Deep Reinforcement Learning for Flow Control Exploits Different Physics for Increasing Reynolds Number Regimes
Abstract
:1. Introduction
2. Methods
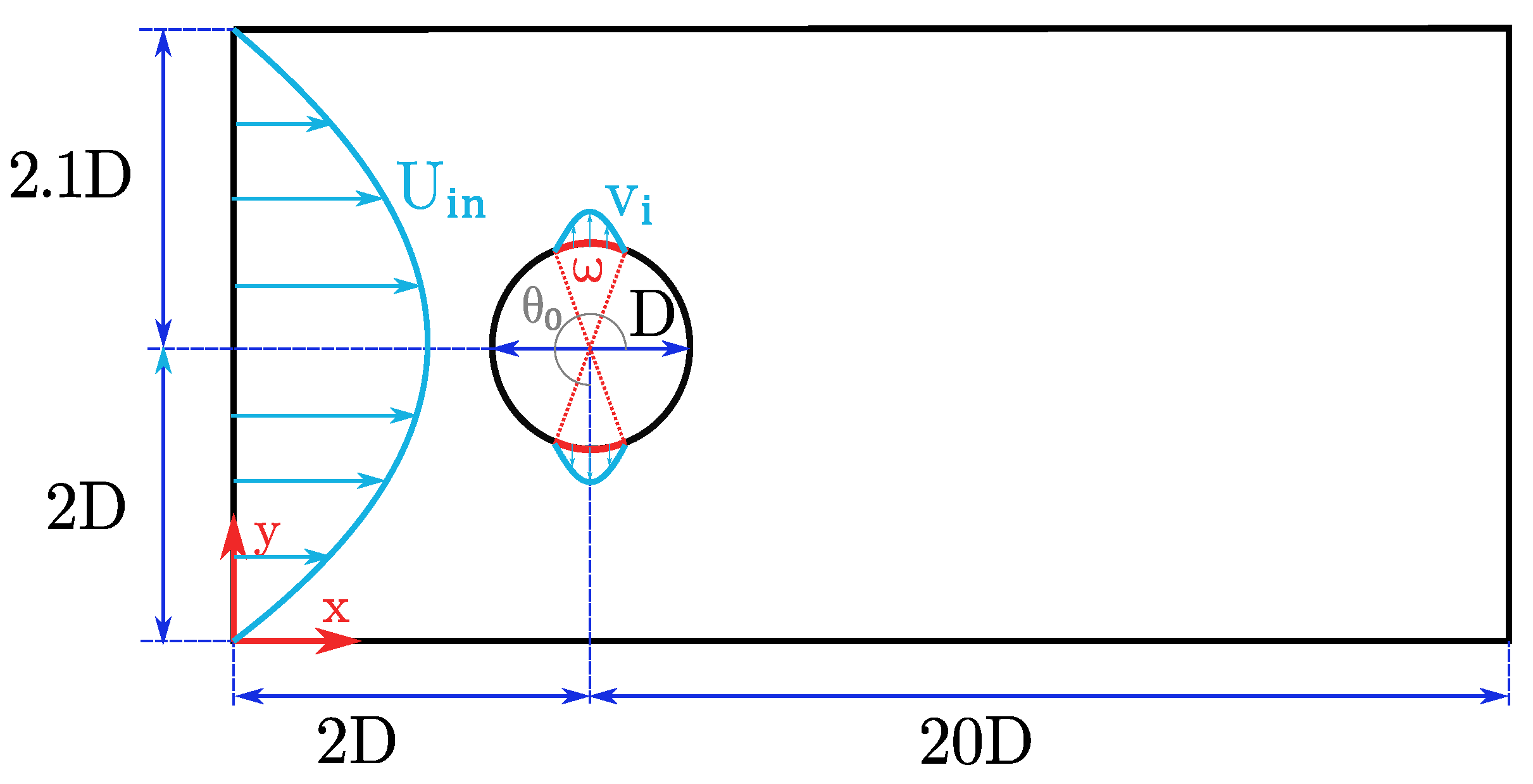
2.1. Problem Configuration and Numerical Setup
2.2. DRL Setup
3. Results and Discussion
3.1. CFD and DRL Code Validation
3.2. DRL Application at Reynolds Number 2000
3.3. Cross-Application of Agents
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | |
| AFC | active flow control |
| ANN | artificial neural network |
| BSC-CNS | Barcelona Supercomputing Center—Centro Nacional de Supercomputación |
| CFD | computational fluid dynamics |
| CFL | Courant–Friedrichs–-Lewy |
| CPU | central processing unit |
| DRL | deep reinforcement learning |
| EMAC | energy-, momentum-, and angular-momentum-conserving equation |
| FEM | finite-element method |
| HPC | high-performance computing |
| PPO | proximal policy optimization |
| PSD | power-spectral density |
| UAV | unmanned aerial vehicle |
| Roman letters | |
| a | action |
| lift coefficient | |
| drag coefficient | |
| offset coefficient of the reward | |
| D | cylinder diameter |
| vector used in force calculation | |
| f | external forces, frequency |
| vortex shedding frequency | |
| F | Force |
| drag force | |
| lift force | |
| H | channel height |
| L | channel length |
| n | unit vector normal to the cylinder |
| Q | mass flow rate |
| normalized mass flow rate | |
| reference mass flow rate | |
| p | pressure |
| r | reward |
| reference value of the reward after control | |
| R | cylinder radius |
| Reynolds number | |
| S | surface |
| s | observation state |
| reference pressure in the observation state | |
| Strouhal number | |
| t | time |
| initial time | |
| final time | |
| action period | |
| vortex-shedding period | |
| u | flow speed |
| mean velocity | |
| inlet boundary velocity in x direction | |
| inlet boundary velocity in the middle of the channel | |
| inlet boundary velocity in y direction | |
| jet velocity | |
| w | lift penalization |
| x | horizontal coordinate |
| y | vertical coordinate |
| Greek letters | |
| velocity strain-rate tensor | |
| kinematic viscosity | |
| domain | |
| jet angular opening | |
| density | |
| standard deviation | |
| Cauchy stress tensor | |
| jet angle | |
| center jet angle | |
References
- Howell, J.P. Aerodynamic Drag Reduction for Low Carbon Vehicles; Woodhead Publishing Limited: Sawston, UK, 2012; pp. 145–154. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bartenwerfer, M. The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech. 1989, 206, 105–129. [Google Scholar] [CrossRef]
- Gad-el Hak, M. Active, and Reactive Flow Management; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Guerrero, J.; Sanguineti, M.; Wittkowski, K. CFD Study of the Impact of Variable Cant Angle Winglets on Total Drag Reduction. Aerospace 2018, 5, 126. [Google Scholar] [CrossRef] [Green Version]
- Tiseira, A.O.; García-Cuevas, L.M.; Quintero, P.; Varela, P. Series-hybridisation, distributed electric propulsion and boundary layer ingestion in long-endurance, small remotely piloted aircraft: Fuel consumption improvements. Aerosp. Sci. Technol. 2022, 120, 107227. [Google Scholar] [CrossRef]
- Serrano, J.R.; García-Cuevas, L.M.; Bares Moreno, P.; Varela Martínez, P. Propeller Position Effects over the Pressure and Friction Coefficients over the Wing of an UAV with Distributed Electric Propulsion: A Proper Orthogonal Decomposition Analysis. Drones 2022, 6, 38. [Google Scholar] [CrossRef]
- Serrano, J.R.; Tiseira, A.O.; García-Cuevas, L.M.; Varela, P. Computational Study of the Propeller Position Effects in Wing-Mounted, Distributed Electric Propulsion with Boundary Layer Ingestion in a 25 kg Remotely Piloted Aircraft. Drones 2021, 5, 56. [Google Scholar] [CrossRef]
- Kametani, Y.; Fukagata, K. Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction. J. Fluid Mech. 2011, 681, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Atzori, M.; Vinuesa, R.; Gatti, D.; Schlatter, P.; Li, W. Decomposition of the mean friction drag on an NACA4412 airfoil under uniform blowing/suction. J. Fluid Mech. 2022, 932, A31. [Google Scholar] [CrossRef]
- Atzori, M.; Vinuesa, R.; Schlatter, P. Control effects on coherent structures in a non-uniform adverse-pressure-gradient boundary layer. Int. J. Heat Fluid Flow 2022, 97, 109036. [Google Scholar] [CrossRef]
- Atzori, M.; Vinuesa, R.; Stroh, A.; Gatti, D.; Frohnapfel, B.; Schlatter, P. Uniform blowing and suction applied to nonuniform adverse-pressure-gradient wing boundary layers. Phys. Rev. Fluids 2021, 6, 113904. [Google Scholar] [CrossRef]
- Fahland, G.; Stroh, A.; Frohnapfel, B.; Atzori, M.; Vinuesa, R.; Schlatter, P.; Gatti, D. Investigation of Blowing and Suction for Turbulent Flow Control on Airfoils. AIAA J. 2021, 4422–4436. [Google Scholar] [CrossRef]
- Voevodin, A.V.; Kornyakov, A.A.; Petrov, A.S.; Petrov, D.A.; Sudakov, G.G. Improvement of the take-off and landing characteristics of wing using an ejector pump. Thermophys. Aeromech. 2019, 26, 9–18. [Google Scholar] [CrossRef]
- Yousefi, K.; Saleh, R. Three-dimensional suction flow control and suction jet length optimization of NACA 0012 wing. Meccanica 2015, 50, 1481–1494. [Google Scholar] [CrossRef]
- Cui, W.; Zhu, H.; Xia, C.; Yang, Z. Comparison of Steady Blowing and Synthetic Jets for Aerodynamic Drag Reduction of a Simplified Vehicle; Elsevier B.V.: Amsterdam, The Netherlands, 2015; Volume 126, pp. 388–392. [Google Scholar] [CrossRef] [Green Version]
- Park, H.; Cho, J.H.; Lee, J.; Lee, D.H.; Kim, K.H. Experimental study on synthetic jet array for aerodynaic drag reduction of a simplified car. J. Mech. Sci. Technol. 2013, 27, 3721–3731. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P.; Kim, J. Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 1994, 262, 75–110. [Google Scholar] [CrossRef]
- Muddada, S.; Patnaik, B.S. An active flow control strategy for the suppression of vortex structures behind a circular cylinder. Eur. J. Mech. B/Fluids 2010, 29, 93–104. [Google Scholar] [CrossRef]
- Rabault, J.; Kuchta, M.; Jensen, A.; Réglade, U.; Cerardi, N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 2019, 865, 281–302. [Google Scholar] [CrossRef] [Green Version]
- Ghraieb, H.; Viquerat, J.; Larcher, A.; Meliga, P.; Hachem, E. Optimization and passive flow control using single-step deep reinforcement learning. Phys. Rev. Fluids 2021, 6. [Google Scholar] [CrossRef]
- Pino, F.; Schena, L.; Rabault, J.; Mendez, M. Comparative analysis of machine learning methods for active flow control. arXiv 2022, arXiv:2202.11664. [Google Scholar]
- Garnier, P.; Viquerat, J.; Rabault, J.; Larcher, A.; Kuhnle, A.; Hachem, E. A review on deep reinforcement learning for fluid mechanics. Comput. Fluids 2021, 225, 104973. [Google Scholar] [CrossRef]
- Rabault, J.; Ren, F.; Zhang, W.; Tang, H.; Xu, H. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization. J. Hydrodyn. 2020, 32, 234–246. [Google Scholar] [CrossRef]
- Vinuesa, R.; Brunton, S.L. Enhancing computational fluid dynamics with machine learning. Nat. Comput. Sci. 2022, 2, 358–366. [Google Scholar] [CrossRef]
- Vinuesa, R.; Lehmkuhl, O.; Lozano-Durán, A.; Rabault, J. Flow Control in Wings and Discovery of Novel Approaches via Deep Reinforcement Learning. Fluids 2022, 7, 62. [Google Scholar] [CrossRef]
- Belus, V.; Rabault, J.; Viquerat, J.; Che, Z.; Hachem, E.; Reglade, U. Exploiting locality and translational invariance to design effective deep reinforcement learning control of the 1-dimensional unstable falling liquid film. AIP Adv. 2019, 9, 125014. [Google Scholar] [CrossRef] [Green Version]
- Rabault, J.; Kuhnle, A. Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach. Phys. Fluids 2019, 31, 094105. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Rabault, J.; Kuhnle, A.; Wang, Y.; Wang, T. Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning. Phys. Fluids 2020, 32, 053605. [Google Scholar] [CrossRef]
- Tokarev, M.; Palkin, E.; Mullyadzhanov, R. Deep reinforcement learning control of cylinder flow using rotary oscillations at low reynolds number. Energies 2020, 13, 5920. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, W.; Deng, J.; Rabault, J. Active flow control with rotating cylinders by an artificial neural network trained by deep reinforcement learning. J. Hydrodyn. 2020, 32, 254–258. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Reinforcement-learning-based control of confined cylinder wakes with stability analyses. J. Fluid Mech. 2022, 932, A44. [Google Scholar] [CrossRef]
- Ren, F.; Rabault, J.; Tang, H. Applying deep reinforcement learning to active flow control in weakly turbulent conditions. Phys. Fluids 2021, 33, 037121. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, L.; Hu, G.; Li, C.; Xiao, Y.; Xiong, H.; Rabault, J.; Noack, B.R. DRLinFluids: An open-source Python platform of coupling deep reinforcement learning and OpenFOAM. Phys. Fluids 2022, 34, 081801. [Google Scholar] [CrossRef]
- Qin, S.; Wang, S.; Rabault, J.; Sun, G. An application of data driven reward of deep reinforcement learning by dynamic mode decomposition in active flow control. arXiv 2021, arXiv:2106.06176. [Google Scholar]
- Vazquez, M.; Houzeaux, G.; Koric, S.; Artigues, A.; Aguado-Sierra, J.; Aris, R.; Mira, D.; Calmet, H.; Cucchietti, F.; Owen, H.; et al. Alya: Towards Exascale for Engineering Simulation Codes. arXiv 2014, arXiv:1404.4881. [Google Scholar]
- Owen, H.; Houzeaux, G.; Samaniego, C.; Lesage, A.C.; Vázquez, M. Recent ship hydrodynamics developments in the parallel two-fluid flow solver Alya. Comput. Fluids 2013, 80, 168–177. [Google Scholar] [CrossRef] [Green Version]
- Lehmkuhl, O.; Houzeaux, G.; Owen, H.; Chrysokentis, G.; Rodriguez, I. A low-dissipation finite element scheme for scale resolving simulations of turbulent flows. J. Comput. Phys. 2019, 390, 51–65. [Google Scholar] [CrossRef]
- Charnyi, S.; Heister, T.; Olshanskii, M.A.; Rebholz, L.G. On conservation laws of Navier–Stokes Galerkin discretizations. J. Comput. Phys. 2017, 337, 289–308. [Google Scholar] [CrossRef] [Green Version]
- Charnyi, S.; Heister, T.; Olshanskii, M.A.; Rebholz, L.G. Efficient discretizations for the EMAC formulation of the incompressible Navier–Stokes equations. Appl. Numer. Math. 2019, 141, 220–233. [Google Scholar] [CrossRef] [Green Version]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Adv. Comput. Math. 1996, 6, 207–226. [Google Scholar] [CrossRef]
- Trias, F.X.; Lehmkuhl, O. A self-adaptive strategy for the time integration of navier-stokes equations. Numer. Heat Transf. Part B Fundam. 2011, 60, 116–134. [Google Scholar] [CrossRef]
- Kuhnle, A.; Schaarschmidt, M.; Fricke, K. Tensorforce: A TensorFlow Library for Applied Reinforcement Learning. 2017. Available online: https://tensorforce.readthedocs.io (accessed on 28 November 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 28 November 2022).
- Schäfer, M.; Turek, S.; Durst, F.; Krause, E.; Rannacher, R. Benchmark Computations of Laminar Flow Around a Cylinder; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1996; pp. 547–566. [Google Scholar] [CrossRef]
- Elhawary, M. Deep reinforcement learning for active flow control around a circular cylinder using unsteady-mode plasma actuators. arXiv 2020, arXiv:2012.10165. [Google Scholar]
- Han, B.Z.; Huang, W.X.; Xu, C.X. Deep reinforcement learning for active control of flow over a circular cylinder with rotational oscillations. Int. J. Heat Fluid Flow 2022, 96, 109008. [Google Scholar] [CrossRef]
- Stabnikov, A.; Garbaruk, A. Prediction of the drag crisis on a circular cylinder using a new algebraic transition model coupled with SST DDES. J. Phys. Conf. Ser. 2020, 1697, 012224. [Google Scholar] [CrossRef]
- Guastoni, L.; Güemes, A.; Ianiro, A.; Discetti, S.; Schlatter, P.; Azizpour, H.; Vinuesa, R. Convolutional-network models to predict wall-bounded turbulence from wall quantities. J. Fluid Mech. 2021, 928, A27. [Google Scholar] [CrossRef]



















| 100 | 1000 | 2000 | |
|---|---|---|---|
| Mesh cells (approximately) | 11,000 | 19,000 | 52,000 |
| Number of witness points | 151 | 151 | 151 |
| 0.088 | 0.04 | 0.04 | |
| 1.7 | 2 | 2 | |
| 3.17 | 3.29 | 3.29 | |
| 5 | 1.25 | 1.25 | |
| w | 0.2 | 1 | 1 |
| 3.37 | 3.04 | 4.39 | |
| 0.25 | 0.2 | 0.2 | |
| Actions per episode | 80 | 100 | 100 |
| Number of episodes | 350 | 1000 | 1400 |
| CPUs per environment | 46 | 46 | 46 |
| Environments | 1 | 1 or 20 | 20 |
| Total CPUs | 46 | 46 or 920 | 920 |
| Baseline duration | 100 | 250 | 100 |
| Work | CD Reduction | Strategy | Configuration | |
|---|---|---|---|---|
| 100 | Present work | E | 2 jets (1 top & 1 bottom) | |
| 100 | Rabault et al. [19] | E | 2 jets (1 top & 1 bottom) | |
| 100 | Tang et al. [28] | E | 4 jets (2 top & 2 bottom) | |
| 200 | Tang et al. [28] | E | 4 jets (2 top & 2 bottom) | |
| 300 | Tang et al. [28] | E | 4 jets (2 top & 2 bottom) | |
| 400 | Tang et al. [28] | E | 4 jets (2 top & 2 bottom) | |
| 1000 | Present work | E | 2 jets (1 top & 1 bottom) | |
| 1000 | Ren et al. [32] | E | 2 jets (1 top & 1 bottom) | |
| 2000 | Present work | D | 2 jets (1 top & 1 bottom) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varela, P.; Suárez, P.; Alcántara-Ávila, F.; Miró, A.; Rabault, J.; Font, B.; García-Cuevas, L.M.; Lehmkuhl, O.; Vinuesa, R. Deep Reinforcement Learning for Flow Control Exploits Different Physics for Increasing Reynolds Number Regimes. Actuators 2022, 11, 359. https://doi.org/10.3390/act11120359
Varela P, Suárez P, Alcántara-Ávila F, Miró A, Rabault J, Font B, García-Cuevas LM, Lehmkuhl O, Vinuesa R. Deep Reinforcement Learning for Flow Control Exploits Different Physics for Increasing Reynolds Number Regimes. Actuators. 2022; 11(12):359. https://doi.org/10.3390/act11120359
Chicago/Turabian StyleVarela, Pau, Pol Suárez, Francisco Alcántara-Ávila, Arnau Miró, Jean Rabault, Bernat Font, Luis Miguel García-Cuevas, Oriol Lehmkuhl, and Ricardo Vinuesa. 2022. "Deep Reinforcement Learning for Flow Control Exploits Different Physics for Increasing Reynolds Number Regimes" Actuators 11, no. 12: 359. https://doi.org/10.3390/act11120359
APA StyleVarela, P., Suárez, P., Alcántara-Ávila, F., Miró, A., Rabault, J., Font, B., García-Cuevas, L. M., Lehmkuhl, O., & Vinuesa, R. (2022). Deep Reinforcement Learning for Flow Control Exploits Different Physics for Increasing Reynolds Number Regimes. Actuators, 11(12), 359. https://doi.org/10.3390/act11120359









