Fractal Dimension Analysis Applied to Soil CO2 Fluxes in Campotosto’s Seismic Area, Central Italy
Abstract
:1. Introduction
2. Methodology and Data Analysis
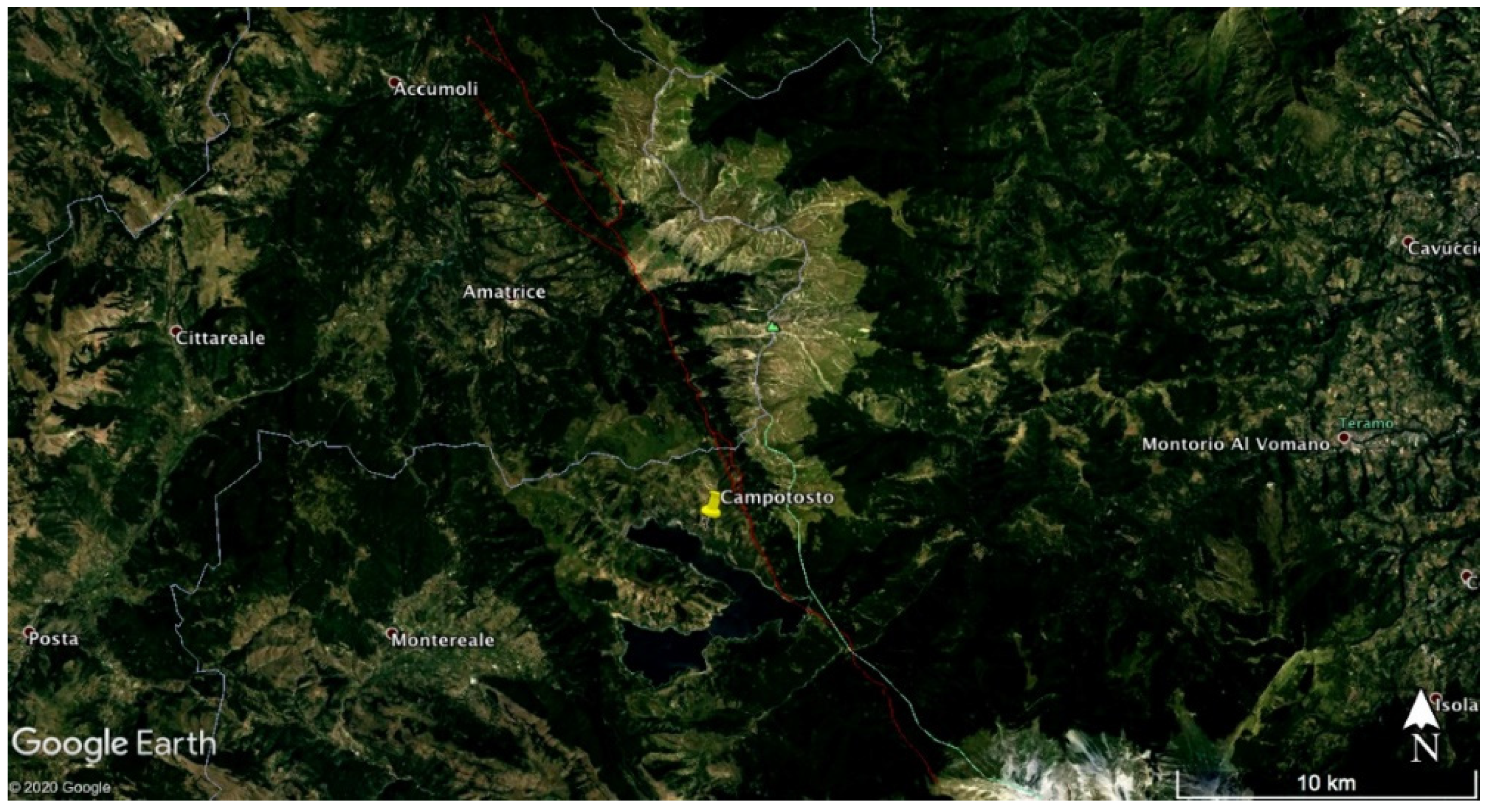
2.1. Experimental
2.2. Mathematical Aspects
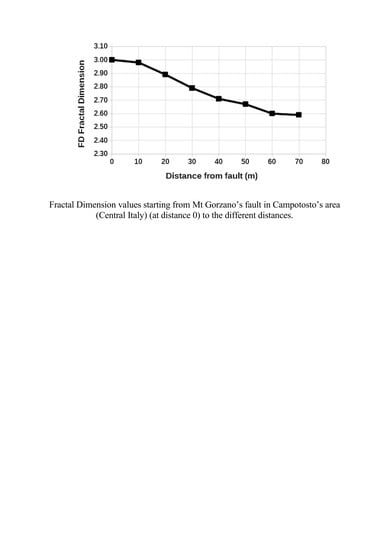
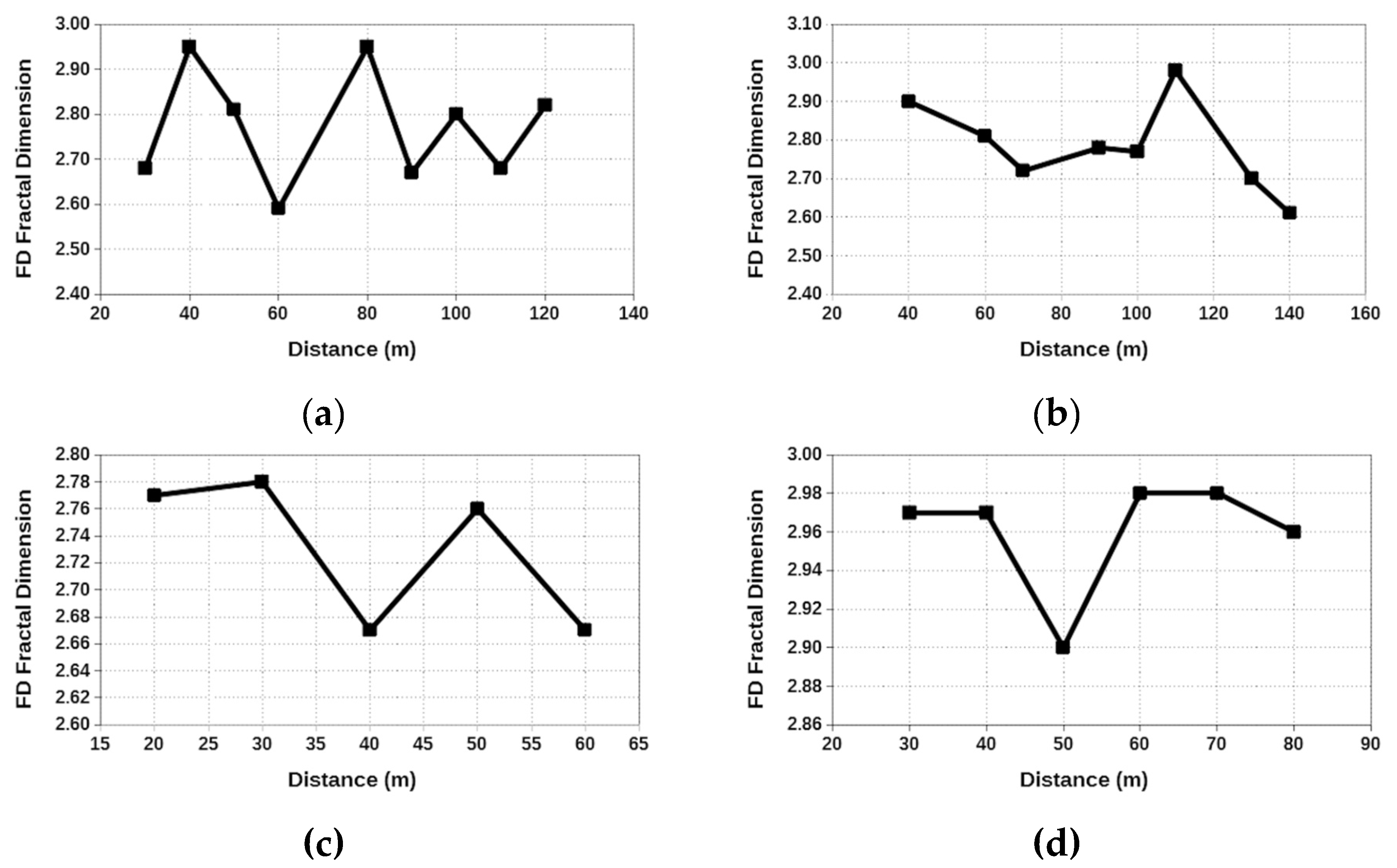
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- King, C.Y. Impulsive radon emanation on a creeping segment of the San Andreas fault, California. Pure Appl. Geophys. 1985, 122, 340–352. [Google Scholar] [CrossRef]
- Ciotoli, G.; Guerra, M.; Lombardi, S.; Vittori, E. Soil gas survey for tracing seismogenic faults: A case study in the Fucino basin, Central Italy. J. Geophys. Res. 1998, 103, 23781–23794. [Google Scholar] [CrossRef]
- Baubron, J.C.; Rigo, A.; Toutain, J.P. Soil gas profiles as a tool to characterize active tectonic areas: The Jaut Pass example (Pyrenees, France). Earth Planet. Sci. Lett. 2002, 196, 69–81. [Google Scholar] [CrossRef]
- Ciotoli, G.; Lombardi, S.; Annunziatellis, A. Geostatistical analysis of soil gas data in a high seismic intermontane basin: Fucino Plain, central Italy. J. Geophys. Res. 2007, 112, B05407. [Google Scholar] [CrossRef]
- Fu, C.C.; Yang, T.F.; Du, J.; Walia, V.; Chen, Y.G. Variations of helium and radon concentrations in soil gases from an active fault zone in Southern Taiwan. Radiat. Meas. 2008, 43, S348–S352. [Google Scholar] [CrossRef]
- Walia, V.; Yang, T.; Hong, W.; Lin, S.; Fu, C. Geochemical variation of soil–gas composition for fault trace and earthquake precursory studies along the Hsincheng fault in NW Taiwan. Appl. Radiat. Isot. 2009, 67, 1855–1863. [Google Scholar] [CrossRef]
- Bigi, S.; Beaubien, S.E.; Ciotoli, G.; D’Ambrogi, C.; Doglioni, C.; Ferrante, V.; Lombardi, S.; Milli, S.; Orlando, L.; Ruggiero, L.; et al. Mantle-derived CO2 migration along active faults within an extensional basin margin (Fiumicino, Rome, Italy). Tectonophysics 2014, 637, 137–149. [Google Scholar] [CrossRef]
- Ciotoli, G.; Sciarra, A.; Ruggiero, L.; Annunziatellis, A.; Bigi, S. Soil gas geochemical behaviour across buried and exposed faults during the 24th August 2016 central Italy earthquake. Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
- Wakita, H.; Nakamura, Y.; Notsu, K.; Noguchi, M.; Asada, T. Radon anomaly: A possible precursor to the 1978 Izu-Oshima-kinkai earthquake. Science 1980, 207, 882–883. [Google Scholar] [CrossRef]
- Reddy, D.V.; Sukhija, B.S.; Nagabhushanam, P.; Kumar, D. A clear case of radon anomaly associated with a microearthquake event in a stable continental region. Geophys. Res. Lett. 2004, 31, L10609. [Google Scholar] [CrossRef]
- Perez, N.M.; Hernandez, P.A.; Padron, E.; Melian, G.; Marrero, R. Precursory Subsurface 222Rn and 220Rn Degassing Signatures of the 2004 Seismic Crisis at Tenerife, Canary Islands. Pure Appl. Geophys. 2007, 164, 2431–2448. [Google Scholar] [CrossRef]
- Cicerone, R.; Ebel, J.E.; Britton, J. A systematic compilation of earthquake precursors. Tectonophysics 2009, 476, 371–396. [Google Scholar] [CrossRef]
- Ghosh, D.; Deb, A.; Sengupta, R. Anomalous radon emission as precursor of earthquake. J. Appl. Geophys. 2009, 69, 67–81. [Google Scholar] [CrossRef]
- Hashemi, S.; Negarestani, A.; Namvaran, M.; Nasab, S.M.M. An analytical algorithm for designing radon monitoring network to predict the location and magnitude of earthquakes. J. Radioanal. Nucl. Chem. 2013, 295, 2249–2262. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Panagiotaras, D.; Cantzos, D.; Yannakopoulos, P. Radon-222: A Potential Short-Term Earthquake Precursor. J. Earth Sci. Clim. Chang. 2015, 6, 282. [Google Scholar] [CrossRef]
- Rice, J.R. Fault stress states, pore pressure redistributions, and the weakness of the San Andreas fault. In Fault Mechanics and Transport Properties of Rock; Evans, B., Wong, T.F., Eds.; Academic Press Ltd.: San Diego, CA, USA, 1992; pp. 476–503. [Google Scholar]
- Sibson, R.H. Fluid involvement in normal faulting. J. Geodyn. 2000, 29, 449–469. [Google Scholar] [CrossRef]
- Collettini, C.; Cardellini, C.; Chiodini, G.; De Paola, N.; Holdsworth, R.E.; Smith, S.A.F. Fault weakening due to CO2 degassing in the Northern Apennines: Short and long-term processes. Geol. Soc. Lond. Spec. Publ. 2008, 299, 175–194. [Google Scholar] [CrossRef]
- King, C.Y.; King, B.S.; Evans, W.C.; Zhang, W. Spatial radon anomalies on active faults in California. Appl. Geochem. 1996, 11, 497–510. [Google Scholar] [CrossRef]
- Annunziatellis, A.; Beaubien, S.E.; Bigi, S.; Ciotoli, G.; Coltella, M.; Lombardi, S. Gas migration along fault systems and through the vadose zone in the Latera caldera (central Italy): Implications for CO2 geological storage. Int. J. Greenh. Gas Control 2008, 2, 353–372. [Google Scholar] [CrossRef]
- Sciarra, A.; Fascetti, A.; Moretti, A.; Cantucci, B.; Pizzino, L.; Lombardi, S.; Guerra, I. Geochemical and radiometric profiles through an active fault in the Sila Massif (Calabria, Italy). J. Geoch. Explor. 2014, 148, 128–137. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The fractal geometry of nature. Review by: Cannon, J.W. Am. Math. Mon. 1984, 91, 594–598. [Google Scholar] [CrossRef]
- Perfect, E.; Kay, B.D. Applications of fractals in soil and tillage research: A review. Soil Till. Res. 1995, 36, 1–20. [Google Scholar] [CrossRef]
- Eghball, B.; Hergert, G.W.; Lesoing, G.W.; Ferguson, R.B. Fractal analysis of spatial and temporal variability. Geoderma 1999, 88, 349–362. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; W.H. Freeman: San Francisco, CA, USA, 1977; p. 365. [Google Scholar]
- Pachepsky, Y.; Crawford, J.W. Fractal analysis. In Encyclopedia of Soils in the Environment; Hillel, D., Ed.; Academic Press: Waltham, MA, USA, 2004; Volume 2, pp. 85–98. [Google Scholar]
- Allaire, S.E.; Lange, S.F.; Lafond, J.A.; Pelletier, B.; Cambouris, A.N.; Dutilleul, P. Multiscale spatial variability of CO2 emissions and correlations with physico-chemical soil properties. Geoderma 2012, 170, 251–260. [Google Scholar] [CrossRef]
- Ryu, S.; Concilio, A.; Chen, J.; North, M.; Ma, S. Prescribed burning and mechanical thinning effects on below-ground conditions and soil respiration in a mixed-conifer forest, California. For. Ecol. Manag. 2009, 257, 1324–1332. [Google Scholar] [CrossRef]
- Panosso, A.R.; Perillo, L.I.; Ferraudo, A.S.; Pereira, G.T.; Miranda, J.G.V.; La Scala, N. Fractal dimension and anisotropy of soil CO2 emission in a mechanically harvested sugarcane production area. Soil Till. Res. 2012, 124, 8–16. [Google Scholar] [CrossRef]
- Burrough, P.A. Fractal dimensions of landscapes and other environmental data. Nature 1981, 294, 240–242. [Google Scholar] [CrossRef]
- Palmer, M.W. Fractal geometry: A tool for describing spatial patterns of plant communities. Vegetatio 1988, 75, 91–102. [Google Scholar] [CrossRef]
- La Scala, N., Jr.; Marques, J., Jr.; Pereira, G.T.; Corà, J.E. Short-term temporal changes in the spatial variability model of CO2 emissions from a Brazilian bare soil. Soil Biol. Biochem. 2000, 32, 1459–1462. [Google Scholar] [CrossRef]
- Ohashi, M.; Gyokusen, K. Temporal change in spatial variability of soil respiration on a slope of Japanese cedar (Cryptomeria japonica D. Don) forest. Soil Biol. Biochem. 2007, 39, 1130–1138. [Google Scholar] [CrossRef]
- Kosugi, Y.; Mitani, T.; Ltoh, M.; Noguchi, S.; Tani, M.; Matsuo, N.; Takanashi, S.; Ohkubo, S.; Nik, A.R. Spatial and temporal variation in soil respiration in a Southeast Asian tropical rainforest. Agric. For. Meteorol. 2007, 147, 35–47. [Google Scholar] [CrossRef]
- Konda, R.; Ohta, S.; Ishizuka, S.; Aria, S.; Ansori, S.; Tanaka, N.; Hardjono, A. Spatial structures of N2O, CO2 and CH4 fluxes from Acacia mangium plantation soils during a relatively dry season in Indonesia. Soil Biol. Biochem. 2008, 40, 3021–3030. [Google Scholar] [CrossRef]
- Bicalho, E.S.; Panosso, A.R.; Teixeira, D.D.B.; Miranda, J.G.V.; Pereira, G.T.; La Scala, N. Spatial variability structure of soil CO2 emission and soil attributes in a sugarcane area. Agric. Ecos. Environ. 2014, 189, 206–215. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Macchiato, M. Multifractal fluctuations in seismic interspike series. Phys. A 2005, 354, 629–640. [Google Scholar] [CrossRef] [Green Version]
- Chamoli, A.; Yadav, R.B.S. Multifractaly in seismic sequences of NW Himalaya. Nat. Hazards 2015, 77, s19–s32. [Google Scholar] [CrossRef]
- Weinlich, F.H. Carbon dioxide controlled earthquake distribution pattern in the NW Bohemian swarm earthquake region, western Eger Rift, Czech Republic—Gas migration in the crystalline basement. Geofluids 2014, 14, 143–159. [Google Scholar] [CrossRef]
- Fischer, T.; Matyska, C.; Heinicke, J. Earthquake-enhanced permeability–evidence from carbon dioxide release following the ML 3.5 earthquake in West Bohemia. Earth Planet. Sci. Lett. 2017, 460, 60–67. [Google Scholar] [CrossRef]
- Boncio, P.; Lavecchia, G.; Milano, G.; Rozzi, B. Seismogenesis in central Appennines, Italy: An integrated analysis of minor earthquake sequences and structural data in the Amatrice-Campotosto Area. Ann. Geophys. 2004, 47, 1723–1742. [Google Scholar]
- Pace, B.; Peruzza, L.; Lavecchia, G.; Boncio, P. Layered seismogenic source model and probabilistic seismic-hazard analyses in central Italy. Bull. Seismol. Soc. Am. 2006, 96, 107–132. [Google Scholar] [CrossRef]
- Lavecchia, G.; Castaldo, R.; de Nardis, R.; De Novellis, V.; Ferrarini, F.; Pepe, S.; Brozzetti, F.; Solaro, G.; Cirillo, D.; Bonano, M.; et al. Ground deformation and source geometry of the 24 August 2016 Amatrice earthquake (Central Italy) investigated through analytical and numerical modelling of DInSAR measurements and structural-geological data. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef]
- Brozzetti, F.; Boncio, P.; Cirillo, D.; Ferrarini, F.; de Nardis, R.; Testa, A.; Liberi, F.; Lavecchia, G. High-resolution field mapping and analysis of the August–October 2016 coseismic surface faulting (central Italy earthquakes): Slip distribution, parameterization, and comparison with global earthquakes. Tectonics 2019, 38. [Google Scholar] [CrossRef] [Green Version]
- Blumetti, A.M.; Guerrieri, L. Fault-generated mountain fronts and the identification of fault segments: Implications for seismic hazard assestment. Boll. Soc. Geol. Ital. 2007, 126, 307–322. [Google Scholar]
- Festa, A. Geometrie e meccanismi di raccorciamento nel settore meridionale del Bacino marchigiano (Monte Gorzano, Appennino centrale). Ital. J. Geosci. 2005, 124, 41–51. [Google Scholar]
- Chiodini, G.; Cioni, R.; Guidi, M.; Raco, B.; Marini, L. Soil CO2 flux measurements in volcanic and geothermal areas. Appl. Geochem. 1998, 13, 543–552. [Google Scholar] [CrossRef]
- Vidal Vazquez, E.; Miranda, J.G.V.; Paz González, A. Characterizing anisotropy and heterogeneity of soil surface microtopography using fractal models. Ecol. Model. 2005, 182, 337–353. [Google Scholar] [CrossRef]
- Huang, C.H.; Bradford, J.M. Applications of a laser scanner to quantify soil microtopography. Soil Sci. Soc. Am. J. Abstr. 1992, 56, 14–21. [Google Scholar] [CrossRef]
- Lewicki, J.L.; Evans, W.C.; Hilley, G.E.; Sorey, M.L.; Rogie, J.D.; Brantley, S.L. Shallow soil CO2 flow along the San Andreas and Calaveras Faults, California. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Walia, V.; Lin, S.J.; Fu, C.C.; Yang, T.F.; Hong, W.L.; Wen, K.L.; Chen, C.H. Soil-gas monitoring: A tool for fault delineation studies along Hsnhua Fault (Tainan), Southern Taiwan. App. Geoch. 2010, 25, 602–607. [Google Scholar] [CrossRef]
- Jung, B.; Garven, G.; Boles, J.R. Effects of episodic fluid flow on hydrocarbon migration in the Newport-Inglewood Fault Zone, Southern California. Geofluids 2014, 14, 234–250. [Google Scholar] [CrossRef]
- Concilio, A.; Chen, J.Q.; Ma, S.; North, M. Precipitation drives interannual vari- ation in summer soil respiration in a Mediterranean-climate, mixed-conifer forest. Clim. Chang. 2009, 92, 109–122. [Google Scholar] [CrossRef]
- Cantero, J.J.; Leon, R.; Cisneros, J.M.; Cantero, A. Habitat structure and vegetation relationships in central Argentina salt marsh landscapes. Plant Ecol. 1998, 137, 79–100. [Google Scholar] [CrossRef]
- Tavares, R.L.M.; Souza, Z.M.; La Scala, N., Jr.; Castioni, G.A.F.; Souza, G.S.; Torres, J.L.T. Spatial and Temporal Variability of Soil CO2 Flux in Sugarcane Green Harvest Systems. Rev. Bras. Cienc. Solo 2016, 40. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Petraki, E.; Yannakopoulos, P.; Cantzos, D.; Panagiotaras, D.; Nomicos, C. Fractal Analysis of Pre-Seismic Electromagnetic and Radon Precursors: A Systematic Approach. J. Earth. Sci. Clim. Chang. 2016, 7. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, D.; Petraki, E.; Vogiannis, E.; Chaldeos, Y.; Yannakopoulos, P.; Kottou, S.; Nomicos, C.; Stonham, J. Traces of self-organisation and long-range memory in variations of environmental radon in soil: Comparative results from monitoring in Lesvos Island and Ileia (Greece). J. Radioanal. Nucl. Chem. 2014, 299, 203–219. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Chaldeos, Y.; Koulouras, G.; Nomicos, C.; Yannakopoulos, P.; Kottou, S.; Stonham, J. Fractal evolution of MHz electromagnetic signals prior to earthquakes: Results collected in Greece during 2009. Geomat. Nat. Hazards Risk 2016, 7, 550–564. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, D.; Matsoukas, C.; Yannakopoulos, P.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Trends in Variation of Environmental Radon in Soil: Results from Measurements in Less Island in Greece. J. Earth Sci. Clim. Chang. 2018, 9, 1–11. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Nomicos, C.; Koulouras, G.; Kottou, S.; Yannakopoulos, P. Long-memory trends in disturbances of radon in soil prior to the twin ML = 5.1 earthquakes of 17 November 2014 Greece. J. Earth Sci. Clim. Chang. 2015, 6, 1–10. [Google Scholar]
- Italiano, F.; Bonfanti, P.; Ditta, M.; Petrini, R.; Slejko, F. Helium and carbon isotopes in the dissolved gases of Friuli Region (NE Italy): Geochemical evidence of CO2 production and degassing over a seismically active area. Chem. Geol. 2009, 266, 76–85. [Google Scholar] [CrossRef]
- Quattrocchi, F.; Pizzi, A.; Gori, S.; Boncio, P.; Voltattorni, N.; Sciarra, A. The contribution of fluid geochemistry to define the structural patterns of the 2009 L’Aquila seismic source. Ital. J. Geosci. 2012, 131, 448–458. [Google Scholar] [CrossRef]
- Martinelli, G.; Plescia, P. Mechanochemical dissociation of calcium carbonate: Laboratory data and relation to natural emission of CO2. Phys. Earth Planet. Inter. 2004, 142, 205–214. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Incecco, S.; Di Carlo, P.; Aruffo, E.; Chatzisavvas, N.; Petraki, E.; Priniotakis, G.; Voyiatzis, I.; Yannakopoulos, P.H.; Nikolopoulos, D. Fractal Dimension Analysis Applied to Soil CO2 Fluxes in Campotosto’s Seismic Area, Central Italy. Geosciences 2020, 10, 233. https://doi.org/10.3390/geosciences10060233
D’Incecco S, Di Carlo P, Aruffo E, Chatzisavvas N, Petraki E, Priniotakis G, Voyiatzis I, Yannakopoulos PH, Nikolopoulos D. Fractal Dimension Analysis Applied to Soil CO2 Fluxes in Campotosto’s Seismic Area, Central Italy. Geosciences. 2020; 10(6):233. https://doi.org/10.3390/geosciences10060233
Chicago/Turabian StyleD’Incecco, Simone, Piero Di Carlo, Eleonora Aruffo, Nikolaos Chatzisavvas, Ermioni Petraki, Georgios Priniotakis, Ioannis Voyiatzis, Panayiotis H. Yannakopoulos, and Dimitrios Nikolopoulos. 2020. "Fractal Dimension Analysis Applied to Soil CO2 Fluxes in Campotosto’s Seismic Area, Central Italy" Geosciences 10, no. 6: 233. https://doi.org/10.3390/geosciences10060233
APA StyleD’Incecco, S., Di Carlo, P., Aruffo, E., Chatzisavvas, N., Petraki, E., Priniotakis, G., Voyiatzis, I., Yannakopoulos, P. H., & Nikolopoulos, D. (2020). Fractal Dimension Analysis Applied to Soil CO2 Fluxes in Campotosto’s Seismic Area, Central Italy. Geosciences, 10(6), 233. https://doi.org/10.3390/geosciences10060233