Assessment of in-Plane Behavior of Metal Compressed Members with Equivalent Geometrical Imperfection
Abstract
:Highlights
- -
- A new procedure is presented to obtain the location of the critical section and the value of the amplitude of unique global and local initial (UGLI) imperfection having the shape of elastic critical buckling mode. The new procedure is also used for the structures consisting of strongly irregular members in compression.
- -
- Validation of the procedure by the investigation of five complex structures made of steel and one made of aluminum alloy solved by other authors.
- -
- Verification of the procedure by comparisons with results of other authors and Geometrically and Materially Nonlinear Analysis with Imperfections (GMNIA) results.
- -
- Information about differences in methods given in four Eurocodes: EN 1993-1-1:2005, EN 1999-1-1:2007, prEN 1993-1-1:2020 and prEN 1999-1-1:2020.
1. Introduction
1.1. Overview and Analysis of Current State
- (i).
- The characteristic value of the initial imperfection amplitude of the equivalent member related to the critical section m:
- (ii).
- Design value of the initial imperfection amplitude of the equivalent member related to the critical section m:
- (iii).
- Design value of UGLI imperfection amplitude :
- (i).
- Current Eurocode EN 1993-1-1:2005 [1] contains the above Equations (2) and (3) but in Corrigendum AC (2009) the index “d“ was removed and some print errors were corrected.
- (ii).
- (iii).
- Working draft Eurocode prEN 1993-1-1:2020 [4] removed from the above Equations (2) and (3) the partial material safety factor γM1 and index “d”. Removing γM1 from Equation (2) destroyed the main assumption of Chladný’s method defined below, but the code committee followed this idea because it leads to an ease of use in practical applications [6]. The authors intend to publish the results of the study showing the consequences of this decision leading to an important difference between the values of UGLI imperfection amplitude calculated according to [4] or [5].
1.2. Research Significance, Contributions and Basic Assumptions of Presented New Method
- (i).
- The first assumption is that the first buckling mode of the examined structural member is dominant and therefore the effect of the higher buckling modes can be neglected. However, in some cases, the higher buckling modes have to be considered in the design. See suggestions by Agüero et al. [17].
- (ii).
- The second assumption is that Chladný’s method given in [3] remains valid. Quoting Chladný [3], where experimentally established values are unavailable, the amplitude of the equivalent imperfection in the shape of the elastic buckling mode may be determined assuming that the buckling resistance of a structure with axially loaded members shall be equal to the buckling resistance of the equivalent member. The buckling resistance of axially loaded columns is defined in clauses 6.3.1.1–6.3.1.4 [1]. The relative slenderness relates to the critical section. The equivalent member has pinned ends, its cross-section and axial force are the same as in the critical cross-section m of the frame and its length is such that its critical force equals the axial force in the critical cross-section m at the critical loading of the structure. The position of the critical cross-section m is determined by the condition that the utilization Um, with allowance for the effect of the axial force and bending moments due to imperfections in the critical cross-section m, is greater than the utilization U(x) at all other cross-sections of the verified member or frame structure.
- (iii).
- (iv).
- The fourth assumption is that if plastic cross-section resistance is taken into account, a maximum plastic shape factor of 1.25 may be taken into account [4,26]. This means that if the criterion is applied with reference to the plastic resistance, the design value of the moment resistance Mc,Rd should be limited to 1.25 Mel,Rd for both a strong axis and weak axis.
- (v).
- The fifth assumption accepts the common method for finding the equivalent local bow imperfections given in [1] 5.3.2 (3). For the new generation of Eurocodes, intensive investigations were done to enhance these values, now in draft [4] see 7.3.3.1 (1) [25,26]. In practice, we often deal with members under compression and bending. If the external bending moments are present, the results may be more unfavorable, because a larger part of the cross-section in longitudinal direction may be plastified, thus leading to a stiffness reduction and therefore higher necessary bow imperfections for simplified calculations. If this is neglected, the load carrying capacity may be underestimated. In our cases of centrally loaded members, there is no need to use the fourth and fifth assumptions.
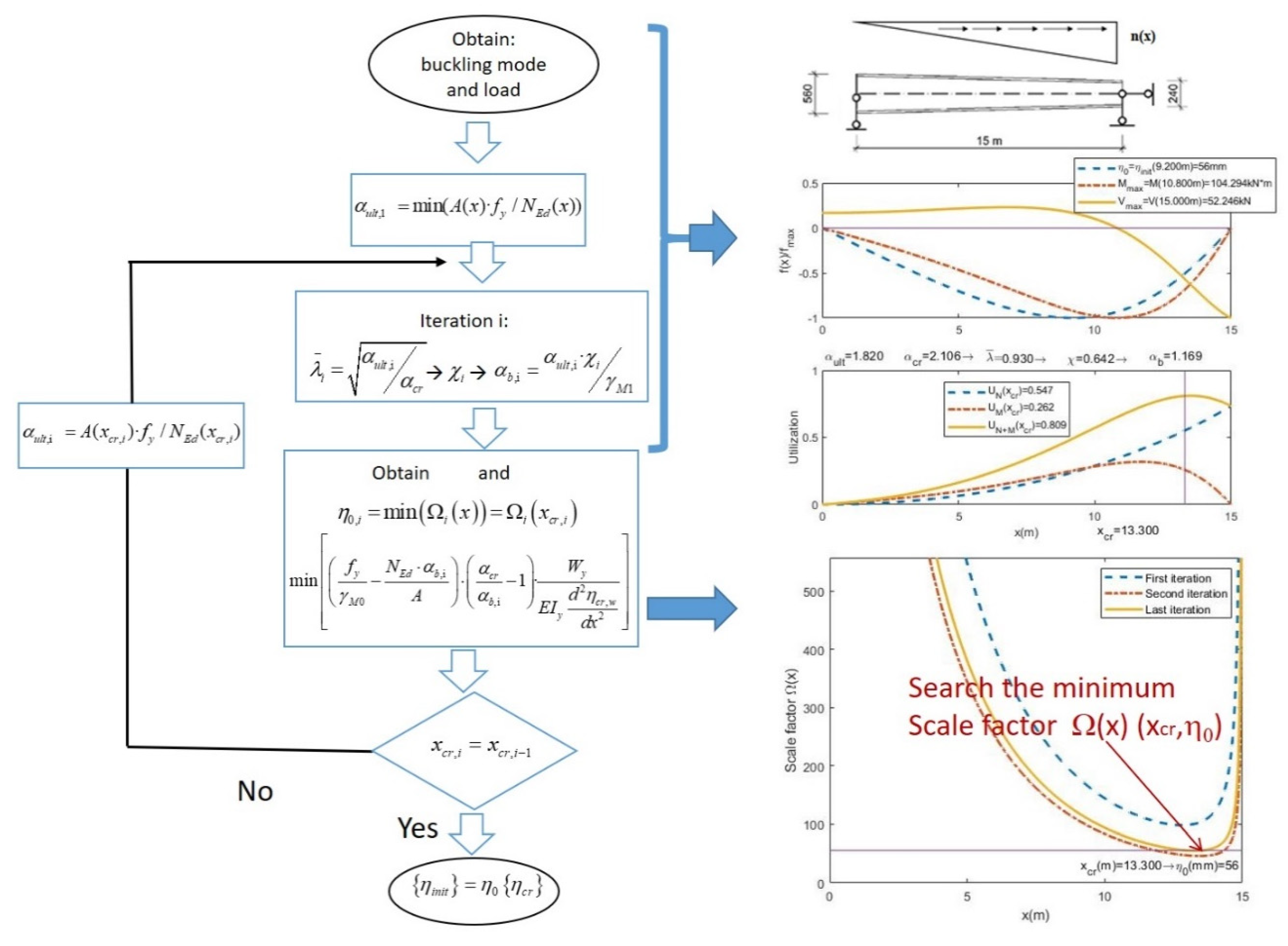
2. Method for Obtaining UGLI Imperfection Amplitude
Steps for Obtaining UGLI Imperfection
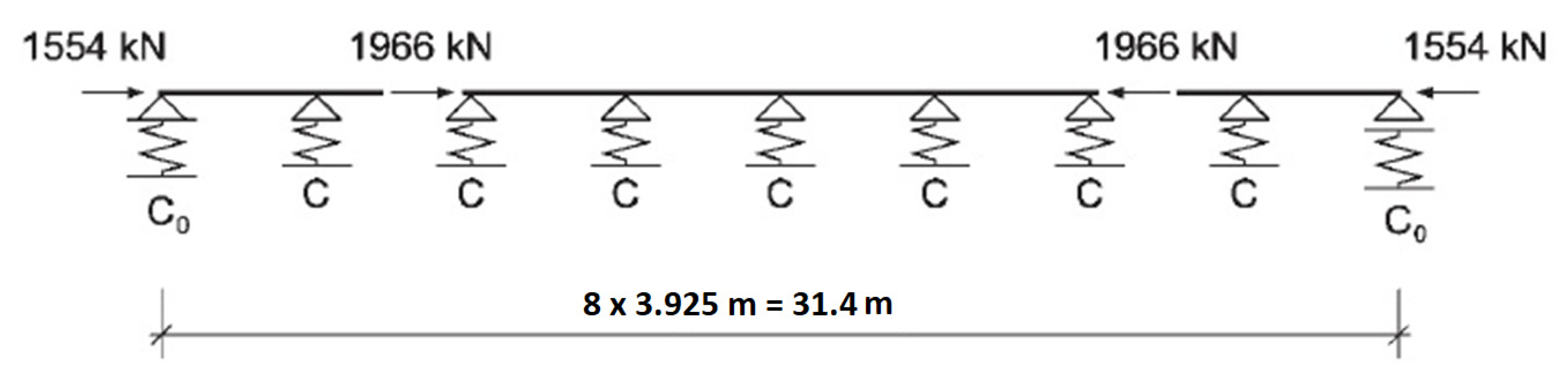
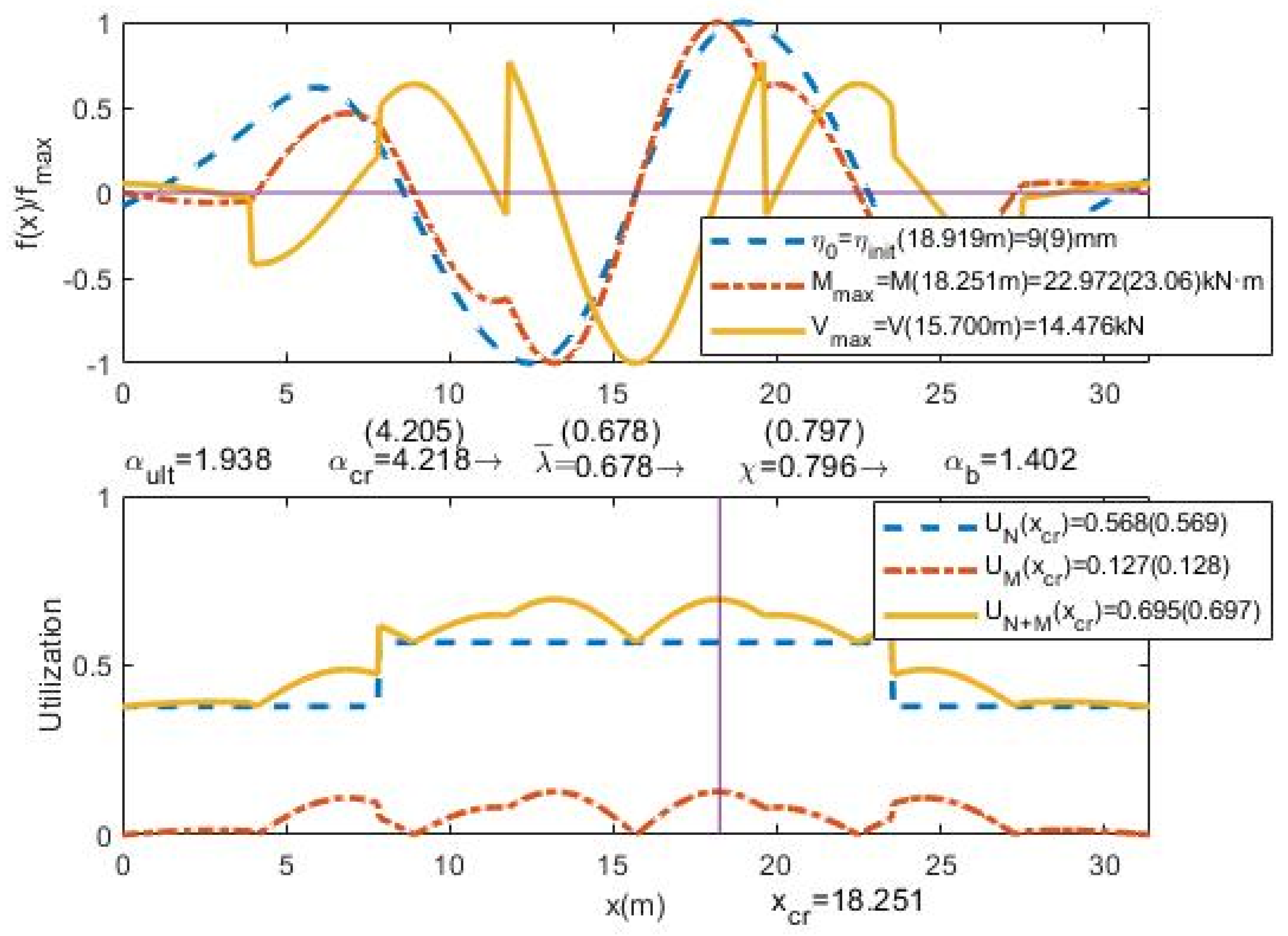
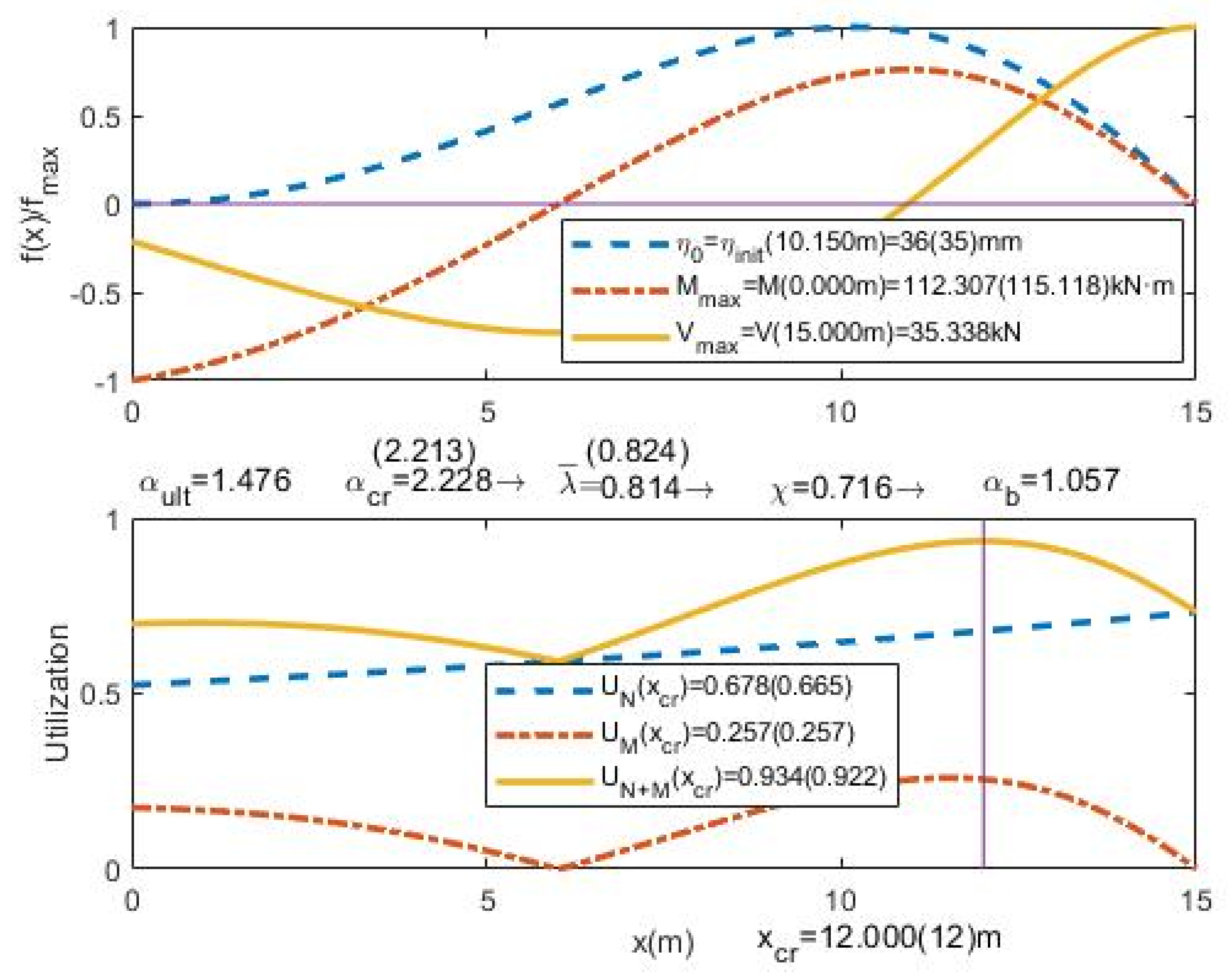
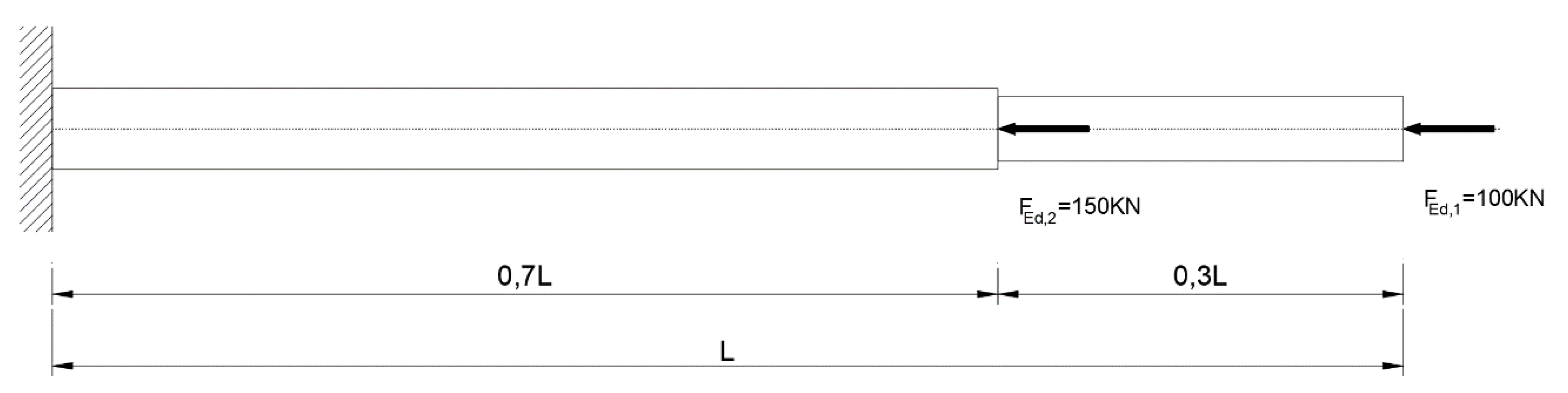
3. Validation of Presented Procedure
- -
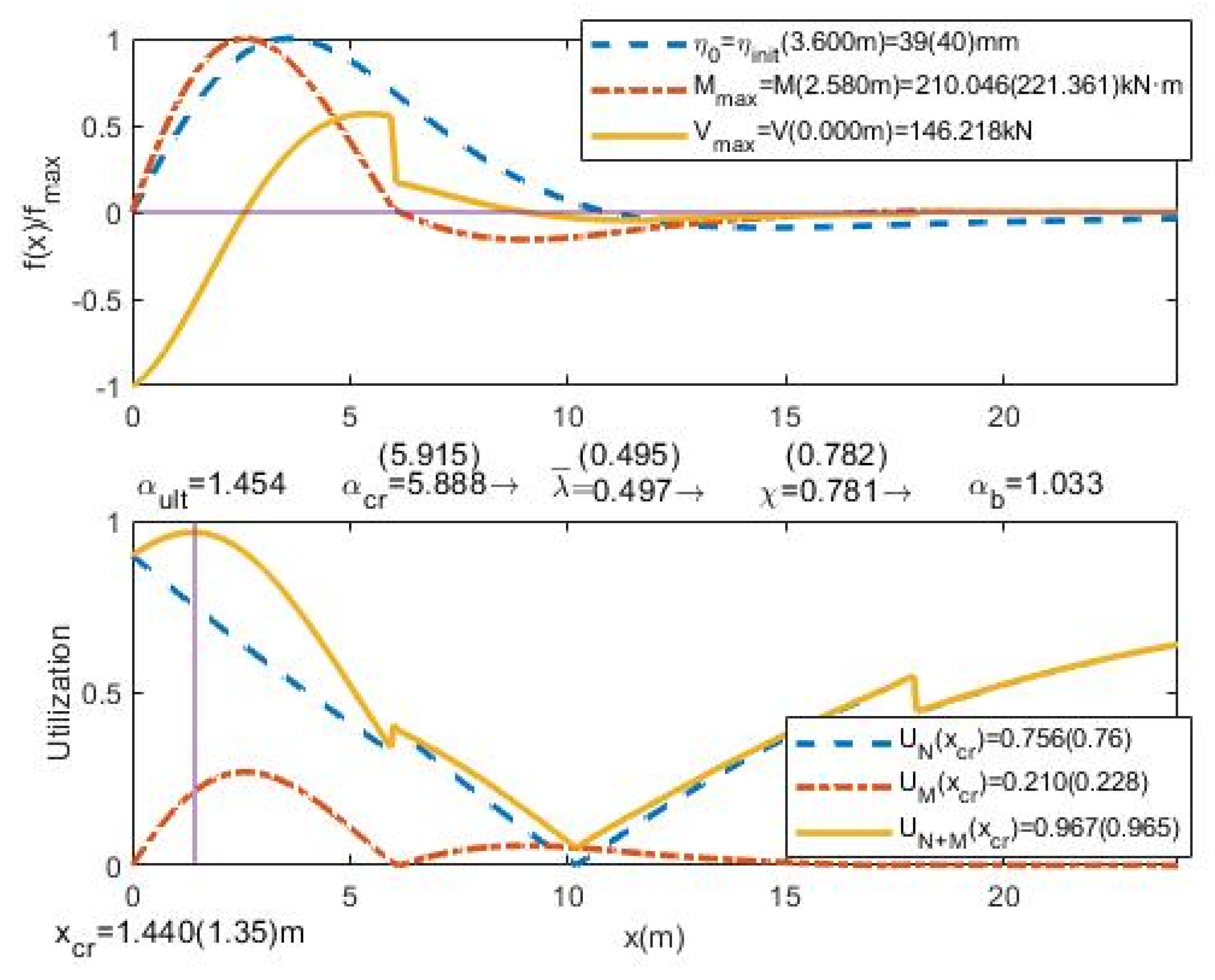
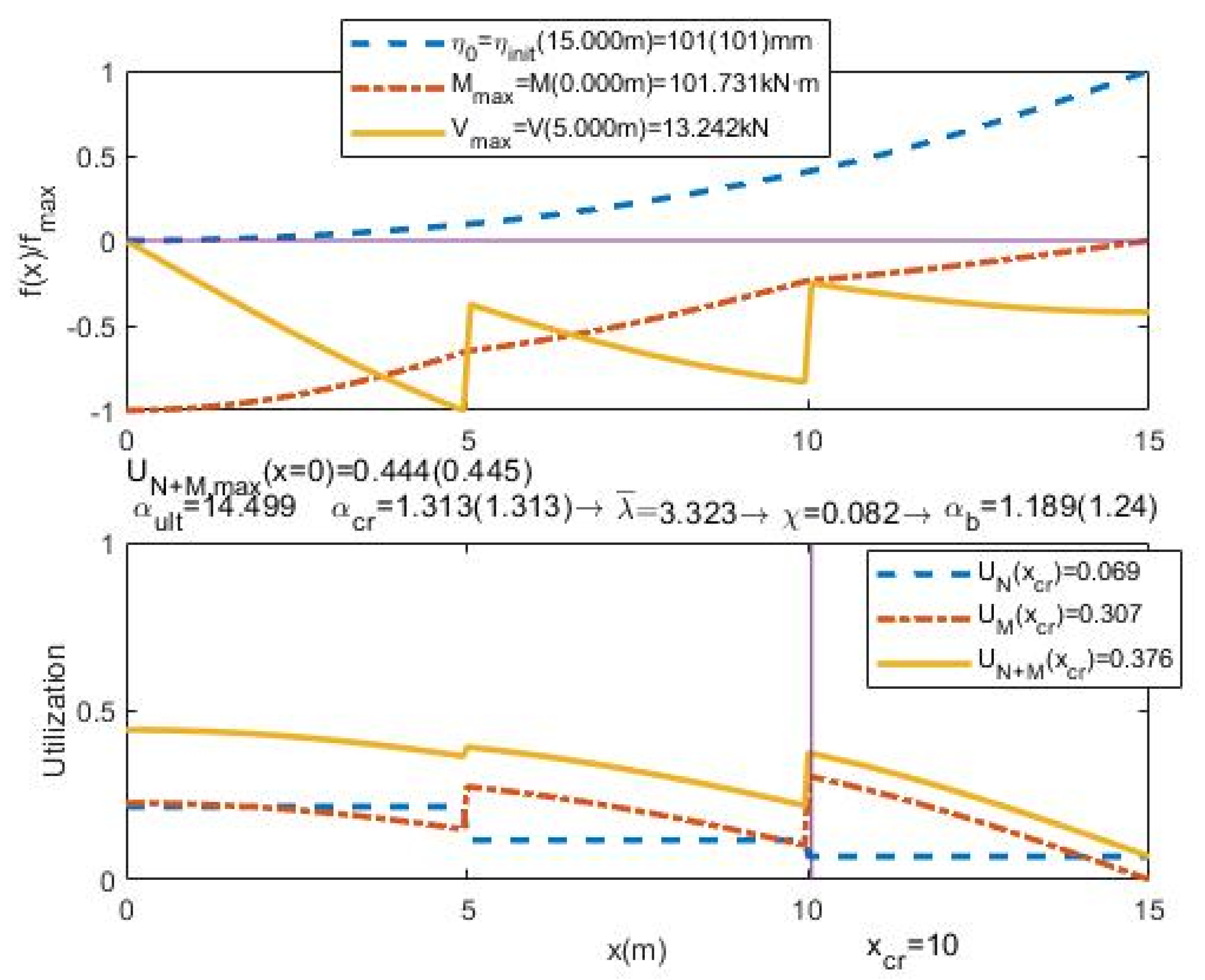
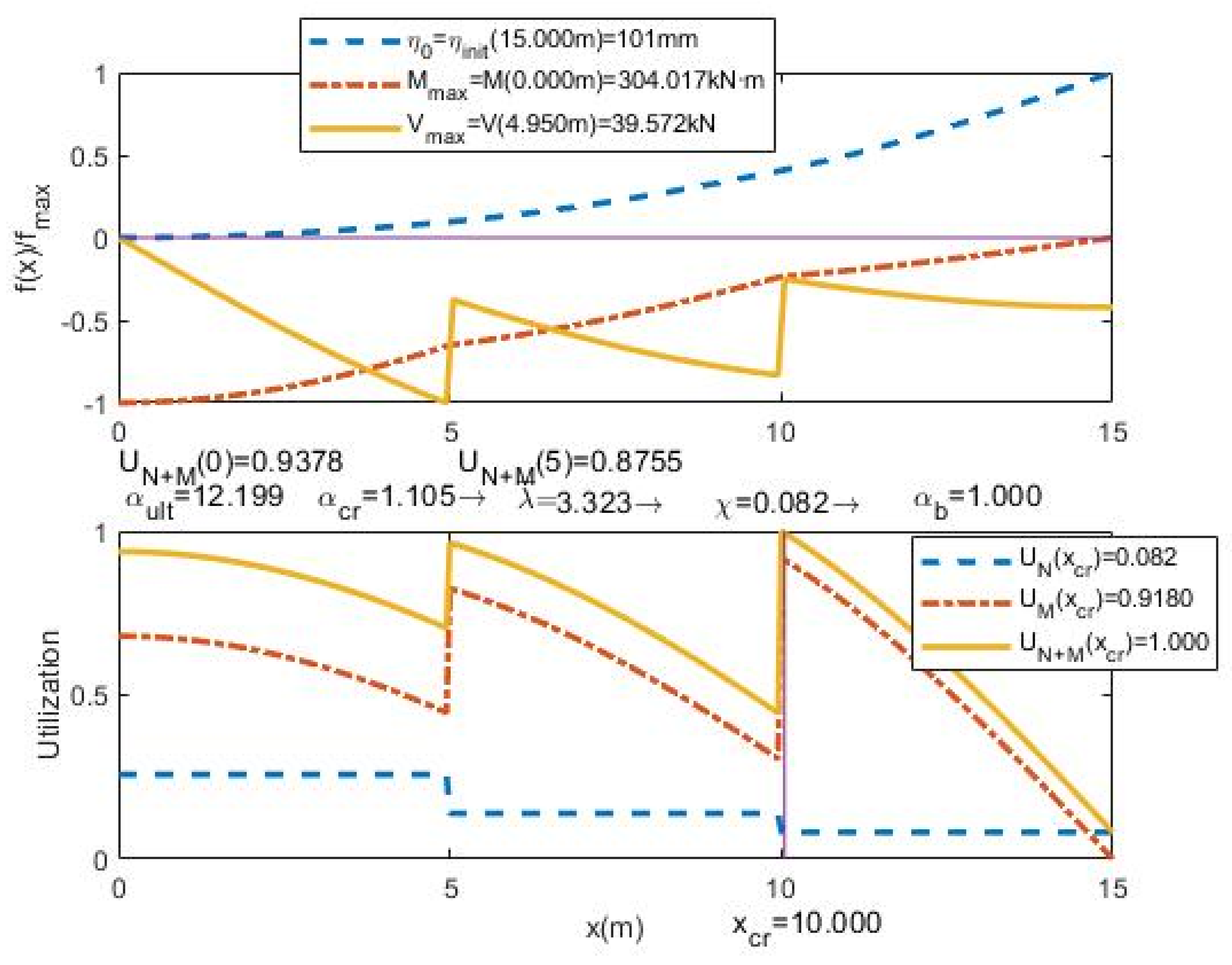
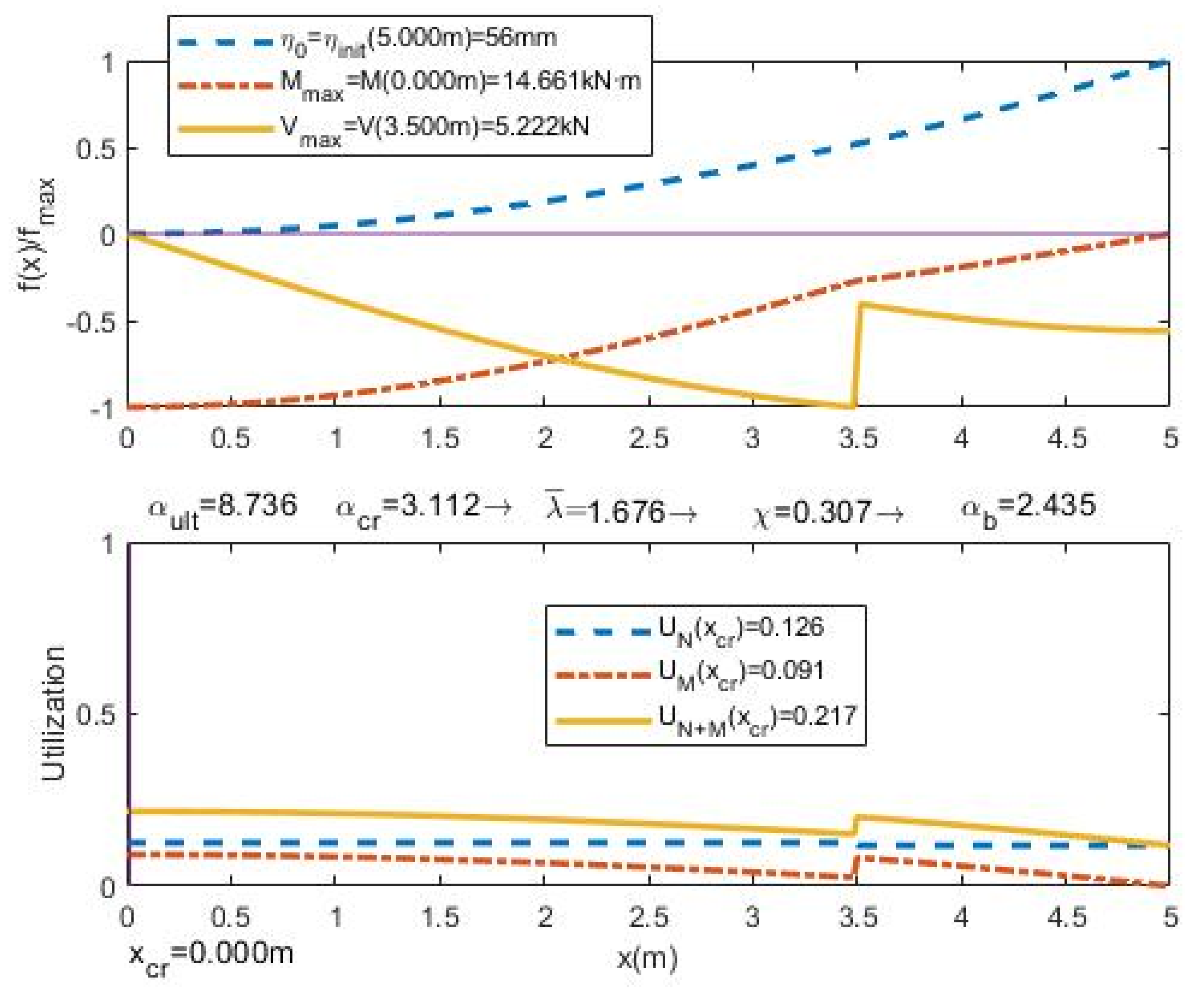
- The relative UGLI imperfection is plotted along the beam. The values are divided by the maximum value of imperfection in order to obtain the relative UGLI imperfection with maximum value 1.0.
- -
- The distribution of relative bending moments due to UGLI imperfection is plotted along the beam, the values are divided by the maximum bending moment value in order to have a maximum value 1.0:
- -
- The distribution of the relative shear forces due to UGLI imperfection is plotted along the beam. The values are divided by the maximum shear force in order to have a maximum value 1.0:
- -
- The plot of utilization factors U distribution: due to axial forces UN, due to bending moments UM and the global utilization factor UN+M. This factor shows how close each section is to its maximum strength and the influence of axial forces and bending moments:
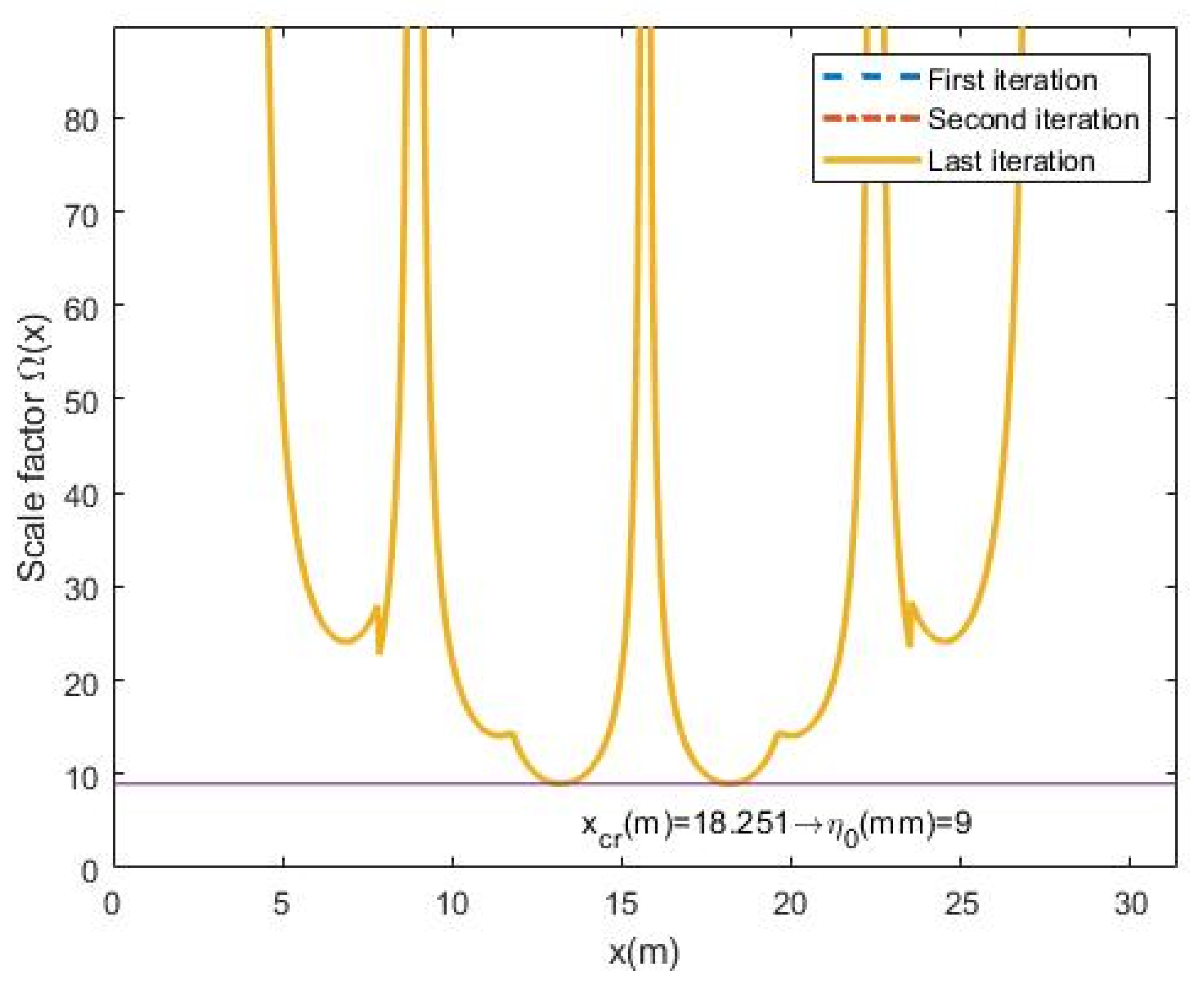
- -
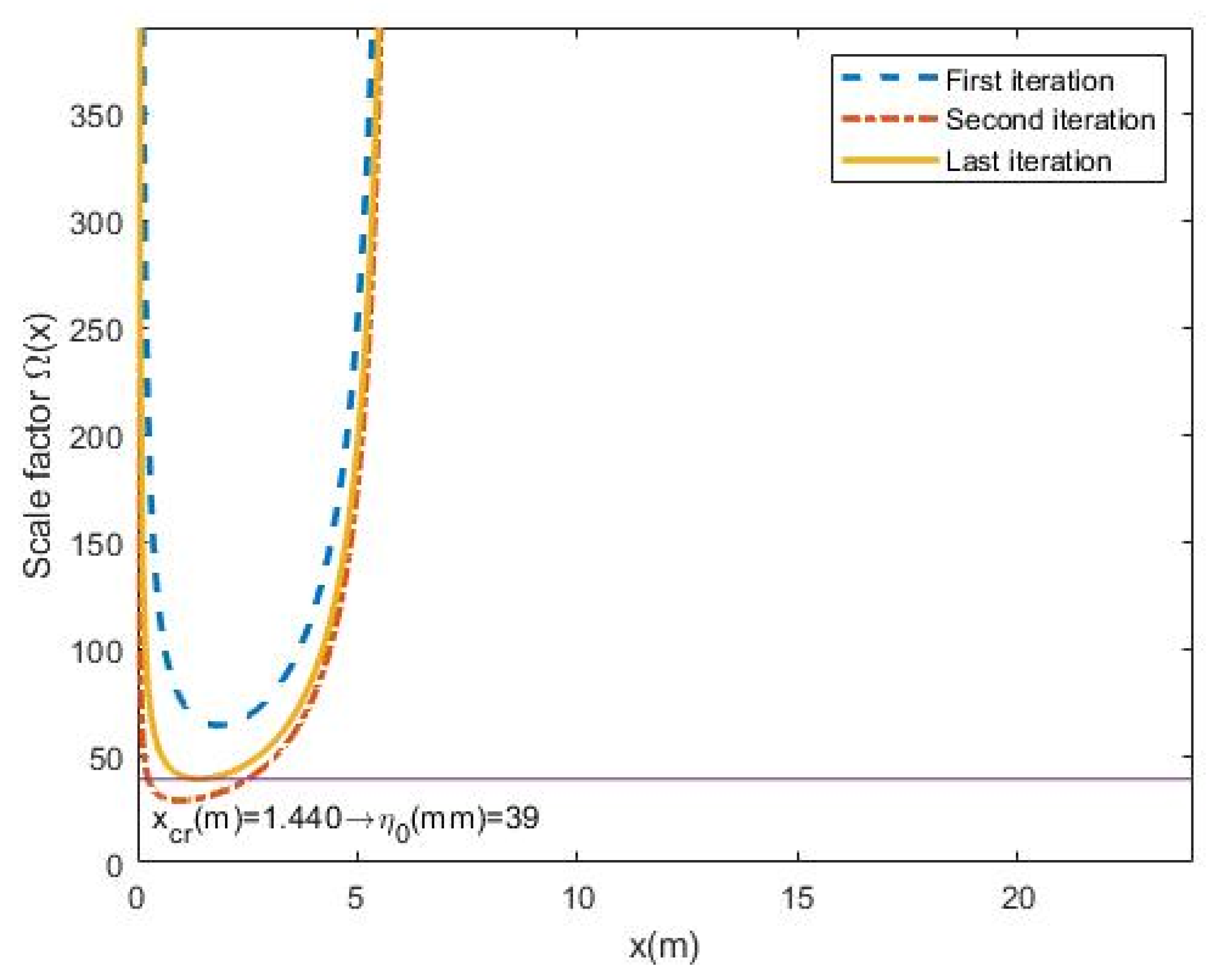
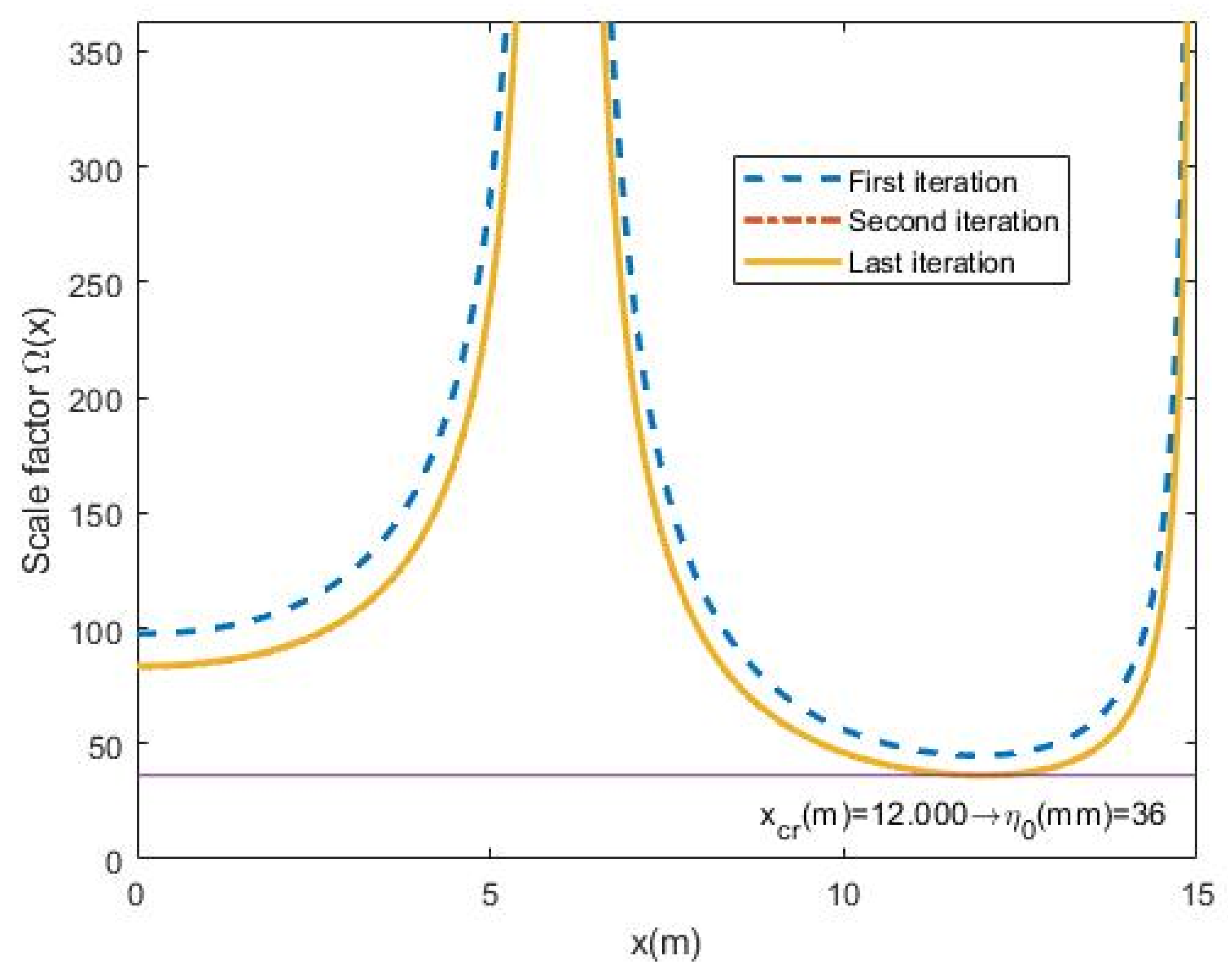
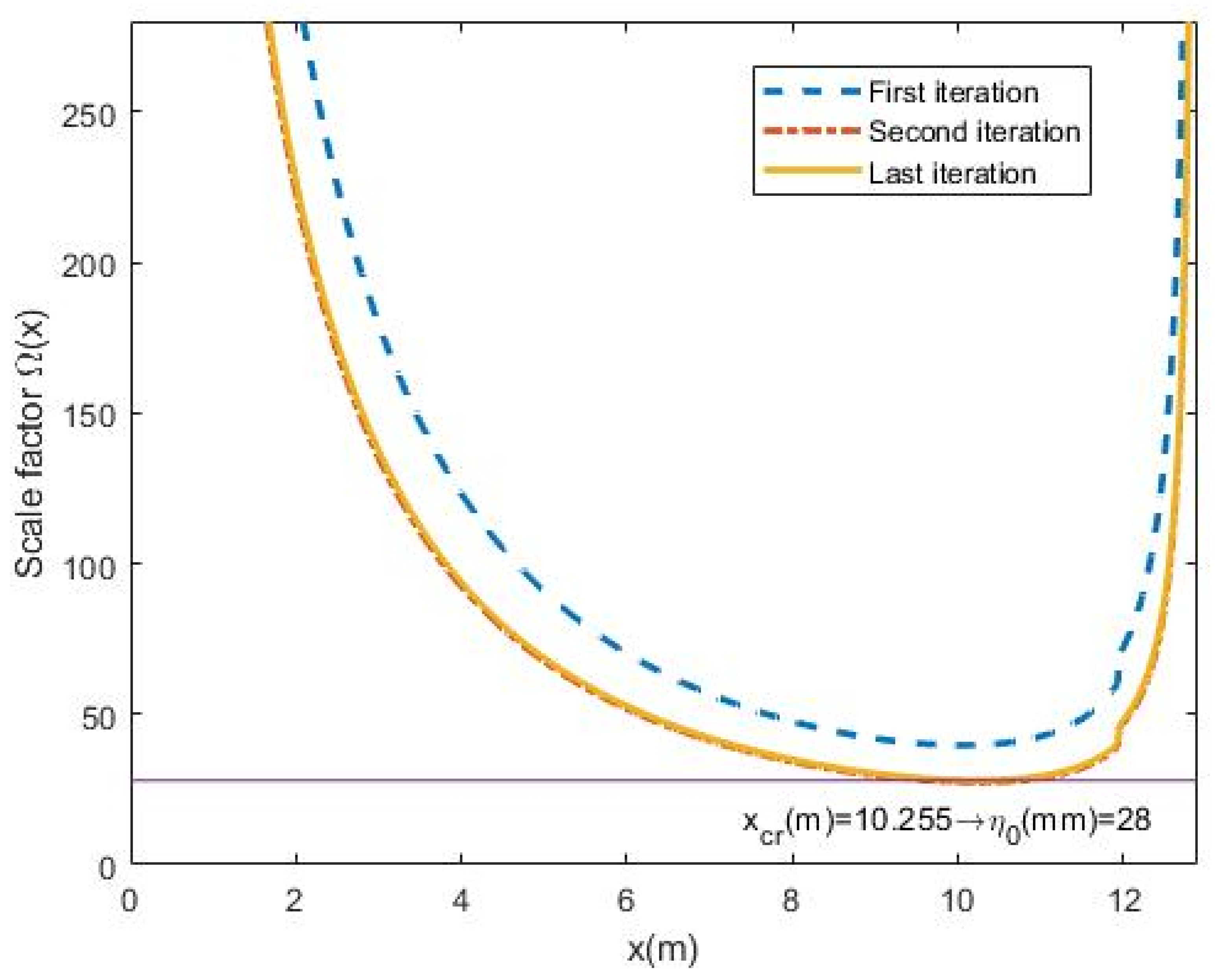
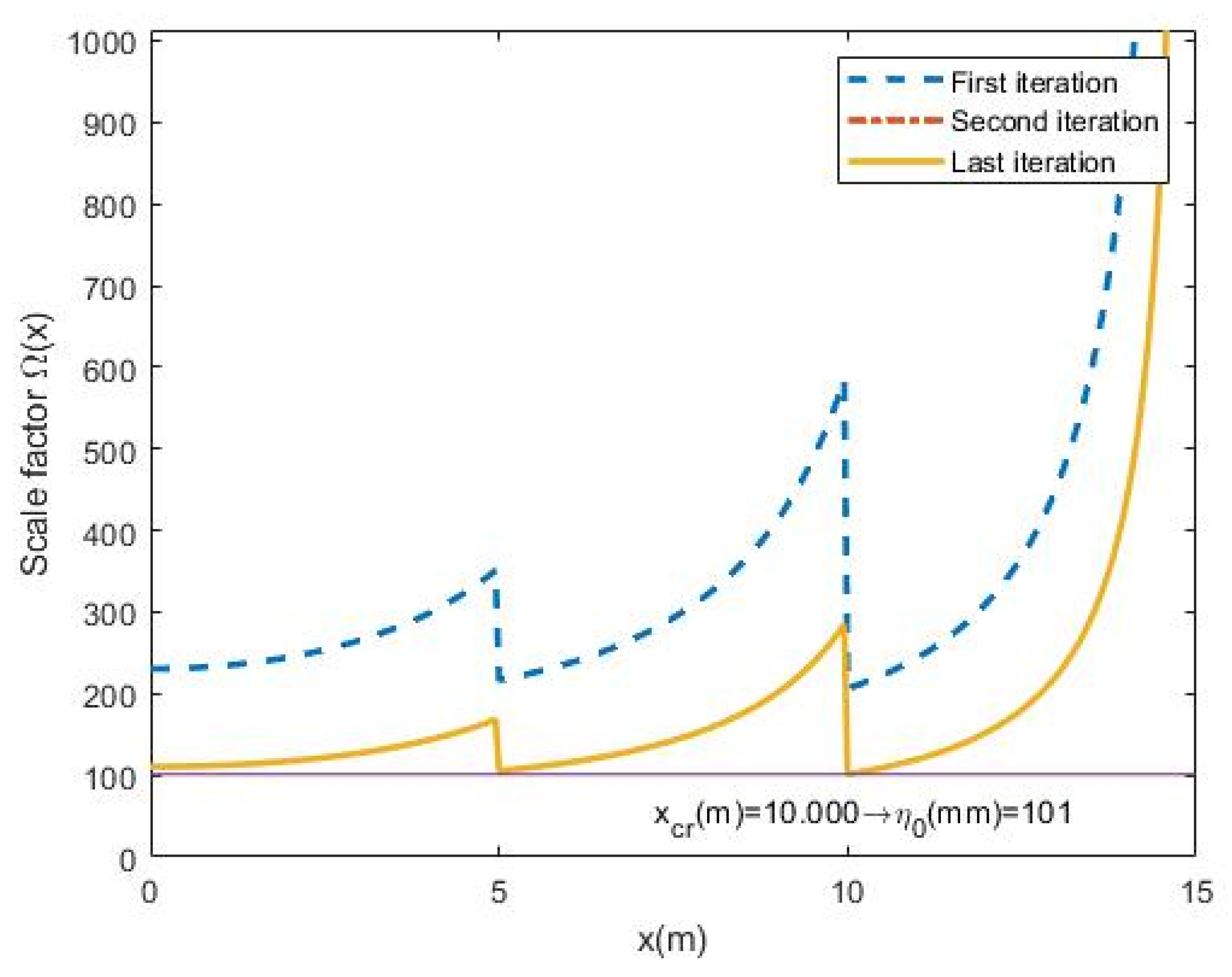
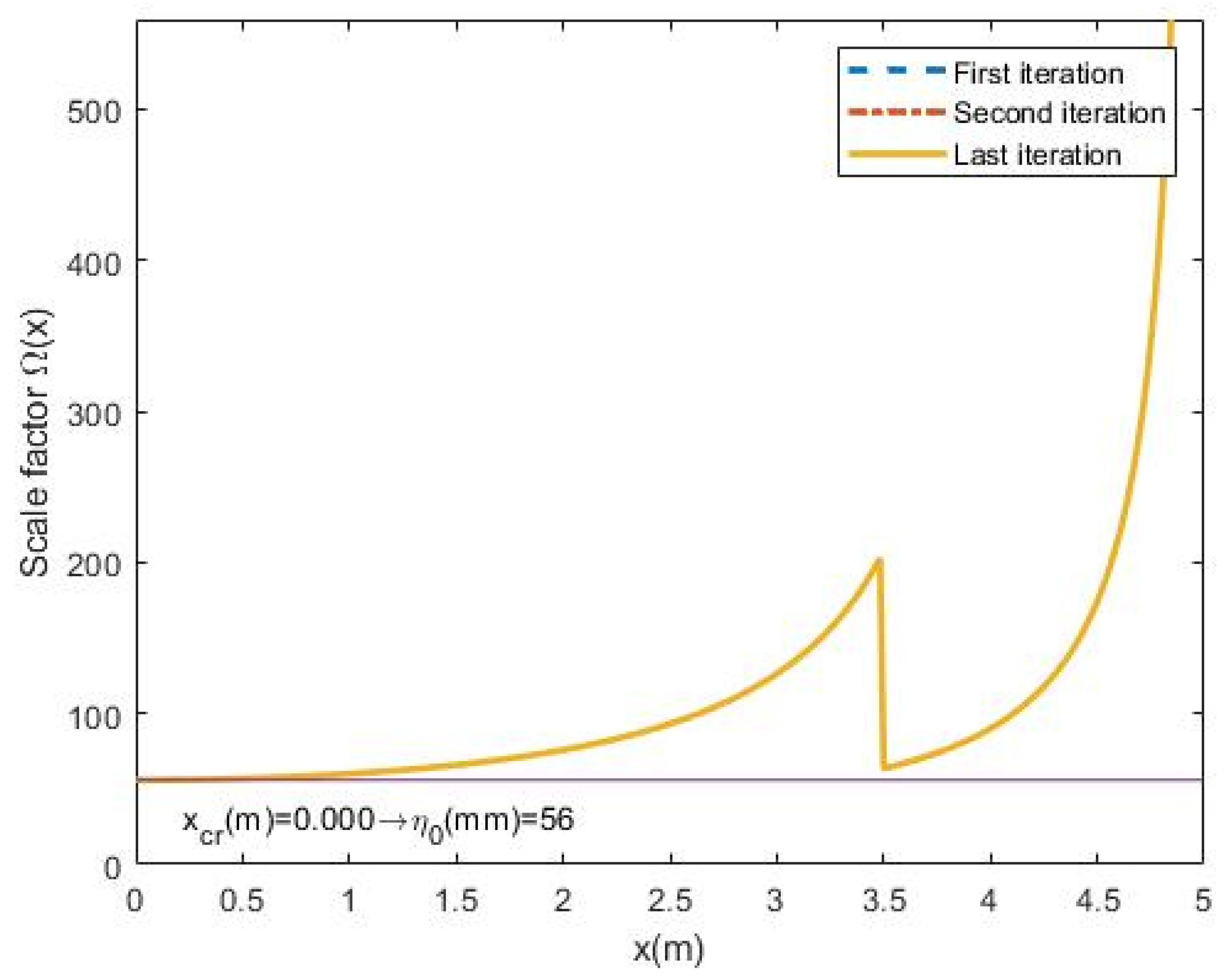
- The value of the scale factor distribution along the member is plotted showing the first, the second and the last iteration. The minimum value of each plot is η0,i. The maximum value shown is 10 times η0:
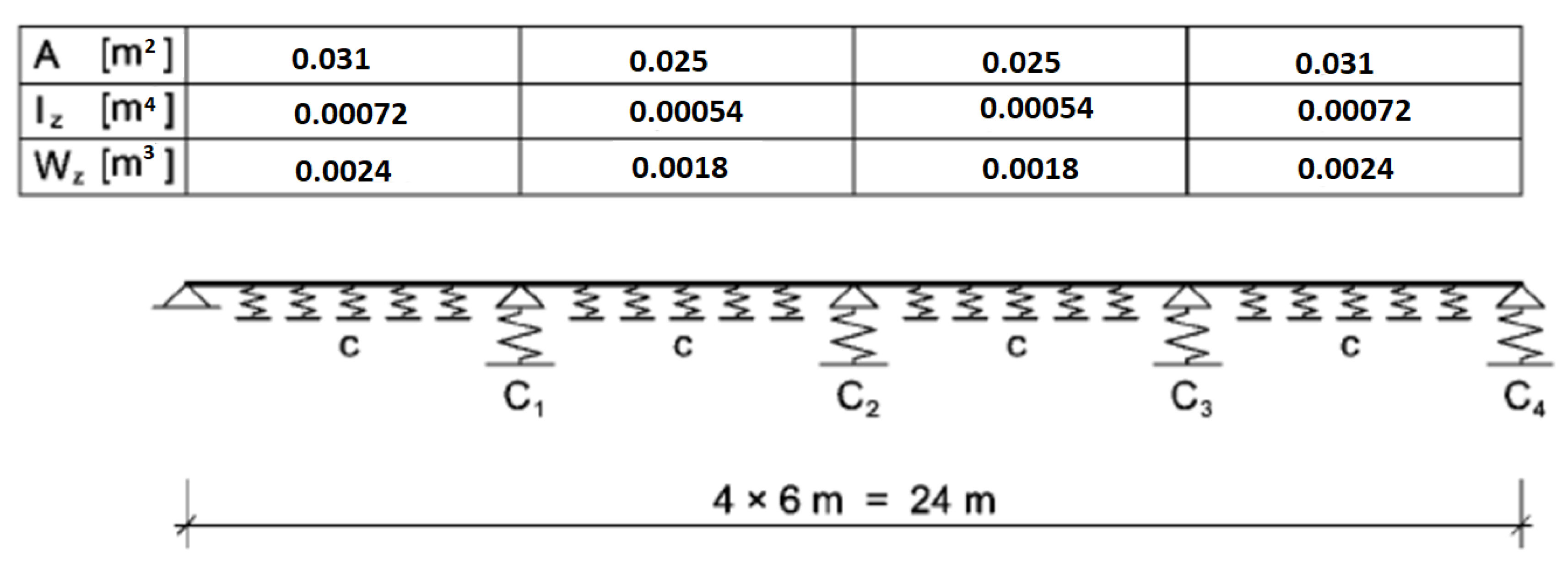
4. Application to the Case Where Problems Were Found to Obtain the Critical Section and to the Member Made of Aluminum Alloy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
References
- EN 1993-1-1:2005 and Corrigendum AC (2006) and Corrigendum AC (2009) and Amendment A1 (2014). Eurocode 3: Design of Steel Structures. In Part 1.1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2005. [Google Scholar]
- EN 1999-1-1:2007 and Amendment A1 (2009) and Amendment A2 (2013). Eurocode 9: Design of Aluminium Structures. In Part 1.1: General Structural Rules; CEN: Brussels, Belgium, 2007. [Google Scholar]
- Chladný, E.; Štujberová, M. Frames with unique global and local imperfection in the shape of the elastic buckling mode (part1). Stahlbau 2013, 8, 609–617. [Google Scholar] [CrossRef]
- prEN 1993-1-1:2020. Eurocode 3: Design of Steel Structures. In Part 1.1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2020. [Google Scholar]
- prEN 1999-1-1:2020. Eurocode 9: Design of aluminium structures. In Part 1.1: General Structural Rules; CEN/TC 250/SC 9 N 888; Secretariat BSI: London, UK, 2020. [Google Scholar]
- Sedlacek, G. Consistency of the Equivalent Geometric Imperfection Used in Design and in the Tolerances for Geometric Imperfection Used in Execution; CEN/TC 250/SC 3 document N1721; CEN: Brussels, Belgium, 2010; pp. 1–144. [Google Scholar]
- Chladný, E.; Štujberová, M. Frames with unique global and local imperfection in the shape of the elastic buckling mode (Part 2). Stahlbau 2013, 9, 684–694. [Google Scholar] [CrossRef]
- Chladný, E.; Štujberová, M. Errata: Frames with unique global and local imperfection in the shape of the elastic buckling mode. Stahlbau 2013, 82, 684–694. [Google Scholar] [CrossRef]
- Chladný, E. Imperfections for global analysis in STN EN 1993-1-1. In Implementation of Eurocodes in Practice. Design of Steel Structures according to STN EN 1993-1-1: November 2006 and STN EN 1993-1-8 April 2007, 1st ed.; SKSI Bratislava: Bratislava, Slovakia, 2007; Chapter 5. (In Slovak) [Google Scholar]
- Chladný, E. Imperfections for Global Analysis in STN EN 1993-1-1. In Implementation of Eurocodes in Practice. Design of Steel Structures According to STN EN 1993-1-1: November 2006 and STN EN 1993-1-8 April 2007 and Their Corrigenda and National Annexes, 2nd ed.; Baláž, I., Ed.; SKSI Bratislava: Bratislava, Slovakia, 2010; Chapter 5. (In Slovak) [Google Scholar]
- Baláž, I. Determination of the flexural buckling resistance of frames with members with non-uniform cross-section and non-uniform axial compression forces. Zborník z XXXIV. In Aktívu Pracovníkov Odboru OK so Zahraničnou Účast’ou “Teoretické a Konštrukčné Problémy Ocel’ových a Drevených Konštruckcií a Mostov”; STU Bratislava: Pezinok, Slovakia, 2008; pp. 17–22. [Google Scholar]
- Baláž, I.; Koleková, Y. Metal frames with non-uniform members and/or nonuniform normal forces with imperfections in the form of elastic buckling mode. Engineering research. In Anniversary Volume Honoring Amália and Miklós Iványi; Univeristy of Pécs: Pécs, Hungary, 2010; pp. 3–15. [Google Scholar]
- Baláž, I.; Koleková, Y. Structures with UGLI imperfections. In Proceedings of the 18th International Conference Engineering Mechanics 2012, Svratka, Czech Republic, 14–17 May 2012; pp. 61–86. [Google Scholar]
- Baláž, I.; Koleková, Y. In plane stability of two hinged arches. In Proceedings of the European Conference on Steel and Composite Structures, Eurosteel, Budapest, Hungary, 31 August–2 September 2011; pp. 1869–1874. [Google Scholar]
- Baláž, I.; Koleková, Y.; Kováč, M.; Živner, T. Generalization of Unique Global and Local Initial Imperfection Used in EN 1993-1-1 and EN 1999-1-1. In Proceedings of the 8th International Conference on Steel and Aluminium Structures, Hong Kong, China, 7–9 December 2016; pp. 1398–1411. [Google Scholar]
- Agüero, A.; Pallarés, F.J. Proposal to evaluate the ultimate limit state of slender structures. Part 1: Technical aspects. Eng. Struct. 2007, 29, 483–497. [Google Scholar] [CrossRef]
- Agüero, A.; Pallarés, L.; Pallares, F.J. Equivalent geometric imperfection definition in steel structures sensitive to flexural and/or torsional buckling due to compression. Eng. Struct. 2015, 91, 160–177. [Google Scholar] [CrossRef]
- Agüero, A.; Pallarés, F.J.; Pallares, L. Equivalent geometric imperfection definition in steel structures sensitive to lateral torsional buckling due to bending moment. Eng. Struct. 2015, 96, 41–55. [Google Scholar] [CrossRef]
- Kováč, M. Buckling Resistance of Metal Members and Frame Structures, Application of New Methods from Eurocodes. Ph.D. Thesis, STU in Bratislava, Bratislava, Slovakia, 2012. [Google Scholar]
- Dallemule, M. In Plane Buckling of Arch Structures. Ph.D. Thesis, STU in Bratislava, Bratislava, Slovakia, 2013. (In Slovak). [Google Scholar]
- Bijlaard, F.; Feldmann, M.; Naumes, J.; Sedlacek, G. The “general method” for assessing the out of plane stability of structural members and frames and the comparison with alternative rules in EN1993—Eurocode3—Part1-1. Steel Constr. 2010, 3, 33. [Google Scholar] [CrossRef]
- Wieschollek, M.; Schillo, N.; Feldmann, M.; Sedlacek, G. Lateral–torsional buckling checks of steel frames using second-order analysis. Steel Constr. 2012, 5, 71–86. [Google Scholar] [CrossRef]
- Papp, F. Buckling assessment of steel members trough overall imperfection method. Eng. Struct. 2016, 106, 124–136. [Google Scholar] [CrossRef]
- Brodniansky, J. Equivalent unique global and local initial imperfection - Imperfection in EN 1993-1-1 and EN 1999-1-1 Clause 5.3.2 (11)—Calculation procedure and discovered obstacles. Pollack Period. 2017, 12, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Lindner, J.; Kuhlmann, U.; Just, A. Verification of Flexural Buckling According to Eurocode 3 Part 1-1 using bow imperfections. Steel Constr. 2016, 9, 349–362. [Google Scholar] [CrossRef]
- Lindner, J.; Kuhlmann, U.; Jörg, F. Initial bow imperfection e0 for the verification of Flexural Buckling According to Eurocode 3 Part 1-1—Additional considerations. Steel Constr. 2018, 11, 30–41. [Google Scholar] [CrossRef]
- Trahair, N.S. Flexural–Torsional Buckling of Structures; E & FNspon: London, UK, 1993. [Google Scholar]
- Marques, L.; Taras, A.; Silva, L.S.; Greiner, R.; Rebelo, C. Development of a consistent. buckling design procedure for tapered columns. J. Constr. Steel Res. 2012, 72, 61–74. [Google Scholar] [CrossRef]
- Chladný, E.; Chladná, M. Some remarks to the application of equivalent bow imperfection in analyses of compressed steel members and structures. In Proceedings of the 10th International Conference on Metal Structures; Ziółko, J., Supernak, E., Eds.; PAN: Gdansk, Poland, 2001; Volume 2, pp. 351–356. [Google Scholar]
- Höglund, T.; Tindall, P. Designer’s Guide to Eurocode 9: Design of Aluminium Structures; EN 1999-1-1 and -1-4; ICE Publishing: London, UK, 2012; ISBN 978-0-7277-5737-1. [Google Scholar]


| Iteration | xcr,i | |||||
|---|---|---|---|---|---|---|
| 1 | 1.2228 | 0.4557 | 0.8106 | 0.9011 | 1.9200 | 1.6435 |
| 2 | 1.5532 | 0.5136 | 0.7698 | 1.0870 | 1.0200 | 0.7413 |
| 3 | 1.3762 | 0.4835 | 0.7910 | 0.9896 | 1.6800 | 1.2012 |
| 4 | 1.5023 | 0.5051 | 0.7757 | 1.0594 | 1.3200 | 0.8779 |
| 5 | 1.4311 | 0.4930 | 0.7842 | 1.0203 | 1.5000 | 1.0586 |
| 6 | 1.4660 | 0.4990 | 0.7800 | 1.0396 | 1.4400 | 0.9702 |
| 7 | 1.4542 | 0.4970 | 0.7814 | 1.0331 | 1.4400 | 1.0000 |
| Iteration | xcr,i | |||||
|---|---|---|---|---|---|---|
| 1 | 1.9376 | 0.6777 | 0.7961 | 1.4023 | 13.2273 | 1 |
| Iteration | xcr,i | |||||
|---|---|---|---|---|---|---|
| 1 | 1.3674 | 0.7834 | 0.7346 | 1.0045 | 11.95 | 1.2343 |
| 2 | 1.4777 | 0.8144 | 0.7155 | 1.0574 | 12 | 1 |
| Iteration | xcr,i | |||||
|---|---|---|---|---|---|---|
| 1 | 1.2828 | 0.8319 | 0.7046 | 0.9038 | 10.0878 | 1.4135 |
| 2 | 1.5123 | 0.9033 | 0.6591 | 0.9967 | 10.268 | 0.9775 |
| 3 | 1.4975 | 0.8989 | 0.6619 | 0.9912 | 10.268 | 1 |
| Iteration | xcr,i | |||||
|---|---|---|---|---|---|---|
| 1 | 3.0523 | 1.5139 | 0.3372 | 1.0292 | 0.0 | 2.0485 |
| 2 | 9.5979 | 2.6845 | 0.1224 | 1.1749 | 10 | 1 |
| Steel | FEd,2 (kN) | 100 | 125 | 150 | 175 | 200 | (225) | 250 | 275 | 300 | 325 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S 235 | (mm) | 68.8 | 71.1 | 73.4 | 75.7 | 78 | 77.7 | 113 | 115.5 | 115.5 | 115.3 |
| S 275 | (mm) | 75 | 77.4 | 80 | 82.4 | 85 | 87.4 | 126.1 | 126 | 126 | 125.8 |
| S 355 | (mm) | 86 | 88.8 | 91.6 | 94.5 | 97.4 | 101 (100.9) | 145 | 145 | 144.9 | 144.7 |
| xcr (m) | 10 | 10 | 10 | 10 | 10 | 10 (10) | 5 | 5 | 5 | 5 |
| Steel | FEd,2 (kN) | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 | 300 | 325 |
|---|---|---|---|---|---|---|---|---|---|---|---|
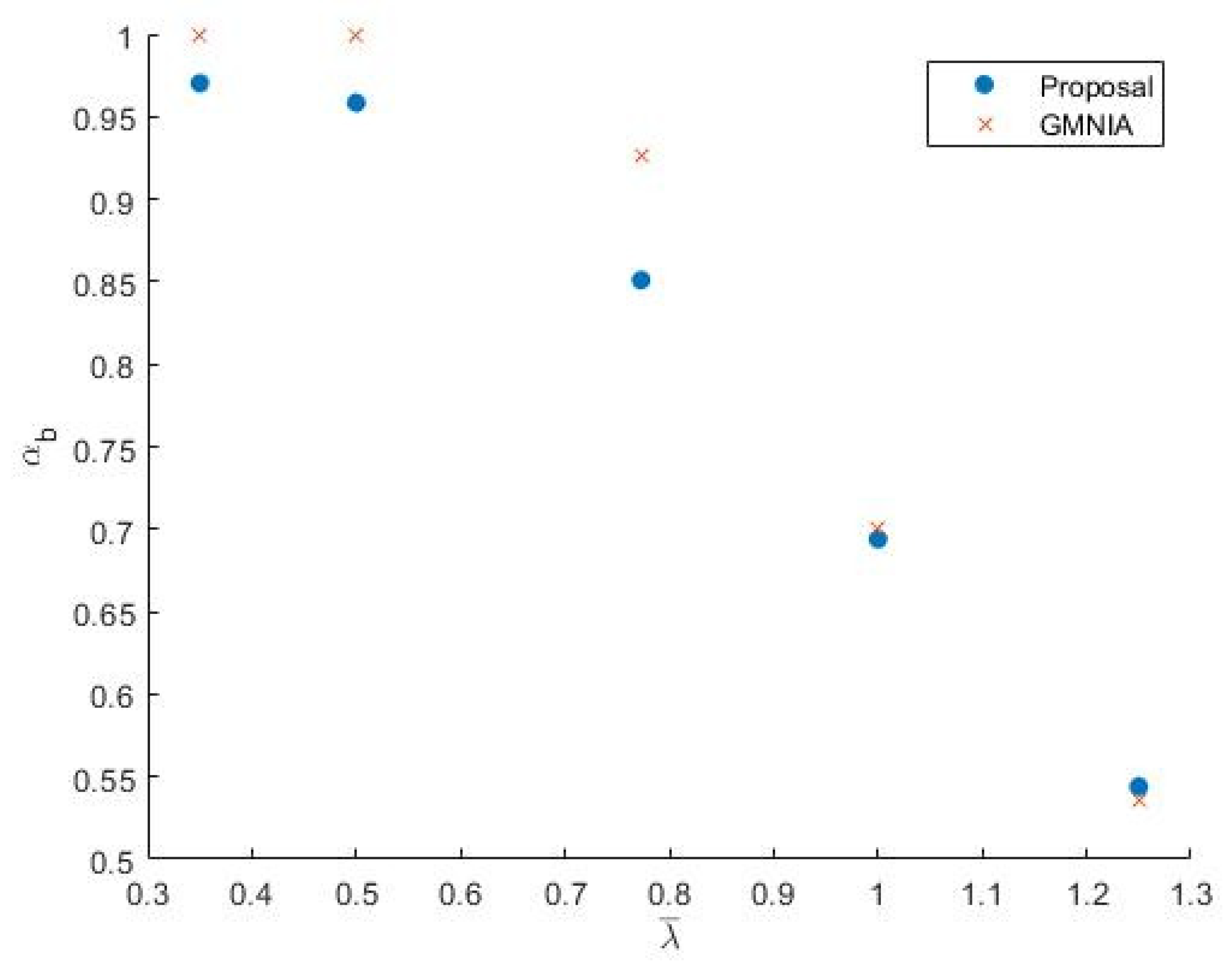
| S 235 | αb (Authors) | 1.381 | 1.333 | 1.287 | 1.242 | 1.2 | 1.159 | 1.065 | 1.023 | 0.985 | 0.949 |
| αb (GMNIA) | 1.455 | 1.396 | 1.346 | 1.294 | 1.246 | 1.193 | 1.138 | 1.09 | 1.07 | 1.03 | |
| S 275 | αb (Authors) | 1.397 | 1.348 | 1.301 | 1.256 | 1.213 | 1.171 | 1.082 | 1.04 | 1.001 | 0.965 |
| αb (GMNIA) | 1.46 | 1.41 | 1.37 | 1.318 | 1.26 | 1.22 | 1.15 | 1.11 | 1.07 | 1.04 | |
| S 355 | αb (Authors) | 1.42 | 1.37 | 1.322 | 1.275 | 1.231 | 1.189 | 1.148 | 1.064 | 1.025 | 0.988 |
| αb (GMNIA) | 1.48 | 1.45 | 1.39 | 1.34 | 1.29 | 1.24 | 1.21 | 1.169 | 1.121 | 1.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agüero, A.; Baláž, I.; Koleková, Y.; Martin, P. Assessment of in-Plane Behavior of Metal Compressed Members with Equivalent Geometrical Imperfection. Appl. Sci. 2020, 10, 8174. https://doi.org/10.3390/app10228174
Agüero A, Baláž I, Koleková Y, Martin P. Assessment of in-Plane Behavior of Metal Compressed Members with Equivalent Geometrical Imperfection. Applied Sciences. 2020; 10(22):8174. https://doi.org/10.3390/app10228174
Chicago/Turabian StyleAgüero, Antonio, Ivan Baláž, Yvona Koleková, and Pedro Martin. 2020. "Assessment of in-Plane Behavior of Metal Compressed Members with Equivalent Geometrical Imperfection" Applied Sciences 10, no. 22: 8174. https://doi.org/10.3390/app10228174








