Enhancing the Iterative Smoothed Particle Hydrodynamics Method

Abstract

Motivated by recent research on the iterative approach proposed for the smoothed particle hydrodynamics (ISPH) method, some ideas to improve the process are introduced. The standard procedure is enhanced iterating on the residuals preserving the matrix-free nature of the process. The method is appealing providing reasonable results with disordered data distribution too and no kernel variations are needed in the approximation. This work moves forward with a novel formulation requiring a lower number of iterations to reach a desired accuracy. The computational procedure is described and some results are introduced to appreciate the proposed formulation.

1. Introduction

Mesh-free methods are promising approaches emerging in recent years as valid computational alternatives to grid-based ones. Grid-based methods adopt a computational frame which is made up of nodes, where the field variables are evaluated, related to each other through a predefined nodal connectivity. Mesh-free methods are independent of a mesh and are well suited for problems with complex geometries or problems which require highly adaptive discretizations maintaining a suitable computational effort [1,2,3]. Smoothed Particle Hydrodynamics is a popular kernel based approach introduced in astrophysics [4,5,6,7,8,9] and it is being increasingly used [3,10,11,12,13,14]. The method provides a spatial approximation via a discrete kernel convolution. In [15] the standard procedure has been improved by means of an iterative approach refining the residuals. An approximant is generated by employing strictly definite positive kernel functions and the method, in convergence, improves the results without requiring evenly spaced data distribution. If the linear approximation order is ensured [16,17], the iterative procedure performs better. In a recent paper [18] some results on this improved approach have been presented, however, the algorithm can become prohibitive for the number of iterations. In this work, starting with the linear approximation order, a formulation which guarantees accuracy with a lower number of iterations is proposed and discussed. The paper is organized as follows. In Section 2 the main ideas of the method are presented. In Section 3 the iterative process and the fast formulation are described. In Section 4 numerical validations are reported choosing the linear approximation order as starting iteration estimate. In Section 5, remarks and ideas on future work are outlined.

2. The Standard Approximation

The method approximates a function f at $\mathbf{x}\in R^d$, for $d\ge 1$, by means of the kernel approximation

$$<f_h\left(\mathbf{x}\right)>={\int }_{\mathsf{\Omega }}f\left(\mathit{\xi }\right)\mathsf{K}(\mathbf{x},\mathit{\xi };h)d\mathsf{\Omega }$$

(1)

where $\mathit{\xi }=({\mathit{\xi }}^{\left(1\right)},...,{\mathit{\xi }}^{\left(d\right)})$ and $\mathsf{K}(\mathbf{x},\mathit{\xi };h$) is the $kernel function$. The spatial kernel influence is localized by the smoothing length h. The continuum is decomposed into a set of arbitrarily distributed data sites $\mathrm{\Xi }={\left({\mathit{\xi }}_j\right)}_{j=1}^N$, where ${\left(f\left({\mathit{\xi }}_j\right)\right)}_{j=1}^N$ are the corresponding measurements and the $particle approximation$ is introduced as

$${\displaystyle f_h\left(\mathbf{x}\right)=\sum _{j=1}^{N}f\left({\mathit{\xi }}_j\right)\mathsf{K}(\mathbf{x},{\mathit{\xi }}_j;h)d{\mathsf{\Omega }}_j}$$

(2)

where $d{\mathsf{\Omega }}_j$ is the measure of the subdomain ${\mathsf{\Omega }}_j$ associated with the data ${\mathit{\xi }}_j$.

Particle approximation often loses its accuracy, especially on the boundary and with non uniform data locations [19]. Making use of the Taylor series expansion, by retaining p terms, multiplying for the kernel function and integrating over $\mathsf{\Omega }$[16,17,19] improvements can be gained. For p = 1 it means

$$f\left(\mathbf{x}\right)=<I_h\left(\mathbf{x}\right)><f_h\left(\mathbf{x}\right)>+O\left(h\right)$$

(3)

with $<I_h\left(\mathbf{x}\right)>=1/{\int }_{\mathsf{\Omega }}\mathsf{K}(\mathbf{x},\mathit{\xi };h)d\mathsf{\Omega }$ and the corresponding discrete formulation is

$$f\left(\mathbf{x}\right)=I_h\left(\mathbf{x}\right)f_h\left(\mathbf{x}\right)+O\left(h\right)$$

(4)

with ${\displaystyle I_h\left(\mathbf{x}\right)=1/\sum _{j=1}^N\mathsf{K}(\mathbf{x},{\mathit{\xi }}_j;h)d{\mathsf{\Omega }}_j}$.

By increasing p, the order of accuracy increases, requiring the solution of linear systems for each evaluation point [16,17]. In [15] an iterative matrix-free approach (ISPH) is introduced to improve the standard method. In [18] it is adopted refining the normalized approach (4) as starting values for the iterations. In the following section an enhanced iterative formulation (E-ISPH) is proposed. For the sake of clarity, a brief overview on the standard iterative formulation is at first described.

3. The Iterative Approximation

3.1. The Iterative Formulation (ISPH)

Let f be the vector collecting the function values at the data in $\mathrm{\Xi }$, $\mathbf{k}\left(\mathbf{x}\right)$ the vector with the kernel values at $\mathrm{\Xi }$ referring to the evaluation point $\mathbf{x}$, $\mathsf{\Omega }$ the diagonal matrix with the significant entries equal to the measures $d{\mathsf{\Omega }}_j$, the SPH approximant (2) can be expressed as

$$f_h\left(\mathbf{x}\right)=k\left(\mathbf{x}\right)\mathsf{\Omega }\mathbf{f}.$$

(5)

By assuming

$$f_h^{\left(0\right)}\left(\mathbf{x}\right)\equiv f_h\left(\mathbf{x}\right)$$

(6)

the sequence $\{f_h^{\left(n\right)}\left(\mathbf{x}\right)\}$ is provided by iterating on the residuals.

Let A a matrix with entries ${\mathbf{A}}_{i,j}=\mathsf{K}({\mathit{\xi }}_i,{\mathit{\xi }}_j;h)d{\mathsf{\Omega }}_j,i,j=1,\dots ,N$, and

$${\mathbf{s}}^{\left(0\right)}=\mathbf{f}-\mathbf{A}\mathbf{f}$$

for $n\in \mathcal{N}$, $n>0$ the term of the succession is obtained as

$$f_h^{\left(n\right)}\left(\mathbf{x}\right)=f_h^{(n-1)}\left(\mathbf{x}\right)+\mathbf{k}\left(\mathbf{x}\right)\mathsf{\Omega }{\mathbf{s}}^{(n-1)}=\mathbf{k}\left(\mathbf{x}\right)\mathsf{\Omega }\sum _{k=0}^n{(\mathbf{I}-\mathbf{A})}^k\mathbf{f}$$

(7)

and

$${\mathbf{s}}^{\left(n\right)}={\mathbf{s}}^{(n-1)}-\mathbf{A}{\mathbf{s}}^{(\mathrm{n}-1)}.$$

For $n\to \infty$, the summation in (7) approximates ${\mathbf{A}}^{-1}$ if and only if ${\parallel \mathbf{I}-\mathbf{A}\parallel }_2<1$[20]; therefore, under this condition the $\{f_h^{\left(n\right)}\left(\mathbf{x}\right)\}$ converges to the interpolant $P_h\left(\mathbf{x}\right)$

The solution for $P_h\left(\mathbf{x}\right)$ is admitted with strictly definite positive kernel functions on pair-wise distinct data sites and this is the only assumption for the data location [21,22]. It is not necessary to ask for evenly spaced data in the construction of $\{f_h^{\left(n\right)}\left(\mathbf{x}\right)\}$.

3.2. The Enhanced Iterative Formulation (E-ISPH)

In order to speed-up the process, the computation is revisited focusing on

$${\mathbf{S}}^{\left(n\right)}=\sum _{k=0}^n{(\mathbf{I}-\mathbf{A})}^{k}n=0,1,2,\dots$$

(8)

For each n, the summation ${\mathbf{S}}^{(2^n-1)}$ of $2^n$ terms is taken into account. Let ${\tilde{\mathbf{S}}}^{\left(n\right)}:={\mathbf{S}}^{(2^n-1)}$, i.e.,

$${\tilde{\mathbf{S}}}^{\left(n\right)}=\sum _{k=0}^{2^n-1}{(\mathbf{I}-\mathbf{A})}^k=\sum _{k=0}^{2^{n-1}-1}{(\mathbf{I}-\mathbf{A})}^k[\mathbf{I}+{(\mathbf{I}-\mathbf{A})}^{2^{n-1}}].$$

(9)

By considering that

$${(\mathbf{I}-\mathbf{A})}^s=\mathbf{I}-[\sum _{j=0}^{s-1}{(\mathbf{I}-\mathbf{A})}^j]\mathbf{A}$$

(10)

by substituting (10) in (9) with $s=2^{n-1}$ the following relation holds

$${\tilde{\mathbf{S}}}^{\left(n\right)}=\sum _{k=0}^{2^{n-1}-1}{(\mathbf{I}-\mathbf{A})}^k\{\mathbf{I}+\mathbf{I}-[\sum _{j=0}^{2^{n-1}-1}{(\mathbf{I}-\mathbf{A})}^j]\mathbf{A}\}.$$

(11)

Consequently, the subsequent recursive formula can be written

$${\tilde{\mathbf{S}}}^{\left(n\right)}=2{\tilde{\mathbf{S}}}^{(n-1)}-{\left({\tilde{\mathbf{S}}}^{(n-1)}\right)}^2\mathbf{A}.$$

(12)

Now, the (12) is employed in the overall computation, giving rise to the new succession {${\tilde{f}}^{\left(n\right)}\left(\mathbf{x}\right)$}. The described enhanced formulation is comparable in accuracy to ISPH, requiring a reduced number of iterations. In the next section, the behavior of the fast procedure E-ISPH is reported and compared with the standard SPH and ISPH formulations.

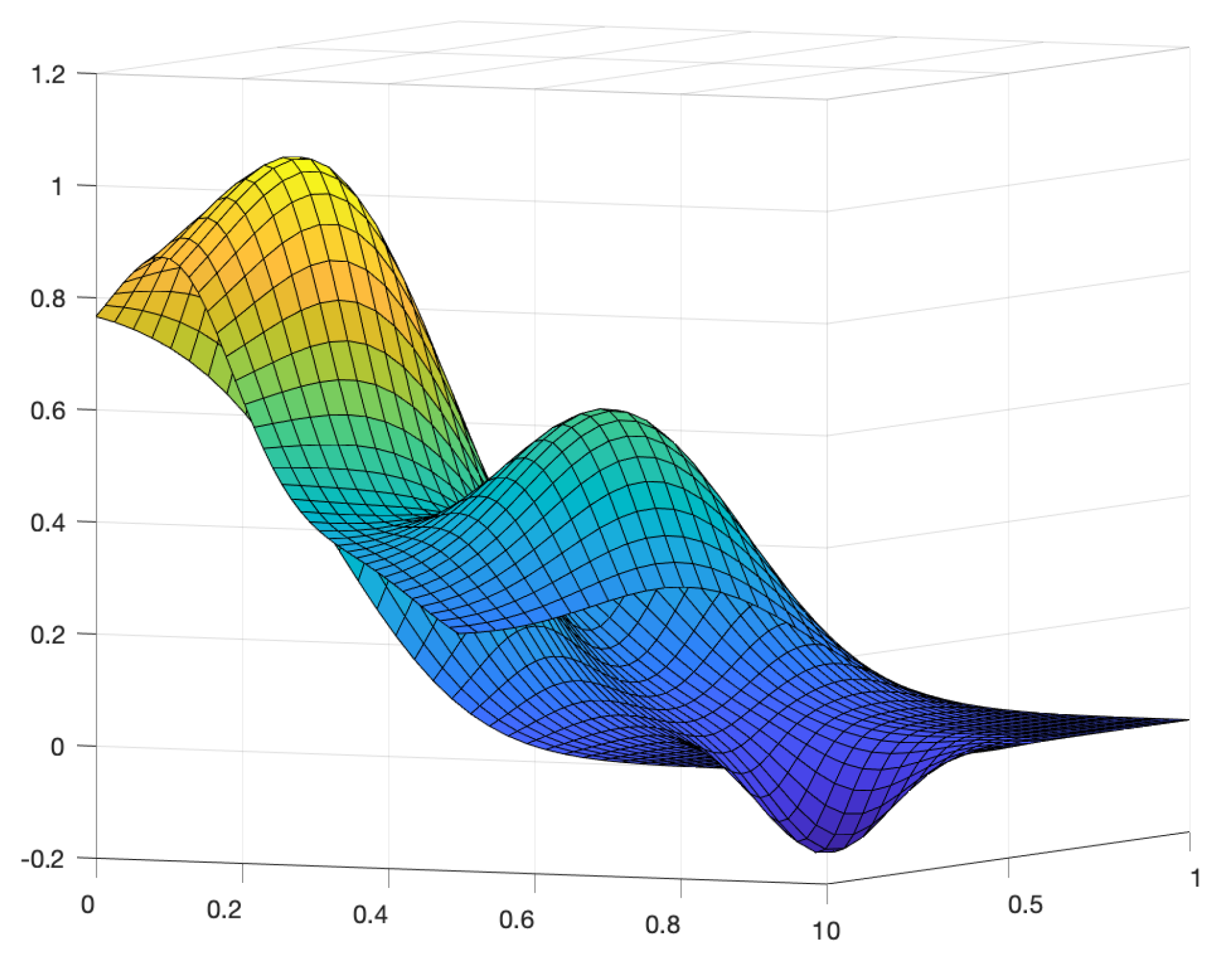
4. Numerical Results

The Franke’s function (13) with d = 2 depicted in Figure 1, taken from the scattered data literature [23,24], is referred to as test function

$$\begin{array}{cc}f(x^{\left(1\right)},x^{\left(2\right)})=\hfill & 0.75exp\left[-\frac{{(9x^{\left(1\right)}-2)}^2+{(9x^{\left(2\right)}-2)}^2}{4}\right]+\hfill \\ \hfill & +0.75exp\left[-\frac{{(9x^{\left(1\right)}+1)}^2}{49}-\frac{{(9x^{\left(2\right)}+1)}^2}{10}\right]+\hfill \\ \hfill & +0.5exp\left[-\frac{{(9x^{\left(1\right)}-7)}^2+{(9x^{\left(2\right)}-3)}^2}{4}\right]+\hfill \\ \hfill & -0.2exp\left[-{(9x^{\left(1\right)}-4)}^2-{(9x^{\left(2\right)}-7)}^2\right].\hfill \end{array}$$

(13)

Two sets of data sites are considered: the gridded ${\mathrm{\Xi }}_G$, composed of regular distribution points, and the Halton ${\mathrm{\Xi }}_H$[25] which consists of unevenly distribution points. The $haltonset$ function of MATLAB© is used to generate ${\mathrm{\Xi }}_H$. The accuracy of the estimates is measured with

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^M{|f_h\left({\mathbf{x}}_i\right)-f\left({\mathbf{x}}_i\right)|}^2}}{M}}$$

(14)

by fixing M = 1600 as the number of evaluation points and $N={(2^t+1)}^2$, t = 1,2,.., as the number of data sites increasing in the unit domain. The kernel function is the Gaussian one.

Some results on the accuracy and on the convergence are illustrated. The improvements in the linear approximation are evident in

Table 1. RMSEs for SPH (standard formulation) and with p = 1. Data sites ${\mathrm{\Xi }}_G$ and ${\mathrm{\Xi }}_H$.

	${\mathrm{\Xi }}_{\mathit{G}}$		${\mathrm{\Xi }}_{\mathit{H}}$
N	SPH	$p$ = 1	SPH	$p$ = 1
9	0.3487	0.2656	0.3376	0.2624
25	0.3136	0.1234	0.2885	0.2206
81	0.2456	0.1617	0.2024	0.1244
289	0.1540	0.0880	0.1215	0.0693
1089	0.0867	0.0403	0.0720	0.0266
4225	0.0621	0.0149	0.0605	0.0137
16641	0.0545	0.0054	0.0541	0.0046
66049	0.0537	0.0023	0.0540	0.0018

, where the RMSEs for the standard and the formulation with p = 1 are included, referring to the ${\mathrm{\Xi }}_G$ and ${\mathrm{\Xi }}_H$ data distributions. In

Table 2. RMSEs for ISPH, $f_h^{\left(0\right)}$ with p = 1. Data sites ${\mathrm{\Xi }}_G$.

N	${\mathit{f}}_{\mathit{h}}^{\left(0\right)}$	${\mathit{f}}_{\mathit{h}}^{\left(10\right)}$	${\mathit{f}}_{\mathit{h}}^{\left(100\right)}$	${\mathit{f}}_{\mathit{h}}^{\left(1000\right)}$
9	0.2656	0.1657	0.1455	0.1834
25	0.1234	0.1355	0.1156	0.0905
81	0.1617	0.0919	0.0525	0.0396
289	0.0880	0.0255	0.0081	0.0042
1089	0.0403	0.0030	2.91 $\times {10}^{-4}$	5.51 $\times {10}^{-5}$
4225	0.0149	9.94 $\times {10}^{-4}$	1.16 $\times {10}^{-4}$	1.29 $\times {10}^{-5}$

and

Table 3. RMSEs for the ISPH, $f_h^{\left(0\right)}$ with p = 1. Data sites ${\mathrm{\Xi }}_H$.

N	${\mathit{f}}_{\mathit{h}}^{\left(0\right)}$	${\mathit{f}}_{\mathit{h}}^{\left(10\right)}$	${\mathit{f}}_{\mathit{h}}^{\left(100\right)}$	${\mathit{f}}_{\mathit{h}}^{\left(1000\right)}$
9	0.2624	0.1626	0.1427	0.1280
25	0.2206	0.1331	0.1023	0.0839
81	0.1244	0.0603	0.0269	0.0167
289	0.0693	0.0133	0.0042	0.0021
1089	0.0266	0.0017	2.35 $\times {10}^{-4}$	4.60 $\times {10}^{-5}$
4225	0.0137	9.15 $\times {10}^{-4}$	1.27 $\times {10}^{-4}$	1.71 $\times {10}^{-5}$

, the error behavior adopting the iterative process ISPH, assuming $f_h^{\left(0\right)}$ with p = 1, is shown for ${\mathrm{\Xi }}_G$ and ${\mathrm{\Xi }}_H$ respectively. A significant reduction, for the two data sequences, can be appreciated by increasing N and the number of the iterations. In

Table 4. RMSEs for the E-ISPH, $f_h^{\left(0\right)}$ with p = 1. Data sites ${\mathrm{\Xi }}_G$.

N	${\mathit{f}}_{\mathit{h}}^{\left(0\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(10\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(20\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(30\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(40\right)}$
9	0.2656	0.1684	0.2239	0.2247	0.2247
25	0.1234	0.0963	0.1365	0.1245	0.1375
81	0.1617	0.0406	0.0241	0.0439	0.0503
289	0.0880	0.0052	0.0019	0.0022	0.0062
1089	0.0403	7.87 $\times {10}^{-5}$	4.18 $\times {10}^{-6}$	9.56 $\times {10}^{-7}$	3.19 $\times {10}^{-5}$
4225	0.0149	2.45 $\times {10}^{-5}$	3.84 $\times {10}^{-7}$	5.89 $\times {10}^{-8}$	3.99 $\times {10}^{-5}$

and

Table 5. RMSEs for the E-ISPH, $f_h^{\left(0\right)}$ with p = 1. Data sites ${\mathrm{\Xi }}_H$.

N	${\mathit{f}}_{\mathit{h}}^{\left(0\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(10\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(20\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(30\right)}$	${\tilde{\mathit{f}}}_{\mathit{h}}^{\left(40\right)}$
9	0.2624	0.1312	0.3210	0.3210	0.3210
25	0.2206	0.0861	0.2719	0.3173	0.3173
81	0.1244	0.0172	0.0545	0.0435	0.0446
289	0.0693	0.0023	0.0011	0.0009	0.0013
1089	0.0266	6.95 $\times {10}^{-5}$	2.64 $\times {10}^{-6}$	9.78 $\times {10}^{-7}$	7.43 $\times {10}^{-5}$
4225	0.0137	3.13 $\times {10}^{-5}$	1.74 $\times {10}^{-7}$	1.31 $\times {10}^{-8}$	3.17 $\times {10}^{-5}$

, the RMSEs refer to the enhanced iterative approach E-ISPH for ${\mathrm{\Xi }}_G$ and ${\mathrm{\Xi }}_H$ showing an accuracy comparable to ISPH requiring a reduced number of iterations. In Figure 2, Figure 3 and Figure 4 the RMSEs behavior is reported in a loglog plot comparing the SPH, ISPH and E-ISPH approaches. In Figure 5, the time (s), required by the ISPH and E-ISPH to reach a comparable accuracy in the approximation, is exhibited in a loglog plot too. All simulations have been executed with a processor 2.3 GHz Intel Core i9 8 core.

5. Conclusions

The iterative procedure adopted via residual iterations gives interesting results into SPH approximation avoiding matrix generation and without changes on the kernel function. A normalized version which guarantees the linear order of approximation is a valid strategy coupled in this paper with a faster approach requiring less number of iterations to achieve the desired accuracy. Work in extending the procedure to differential operators is in progress, so allowing one to adopt the method for a large variety of problems in the applied sciences.