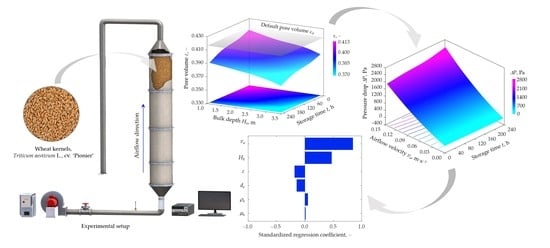
Influence of Self-Compaction on the Airflow Resistance of Aerated Wheat Bulks (Triticum aestivum L., cv. ‘Pionier’)
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Material and Sample Preparation
2.2. Characterization of Grain Physical Properties
2.3. Experimental Test Bench
2.4. Experimental Procedure
2.5. Semi-Empirical Modelling of Airflow Resistance
2.6. Statistical Analysis and Graphical Presentation
3. Results and Discussion
3.1. Characterization of Grain Physical Properties
3.2. Bulk Conditions during Experimentation
3.3. Determination of the Product Factor k
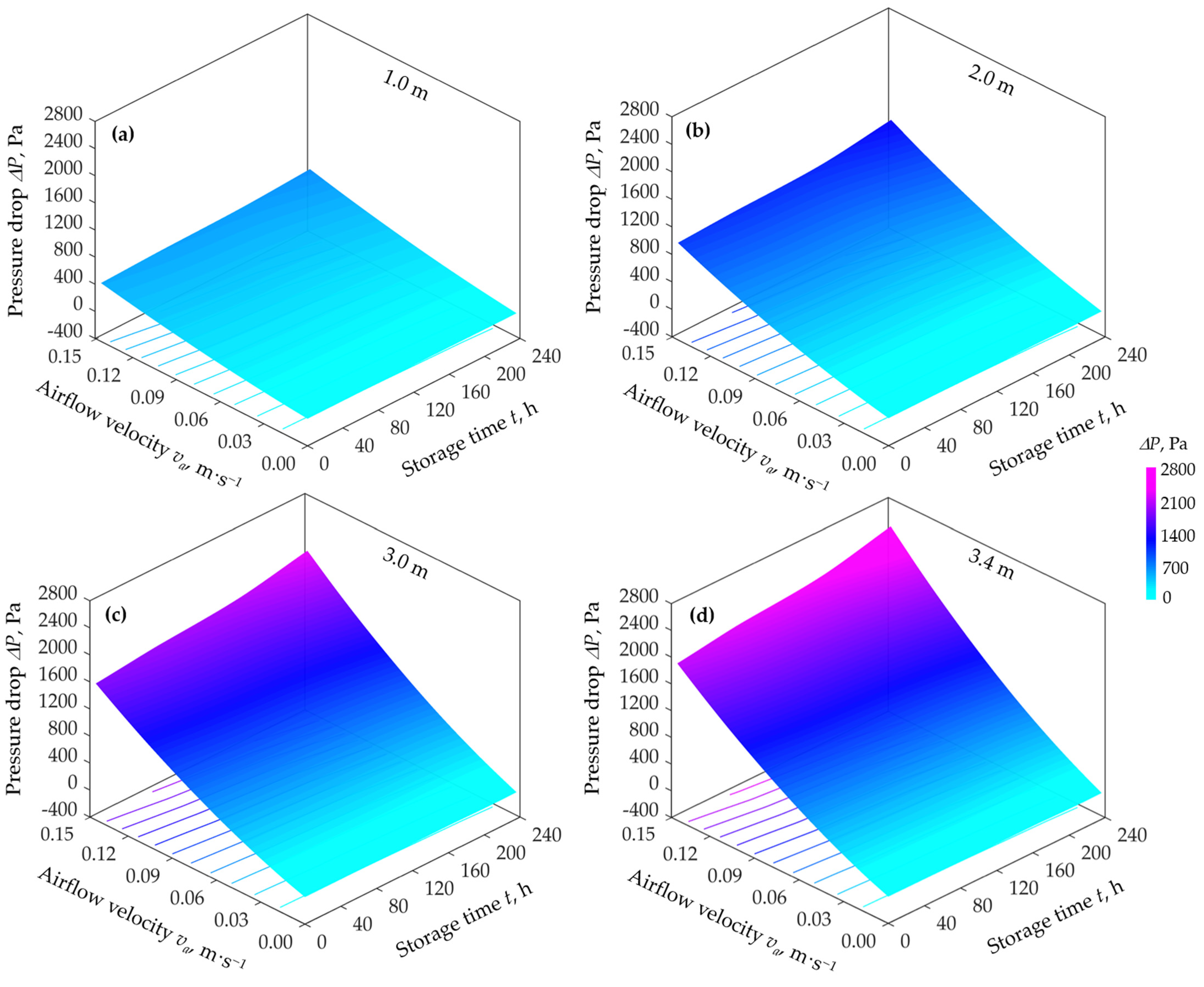
3.4. Influence of Self-Compaction on the Airflow Resistance
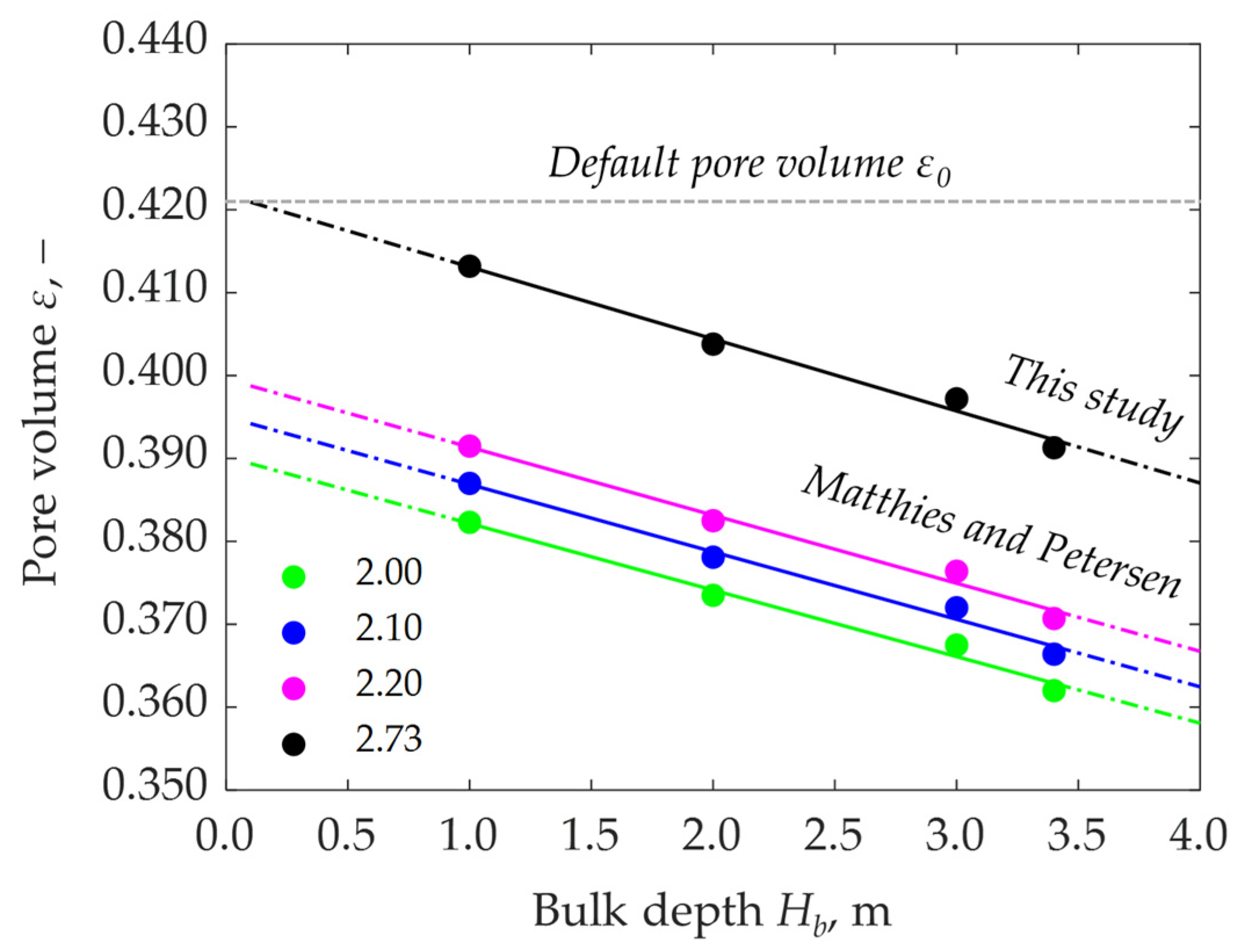
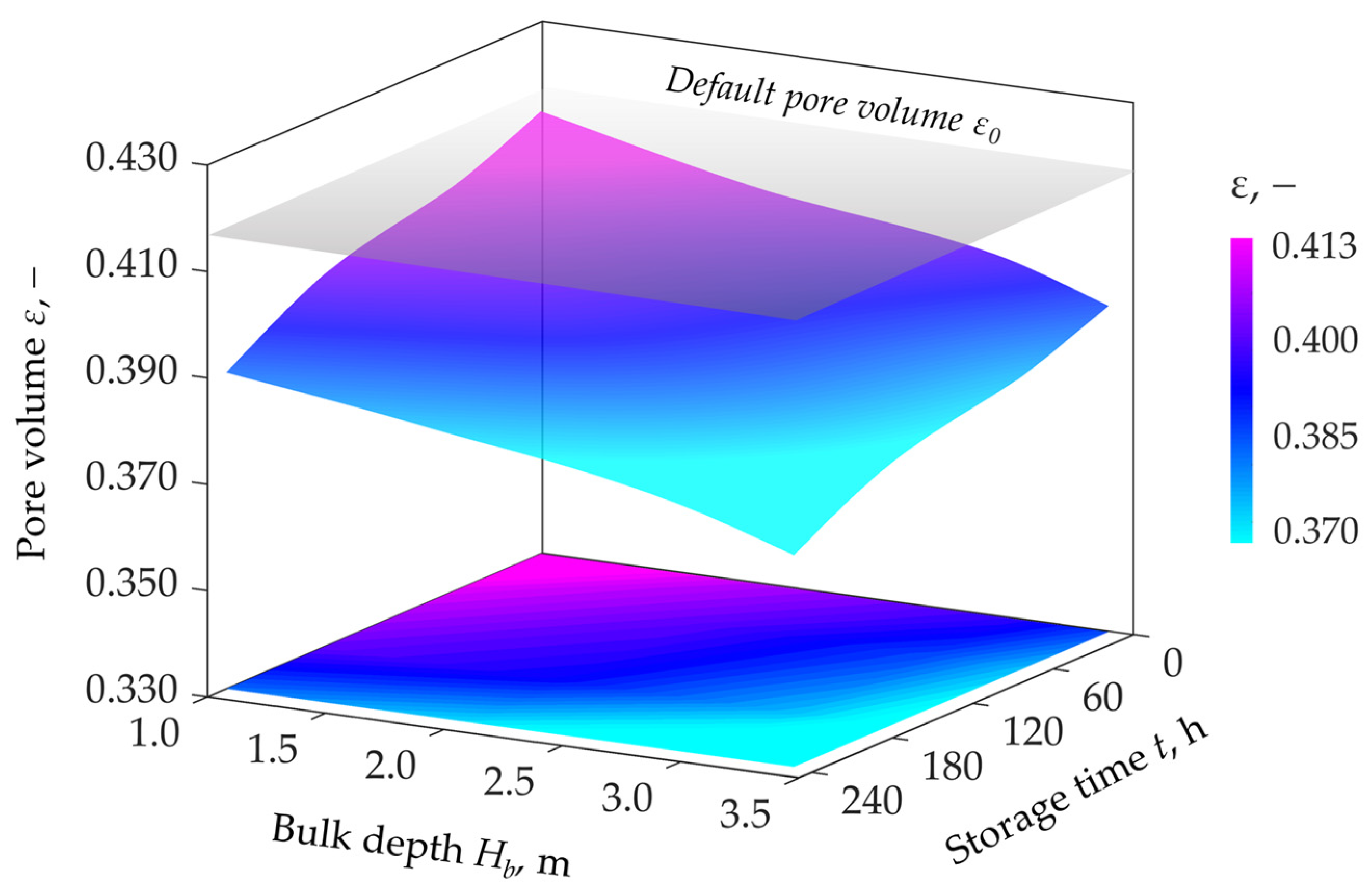
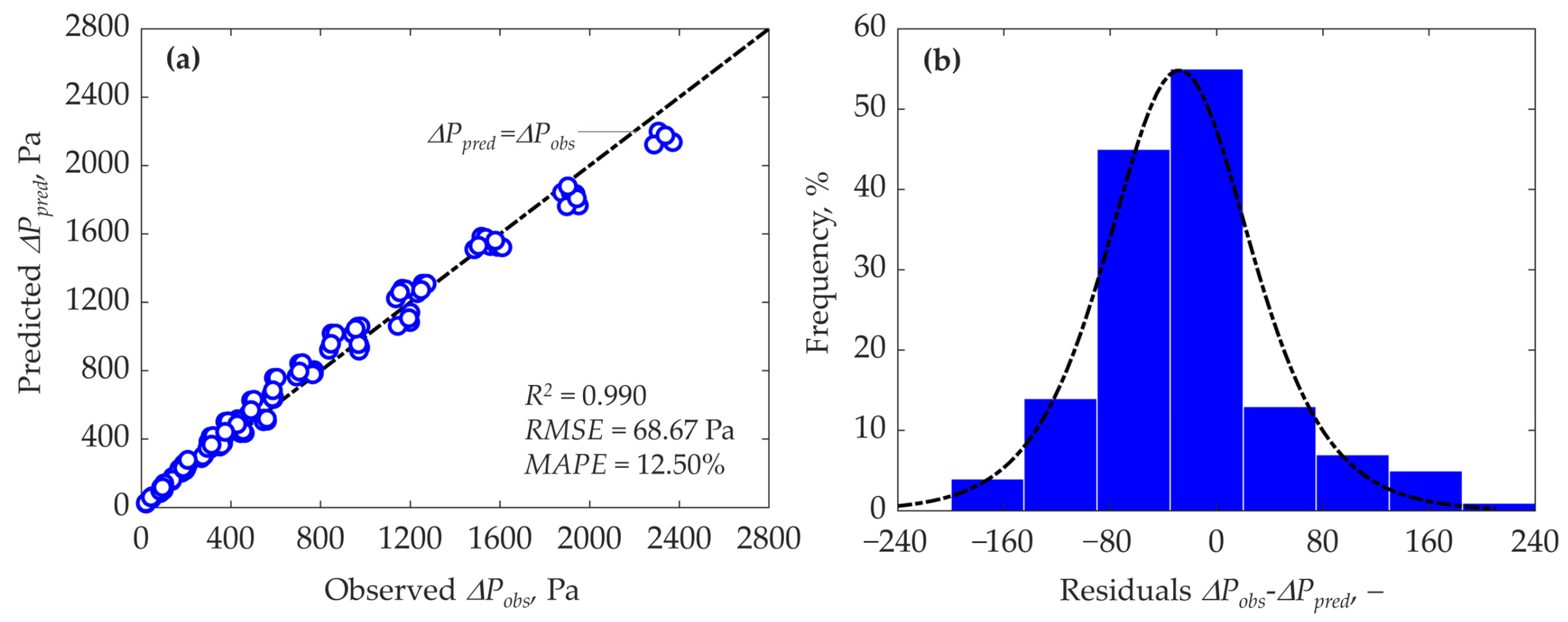
3.5. Modelling of Pore Volume Variation in Bulk
3.6. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a, c | Empirical constants, - |
| A | Kernel surface area, mm2 |
| da | Kernel arithmetic diameter, mm |
| de | Kernel equivalent diameter, mm |
| dg | Kernel geometric diameter, mm |
| d.b. | Dry basis, - |
| f | Fan frequency, Hz |
| Hb | Grain bulk depth, mm |
| L | Kernel length, mm |
| k | Product factor, - |
| ṁ | Air mass flow rate, kg·h−1 |
| m | Kernel unit mass, g |
| mc | Aggregate mass of kernels in the container, g |
| mgr | Mass of kernels soaked in toluene, g |
| mfl,tol | Mass of pycnometer flask filled with toluene, g |
| mgr,fl,tol | Mass of kernels, toluene solution and pycnometer flask, g |
| n | Number of observations, - |
| MAPE | Mean absolute percentage error, % |
| p | Probability level, - |
| Q | Air volume flow rate, m3·h−1 |
| R2 | Coefficient of determination, - |
| Ra | Kernel aspect ratio, - |
| Re | Reynolds number, - |
| RMSE | Root mean square error, Pa |
| t | Elapsed storage time, h |
| Ta | Air temperature, °C |
| T | Kernel thickness, mm |
| va | Airflow velocity, m·s−1 |
| V | Kernel unit volume, mm3 |
| Vb | Test bin volume, m3 |
| Vc | Container volume, m3 |
| Vp | Pycnometer volume, mm3 |
| W | Kernel width, mm |
| X | Moisture content, - |
| x,y | Independent and dependent variables in linear models, - |
| xa | Air absolute humidity, g·kg−1 |
| Δxa | Air saturation deficit, g·kg−1 |
| P | Pressure, Pa |
| ΔP | Pressure drop, Pa |
| ΔPobs | Observed pressure drop, Pa |
| ΔPpred | Predicted pressure drop, Pa |
| ε | Bulk pore volume, - |
| ε0 | Default pore volume, - |
| εmin | Pore volume at the highest bulk depth, - |
| ζ | Friction factor, - |
| ϑ | Kernel sphericity, % |
| φa | Air relative humidity, % |
| ω | Fan rotational speed, min−1 |
| μa | Air dynamic viscosity, kg·m−1·s−1 |
| ρa | Air density, kg·m−3 |
| ρb | Bulk density, kg·m−3 |
| ρb0 | Default bulk density, kg·m−3 |
| ρs | Solid density, kg·m−3 |
| ρtol | Toluene density, kg·m−3 |
Appendix A
| Storage Time t, h | Moisture Content X, kg·kg−1 d.b. | Temperature T, °C | Relative Humidity φa, % | Absolute Humidity xa, g·kg−1 | Saturation Deficit Δxa, g·kg−1 | Viscosity μa × 10−5, kg·m−1·s−1 | Density ρa, kg·m−3 |
|---|---|---|---|---|---|---|---|
| 1 | 0.123 ± 0.001 | 17.18 ± 0.09 | 39.83 ± 0.69 | 4.84 ± 0.07 | 2.85 ± 0.04 | 1.80 ± 0.00 | 1.22 ± 0.00 |
| 65 | - | 15.02 ± 0.10 | 39.54 ± 0.19 | 4.23 ± 0.02 | 2.65 ± 0.04 | 1.79 ± 0.00 | 1.23 ± 0.00 |
| 164 | - | 16.30 ± 0.02 | 40.87 ± 0.02 | 4.70 ± 0.01 | 2.72 ± 0.00 | 1.80 ± 0.00 | 1.22 ± 0.00 |
| 236 | 0.122 ± 0.001 | 12.29 ± 0.02 | 34.04 ± 0.02 | 3.01 ± 0.01 | 2.66 ± 0.00 | 1.78 ± 0.00 | 1.24 ± 0.00 |
References
- FAO. Food and Agriculture Data. Available online: http://www.fao.org/faostat/en/#data (accessed on 28 June 2022).
- Awika, J.M. Major cereal grains production and use around the world. In Advances in Cereal Science: Implications to Food Processing and Health Promotion; ACS Publications: Washington, DC, USA, 2011; pp. 1–13. [Google Scholar]
- Ziegler, V.; Paraginski, R.T.; Ferreira, C.D. Grain storage systems and effects of moisture, temperature and time on grain quality—A review. J. Stored Prod. Res. 2021, 91, 101770. [Google Scholar] [CrossRef]
- Anukiruthika, T.; Jian, F.; Jayas, D.S. Movement and behavioral response of stored product insects under stored grain environments—A review. J. Stored Prod. Res. 2021, 90, 101752. [Google Scholar] [CrossRef]
- Collins, D.A. A review on the factors affecting mite growth in stored grain commodities. Exp. Appl. Acarol. 2012, 56, 191–208. [Google Scholar] [CrossRef] [PubMed]
- Mesterházy, Á.; Oláh, J.; Popp, J. Losses in the Grain Supply Chain: Causes and Solutions. Sustainability 2020, 12, 2342. [Google Scholar] [CrossRef]
- Navarro, S.; Noyes, R.T. The Mechanics and Physics of Modern Grain Aeration Management; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Labuza, T.P. Sorption phenomena in foods: Theoretical and practical aspects. In Theory, Determination and Control of Physical Properties of Food Materials; Springer: Berlin, Germany, 1975; pp. 197–219. [Google Scholar]
- Lenovich, L.M. Survival and death of microorganisms as influenced by water activity. In Water Activity: Theory and Applications to Food, 1st ed.; Routledge: Oxfordshire, UK, 2017; pp. 119–136. [Google Scholar]
- Chakraverty, A.; Singh, R.P. Grain storage. In Postharvest Technology and Food Process Engineering; CRC Press: Boca Raton, FL, USA, 2014; pp. 131–157. [Google Scholar]
- Brooker, D.B.; Bakker-Arkema, F.W.; Hall, C.W. Drying and Storage of Grains and Oilseeds, 1st ed.; Springer Science & Business Media: New York, NY, USA, 1992. [Google Scholar]
- Giner, S.A.; Denisienia, E. Pressure drop through wheat as affected by air velocity, moisture content and fines. J. Agric. Eng. Res. 1996, 63, 73–85. [Google Scholar] [CrossRef]
- Kashaninejad, M.; Maghsoudlou, Y.; Khomeiri, M.; Tabil, L. Resistance to airflow through bulk pistachio nuts (Kalleghochi variety) as affected by moisture content, airflow rate, bed depth and fill method. Powder Technol. 2010, 203, 359–364. [Google Scholar] [CrossRef]
- Olatunde, G.; Atungulu, G.G.; Sadaka, S. CFD modeling of air flow distribution in rice bin storage system with different grain mass configurations. Biosyst. Eng. 2016, 151, 286–297. [Google Scholar] [CrossRef]
- Neethirajan, S.; Karunakaran, C.; Jayas, D.S.; White, N.D.G. X-ray Computed Tomography Image Analysis to explain the Airflow Resistance Differences in Grain Bulks. Biosyst. Eng. 2006, 94, 545–555. [Google Scholar] [CrossRef]
- Alagusundaram, K.; Jayas, D. Airflow resistance of grains and oilseeds. Postharvest News Inf. 1990, 1, 279–283. [Google Scholar] [CrossRef]
- Shedd, C.K. Resistance of grains and seeds to air flow. Agric. Eng. 1953, 34, 616–619. [Google Scholar]
- Hukill, W.; Ives, N. Radial airflow resistance of grain. Agric. Eng. 1955, 36, 332–335. [Google Scholar]
- Gunasekaran, S.; Jackson, C.Y. Resistance to airflow of grain sorghum. Trans. ASAE 1988, 31, 1237–1240. [Google Scholar] [CrossRef]
- Nimkar, P.M.; Chattopadhyay, P.K. PH—Postharvest Technology: Airflow Resistance of Green Gram. Biosyst. Eng. 2002, 82, 407–414. [Google Scholar] [CrossRef]
- Agullo, J.O.; Marenya, M.O. Airflow Resistance of Parchment Arabica Coffee. Biosyst. Eng. 2005, 91, 149–156. [Google Scholar] [CrossRef]
- Hunter, A.J. Pressure difference across an aerated seed bulk for some common duct and store cross-sections. J. Agric. Eng. Res. 1983, 28, 437–450. [Google Scholar] [CrossRef]
- Haque, E.; Ahmed, Y.N.; Deyoe, C.W. Static pressure drop in a fixed bed of grain as affected by grain moisture content. Trans. ASAE 1982, 25, 1095–1098. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow Through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1997, 75, S32–S48. [Google Scholar] [CrossRef]
- Burke, S.P.; Plummer, W.B. Gas flow through packed columns. Ind. Eng. Chem. 1928, 20, 1196–1200. [Google Scholar] [CrossRef]
- Patterson, R.J. Airflow-Pressure Drop Characteristics of Packed Beds of Biological Particles; Michigan State University: East Lansing, MI, USA, 1969. [Google Scholar]
- Li, W.; Sokhansanj, S. Generalized equation for airflow resistance of bulk grains with variable density, moisture content and fines. Dry. Technol. 1994, 12, 649–667. [Google Scholar] [CrossRef]
- Bern, C.J.; Charity, L.F. Airflow resistance characteristics of corn as influenced by bulk density. ASAE Pap. 1975, 48, 1137–1145. [Google Scholar]
- Leva, M. Fluidization; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Matthies, H.J.; Petersen, H. New data for calculating the resistance to air flow of stored granular materials. Trans. ASAE 1974, 17, 1144–1149. [Google Scholar] [CrossRef]
- Kumar, A.; Muir, W.E. Airflow resistance of wheat and barley affected by airflow direction, filling method and dockage. Trans. ASAE 1986, 29, 1423–1426. [Google Scholar] [CrossRef]
- Turner, A.P.; Montross, M.D.; McNeill, S.G.; Sama, M.P.; Casada, M.C.; Boac, J.M.; Bhadra, R.E.; Maghirang, R.G.; Thompson, S.A. Modeling the compressibility behavior of hard red wheat varieties. Trans. ASABE 2016, 59, 1029–1038. [Google Scholar] [CrossRef] [Green Version]
- Thompson, S.; McNeill, S.; Ross, I.; Bridges, T. Packing factors of whole grains in storage structures. Appl. Eng. Agric. 1987, 3, 215–221. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Q.; Yan, X.; Shi, C. Compressibility and equivalent bulk modulus of shelled corn. Biosyst. Eng. 2015, 140, 91–97. [Google Scholar] [CrossRef]
- Rocha, J.C.d.; Pohndorf, R.S.; Meneghetti, V.L.; Oliveira, M.d.; Elias, M.C. Effects of mass compaction on airflow resistance through paddy rice grains. Biosyst. Eng. 2020, 194, 28–39. [Google Scholar] [CrossRef]
- Molenda, M.; Montross, M.D.; McNeill, S.G.; Horabik, J. Airflow resistance of seeds at different bulk densities using Ergun’s equation. Trans. ASAE 2005, 48, 1137–1145. [Google Scholar] [CrossRef]
- Łukaszuk, J.; Molenda, M.; Horabik, J.; Szot, B.; Montross, M.D. Airflow resistance of wheat bedding as influenced by the filling method. Res. Agric. Eng. 2008, 54, 50. [Google Scholar] [CrossRef]
- AOAC. Official Methods of Analysis, 16th ed.; Association of Analytical Chemist: Arlington, VA, USA, 1998. [Google Scholar]
- Karaj, S.; Müller, J. Determination of physical, mechanical and chemical properties of seeds and kernels of Jatropha curcas L. Ind. Crops Prod. 2010, 32, 129–138. [Google Scholar] [CrossRef]
- Sirisomboon, P.; Kitchaiya, P.; Pholpho, T.; Mahuttanyavanitch, W. Physical and mechanical properties of Jatropha curcas L. fruits, nuts and kernels. Biosyst. Eng. 2007, 97, 201–207. [Google Scholar] [CrossRef]
- Mohsenin, N.N. Physical Properties of Plant and Animal Materials; Gordon & Breach Science Publishers Ltd.: Philadelphia, PA, USA, 1968. [Google Scholar]
- ASAE. ASAE D272: Resistance to airflow of grains, seeds, other agricultural products, and perforated metal sheets. Am. Soc. Agric. Biol. Eng. 2003, 3, 569–576. [Google Scholar]
- Miller, R.W. Flow Measurement Engineering Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Mühlbauer, W. Handbuch der Getreidetrocknung: Grundlagen und Verfahren; Agrimedia: Clenze, Germany, 2009. [Google Scholar]
- Tabatabaeefar, A. Moisture-dependent physical properties of wheat. Int. Agrophys. 2003, 17, 207–211. [Google Scholar]
- Karimi, M.; Kheiralipour, K.; Tabatabaeefar, A.; Khoubakht, G.; Naderi, M.; Heidarbeigi, K. The effect of moisture content on physical properties of wheat. Pak. J. Nutr. 2009, 8, 90–95. [Google Scholar] [CrossRef]
- Molenda, M.; Horabik, J. Mechanical Properties of Granular Agro-Materials and Food Powders for Industrial Practice. In Part I: Characterization of Mechanical Properties of Particulate Solids for Storage and Handling; Institute of Agrophysics Polish Academy of Sciences: Lublin, Poland, 2005; p. 145. [Google Scholar]
- Wang, D.; Dowell, F.E.; Lacey, R.E. Single wheat kernel size effects on near-infrared reflectance spectra and color classification. Cereal Chem. 1999, 76, 34–37. [Google Scholar] [CrossRef]
- Nelson, S. Moisture-Dependent Kernel- and Bulk-Density Relationships for Wheat and Corn. Trans. ASAE 1980, 23, 139–0143. [Google Scholar] [CrossRef]
- Petingco, M.C.; Casada, M.E.; Maghirang, R.G.; Thompson, S.A.; McNeill, S.G.; Montross, M.D.; Turner, A.P. Influence of kernel shape and size on the packing ratio and compressibility of hard red winter wheat. Trans. ASABE 2018, 61, 1437–1448. [Google Scholar] [CrossRef]
- Markowski, M.; Żuk-Gołaszewska, K.; Kwiatkowski, D. Influence of variety on selected physical and mechanical properties of wheat. Ind. Crops Prod. 2013, 47, 113–117. [Google Scholar] [CrossRef]
- Gürsoy, S.; Güzel, E. Determination of physical properties of some agricultural grains. Res. J. Appl. Sci. Eng. Technol. 2010, 2, 492–498. [Google Scholar]
- Jayas, D.S.; Cenkowski, S. Grain Property Values and Their Measurement. In Handbook of Industrial Drying, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Muir, W.; Sinha, R. Physical properties of cereal and oilseed cultivars grown in western Canada. Can. Agric. Eng. 1988, 30, 51–55. [Google Scholar]
- Kraszewski, A.W. Wheat moisture content and bulk density determination by microwave parameters measurement. Can. Agric. Eng. 1992, 34, 327–335. [Google Scholar]
- Petingco, M.C.; Casada, M.E.; Maghirang, R.G.; Thompson, S.A.; Turner, A.P.; McNeill, S.G.; Montross, M. Discrete Element Method Simulation of Wheat Bulk Density as Affected by Grain Drop Height and Kernel Size Distribution. J. ASABE 2022, 65, 555–566. [Google Scholar] [CrossRef]
- Stephens, L.E.; Foster, G.H. Grain Bulk Properties as Affected by Mechanical Grain Spreaders. Trans. ASAE 1976, 19, 354–0358. [Google Scholar] [CrossRef]
- White, F.M.; Majdalani, J. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Bakker-Arkema, F.W.; Patterson, R.J.; Bickert, W.G. Static pressure-airflow relationships in packed beds of granular biological materials such as cherry pits. Trans. ASAE 1969, 12, 134–0136. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Q.; Shi, C.; Yan, X. Model for the prediction of grain density and pressure distribution in hopper-bottom silos. Biosyst. Eng. 2017, 163, 159–166. [Google Scholar] [CrossRef]
- Guillard, F.; Golshan, P.; Shen, L.; Valdes, J.R.; Einav, I. Dynamic patterns of compaction in brittle porous media. Nat. Phys. 2015, 11, 835–838. [Google Scholar] [CrossRef]
- Grundas, S.; Szot, B.; Wozniak, W. Variability of the porosity of cereal grain layer under the influence of static loading. Zesz. Probl. Postępów Nauk. Rol. 1978, 203, 33–40. [Google Scholar]
- Jayas, D.S.; Sokhansanj, S.; Moysey, E.B.; Barber, E.M. Airflow resistance of canola (rapeseed). Trans. ASAE 1987, 30, 1484–1488. [Google Scholar] [CrossRef]
- Kay, R.L.; Bern, C.J.; Hurburgh, C.R., Jr. Horizontal and Vertical Airflow Resistance of Shelled Corn at Various Bulk Densities. Trans. ASAE 1989, 32, 733–0736. [Google Scholar] [CrossRef]
- Siebenmorgen, T.J.; Jindal, V.K. Airflow resistance of rough rice as affected by moisture content, fines concentration and bulk density. Trans. ASAE 1987, 30, 1138–1143. [Google Scholar] [CrossRef] [Green Version]
- Haque, E. Void fraction as a function of depth and pressure drops of packed beds of porous media formed by granular materials. Trans. ASABE 2011, 54, 2239–2243. [Google Scholar] [CrossRef]
- Khatchatourian, O.A.; Savicki, D.L. Mathematical Modelling of Airflow in an Aerated Soya Bean Store under Non-uniform Conditions. Biosyst. Eng. 2004, 88, 201–211. [Google Scholar] [CrossRef]
- Gao, M.; Cheng, X.; Du, X. Simulation of bulk density distribution of wheat in silos by finite element analysis. J. Stored Prod. Res. 2018, 77, 1–8. [Google Scholar] [CrossRef]



| Source | Year | Model Type | Applicability | Comments | |
|---|---|---|---|---|---|
| Velocity va, m·s−1 | Type of Grains | ||||
| Ergun [24] | 1952 | Semi-empirical | ≥0.01 | Maize, rice, sorghum, wheat | Covers both laminar and turbulent flow; suitable for spherical particles |
| Shedd [17] | 1953 | Empirical | 0.005–0.30 | Barley, maize, oat, rice, sorghum, soybean, wheat | Appropriate for low airflow velocities and uncompacted grain bulk; outperformance at high velocities |
| Hukill and Ives [18] | 1955 | Empirical | 0.0003–1.0 | Barley, maize, oat, rice, sorghum, soybean, wheat | Encompasses a wide range of velocities; limited to specific grain and air conditions |
| Leva [30] | 1959 | Semi-empirical | ≥0.0001 | Barley, maize, oat, wheat | Tedious to solve; includes a friction-factor for the state-of-flow and a shape factor for non-spherical shape of grains |
| Patterson [27] | 1969 | Semi-empirical | 0.05–0.61 | Beans, maize | Adjusted model for grains with different size distributions and shape irregularities |
| Matthies and Petersen [31] | 1974 | Semi-empirical | 0.02–0.61 | Barley, maize, rice, rye, wheat | Established for high bulks; considers several influencing parameters |
| Bern and Charity [29] | 1975 | Semi-empirical | 0.015–0.60 | Maize | Easy to solve; considers solely pore volume and airflow velocity; limited to maize |
| Haque, Ahmed and Deyoe [23] | 1982 | Empirical | 0.01–0.22 | Maize, sorghum, wheat | Includes the effect of moisture content on the calculation basis |
| Hunter [22] | 1983 | Empirical | 0.006–0.21 | Barley, maize, oat, rice, sorghum, soybean, wheat | Better fit compared to Shedd; considers the non-uniform nature of grain bulks; lacks insight into parameters affecting airflow resistance |
| Li and Sokhansanj [28] | 1992 | Semi-empirical | 0.0001–0.90 | Barley, maize, oat, wheat | Similar to Ergun; suitable for grains; established for a wide range of airflow velocities |
| Frequency | Rotational Speed | Airflow Velocity | Mass Flow Rate | Volume Flow Rate |
|---|---|---|---|---|
| f, Hz | ω, min−1 | va, m·s−1 | ṁ, kg·h−1 | Q, m3·h−1 |
| 10.0 | 578 | 0.011 ± 0.000 | 8.57 ± 0.36 | 7.00 ± 0.29 |
| 15.0 | 867 | 0.021 ± 0.001 | 20.15 ± 0.96 | 16.46 ± 0.79 |
| 20.0 | 1156 | 0.037 ± 0.004 | 32.93 ± 3.40 | 26.90 ± 2.78 |
| 25.0 | 1445 | 0.056 ± 0.005 | 47.48 ± 4.25 | 38.79 ± 3.47 |
| 30.0 | 1734 | 0.074 ± 0.006 | 61.37 ± 4.66 | 50.14 ± 3.81 |
| 35.0 | 2023 | 0.092 ± 0.006 | 74.99 ± 5.04 | 61.27 ± 4.12 |
| 40.0 | 2312 | 0.109 ± 0.008 | 88.14 ± 6.28 | 72.01 ± 5.14 |
| 45.0 | 2601 | 0.125 ± 0.008 | 100.78 ± 6.61 | 82.34 ± 5.40 |
| 50.0 | 2890 | 0.141 ± 0.010 | 113.16 ± 8.37 | 92.45 ± 6.84 |
| Properties | Unit | Value |
|---|---|---|
| Length L | mm | 6.87 ± 0.25 |
| Width W | mm | 3.75 ± 0.22 |
| Thickness T | mm | 3.11 ± 0.17 |
| Arithmetic diameter da | mm | 4.57 ± 0.15 |
| Geometric diameter dg | mm | 4.30 ± 0.15 |
| Equivalent diameter de | mm | 4.49 ± 0.14 |
| Aspect ratio Ra | - | 0.55 ± 0.03 |
| Sphericity ϑ | % | 62.72 ± 1.94 |
| Surface area A | mm2 | 64.06 ± 5.42 |
| Volume V | mm3 | 41.95 ± 4.34 |
| Unit mass m | g | 0.06 ± 0.01 |
| Bulk density ρb0 | kg·m−3 | 782.46 ± 6.68 |
| Solid density ρs | kg·m−3 | 1351.40 ± 4.62 |
| Pore volume ε0 | - | 0.421 ± 0.07 |
| Product Factor k, - | Mathematical Model | R2, - |
|---|---|---|
| 2.00 | y = −8.027 × 10−3 x + 0.390 | 0.986 |
| 2.10 | y = −8.141 × 10−3 x + 0.395 | 0.986 |
| 2.20 | y = −8.215 × 10−3 x + 0.400 | 0.985 |
| 2.73 | y = −8.693 × 10−3 x + 0.422 | 0.986 |
| Storage Time t, h | Bulk Depth Hb, m | Pore Volume ε, - | Bulk Density ρb, kg·m−3 | Statistical Indicators | ||
|---|---|---|---|---|---|---|
| R2, - | RMSE, Pa | MAPE, % | ||||
| 1.0 | 1.0 | 0.413 | 793.00 | 0.995 | 15.18 | 8.21 |
| 2.0 | 0.404 | 805.70 | 0.995 | 33.28 | 8.32 | |
| 3.0 | 0.397 | 814.62 | 0.995 | 52.39 | 7.19 | |
| 3.4 | 0.391 | 822.60 | 0.996 | 61.93 | 7.62 | |
| 65.0 | 1.0 | 0.406 | 802.33 | 0.983 | 29.19 | 14.75 |
| 2.0 | 0.400 | 811.38 | 0.983 | 62.74 | 15.12 | |
| 3.0 | 0.391 | 822.46 | 0.983 | 100.65 | 14.40 | |
| 3.4 | 0.385 | 830.98 | 0.982 | 123.77 | 13.97 | |
| 164.0 | 1.0 | 0.400 | 810.98 | 0.987 | 26.58 | 16.16 |
| 2.0 | 0.395 | 817.73 | 0.987 | 54.16 | 14.44 | |
| 3.0 | 0.385 | 831.11 | 0.987 | 89.30 | 13.28 | |
| 3.4 | 0.379 | 838.95 | 0.987 | 106.91 | 13.66 | |
| 236.0 | 1.0 | 0.390 | 825.03 | 0.993 | 21.04 | 14.61 |
| 2.0 | 0.383 | 833.27 | 0.993 | 45.24 | 15.11 | |
| 3.0 | 0.375 | 844.08 | 0.993 | 68.35 | 10.66 | |
| 3.4 | 0.370 | 851.65 | 0.993 | 84.17 | 12.75 | |
| Storage Time t, h | Mathematical Model | R2, - |
|---|---|---|
| 1 | 0.987 | |
| 65 | 0.977 | |
| 164 | 0.963 | |
| 236 | 0.980 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramaj, I.; Schock, S.; Karaj, S.; Müller, J. Influence of Self-Compaction on the Airflow Resistance of Aerated Wheat Bulks (Triticum aestivum L., cv. ‘Pionier’). Appl. Sci. 2022, 12, 8909. https://doi.org/10.3390/app12178909
Ramaj I, Schock S, Karaj S, Müller J. Influence of Self-Compaction on the Airflow Resistance of Aerated Wheat Bulks (Triticum aestivum L., cv. ‘Pionier’). Applied Sciences. 2022; 12(17):8909. https://doi.org/10.3390/app12178909
Chicago/Turabian StyleRamaj, Iris, Steffen Schock, Shkelqim Karaj, and Joachim Müller. 2022. "Influence of Self-Compaction on the Airflow Resistance of Aerated Wheat Bulks (Triticum aestivum L., cv. ‘Pionier’)" Applied Sciences 12, no. 17: 8909. https://doi.org/10.3390/app12178909
APA StyleRamaj, I., Schock, S., Karaj, S., & Müller, J. (2022). Influence of Self-Compaction on the Airflow Resistance of Aerated Wheat Bulks (Triticum aestivum L., cv. ‘Pionier’). Applied Sciences, 12(17), 8909. https://doi.org/10.3390/app12178909