Research on the Dual-Objective Scheduling of the Pipeline Path of Liquid Terminal Resources Based on a Hybrid Algorithm
Abstract
:1. Introduction
- (1)
- PAVP is proposed, highlighting the scarcity of research on internal scheduling issues at liquid ports, which primarily focus on export and import operations.
- (2)
- A dual-objective model for the PAVP is formulated, aiming to minimize the total cost of handling within the port and the overall vessel time at the port, while ensuring operational safety.
- (3)
- An improved NSGA-II-Dijkstra (INIIDA) is proposed to address the PAVP. This hybrid algorithm integrates NSGA-II with Dijkstra’s algorithm to solve the PAVP. Then the hybrid algorithm is ameliorated by the adaptive dynamic probability based on the Pareto level and heaps in the shortest path, making the algorithm adaptable to the PAVP.
2. Literature Review
2.1. Research on Pipelines
2.2. Related Algorithms
2.3. Research Overview
3. Problem Definition and Optimization Model
3.1. Problem Definition
3.2. Model Formulation
3.2.1. Basic Assumptions
- (1)
- The type of liquid cargo, carrying capacity, handling process requirements and other information loaded of the arriving vessel in a planning cycle are known. The port production operation plan must collect this information before the vessel arrives at the port.
- (2)
- Only the unloading path of liquid cargo is considered, and the cargo of pipeline is flowed in a single direction.
- (3)
- When the vessel reaches at the designated berth, before the cargo is unloaded, the oil sampling and analysis should be carried out in the cargo hold to determine the quality of the cargo and the fuel quantity should be calculated. Unloading operations shall not be carried out until the oil quantity calculation and oil sample analysis are completed. The unloading time is calculated from the initiation of the oil transfer arm’s operation until it ceases. The early sampling time is included in the preparation and handling duration of the oil transfer arm.
- (4)
- A vessel may be carrying multiple types of cargo at the same time, and unloading one type of cargo counts as one operation. And each type of cargo on the same vessel is carried out only once per operation.
- (5)
- The flow velocity of liquid cargo in the pipeline is constant.
- (6)
- The inner diameter of all pipelines is constant, i.e., the cross-sectional area is uniform.
- (7)
- The time required for the valve to open or close is not considered, and the time for liquid cargo to wait for the valve to open is not considered. Only the number of valve operations is calculated. Valves are assumed to be initially fully closed.
- (8)
- Long-distance pipeline docking and transshipment are not considered; only the internal transportation from the berth to the oil storage tank within the terminal is included. The vessel’s onboard pump is assumed to provide sufficient pressure for unloading from the vessel to the tank.
- (9)
- Operations such as cargo oil sweeping, checking bilge oil levels, and crude oil washing are considered part of the pipeline oil circuit emptying time.
3.2.2. Symbol Description
3.2.3. PAVP Model
4. INIIDA
- Step 1:
- Encode the number of oil transfer arms and number of oil tanks into two subchromosomes. Generate an initial population of twenty distinct chromosomes randomly, specifying the quantities and specific assignments of oil transfer arms and tanks per vessel in an operational planning cycle for the genetic algorithm;
- Step 2:
- Perform non-dominated sorting of the initial population and determine dynamic crossover and mutation probabilities;
- Step 3:
- Select two chromosomes from a vessel for crossover. Randomly select two vessels in a plan for single-point crossover, creating two new chromosomes to complete a generational crossover;
- Step 4:
- Choose one chromosome from a vessel for mutation. Randomly select a chromosome in a plan to form a new chromosome for mutation;
- Step 5:
- Compute the shortest path for each chromosome based on chromosome characteristics and valve distances, utilizing the Dijkstra algorithm;
- Step 6:
- Evaluate fitness and ensure consistency between parents and offspring. Discrepancies between parents and offspring are managed to maintain solution validity while promoting genetic diversity within the population;
- Step 7:
- Parent and child confluence, Pareto level is calculated by nondominated ordering;
- Step 8:
- Dynamically adjust crossover probability of parents and mutation probability of offspring based on their Pareto levels within the population. This adjustment aims to enhance individual performance, favoring greater crossover probabilities;
- Step 9:
- Integrate Pareto levels into the next generation starting from the top level until the population size meets the required level, using crowding levels for selection;
- Step 10:
- Check termination conditions to determine if the algorithm should end. If conditions are met, terminate; otherwise, return to Step 3.
4.1. Population Initialization and Chromosome Encoding
4.2. Crossover and Mutation
4.3. Adaptive Dynamic Probabilities Based on Pareto Level
4.4. Optimizing Dijkstra with Heaps
5. Experiments and Analysis
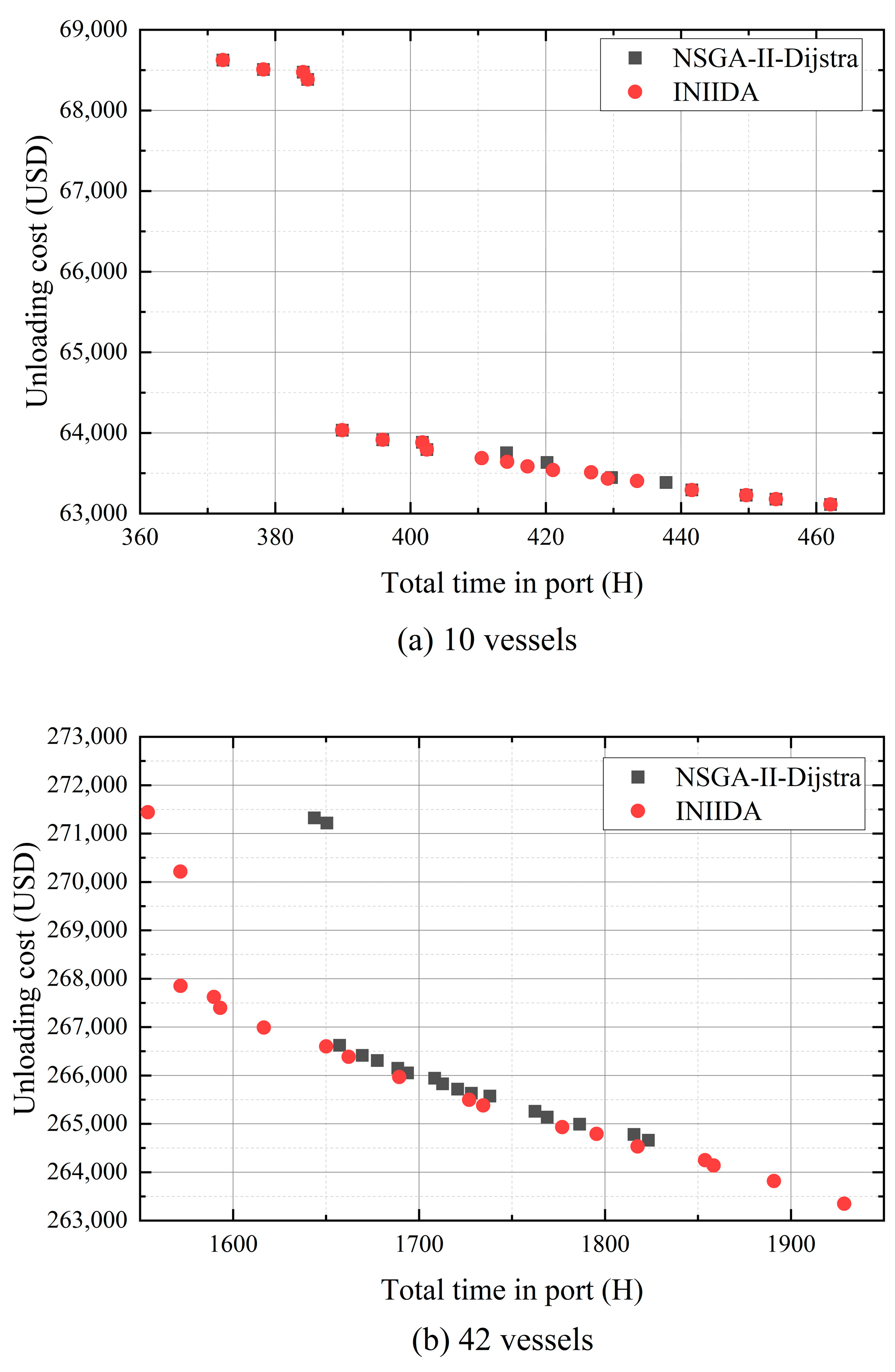
5.1. Small-Scale Berths
5.2. Mixed Berths
5.3. Algorithm Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Russo, F.; Musolino, G. Industrial and oil ports: Case studies and theoretical approaches. Transp. Res. Pro. 2023, 69, 703–710. [Google Scholar] [CrossRef]
- Suffia, I.; Locatelli, A.M.; Romano, M. Oil transportation: Eni’s fleet, Italian ports and pipelines, 1950–1980. Int. J. Marit. Hist. 2021, 32, 900–927. [Google Scholar] [CrossRef]
- Elena, K. Analysis of the interconnected development potential of the oil, gas and transport industries in the Russian Arctic. Energies 2023, 16, 3124. [Google Scholar] [CrossRef]
- Foroni, C.; Stracca, L. The shale oil revolution and the global oil supply curve. J. Appl. Econ. 2023, 38, 370–387. [Google Scholar] [CrossRef]
- Peng, P.; Claramunt, C.; Cheng, S.F.; Lu, F. How Does a Port Build Influence? Diffusion Patterns in Global Oil Transportation. Sensors 2022, 22, 8595. [Google Scholar] [CrossRef]
- Zhou, Y.M.; Wang, Y.; Yang, L.K.; Kong, Q.; Zhang, H.X. Microbial degradation mechanisms of surface petroleum contaminated seawater in a typical oil trading port. Environ. Pollut. 2023, 324, 121420. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.Y.; Song, Y.H.; Zhang, X.S.; Dong, L.J.; Xi, Y.C.; Zeng, D.Z.; Liu, Q.L.; Zhang, H.L.; Zhang, Z.; Yan, R.; et al. Evolution of corrosion prediction models for oil and gas pipelines: From empirical-driven to data-driven. Eng. Fail. Anal. 2023, 146, 107097. [Google Scholar] [CrossRef]
- Chen, P.C.; Li, R.; Jia, G.M.; Lan, H.; Fu, K.; Liu, X.B. A Decade review of the art of inspection and monitoring technologies for long-distance oil and gas pipelines in permafrost areas. Energies 2023, 16, 1751. [Google Scholar] [CrossRef]
- Mgbemena, C.E.; Onuoha, D.O.; Godwin, H.C. Development of a novel virtual reality-enabled remote monitoring device for maintenance of cathodic protection systems on oil and gas pipelines. Sci. Rep. 2023, 13, 15874. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.H.; Liao, K.X.; Li, X.X.; He, G.X.; Xia, F.; Zeng, Q. Collaborative detection and on-line monitoring of pipeline stress in oil and gas stations. Meas. Sci. Technol. 2022, 33, 105001. [Google Scholar] [CrossRef]
- Yan, Y.; Xiong, G.L.; Zhou, J.J.; Wang, R.H.; Huang, W.Y.; Yang, M.; Wang, R.C.; Geng, D.X. A whole process risk management system for the monitoring and early warning of slope hazards affecting gas and oil pipelines. Front. Earth Sci. 2022, 9, 812527. [Google Scholar] [CrossRef]
- Xu, C.X.; Wu, J.; Feng, H.L.; Ibrom, A.; Zeng, Q.; Zhang, J.F.; Li, N.; Hu, Q. Operation of off-grid power supply system using IoT monitoring platform for oil and gas pipeline based on RESOC. CSEE J. Power Energy Syst. 2020, 6, 12–21. [Google Scholar]
- Salman, A.; Ashraf, A.; Qaisar, S.B.; Afridi, M.K.; Saeed, H.; Rashid, S.; Felemban, E.A.; Sheikh, A.A. SimpliMote: A wireless sensor network monitoring platform for oil and gas pipelines. IEEE Syst. J. 2018, 12, 778–789. [Google Scholar]
- Chen, X.L.; Wang, M.Q.; Wang, B.; Hao, H.D.; Shi, H.L.; Wu, Z.N.; Chen, J.X.; Gai, L.M.; Tao, H.C.; Zhu, B.K.; et al. Energy consumption reduction and sustainable development for oil & gas transport and storage engineering. Energies 2023, 16, 1775. [Google Scholar] [CrossRef]
- Zhang, H.R.; Liang, Y.T.; Liao, Q.; Gao, J.; Yan, X.H.; Zhang, W. Mixed-time mixed-integer linear programming for optimal detailed scheduling of a crude oil port depot. Chem. Eng. Res. Des. 2018, 137, 434–451. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Wu, N.Q.; Li, Z.W.; Qu, T. A novel solution approach to a priority-slot-based continuous-time mixed integer nonlinear programming formulation for a crude-oil scheduling problem. Ind. Eng. Chem. Res. 2016, 55, 10955–10967. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Zhang, H.R.; Qiu, R.; Liang, Y.T.; Wu, G.M.; Xiang, C.C.; Yan, X.H. A hybrid time MILP model for the pump scheduling of multi-product pipelines based on the rigorous description of the pipeline hydraulic loss changes. Comput. Chem. Eng. 2019, 121, 174–199. [Google Scholar] [CrossRef]
- Cano-Acosta, A.; Fontecha, J.; Velasco, N.; Muñoz-Giraldo, F. Shortest path algorithm for optimal sectioning of hydrocarbon transport pipeline. IFAC 2016, 49, 532–537. [Google Scholar] [CrossRef]
- Yang, Z.M.; Su, H.; Du, X.K.; Zio, E.; Xiang, Q.; Peng, S.L.; Fan, L.; Faber, M.H.; Zhang, J.J. Supply resilience assessment of natural gas pipeline network systems. J. Clean. Prod. 2023, 385, 135654. [Google Scholar] [CrossRef]
- Dbouk, H.M.; Hayek, H.; Ghorayeb, K. Modular approach for optimal pipeline layout. J. Pet. Sci. Eng. 2020, 197, 107934. [Google Scholar] [CrossRef]
- Kang, J.Y.; Lee, B.S. Optimisation of pipeline route in the presence of obstacles based on a least cost path algorithm and laplacian smoothing. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 492–498. [Google Scholar] [CrossRef]
- Nasiri, M.M.; Khaleghi, A.; Govindan, K.; Bozorgi-Amiri, A. Sustainable hierarchical multi-modal hub network design problem: Bi-objective formulations and solution algorithms. Oper. Res. 2023, 23, 35. [Google Scholar] [CrossRef]
- Wang, Y.C.; Shi, G.Y.; Hirayama, K. Many-objective container stowage optimization based on improved NSGA-III. J. Mar. Sci. Eng. 2022, 10, 517. [Google Scholar] [CrossRef]
- Li, J.J.; Zhang, X.Y.; Yang, B.D.; Wang, N.N. Vessel traffic scheduling optimization for restricted channel in ports. Comput. Ind. Eng. 2021, 152, 107014. [Google Scholar] [CrossRef]
- Zhong, H.L.; Zhang, Y.G.; Gu, Y.M. A bi-objective green tugboat scheduling problem with the tidal port time windows. Transp. Res. D Transp Environ. 2022, 110, 103409. [Google Scholar] [CrossRef]
- Shi, J.T.; Li, H.D. Operational planning of international freight trains considering the dynamic demands and capacities of border ports. Comput. Ind. Eng. 2023, 185, 109658. [Google Scholar] [CrossRef]
- Duan, Y.; Ren, H.; Xu, F.; Yang, X.; Meng, Y. Bi-Objective Integrated Scheduling of Quay Cranes and Automated Guided Vehicles. J. Mar. Sci. Eng. 2023, 11, 1492. [Google Scholar] [CrossRef]
- Jiang, X.; Zhong, M.; Shi, J.; Li, W.; Sui, Y.; Dou, Y. Overall Scheduling Model for Vessels Scheduling and Berth Allocation for Ports with Restricted Channels That Considers Carbon Emissions. J. Mar. Sci. Eng. 2022, 10, 1757. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.H.; Yuan, Y.B. Modified NSGA-II for solving continuous berth allocation problem: Using multiobjective constraint-handling strategy. J. IEEE Trans. Cybern. 2017, 47, 2885–2895. [Google Scholar] [CrossRef] [PubMed]
- Silveira, P.; Teixeira, Â.P.; Soares, C.G. AIS based shipping routes using the Dijkstra algorithm. TransNav Int. J. Mar. Nav. Saf. Sea Transp. 2019, 13, 565–571. [Google Scholar] [CrossRef]
- Baeza, D.; Ihle, C.F.; Ortiz, J.M. A comparison between ACO and Dijkstra algorithms for optimal ore concentrate pipeline routing. J. Clean. Prod. 2017, 144, 149–160. [Google Scholar] [CrossRef]
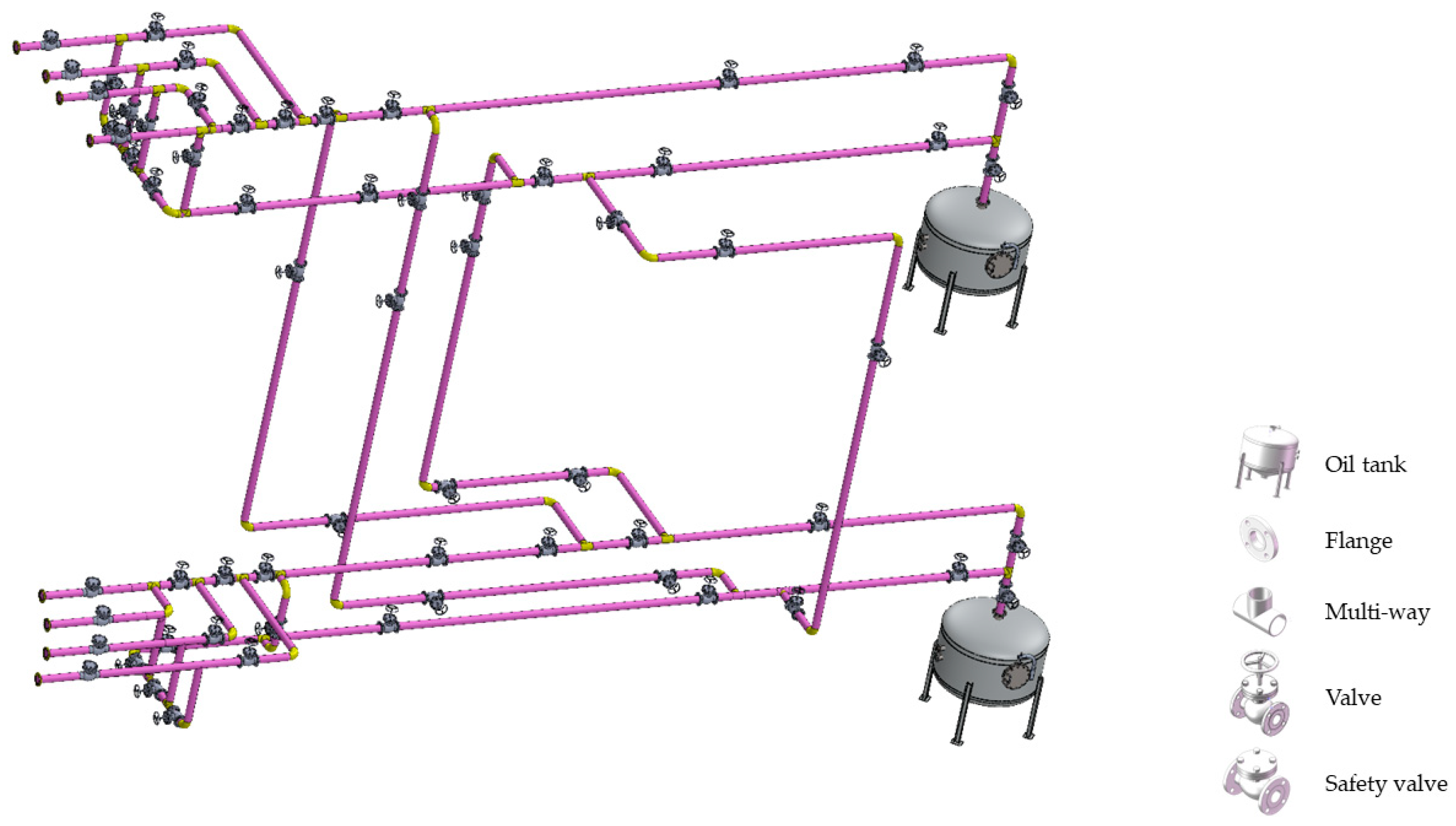
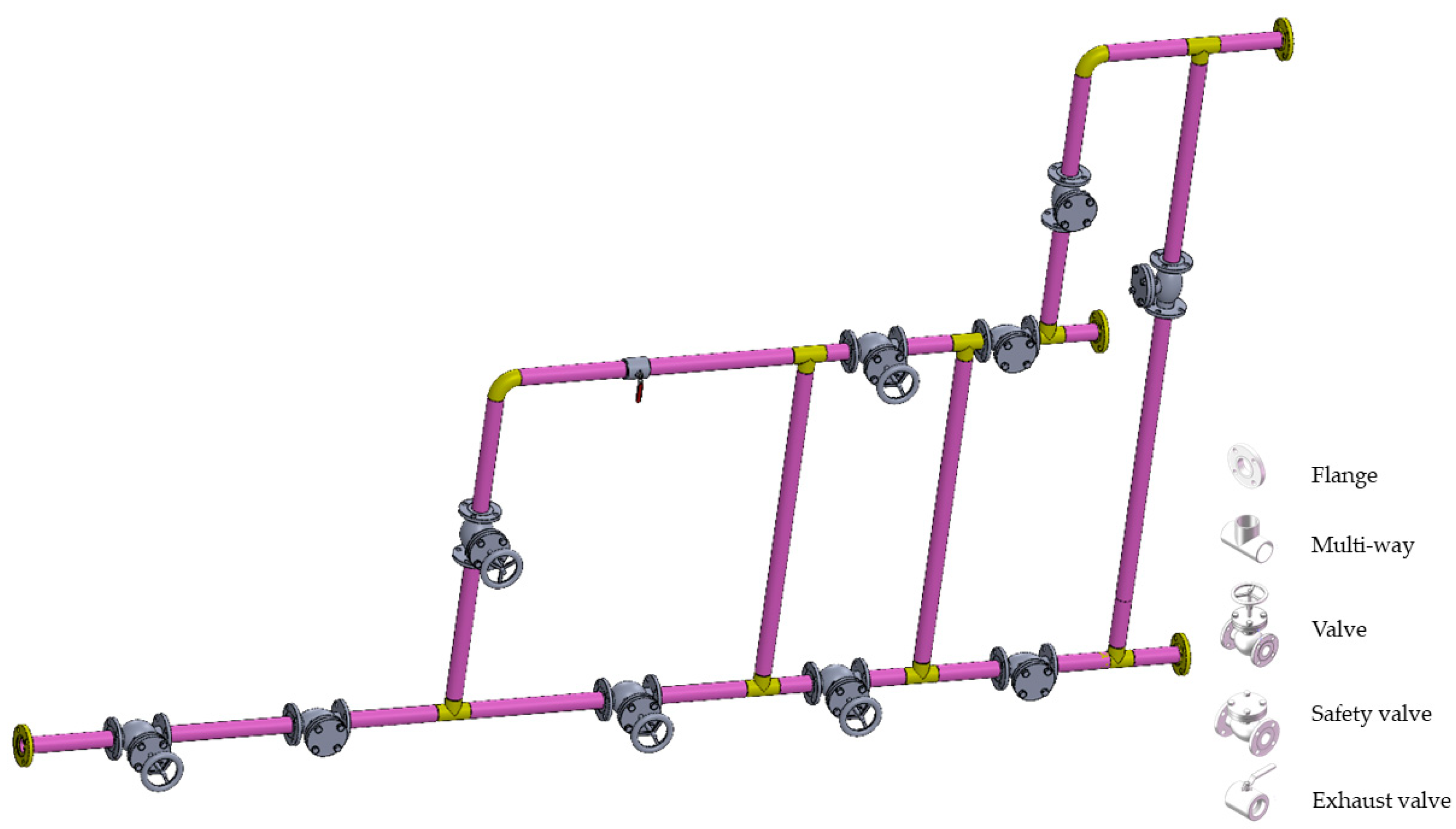

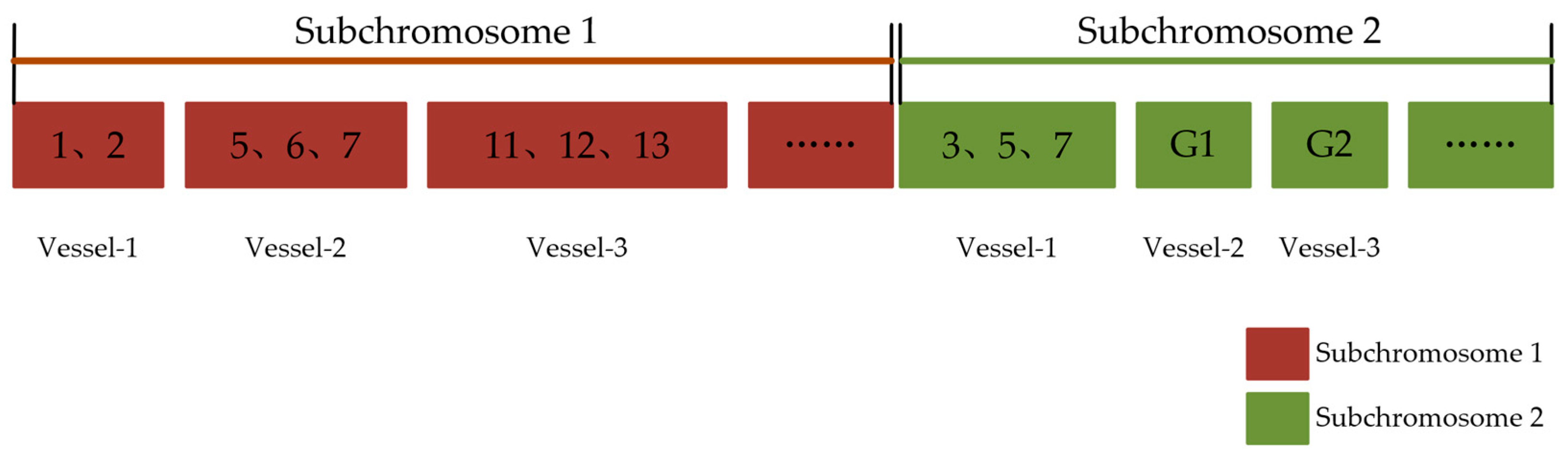






| Region | 2020 | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 | 2028 |
|---|---|---|---|---|---|---|---|---|---|
| North America | 22.1 | 23.9 | 24.6 | 24.7 | 24.5 | 24.3 | 24.0 | 23.8 | 23.5 |
| S&C America | 5.8 | 6.4 | 6.6 | 6.7 | 6.8 | 6.9 | 7.0 | 7.1 | 7.2 |
| Europe | 13.7 | 14.5 | 14.9 | 14.9 | 14.8 | 14.7 | 14.6 | 14.5 | 14.3 |
| Africa | 3.8 | 4.0 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 |
| Middle East | 8.1 | 8.5 | 9.0 | 9.2 | 9.3 | 9.4 | 9.6 | 9.7 | 9.8 |
| Eurasia | 4.2 | 4.5 | 4.6 | 4.6 | 4.6 | 4.6 | 4.7 | 4.7 | 4.7 |
| Asia Pacific | 34.0 | 35.7 | 35.8 | 37.8 | 38.8 | 39.7 | 40.3 | 40.9 | 41.3 |
| World | 91.7 | 97.5 | 99.8 | 102.3 | 103.1 | 104.1 | 104.8 | 105.3 | 105.7 |
| Symbol | Descriptions |
|---|---|
| A | Set of vessels, A = {1, 2, 3, …, a}, |
| B | Set of berths, B = {1, 2, 3, …, b}, |
| Cb | Set of oil transfer arms of berth b, Cb = {1, 2, 3, …, c}, |
| D | Set of pipelines, D = {1, 2, 3, …, d}, |
| E | Set of tanks, E = {1, 2, 3, …, e}, |
| F | Set of valves, |
| G | Set of cargoes, G = {1, 2, 3, …, g}. |
| Symbol | Descriptions |
|---|---|
| ATAa | Actual time of arrival of vessel a |
| C | Total cost of vessels of a plan, unit: USD |
| C1 | Cost of oil transfer arms, unit: USD |
| C2 | Cost of pipelines, unit: USD |
| C3 | Cost of valves, unit: USD |
| Cfj | Cost of operations of valve j, unit: USD/unit |
| Cl | Fixed cost of pipelines occupation, unit: USD/m |
| Cs | Fixed cost of oil transfer arms handling, unit: USD/unit |
| Ct | Fixed cost of oil transfer arms occupation, unit: USD/h/unit |
| Ds | Pipeline section, unit: m2 |
| ECfj | Energy consumption of valve j |
| ETDa | Estimated time of departure of vessel a |
| ga | Type of liquid cargo of vessel a |
| ge | Type of liquid cargo of tank e |
| gd | Type of liquid cargo of pipeline d |
| La | Total length of operation pipeline of vessel a, unit: m |
| lij | Pipeline length from valve i to valve j, unit: m |
| Nca | Quantity of oil transfer arm occupation |
| Ncb | Quantity of oil transfer arm in berth b |
| njF | Operation times of valve j, j∈F |
| T | Total time of vessels of a plan, unit: h |
| Tc | Preparation and handling time of oil transfer arm, unit: h |
| Tca | Unloading time of cargo of vessel a, unit: h |
| Te(in) | The moment when the oil tank e starts to feed oil |
| Te(max) | The moment when the oil tank e reaches its maximum storage capacity |
| Te(min) | The moment when the oil tank e reaches its minimum storage capacity |
| Te(out) | The moment when the oil tank e starts to drain oil |
| Tpa | Pipeline oil circuit emptying time, unit: h |
| v | Maximum passable flow velocity of pipeline, unit: m/s |
| Va | Standard flow rate of oil transfer arm of vessel a, unit: m3/h |
| Vca | Unloading actual flow rate of oil transfer arm of vessel a, unit: m3/h |
| Wa | Liquid cargo unloading volume of vessel a, unit: m3 |
| Weu | Vacant space of tank e, unit: m3 |
| Symbol | Descriptions |
|---|---|
| pj | Status of valve j |
| qdij | Status of pipeline from valve i to valve j |
| ω(alij) | Pipeline path from valve i to valve j of vessel a |
| ω(lij) | Connection status of pipeline from valve i to valve j |
| Parameters | Design Value |
|---|---|
| Cl | 30 USD/m |
| Cs | 50 USD/unit/h |
| Ct | 1000 USD/unit |
| Cost of electric ball valves | 5 USD/once |
| Cost of electric gate valve | 3 USD/once |
| Cost of exhaust valves | 2 USD/once |
| Cost of manual ball valves | 10 USD/once |
| Cost of manual gate valves | 8 USD/once |
| Cost of multi-way valves | 12 USD/once |
| Cost of ordinary valves | 2 USD/once |
| Cost of safety valves | 2 USD/once |
| Rated power of pump, level 1 | 4000 m3/h |
| Rated power of pump, level 2 | 2250 m3/h |
| Rated power of pump, level 3 | 1560 m3/h |
| V | 4.5 m/s |
| Quantity of Vessels | Iterations | Time of NSGA-II-Dijkstra | Time of INIIDA | Speed Increase % |
|---|---|---|---|---|
| 10 | 100 | 1:02:19 | 00:18:43 | 69.97% |
| 10 | 500 | 2:01:31 | 00:45:23 | 62.65% |
| 10 | 1000 | 11:47:15 | 03:09:57 | 73.14% |
| 27 | 100 | 1:01:36 | 00:22:35 | 63.33% |
| 27 | 500 | 5:00:58 | 01:32:18 | 69.33% |
| 27 | 1000 | 10:05:41 | 03:27:57 | 65.67% |
| 42 | 100 | 1:48:12 | 00:38:25 | 64.49% |
| 42 | 500 | 8:09:58 | 02:51:26 | 65.01% |
| 42 | 1000 | 17:02:58 | 05:41:07 | 66.65% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Xiao, H.; Wang, C.; Yuan, X.; Liu, M. Research on the Dual-Objective Scheduling of the Pipeline Path of Liquid Terminal Resources Based on a Hybrid Algorithm. Appl. Sci. 2024, 14, 6195. https://doi.org/10.3390/app14146195
Kong L, Xiao H, Wang C, Yuan X, Liu M. Research on the Dual-Objective Scheduling of the Pipeline Path of Liquid Terminal Resources Based on a Hybrid Algorithm. Applied Sciences. 2024; 14(14):6195. https://doi.org/10.3390/app14146195
Chicago/Turabian StyleKong, Lingxin, Hanbin Xiao, Chaoyu Wang, Xinjie Yuan, and Min Liu. 2024. "Research on the Dual-Objective Scheduling of the Pipeline Path of Liquid Terminal Resources Based on a Hybrid Algorithm" Applied Sciences 14, no. 14: 6195. https://doi.org/10.3390/app14146195
APA StyleKong, L., Xiao, H., Wang, C., Yuan, X., & Liu, M. (2024). Research on the Dual-Objective Scheduling of the Pipeline Path of Liquid Terminal Resources Based on a Hybrid Algorithm. Applied Sciences, 14(14), 6195. https://doi.org/10.3390/app14146195









