A General Method for Solving Differential Equations of Motion Using Physics-Informed Neural Networks
Abstract
:1. Introduction
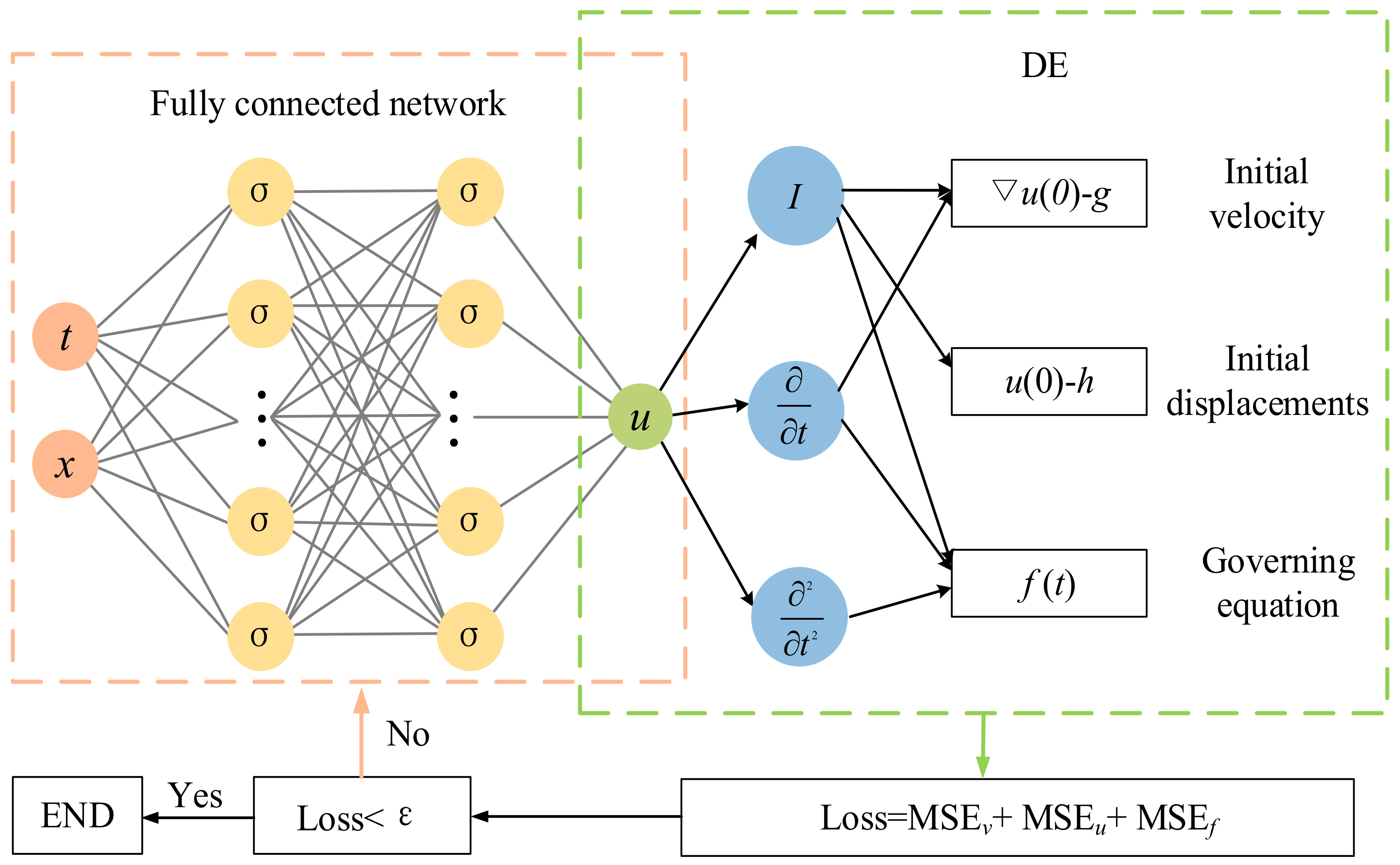
2. Physics-Informed Neural Networks
2.1. Fully Connected Neural Network
2.2. Differential Equations
2.3. Training Process of Neural Network
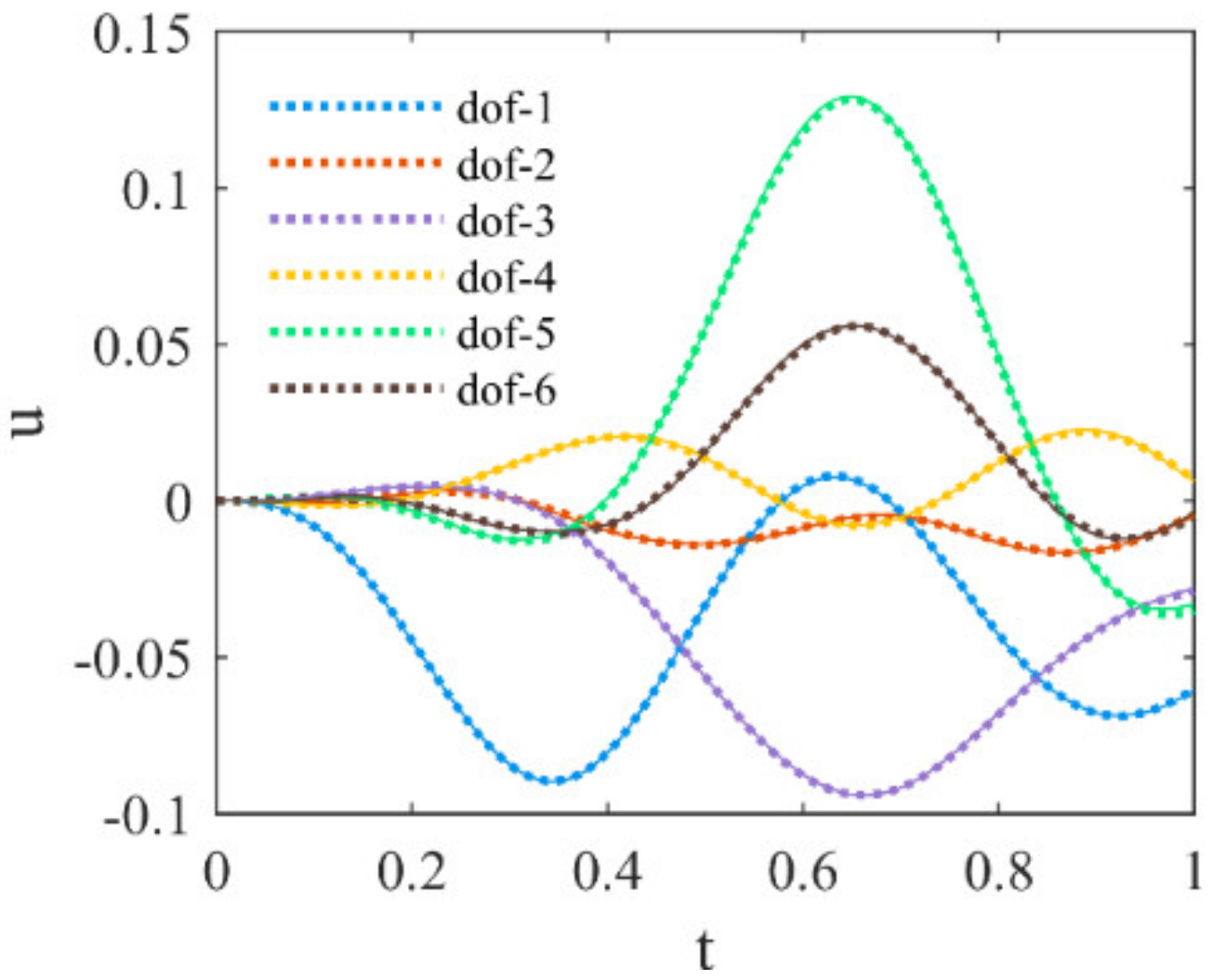
3. Numerical Studies
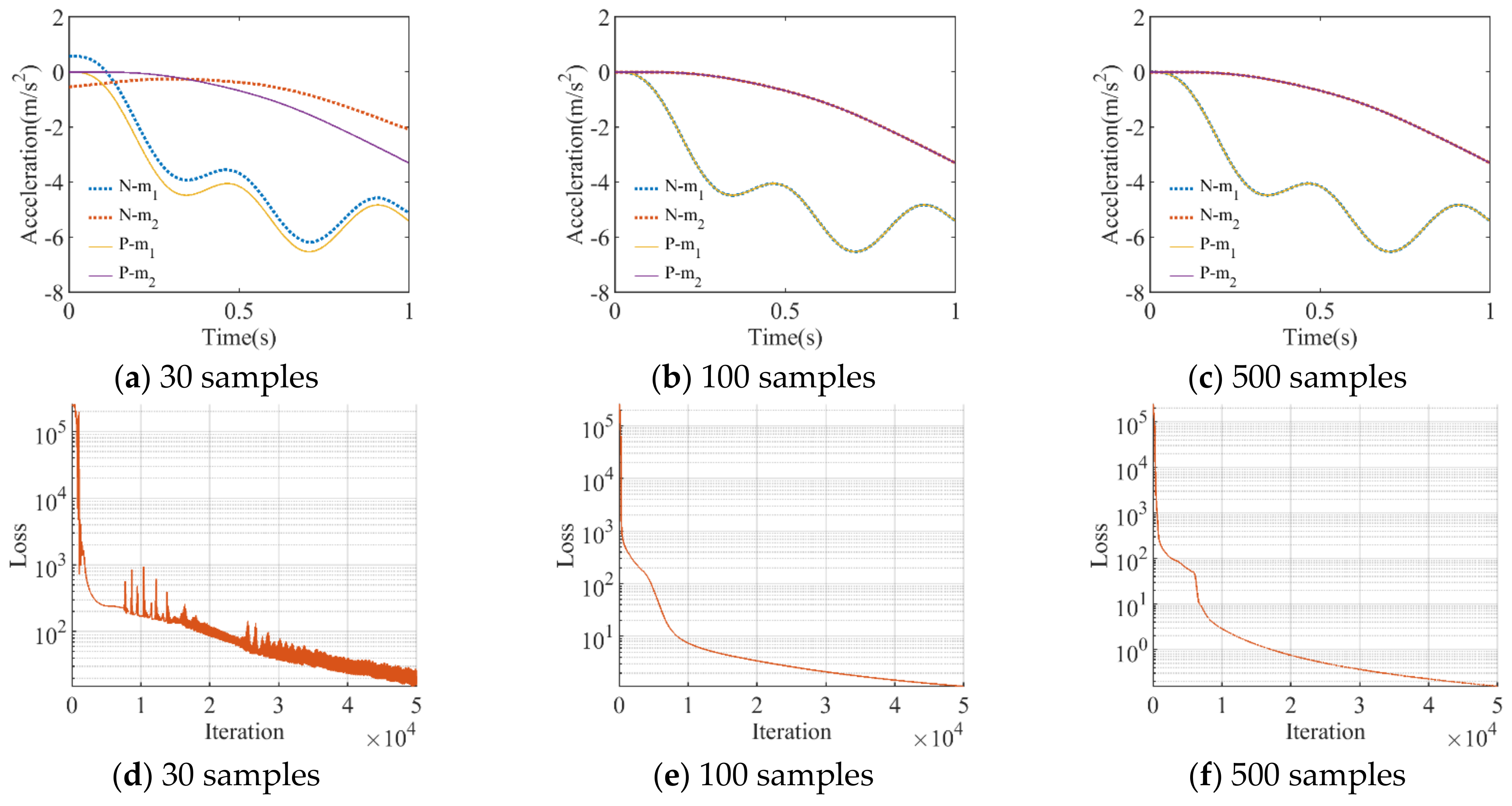
3.1. Two-Degree-of-Freedom System
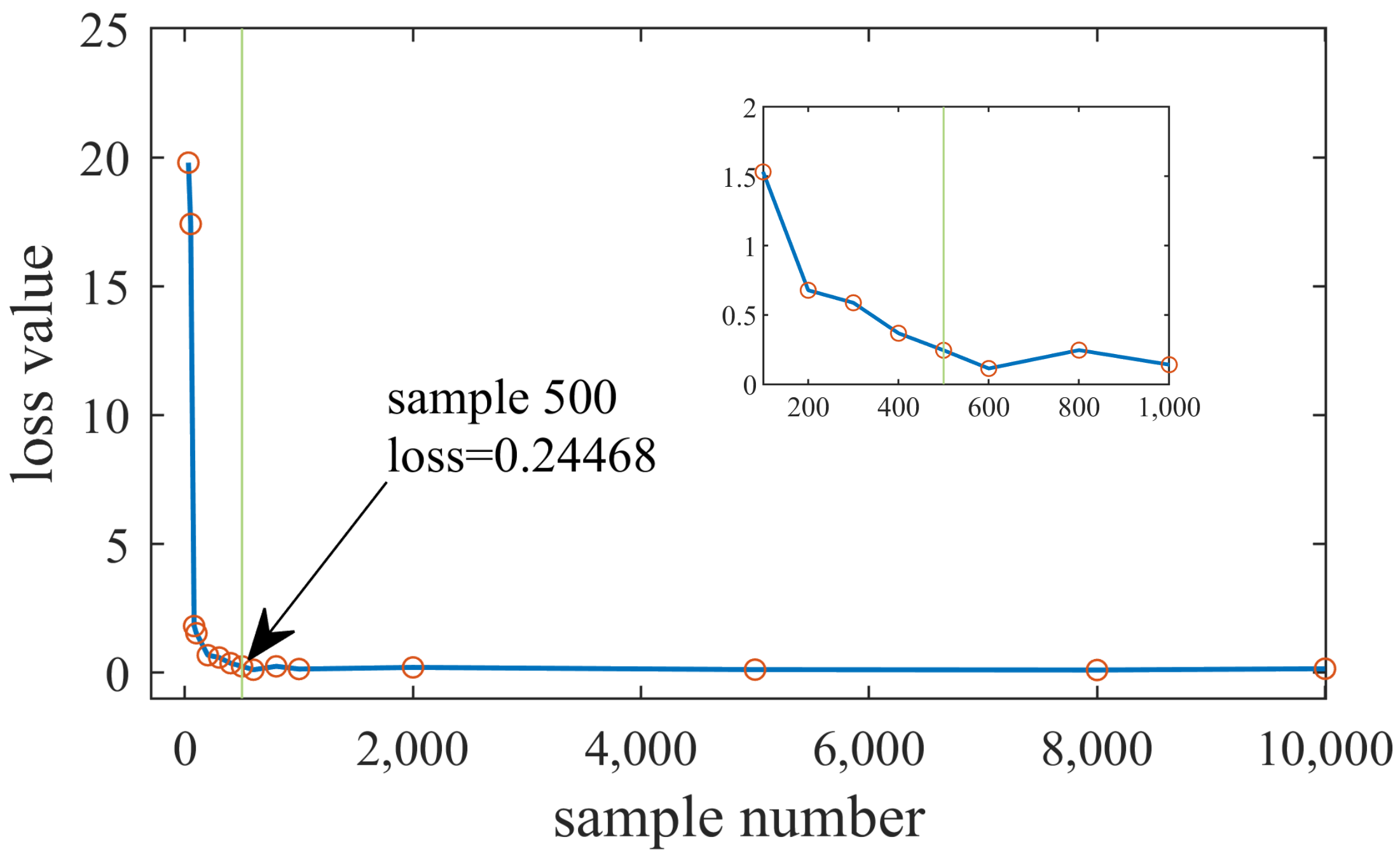
3.1.1. Training Sample Number
3.1.2. Number of Hidden Layers and Neurons
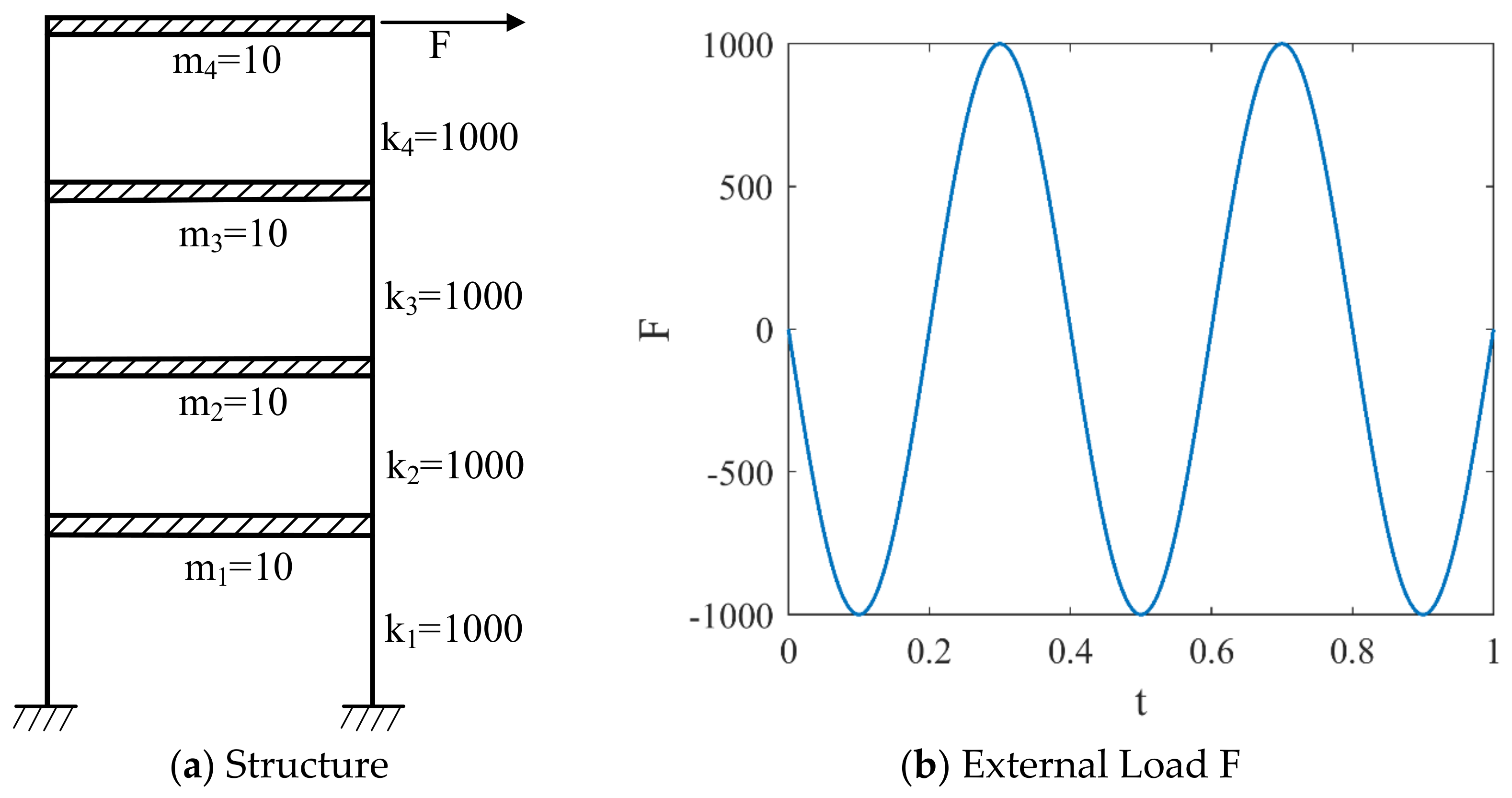
3.2. Four-Layer Framework Structure
3.2.1. Activation Function
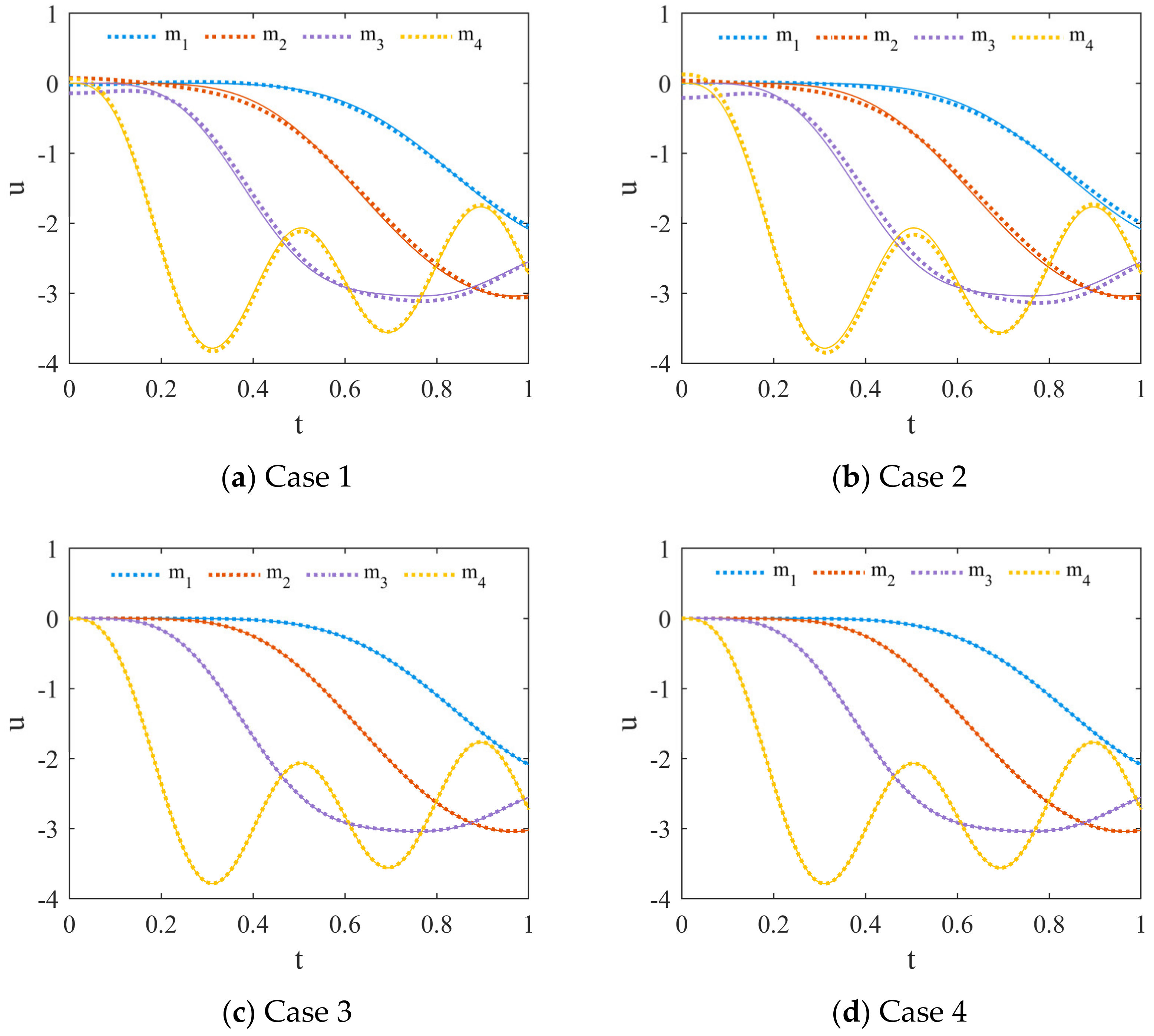
3.2.2. The Weight Coefficients of the Loss Function
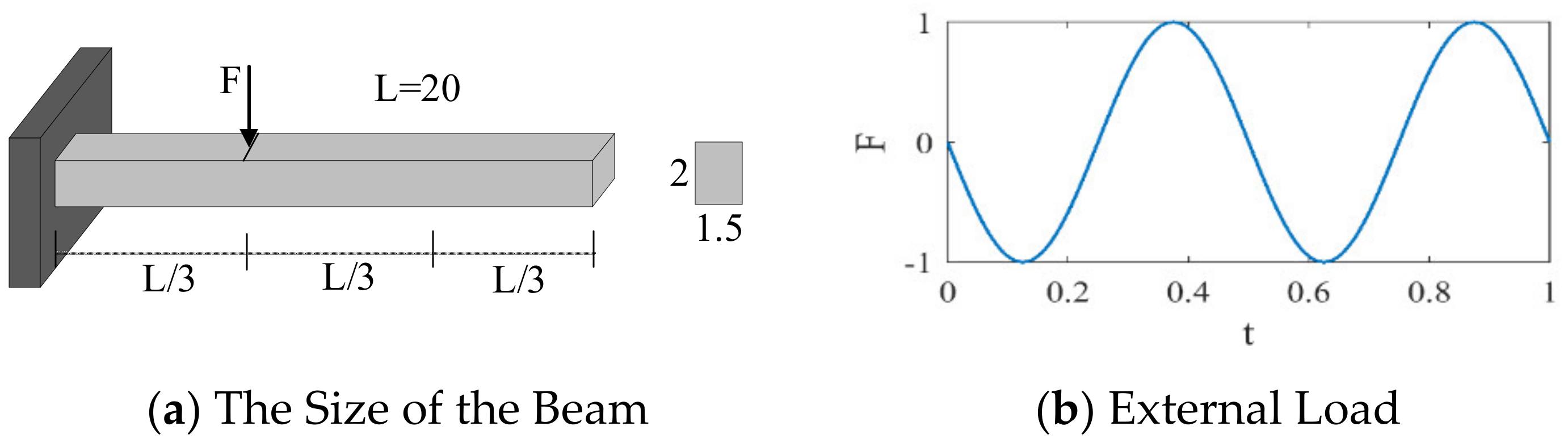
3.3. Cantilever Beam
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farlow, S.J. Partial Differential Equations for Scientists and Engineers; Courier Corporation: Chelmsford, MA, USA, 1993. [Google Scholar]
- Ames, W.F. Numerical Methods for Partial Differential Equations; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Johnson, C. Numerical Solution of Partial Differential Equations by the Finite Element Method; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Smith, G.D.; Smith, G.D.; Smith, G.D.S. Numerical Solution of Partial Differential Equations: Finite Difference Methods; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Belytschko, T.; Schoeberle, D. On the unconditional stability of an implicit algorithm for nonlinear structural dynamics. J. Appl. Mech. 1975, 42, 865–869. [Google Scholar] [CrossRef]
- Ijari, K.; Paternina-Arboleda, C.D. Sustainable Pavement Management: Harnessing Advanced Machine Learning for Enhanced Road Maintenance. Appl. Sci. 2024, 14, 6640. [Google Scholar] [CrossRef]
- Feretzakis, G.; Sakagianni, A.; Anastasiou, A.; Kapogianni, I.; Tsoni, R.; Koufopoulou, C.; Karapiperis, D.; Kaldis, V.; Kalles, D.; Verykios, V.S. Machine Learning in Medical Triage: A Predictive Model for Emergency Department Disposition. Appl. Sci. 2024, 14, 6623. [Google Scholar] [CrossRef]
- Li, Q.; Ni, P.; Du, X.; Han, Q.; Xu, K.; Bai, Y. Bayesian finite element model updating with a variational autoencoder and polynomial chaos expansion. Eng. Struct. 2024, 316, 118606. [Google Scholar] [CrossRef]
- Ni, P.; Han, Q.; Du, X.; Fu, J.; Xu, K. Probabilistic model updating of civil structures with a decentralized variational inference approach. Mech. Syst. Signal Process. 2024, 209, 111106. [Google Scholar] [CrossRef]
- Michoski, C.; Milosavljević, M.; Oliver, T.; Hatch, D.R. Solving differential equations using deep neural networks. Neurocomputing 2020, 399, 193–212. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Rudd, K.; Ferrari, S. A constrained integration (CINT) approach to solving partial differential equations using artificial neural networks. Neurocomputing 2015, 155, 277–285. [Google Scholar] [CrossRef]
- Piscopo, M.L.; Spannowsky, M.; Waite, P. Solving differential equations with neural networks: Applications to the calculation of cosmological phase transitions. Phys. Rev. D 2019, 100, 016002. [Google Scholar] [CrossRef]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, X.-W. Fatigue life evolution of steel wire considering corrosion-fatigue coupling effect: Analytical model and application. Steel Compos. Struct. 2024, 50, 363–374. [Google Scholar]
- Zhang, S.; Ni, P.; Wen, J.; Han, Q.; Du, X.; Xu, K. Automated vision-based multi-plane bridge displacement monitoring. Autom. Constr. 2024, 166, 105619. [Google Scholar] [CrossRef]
- Li, Q.; Du, X.; Ni, P.; Han, Q.; Xu, K.; Yuan, Z. Efficient Bayesian inference for finite element model updating with surrogate modeling techniques. J. Civ. Struct. Health Monit. 2024, 14, 997–1015. [Google Scholar] [CrossRef]
- Li, Q.; Du, X.; Ni, P.; Han, Q.; Xu, K.; Bai, Y. Improved hierarchical Bayesian modeling framework with arbitrary polynomial chaos for probabilistic model updating. Mech. Syst. Signal Process. 2024, 215, 111409. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, M.; Du, X.; Gao, Z.; Ni, P. Probabilistic machine learning approach for structural reliability analysis. Probabilistic Eng. Mech. 2023, 74, 103502. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, X.-W.; Guo, Y. Copula-based JPDF of wind speed, wind direction, wind angle, and temperature with SHM data. Probabilistic Eng. Mech. 2023, 73, 103483. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Haghighat, E.; Raissi, M.; Moure, A.; Gomez, H.; Juanes, R. A physics-informed deep learning framework for inversion and surrogate modeling in solid mechanics. Comput. Methods Appl. Mech. Eng. 2021, 379, 113741. [Google Scholar] [CrossRef]
- Wei, S.; Jin, X.; Li, H. General solutions for nonlinear differential equations: A rule-based self-learning approach using deep reinforcement learning. Comput. Mech. 2019, 64, 1361–1374. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks for heat transfer problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z.; Zhang, D.; Karniadakis, G.E. PPINN: Parareal physics-informed neural network for time-dependent PDEs. Comput. Methods Appl. Mech. Eng. 2020, 370, 113250. [Google Scholar] [CrossRef]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Bolandi, H.; Sreekumar, G.; Li, X.; Lajnef, N.; Boddeti, V.N. Physics Informed Neural Network for Dynamic Stress Prediction. arXiv 2022, arXiv:2211.16190. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Marchine Learn. Res. 2018, 18, 1–43. [Google Scholar]
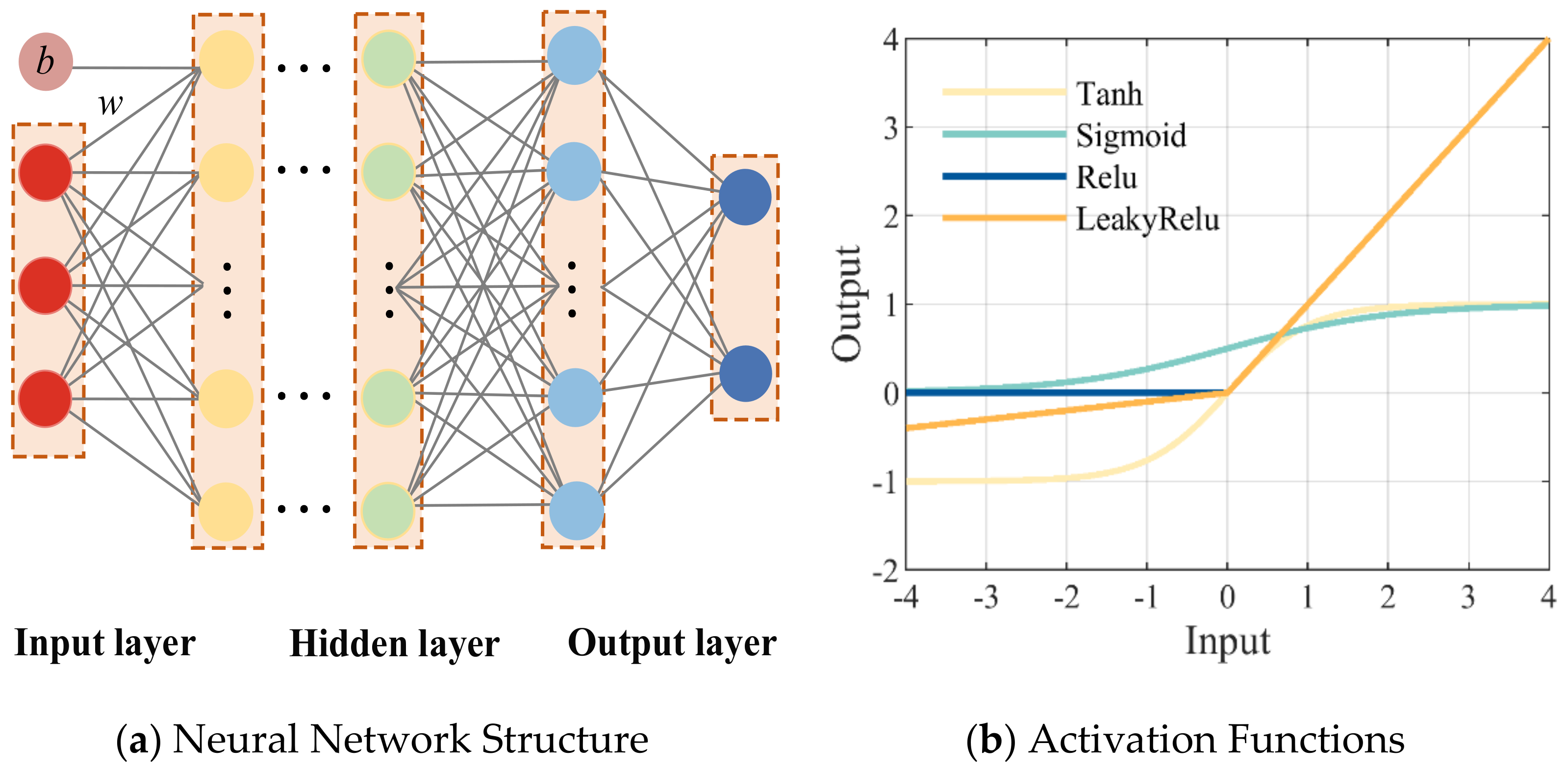



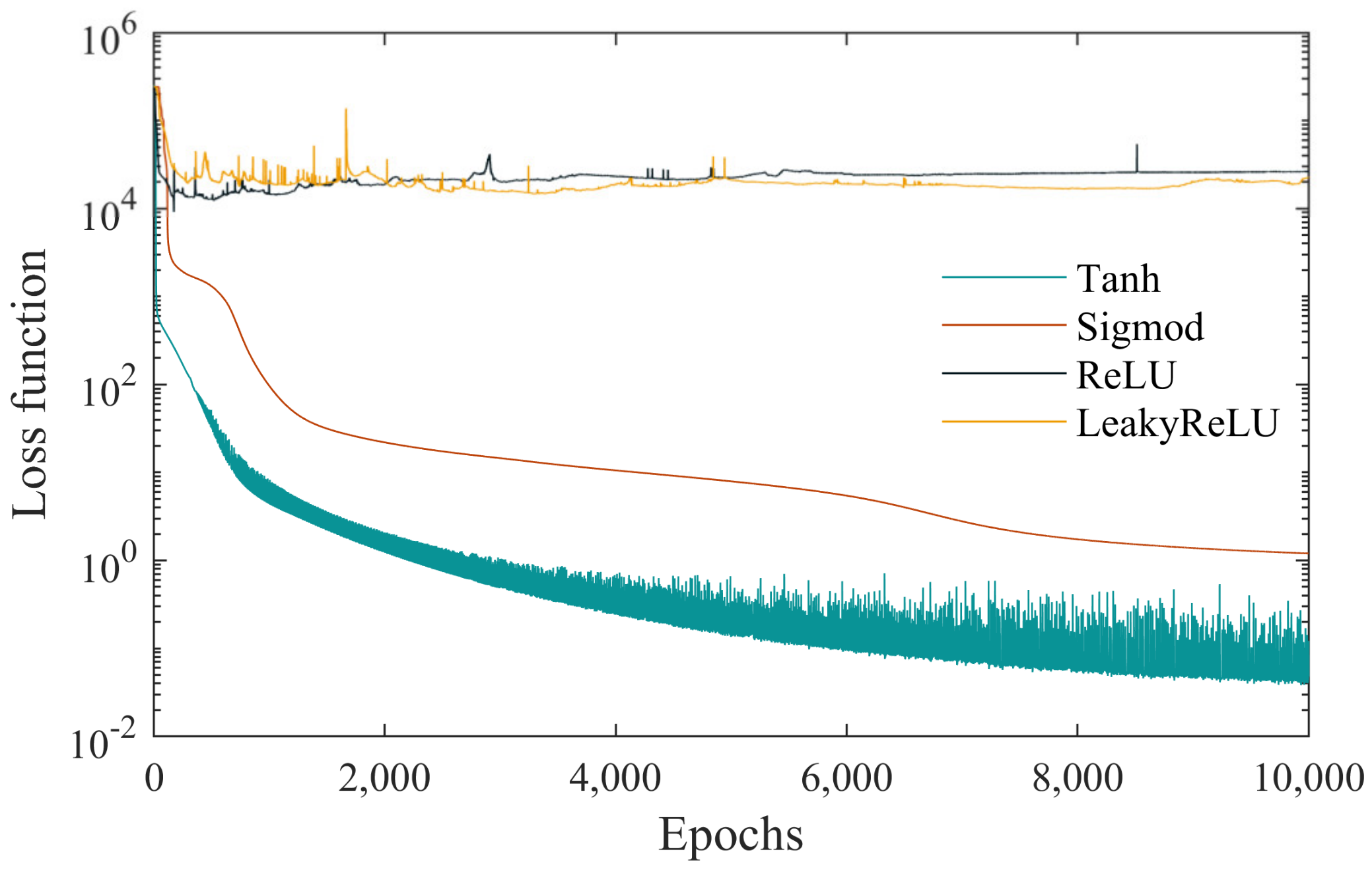


| Tanh | Sigmoid | ReLU | LeakyReLU |
|---|---|---|---|
| Case | Active Function | Hidden Layers | Neurons | Loss Value |
|---|---|---|---|---|
| 1 | Tanh | 2 | 10 | 5259.4248 |
| 2 | Tanh | 4 | 10 | 72.4586 |
| 3 | Tanh | 6 | 10 | 11.2092 |
| 4 | Tanh | 2 | 20 | 138.7688 |
| 5 | Tanh | 4 | 10 | 0.89231 |
| 6 | Tanh | 6 | 20 | 0.24468 |
| Case | Hidden Layers | Neuron Nodes | Active Function | ||
|---|---|---|---|---|---|
| 1 | 8 | 20 | Tanh | 1 | 1 |
| 2 | 8 | 20 | Tanh | 1 | 1000 |
| 3 | 8 | 20 | Tanh | 1000 | 1 |
| 4 | 8 | 20 | Tanh | 1000 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Ni, P.; Zhao, M.; Du, X. A General Method for Solving Differential Equations of Motion Using Physics-Informed Neural Networks. Appl. Sci. 2024, 14, 7694. https://doi.org/10.3390/app14177694
Zhang W, Ni P, Zhao M, Du X. A General Method for Solving Differential Equations of Motion Using Physics-Informed Neural Networks. Applied Sciences. 2024; 14(17):7694. https://doi.org/10.3390/app14177694
Chicago/Turabian StyleZhang, Wenhao, Pinghe Ni, Mi Zhao, and Xiuli Du. 2024. "A General Method for Solving Differential Equations of Motion Using Physics-Informed Neural Networks" Applied Sciences 14, no. 17: 7694. https://doi.org/10.3390/app14177694






