Understanding the Flows of Signals and Gradients: A Tutorial on Algorithms Needed to Implement a Deep Neural Network from Scratch
Abstract
:1. Introduction
- automatic differentiation—i.e., a backpropagation algorithm with suitable inductive steps for different layer types and the activation functions;
- initialization of weights—to avoid exploding or vanishing signals/gradients and to guarantee convergence;
- learning algorithms (optimizers)—to guarantee suitably fast convergence;
- regularization—to avoid overfitting;
- organization of computations—to plan when and how to use CPU or GPU computations.
1.1. Motivation and Contributions
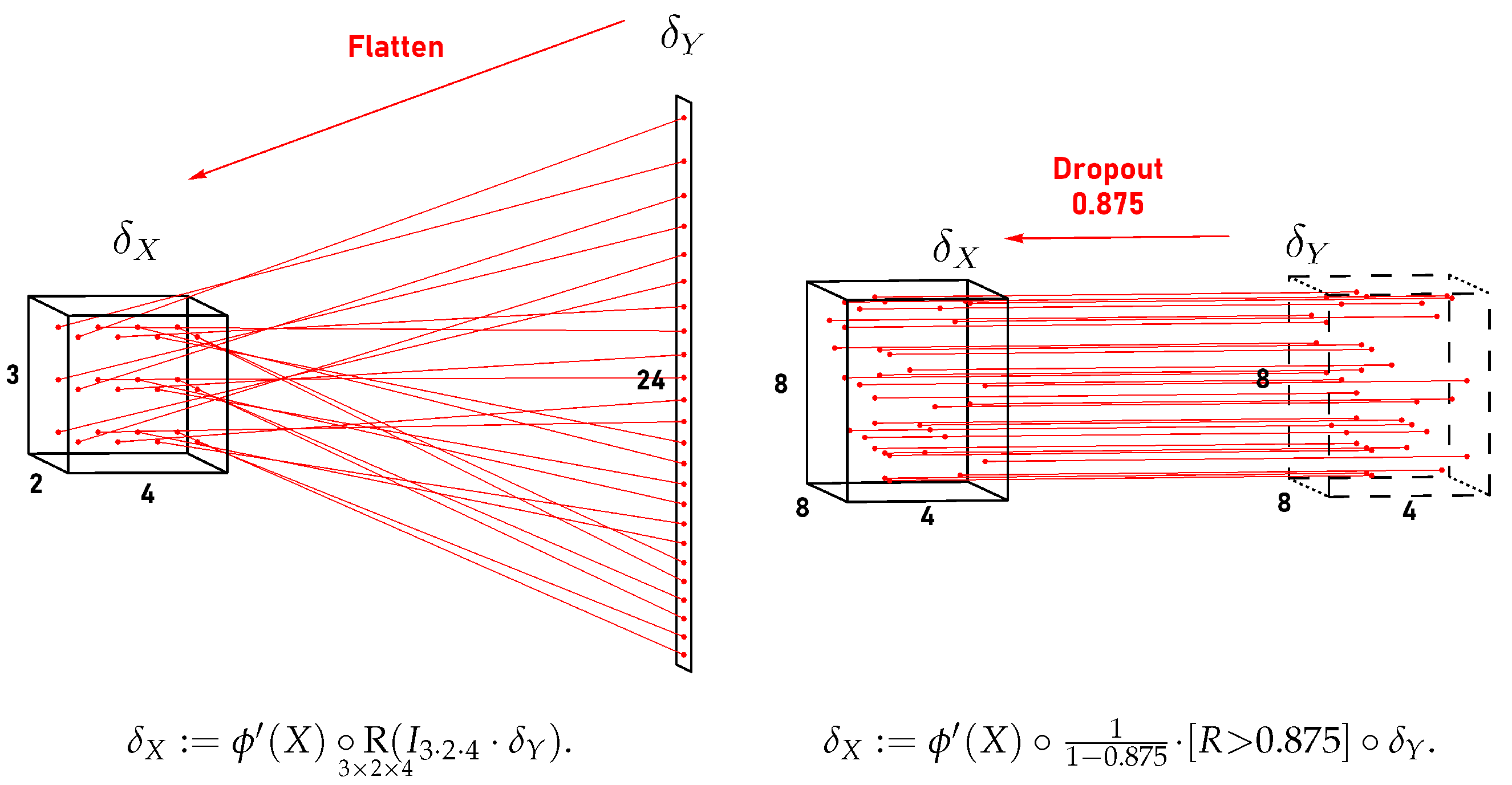
- The proposition of R and S operators for tensors—rashape and stack, respectively—that facilitate algebraic notation for computations (forward and backward) involved in convolutional, pooling, and flattening layers;
- A Python project named hmdl (“home-made deep learning”)—a practical implementation of the ideas presented in this tutorial;
- A careful analysis of a small example—tracking flows of signals and gradients through a four-layer convolutional network (Section 3);
- A concise explanation of DL computations (the aforementioned topics)—automatic differentiation, initialization of weights, learning algorithms, and regularization;
- Clear and consistent notation across all mathematical contexts involved.
1.2. Organization of the Remaining Content
2. Background
2.1. Milestones in the Not-So-Long History of Deep Learning
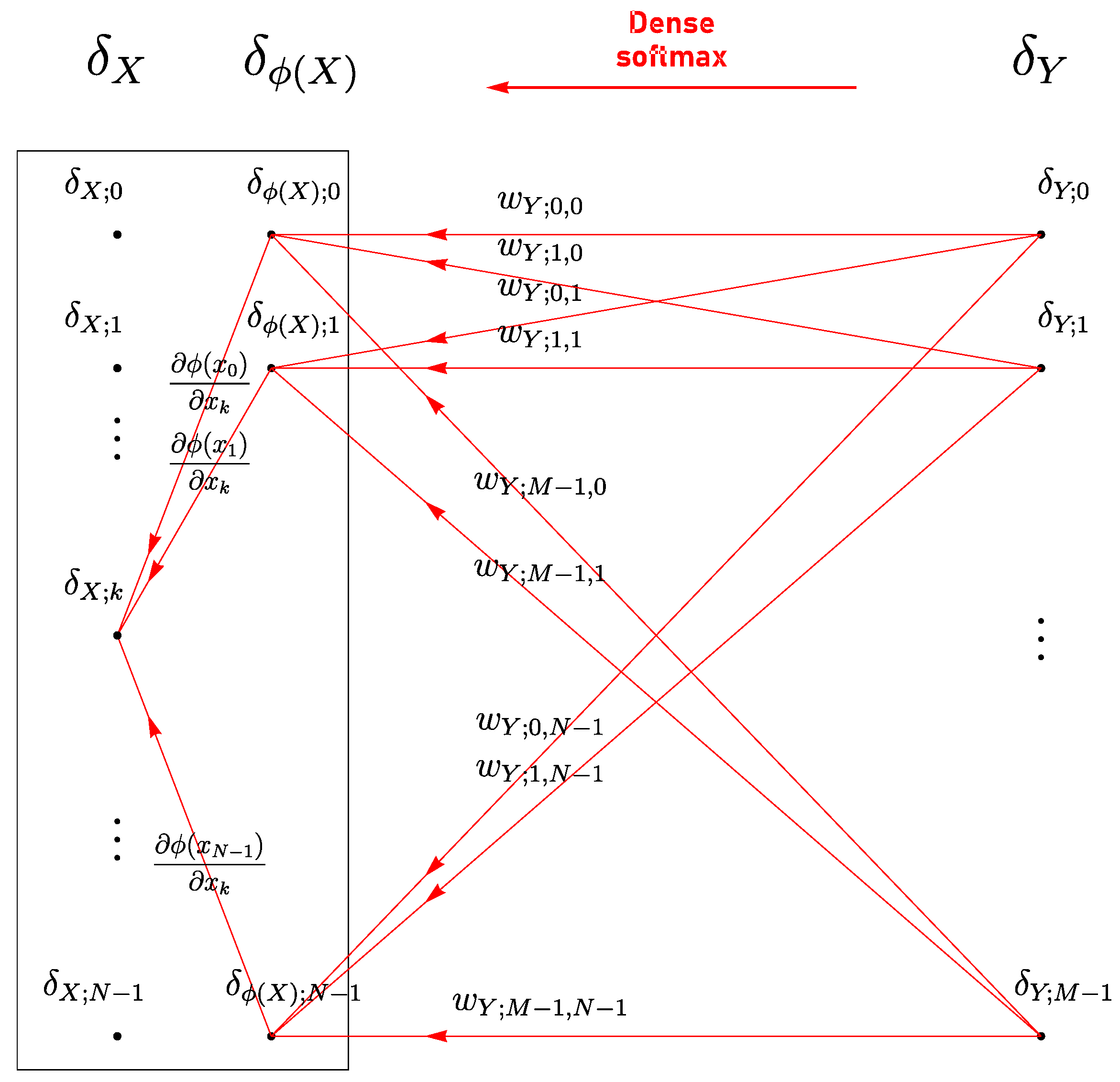
2.2. Backpropagation
2.3. Notation
3. Flows of Signals and Gradients—Direct Derivation for a Small Network Example
3.1. Forward Pass
3.2. Backward Pass
- Backward pass:
- 1
- Compute initial error quantity —see (18).
- 2
- Rule 1: compute as a function of , , —see (19).
- 3
- Rule 2: compute , as a function of , —see (20), (21).
- 4
- Rule 1: compute as a function of , , —see (23).
- 5
- Rule 2: do not compute (no tunable parameters in layer ).
- 6
- Rule 1: compute as a function of , , —see (25).
- 7
- Rule 2: compute , as a function of , —see (28), (29).
- 8
- Rule 1: compute as a function of , , —see (32).
- 9
- 10
- Rule 1: do not compute (not needed since X is the initial layer).
- Corrections (simple SGD):
- 1
- Compute corrections for layer Y:
- 2
- Do not compute corrections for layer (no tunable parameters).
- 3
- Compute corrections for layer :
- 4
- Compute corrections for layer :
4. General Formulas for Common Layer Types
4.1. Convolutional Layers (2D)
4.2. Max Pooling Layers (2D)
4.3. Average Pooling Layers (2D)
4.4. Flattening Layers
4.5. Dropout Layers
4.6. Dense Layers
4.7. Softmax Activation
5. Weight Initialization
- Its execution produces the printout “nan, nan” which informs us about the numerically unwanted behavior. In fact, it is easy to check that, after 28 iterations, all elements inside x are at least of order and some of order —close to the maximum non-infinity value allowed for floating-point numbers of single precision. One iteration later, there are already 503 nan values and 9 inf values inside x.
- And the program execution produces the printout “0.0, 0.0”—the signals have vanished.
- And the obtained printout is “-0.016219143 0.81295455”—the signals have neither exploded nor vanished.
5.1. Randomness and Variance Analysis Setup
- Random elements in each are mutually independent and share the same distribution (i.i.d.—independent, identically distributed);
- Likewise, elements in each are i.i.d.;
- and are independent of each other;
- Biases are initialized with zeros.
5.2. Glorot Initialization
- Glorot normal initialization:
- Glorot uniform initialization:
5.3. He Initialization
- He normal initialization:
- He uniform initialization:
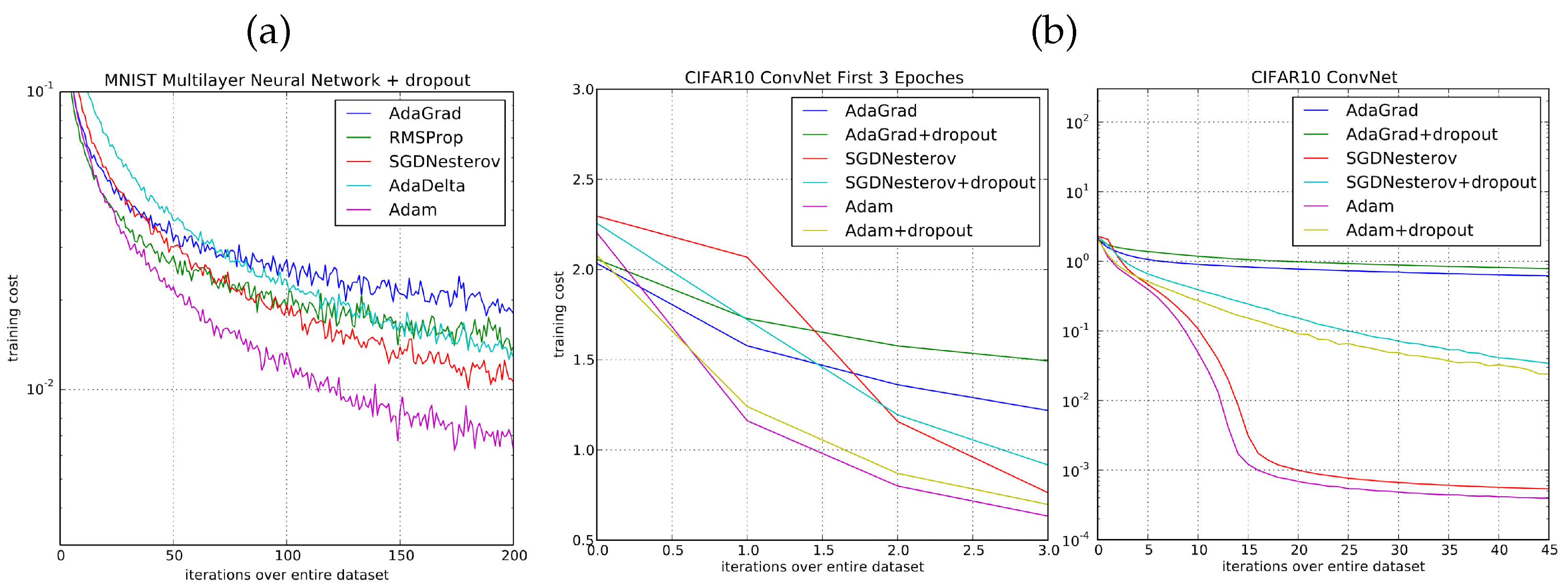
6. Learning Algorithms (Optimizers)
6.1. Exponential Moving Average (EMA)
6.2. AdaGrad and RMSProp
6.3. Adam
6.4. Other Ideas: Nadam, Adamax, AMSGrad
7. Regularization
7.1. Regularization (Weight Decay)
7.2. Regularization (Lasso)
7.3. Dropout Regularization
8. Implementation and Experiments
- Note on source codes: When presenting excerpts of hmdl source code in this manuscript, we have removed, for clarity and brevity, the auxiliary code parts, such as verbosity printouts, time measurements, etc. (for full codes, we direct the reader to the repository).
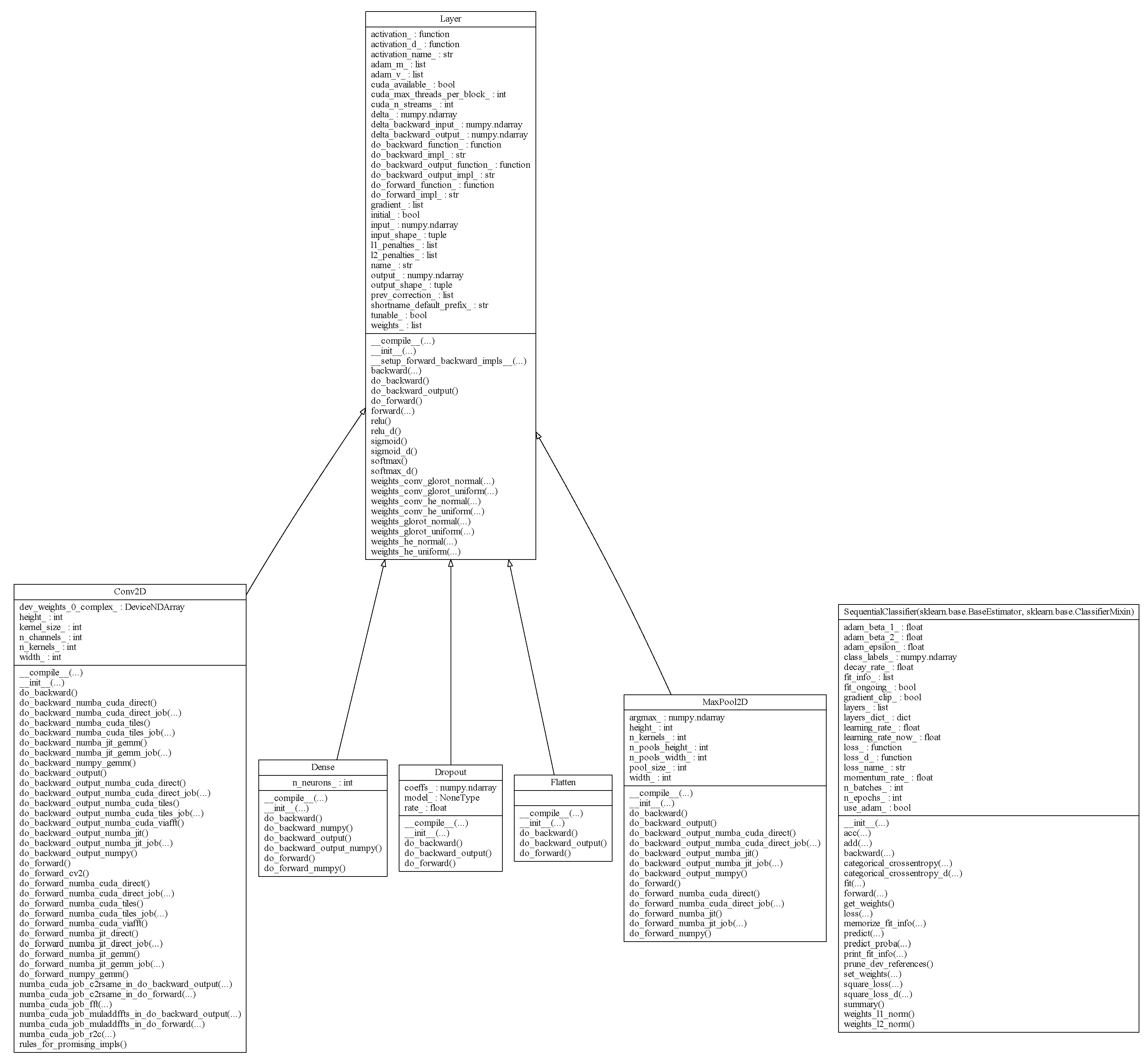
8.1. “Home-Made Deep Learning” Project—A High-Level View
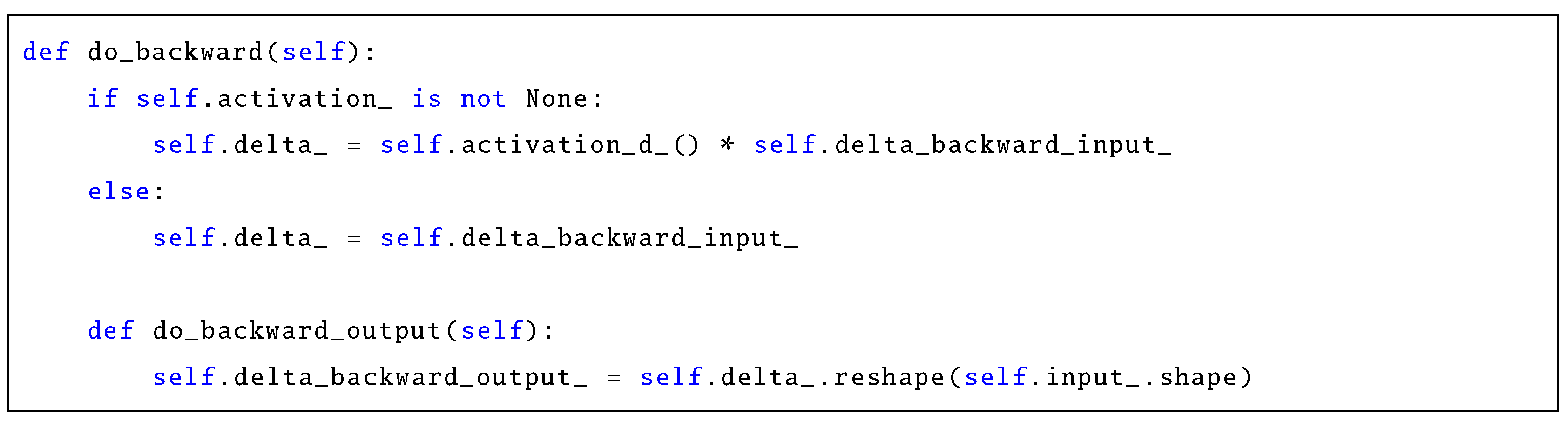
8.2. Executions of Forward and Backward Computations
8.3. Automatic Differentiation (Backward Computations) for Common Layer Types
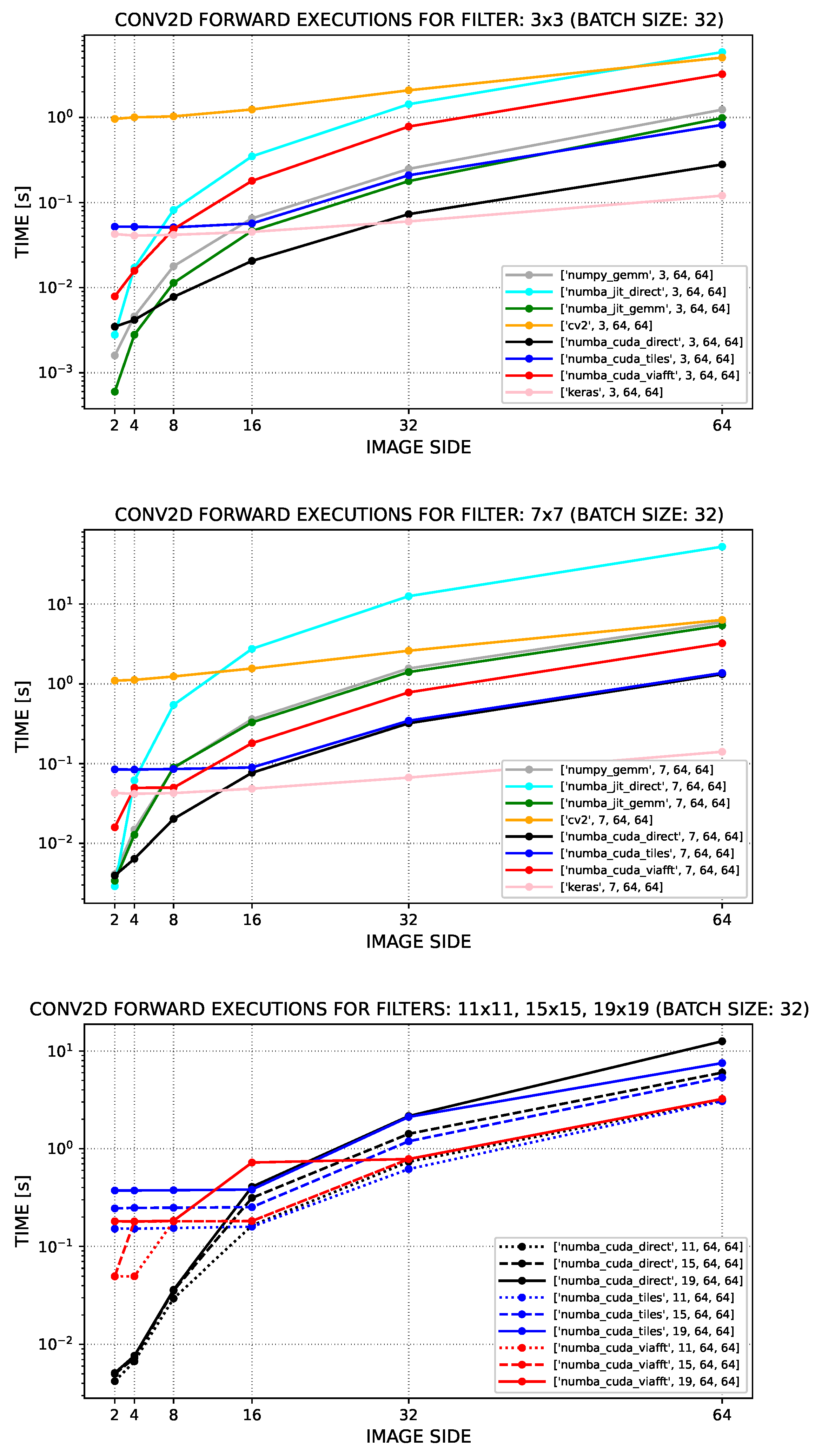
8.4. Efficiency of Forward Computations in Convolutional Layers for Different Implementation Variants
- numpy_gemm—GEMM-based convolution; see (9), involving image-to-matrix and weights-to-matrix transformations. and a numpy.dot multiplication of matrices, executed from regular Python code.
- numba_jit_direct—definition-based convolution; see (8), implemented directly by multiple loops and compiled and executed by means of numba.jit.
- numba_jit_gemm—GEMM-based convolution (as in variant 1); compiled and executed by means of numba.jit.
- cv2—convolution based on an OpenCV function cv2.filter2D (faster than scipy.signal.convolve2d); involves multiple invocations of the function to suitably handle input–output channels.
- numba_cuda_direct—definition-based convolution (as in 2); compiled and executed on GPU via numba.cuda.
- numba_cuda_tiles—definition-based convolution that partitions inputs into tiles associated with CUDA thread blocks and involves collaboration of threads in order to copy inputs and weights into efficient shared memory; compiled and executed on the GPU by means of numba.cuda.
- numba_cuda_viafft—takes advantage of the fact that convolution (for q-th output channel) can be computed as , where p iterates over input channels; involves invocations of multiple GPU kernels and is compiled and executed on the GPU by means of numba.cuda.
- Winograd-based implementations are currently not provided in the hmdl project.
- “NVIDIA Quadro M4000M” environment—hardware: Lenovo ThinkPad P70, Intel Xeon CPU E3-1505M v5 2.8 GHz (3.7 GHz boost), 64 GB RAM, and NVIDIA Quadro M4000M GPU (4 GB/32 GB of dedicated/shared memory), manufactured by: Lenovo Group Limited, Beijing, China; software: nvcc 11.6 (V11.6.112), Python 3.9.7, numpy 1.20.0, numba 0.54.1, cv2 4.5.5-dev keras 2.8.0, and tensorflow 2.8.0; OS: Windows 10 Pro (22H2).
8.5. Implementation of Weight Initialization
8.6. Implementation of Adam Coupled with Regularizations
8.7. Deep Learning Experiments
- “GRID A100-7-40C MIG 7g.40gb” environment—hardware: Ubuntu Server 20.4.03, 4 CPUs: AMD EPYC 7H12 64-Core (2.6 GHz), 128 GB RAM, and NVIDIA GRID A100-7-40C vGPU, manufactured by: Supermicro (Super Micro Computer, Inc.), San Jose, CA 95131, USA; software: nvcc 11.4 (V11.4.48), Python 3.8.10, numpy 1.23.5, numba 0.56.4, cv2 4.7.0, keras 2.12.0, and tensorflow 2.12.0; OS: Ubuntu 20.04.3 LTS.
8.8. Reproducing Experiments (or Running New Ones)
9. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Implementation Variants Supported by Numba for Max Pooling Layers (Hmdl Project)
Appendix A.1. Variant Accelerated Using Low-Level Compilation by numba.jit


Appendix A.2. Variant Accelerated Using GPU Computations and numba.cuda




Appendix B. Implementation Variants Supported by Numba for Convolutional Layers (Hmdl Project)—Backward Computations
Appendix B.1. Variant Accelerated Using Low-Level Compilation via numba.jit

Appendix B.2. Variant Based Directly on Definition Accelerated Using GPU Computations and numba.cuda


Appendix B.3. Variant Based on Tiles Accelerated Using GPU Computations Using and numba.cuda


References
- Rabiner, L. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- McCulloch, W.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Perceiving and Recognizing Automaton; Technical Report 85–460–1; Cornell Aeronautical Laboratory, Inc.: Buffalo, NY, USA, 1957. [Google Scholar]
- Linnainmaa, S. Algoritmin Kumulatiivinen Pyoristysvirhe Yksittaisten Pyoristysvirheiden Taylor-Kehitelmana. Master’s Thesis, University of Helsinki, Tapiola, Finland, 1970. [Google Scholar]
- Fukushima, K. Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning Representations by Back-propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Aizenberg, I.; Aizenberg, N.N.; Vandewalle, J. Multi-Valued and Universal Binary Neurons: Theory, Learning and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Heck, L.; Konig, Y.; Sönmez, M.; Weintraub, M. Robustness to Telephone Handset Distortion in Speaker Recognition by Discriminative Feature Design. Speech Commun. 2000, 31, 181–192. [Google Scholar] [CrossRef]
- Ng, A. Feature Selection, L1 vs. L2 Regularization, and Rotational Invariance. In Proceedings of the 21st International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; ICML’04. pp. 78–85. [Google Scholar] [CrossRef]
- Hinton, G.; Osindero, S.; Teh, Y. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the CVPR 2009, Miami, FL, USA, 22–24 June 2009; pp. 248–255. [Google Scholar]
- Huang, J. The Intelligent Industrial Revolution. Online. NVIDIA Article on GTC (GPU Technology Conference). 2016. Available online: https://blogs.nvidia.com/blog/intelligent-industrial-revolution/ (accessed on 10 August 2022).
- Raina, R.; Madhavan, A.; Ng, A. Large-scale Deep Unsupervised Learning Using Graphics Processors. In Proceedings of the ICML ’09: Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 873–880. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. Res. Proc. Track 2010, 9, 249–256. [Google Scholar]
- Nair, V.; Hinton, G. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the ICML 2010, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Hinton, G.; Srivastava, N.; Swersky, K. Overview of Mini-Batch Gradient Descent. Online. Lecture 6, Unpublished as a Paper. 2012. Available online: http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 10 July 2022).
- Ciresan, D.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the CVPR 2012, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Hinton, G.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. CoRR 2012. Available online: http://arxiv.org/abs/1207.0580 (accessed on 22 October 2024).
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 1, pp. 1097–1105. [Google Scholar]
- Mathieu, M.; Henaff, M.; LeCun, Y. Fast Training of Convolutional Networks through FFTs. arXiv 2013. Available online: https://arxiv.org/abs/1312.5851 (accessed on 22 October 2024).
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR (Poster), Banff, AB, Canada, 14–16 April 2014; Available online: https://arxiv.org/pdf/1412.6980.pdf (accessed on 22 October 2024).
- Simoyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014. Available online: https://arxiv.org/abs/1409.1556v6 (accessed on 22 October 2024).
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014. Available online: https://arxiv.org/abs/1409.4842 (accessed on 22 October 2024).
- Lavin, A.; Gray, S. Fast Algorithms for Convolutional Neural Networks. arXiv 2015. Available online: https://arxiv.org/abs/1509.09308 (accessed on 22 October 2024).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015. Available online: https://arxiv.org/abs/1512.03385 (accessed on 22 October 2024).
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the 4th International Conferenc on Learning Representations (ICLR), San Juan, PR, USA, 2–4 May 2016; pp. 1–4. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017. Available online: https://arxiv.org/abs/1706.03762 (accessed on 22 October 2024).
- Reddi, S.; Kale, S.; Kumar, S. On the Convergence of Adam and Beyond. In Proceedings of the 6th International Conferenc on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Goyal, A.; Lamb, A.; Hoffmann, J.; Sodhani, S.; Levine, S.; Bengio, Y.; Schölkopf, B. Recurrent Independent Mechanisms. arXiv 2020. Available online: https://arxiv.org/abs/1909.10893 (accessed on 22 October 2024).
- Xue, Y.; Tong, Y.; Neri, F. An ensemble of differential evolution and Adam for training feed-forward neural networks. Inf. Sci. 2022, 608, 453–471. [Google Scholar] [CrossRef]
- Bengio, Y.; Lecun, Y.; Hinton, G. Deep Learning for AI. Commun. ACM 2021, 64, 58–65. [Google Scholar] [CrossRef]
- Rumelhart, D.; McClelland, J. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Fukushima, K. Visual feature extraction by a multilayered network of analog threshold elements. IEEE Trans. Syst. Sci. Cybern. 1969, 5, 322–333. [Google Scholar] [CrossRef]
- Tong, G.; Huang, L. Fast Convolution based on Winograd Minimum Filtering: Introduction and Development. CS & IT-CSCP 2021; pp. 177–191 abs/2111.00977. Available online: https://arxiv.org/abs/2111.00977 (accessed on 22 October 2024).
- Delvin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the ACL’2019, Austin, TX, USA, 4–13 October 2019; pp. 4171–4186. [Google Scholar]
- Wolfram, S. What Is ChatGPT Doing… and Why Does It Work? Online. 2023. Available online: https://writings.stephenwolfram.com/2023/02/what-is-chatgpt-doing-and-why-does-it-work (accessed on 22 October 2024).
- Mazzia, V.; Salvetti, F.; Chiaberge, M. Efficient-CapsNet: Capsule network with self-attention routing. Sci. Rep. 2021, 11, 14634. [Google Scholar] [CrossRef] [PubMed]
- Byerly, A.; Kalganova, T.; Dear, I. No Routing Needed Between Capsules. arXiv 2021. Available online: https://arxiv.org/abs/2001.09136 (accessed on 22 October 2024). [CrossRef]
- Dhakad, N.; Malhotra, Y.; Vishvakarma, S.K.; Roy, K. SHA-CNN: Scalable Hierarchical Aware Convolutional Neural Network for Edge AI. arXiv 2024. Available online: https://arxiv.org/abs/2407.21370 (accessed on 22 October 2024).
- Touvron, H.; Cord, M.; El-Nouby, A.; Verbeek, J.; Jégou, H. Three things everyone should know about Vision Transformers. arXiv 2022. Available online: https://arxiv.org/abs/2203.09795 (accessed on 22 October 2024).
- Antonio, B.; Moroni, D.; Martinelli, M. Efficient adaptive ensembling for image classification. Expert Syst. 2023. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Huang, K.; Wang, Y.; Tao, M.; Zhao, T. Why do deep residual networks generalize better than deep feedforward networks?—A neural tangent kernel perspective. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Curran Associates Inc.: Red Hook, NY, USA, 2020. NIPS ’20. [Google Scholar]
- Ma, L.; Li, N.; Yu, G.; Geng, X.; Huang, M.; Wang, X. Pareto-Wise Ranking Classifier for Multiobjective Evolutionary Neural Architecture Search. IEEE Trans. Evol. Comput. 2024, 28, 570–581. [Google Scholar] [CrossRef]
- Dellinger, J. Weight Initialization in Neural Networks: A Journey from the Basics to Kaiming. Online. 2019. Available online: https://towardsdatascience.com/weight-initialization-in-neural-networks-a-journey-from-the-basics-to-kaiming-954fb9b47c79 (accessed on 23 June 2022).
- Polyak, B. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. RPROP—A Fast Adaptive Learning Algorithm. In Proceedings of the 1992 International Symposium on Computer and Information Sciences, Antalya, Turkey, 2–4 November 1992; pp. 279–285. [Google Scholar]
- Nesterov, Y. A method for unconstrained convex minimization problem with the rate of convergence O(1/k2). In Proceedings of the Doklady ANSSSR (Translated as Soviet. Math. Docl.); 1983; Volume 269, pp. 543–547. Available online: https://api.semanticscholar.org/CorpusID:202149403 (accessed on 22 October 2024).
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. 2016. Available online: https://ruder.io/optimizing-gradient-descent/index.html (accessed on 10 July 2022).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Korzeń, M.; Jaroszewicz, S.; Klęsk, P. Logistic regression with weight grouping priors. Comput. Stat. Data Anal. 2013, 64, 281–298. [Google Scholar] [CrossRef]
- Tessier, H.; Gripon, V.; Léonardon, M.; Arzel, M.; Hannagan, T.; Bertrand, D. Rethinking Weight Decay for Efficient Neural Network Pruning. J. Imaging 2022, 8, 64. [Google Scholar] [CrossRef]
- Nowlan, S.; Hinton, G. Simplifying Neural Networks by Soft Weight-Sharing. Neural Comput. 1992, 4, 473–493. [Google Scholar] [CrossRef]
- Plaut, D.C.; Nowlan, S.J.; Hinton, G.E. Experiments on Learning by Back-Propagation; Technical Report CMU–CS–86–126; Carnegie–Mellon University: Pittsburgh, PA, USA, 1986. [Google Scholar]
- Kim, C.; Kim, S.; Kim, J.; Lee, D.; Kim, S. Automated Learning Rate Scheduler for Large-batch Training. arXiv 2021. Available online: https://arxiv.org/abs/2107.05855 (accessed on 22 October 2024).
- d’Ascoli, S.; Refinetti, M.; Biroli, G. Optimal learning rate schedules in high-dimensional non-convex optimization problems. arXiv 2022. Available online: https://arxiv.org/abs/2202.04509 (accessed on 22 October 2024).
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Centofani, F.; Fontana, M.; Lepore, A.; Vantini, S. Smooth LASSO estimator for the Function-on-Function linear regression model. Comput. Stat. Data Anal. 2022, 176, 107556. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Hahn, G.; Lutz, S.M.; Laha, N.; Cho, M.H.; Silverman, E.K.; Lange, C. A fast and efficient smoothing approach to Lasso regression and an application in statistical genetics: Polygenic risk scores for chronic obstructive pulmonary disease (COPD). Stat. Comput. 2021, 31, 35. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Breiman, L. Combining Predictors; Technical Report; Department of Statistics, University of California: Berkeley, CA, USA, 1998. [Google Scholar]
- Keras. GitHub. 2015. Available online: https://github.com/fchollet/keras (accessed on 22 October 2024).
- Roweis, S. Olivetti Faces Dataset; AT&T Laboratories: Cambridge, UK, 1994. [Google Scholar]
- MNIST Handwritten Digit Database; Data Set. 1998. Available online: https://yann.lecun.com/exdb/mnist/ (accessed on 22 October 2024).
- Krizhevsky, A.; Nair, V.; Hinton, G. CIFAR-10; Data Set; Canadian Institute for Advanced Research: Toronto, ON, Canada, 2010. [Google Scholar]

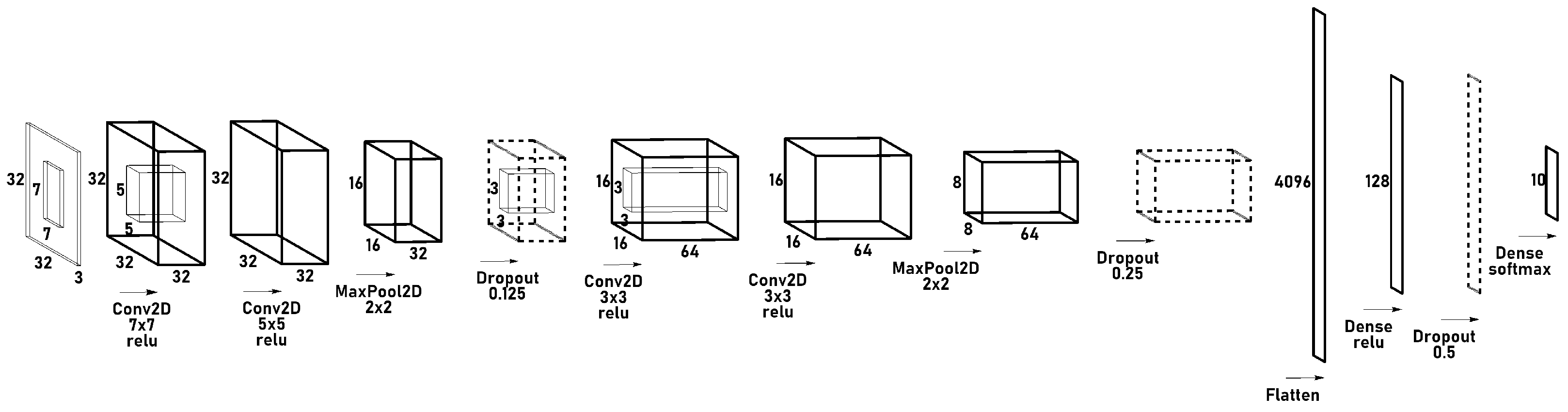
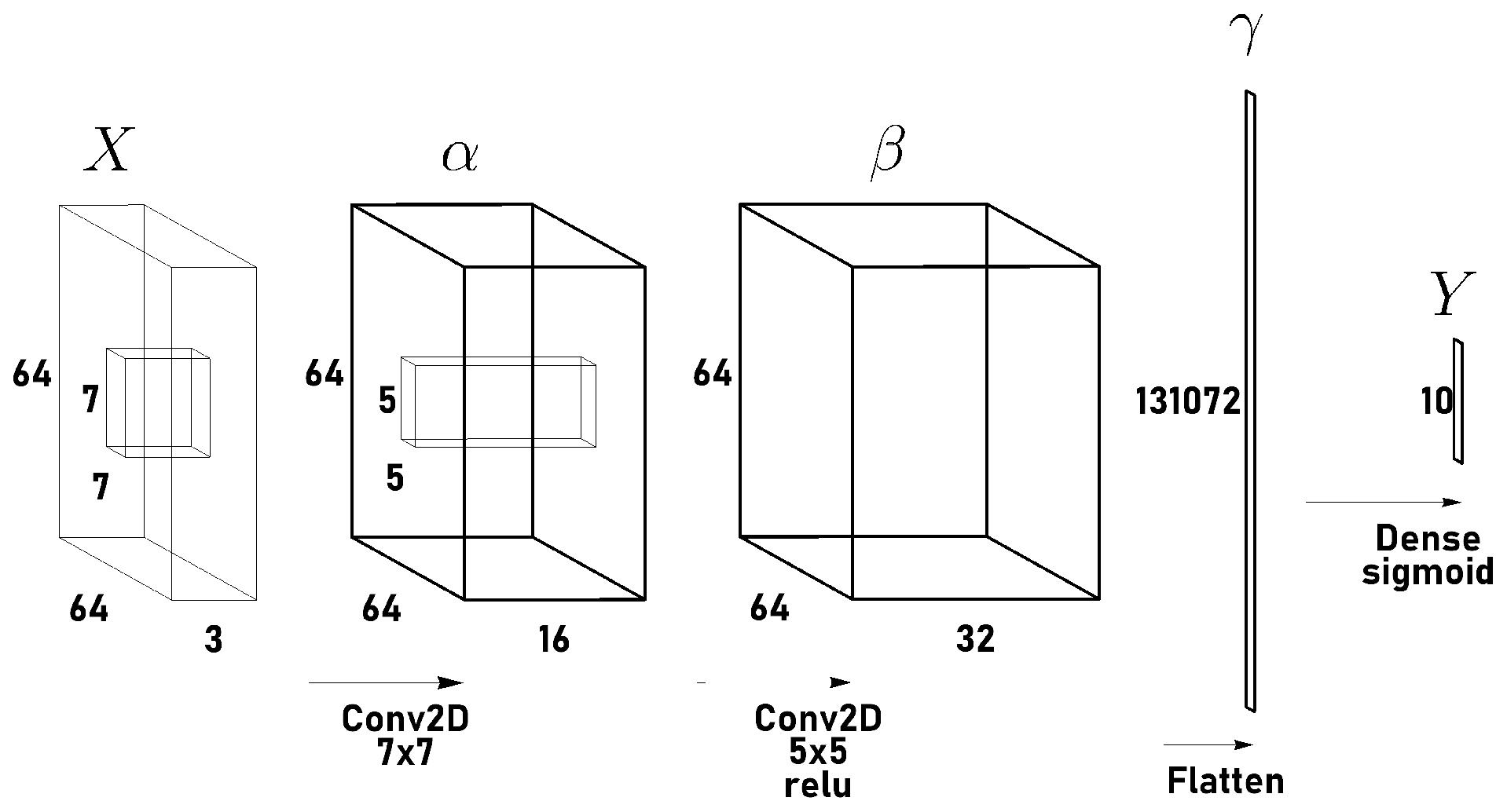
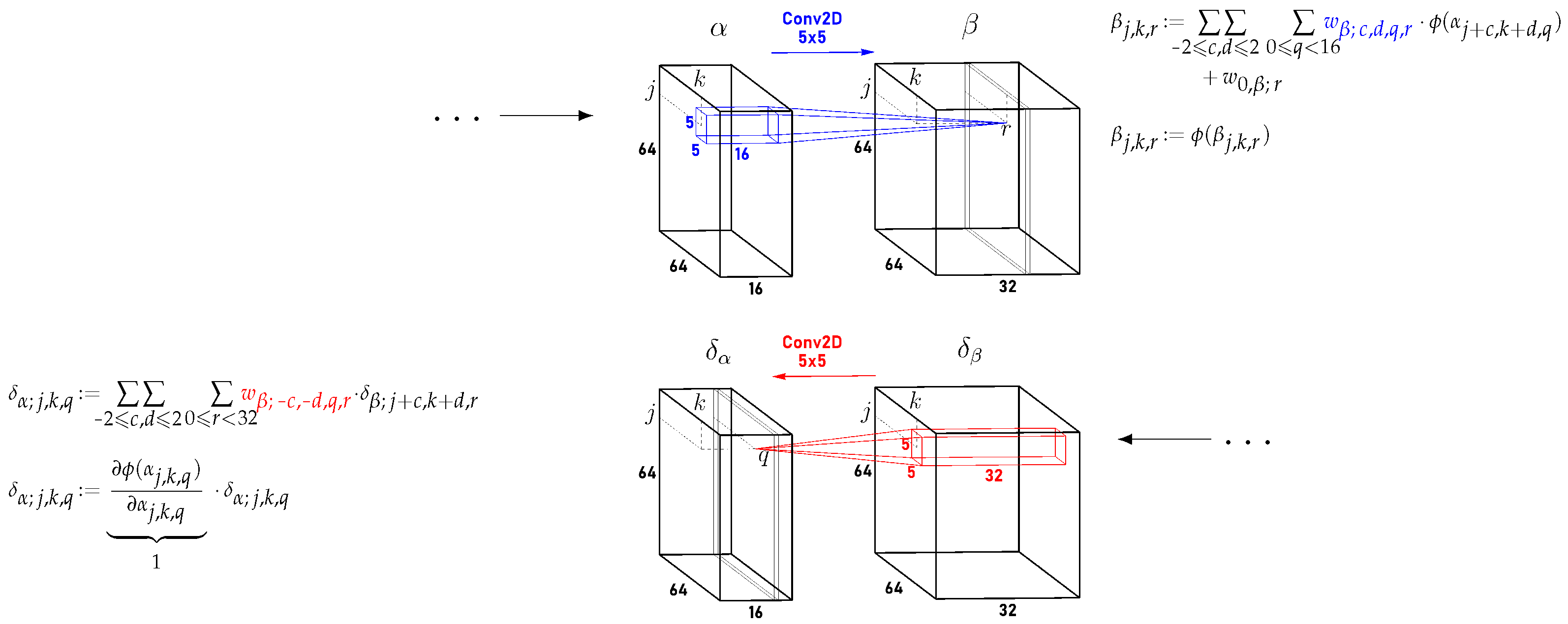
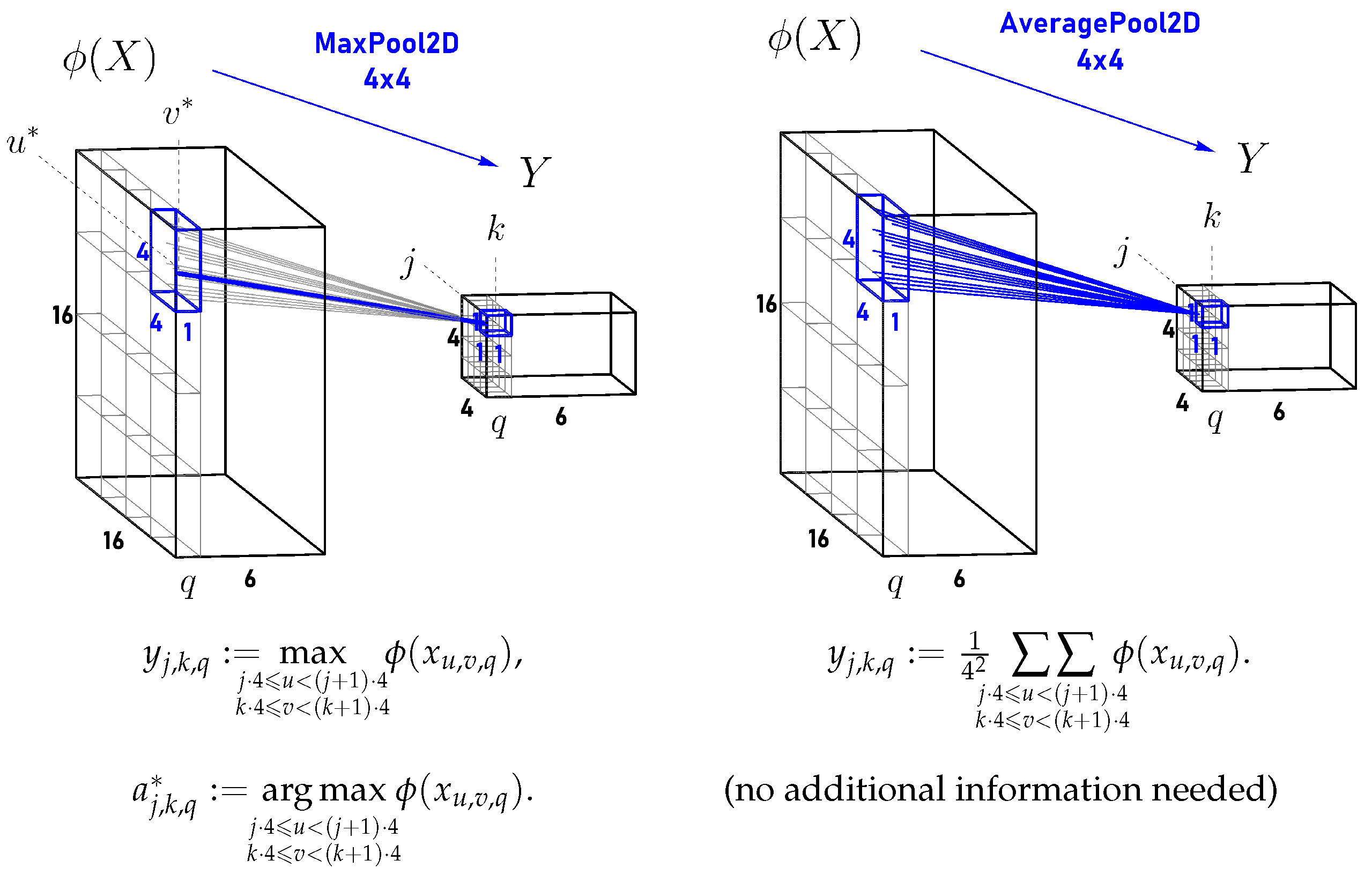


















| Data Set: Olivetti | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| hmdl | Keras | Diffs [%] | |||||||||
| No. | Structure String | Expt. ID (hash) | Params | Fit Time [s] | Test Acc. | Test Loss | Fit Time [s] | Test Acc. | Test Loss | Acc. | Loss |
| GPU device: NVIDIA Quadro M4000M | |||||||||||
| 1 | F();D(8,r);DR(0.25);D(40,sm); | 0979993065 | 33 136 | 2.2 | 0.6817 | 1.258 | 4.4 | 0.7058 | 1.186 | 3.54 | 5.7 |
| 2 | F();D(64,r);DR(0.25);D(40,sm); | 1781687523 | 264 808 | 8.7 | 0.9542 | 0.1738 | 4.6 | 0.9433 | 0.2555 | 1.16 | 32.0 |
| 3 | F();D(64,r);DR(0.25);D(64,r);DR(0.25);D(40,sm); | 3416029629 | 268 968 | 8.9 | 0.9467 | 0.2246 | 5.2 | 0.9475 | 0.2330 | 0.08 | 3.6 |
| 4 | C(5,8,r);M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 2855585004 | 133 944 | 38.1 | 0.9633 | 0.1456 | 7.2 | 0.9667 | 0.1380 | 0.35 | 5.2 |
| 5 | C(9,16,r);M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 4283815439 | 266 120 | 62.8 | 0.9567 | 0.1764 | 9.1 | 0.9575 | 0.1699 | 0.08 | 3.7 |
| 6 | C(5,8,r);M(4);DR(0.25);C(3,16,r);M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 1035804442 | 69 576 | 62.3 | 0.9492 | 0.1677 | 8.2 | 0.9558 | 0.1503 | 0.70 | 10.4 |
| 7 | C(5,8,r);M(2);DR(0.25);C(3,16,r);M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 3391566488 | 266 184 | 82.4 | 0.9217 | 0.2963 | 9.1 | 0.9183 | 0.3415 | 0.37 | 13.2 |
| 8 | C(5,8,r)×2;M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 3923102291 | 135 552 | 97.1 | 0.9583 | 0.1611 | 14.3 | 0.9600 | 0.1652 | 0.18 | 2.5 |
| 9 | C(3,8,r)×2;M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 1455896911 | 134 400 | 85.4 | 0.9600 | 0.1528 | 12.3 | 0.9592 | 0.1939 | 0.08 | 21.2 |
| 10 | C(5,8,r)×2;M(2);DR(0.25);C(3,16,r)×2;M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 2185109709 | 270 112 | 175.9 | 0.9358 | 0.3113 | 17.9 | 0.9233 | 0.3771 | 1.35 | 17.4 |
| 11 | C(5,8,r)×2;M(4);DR(0.25);C(3,32,r)×2;M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 1466991051 | 147 136 | 148.0 | 0.9500 | 0.1941 | 16.4 | 0.9483 | 0.2060 | 0.18 | 5.8 |
| GPU device: GRID A100-7-40C MIG 7g.40gb | |||||||||||
| 1 | F();D(8,r);DR(0.25);D(40,sm); | 0979993065 | 33 136 | 1.2 | 0.6817 | 1.258 | 2.5 | 0.6908 | 1.229 | 1.33 | 2.3 |
| 2 | F();D(64,r);DR(0.25);D(40,sm); | 1781687523 | 264 808 | 2.3 | 0.9542 | 0.1740 | 2.5 | 0.9550 | 0.2310 | 0.08 | 24.7 |
| 3 | F();D(64,r);DR(0.25);D(64,r);DR(0.25);D(40,sm); | 3416029629 | 268 968 | 2.5 | 0.9508 | 0.2212 | 5.2 | 0.9475 | 0.2266 | 0.35 | 2.4 |
| 4 | C(5,8,r);M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 2855585004 | 133 944 | 27.1 | 0.9625 | 0.1464 | 3.2 | 0.9608 | 0.1683 | 0.18 | 13.0 |
| 5 | C(9,16,r);M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 4283815439 | 266 120 | 35.9 | 0.9542 | 0.1754 | 3.3 | 0.9575 | 0.1720 | 0.35 | 1.9 |
| 6 | C(5,8,r);M(4);DR(0.25);C(3,16,r);M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 1035804442 | 69 576 | 43.7 | 0.9483 | 0.1799 | 3.9 | 0.9617 | 0.1295 | 1.41 | 28.4 |
| 7 | C(5,8,r);M(2);DR(0.25);C(3,16,r);M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 3391566488 | 266 184 | 55.1 | 0.9242 | 0.2890 | 3.9 | 0.9442 | 0.2134 | 2.16 | 26.2 |
| 8 | C(5,8,r)×2;M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 3923102291 | 135 552 | 52.5 | 0.9608 | 0.1532 | 3.8 | 0.9683 | 0.1362 | 0.78 | 11.1 |
| 9 | C(3,8,r)×2;M(4);DR(0.25);F();D(64,r);DR(0.25);D(40,sm); | 1455896911 | 134 400 | 51.3 | 0.9533 | 0.1760 | 4.0 | 0.9708 | 0.1334 | 1.84 | 24.2 |
| 10 | C(5,8,r)×2;M(2);DR(0.25);C(3,16,r)×2;M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 2185109709 | 270 112 | 97.6 | 0.9358 | 0.3081 | 4.9 | 0.9433 | 0.2224 | 0.80 | 27.8 |
| 11 | C(5,8,r)×2;M(4);DR(0.25);C(3,32,r)×2;M(2);DR(0.25); F();D(64,r);DR(0.25);D(40,sm); | 1466991051 | 147 136 | 83.7 | 0.9517 | 0.1879 | 5.1 | 0.9558 | 0.1753 | 0.43 | 6.7 |
| Data Set: MNIST | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| hmdl | Keras | Diffs [%] | |||||||||
| No. | Structure String | Expt. ID (hash) | Params | Fit Time | Test Acc. | Test Loss | Fit Time | Test Acc. | Test Loss | Acc. | Loss |
| GPU device: NVIDIA Quadro M4000M | |||||||||||
| 1 | F();D(128,r);DR(0.125);D(128,r);DR(0.125);D(10,sm); | 1321552096 | 118 282 | 133 | 0.9759 | 0.0769 | 18 | 0.9805 | 0.0765 | 0.47 | 0.5 |
| 2 | F();D(512,r);DR(0.125);D(512,r);DR(0.125);D(10,sm); | 0643554048 | 669 706 | 275 | 0.9849 | 0.0584 | 31 | 0.9855 | 0.0752 | 0.06 | 22.3 |
| 3 | F();D(512,r);DR(0.125);D(512,r);DR(0.125); D(512,r);DR(0.125);D(10,sm); | 0491196249 | 932 362 | 352 | 0.9808 | 0.0800 | 39 | 0.9846 | 0.0902 | 0.39 | 11.3 |
| 4 | C(7,64,r);M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 2044490280 | 1 610 250 | 6 861 | 0.9875 | 0.0407 | 393 | 0.9876 | 0.0493 | 0.01 | 17.4 |
| 5 | C(7,64,r);M(2);DR(0.125);C(5,128,r);M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 2037082629 | 1 012 362 | 67 425 | 0.9927 | 0.0250 | 1 395 | 0.9936 | 0.0274 | 0.09 | 8.8 |
| 6 | C(5,64,r);M(2);DR(0.125);C(3,128,r);M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 0549589385 | 879 754 | 27 840 | 0.9920 | 0.0254 | 814 | 0.9932 | 0.0333 | 0.12 | 23.7 |
| 7 | C(5,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 1685817126 | 484 714 | 46 803 | 0.9944 | 0.0205 | 1 101 | 0.9937 | 0.0301 | 0.07 | 31.9 |
| 8 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); C(3,128,r)×2;M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 1224383397 | 435 306 | 49 391 | 0.9959 | 0.0219 | 1 093 | 0.9951 | 0.0343 | 0.08 | 36.2 |
| 9 | C(5,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); C(3,128,r)×2;M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 3604054245 | 452 202 | 64 678 | 0.9953 | 0.0161 | 1 343 | 0.9943 | 0.0247 | 0.10 | 34.8 |
| 10 | C(5,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.25); C(3,128,r)×2;M(2);DR(0.5);F();D(128,r);DR(0.5);D(10,sm); | 1584841448 | 452 202 | 65 518 | 0.9929 | 0.0241 | 1 776 | 0.9957 | 0.0198 | 0.28 | 17.8 |
| GPU device: GRID A100-7-40C MIG 7g.40gb | |||||||||||
| 1 | F();D(128,r);DR(0.125);D(128,r);DR(0.125);D(10,sm); | 1321552096 | 118 282 | 100 | 0.9750 | 0.0778 | 11 | 0.9816 | 0.0760 | 0.68 | 2.3 |
| 2 | F();D(512,r);DR(0.125);D(512,r);DR(0.125);D(10,sm); | 0643554048 | 669 706 | 190 | 0.9838 | 0.0582 | 11 | 0.9840 | 0.0931 | 0.02 | 37.5 |
| 3 | F();D(512,r);DR(0.125);D(512,r);DR(0.125); D(512,r);DR(0.125);D(10,sm); | 0491196249 | 932 362 | 292 | 0.9801 | 0.0816 | 16 | 0.9841 | 0.0930 | 0.41 | 12.3 |
| 4 | C(7,64,r);M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 2044490280 | 1 610 250 | 2 681 | 0.9877 | 0.0409 | 83 | 0.9869 | 0.0602 | 0.08 | 32.1 |
| 5 | C(7,64,r);M(2);DR(0.125);C(5,128,r);M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 2037082629 | 1 012 362 | 8 254 | 0.9927 | 0.0220 | 82 | 0.9946 | 0.0250 | 0.19 | 12.0 |
| 6 | C(5,64,r);M(2);DR(0.125);C(3,128,r);M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 0549589385 | 879 754 | 5 432 | 0.9926 | 0.0248 | 68 | 0.9935 | 0.0316 | 0.09 | 21.5 |
| 7 | C(5,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 1685817126 | 484 714 | 6 592 | 0.9943 | 0.0189 | 82 | 0.9942 | 0.0312 | 0.01 | 39.4 |
| 8 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); C(3,128,r)×2;M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 1224383397 | 435 306 | 8 308 | 0.9947 | 0.0243 | 82 | 0.9955 | 0.0239 | 0.08 | 1.6 |
| 9 | C(5,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); C(3,128,r)×2;M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 3604054245 | 452 202 | 9 666 | 0.9954 | 0.0174 | 93 | 0.9952 | 0.0259 | 0.02 | 32.8 |
| 10 | C(5,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.25); C(3,128,r)×2;M(2);DR(0.5);F();D(128,r);DR(0.5);D(10,sm); | 1584841448 | 452 202 | 9 440 | 0.9928 | 0.0240 | 143 | 0.9954 | 0.0187 | 0.26 | 22.1 |
| Data Set: CIFAR-10 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| hmdl | Keras | Diffs [%] | |||||||||
| No. | Structure String | Expt. ID (hash) | Params | Fit Time | Test Acc. | Test Loss | Fit Time | Test Acc. | Test Loss | Acc. | Loss |
| GPU device: NVIDIA Quadro M4000M | |||||||||||
| 1 | F();D(512,r);DR(0.25);D(512,r);DR(0.25); D(512,r);DR(0.25);D(10,sm); | 0112184563 | 2 103 818 | 619 | 0.5589 | 1.573 | 75 | 0.5700 | 1.642 | 1.99 | 4.2 |
| 2 | F();D(512,r);DR(0.125);D(512,r);DR(0.125); D(512,r);DR(0.125);D(10,sm); | 3617925328 | 2 103 818 | 610 | 0.5671 | 2.259 | 80 | 0.5624 | 2.436 | 0.84 | 7.3 |
| 3 | C(3,32,r);M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 1176787770 | 1 050 890 | 3 981 | 0.6557 | 1.116 | 234 | 0.6410 | 1.068 | 2.29 | 4.3 |
| 4 | C(3,32,r);M(2);DR(0.125);F();D(128,r);DR(0.25);D(10,sm) | 4064952781 | 1 050 890 | 4 071 | 0.6582 | 1.009 | 234 | 0.6500 | 1.061 | 1.26 | 4.9 |
| 5 | C(7,32,r);M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 2176511806 | 1 054 730 | 5 699 | 0.6581 | 1.139 | 309 | 0.6542 | 1.062 | 0.60 | 6.8 |
| 6 | C(7,32,r);M(2);DR(0.125);C(5,64,r);M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 3250393598 | 581 706 | 20 149 | 0.7148 | 1.363 | 628 | 0.7248 | 1.134 | 1.40 | 16.8 |
| 7 | C(3,32,r);C(5,16,r);M(2);DR(0.125); F();D(128,r);DR(0.25);D(10,sm); | 4064194389 | 539 418 | 17 091 | 0.6665 | 1.607 | 777 | 0.6631 | 1.625 | 0.51 | 1.1 |
| 8 | C(7,32,r);C(5,32,r);M(2);DR(0.125); C(3,64,r)×2;M(2);DR(0.25);F();D(128,r);DR(0.5);D(10,sm); | 3392187021 | 611 498 | 49 819 | 0.7741 | 0.8160 | 1 282 | 0.7739 | 0.7324 | 0.03 | 10.2 |
| 9 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 1676196221 | 591 274 | 33 930 | 0.7654 | 1.137 | 961 | 0.7607 | 1.178 | 0.62 | 3.5 |
| 10 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.25); F();D(128,r);DR(0.5);D(10,sm); | 4191965583 | 591 274 | 34 161 | 0.7968 | 0.6892 | 959 | 0.7855 | 0.6926 | 1.44 | 0.5 |
| 11 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); C(3,128,r)×2;M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 0843263662 | 550 570 | 52 878 | 0.8093 | 1.005 | 1 229 | 0.8086 | 1.024 | 0.09 | 1.9 |
| 12 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.25); C(3,128,r)×2;M(2);DR(0.5);F();D(128,r);DR(0.5);D(10,sm); | 0715119487 | 550 570 | 52 614 | 0.8217 | 0.5949 | 1 228 | 0.8359 | 0.5497 | 1.73 | 7.6 |
| GPU device: GRID A100-7-40C MIG 7g.40gb | |||||||||||
| 1 | F();D(512,r);DR(0.25);D(512,r);DR(0.25); D(512,r);DR(0.25);D(10,sm); | 0112184563 | 2 103 818 | 383 | 0.5646 | 1.567 | 29 | 0.5681 | 1.654 | 0.62 | 5.3 |
| 2 | F();D(512,r);DR(0.125);D(512,r);DR(0.125); D(512,r);DR(0.125);D(10,sm); | 3617925328 | 2 103 818 | 386 | 0.5543 | 2.331 | 28 | 0.5595 | 2.575 | 0.94 | 9.5 |
| 3 | C(3,32,r);M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 1176787770 | 1 050 890 | 1 491 | 0.6565 | 1.124 | 41 | 0.6450 | 1.069 | 1.78 | 4.9 |
| 4 | C(3,32,r);M(2);DR(0.125);F();D(128,r);DR(0.25);D(10,sm) | 4064952781 | 1 050 890 | 1 496 | 0.6580 | 1.004 | 42 | 0.6406 | 1.052 | 2.72 | 4.6 |
| 5 | C(7,32,r);M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 2176511806 | 1 054 730 | 1 646 | 0.6579 | 1.167 | 49 | 0.6578 | 1.045 | 0.02 | 10.5 |
| 6 | C(7,32,r);M(2);DR(0.125);C(5,64,r);M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 3250393598 | 581 706 | 3 487 | 0.7145 | 1.335 | 83 | 0.7197 | 1.241 | 0.73 | 7.0 |
| 7 | C(3,32,r);C(5,16,r);M(2);DR(0.125); F();D(128,r);DR(0.25);D(10,sm); | 4064194389 | 539 418 | 2 804 | 0.6664 | 1.626 | 83 | 0.6624 | 1.606 | 0.45 | 1.2 |
| 8 | C(7,32,r);C(5,32,r);M(2);DR(0.125); C(3,64,r)×2;M(2);DR(0.25);F();D(128,r);DR(0.5);D(10,sm); | 3392187021 | 611 498 | 7 043 | 0.7741 | 0.7779 | 107 | 0.7774 | 0.7439 | 0.43 | 4.4 |
| 9 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); F();D(128,r);DR(0.125);D(10,sm); | 1676196221 | 591 274 | 5 795 | 0.7738 | 1.106 | 143 | 0.7656 | 1.093 | 1.07 | 1.2 |
| 10 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.25); F();D(128,r);DR(0.5);D(10,sm); | 4191965583 | 591 274 | 5 784 | 0.7948 | 0.7195 | 89 | 0.7938 | 0.6612 | 0.13 | 8.1 |
| 11 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.125); C(3,128,r)×2;M(2);DR(0.125);F();D(128,r);DR(0.125);D(10,sm); | 0843263662 | 550 570 | 8 625 | 0.8032 | 1.014 | 103 | 0.8172 | 0.9271 | 1.74 | 8.6 |
| 12 | C(3,32,r)×2;M(2);DR(0.125);C(3,64,r)×2;M(2);DR(0.25); C(3,128,r)×2;M(2);DR(0.5);F();D(128,r);DR(0.5);D(10,sm); | 0715119487 | 550 570 | 8 759 | 0.8190 | 0.6119 | 103 | 0.8441 | 0.5184 | 3.06 | 15.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klęsk, P. Understanding the Flows of Signals and Gradients: A Tutorial on Algorithms Needed to Implement a Deep Neural Network from Scratch. Appl. Sci. 2024, 14, 9972. https://doi.org/10.3390/app14219972
Klęsk P. Understanding the Flows of Signals and Gradients: A Tutorial on Algorithms Needed to Implement a Deep Neural Network from Scratch. Applied Sciences. 2024; 14(21):9972. https://doi.org/10.3390/app14219972
Chicago/Turabian StyleKlęsk, Przemysław. 2024. "Understanding the Flows of Signals and Gradients: A Tutorial on Algorithms Needed to Implement a Deep Neural Network from Scratch" Applied Sciences 14, no. 21: 9972. https://doi.org/10.3390/app14219972
APA StyleKlęsk, P. (2024). Understanding the Flows of Signals and Gradients: A Tutorial on Algorithms Needed to Implement a Deep Neural Network from Scratch. Applied Sciences, 14(21), 9972. https://doi.org/10.3390/app14219972






