Numerical and Experimental Characterization of Fiber-Reinforced Thermoplastic Composite Structures with Embedded Piezoelectric Sensor-Actuator Arrays for Ultrasonic Applications †
Abstract
:1. Introduction
2. Phenomenological Description
2.1. Ultrasound Radiation and Reception
2.2. Transducer Arrays for the Generation of Directional Waves in a Plate
3. Application of Integrated Transducer Arrays for Generation of Sound Waves
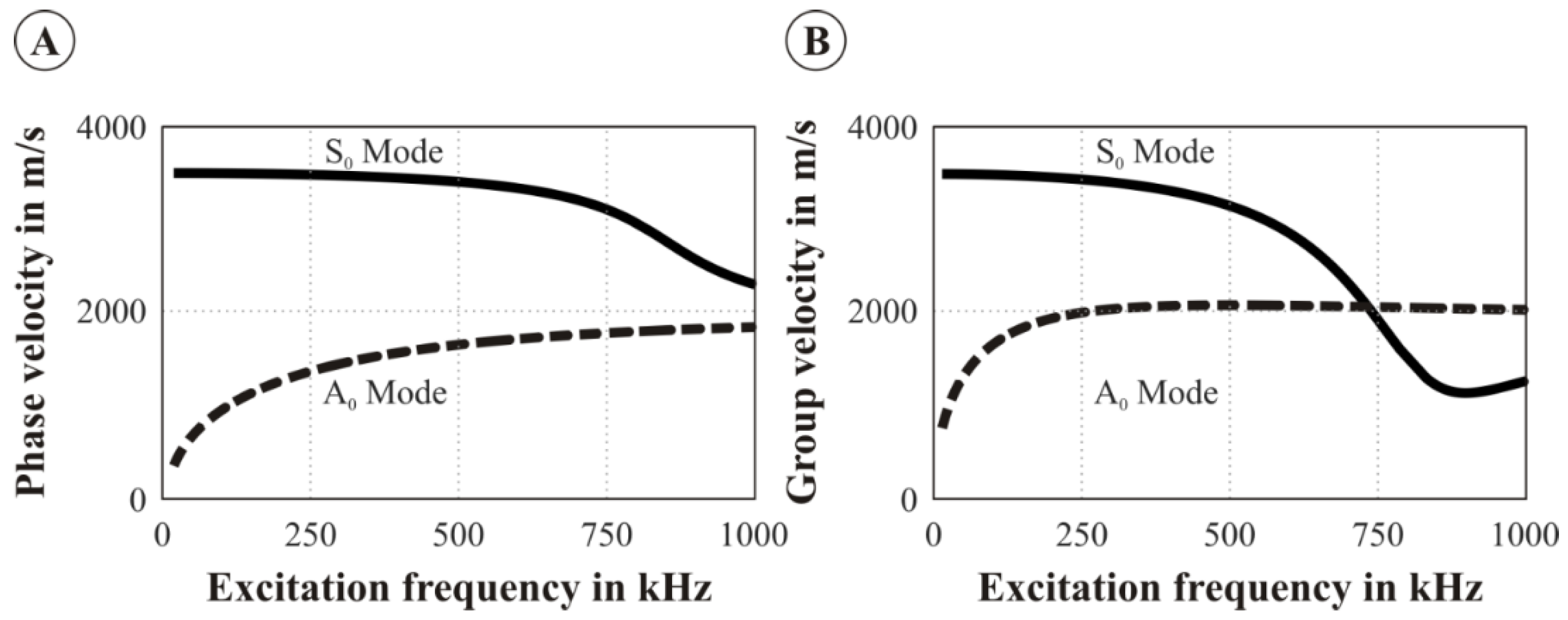
3.1. Numerical Investigations
- the wave has to propagate through some distance in order to reveal its directivity and plate mode character; and
- the reflections of higher Lamb modes—if any present—from the plate edges should not interfere with the main wave front;
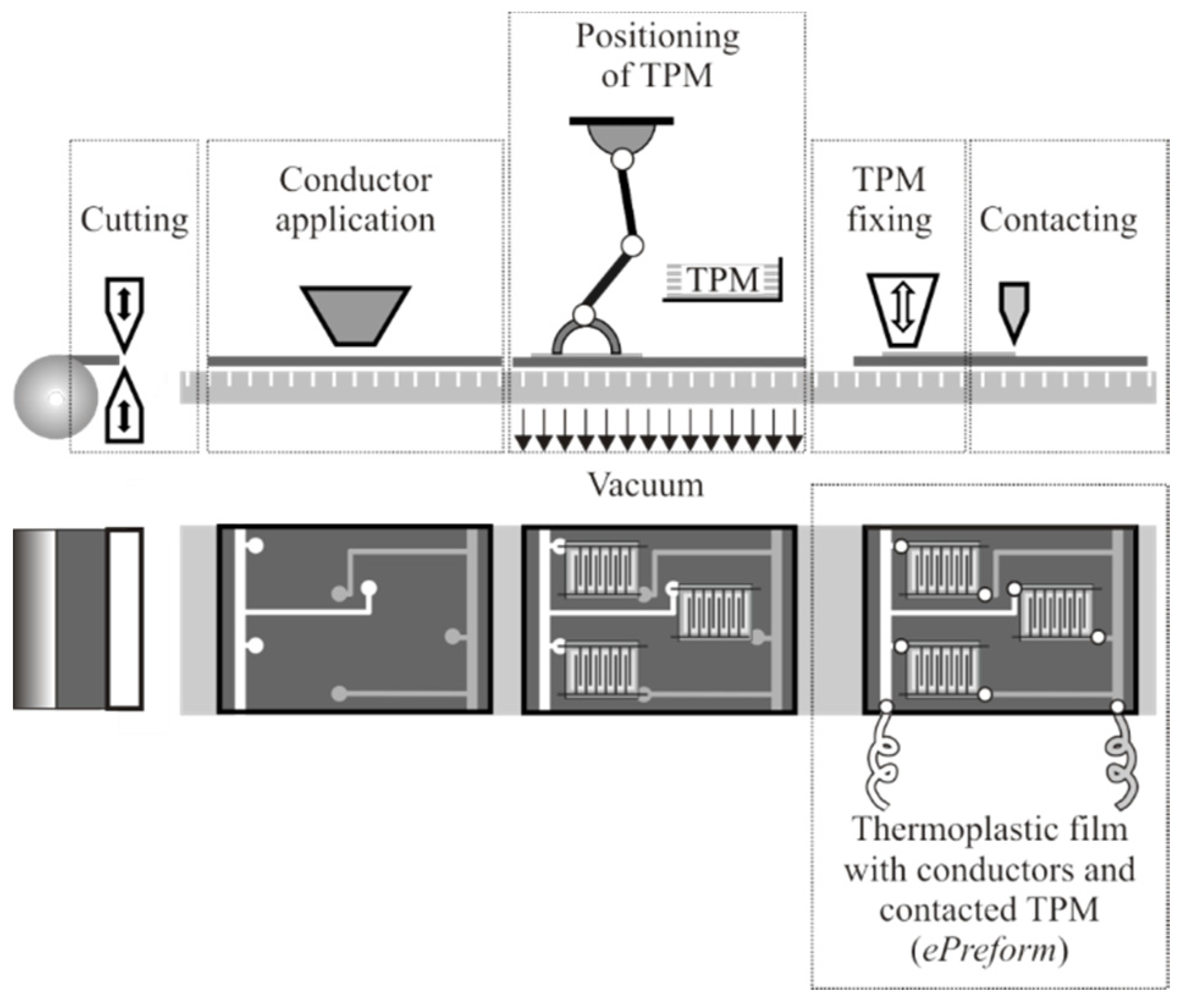
3.2. Manufacturing Process
3.3. Experimental Investigations
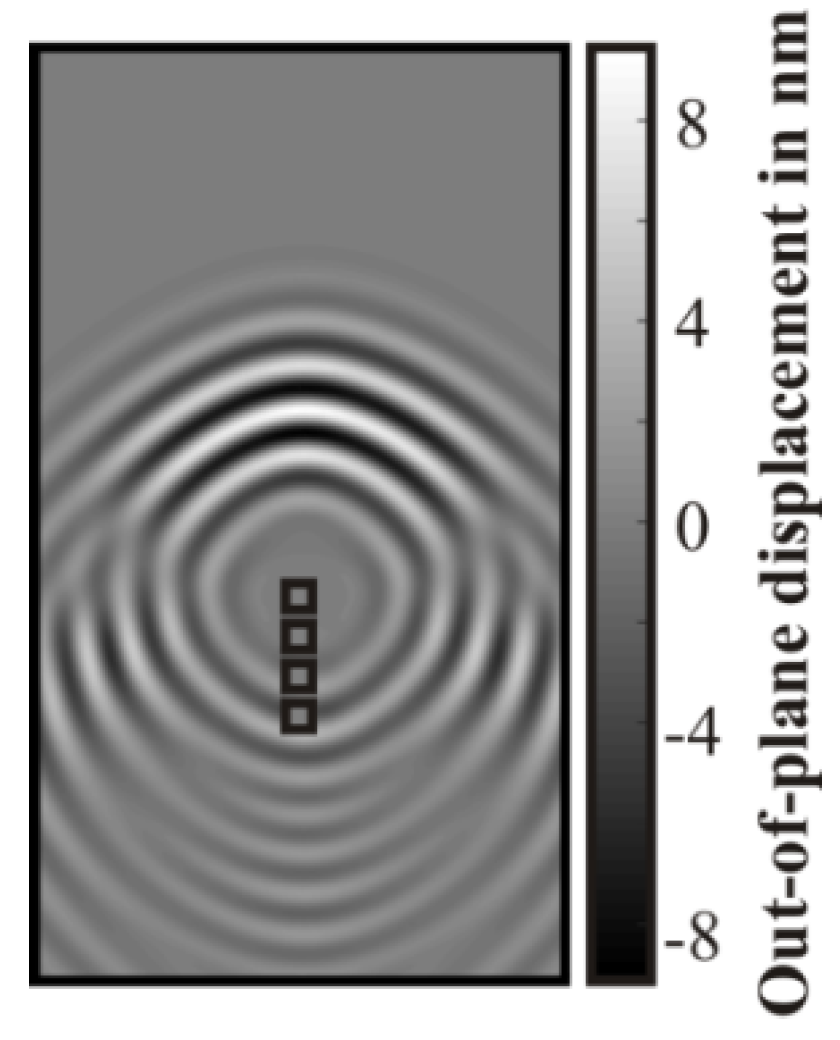
3.3.1. Laser Doppler Vibrometry
3.3.2. Microphone Measurements
3.3.3. Propagation of Structural Mechanical Waves
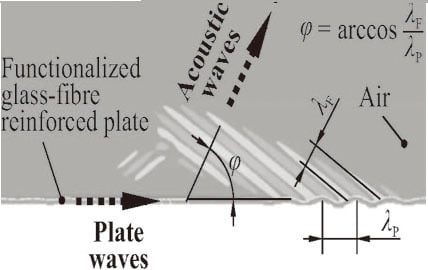
3.3.4. Propagation of Acoustic Waves
4. Conclusions and Outlook
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Property | Symbol | Value and Unit |
|---|---|---|
| Young’s Modulus | E∥ | 19.83 GPa |
| E⊥ | 19.37 GPa | |
| Shear Modulus | G# | 7.3 GPa |
| Poisson’s ratio | υ∥⊥ | 0.17 |
| Density | ρ | 1.8 g/cm3 |
| Property | Symbol | Value and Unit |
|---|---|---|
| Density | ρ | 7.8 g/cm3 |
| Young’s Modulus | E11 | 122 GPa |
| E21 | 57 GPa | |
| E31 | 54 GPa | |
| E22 | 122 GPa | |
| E23 | 54 GPa | |
| E33 | 103 GPa | |
| E44 | 34 GPa | |
| E55 | 33 GPa | |
| E66 | 33 GPa | |
| Permittivity in vacuum | ε0 | 8.85 × 10−12 F/m |
| Relative permittivity | εT11 | 413 |
| εT33 | 877 | |
| Piezoelectric stress coefficients | e31 | −7.1 C/m2 |
| e33 | 14.4 C/m2 | |
| e15 | 15.2 C/m2 |
References
- Dumstorff, G.; Paul, S.; Lang, W. Integration without disruption: The basic challenge of sensor integration. Sens. J. IEEE 2014, 14, 2102–2111. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg grating sensors toward structural health monitoring in composite materials: Challenges and solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef] [PubMed]
- Reddy, J.N. On laminated composite plates with integrated sensors and actuators. Eng. Struct. 1999, 21, 568–593. [Google Scholar] [CrossRef]
- Zysset, C.; Kinkeldei, T.W.; Münzenrieder, N.; Cherenack, K.; Tröster, G. Integration method for electronics in woven textiles. Compon. Packag. Manuf. Technol. IEEE Trans. 2012, 2, 1107–1117. [Google Scholar] [CrossRef]
- Pfeifer, G.; Starke, E.; Fischer, W.J.; Roscher, K.U.; Landgraf, J. Sensornetzwerke in faserverstärkten Verbundwerkstoffen mit drahtloser Signalübertragung. Z. Kunststofftechnik/J. Plast. Technol. 2007, 5, 1–15. (In German) [Google Scholar]
- Roscher, K.-U.; Grätz, H.; Heinig, A.; Fischer, W.-J.; Pfeifer, G.; Starke, E. Integrated sensor network with event-driven activation for recording impact events in textile-reinforced composites. In Proceedings of the 2007 IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007; pp. 128–131.
- Hufenbach, W.; Adam, F.; Körner, I.; Winkler, A.; Weck, D. Combined joining technique for thermoplastic composites with embedded sensor networks. Available online: http://jim.sagepub.com/content/early/2013/01/03/1045389X12471870 (accessed on 13 February 2016).
- Kostka, P.; Holeczek, K.; Filippatos, A.; Langkamp, A.; Hufenbach, W. In situ integrity assessment of a smart structure based on the local material damping. J. Intel. Mater. Syst. and Struct. 2013, 24, 299–309. [Google Scholar] [CrossRef]
- Kostka, P.; Holeczek, K.; Hufenbach, W. Structure-integrated active damping system: Integral strain-based design strategy for the optimal placement of functional elements. Int. J. Compos. Mater. 2013, 3, 53–58. [Google Scholar]
- Hufenbach, W.; Gude, M.; Heber, T. Embedding versus adhesive bonding of adapted piezoceramic modules for function-integrative thermoplastic composite structures. Compos. Sci. Technol. 2011, 71, 1132–1137. [Google Scholar] [CrossRef]
- Moharana, S.; Bhalla, S. Influence of adhesive bond layer on power and energy transduction efficiency of piezo-impedance transducer. J. Intell. Mater. Syst. Struct. 2014, 26, 247–259. [Google Scholar] [CrossRef]
- Hufenbach, W.; Gude, M.; Heber, T. Development of novel piezoceramic modules for adaptive thermoplastic composite structures capable for series production. In 22nd Eurosensors Conference, Dersden, Germany, 7–10 September 2008; pp. 22–27.
- Hufenbach, W.; Modler, N.; Winkler, A. Sensitivity analysis for the manufacturing of thermoplastic e-preforms for active textile reinforced thermoplastic composites. Procedia Mater. Sci. 2013, 2, 1–9. [Google Scholar] [CrossRef]
- Raghavan, A.; Cesnik, C.E.S. Review of guided-wave structural health monitoring. Shock. Vib. Dig. 2007, 39, 91–114. [Google Scholar] [CrossRef]
- Staszewski, W.J.; Lee, B.C.; Mallet, L.; Scarpa, F. Structural health monitoring using scanning laser vibrometry: I. Lamb wave sensing. Smart Mater. Struct. 2004, 13, 251–260. [Google Scholar] [CrossRef]
- Holeczek, K.; Kostka, P.; Modler, N. Dry friction contribution to damage-caused increase of damping in fiber-reinforced polymer-based composites. Adv. Eng. Mater. 2014, 16, 1284–1292. [Google Scholar] [CrossRef]
- Kostka, P.; Holeczek, K.; Hufenbach, W. A new methodology for the determination of material damping distribution based on tuning the interference of solid waves. Eng. Struct. 2015, 83, 1–6. [Google Scholar] [CrossRef]
- Holeczek, K.; Dannemann, M.; Modler, N. Auslegung reflexionsfreier Dämpfungsmaßnahmen für mechanische Festkörperwellen. In Proceedings of the VDI-Fachtagung Schwingungsdämpfun, Leonberg, Germany, 22–23 September 2015; pp. 155–170. (In German)
- Brekhovskikh, L. Waves in Layered Media, 2nd ed.; Elsevier Science: Oxford, UK, 1980. [Google Scholar]
- Kunadt, A.; Pfeifer, G.; Fischer, W.J. Ultrasound flow sensor based on arrays of piezoelectric transducers integrated in a composite: Materials Science Engineering, Symposium B6—Hybrid Structures. Procedia Mater. Sci. 2013, 2, 160–165. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge Univ. Press: Cambridge, UK, 2004. [Google Scholar]
- Li, J.; Rose, J.L. Implementing guided wave mode control by use of a phased transducer array. Ultrason. Ferroelectr. Freq. Control, IEEE Trans. 2001, 48, 761–768. [Google Scholar] [CrossRef]
- Yu, L.; Giurgiutiu, V. In-situ optimized PWAS phased arrays for Lamb wave structural health monitoring. J. Mech. Mater. Struct. 2007, 2, 459–487. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Tuned Lamb Wave Excitation and Detection with Piezoelectric Wafer Active Sensors for Structural Health Monitoring. J. Intell. Mater. Syst. Struct. 2005, 16, 291–305. [Google Scholar] [CrossRef]
- Moulin, E.; Bourasseau, N.; Assaad, J.; Delebarre, C. Lamb-wave beam-steering for integrated health monitoring applications. In Proceedings of the Nondestructive Evaluation and Health Monitoring of Aerospace Materials and Composites, Gyekenyesi, San Diego, CA, USA, March 2003; pp. 124–131.
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors; Elsevier/Academic Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- ANSYS, Release 15.0; Software for Engineering Analysis; ANSYS® Academic Research: Pittsburgh, Pennsylvania, USA, 2013.
- Winkler, A.; Modler, N. Online poling of thermoplastic-compatible piezoceramic modules during the manufacturing process of active fiber-reinforced composites. Mater. Sci. Forum, 2015, 825–826, 787–794. [Google Scholar] [CrossRef]
- Bond-Laminates GmbH. Material Data Sheet: Tepex® dynalite 102-RG600(x)/47% Roving Glass–PA 6 Consolidated Composite Laminate, 2014. MatWeb: Material property data. Available online: http://bond-laminates.com/uploads/tx_lxsmatrix/ MDS_102-RG600_x_-47_.pdf (accessed on 13 February 2016).
- Physik Instrumente (PI) GmbH & Co. KG. Available online: http://www.piceramic.com/download/PI_Ceramic_Material_Data.pdf (accessed on 13 February 2016).












© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holeczek, K.; Starke, E.; Winkler, A.; Dannemann, M.; Modler, N. Numerical and Experimental Characterization of Fiber-Reinforced Thermoplastic Composite Structures with Embedded Piezoelectric Sensor-Actuator Arrays for Ultrasonic Applications. Appl. Sci. 2016, 6, 55. https://doi.org/10.3390/app6030055
Holeczek K, Starke E, Winkler A, Dannemann M, Modler N. Numerical and Experimental Characterization of Fiber-Reinforced Thermoplastic Composite Structures with Embedded Piezoelectric Sensor-Actuator Arrays for Ultrasonic Applications. Applied Sciences. 2016; 6(3):55. https://doi.org/10.3390/app6030055
Chicago/Turabian StyleHoleczek, Klaudiusz, Eric Starke, Anja Winkler, Martin Dannemann, and Niels Modler. 2016. "Numerical and Experimental Characterization of Fiber-Reinforced Thermoplastic Composite Structures with Embedded Piezoelectric Sensor-Actuator Arrays for Ultrasonic Applications" Applied Sciences 6, no. 3: 55. https://doi.org/10.3390/app6030055
APA StyleHoleczek, K., Starke, E., Winkler, A., Dannemann, M., & Modler, N. (2016). Numerical and Experimental Characterization of Fiber-Reinforced Thermoplastic Composite Structures with Embedded Piezoelectric Sensor-Actuator Arrays for Ultrasonic Applications. Applied Sciences, 6(3), 55. https://doi.org/10.3390/app6030055