Influence of Membrane Vibration on Particles Rejection Using a Slotted Pore Membrane Microfiltration
Abstract
:1. Introduction
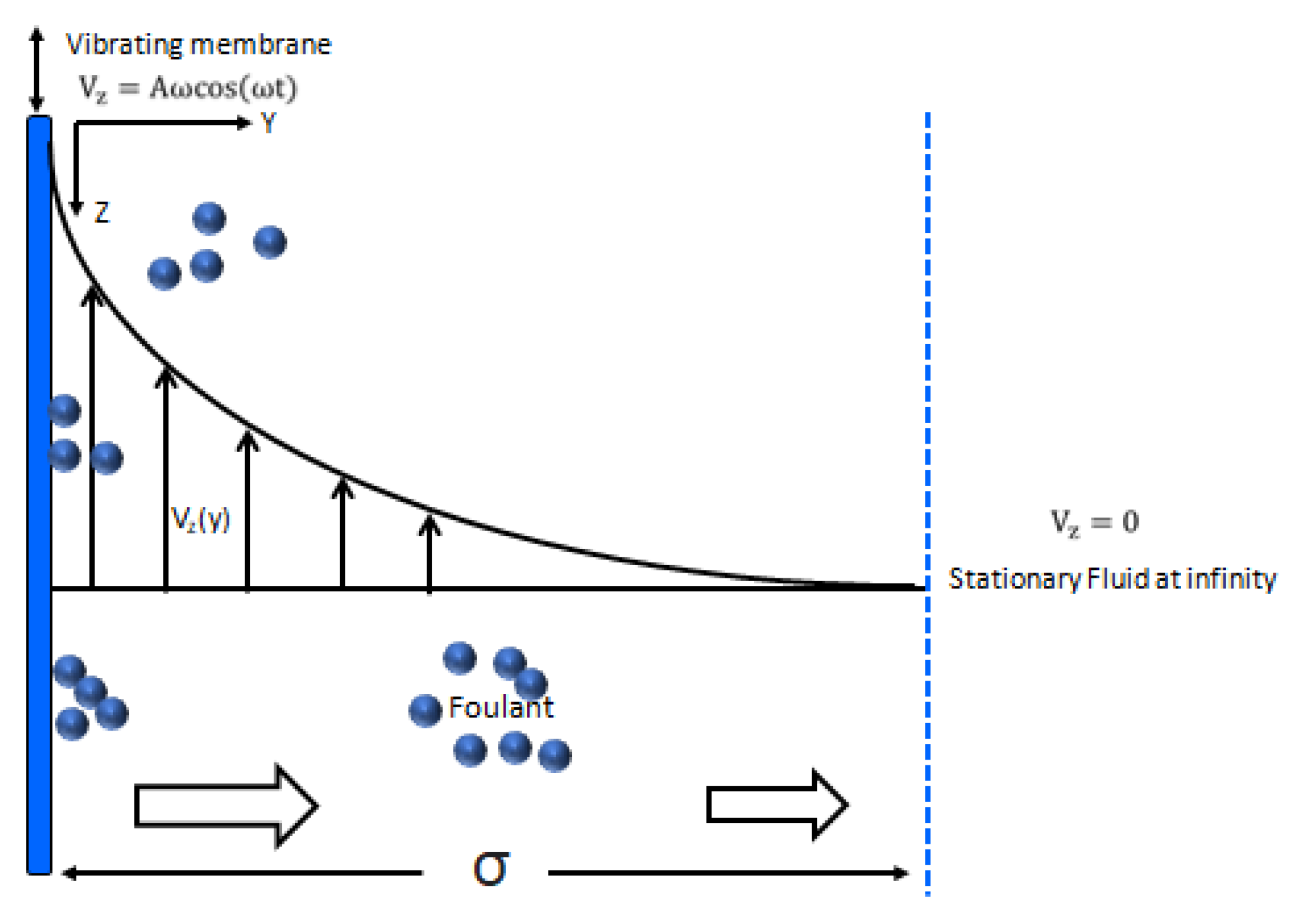
2. Mathematical Model
3. Experimental Methodology
3.1. Oscilating Membrane Filtration
3.2. Materials Used
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Amplitude of oscillation (m) |
| Z(y,t) | Instantaneous displacement of an immersed oscillating membrane along z-axis (m) |
| t | Time (s) |
| Vz | Velocity of the fluid in z direction (m/s) |
| y | Lateral coordinates (m) |
| z | Directional Coordinate (m) |
| Greek Symbols | |
| γ | Shear rate (1/s) |
| γs | Shear rate at membrane surface (1/s) |
| µ | Fluid dynamic viscosity (kg/ms) |
| ʋ | Fluid kinematic viscosity (m2/s) |
| ρ | Fluid density (kg/m3) |
| ω | Angular Frequency (rad/s) |
| I | |
| ℜe | Real part |
Appendix A
References
- Cheryan, M.; Rajagopalan, N. Membrane processing of oily streams. Wastewater treatment and waste reduction. J. Membr. Sci. 1998, 151, 13–28. [Google Scholar] [CrossRef]
- Faksness, L.-G.; Grini, P.G.; Daling, P.S. Partitioning of semi-soluble organic compounds between the water phase and oil droplets in produced water. Mar. Pollut. Bull. 2004, 48, 731–742. [Google Scholar] [CrossRef] [PubMed]
- Fakhru’L-Razi, A.; Pendashteh, A.; Abdullah, L.C.; Biak, D.R.A.; Madaeni, S.S.; Abidin, Z.Z. Review of technologies for oil and gas produced water treatment. J. Hazard. Mater. 2009, 170, 530–551. [Google Scholar] [CrossRef] [PubMed]
- Jiménez, S.; Micó, M.M.; Arnaldos, M.; Medina, F.; Contreras, S. State of the art of produced water treatment. Chemosphere 2018, 192, 186–208. [Google Scholar] [CrossRef]
- Rezakazemi, M.; Khajeh, A.; Mesbah, M. Membrane filtration of wastewater from gas and oil production. Environ. Chem. Lett. 2017, 16, 367–388. [Google Scholar] [CrossRef]
- Dezhi, S.; Chung, J.S.; Xiaodong, D.; Ding, Z. Demulsification of water-in-oil emulsion by wetting coalescence materials in stirred- and packed-columns. Colloids Surf. A Physicochem. Eng. Asp. 1999, 150, 69–75. [Google Scholar] [CrossRef]
- Eow, J.S.; Ghadiri, M.; Sharif, A.O.; Williams, T.J. Electrostatic enhancement of coalescence of water droplets in oil: A review of the current understanding. Chem. Eng. J. 2001, 84, 173–192. [Google Scholar] [CrossRef]
- Partovinia, A.; Naeimpoor, F. Phenanthrene biodegradation by immobilized microbial consortium in polyvinyl alcohol cryogel beads. Int. Biodeterior. Biodegrad. 2013, 85, 337–344. [Google Scholar] [CrossRef]
- Partovinia, A.; Naeimpoor, F. Comparison of phenanthrene biodegradation by free and immobilized cell systems: Formation of hydroxylated compounds. Environ. Sci. Pollut. Res. 2014, 21, 5889–5898. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, D.; Jiang, L.; Jin, J. Recent progress in developing advanced membranes for emulsified oil/water separation. NPG Asia Mater. 2014, 6, e101. [Google Scholar] [CrossRef]
- Jepsen, K.L.; Bram, M.V.; Pedersen, S.; Yang, Z. Membrane Fouling for Produced Water Treatment: A Review Study From a Process Control Perspective. Water 2018, 10, 847. [Google Scholar] [CrossRef] [Green Version]
- Widodo, S.; Ariono, D.; Khoiruddin, K.; Hakim, A.N.; Wenten, I.G. Recent advances in waste lube oils processing technologies. Environ. Prog. Sustain. Energy 2018, 37, 1867–1881. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wachinski, A. Membrane Processes for Water Reuse; McGraw Hill Professional: London, UK, 2012. [Google Scholar]
- Padaki, M.; Murali, R.S.; Abdullah, M.S.; Misdan, N.; Moslehyani, A.; Kassim, M.A.; Hilal, N.; Ismail, A.F. Membrane technology enhancement in oil—Water separation. Rev. Desalin. 2015, 357, 197–207. [Google Scholar] [CrossRef]
- Fane, A.; Tang, C.; Wang, R. Membrane Technology for Water: Microfiltration, Ultrafiltration, Nanofiltration, and Reverse Osmosis. Treatise Water Sci. 2011, 301–335. [Google Scholar] [CrossRef]
- Patterson, J.W. Industrial Wastewater Treatment Technology; United States 1985. Available online: https://www.osti.gov/biblio/7253209 (accessed on 9 September 2021).
- Bilstad, T.; Espedal, E. Membrane separation of produced water. Water Sci. Technol. 1996, 34, 239–246. [Google Scholar] [CrossRef]
- Huang, S.; Ras, R.H.; Tian, X. Antifouling membranes for oily wastewater treatment: Interplay between wetting and membrane fouling. Curr. Opin. Colloid Interface Sci. 2018, 36, 90–109. [Google Scholar] [CrossRef] [Green Version]
- Nazzal, F.F.; Wiesner, M.R. Microfiltration of oil-in-water emulsions. Water Environ. Res. 1996, 68, 1187–1191. [Google Scholar] [CrossRef] [Green Version]
- Pope, J.; Yao, S.; Fane, A. Quantitative measurements of the concentration polarisation layer thickness in membrane filtration of oil-water emulsions using NMR micro-imaging. J. Membr. Sci. 1996, 118, 247–257. [Google Scholar] [CrossRef]
- Holdich, R.; Cumming, I.; Smith, I. Crossflow microfiltration of oil in water dispersions using surface filtration with imposed fluid rotation. J. Membr. Sci. 1998, 143, 263–274. [Google Scholar] [CrossRef]
- Cumming, I.; Holdich, R.; Smith, I. The rejection of oil by microfiltration of a stabilised kerosene/water emulsion. J. Membr. Sci. 2000, 169, 147–155. [Google Scholar] [CrossRef]
- Ullah, A.; Starov, V.; Naeem, M.; Holdich, R. Microfiltration of deforming oil droplets on a slotted pore membrane and sustainable flux rates. J. Membr. Sci. 2011, 382, 271–277. [Google Scholar] [CrossRef]
- Ullah, A.; Habib, M.; Khan, S.W.; Ahmad, M.; Starov, V. Membrane oscillation and oil drop rejection during produced water purification. Sep. Purif. Technol. 2015, 144, 16–22. [Google Scholar] [CrossRef]
- Ullah, A.; Holdich, R.; Naeem, M.; Starov, V. Stability and deformation of oil droplets during microfiltration on a slotted pore membrane. J. Membr. Sci. 2012, 401–402, 118–124. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Aurelle, Y.; Roques, H. Concentration polarization, membrane fouling and cleaning in ultrafiltration of soluble oil. J. Membr. Sci. 1984, 19, 23–38. [Google Scholar] [CrossRef]
- Lipp, P.; Lee, C.; Fane, A.; Fell, C. A fundamental study of the ultrafiltration of oil-water emulsions. J. Membr. Sci. 1988, 36, 161–177. [Google Scholar] [CrossRef]
- Nabi, N.; Aimar, P.; Meireles, M. Ultrafiltration of an olive oil emulsion stabilized by an anionic surfactant. J. Membr. Sci. 2000, 166, 177–188. [Google Scholar] [CrossRef]
- Chakrabarty, B.; Ghoshal, A.; Purkait, M.K. Ultrafiltration of stable oil-in-water emulsion by polysulfone membrane. J. Membr. Sci. 2008, 325, 427–437. [Google Scholar] [CrossRef]
- Falahati, H.; Tremblay, A. Flux dependent oil permeation in the ultrafiltration of highly concentrated and unstable oil-in-water emulsions. J. Membr. Sci. 2011, 371, 239–247. [Google Scholar] [CrossRef]
- Lu, D.; Zhang, T.; Ma, J. Ceramic Membrane Fouling during Ultrafiltration of Oil/Water Emulsions: Roles Played by Stabilization Surfactants of Oil Droplets. Environ. Sci. Technol. 2015, 49, 4235–4244. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, T.; Kazemimoghadam, M.; Saadabadi, M. Modeling of membrane fouling and flux decline in reverse osmosis during separation of oil in water emulsions. Desalination 2003, 157, 369–375. [Google Scholar] [CrossRef]
- Peng, H.; Volchek, K.; MacKinnon, M.; Wong, W.; Brown, C. Application on to nanofiltration to water management options for oil sands operation. Desalination 2004, 170, 137–150. [Google Scholar] [CrossRef]
- Ullah, A.; Khan, S.W.; Shakoor, A.; Starov, V. Passage and deformation of oil drops through non-converging and converging micro-sized slotted pore membranes. Sep. Purif. Technol. 2013, 119, 7–13. [Google Scholar] [CrossRef]
- Chandler, M.; Zydney, A. Effects of membrane pore geometry on fouling behavior during yeast cell microfiltration. J. Membr. Sci. 2006, 285, 334–342. [Google Scholar] [CrossRef]
- Kuiper, S.; Brink, R.; Nijdam, W.; Krijnen, G.J.; Elwenspoek, M. Ceramic microsieves: Influence of perforation shape and distribution on flow resistance and membrane strength. J. Membr. Sci. 2002, 196, 149–157. [Google Scholar] [CrossRef]
- Van Rijn, C.J.M.; Veldhuis, G.J.; Kuiper, S. Nanosieves with microsystem technology for microfiltration applications. Nanotechnology 1998, 9, 343–345. [Google Scholar] [CrossRef]
- Kuiper, S.; van Rijn, C.; Nijdam, W.; Raspe, O.; van Wolferen, H.; Krijnen, G.; Elwenspoek, M. Filtration of lager beer with microsieves: Flux, permeate haze and in-line microscope observations. J. Membr. Sci. 2002, 196, 159–170. [Google Scholar] [CrossRef]
- Ullah, A.; Naeem, M.; Holdich, R.G.; Starov, V.M.; Semenov, S. Microfiltration of Deforming Droplets. In UK Colloids 2011; Progress in Colloid and Polymer Science; Starov, V., Griffiths, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 139. [Google Scholar] [CrossRef]
- Ullah, A.; Holdich, R.; Naeem, M.; Starov, V. Shear enhanced microfiltration and rejection of crude oil drops through a slotted pore membrane including migration velocities. J. Membr. Sci. 2012, 421–422, 69–74. [Google Scholar] [CrossRef] [Green Version]
- Ullah, A.; Starov, V.; Naeem, M.; Holdich, R.; Semenov, S. Filtration of suspensions using slit pore membranes. Sep. Purif. Technol. 2012, 103, 180–186. [Google Scholar] [CrossRef]
- Ullah, A.; Holdich, R.; Naeem, M.; Khan, S.W.; Starov, V. Prediction of size distribution of crude oil drops in the permeate using a slotted pore membrane. Chem. Eng. Res. Des. 2014, 92, 2775–2781. [Google Scholar] [CrossRef] [Green Version]
- Ullah, A.; Ahmad, J.; Khan, H.; Khan, S.W.; Zamani, F.; Hasan, S.W.; Starov, V.M.; Chew, J.W. Membrane oscillation and slot (pore) blocking in oil–water separation. Chem. Eng. Res. Des. 2018, 142, 111–120. [Google Scholar] [CrossRef]
- Ullah, A.; Shahzada, K.; Khan, S.W.; Starov, V. Purification of produced water using oscillatory membrane filtration. Desalination 2020, 491, 114428. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, X.; Yan, L.; Bai, Y.; Li, S.; Sorokin, P.; Shao, L. Biomimetic nanoparticle-engineered superwettable mem-branes for efficient oil/water separation. J. Membr. Sci. 2021, 618, 118525. [Google Scholar] [CrossRef]
- Yang, J.; Cui, J.; Xie, A.; Dai, J.; Li, C.; Yan, Y. Facile preparation of superhydrophilic/underwater superoleophobic cellu-lose membrane with CaCO3 particles for oil/water separation. Colloids Surf. A Physicochem. Eng. Asp. 2021, 608, 125583. [Google Scholar] [CrossRef]
- Dhumal, P.S.; Khose, R.V.; Wadekar, P.H.; Lokhande, K.D.; Some, S. Graphene-bentonite supported free-standing, flexible membrane with switchable wettability for selective oil–water separation. Sep. Purif. Technol. 2021, 266, 118569. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Z.; Han, X.; Zhou, X.; Zhang, Y.; Jiang, S.; Yu, Z.; Zhou, X.; Liu, C.; Chu, H. The interaction between microalgae and membrane surface in filtration by uniform shearing vibration membrane. Algal Res. 2020, 50, 102012. [Google Scholar] [CrossRef]






| Frequency (Hz) | No of Drops per 0.4 mL Sample | Concentration of Crude Oil in the Feed (ppm) | Concentration of Crude Oil in the Permeate (ppm) |
|---|---|---|---|
| 25 | 1020 | 400 | 5 |
| 21 | 1606 | 400 | 7 |
| 0 | 5092 | 400 | 21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, A.; Alam, K.; Khan, S.U.; Starov, V.M. Influence of Membrane Vibration on Particles Rejection Using a Slotted Pore Membrane Microfiltration. Membranes 2021, 11, 709. https://doi.org/10.3390/membranes11090709
Ullah A, Alam K, Khan SU, Starov VM. Influence of Membrane Vibration on Particles Rejection Using a Slotted Pore Membrane Microfiltration. Membranes. 2021; 11(9):709. https://doi.org/10.3390/membranes11090709
Chicago/Turabian StyleUllah, Asmat, Kamran Alam, Saad Ullah Khan, and Victor M. Starov. 2021. "Influence of Membrane Vibration on Particles Rejection Using a Slotted Pore Membrane Microfiltration" Membranes 11, no. 9: 709. https://doi.org/10.3390/membranes11090709
APA StyleUllah, A., Alam, K., Khan, S. U., & Starov, V. M. (2021). Influence of Membrane Vibration on Particles Rejection Using a Slotted Pore Membrane Microfiltration. Membranes, 11(9), 709. https://doi.org/10.3390/membranes11090709








