Dynamic Characteristics Analysis of the DI-SO Cylindrical Spur Gear System Based on Meshing Conditions
Abstract
:1. Introduction
2. Analysis of Meshing Characteristics in the DI-SO Cylindrical Spur Gear System
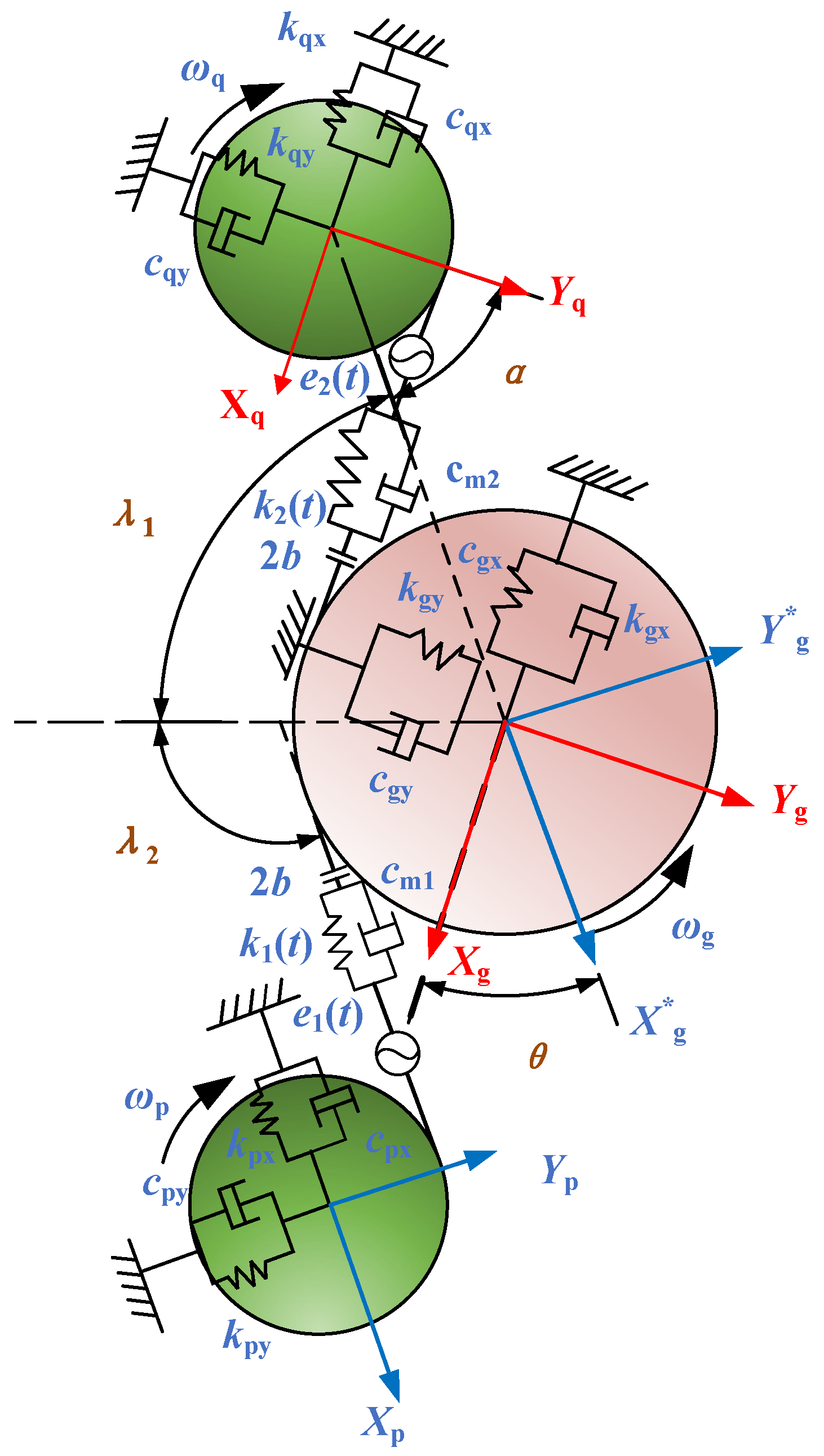
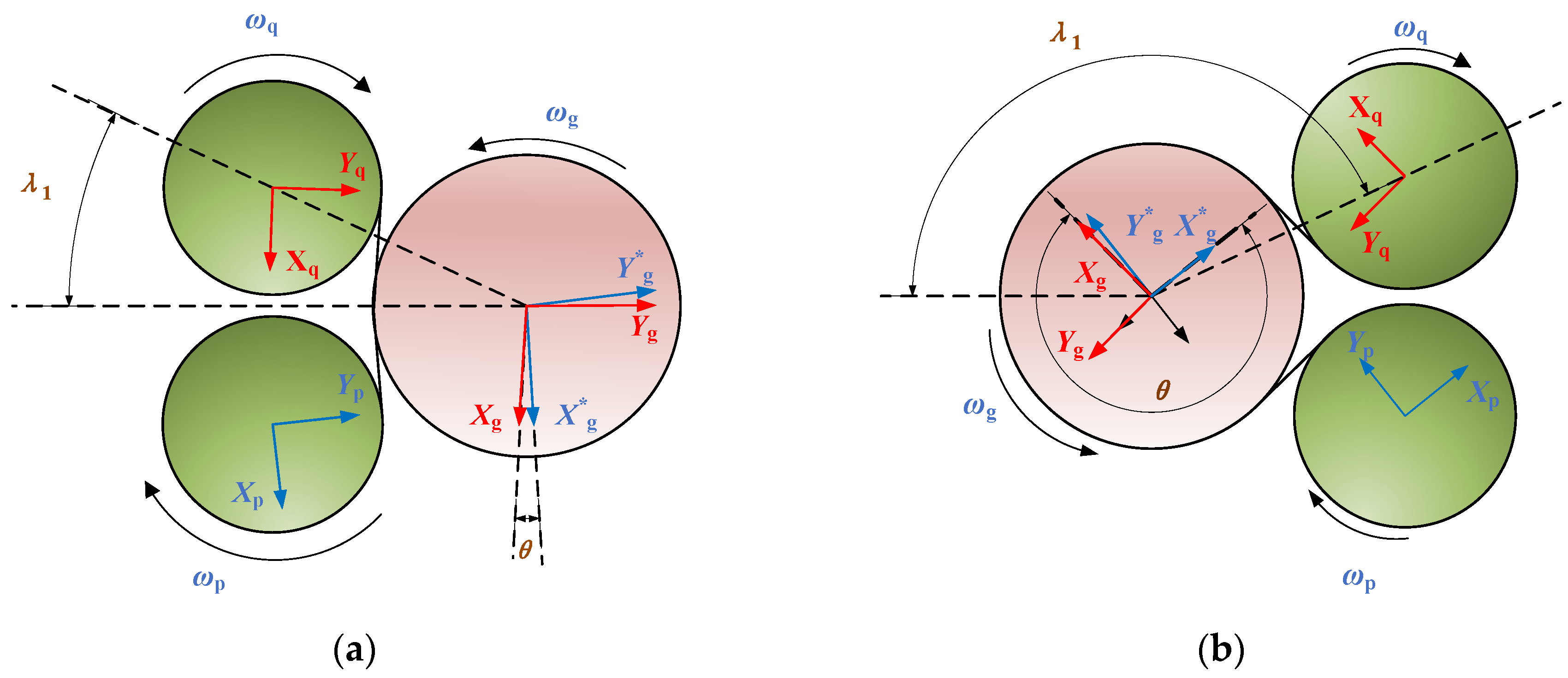
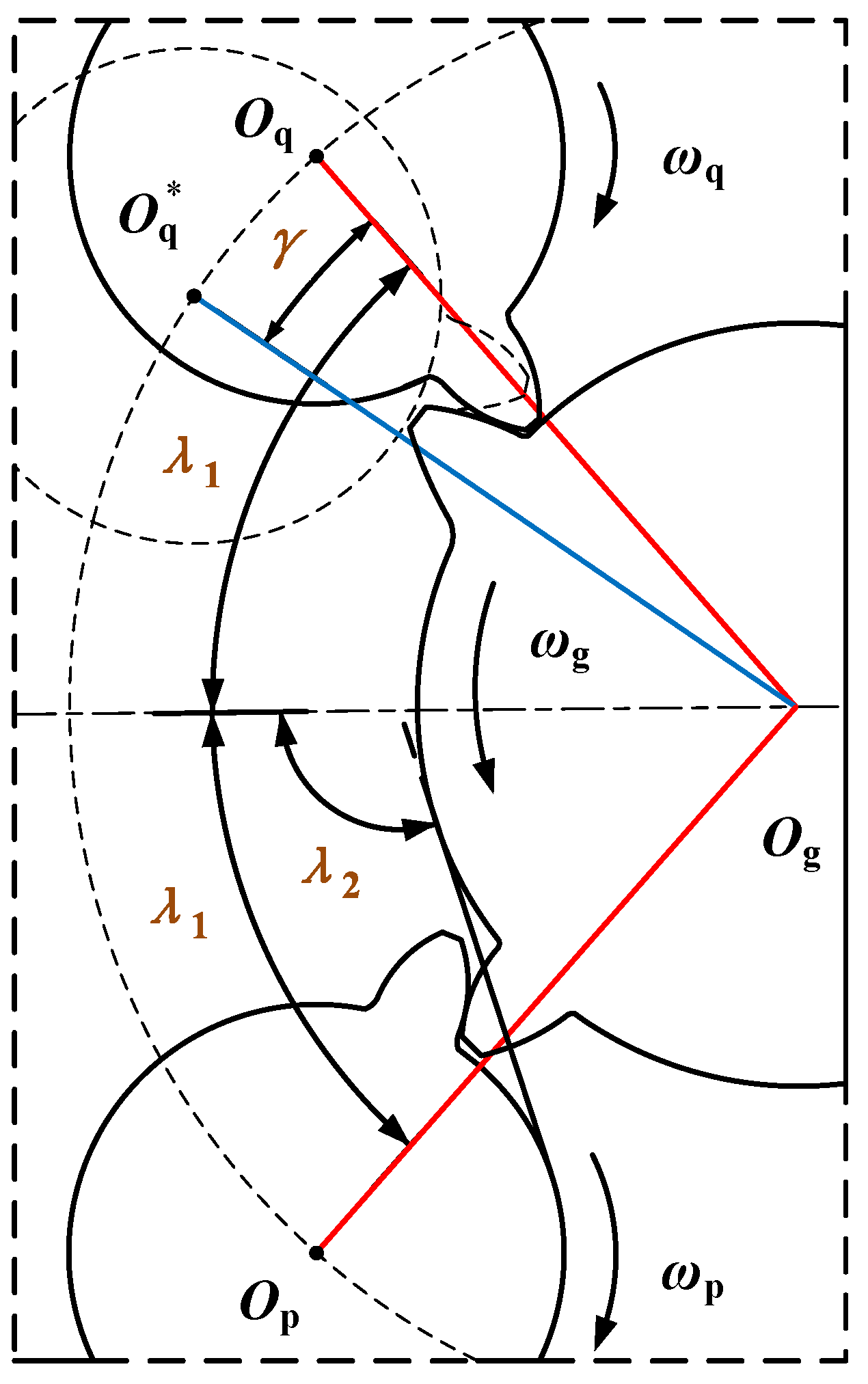
2.1. Analysis of Assembly Angles in the DI-SO Cylindrical Spur Gear System
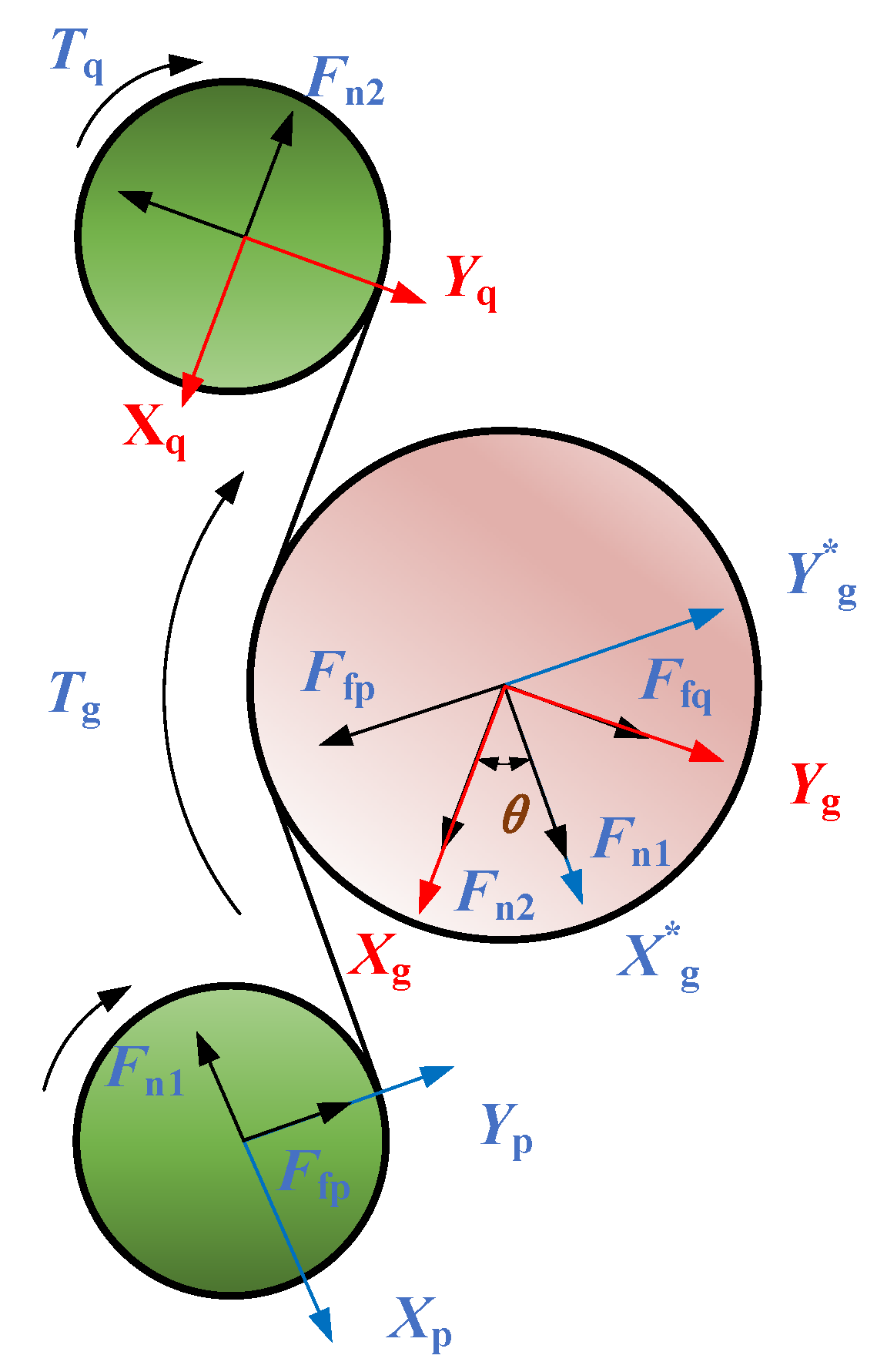
2.2. Analysis of Meshing Force in the DI-SO Cylindrical Spur Gear System
2.3. Analysis of Meshing Conditions in the DI-SO Cylindrical Spur Gear System
3. Dynamic Modeling of the DI-SO Cylindrical Spur Gear System
3.1. Mathematical Description of Time-Varying Parameters
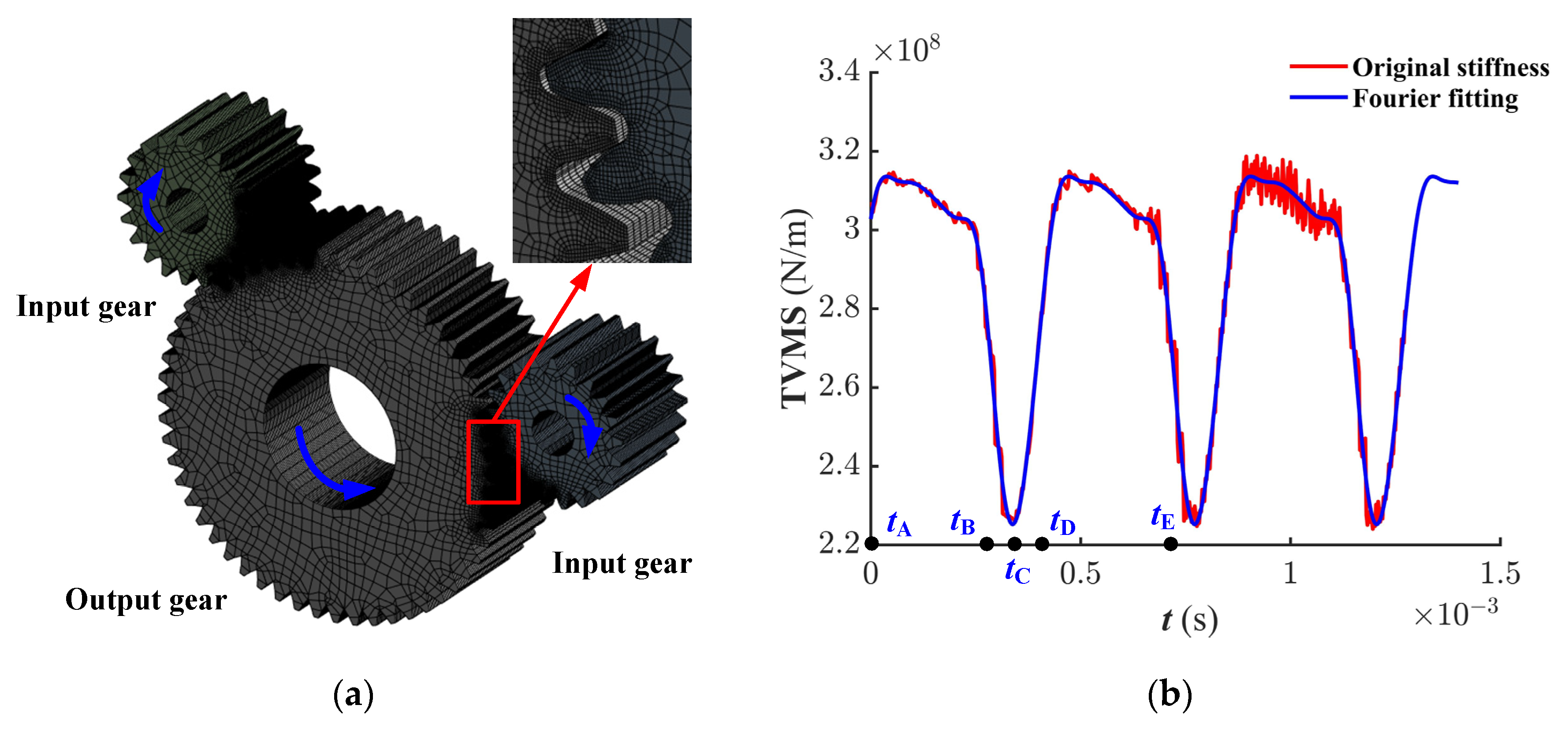
3.1.1. Time-Varying Meshing Stiffness
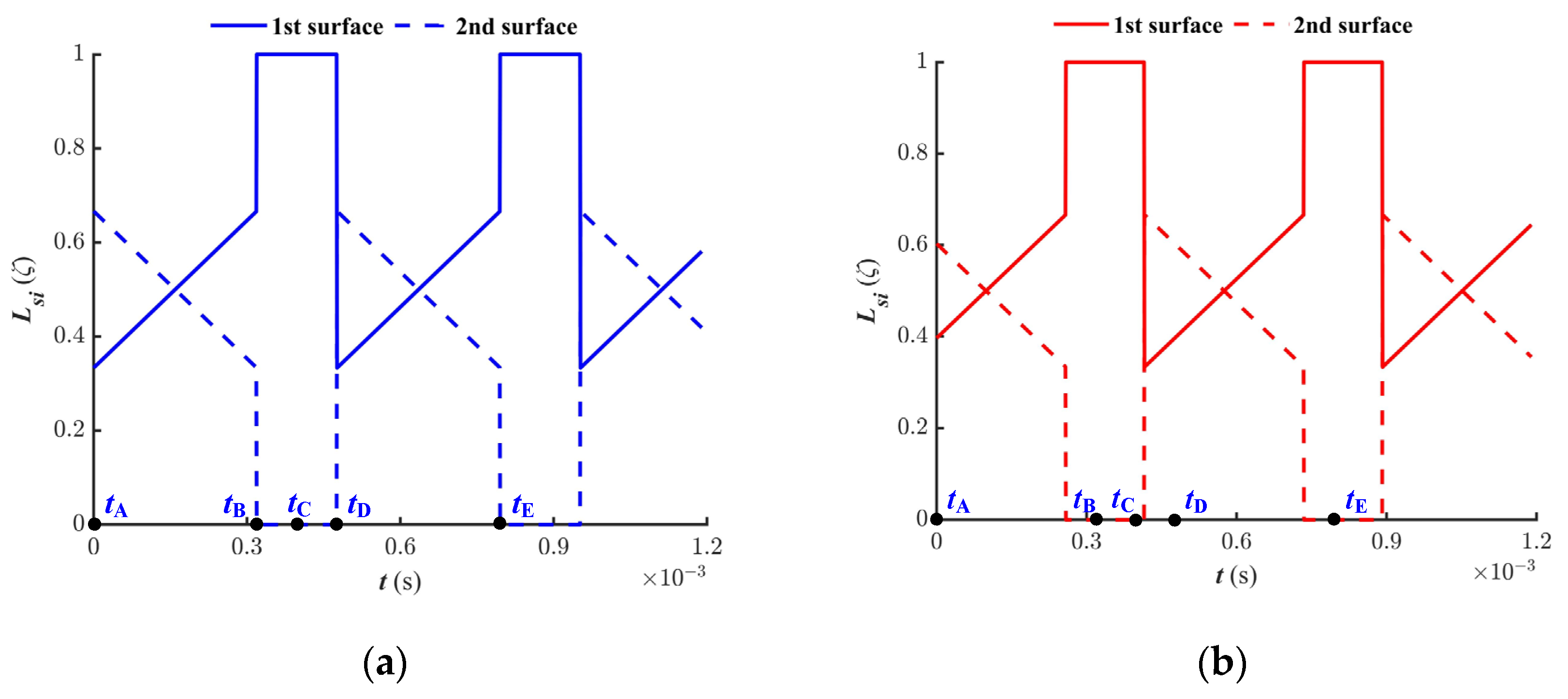
3.1.2. Load-Sharing Ratio
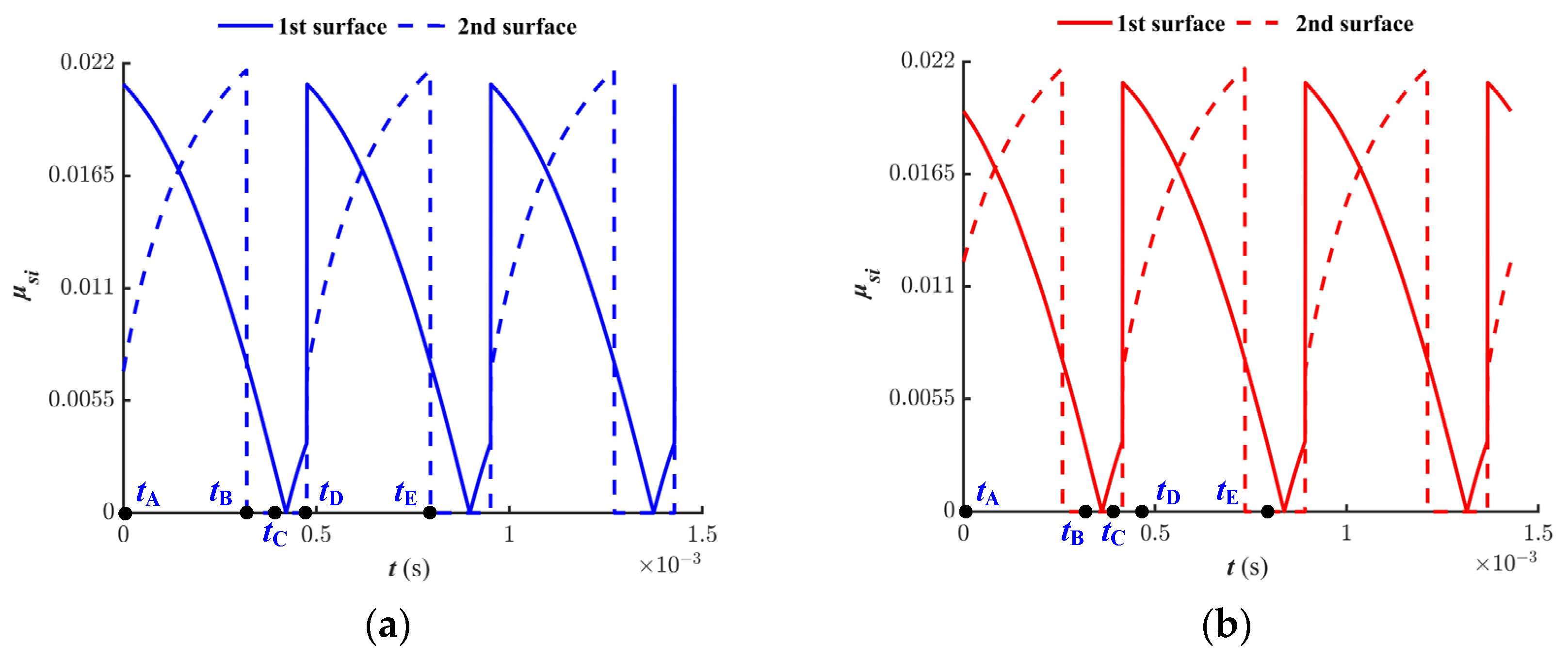
3.1.3. Time-Varying Friction
3.2. The Dynamic Equations of the DI-SO Cylindrical Spur Gear System
4. Nonlinear Dynamic Characteristics of the DI-SO Cylindrical Spur Gear System under Different Meshing Conditions
4.1. The Influence of Meshing Frequency on the Dynamic Characteristics of the DI-SO Cylindrical Spur Gear System
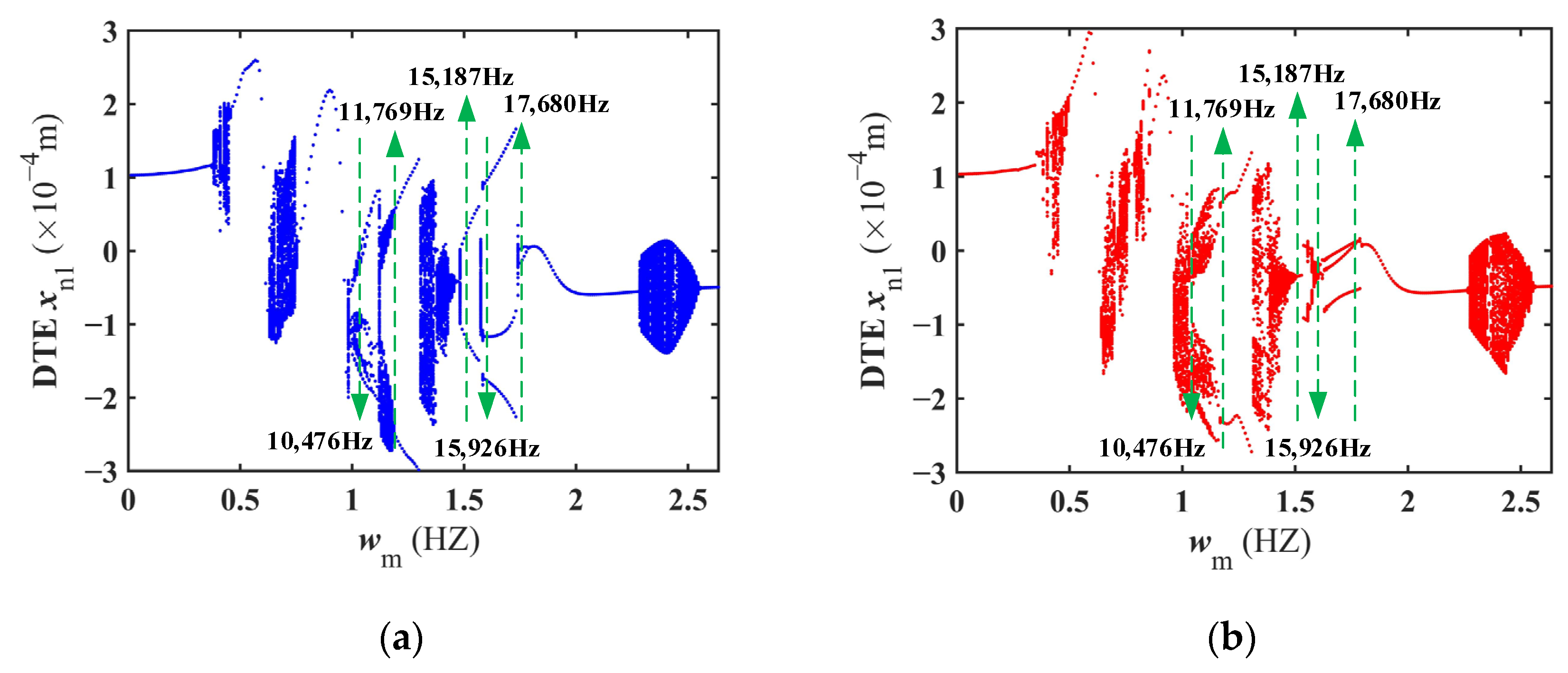
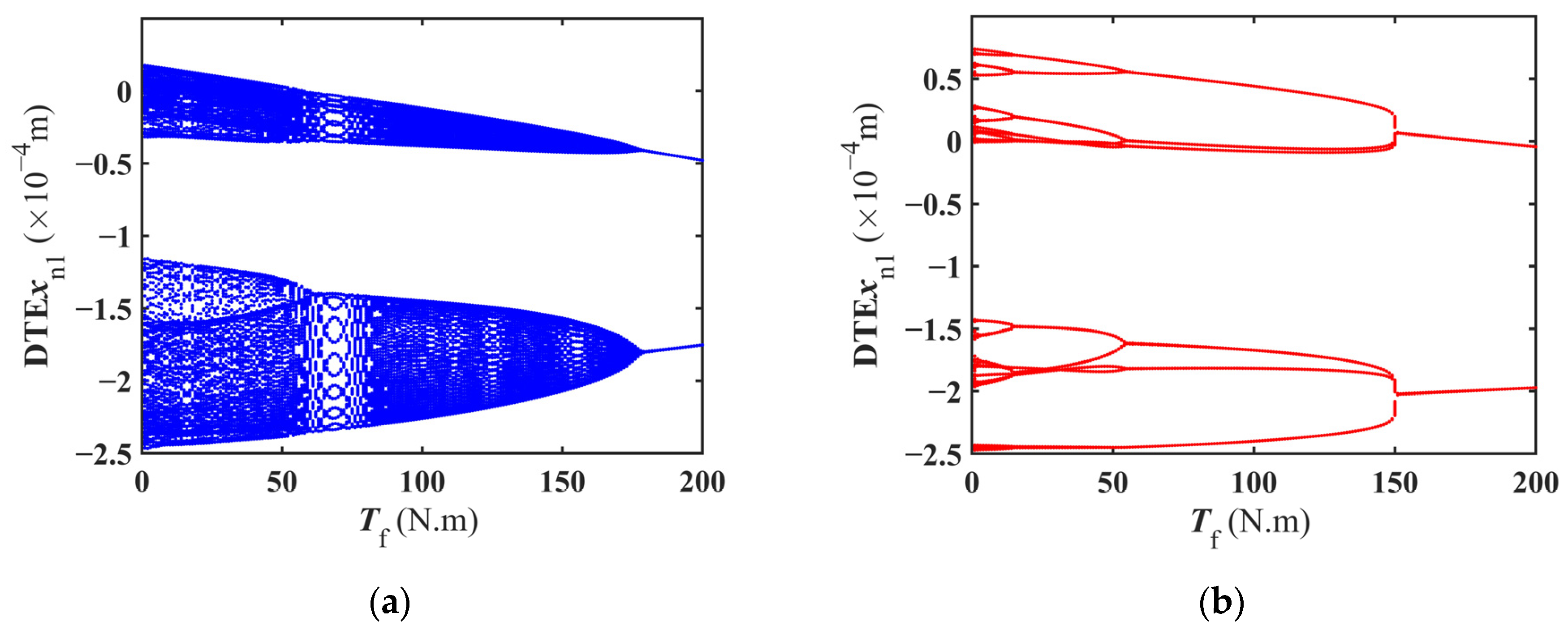
4.1.1. Bifurcation Characteristics of Meshing Frequency
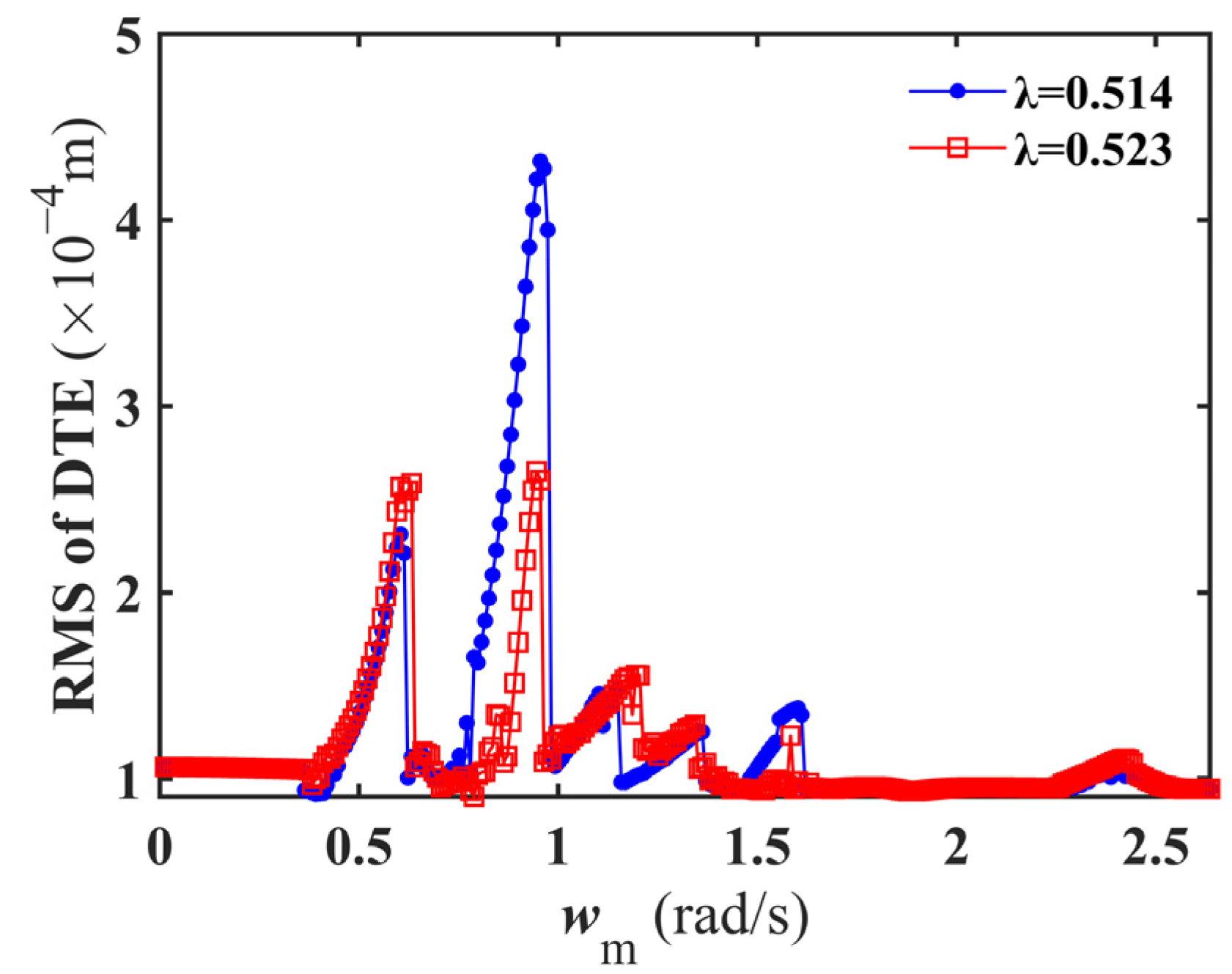
4.1.2. RMS of DTE Vibration Response with Meshing Frequency
4.1.3. Nonlinear Dynamic Behavior at the Medium-Frequency Meshing Stage
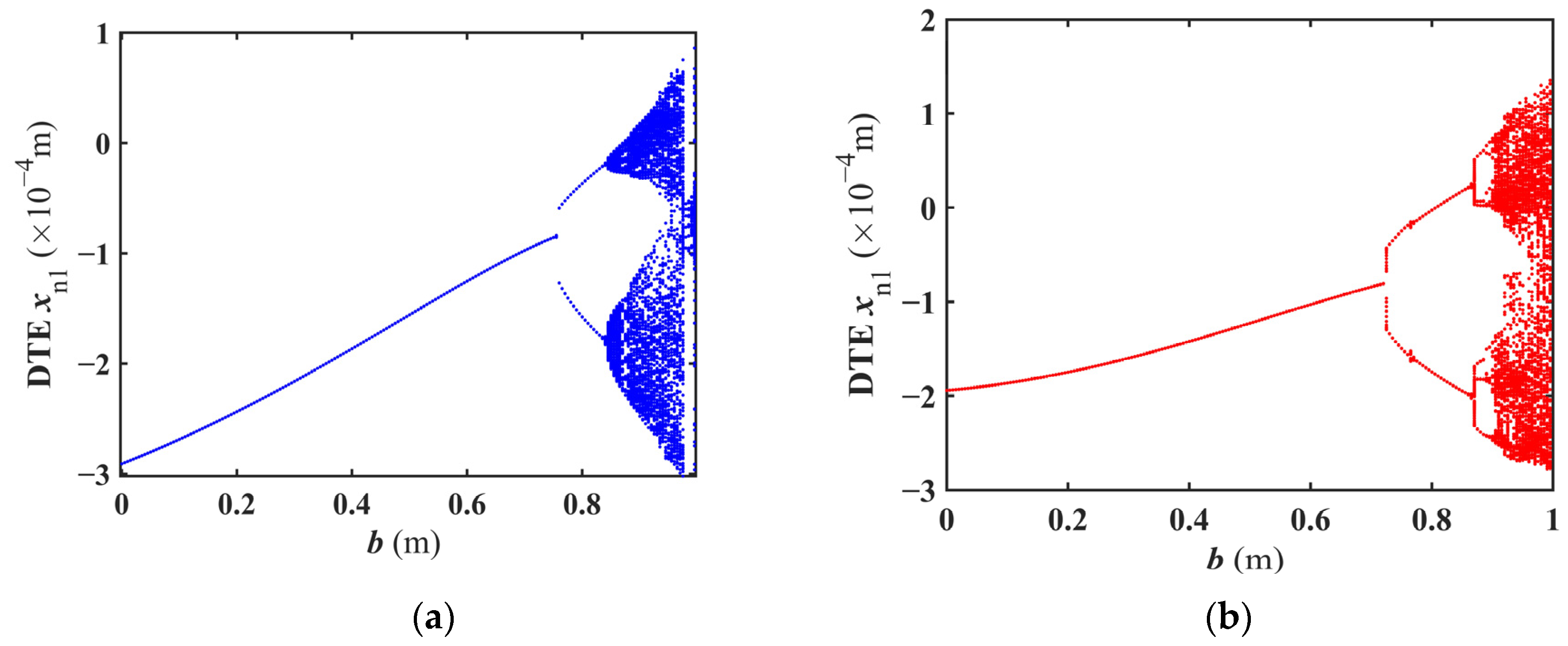
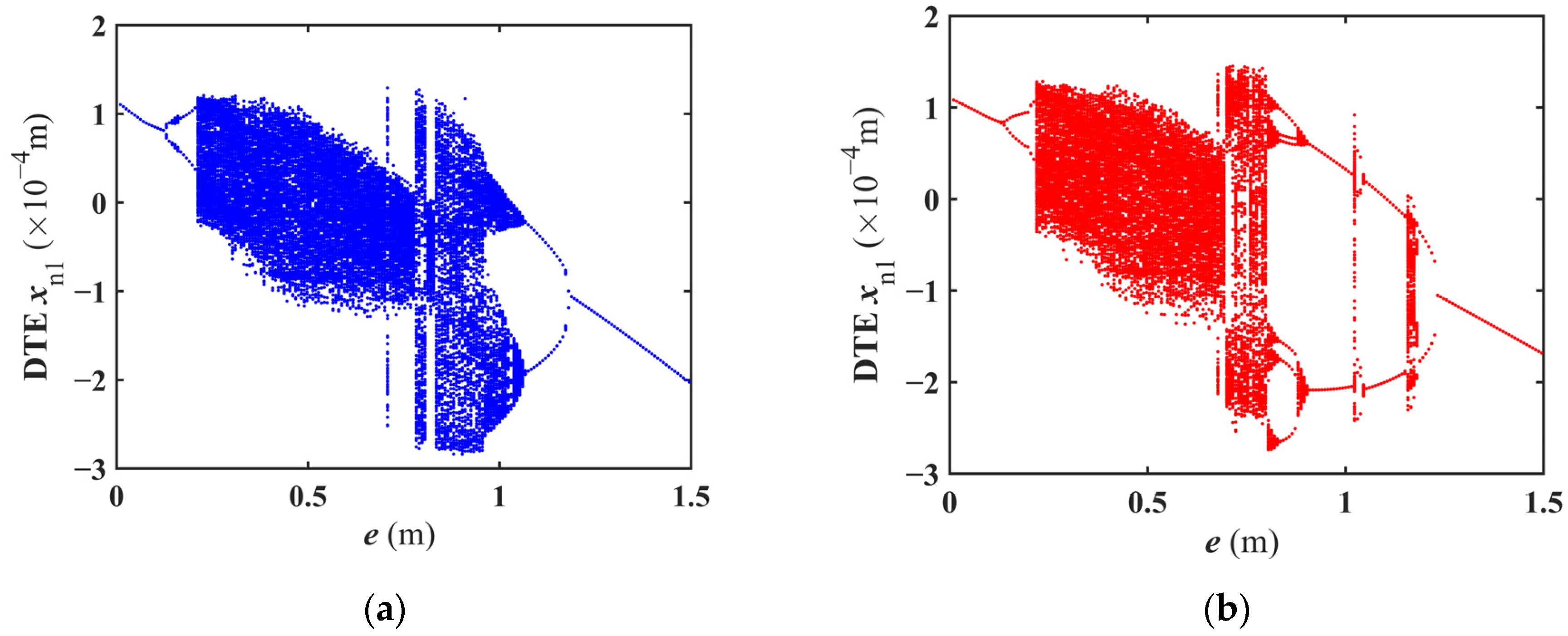
4.2. The Impact of Meshing Frequency on the Dynamic Characteristics of the DI-SO Cylindrical Spur Gear System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kambrath, J.; Yoon, C.; Mathew, J.; Liu, X.; Wang, Y.; Gajanayake, C.; Gupta, A.; Yoon, Y. Mitigation of resonance vibration effects in marine propulsion. IEEE Trans. Ind. Electron. 2018, 66, 6159–6169. [Google Scholar] [CrossRef]
- Manngård, M.; Koene, I.; Lund, W.; Haikonen, S.; Fagerholm, F.A.; Wilczek, M.; Mnich, K.; Keski-Rahkonen, J.; Viitala, R.; Björkqvist, J.; et al. Torque estimation in marine propulsion systems. Mech. Syst. Signal Process. 2022, 172, 108969. [Google Scholar] [CrossRef]
- Tang, S.; Khoo, B.C.; Zhu, Y.; Lim, K.M.; Yuan, S. A light deep adaptive framework toward fault diagnosis of a hydraulic piston pump. Appl. Acoust. 2024, 217, 109807. [Google Scholar] [CrossRef]
- Gürgen, S.; Yazır, D.; Konur, O. Fuzzy fault tree analysis for loss of ship steering ability. Ocean Eng. 2023, 279, 114419. [Google Scholar] [CrossRef]
- Xu, J.; Jiao, C.; Zou, D.; Ta, N.; Rao, Z. Dynamic evolution laws of the DI-SO helical gear system with unsymmetrical load inputs. J. Vib. Eng. Technol. 2021, 9, 1317–1334. [Google Scholar] [CrossRef]
- Mo, S.; Tang, X.; Chen, K.; Zhang, W. Analysis of vibration characteristics of face gear powering-split transmission system. Commun. Nonlinear Sci. 2024, 130, 107750. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Yuan, S. Multiple-signal defect identification of hydraulic pump using an adaptive normalized model and S transform. Eng. Appl. Artif. Intel. 2023, 124, 106548. [Google Scholar] [CrossRef]
- Senjanović, I.; Hadžić, N.; Murawski, L.; Vladimir, N.; Alujević, N.; Cho, D. Analytical procedures for torsional vibration analysis of ship power transmission system. Eng. Struc. 2019, 178, 227–244. [Google Scholar] [CrossRef]
- Liu, Z.; Chang, C.; Hu, H.; Ma, H.; Yuan, K.; Li, X.; Zhao, X.; Peng, Z. Dynamic characteristics of spur gear system with tooth root crack considering gearbox flexibility. Mech. Syst. Signal Process. 2024, 208, 110966. [Google Scholar] [CrossRef]
- Yang, X.; Lei, Y.; Liu, H.; Yang, B.; Li, X.; Li, N. Rigid-flexible coupled modeling of compound multistage gear system considering flexibility of shaft and gear elastic deformation. Mech. Syst. Signal Process. 2023, 200, 110632. [Google Scholar] [CrossRef]
- Inalpolat, M.; Handschuh, M.; Kahraman, A. Influence of indexing errors on dynamic response of spur gear pairs. Mech. Syst. Signal Process. 2015, 60, 391–405. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, C.; Liu, H.; Gu, Z. Mesh stiffness and nonlinear dynamic response of a spur gear pair considering tribo-dynamic effect. Mech. Mach. Theory 2020, 153, 103989. [Google Scholar] [CrossRef]
- Xie, C.; Hua, L.; Lan, J.; Han, X.; Wan, X.; Xiong, X. Improved analytical models for mesh stiffness and load sharing ratio of spur gears considering structure coupling effect. Mech. Syst. Signal Process. 2018, 111, 331–347. [Google Scholar] [CrossRef]
- Yu, W.; Mechefske, C.K.; Timusk, M. The dynamic coupling behaviour of a cylindrical geared rotor system subjected to gear eccentricities. Mech. Mach. Theory 2017, 107, 105–122. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, K.; Huai, T.; Ma, H.; Wang, K. A mesh stiffness method using slice coupling for spur gear pairs with misalignment and lead crown relief. Appl. Math. Model. 2021, 90, 845–861. [Google Scholar] [CrossRef]
- Liu, N.; Ma, H.; Zhao, Z.; Wang, P.; Zhao, X. Dynamic characteristics of gear-rotor system with gear eccentricity and wear fault. Nonlinear Dynam. 2024, 2, 112. [Google Scholar] [CrossRef]
- Xiang, L.; Gao, N.; Hu, A. Dynamic analysis of a planetary gear system with multiple nonlinear parameters. J. Comput. Appl. Math. 2018, 327, 325–340. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yao, Z.; Yang, X.; Sun, R.; Zhao, Y. Nonlinear characteristics of a multi-degree-of-freedom spur gear system with bending-torsional coupling vibration. Mech. Syst. Signal Process. 2019, 121, 810–827. [Google Scholar] [CrossRef]
- Xue, S.; Howard, I.; Wang, C.; Lian, P.; Wang, Y.; Liu, G. Dynamic modelling of the gear system under non-stationary conditions using the iterative convergence of the tooth mesh stiffness. Eng. Fail. Anal. 2022, 131, 105908. [Google Scholar] [CrossRef]
- Yue, K.; Kang, Z.; Zhang, M.; Wang, L.; Shao, Y.; Chen, Z. Study on gear meshing power loss calculation considering the coupling effect of friction and dynamic characteristics. Tribol. Int. 2023, 183, 108378. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, R.; Hu, Z.; Tang, J.; Sun, Z.; Ning, A.; Yang, S. Dynamic modeling and analysis considering friction-wear coupling of gear system. Int. J. Mech. Sci. 2024, 275, 109343. [Google Scholar] [CrossRef]
- Samani, F.S.; Salajegheh, M.; Molaie, M. Nonlinear vibration of the spiral bevel gear under periodic torque considering multiple elastic deformation evaluations due to different bearing supports. SN Appl. Sci. 2021, 3, 772. [Google Scholar] [CrossRef]
- Li, H.; Chen, S.; Tang, J.; Sun, Z.; Hu, Y. Nonlinear dynamic modeling and analysis of spur gear based on gear compatibility conditions. Mech. Mach. Theory 2022, 171, 104767. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, T.; Shao, Y.; Wang, G. The influence of time-varying mesh stiffness on natural characteristics of planetary gear system. J. Phys. Conf. Ser. 2021, 1948, 012079. [Google Scholar] [CrossRef]
- Esmail, E.; Pennestrì, E.; Juber, A. Power losses in two-degrees-of-freedom planetary gear trains: A critical analysis of Radzimovsky’s formulas. Mech. Mach. Theory 2018, 128, 191–204. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Wang, H.; Guo, L. Influence of the random system parameters on the nonlinear dynamic characteristics of gear transmission system. Int. J. of Nonlin. Sci. Num. 2017, 18, 619–630. [Google Scholar] [CrossRef]
- Marques, P.M.; Martins, R.C.; Seabra, J. Gear dynamics and power loss. Tribol. Int. 2016, 97, 400–411. [Google Scholar] [CrossRef]
- Geng, Z.; Chen, M.; Wang, J.; Xia, Y.; Kong, Y.; Xiao, K. Nonlinear dynamic analysis of a spur gear pair system with wear considering the meshing position. Lubricants 2024, 12, 25. [Google Scholar] [CrossRef]
- Duan, L.; Wang, L.; Du, W.; Shao, Y.; Chen, Z. Analytical method for time-varying meshing stiffness and dynamic responses of modified spur gears considering pitch deviation and geometric eccentricity. Mech. Syst. Signal Process. 2024, 218, 111590. [Google Scholar] [CrossRef]
- Wei, S.; Chu, F.L.; Ding, H.; Chen, L. Dynamic analysis of uncertain spur gear systems. Mech. Syst. Signal Process. 2021, 150, 107280. [Google Scholar] [CrossRef]
- Yang, Y. Nonlinear Dynamics of a multi-shaft gear system in parameter-state space. Int. J. Automot. Mech. Eng. 2023, 20, 10684–10694. [Google Scholar] [CrossRef]
- Parker, R.G.; Lin, J. Mesh phasing relationships in planetary and epicyclic gears. J. Mech. Des. 2004, 126, 365–370. [Google Scholar] [CrossRef]
- Zhan, J.; Fard, M.; Jazar, R. A CAD-FEM-QSA integration technique for determining the time-varying meshing stiffness of gear pairs. Measurement 2017, 100, 139–149. [Google Scholar] [CrossRef]
- Shi, J.F.; Gou, X.F.; Zhu, L.Y. Modeling and analysis of a spur gear pair considering multi-state mesh with time-varying parameters and backlash. Mech. Mach. Theory 2019, 134, 582–603. [Google Scholar] [CrossRef]
- Xu, H. Development of a Generalized Mechanical Efficiency Prediction Methodology for Gear Pairs; The Ohio State University: Columbus, OH, USA, 2005. [Google Scholar]
- Tan, L.; Hu, Z.; Tang, J.; Sun, Z.; Wang, Z.; Fu, Z.; Wang, Q. Dynamic characteristics analysis of profile-shifted planetary gears considering friction. Meccanica 2024, 59, 193–215. [Google Scholar] [CrossRef]
- Han, L.; Qi, H. Dynamic response analysis of helical gear pair considering the interaction between friction and mesh stiffness. Meccanica 2019, 54, 2325–2337. [Google Scholar] [CrossRef]
- Omar, F.K.; Moustafa, K.A.; Emam, S. Mathematical modeling of gearbox including defects with experimental verification. J. Vib. Control 2012, 18, 1310–1321. [Google Scholar] [CrossRef]
- Tang, S.; Ma, J.; Yan, Z.; Zhu, Y.; Khoo, B.C. Deep transfer learning strategy in intelligent fault diagnosis of rotating machinery. Eng. Appl. Artif. Intel. 2024, 134, 108678. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Xin, X.; Yu, S.; Ma, H.; Han, Q. Dynamic modelling considering nonlinear factors of coupled spur gear system and its experimental research. IEEE Access 2020, 8, 84971–84980. [Google Scholar] [CrossRef]
- Aihara, T.; Sakamoto, K. Theoretical analysis of nonlinear vibration characteristics of gear pair with shafts. Theor. Appl. Mech. Lett. 2022, 12, 100324. [Google Scholar] [CrossRef]


| Harmonic Order j | Amplitude kj (×107 N/m) | Phase Angle ϕj (rad) |
|---|---|---|
| 0 | 28.723 | 0 |
| 1 | 3.661 | 1.434 |
| 2 | 1.932 | −0.548 |
| 3 | 0.659 | 0.874 |
| Parameter Type | Symbol | Input/Output Gear Values |
|---|---|---|
| Number of teeth | Zp (Zq)/Zg | 21/55 |
| Pressure angle (°) | α | 20 |
| Modulus (mm) | m | 5 |
| Tooth width (mm) | B | 90 |
| Poisson’s ratio | v | 0.3 |
| Elastic modulus (GPa) | E | 207 |
| Overlap ratio | εα | 1.67 |
| Torque load (N·m) | Tp | 200 |
| Backlash (m) | b | 0.9 × 10−4 |
| Rotational speed of driving Gear (r/s) | np | 85 |
| Supporting stiffness (N/m) | kpx | 1.8 × 109 |
| kpy | 1.8 × 109 | |
| kqx | 1.8 × 109 | |
| kqy | 1.8 × 109 | |
| kgx | 1.8 × 109 | |
| kgy | 1.8 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Zhang, S.; Tang, S.; Chang, Z.; Lin, R.; Zhang, L. Dynamic Characteristics Analysis of the DI-SO Cylindrical Spur Gear System Based on Meshing Conditions. J. Mar. Sci. Eng. 2024, 12, 1589. https://doi.org/10.3390/jmse12091589
Zhu Y, Zhang S, Tang S, Chang Z, Lin R, Zhang L. Dynamic Characteristics Analysis of the DI-SO Cylindrical Spur Gear System Based on Meshing Conditions. Journal of Marine Science and Engineering. 2024; 12(9):1589. https://doi.org/10.3390/jmse12091589
Chicago/Turabian StyleZhu, Yong, Shida Zhang, Shengnan Tang, Zhengxi Chang, Renyong Lin, and Lingbo Zhang. 2024. "Dynamic Characteristics Analysis of the DI-SO Cylindrical Spur Gear System Based on Meshing Conditions" Journal of Marine Science and Engineering 12, no. 9: 1589. https://doi.org/10.3390/jmse12091589







