Convex Optimisation Model for Ship Speed Profile: Optimisation under Fixed Schedule

Abstract

We present a novel convex optimisation model for ship speed profile optimisation under varying environmental conditions, with a fixed schedule for the journey. To demonstrate the efficacy of the proposed method, a combined speed profile optimisation model was developed that employed an existing dynamic programming approach, along the novel convex optimisation model. The proposed model was tested with 5 different ships for 20 journeys from Houston, Texas to London Gateway, with differing environmental conditions, which were retrieved from actual weather forecasts. As a result, it was shown that the combined model with both dynamic programming and convex optimisation was approximately 22% more effective in developing a fuel saving speed profile compared to dynamic programming alone. Overall, average fuel savings for the studied voyages with speed profile optimisation was approximately 1.1% compared to operation with a fixed speed and 3.5% for voyages where significant variance in environmental conditions was present. Speed profile optimisation was found to be especially beneficial in cases where detrimental environmental conditions could be avoided with minor speed adjustments. Relaxation of the fixed schedule constraint likely leads to larger savings but makes comparison virtually impossible as a lower speed leads to lower propulsion energy needed.

1. Introduction

The international maritime organization has made a preliminary plan on how to reduce shipping-related greenhouse gas emissions by 50% by 2050 compared to emissions values in 2008 [1]. To reach this target, emissions from shipping are regulated in MARPOL Annex VI [2], which limits shipping-related carbon dioxide emissions via an energy efficiency design index (EEDI) that applies to newbuilds. In addition, MARPOL Annex VI regulates the emission of sulfur oxides, nitrogen oxides, and particulate matter.

While the current revision of EEDI only applies to the technical design aspects of newbuilds, amendments are planned for MARPOL Annex VI that would also regulate the allowed emissions of existing ships from a technical standpoint, through an instrument called the energy efficiency design index for existing ships (EEXI). The main technical measure to conform to EEXI is expected to be the de-rating of main engines, in addition to the instalment of various energy efficiency increasing technologies. In addition, a carbon intensity indicator (CII) is planned to be put into effect in the near future, that would limit the actual measured carbon dioxide emissions of ships. This indicator would be the first emission regulation in shipping that would incentivise the carbon intensity reduction of ships through operational measures [3].

Decreasing ship emissions through operational measures is an attractive alternative to expensive technical design choices such as using LNG instead of heavy fuel oil or hybridising the energy system of the ship [4]. In addition, their effect is immediate whereas technical changes occur either through the renewal of the tonnage or through expensive retrofitting. According to [5], operational measures such as speed optimisation, capacity utilisation, and voyage optimisation are projected to have a prominent impact on future greenhouse gas emission mitigation in shipping.

Speed optimisation in shipping usually refers to the act of minimising the ship’s speed by manipulating the schedule of a journey and the ordering of port visits [6,7]. This is done because the fuel consumption of a ship is roughly proportional to the third power of the ship’s speed. This concept is tightly tied to capacity utilisation, which refers to utilising an existing fleet with intelligent methods as efficiently as possible to transfer cargo. Literature concerning these topics was combined and reviewed in [8]. On the other hand, voyage optimisation refers to the optimisation of a ship’s route and speed on a journey with varying weather conditions, typically with a fixed schedule. A clarification must be made regarding the terms used for these operational methods. The logistics problem of fleet schedule management and speed optimisation as defined above is a separate problem from voyage optimisation. When referring to fleet management, speed optimisation is focused on solving a travelling salesman-type of problem, often for multiple ships visiting multiple ports, without necessarily accounting for the detailed route taken between ports or the detailed speed profile used. On the other hand, speed profile optimisation in the context of voyage optimisation is focused on solving the detailed route and speed profile of a single ship, travelling between two ports under varying weather conditions.

Encountered resistance increases quadratically as a function of the ship’s speed, so in a simplified calm water scenario the optimal solution is to always traverse with a fixed speed as slow as possible to reach the target destination in time. However, such conditions as sea currents, wind, and waves complicate the matter. Roughly speaking, in the presence of significantly rough weather conditions somewhere along a journey, such as high waves and strong wind, it is better to operate at a slower speed during those conditions, and to operate at a higher speed in calm waters or when traversing downwind. Safety aspects also support using lower, or specific, speeds in harsh conditions, but they were not considered in this study. Furthermore, adverse conditions may be avoided completely by controlling the ships speed so that it arrives to the location before or after the adverse conditions.

Various studies related to voyage optimisation are collected and explored in [9,10]. These studies present methods that optimise a ship’s route from port A to port B, and may or may not take speed profile optimisation into account. Used methods include the isochrone method and its variants [11,12,13], various dynamic programming approaches including forward dynamic programming [14,15], path-finding algorithms [16,17], and the Bellman–Ford algorithm [18], and methods that employ a non-linear solver, such as a genetic algorithm, to solve the voyage optimisation problem [19]. These methods were originally developed to solve the problem of routing only, assuming a fixed speed for the vessel. However, recent modifications to the methods enabled optimisation of the speed profile of the ship as well.

A commonality in these studies is that the voyage is separated into a set of states, where an individual state is defined by a set of parameters such as the position of the ship, time spent on journey, and speed over ground. The developed method then solves the optimal sequence of traversing these states, depending on the cost function between each state. This cost function usually takes the form of a ship performance model that accounts for weather conditions. A hindrance in such formulations is that computational load increases drastically by increasing the resolution of state variables between adjacent states. As a result, existing voyage optimisation methods are subject to a trade-off between the spatial and temporal resolution of the result, and the time it takes to compute the solution. The convex optimisation method proposed in this paper increases the spatial and temporal resolution of the result, with a negligible increase in computational load.

Speed profile optimisation in relation to voyages from port A to port B with a fixed schedule were studied in [14,20,21,22,23,24,25]. In [14], the authors developed a forward dynamic programming algorithm for solving the route and speed profile of a ship. The algorithm was used to solve the route and speed selection problem of a cross Atlantic voyage, by representing the voyage as a three dimensional grid. The control variables were set as the heading and the engine power of the ship. The authors reported 3.1% of possible fuel savings with the method, compared to a similar algorithm that optimised the routing by only assuming a fixed speed. The case study voyage featured storm regions during the voyage where wave heights exceeded 8 meters. In [20] the authors solved the optimal fixed speed for a journey between ports for a ship with multiple port calls, taking varying sea conditions into account. The authors reported 21% of possible average fuel savings with their method compared to the operation with the design speed of the studied ship. In [21], a model predictive control framework was formulated to optimise the speed of a vessel using a non-linear solver. The authors reported 28% of possible fuel savings for their method. However, the proposed method had the opportunity to arrive at the target location later than the voyage data it was compared to. This makes it hard to evaluate the overall impact of the method. The authors in [22] formulated the speed profile optimisation problem along a fixed route and schedule as an optimisation problem with spatial weather condition vectors and a simplified ship performance model. The authors reported 0.72% of fuel savings with the developed method. This research in particular is quite close to the method presented in this paper, although significant differences include the accounting of temporal weather dynamics and the level of detail in modelling ship performance.

A robust optimisation algorithm was developed to solve the fuel budget problem of a liner container ship in [23]. The authors demonstrated the effectiveness of the method by optimising the sailing schedule of the Asia-Europe service LP4. This was done by solving the schedule between port calls, i.e., the average speed of the vessel between port calls, taking into account stochastic weather patterns. The authors demonstrated that the developed optimisation model was capable of producing a robust fuel budget under varying environmental conditions for the studied route. The authors in [24] developed a two-stage weather routing algorithm where first the route was optimised with A* by keeping the speed of the vessel constant. Once the optimal route was found, a novel geometric program was employed to find the optimal speed profile for the vessel. The developed speed profile optimisation model shares similarities in methodology to the one presented in this paper. The method was tested for a voyage between Tokyo and San Francisco and roughly 2.5% of fuel savings were attained compared to the solution using a fixed speed for the vessel. In [25], the authors developed a ship weather routing system utilising a genetic algorithm to solve both the route and speed profile of a vessel simultaneously. On the basis of the results, the algorithm seemed to be computationally efficient, taking approximately 10 min to solve the route and speed profile for the whole voyage. The authors did not compare fuel savings attained from speed profile optimisation specifically, but the algorithm seemed to prefer operating at a fixed speed.

An important distinction between non-linear solvers and mathematical optimisation and dynamic programming is that the latter two are guaranteed to find a global optimal solution to the presented problem. Furthermore, these methods find the solution in a predictable amount of time, whereas non-linear solvers must typically be tuned with hyperparameters to a certain accuracy. The time complexity of general dynamic programming methods is exponential, although specialised dynamic programs such as path-finding algorithms can be solved faster. However, these specialised dynamic programs require that the entire graph structure of the problem must be calculated beforehand, which is infeasible for larger problems. On the other hand, mathematical optimisation problems can be typically solved in polynomial time, which is a clear benefit compared to other methods. However, they are much more rigid in terms of what can be modelled compared to dynamic programming or non-linear programs.

This work presents a novel convex optimisation model for the optimisation of a ship’s speed profile with high spatial and temporal resolution. The proposed model can be used as an extension to existing speed profile optimisation frameworks, improving the results with minimal computational overhead. The model was tested for five different ships on the 20 shortest path journeys from Houston, Texas to London Gateway. Hydro-meteorological condition predictions for the voyages were gathered from NAPA Voyage Optimisation [26], which acquires the predictions from Tidetech [27]. Information on the weather forecast and related uncertainties can be found in [28]. Operation in detrimental conditions such as high wave heights was not restricted in the demonstrations, although such a feature could easily be added into the model. This approach was selected to study the impact of speed profile optimisation under a fixed schedule specifically, whereas a model that restricts operation under certain conditions would require a flexible schedule. The original motivation for this study stemmed from previous work of the authors in [29], where the power demand profile of a ship was predicted based on the expected speed profile during a voyage. To establish an adequate power demand prediction, the expected speed profile had to be of high resolution and obtained with reasonable computational efficiency. Furthermore, speed profile optimisation has a direct impact on monetary savings due to fuel consumption reduction, which also translates to reduced CO₂ emission. This may help in conforming to the future CII tiers. In the context of EEXI, the developed methods in this paper may alleviate the impact of a de-rated engine indirectly due to the avoidance of detrimental weather conditions which require high propulsive power. The contributions of this work are the following:

• A ship speed profile optimisation formulation in the convex optimisation modelling framework;
• A demonstration of how to link the developed convex optimisation model to existing optimisation methods, increasing their efficacy further; and
• A comprehensive study on the effectiveness of ship speed profile optimisation under a fixed schedule for various ship types.

2. Methods

The developed methodology combines dynamic programming and convex optimisation in ship speed profile optimisation. The resulting model is capable of accounting for both spatial and temporal variation in weather conditions due to the utilization of dynamic programming, while still retaining high solution granularity and computational efficiency with convex optimisation. Individually, the computational load of dynamic programming is tremendous for a solution of reasonable accuracy, whereas convex optimisation alone cannot account for both temporal and spatial weather changes. This leads to the motivation for the combination of these two methods.

Key aspects of dynamic programming and convex optimisation are compared in

Table 1. Dynamic programming vs. convex optimisation.

	Dynamic Programming	Convex Optimisation
Computational speed	slow	very fast
Memory load	very high	very low
Spatial/temporal resolution of solution	low	high
Resolution of speed selection	low	continuous
Modelling flexibility	no restrictions	needs to be convex
Other limitations	none	no temporal changes in weather

. Concisely, dynamic programming has large computational overhead but it benefits greatly from the allowed flexibility in what models can be solved. Conversely, convex optimisation is computationally highly efficient, but establishing the solved model in a convex format can be challenging. In the context of speed optimisation, the limitation of only considering spatial changes in weather conditions is a large hindrance. As a result of this, the convex optimisation model by itself cannot avoid detrimental conditions at a certain location by controlling when that location is reached.

This section introduces both methods individually, and finally shows how they can be combined into a holistic speed optimisation model. The resulting model can be solved faster and with less computing resources compared to dynamic programming or non-linear optimisation approaches of similar resolution. Both the dynamic programming method and convex optimisation are based on a ship’s performance model, which will be introduced first.

2.1. Ship Performance Model

In this study, the ship performance model approximates fuel consumption by calculating ship resistance, i.e., the required propeller thrust to move the ship at a given speed, using real weather data as input to the model. The total resistance is modelled as the sum of calm water resistance, resistance caused by waves, resistance caused by sea currents, and air resistance. Once the resistance is known, fuel consumption is estimated by assuming fixed hull, shaft and propeller efficiencies, and a standard marine engine specific fuel oil consumption curve.

It is important to note that the employment of a convex optimisation model necessitates that the cost function be also convex. This has an impact on the range of possibilities how certain resistance terms can be modelled.

The ship’s calm water resistance opposing its motion is derived from [30]:

$$R_{calm}\left(v\right)=\frac{1}{2}{C}_t{\rho }_w{v}^{2}S$$

(1)

where $C_t$ is the total drag coefficient, ${\rho }_w$ is the density of water, v is the ship’s speed through water, and S is the wetted area of the hull.

The total drag coefficient $C_t$ is defined as:

$$C_t=C_f+C_i+C_r$$

(2)

where $C_f$ is the coefficient of viscous water resistance according to the ITTC-1957 frictional correlation line [31]: $C_f=0.075/{(logRe-2)}^2$ where $Re$ is the Reynold’s number, $C_i$ is the incremental resistance coefficient, selected to be $C_i=0.0004$ for this study as suggested in [30], and $C_r$ is the residual resistance coefficient, which was retrieved from graphs originally proposed by Harvald [32]. The wetted area of the hull was approximated with Mumford’s formula: $S=1.025\ast L_{pp}\ast (C_B\ast B+1.7\ast T)$, where $L_{pp}$ is the ship’s length between perpendiculars, $C_B$ is the block coefficient, and T is draft.

The additional resistance encountered by the ship due to waves was approximated as a function of the ship’s speed over ground v, wave height h, and circular wave frequency $\omega$ according to the methodology laid out in [33], where the wave resistance component is expressed as:

$$R_{waves}(v,h,\omega )=R_{AWR}(v,h)+R_{AWM}(v,h,\omega )$$

(3)

where $R_{AWR}$ is the wave reflection effect and $R_{AWM}$ is the added resistance due to motion effects $R_{AWM}$.

The equivalent calm water speed of a vessel in a sea-current can be calculated with analytical geometry:

$$v^{\prime }=\sqrt{(u^2+v^2-2uv·cos\left(\theta \right))}$$

(4)

where $v^{\prime }$ is the equivalent calm water speed of the vessel, u is the speed of the current, v is the vessel’s speed over ground, and $\theta$ is the relative angle between the speed vectors of the ship and current. [34] The resistance addition of sea currents can then be approximated as a function of v, u, and $\theta$ with:

$$\begin{array}{cc}\hfill R_{current}(v,u,\theta )& =({v^{\prime }}^2-v^2)\frac{1}{2}{C}_t{\rho }_{w}S\hfill \\ \hfill & =(u^2-2uv·cos\left(\theta \right))\frac{1}{2}{C}_t{\rho }_{w}S.\hfill \end{array}$$

(5)

Added resistance due to the wind was calculated according to [35]:

$$R_{air}(v,\gamma ,w)=\frac{1}{2}{C}_a\left({\gamma }_R\right){\rho }_a{w}_R^{2}A-\frac{1}{2}{C}_a\left(0\right){\rho }_a{v}^{2}A$$

(6)

where $C_a$ is the air resistance coefficient as a function of ${\gamma }_R$; the relative angle between wind direction and the ship’s motion, ${\rho }_a$ is air density, A is the ship surface area opposed to the wind, v is the ship’s speed over ground, and $w_R$ is the relative wind speed. $C_a$ was fitted for this study according to laden conditions of a container ship described in [36], which was then used to model the air resistance coefficients dependency on wind direction for all of the studied ships. This was deemed reasonable, as the shape of the function does not differ substantially across ship types, and $C_a$ functions were not publicly available for the studied ships specifically. The relative wind speed and angle can be calculated with:

$$\begin{array}{cc}\hfill w_R& =\sqrt{w^2+v^2+2wvcos\left(\gamma \right)}\hfill \\ \hfill {\gamma }_R& =arccos\left(\frac{w·cos\left(\gamma \right)+v}{\sqrt{w^2+v^2+2wvcos\left(\gamma \right)}}\right)\hfill \end{array}$$

(7)

where w is the true wind speed and $\gamma$ is the angle between true wind and the heading of the ship.

The total resistance affecting the ship can be expressed as the sum of these resistance  terms:

$$R_{total}(v,h,u,\theta ,\gamma ,\omega )=R_{calm}\left(v\right)+R_{waves}(v,h,\omega )+R_{current}(v,u,\theta )+R_{air}(v,\gamma ,w),$$

(8)

which is a function of the ship’s speed v and the hydro-meteorological conditions $h,u,\theta ,\gamma$, w, and $\omega$. In this work, the speed of the ship is a decision variable in the models, whereas the hydro-meteorological conditions depend on the location and time the ship is at a given location. We represent each of the conditions as a $a\times b$ matrix, where a is the amount of discretised distances considered and b the amount of discretised time values considered.

A condition matrix is notated as the conditions upper-case variant, a vector of conditions as a bold lower-case letter and individual condition values are notated as a regular lower-case letter, indexed by a single variable when referring to a value in a vector, or two variables when referring to the matrix. For example, all possible angles between the ship’s motion and the true wind during a journey are contained in the matrix $\Gamma$ while $\mathit{\gamma }$ refers to a vector of angle values. ${\gamma }_i$ refers to the specific angle value at index i of a vector $\mathit{\gamma }$ and ${\gamma }_{d,t}$ refers to the angle value at indices d and t in matrix $\Gamma$. It should be clear from the context which vector $\mathit{\gamma }$ is referred to when using the notation of ${\gamma }_i$. The amount of rows and columns in a condition matrix, i.e., the resolution of the prediction of hydro-meteorological conditions, is a hyperparameter in the model. Conditions are interpolated for d and t entries when data is not available.

The propulsion power demand of the ship was calculated as:

$$P(v,h,u,\theta ,\gamma ,\omega )=\frac{R_{total}(v,h,u,\theta ,\gamma ,\omega )v}{{\eta }_h{\eta }_p,{\eta }_s}$$

(9)

where ${\eta }_h$ is the hull efficiency, ${\eta }_p$ is the propeller efficiency, and ${\eta }_s$ is the shaft efficiency. ${\eta }_p$ was fixed at 0.65 in this study, and ${\eta }_h$ and ${\eta }_s$ are fixed at 0.98.

Once the propulsion power demand is known, the fuel consumption ($C_{fc}$) of the ship can be retrieved with the help of the specific fuel oil consumption (SFOC) curve of the engine:

$$C_{fc}(v,h,u,\theta ,\gamma ,\omega )=P(v,h,u,\theta ,\gamma ,\omega )SFOC\left(E_{op}\right)T_{\Delta }$$

(10)

where $E_{op}$ is the operating point of the engine i.e., current engine power divided by maximum engine power and $T_{\Delta }$ is the time step of the used model. A standard marine engine product guide was used to fit the SFOC curve for this study [37].

2.2. Dynamic Programming

Dijkstra’s algorithm was selected as the method for solving the dynamic programming problem in this study, relying heavily on the example set in [17]. Dijkstra’s algorithm finds the shortest path between nodes on a graph with positive edge weights. As such, before the algorithm can be employed, the problem of speed selection must first be formalized in a graph structure.

We define a graph $G=(N,E)$, where N denotes a set of nodes and E a set of edges. A single node is defined as the pair $(d,t)$, where d is the distance travelled and t is the time spent on a journey. The set of nodes N is formed by the Cartesian product of possible ship state variable sets $N=D\times T$, where D is the set of discretised possible distances travelled and T a discretised set of possible time durations spent on the journey.

The number of nodes decides the computational complexity of the problem, and is dependent on journey length $D_{trip}$ and its discretisation factor $D_{\Delta }$, and maximum allowed time for trip $T_{trip}$ along with its discretisation factor $T_{\Delta }$. Since the discretisation factors are model hyperparameters, they should be selected with care so that the size of the graph remains manageable. For example, assume a trip of 500 km with a target time of 17 h. We could set the distance discretisation factor as 10 km so that $D=\{0,10,20\dots 490,500\}$, and the time discretisation factor as 0.5 h so that $T=\{0,0.5,1\dots 16.5,17\}$. The resulting graph would then contain 1785 nodes.

The nodes are essentially abstractions of ship states. Similarly, the edges connecting the nodes are abstractions of speed selection actions in a state. Possible speed selection actions a is a vector that contains the interval $[0,v_{max}·T_{\Delta }]$, discretised by $D_{\Delta }$, where $v_{max}$ is the maximum speed of the ship. The set of edges E contains all possible pairs of nodes $((d_{parent},t_{parent}),(d_{child},t_{child}))\in N\times N$, that fulfill the following conditions:

• $t_{child}=t_{parent}+T_{\Delta }$;
• $d_{child}\in d_{parent}\times a$.

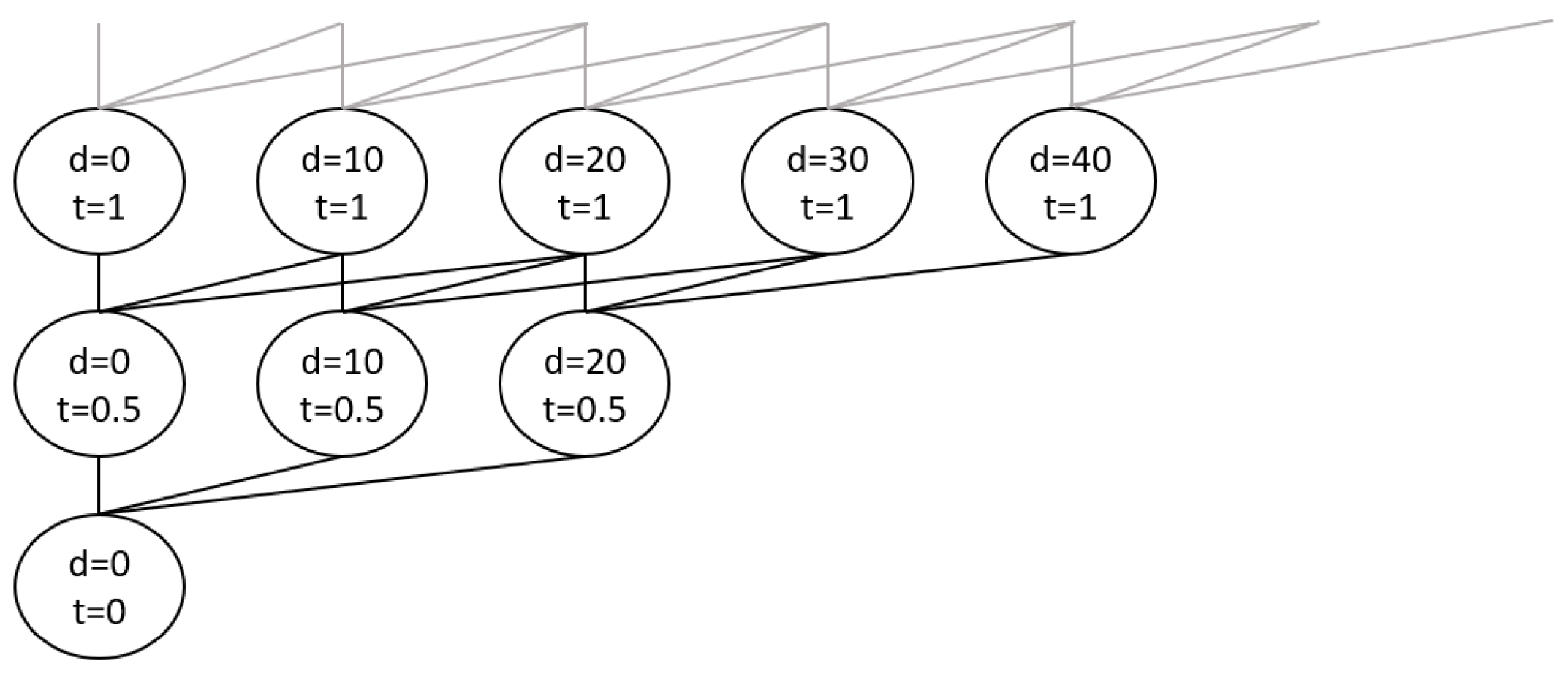
This forms a directed and acyclic graph with a tree structure. The expansion of the graph from an exemplary source node $(0,0)$ is shown in Figure 1. In the example, $T_{\Delta }$ is 0.5 h, $D_{\Delta }$ is 10 km, and $v_{max}$ is 40 km/h. The goal node is determined to be any node where distance is equal to the length of the trip. Notice that traversing the graph along the right-most nodes is equivalent to completing the journey at maximum speed, whereas the leftmost nodes signify staying still at the starting location.

The edge weight $W((d_{parent},t_{parent}),(d_{child},t_{child}))$ between nodes $(d_{parent},t_{parent})$ and $(d_{child},t_{child})$ is determined as the cumulative fuel consumption between the distances $d_{parent}$ and $d_{child}$. The speed of the ship between these nodes can be determined with $v=\frac{d_{child}-d_{parent}}{t_{child}-t_{parent}}$. The weight between the nodes can then be calculated with the help of Equation (10).

$$W((d_{parent},t_{parent}),(d_{child},t_{child}))=\sum _{i=0}^n{C}_{fc}(v,h_i,u_i,{\theta }_i,{\gamma }_i,{\omega }_i)$$

(11)

where condition vectors are extracted from their corresponding matrices at matrix indices between $(d_{parent},t_{parent})$ and $(d_{child},t_{child})$.

In addition, the computational efficiency of Dijkstra’s algorithm can be improved by checking whether the node $(d_{child},t_{child})$ is such that that the goal node can still be reached in the remaining time available. If not, we manually set the weight to the node to be infinite. If detrimental conditions exist on the route at some region of time and distance, they manifest as a collection of unusually high edge weights in that region of the graph. The primary task of Dijkstra’s algorithm is to find such speed selections that the path along the graph avoids these high edge weight regions.

Once the edge weights have been determined, Dijkstra’s algorithm can be used to find the path of speed selections that results in the lowest cumulative fuel consumption. The operation of Dijkstra’s algorithm in pseudocode, with the help of a priority queue, can be seen in Appendix A.

Once the algorithm finds the goal node, the optimal speed selection path can be recovered by traversing backwards from the goal node. The result is represented as an ordered set of tuples $\{(d_1,t_1),(d_2,t_2)\dots (D_{trip},T_{trip})\}$ where each node in the set is along the optimal path to the goal node $(D_{trip},T_{trip})$.

2.3. Convex Optimisation

The convex optimisation model takes spatial condition vectors as input, and produces an optimal speed profile with high spatial resolution as a result. Whereas the dynamic programming model minimised fuel consumption, the performance model of the ship cannot be configured to produce fuel consumption as the output while still remaining convex. This subsection describes the simplifications and modifications made to the performance model in order to arrive at a convex formulation.

A convex function f is geometrically defined as as a function where all points in a line segment drawn between any two points along f must be larger than or equal to f. In general, a function is convex if the second derivative of the function is strictly positive. Mathematically, a convex function is defined as:

$$f(\delta x+(1-\delta \left)y\right)\le \delta f\left(x\right)+(1-\delta )f\left(y\right)$$

(12)

for all $x,y$ in dom f and with $0\le \delta \le 1$, when the domain of f is a convex set. Such a function can be minimised over a convex set, which is formed by optimisation constraints, to form a convex optimisation model. Convex optimisation models can be solved in polynomial time by a variety of algorithms, such as interior-point methods, cutting-plane methods, or the ellipsoid method [38].

Foremost, the wave resistance model explained in more detail in [33], is not a convex function of the ship’s speed. However, the model seems to behave quite linearly with respect to the speed with fixed wave heights and circular wave frequencies, except in extreme conditions. A linear function was fitted to the wave resistance model for wave zero-crossing periods ranging between 0–6 s, and wave heights ranging from 0–10 m.

Figure 2 shows the root-mean-square error between resistance values calculated with the accurate wave resistance model, and the linear approximations for the modelled bulk carrier ship. As can be seen from the figure, the linear approximations perform well for the majority of wave height and zero-crossing periods, except for extreme conditions where wave heights exceed 8 meters. The root-mean-square error surface plots are similar across the modelled ships, differing slightly in at which wave heights the performance of the linear models starts to degrade.

Based on the analysis above, it was concluded that wave resistance can be approximated reasonably well with a linear fit in the convex optimisation model $R_{wave}=a_{wave}v+b_{wave}$, where $a_{wave}$ and $b_{wave}$ are the slope and intercept of the fitted linear function for specific values of wave zero-crossing period and wave height and v is the ship’s speed. Sea conditions where the linear models performance degrades are extremely rare for a ship to encounter, and such conditions are usually avoided through routing.

The formula of air resistance (Equation (6)) is not convex with regards to the formulation of the relative wind angle and the wind resistance coefficients dependency on it. Thus, values for the $C_a\left({\gamma }_R\right)$ term were calculated beforehand, using the mean speed required for the journey as an approximation of the true optimised speed. The air resistance term then becomes:

$$R_{air}=\frac{1}{2}\psi {\rho }_{a}A(w^2+v^2+2wv·cos\left(\gamma \right))-\frac{1}{2}{C}_a\left(0\right){\rho }_a{v}^{2}A$$

(13)

where $\psi$ is the pre-computed $C_a\left(\gamma \right)$ term. This approximation causes the relative wind angles in the optimisation model to be slightly shifted compared to what they would actually be. The effect of this is negligible unless the optimised speed differs drastically from the required mean speed for the journey.

Using the linear wave resistance model and the simplified air resistance formula and dropping terms that do not depend on the speed of the ship, the convex resistance model can then be declared as:

$$\begin{array}{cc}\hfill R_{total}& =\frac{1}{2}{C}_t{\rho }_w{v}^{2}S+a_{wave}v-uv·cos\left(\theta \right)C_t{\rho }_{w}S+\frac{1}{2}{\rho }_{a}A(\psi v^2+2wv\psi ·cos\left(\gamma \right)-C_a\left(0\right)v^2)\hfill \\ \hfill & =v^2(\frac{1}{2}{C}_t{\rho }_{w}S+\frac{1}{2}{\rho }_{a}A(\psi -C_a\left(0\right)))+v(a_{wave}-u·cos\left(\theta \right)C_t{\rho }_{w}S+2w\psi ·cos\left(\gamma \right))\hfill \end{array}$$

(14)

which is convex, since the second order term multiplier is positive ($\frac{1}{2}{C}_t{\rho }_{w}S>|mi{n}_{\psi }\left(\frac{1}{2}{\rho }_{a}A(\psi -C_a\left(0\right))\right)\left|\right)$ and $a{x}^2$ is convex for $a>0$, and the second term is linear in v. However, if we multiply the resistance with the ship’s speed to get propulsion power demand as in Equation (9), the multiplier of the new second order term is not strictly positive and thus, the model is not convex.

For this reason, it was decided that rather than minimising actual fuel consumption, the convex optimisation model would minimise the cumulative encountered resistance instead, as a proxy for the fuel consumption. Such a decision is not drastic, as power demand is a linear function of resistance, and an engine’s fuel flow rate is close to a linear function of power demand [29].

Minimising the total cumulative encountered resistance is the same as minimising total energy expenditure to counter the resistance, since $E_{step}=R_{step}\ast s_{step}$, where $E_{step}$, $R_{step}$ and $s_{step}$ refer to the energy expenditure, resistance force, and distance travelled for one optimisation step respectively. Since the optimisation model operates in the spatial domain, each optimisation step is affiliated with a constant distance step $s_{step}$. $s_{step}$ does not depend on the speed of the vessel. Thus, minimising $\sum {}_{i=1}^S{E}_i$ with respect to v is the same as minimising $\sum {}_{i=1}^S{R}_i$ with respect to v, with S being the vector of discretised distances.

Minimising the encountered cumulative resistance also allows us to drop all of the resistance terms that do not depend on v, as was done in Equation (14). This is because v is the only optimisation variable and any non-dependent term will not affect the end result.

Before optimisation, the journey distance is spatially discretised into S steps with equal distance, which determines the resolution of the result. In addition, a penalty term for changes in speed (i.e., acceleration) is added. Even though modelling the longitudinal dynamics of the ship is outside the scope of this study, we do not want our model to frequently change the speed of the vessel without penalty. The penalty of accelerating was approximated with an exponential function of the form $e^{v_i-v_{i-1}}$, where $v_i$ refers to the speed at step i and $v_{i-1}$ the speed at the previous step. This way, positive changes in speed were penalized in the objective function.

Given a discretised set of distances S and condition vectors $\mathit{h},\mathit{u},\mathit{\theta },\mathit{\gamma },\mathit{\omega }$ that match the discretised distance set, we first transformed wave height vector $\mathit{h}$ and wave circular frequency $\mathit{\omega }$ into a vector of linear wave resistance slopes ${\mathit{a}}_{\mathit{wave}}$. Secondly, the wind resistance coefficients were pre-computed using the mean speed required for the journey to form vector $\mathit{\psi }$. The full optimisation problem is then:

$$\mathrm{Minimize}$$

$$v$$

$$\sum {}_{i=1}^S{v}^2(\frac{1}{2}{C}_t{\rho }_{w}S+\frac{1}{2}{\rho }_{a}A({\psi }_i-C_a\left(0\right)))+v(a_{wav{e}_i}-u_i·cos\left({\theta }_i\right)C_t{\rho }_{w}S+2w_i{\psi }_i·cos\left({\gamma }_i\right))$$

(15)

subject to:

$${\tau }_{i=1}==0$$

(16)

$${\tau }_i+\frac{s_{step}}{v_i}\le {\tau }_{i+1},\forall i$$

(17)

$${\tau }_{i=S}\le T_{trip}$$

(18)

$$v_{i=1}\le a_{max}$$

(19)

$$-a_{max}\le \frac{v_i-v_{i-1}}{{\tau }_i-{\tau }_{i-1}}\le a_{max},\forall i$$

(20)

$v\in {\mathbb{R}}_{>0}$.

The vector $\mathit{\tau }$ in Equations (16)–(18) contains the cumulative time spent to reach each step i. Equation (16) simply states that counting the cumulative time spent starts from zero. Equation (17) ensures that each time increment in $\tau$ is equivalent to actual time taken to traverse that increment. This constraint is implemented as an inequality constraint since $\frac{s_{step}}{v_i}$ is convex, not linear. The next constraint, Equation (18), ensures that the journey is completed in the given time limit, and also forces constraint (17) to be tight. Equations (19) and (20) constrain the ship to start from a stationary position and constrain the maximum acceleration of the ship to $a_{max}$, respectively.

2.4. Combining Dijkstra’s Algorithm Solution with Convex Optimisation

This chapter explains how the two approaches of dynamic programming and convex optimisation can be combined together. Essentially, this combined approach consists of these four steps:

• Calculate speed profile with dynamic programming;
• Transform dynamic programming solution into a set of checkpoint constraints;
• Extract spatial vectors of hydro-meteorological conditions along the path of the dynamic programming solution; and
• Solve optimal speed profile with the convex optimisation model, respecting the checkpoint constraints and using the extracted spatial condition vectors.

The concept of checkpoint constraints mentioned in steps 2 and 4 requires additional explanation. The function of the dynamic programming solution in this combined model is to provide two inputs to the convex optimisation model. Foremost, in case the dynamic programming solution is such that adverse conditions were avoided or beneficial conditions reached via speed selection, this behaviour must be passed on to the optimisation model. Secondly, spatial condition vectors for the optimisation model are extracted based on the dynamic programming solution.

The behaviour of avoiding or seeking certain conditions can be passed onto the optimisation model by introducing constraints that specify when a certain distance should be reached. In this work, such constraints are referred to as checkpoint constraints. The main problem of this transfer process is determining how many checkpoint constraints to create and how to specify the locations of the checkpoints.

Locations of the checkpoint constraints were set by identifying detrimental conditions based on the power demand vector of the ship, ${\mathbf{P}}_{\mathbf{f}\mathbf{s}}$, when simulating the journey with fixed speed. A detrimental propulsion power limit, referred to as $P_{threshold}$ was then calculated according to Equation (9), with the conditions listed in

Table 2. Selected detrimental conditions. 0 degrees refers to tail conditions.

Condition	Value
w	20 m/s
$\gamma$	0
h	5 m
u	0 m/s
$\theta$	0
$\omega$	1 Hz

and speed set at the mean fixed speed required for the journey.

The selection of these detrimental condition limits is a hyperparameter in the model that controls the degree to which the end speed profile adheres to the dynamic programming solution. Checkpoints can then be expressed as a set of distances travelled $d_n$ and a set of times spent $t_n$, where $d_n$ are retrieved from indices where ${\mathbf{P}}_{\mathbf{f}\mathbf{s}}>P_{threshold}$ and $t_n$ are retrieved from the dynamic programming solution at distances $d_n$.

The checkpoints can then be turned into optimisation constraints with:

$${\tau }_{s=d_n}\le t_n,\forall d_n\in D,\forall t_n\in T$$

(21)

where D is the set of distances travelled in the identified checkpoints and T the set of times spent by the dynamic programming solution to reach those distances. Finally, condition vectors can be retrieved along the dynamic programming solution, and they can be passed onto the optimisation model. Since the optimisation model is now constrained by the inequality constraints in Equation (21), the hydro-meteorological conditions along the dynamic programming solution are close to the actual conditions that would be encountered with the speed profile that convex optimisation produces. The full scheme of the proposed combined model is illustrated in Figure 3.

The main particulars of the tested ships are described in

Table 3. The main particulars of tested ships. The cruise ship is based on the ship: “Mein Schiff 6”. Engine power ratings were estimated so that the engine operated at 80% load when travelling at design speed under conditions listed in Table 2. The design speeds were estimated based on [39].

Parameter	Bulk Carrier [33]	Cruise Ship	KVLCC2 [40]	S175 [41]	WILS II [42]
Area opposed to wind [m${}^2$]	1000 *	1600 *	1600 *	700 *	1600 *
Beam [m]	50	42.39	58	25.4	38.4
Length [m]	285	295.26	320	175	321
Draft [m]	18.5	8.25	20.8	9.5	15
Displacement [tons]	218,752	75,000 *	312,622	24,742	140,200
Engine power rating [MW]	52	32.5	65	26	55
Design speed [knots]	14.5 *	20 *	15 *	23 *	23 *

* Value estimated roughly due to missing data.

. KVLCC2 is a tanker and S175 and WILS II are container ships.

3. Results

The proposed method was tested with the hydro-meteorological conditions of 20 Cross-Atlantic journeys from Houston, Texas to London Gateway, 9280 km in length. The journey occurred between 26 May 2020 and 16 February 2021. Speed profiles of 5 different ships were optimised with the combined method for each of the 20 journeys, and the time limit for the journeys was varied between 282 h and 408 h, so that the analysis contained a mix of slower and faster journeys.

The voyages were discretised with a distance step of $D_{\Delta }=20$ km and a time step of $T_{\Delta }=6$ h. This results in a graph structure with 31,552 nodes at maximum, and a speed selection step size of $3.33$ km/h for dynamic programming. $D_{\Delta }$ and $T_{\Delta }$ were selected so that a fairly accurate result was still attainable by dynamic programming, and so that the graph structure could still be stored into the memory of a standard desktop computer with 16 GB of random-access memory. Hydro-meteorological conditions for each possible distance and time tuple were retrieved from NAPA Voyage Optimization [26].

Figure 4 shows the average fuel savings by ship type of the proposed combined method and dynamic optimisation, compared to fuel consumption by operating with a fixed speed. The results for the bulk carrier and KVLCC2 were filtered so that no journeys were considered where the required constant speed was higher than their design speed. It is evident that the combined approach is more effective in producing a fuel saving speed profile than the dynamic programming approach. Overall, the combined approach was approximately 22% more effective in saving fuel across all of the tested journeys and ships. The fuel saving potential of speed profile optimisation was higher for ships with a higher design speed. The trend in Figure 4 is that speed profile optimisation is most effective for the fastest ships under consideration: The S175 and WILS II. The fuel consumption assessments were calculated according to the more accurate ship performance model described in Section 2.1, rather than the convex variant. Furthermore, fuel consumption was assessed based on the realised weather conditions with the final speed profile, rather than the condition approximations passed onto the convex optimisation model. Overall, the speed profiles produced by the combined method saved 1.1% of fuel on average across all ship types.

In many of the tested journeys, weather conditions were mild for the entirety of the journey. In such conditions, it is of course optimal to operate at a near fixed speed, which in turn results in the fuel saving difference between the optimal and fixed speed result being very small. A histogram of the standard deviation (STD) of the constant speed propulsion power demand vector is shown in Figure 5a, and a histogram of achieved fuel savings in Figure 5b. As can be seen, the STD of fixed speed power demand across the journeys is primarily low, which indicates a large population of journeys where weather conditions did not vary significantly. This is also reflected in the histogram of achieved savings. If we filter the studied journeys to those where fixed speed power demand STD exceeded 1.5 MW, the average attained fuel savings with the combined method reach 3.5%. This filtration is fast and simple to perform before proceeding to assess the potential benefit of speed profile optimisation.

3.1. Computational Load Analysis

Computing times of graph initialisation for dynamic programming, Dijkstra’s algorithm and convex optimisation are shown in

Table 4. Average computing time for various phases of the combined method.

Phase	Computing Time
Graph initialisation	2.84 min
Dijkstra’s algorithm	1.00 s
Convex optimisation	4.69 s

. The computing times were calculated as the average time it took to compute the various phases in the 100 conducted speed profile optimisations. The convex optimisation model was created with CVXPY [43,44] and solved with ECOS [45]. The rest of the model was coded in Python, utilising standard libraries for scientific computing such as NumPy [46].

The tests were computed with a standard desktop environment, with an AMD Ryzen 5 3600 6-core processor and 16 GiB of random-access memory. Initialising the dynamic programming graph takes up the vast majority of total computing time, whereas the time it takes to solve the dynamic programming graph with Dijkstra’s algorithm is negligible. Furthermore, the computing overhead induced by the proposed convex optimisation model is also very small. It can be stated that including the convex optimisation model does not influence the performance of the model in a drastic way. The graph initialisation portion of the method could be parallelised as in [17] to decrease the computing time required. This does not however decrease the memory load required for the graphs.

3.2. Example Voyage Analysis

Figure 6 shows the resistance profile from all sources with the combined approach, dynamic optimisation and operation according to a fixed speed profile for one of the studied journeys with the S175 container ship. Fuel savings of 3.8%, or 43 tons, were attained on this example journey with the speed profile produced by the combined approach, compared to the constant speed result. Assuming heavy fuel oil as the used fuel with 40 MJ/kg energy density [47] and a CO₂ emission factor of 79 t CO₂/TJ [48], such savings would have resulted in a CO₂ reduction of approximately 136 tons. The effect of wind resistance and ocean currents was small for the entirety of the journey. However, the end of the journey is characterised by high wave resistance values, signifying the presence of a storm in this region. The combined method and dynamic optimisation solutions operate at a slightly higher speed for the initial two-thirds of the journey so that they arrive at the distance of 7000 km before the storm has elevated. Thus, they encounter significantly smaller wave resistance values in the end of the journey compared to the journey with fixed speed.

Figure 7 shows the encountered wave heights when operating according to constant speed and with the optimised speed. The wave heights between 7000–8000 km reach 6 m at maximum when operating with constant speed. Conversely, the wave heights reach 5 m at maximum for the same region when operating according to optimised speed. Furthermore, the adverse conditions are in effect for a longer distance with constant speed operation. Even though the difference between these adverse conditions is not huge, the combination of reducing speed in this region and reaching the storm at a slightly more favourable time reduces the total encountered resistance substantially.

Figure 8 shows the speed profile solutions of the different methods for all ships for the studied journey. For S175 and WILS II, the combined approach follows the same trend as the dynamic optimisation solution, in that it controls the speed of the vessel so that it arrives at 7000 km roughly at the same time as the dynamic optimisation solution. However, the dynamic programming solution is limited in the sense that it must make quite drastic speed adjustments along the way due to its limited speed selection resolution, whereas the solution passed through convex optimisation manages to capture the actual optimal speed of roughly 16.5 knots for the first two thirds of the journey. This highlights the benefit of the proposed method as an extension to the existing speed optimisation methodologies. In this particular journey, the slower ships did not gain a fuel advantage from adjusting the speed profile, and as such operate close to the constant speed. However, some minor speed reduction can be seen during the region of adverse conditions for KVLCC2, the Cruise ship, and the Bulk carrier.

4. Discussion

The fuel saving potential of speed profile optimisation in the voyages studied was 1.1% across all studied ships, which is in line with the results of similar studies on speed profile optimisation [14,22,24]. This value is not all that significant considering that the error margins of the model and uncertainty in weather predictions may also shift the actual result. Our finding raises a critical question regarding the usefulness of speed profile optimisation specifically. Would 1.1% average fuel savings in general incentivise investment from ship operators? However, the modelled savings were larger for journeys with easily identifiable deviations in upcoming weather conditions. Speed profile optimisation may see potential in journeys when it can be easily discerned that conditions along the voyage are variable. In addition, speed profile optimisation is an addition to weather routing which does not necessarily represent an additional investment to the operators.

Models for liner network design and industrial and tramp routing and scheduling typically assume a fixed speed between ports [49]. This is because the higher-level models would become unnecessarily complex and infeasible to solve if high fidelity speed optimisation would be taken into account. Furthermore, the time horizon of such models extends beyond available weather forecasts. Based on the results of the presented research, this assumption of fixed speed between ports does not interfere with the accuracy of such models in a major way. Similarly, this logic holds for establishing a power demand prediction based on the speed profile of the ship as was done in [29]. It is expected that a reasonably accurate power demand prediction could be calculated assuming a fixed speed for the voyage under study.

Ships are typically routed so that they specifically avoid detrimental conditions. This in turn makes the speed profile optimisation of ships less effective in saving fuel, which was not taken into account for this study. It is expected that detrimental conditions would be less prevalent than in the analysed journeys if measured data would be used from actual traversed journeys with route optimisation. Route optimisation could be implemented in the proposed combined model as well, if the used dynamic programming model was replaced with a variant that also takes routing into account, such as the model developed in [17].

Fuel saving potential of speed profile optimisation is a result of two mechanisms: Avoiding detrimental conditions by controlling the ship’s speed and operating slower in unavoidable detrimental conditions. The former of these mechanisms offers higher fuel saving potential, but there are limited opportunities for such control under a fixed schedule, according to the studied journeys. On the other hand, the latter mechanism offers marginal benefits due to the fact that speed must also be increased in some other portion of the journey, if it is lowered for detrimental conditions. The potential for such optimisation depends also on the occurrence of beneficial conditions along the journey.

The results reflected that speed profile optimisation offered more benefits for ships that were operating with a slow speed relative to their design speed. This is reasonable since such ships have more opportunities to save fuel via the two mechanisms described above. The calm water resistance curve of such ships is not as steep at lower speeds compared to ships that operate close to their design speed. Consequently, the relative cost of changing the speed is lower.

The developed model did not restrict the ship from operating in highly detrimental conditions in the studied voyages. Detrimental conditions could include for example wave surfing, parametric rolling, or dangerously high waves. Such a feature could easily be implemented into the dynamic programming solution, by setting edge weights to infinity in case the edge leads to a node with unacceptable conditions. Consequently, the combined model would then also avoid these conditions via speed profile optimisation. This would inadvertently lead to the necessity of having a flexible schedule for the ship and implementing that into the model. The presented results of this research were directed to emphasis the potential of speed profile optimisation in terms of fuel savings specifically, and an optimisation problem with a flexible schedule would lead to the different issue of time charter equivalent maximisation.

The proposed model could be improved in various ways. Firstly, the dynamic programming model could be replaced with one that also takes routing into account, such as the one proposed in [17]. Such an implementation could also include operational restrictions in certain conditions without relaxing the fixed schedule constraint, since the model could avoid such detrimental conditions through routing and still arrive on time.

Secondly, the ship performance model could be improved in various ways, such as including a more detailed propeller efficiency model or modelling the calm water resistance in a more comprehensive manner. The effect of wave direction on encountered wave resistance could be included as well, based on the methodology developed in [50]. The limitations of the chosen methods for resistance calculation are acknowledged. However, the focus of this study was on developing the novel optimisation model for increased computational efficacy rather than the precise modelling of ship resistance. In practice, commercial providers of voyage optimisation software [26] and services dispose of more accurate methods for resistance estimation, often backed up by onboard measurements [51] and other monitoring data [52], which allow them to update and further tune the models. However, the authors believe that the qualitative comparisons can be performed with chosen methods. These more accurate methods and tuned and updated models can be combined with the presented computational method for the optimization. Thus the improvement of computational efficacy is deemed important for a practical point of view.

Finally, the juxtaposition between a fixed and flexible schedule came up multiple times during research. Allowing a flexible schedule for the voyage and associating a penalty for late arrival would lead to a more comprehensive and realistic model for ship owners and operators. Such a model could also include additional costs such as crew salaries and port fees. These subjects were left outside the scope of this work purposefully, and are rather subjects of further research.

This research focused on a single route in the Atlantic Ocean. To study the impact of speed profile optimisation further, and to generalise the achieved results, it would be valuable to study other routes as well. Particularly routes with significant ocean current activity should provide interesting results. As ocean currents are temporally static in the time frame of a single voyage, the application of the convex optimisation model alone could provide interesting benefits in such voyages.

5. Conclusions

As marine emission regulations become more strict and stakeholders more environmentally aware, ship operators are looking for cost efficient ways for reducing emissions. Operational methods for emission reduction are a lucrative option due to the low capital investment compared to technical changes for example. This paper focused on ship speed profile optimisation with a fixed schedule in relation to the broader concept of voyage optimisation.

We presented a novel convex optimisation extension to existing ship speed profile optimisation frameworks. The developed model was connected to a dynamic program for speed profile optimisation, and it was demonstrated how this connection reinforced the benefits of both methodologies, while alleviating their negative aspects. The combined model with dynamic programming and convex optimisation tolerated larger temporal and spatial resolutions for the dynamic programming model, thus increasing the computational performance of the method significantly compared to dynamic programming alone.

The combined method with both dynamic programming and convex optimisation was 22% more effective in saving fuel via speed profile optimisation, compared to using only dynamic programming. The performance of dynamic programming by itself could be improved further by increasing the temporal and spatial resolution of the model, but this comes at a significant computational cost, whereas including the convex optimisation extension induced negligible computational cost.

The fuel saving performance of the proposed methodology was demonstrated with the 20 shortest path journeys from Houston, Texas to London Gateway simulating five different vessels. Actual hydro-meteorological conditions active during the journeys were gathered from NAPA Voyage Optimisation [26]. On average, the developed combined method saved 1.1% of fuel across all studied journeys and vessels. Focusing only on journeys where meaningful changes in weather conditions were present, the attained fuel savings were 3.5% on average. A significant variation in potential fuel savings via speed profile optimisation was also identified depending on ship type within the studied time constraints depending on the ship design speed.

As a conclusion, it can be stated that the fuel saving impact of speed profile optimisation of ships with a fixed schedule in general is small, although not negligible. Speed profile optimisation provides more substantial benefits in cases where significant variation in weather conditions are present in the upcoming journey. The fuel saving impact of such methods is increased for fast vessels, operating well under their design speed.