Exploiting Distance-Based Structures in Data Using an Explainable AI for Stock Picking
Abstract
:1. Introduction
2. Related Works
3. Materials and Methods
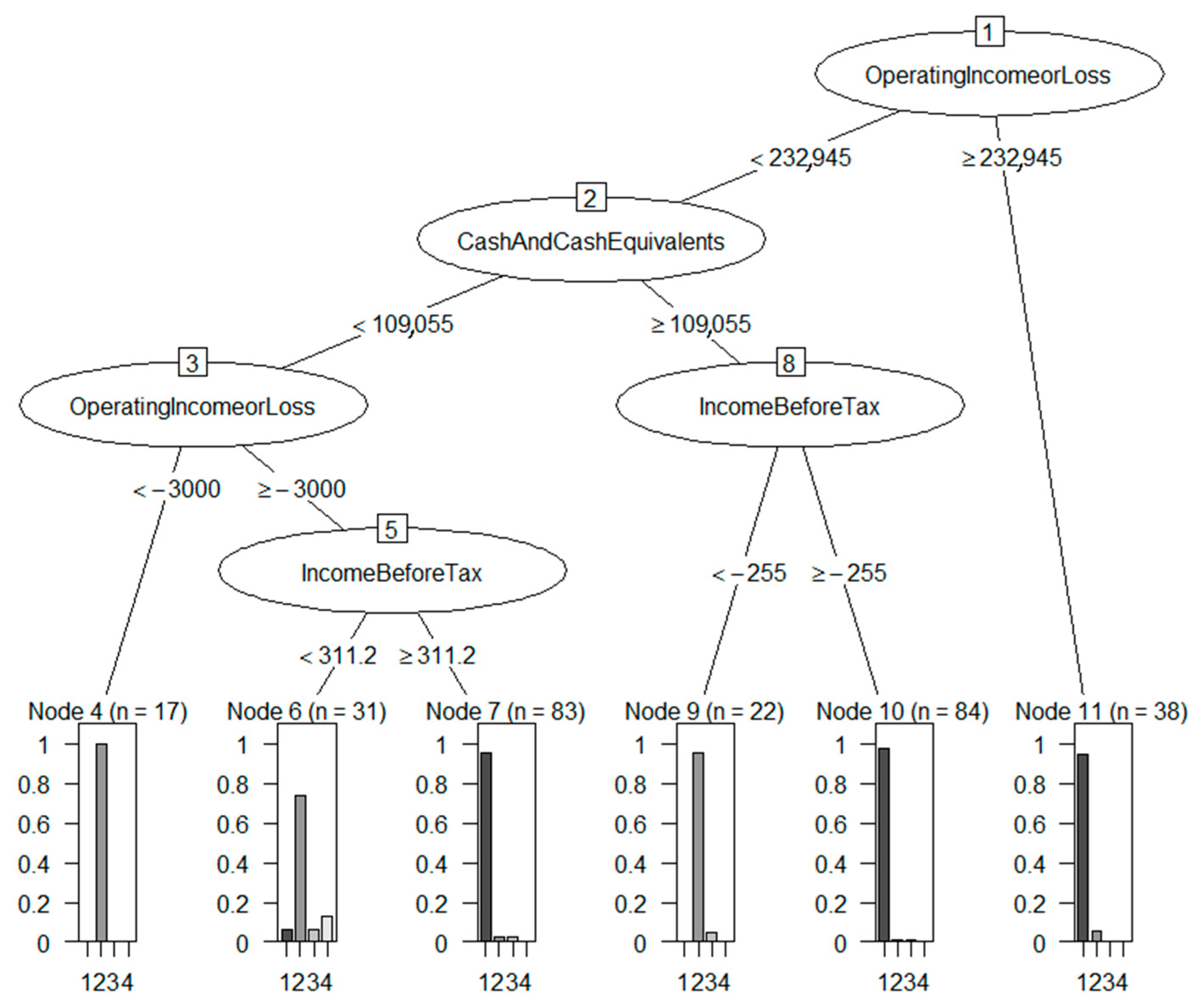
3.1. Identification of DSD
Validation of DSD
3.2. Fundamental Analysis
3.3. Searching for Meaningful Explanations Using the Grice’s Maxims
3.3.1. Rating of Explanations
3.3.2. Validation by Evaluation of the Relevance of Explanations
3.4. Access to Data and Open-Source Code
4. Results
4.1. Meaningfulness of DSD-XAI Explanations
4.2. Relevance of DSD-XAI Explanations by Simulated Stock Picking
4.3. DSD Identification by Cluster Analysis and Validation
5. Discussion
6. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Code Availability
References
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, Fl, USA, 1984. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Blockeel, H.; De Raedt, L.; Ramon, J. Top-down induction of clustering trees. In Proceedings of the 15th International Conference on Machine Learning, San Francisco, CA, USA, 21–27 July 1998; Shavlik, J., Ed.; Morgan Kaufmann: Burlington, MA, USA, 1998; pp. 55–63. [Google Scholar]
- Burkart, N.; Huber, M.F. A survey on the explainability of supervised machine learning. J. Artif. Intell. Res. 2021, 70, 245–317. [Google Scholar] [CrossRef]
- Dasgupta, S.; Frost, N.; Moshkovitz, M.; Rashtchian, C. Explainable K-means and K-medians clustering. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; PMLR: Vienna, Austria, 2020; pp. 7055–7065. [Google Scholar]
- Loyola-González, O.; Gutierrez-Rodríguez, A.E.; Medina-Pérez, M.A.; Monroy, R.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A.; García-Borroto, M. An Explainable Artificial Intelligence Model for Clustering Numerical Databases. IEEE Access 2020, 8, 52370–52384. [Google Scholar] [CrossRef]
- Thrun, M.C. The Exploitation of Distance Distributions for Clustering. Int. J. Comput. Intell. Appl. 2021, 20, 2150016. [Google Scholar] [CrossRef]
- Thrun, M.C.; Ultsch, A. Using projection based clustering to find distance and density based clusters in high-dimensional data. J. Classif. 2020, 38, 280–312. [Google Scholar] [CrossRef]
- Grice, H.P. Logic and conversation. In Speech Acts; Academic Press: New York, NY, USA, 1975; Volume 3, pp. 41–58. [Google Scholar]
- Thrun, M.C.; Ultsch, A.; Breuer, L. Explainable AI Framework for Multivariate Hydrochemical Time Series. Mach. Learn. Knowl. Extr. 2021, 3, 170–205. [Google Scholar] [CrossRef]
- Tsaih, R.; Hsu, Y.; Lai, C.C. Forecasting S&P 500 stock index futures with a hybrid AI system. Decis. Support Syst. 1998, 23, 161–174. [Google Scholar]
- Gelistete Unternehmen in Prime Standard, G.S.u.S. Available online: http://www.deutsche-boerse-cash-market.com/dbcm-de/instrumente-statistiken/statistiken/gelistete-unternehmen (accessed on 18 September 2018).
- Prime-Standard. Teilbereich des Amtlichen Marktes und des Geregelten Marktes der Deutschen Börse für Unternehmen, die Besonders hohe Transparenzstandards Erfüllen. Available online: http://deutsche-boerse.com/dbg-de/ueber-uns/services/know-how/boersenlexikon/boersenlexikon-article/Prime-Standard/2561178 (accessed on 18 September 2018).
- Nazário, R.T.F.; e Silva, J.L.; Sobreiro, V.A.; Kimura, H. A literature review of technical analysis on stock markets. Q. Rev. Econ. Financ. 2017, 66, 115–126. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock and stock price index movement using trend deterministic data preparation and machine learning techniques. Expert Syst. Appl. 2015, 42, 259–268. [Google Scholar] [CrossRef]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock market index using fusion of machine learning techniques. Expert Syst. Appl. 2015, 42, 2162–2172. [Google Scholar] [CrossRef]
- O'Neil, W.J. How to Make Money in Stocks; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Deboeck, G.J.; Ultsch, A. Picking stocks with emergent self-organizing value maps. Neural Netw. World 2000, 10, 203–216. [Google Scholar]
- Mohanram, P.S. Separating winners from losers among lowbook-to-market stocks using financial statement analysis. Rev. Account. Stud. 2005, 10, 133–170. [Google Scholar] [CrossRef]
- Ou, J.A.; Penman, S.H. Financial statement analysis and the prediction of stock returns. J. Account. Econ. 1989, 11, 295–329. [Google Scholar] [CrossRef]
- Richardson, S.; Tuna, I.; Wysocki, P. Accounting anomalies and fundamental analysis: A review of recent research advances. J. Account. Econ. 2010, 50, 410–454. [Google Scholar] [CrossRef]
- Gite, S.; Khatavkar, H.; Kotecha, K.; Srivastava, S.; Maheshwari, P.; Pandey, N. Explainable stock prices prediction from financial news articles using sentiment analysis. PeerJ Comput. Sci. 2021, 7, e340. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Ultsch, A. The integration of connectionist models with knowledge-based systems: Hybrid systems. In Proceedings of the SMC'98 Conference Proceedings, 1998 IEEE International Conference on Systems, Man, and Cybernetics (Cat. No.98CH36218), San Diego, CA, USA, 14 October 1998; IEEE: San Diego, CA, USA, 1998; pp. 1530–1535. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Ultsch, A.; Korus, D. Integration of neural networks and knowledge-based systems. In Proceedings of the International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Perth, Australia, 1995; pp. 1–6. [Google Scholar]
- Biran, O.; Cotton, C. Explanation and justification in machine learning: A survey. In IJCAI-17 Workshop Explainable AI (XAI); IJCAI: Macao, SA, USA, 2017; pp. 8–13. [Google Scholar]
- Adadi, A.; Berrada, M. Peeking inside the black-box: A survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Lipton, Z.C. The mythos of model interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Ultsch, A.; Halmans, G.; Mantyk, R. CONKAT: A connectionist knowledge acquisition tool. In Proceedings of the 24th Annual Hawaii International Conference on System Sciences, Kauai, HI, USA, 8–11 January 1991; IEEE: Kauai, HI, USA, 1991; pp. 507–513. [Google Scholar]
- Ultsch, A.; Korus, D.; Kleine, T. Integration of neural networks and knowledge-based systems in medicine. In Proceedings of the Conference on Artificial Intelligence in Medicine in Europe, Pavia, Italy, 25–28 June 1995; Barahona, P., Stefanelli, M., Wyatt, J., Eds.; Springer: Berlin, Heidelberg, 1995; pp. 425–426. [Google Scholar]
- Letham, B.; Rudin, C.; McCormick, T.H.; Madigan, D. An interpretable stroke prediction model using rules and bayesian analysis. In Proceedings of the 17th AAAI Conference on Late-Breaking Developments in the Field of Artificial Intelligence, Bellevue, WD, USA, 14–18 July 2013; AAAI Press: New York, NY, USA, 2013; pp. 65–67. [Google Scholar]
- Riid, A.; Sarv, M. Determination of regional variants in the versification of estonian folksongs using an interpretable fuzzy rule-based classifier. In Proceedings of the 8th Conference of the European Society for Fuzzy logic and Technology (EUSFLAT-13), Milano, Italy, 11–13 September 2013; Atlantis Press: Amsterdam, The Netherlands, 2013; pp. 61–66. [Google Scholar]
- Nauck, D.; Kruse, R. Obtaining interpretable fuzzy classification rules from medical data. Artif. Intell. Med. 1999, 16, 149–169. [Google Scholar] [CrossRef]
- Lakkaraju, H.; Bach, S.H.; Leskovec, J. Interpretable decision sets: A joint framework for description and prediction. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; IEEE: New York, NY, USA, 2016; pp. 1675–1684. [Google Scholar]
- Hewett, R.; Leuchner, J. The power of second-order decision tables. In Proceedings of the 2nd SIAM International Conference on Data Mining, Arlington, VA, USA, 11–13 April 2002; SIAM: New Delhi, India, 2002; pp. 384–399. [Google Scholar]
- Dehuri, S.; Mall, R. Predictive and comprehensible rule discovery using a multi-objective genetic algorithm. Knowl. Based Syst. 2006, 19, 413–421. [Google Scholar] [CrossRef]
- Basak, J.; Krishnapuram, R. Interpretable hierarchical clustering by constructing an unsupervised decision tree. IEEE Trans. Knowl. Data Eng. 2005, 17, 121–132. [Google Scholar] [CrossRef]
- Kim, B.; Shah, J.A.; Doshi-Velez, F. Mind the gap: A generative approach to interpretable feature selection and extraction. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; pp. 2260–2268. [Google Scholar]
- Thrun, M.C.; Gehlert, T.; Ultsch, A. Analyzing the Fine Structure of Distributions. PLoS ONE 2020, 15, e0238835. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Hartigan, P.M. The dip test of unimodality. Ann. Stat. 1985, 13, 70–84. [Google Scholar] [CrossRef]
- Orloci, L. An agglomerative method for classification of plant communities. J. Ecol. 1967, 55, 193–206. [Google Scholar] [CrossRef] [Green Version]
- Thrun, M.C.; Ultsch, A. Swarm intelligence for self-organized clustering. Artif. Intell. 2021, 290, 103237. [Google Scholar] [CrossRef]
- Van der Merwe, D.; Engelbrecht, A.P. Data clustering using particle swarm optimization. In Proceedings of the Evolutionary Computation, CEC'03, Canberra, Australia, 8–12 December 2003; IEEE: Canberra, Australia, 2003; pp. 215–220. [Google Scholar]
- Thrun, M.C. Projection Based Clustering through Self-Organization and Swarm Intelligence; Ultsch, A., Hüllermeier, E., Eds.; Springer: Heidelberg, Germany, 2018. [Google Scholar] [CrossRef] [Green Version]
- Ultsch, A.; Lötsch, J. Machine-learned cluster identification in high-dimensional data. J. Biomed. Inform. 2017, 66, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Thrun, M.C. Distance-Based Clustering Challenges for Unbiased Benchmarking Studies. Nat. Sci. Rep. 2021, 11, 18988. [Google Scholar] [CrossRef]
- Murtagh, F. On ultrametricity, data coding, and computation. J. Classif. 2004, 21, 167–184. [Google Scholar] [CrossRef]
- Adolfsson, A.; Ackerman, M.; Brownstein, N.C. To cluster, or not to cluster: An analysis of clusterability methods. Pattern Recognit. 2019, 88, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.O.; Walther, G. Investigating the multimodality of multivariate data with principal curves. Comput. Stat. Data Anal. 2012, 56, 4462–4469. [Google Scholar] [CrossRef]
- Thrun, M.C. Improving the sensitivity of statistical testing for clusterability with mirrored-density plot. In Machine Learning Methods in Visualisation for Big Data; Archambault, D., Nabney, I., Peltonen, J., Eds.; The Eurographics Association: Norrköping, Sweden, 2020; pp. 1–17. [Google Scholar]
- Thrun, M.C.; Ultsch, A. Uncovering High-Dimensional Structures of Projections from Dimensionality Reduction Methods. MethodsX 2020, 7, 101093. [Google Scholar] [CrossRef]
- Thrun, M.C.; Lerch, F.; Lötsch, J.; Ultsch, A. Visualization and 3D printing of multivariate data of biomarkers. In Proceedings of the International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Plzen, Czech Republic, 30 May–3 June 2016; Skala, V., Ed.; WSCG: Plzen, Czech Republic, 2016; pp. 7–16. [Google Scholar]
- Dasgupta, S.; Gupta, A. An elementary proof of a theorem of Johnson and Lindenstrauss. Random Struct. Algorithms 2003, 22, 60–65. [Google Scholar] [CrossRef]
- Johnson, W.B.; Lindenstrauss, J. Extensions of lipschitz mappings into a hilbert space. Contemp. Math. 1984, 26, 189–206. [Google Scholar] [CrossRef]
- Silver, C.; Chen, J.; Hong, E.; Kagan, J.; Kenton, W.; Krishna, M. Operating Income; Investopedia LLC: New York, NY, USA, 2014. [Google Scholar]
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Cowan, N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behav. Brain Sci. 2001, 24, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Miller, G.A. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 101, 343–352. [Google Scholar] [CrossRef]
- Mörchen, F.; Ultsch, A.; Hoos, O. Extracting interpretable muscle activation patterns with time series knowledge mining. Int. J. Knowl. Based Intell. Eng. Syst. 2005, 9, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Miller, T.; Howe, P.; Sonenberg, L.; AI, E. Explainable AI: Beware of inmates running the asylum. In IJCAI 2019 Workshop on Explainable Artificial Intelligence (XAI); IJCAI: Melbourne, Australia, 2017; pp. 36–42. [Google Scholar]
- Ultsch, A. Is Log Ratio a Good Value for Measuring Return in Stock Investments? In Advances in Data Analysis, Data Handling and Business Intelligence; Springer: Berlin/Heidelberg, Germany, 2009; pp. 505–511. [Google Scholar]
- Welch, B.L. The significance of the difference between two means when the population variances are unequal. Biometrika 1938, 29, 350–362. [Google Scholar] [CrossRef]
- Cormack, R.M. A review of classification. J. Roy. Stat. Soc. Ser. A (Gen.) 1971, 134, 321–367. [Google Scholar] [CrossRef]
- Grubinger, T.; Zeileis, A.; Pfeiffer, K.-P. evtree: Evolutionary learning of globally optimal classification and regression trees in R. J. Stat. Softw. 2014, 61, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Ultsch, A. Pareto density estimation: A density estimation for knowledge discovery. In Innovations in Classification, Data Science, and Information Systems; Baier, D., Werrnecke, K.D., Eds.; Springer: Berlin, Germany, 2005; pp. 91–100. [Google Scholar]
- Joshi, G.; Walambe, R.; Kotecha, K. A Review on Explainability in Multimodal Deep Neural Nets. IEEE Access 2021, 9, 59800–59821. [Google Scholar] [CrossRef]
- Mimmack, G.M.; Mason, S.J.; Galpin, J.S. Choice of distance matrices in cluster analysis: Defining regions. J. Clim. 2001, 14, 2790–2797. [Google Scholar] [CrossRef]
- Mörchen, F. Time Series Knowledge Mining; Citeseer/Görich & Weiershäuser: Marburg, Germany, 2006. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for clustering data. In Prentice Hall Advanced Reference Series: Computer Science; Marttine, B., Ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1988; pp. 1–320. [Google Scholar]
- Hennig, C.; Meila, M.; Murtagh, F.; Rocci, R. Handbook of cluster analysis. In Handbook of Modern Statistical Methods; Hennig, C., Meila, M., Murtagh, F., Rocci, R., Eds.; Chapman & Hall/CRC Press: New York, NY, USA, 2015; pp. 1–730. [Google Scholar]
- Wachter, S.; Mittelstadt, B.; Russell, C. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harv. JL Tech. 2017, 31, 841. [Google Scholar] [CrossRef] [Green Version]
- Karimi, A.-H.; Schölkopf, B.; Valera, I. Algorithmic recourse: From counterfactual explanations to interventions. In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, Virtual Event, 3–10 March 2021; pp. 353–362. [Google Scholar]










| Quarter Cluster Analysis | Quarter of Stock Prices | Price Development of Selected Stocks in DSD-XAI | Random | Rate of Success (Significance of t-Test) |
|---|---|---|---|---|
| 2018, Q4 | 2019, Q1 | 61% of stocks fall with an average rate of return of −8% | 51% of stocks fall with an average rate of return of −1% | 10% |
| 2018, Q1 | 2018, Q2 | 57% of stocks rise with an average rate of return of 2% | 43% of stocks rise with an average rate of return of −4 % | 14% |
| 2018, Q2 | 2018, Q3 | 95% of stocks fall with an average rate of return of −31% | 91% of stocks fall with an average rate of return of −22% | 4% with |
| 2018, Q3 | 2018, Q4 | 52% of stocks fall with an average rate of return of −2% | 30% of stocks fall with an average rate of return of 9% | 22% with |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thrun, M.C. Exploiting Distance-Based Structures in Data Using an Explainable AI for Stock Picking. Information 2022, 13, 51. https://doi.org/10.3390/info13020051
Thrun MC. Exploiting Distance-Based Structures in Data Using an Explainable AI for Stock Picking. Information. 2022; 13(2):51. https://doi.org/10.3390/info13020051
Chicago/Turabian StyleThrun, Michael C. 2022. "Exploiting Distance-Based Structures in Data Using an Explainable AI for Stock Picking" Information 13, no. 2: 51. https://doi.org/10.3390/info13020051
APA StyleThrun, M. C. (2022). Exploiting Distance-Based Structures in Data Using an Explainable AI for Stock Picking. Information, 13(2), 51. https://doi.org/10.3390/info13020051






