Enhancing Frequency Regulation Support through Several Synthetic Inertial Approaches for WDPS
Abstract
:1. Introduction
- (1)
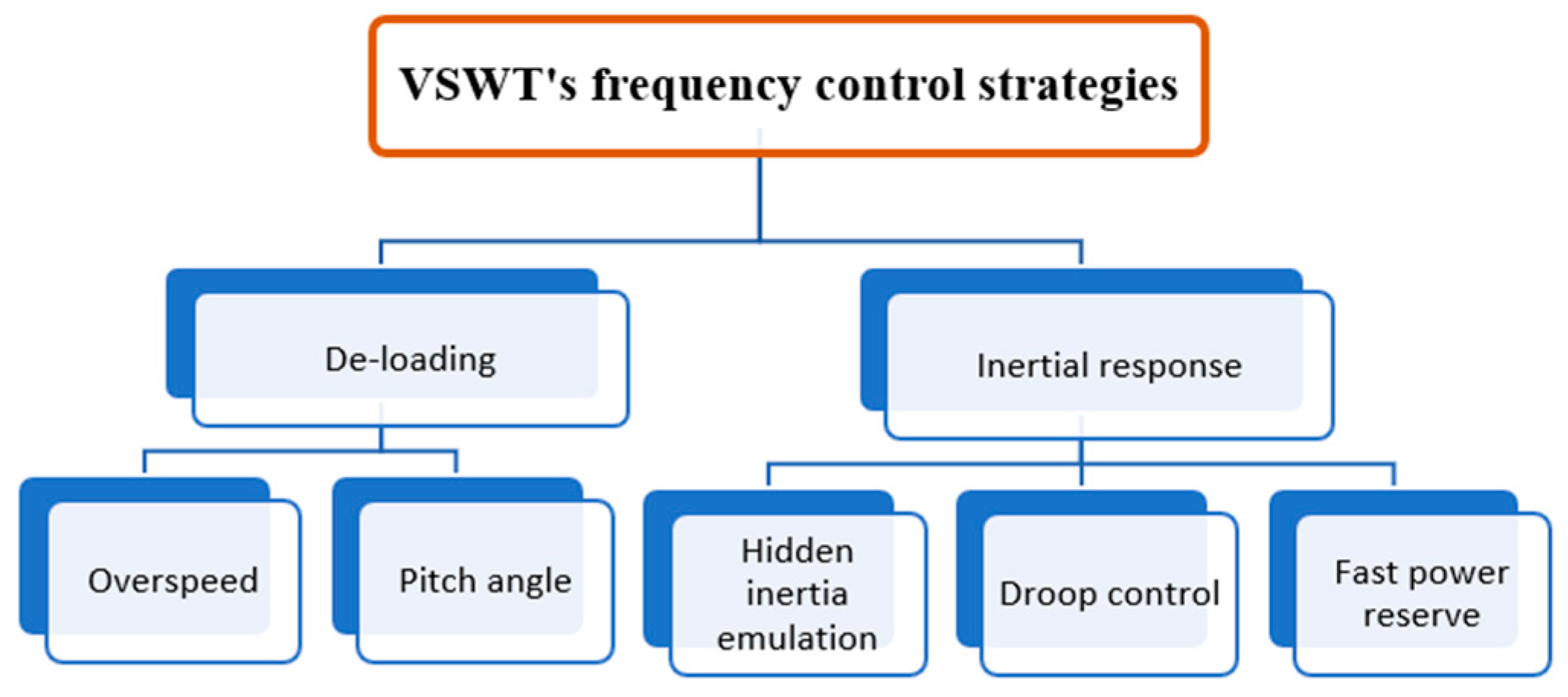
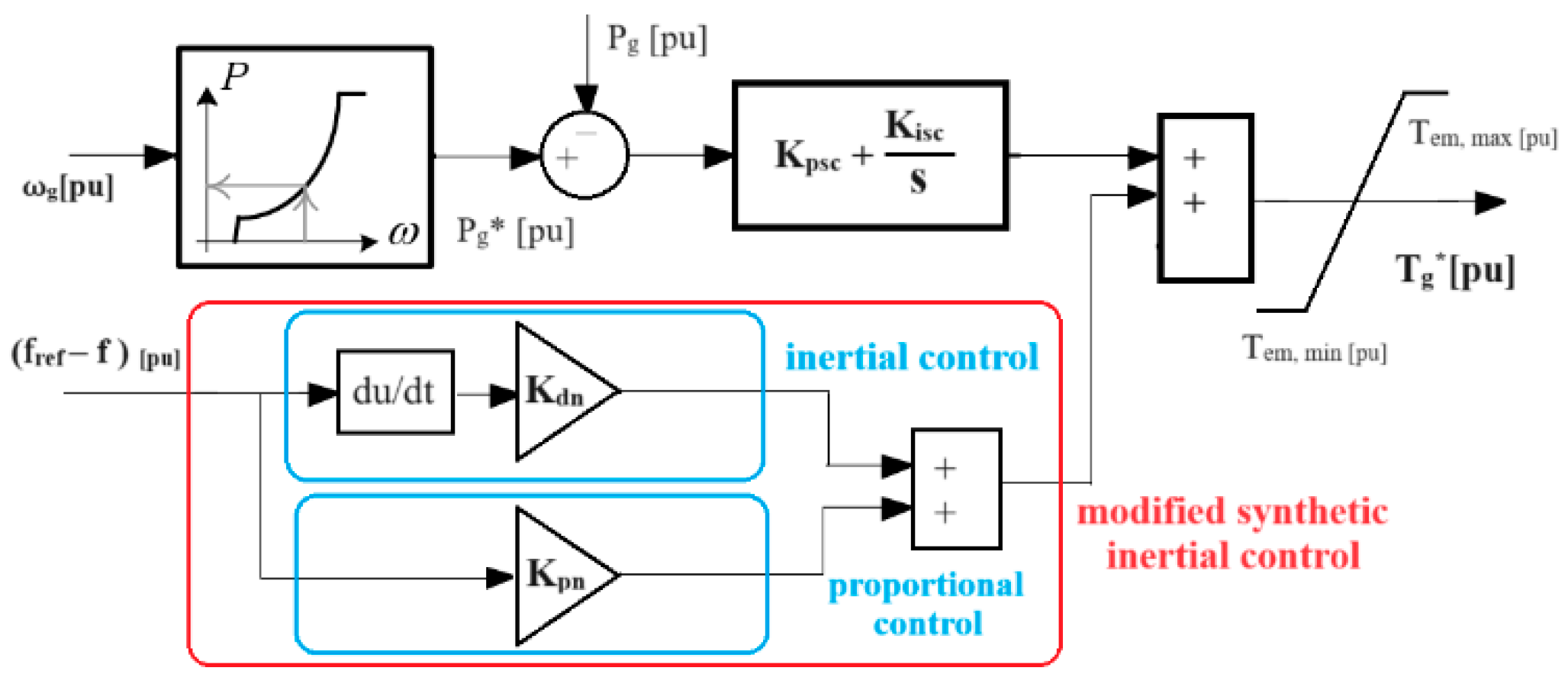
- New controls were introduced (modified synthetic inertial control, droop control, traditional inertial control) into VSWT that enable them to contribute, by releasing synthetic inertia, during contingencies;
- (2)
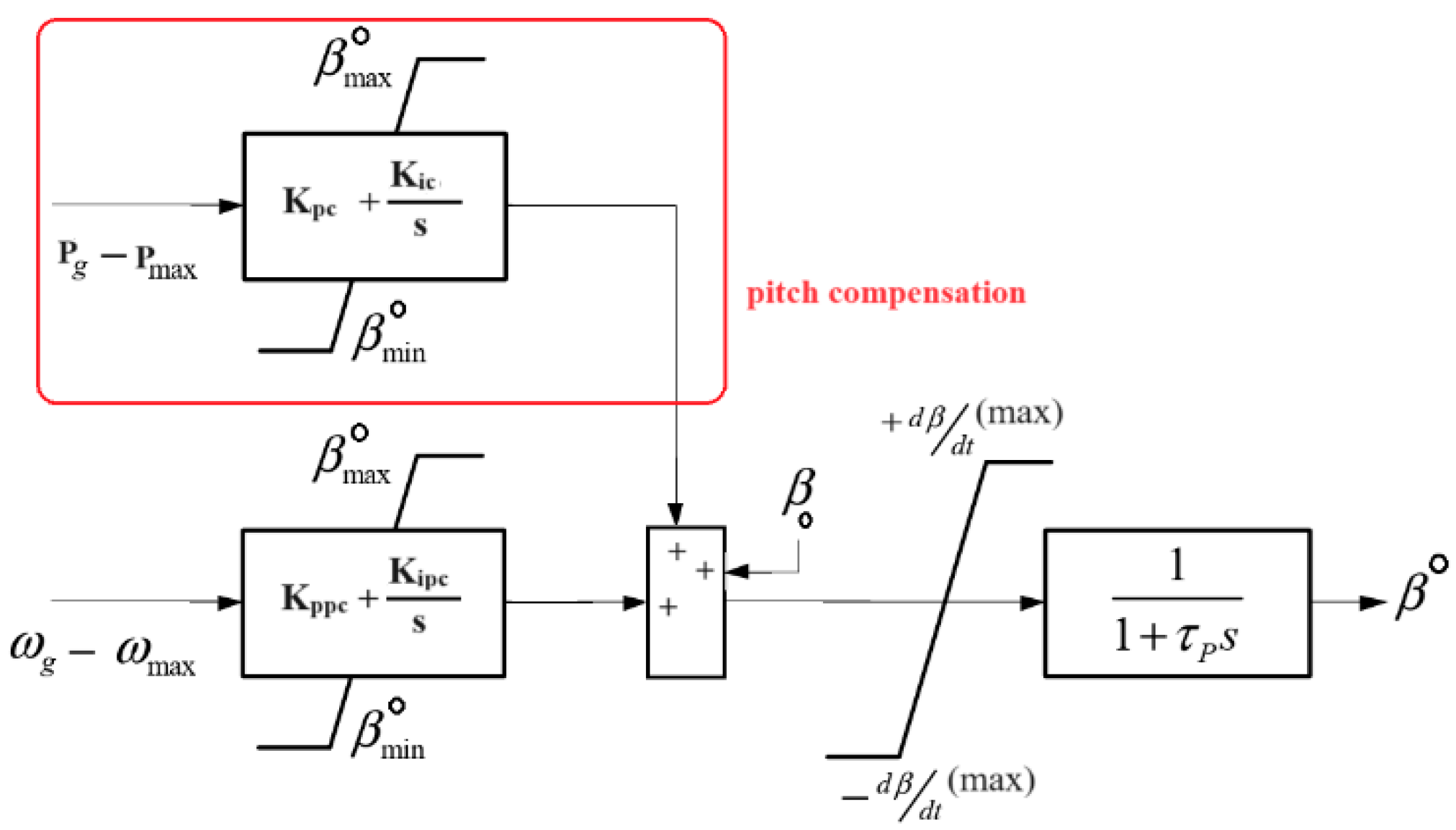
- Pitch compensation control was introduced in BPAC that returned the system to normal after perturbations. In addition, it enhanced the BPAC smoothness;
- (3)
- The SPBA optimization algorithm is used to optimally tune the hybrid power system. Major benefits are achieved by using SPBA, as discussed in Section 5;
- (4)
- The hybrid WDPS control strategies’ performance was evaluated and compared against seven different scenarios to highlight their pros and cons. Moreover, it is concluded that droop control is the best alternative to modified synthetic inertial control in terms of robustness because it reduced noise by eliminating the derivative function from the control loop. Moreover, it reduced the steady-state error which made the power system more stable;
- (5)
- The controller performance was tested under various real-world scenarios to highlight its reliability.
2. Wind Turbine Modeling
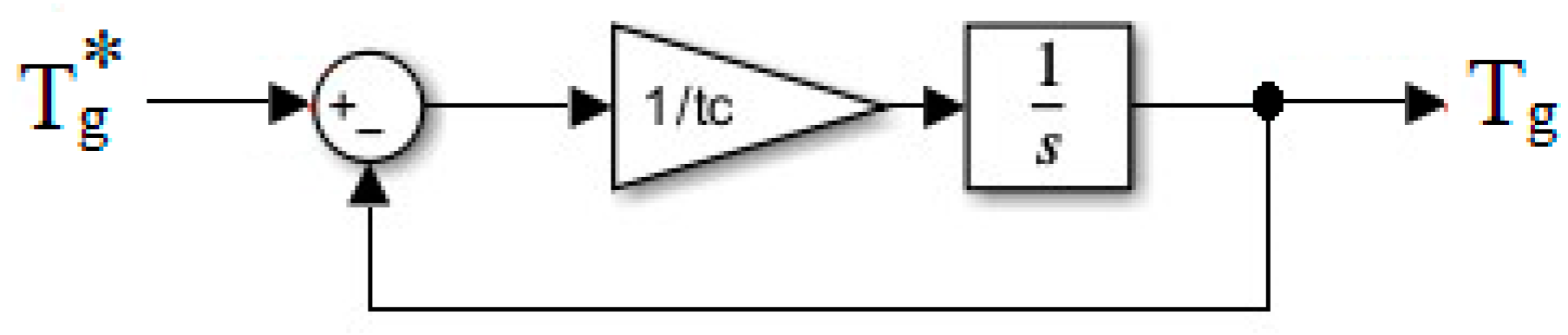
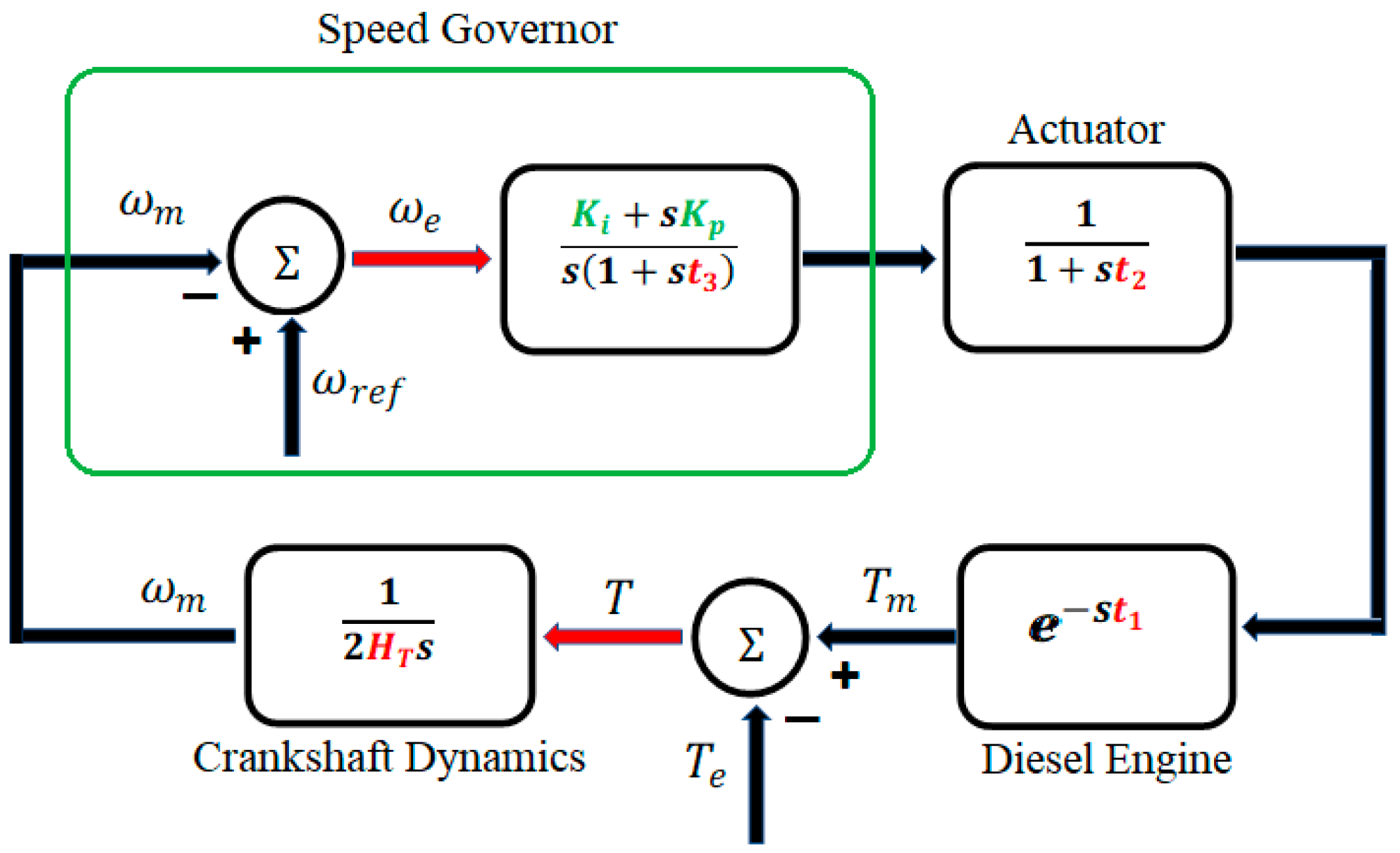
3. Diesel Power Plant Modeling
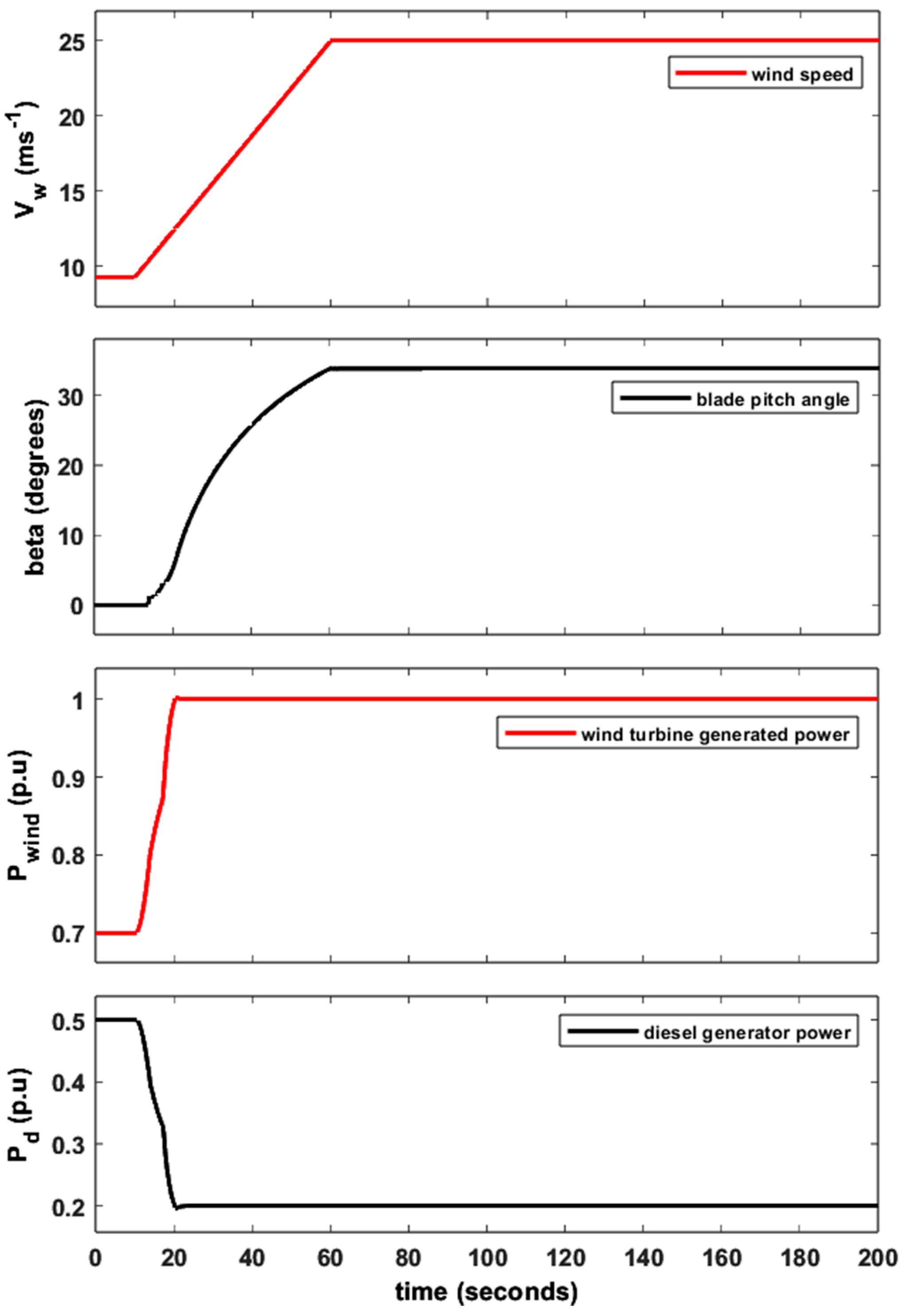
4. Proposed Control Loop: San Cristobal Island WT
5. Student Psychology-Based Algorithm (SPBA) Optimization
- Provide unique and best optimal controller gain parameters;
- Reduce the NADIR and FD;
- Provide the minimum ISE at the optimal operating point;
- Provide the minimum IAE at the optimal operating point;
- Reduce the number of sign changes in the frequency derivative.
6. Simulations and Results
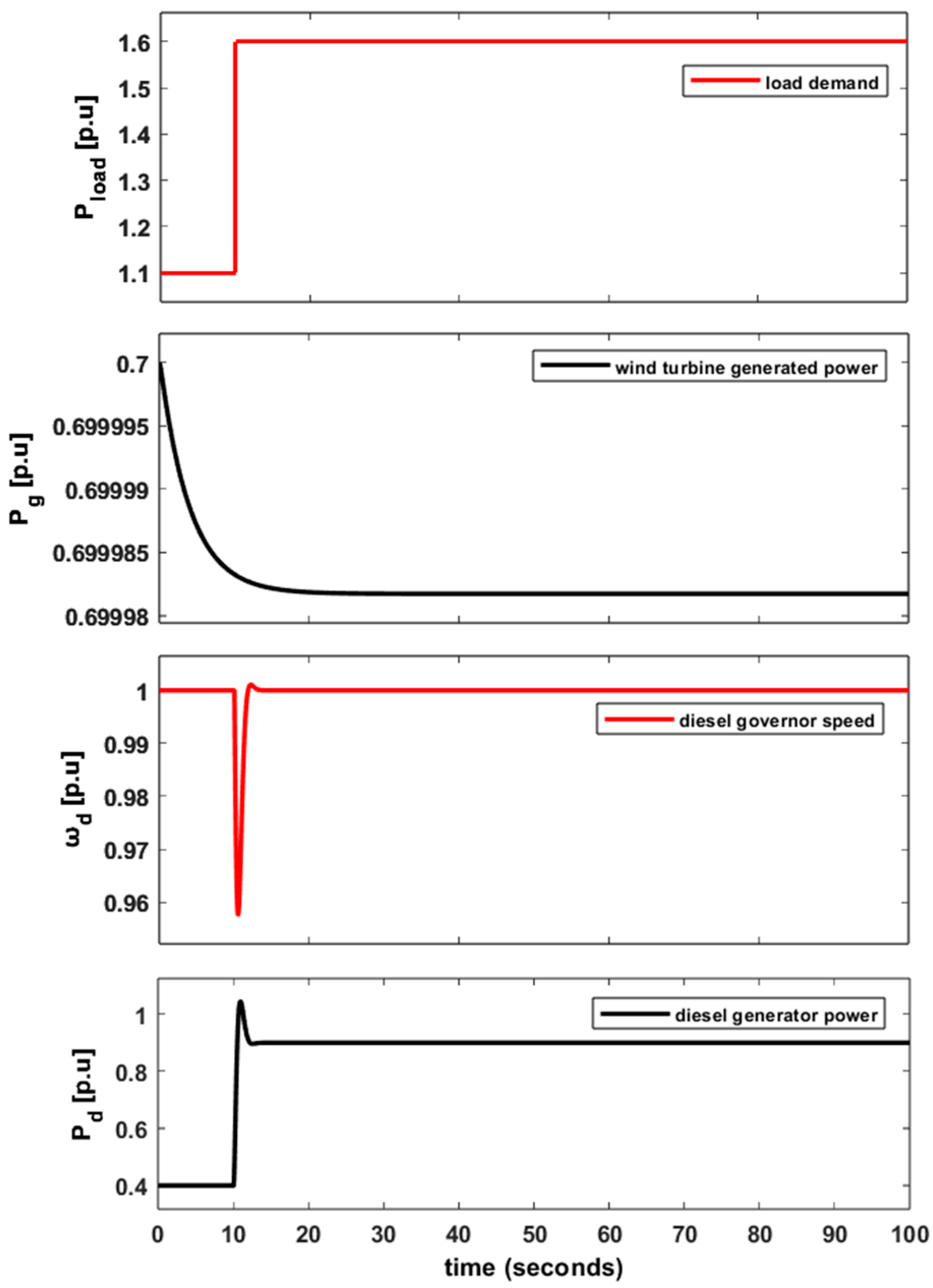
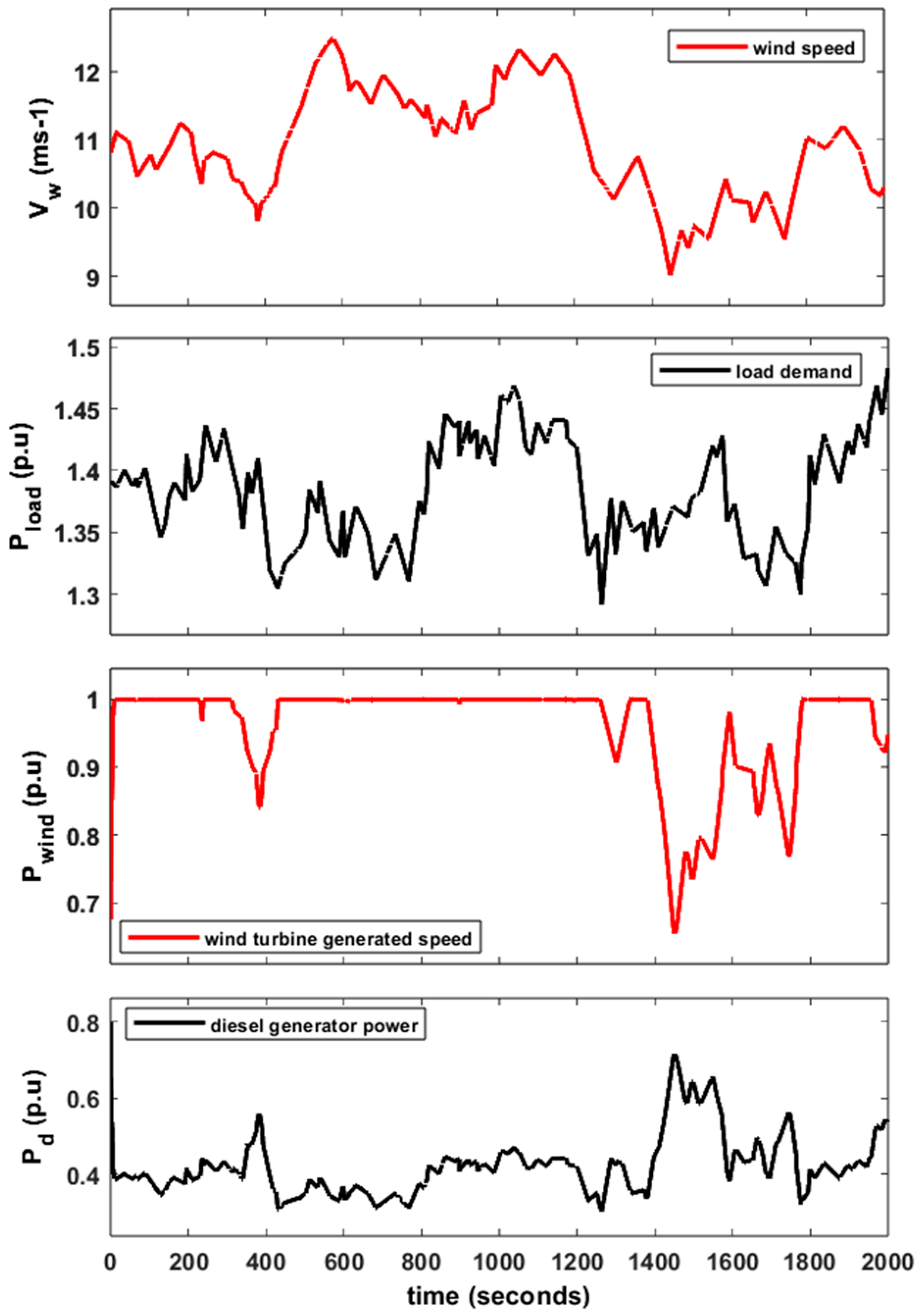
6.1. Base Case: San Cristobal Island Hybrid WDPS
6.2. Case T: Tuned DPP Effects on Synthetic Inertia
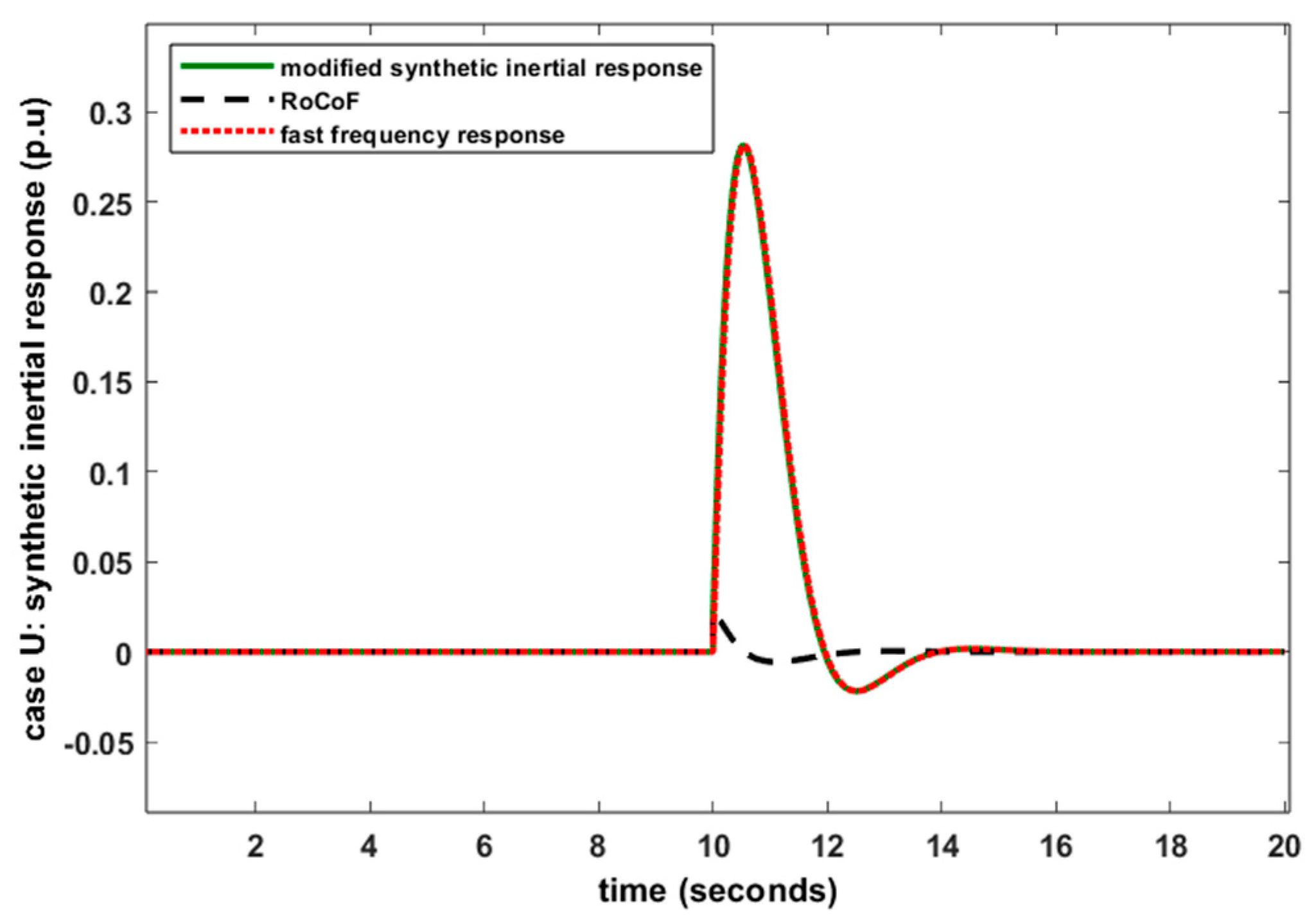
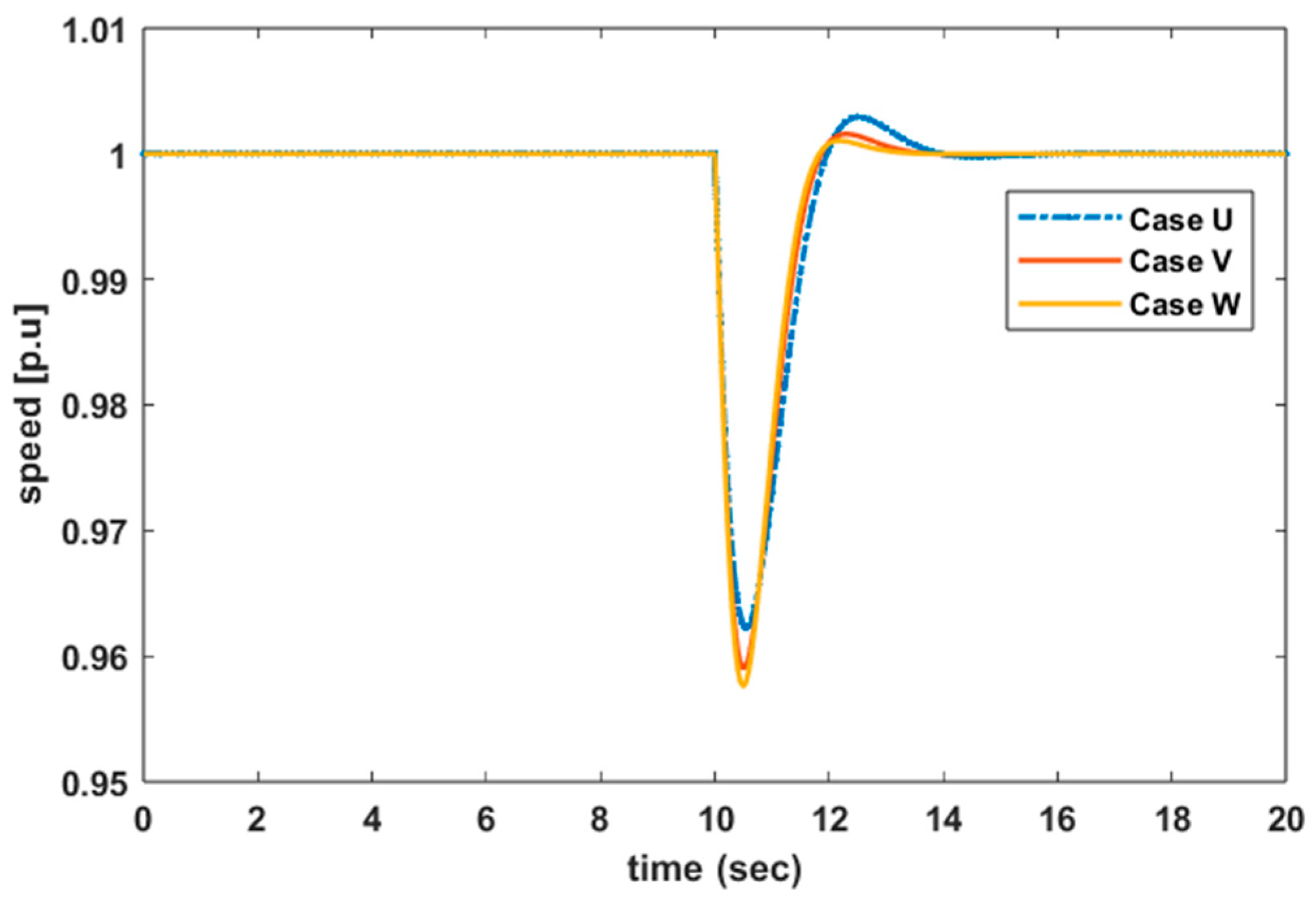
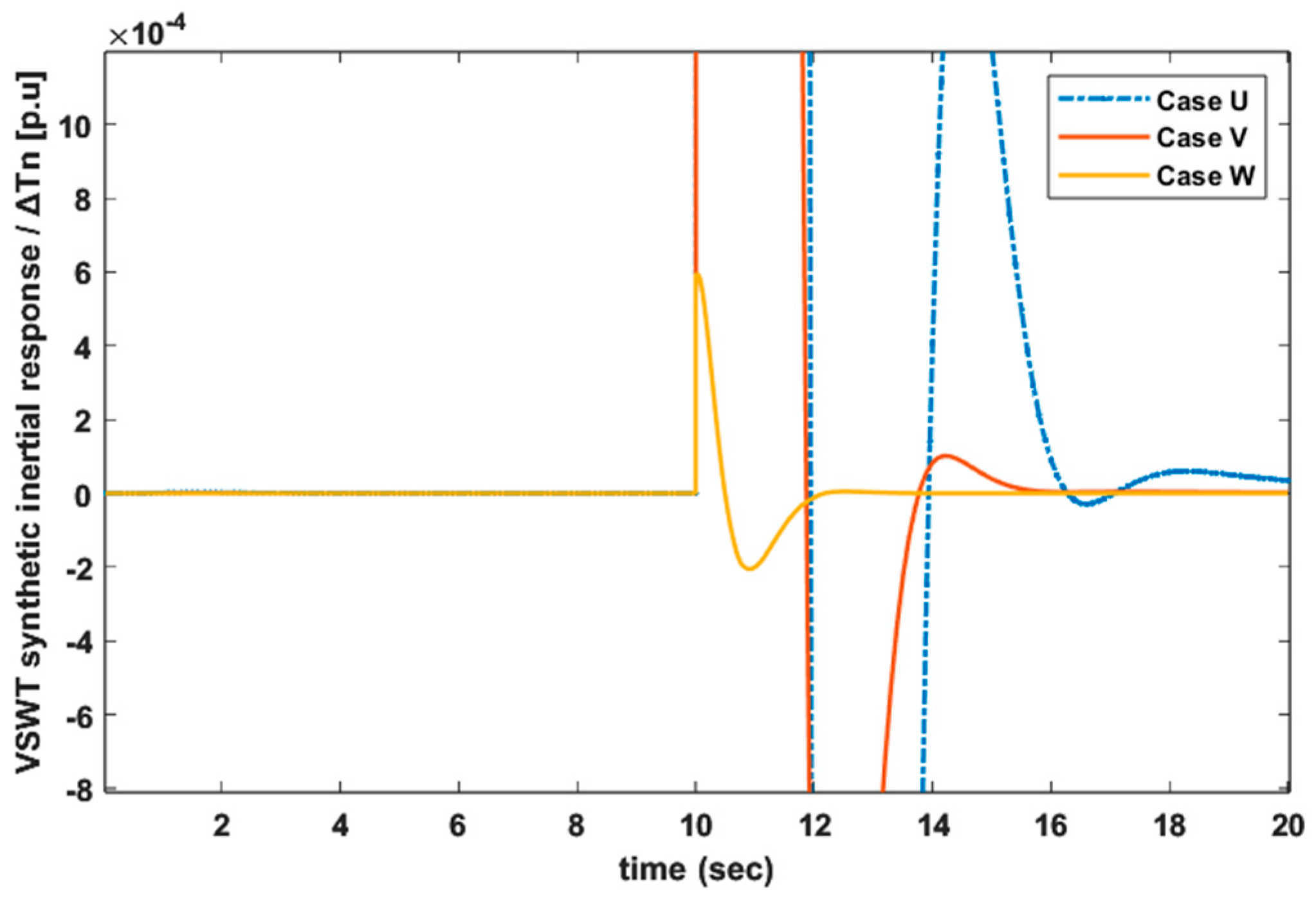
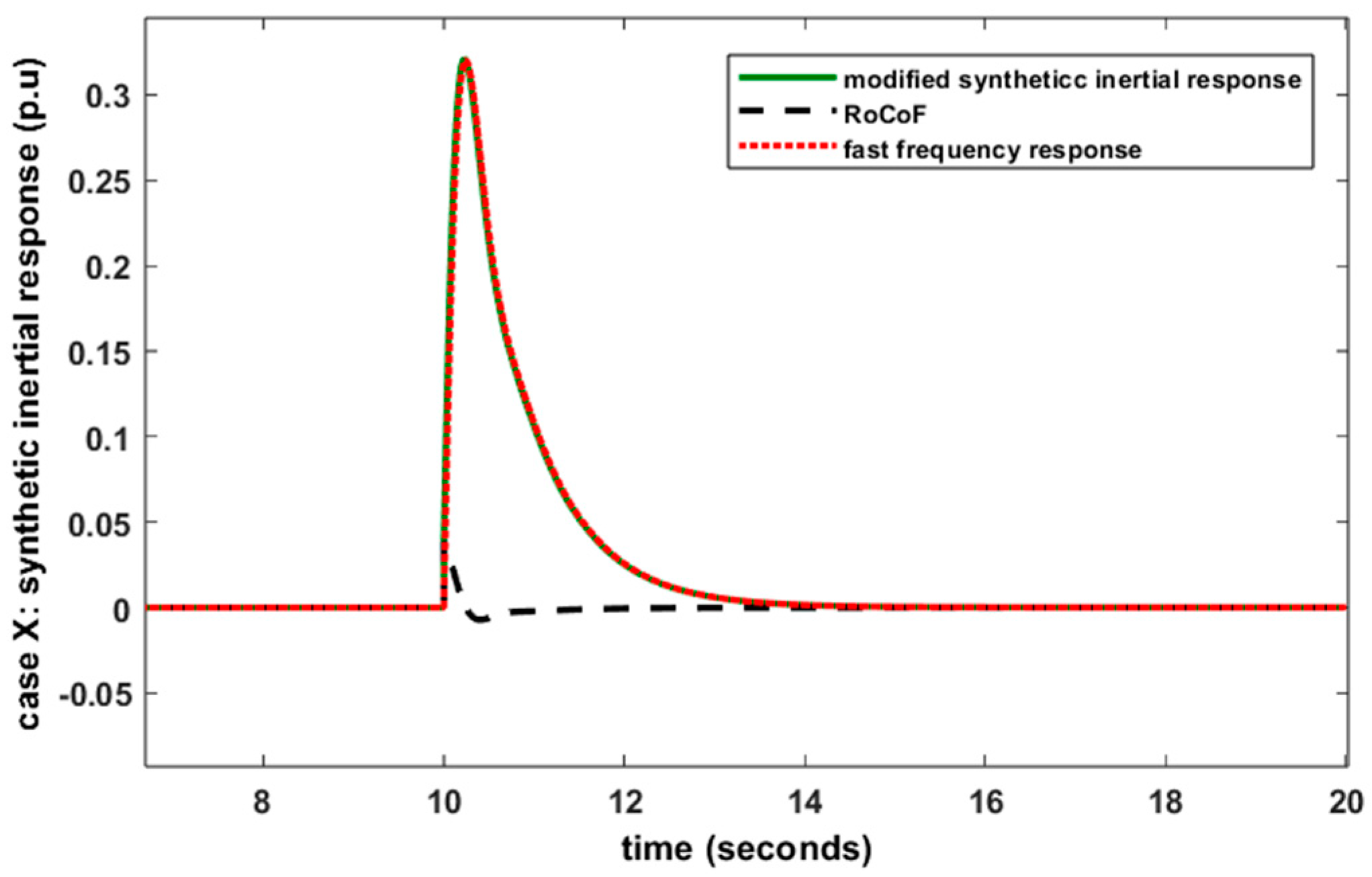
6.3. Case U: FR Provided by VSWT Using Modified Synthetic Inertial Control
6.4. Case V: FR Provided by VSWT Using Proportional Control
6.5. Case W: FR Provided by VSWT Using Inertial Control
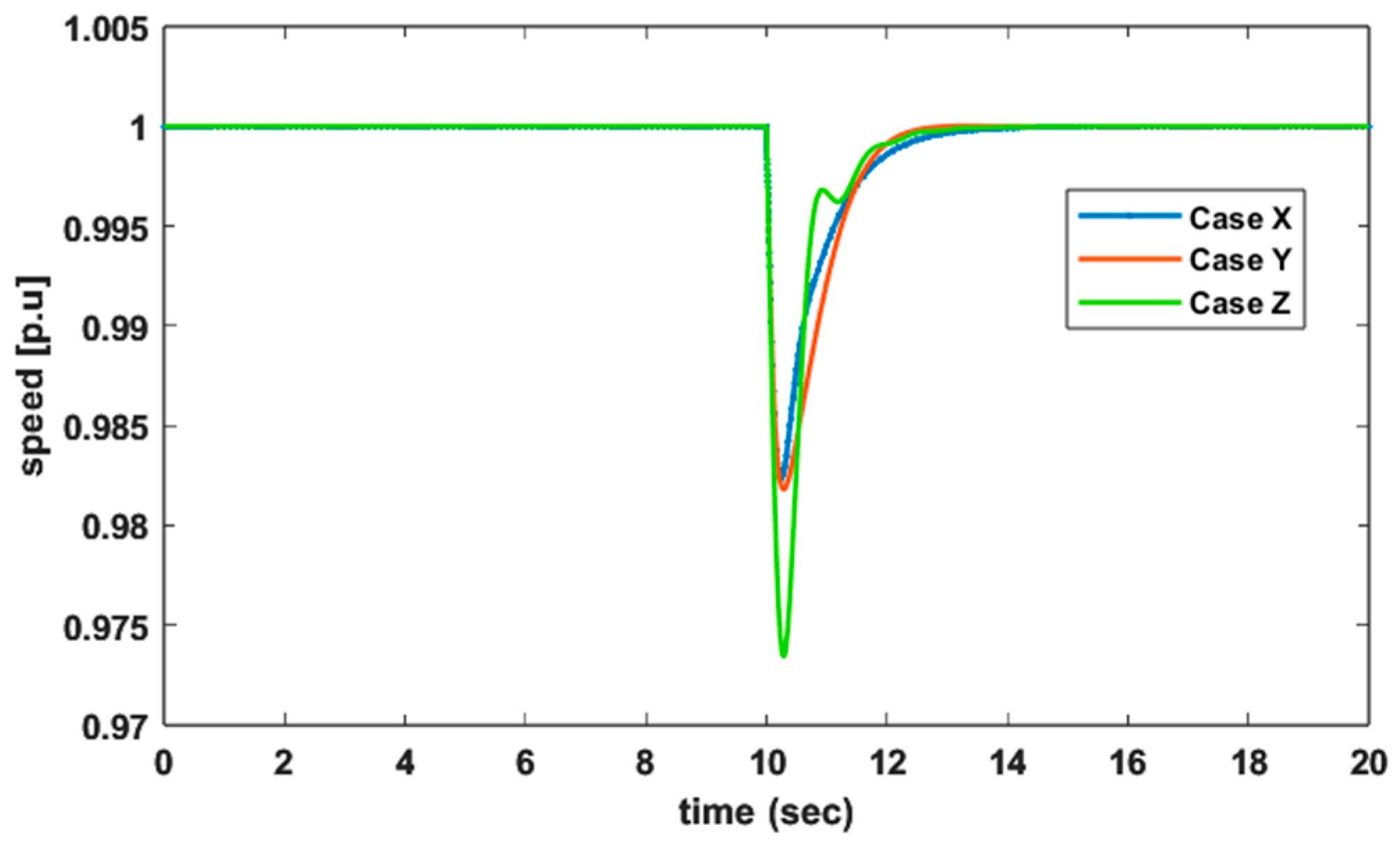
6.6. Case X: Simultaneously Tuned: DPP and VSWT with Modified Synthetic Inertial Control
6.7. Case Y: Simultaneously Tuned: DPP and VSWT with Droop Control
6.8. Case Z: Simultaneously Tuned: DPP and VSWT with Traditional Inertial Control
7. Controller Performance Evaluation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Case | NADIR (p.u.) | ISE | IAE | Q (p.u.) |
|---|---|---|---|---|
| Base | 0.8701 | 0.0410 | 0.4804 | 1.1373 × 103 |
| T | 0.9576 | 0.0012 | 0.0391 | 1.3665 × 103 |
| U | 0.9623 | 0.0011 | 0.0438 | 1.6790 × 103 |
| V | 0.9591 | 0.0012 | 0.0404 | 1.1371 × 103 |
| W | 0.9576 | 0.0012 | 0.0391 | 1.19224 × 104 |
| X | 0.9824 | 1.5215 × 10−4 | 0.0193 | 1.5206 × 104 |
| Y | 0.9818 | 2.0568 × 10−4 | 0.0169 | 1.5658 × 104 |
| Z | 0.9734 | 2.5728 × 10−4 | 0.0161 | 3.554 × 103 |

References
- Asad, M. Improving Power Flow Using Static Synchronous Series Compensator. Egypt. J. Eng. Sci. Technol. 2021, 33, 69–74. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, S.; Yang, Z. Recent Progress on Flutter-based Wind Energy Harvesting. Int. J. Mech. Syst. Dyn. 2022, 2, 82–98. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Muljadi, E.; Molina-García, A. Frequency Control Studies: A Review of Power System, Conventional and Renewable Generation Unit Modeling. Electr. Power Syst. Res. 2022, 211, 108191. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Martínez-Lucas, G.; Molina-García, Á.; Sarasua, J.I. An Adaptive Control Scheme for Variable Speed Wind Turbines Providing Frequency Regulation in Isolated Power Systems with Thermal Generation. Energies 2020, 13, 3369. [Google Scholar] [CrossRef]
- ENTSO-E. Electricity Balancing in Europe. Available online: https://docstore.entsoe.eu/ (accessed on 10 December 2023).
- Ochoa, D.; Martinez, S. Proposals for Enhancing Frequency Control in Weak and Isolated Power Systems: Application to the Wind-Diesel Power System of San Cristobal Island-Ecuador. Energies 2018, 11, 910. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. Overview of Wind Power Intermittency Impacts on Power Systems. Electr. Power Syst. Res. 2010, 80, 627–632. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.; Sánchez-Fernández, J. Frequency Regulation of a Hybrid Wind–Hydro Power Plant in an Isolated Power System. Energies 2018, 11, 239. [Google Scholar] [CrossRef]
- Lazarewicz, M.L.; Ryan, T.M. Integration of Flywheel-Based Energy Storage for Frequency Regulation in Deregulated Markets. In Proceedings of the PES 2010 IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Liu, L.; Senjyu, T.; Kato, T.; Mandal, P.; Hemeida, A.M.; Howlader, A.M. Renewable Energy Power System Frequency Control by Using PID Controller and Genetic Algorithm. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; pp. 1–5. [Google Scholar]
- Guha, D.; Roy, P.K.; Banerjee, S. Frequency Control of a Wind-Diesel-Generator Hybrid System with Squirrel Search Algorithm Tuned Robust Cascade Fractional Order Controller Having Disturbance Observer Integrated. Electr. Power Compon. Syst. 2022, 50, 814–839. [Google Scholar] [CrossRef]
- Afzal Thoker, Z.; Ahmad Lone, S. Dynamic Performance Improvement of Wind-Diesel Power System through Robust Sliding Mode Control of Hybrid Energy Storage System. Wind Eng. 2022, 46, 1065–1079. [Google Scholar] [CrossRef]
- Mi, Y.; Chen, B.; Cai, P.; He, X.; Liu, R.; Yang, X. Frequency Control of a Wind-Diesel System Based on Hybrid Energy Storage. Prot. Control Mod. Power Syst. 2022, 7, 31. [Google Scholar] [CrossRef]
- Panwar, A.; Sharma, G.; Bansal, R.C. Optimal AGC Design for a Hybrid Power System Using Hybrid Bacteria Foraging Optimization Algorithm. Electr. Power Compon. Syst. 2019, 47, 955–965. [Google Scholar] [CrossRef]
- Kumar, N.K.; Gopi, R.S.; Kuppusamy, R.; Nikolovski, S.; Teekaraman, Y.; Vairavasundaram, I.; Venkateswarulu, S. Fuzzy Logic-Based Load Frequency Control in an Island Hybrid Power System Model Using Artificial Bee Colony Optimization. Energies 2022, 15, 2199. [Google Scholar] [CrossRef]
- Fox, B.; Flynn, D.; Bryans, L.; Jenkins, N.; Milborrow, D.; O’Malley, M.; Watson, R.; Anaya-Lara, O. Wind Power Integration: Connection and System Operational Aspects; Institution of Engineering and Technology: Stevenage, UK, 2007; ISBN 9780863414497. [Google Scholar]
- Abad, G.; López, J.; Rodríguez, M.A.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; ISBN 9781118104965. [Google Scholar]
- Ackermann, T. Wind Power in Power Systems; Ackermann, T., Ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 9780470974162. [Google Scholar]
- Cai, T.; Liu, S.; Yan, G.; Liu, H. Analysis of Doubly Fed Induction Generators Participating in Continuous Frequency Regulation with Different Wind Speeds Considering Regulation Power Constraints. Energies 2019, 12, 635. [Google Scholar] [CrossRef]
- Serrano-González, J.; Lacal-Arántegui, R. Technological Evolution of Onshore Wind Turbines—A Market-based Analysis. Wind Energy 2016, 19, 2171–2187. [Google Scholar] [CrossRef]
- Vázquez-Hernández, C.; Serrano-González, J.; Centeno, G. A Market-Based Analysis on the Main Characteristics of Gearboxes Used in Onshore Wind Turbines. Energies 2017, 10, 1686. [Google Scholar] [CrossRef]
- Quan, Y.; Hang, L.; He, Y.; Zhang, Y. Multi-Resonant-Based Sliding Mode Control of DFIG-Based Wind System under Unbalanced and Harmonic Network Conditions. Appl. Sci. 2019, 9, 1124. [Google Scholar] [CrossRef]
- Liserre, M.; Cardenas, R.; Molinas, M.; Rodriguez, J. Overview of Multi-MW Wind Turbines and Wind Parks. IEEE Trans. Ind. Electron. 2011, 58, 1081–1095. [Google Scholar] [CrossRef]
- Shen, Y.-W.; Ke, D.-P.; Sun, Y.-Z.; Kirschen, D.S.; Qiao, W.; Deng, X.-T. Advanced Auxiliary Control of an Energy Storage Device for Transient Voltage Support of a Doubly Fed Induction Generator. IEEE Trans. Sustain. Energy 2016, 7, 63–76. [Google Scholar] [CrossRef]
- Molina-Garcia, A.; Fernandez-Guillamon, A.; Gomez-Lazaro, E.; Honrubia-Escribano, A.; Bueso, M.C. Vertical Wind Profile Characterization and Identification of Patterns Based on a Shape Clustering Algorithm. IEEE Access 2019, 7, 30890–30904. [Google Scholar] [CrossRef]
- Alsharafi, A.; Besheer, A.; Emara, H. Primary Frequency Response Enhancement for Future Low Inertia Power Systems Using Hybrid Control Technique. Energies 2018, 11, 699. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power Systems with High Renewable Energy Sources: A Review of Inertia and Frequency Control Strategies over Time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef]
- Fang, X.; Krishnan, V.; Hodge, B.-M. Strategic Offering for Wind Power Producers Considering Energy and Flexible Ramping Products. Energies 2018, 11, 1239. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M.; Bonfiglio, A.; Procopio, R.; Verduci, B. Evaluation of Inertial Response Controllers for Full-Rated Power Converter Wind Turbine (Type 4). In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Renuka, T.K.; Reji, P. Frequency Control of Wind Penetrated Hydro-Dominated Power System. In Proceedings of the 2015 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 24–26 June 2015; pp. 316–321. [Google Scholar]
- Morren, J.; Pierik, J.; de Haan, S.W.H. Inertial Response of Variable Speed Wind Turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Ramtharan, G.; Jenkins, N.; Ekanayake, J.B. Frequency Support from Doubly Fed Induction Generator Wind Turbines. IET Renew. Power Gener. 2007, 1, 3. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, X.; Hei, Y.; Wang, H. Active Participation of Variable Speed Wind Turbine in Inertial and Primary Frequency Regulations. Electr. Power Syst. Res. 2017, 147, 174–184. [Google Scholar] [CrossRef]
- Ekanayake, J.; Jenkins, N. Comparison of the Response of Doubly Fed and Fixed-Speed Induction Generator Wind Turbines to Changes in Network Frequency. IEEE Trans. Energy Convers. 2004, 19, 800–802. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Chikuni, E.; Stemmet, W.; Folly, K. Effects of the Synthetic Inertia from Wind Power on the Total System Inertia after a Frequency Disturbance. In Proceedings of the IEEE Power and Energy Society Conference and Exposition in Africa: Intelligent Grid Integration of Renewable Energy Resources (PowerAfrica), Johannesburg, South Africa, 9–13 July 2012; pp. 1–7. [Google Scholar]
- Bonfiglio, A.; Invernizzi, M.; Labella, A.; Procopio, R. Design and Implementation of a Variable Synthetic Inertia Controller for Wind Turbine Generators. IEEE Trans. Power Syst. 2019, 34, 754–764. [Google Scholar] [CrossRef]
- Morren, J.; de Haan, S.W.H.; Kling, W.L.; Ferreira, J.A. Wind Turbines Emulating Inertia and Supporting Primary Frequency Control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Marano, A.; Gomez-Exposito, A.; Martinez Ramos, J.L. Frequency Regulation Contribution Through Variable-Speed Wind Energy Conversion Systems. IEEE Trans. Power Syst. 2009, 24, 173–180. [Google Scholar] [CrossRef]
- Díaz-González, F.; Hau, M.; Sumper, A.; Gomis-Bellmunt, O. Participation of Wind Power Plants in System Frequency Control: Review of Grid Code Requirements and Control Methods. Renew. Sustain. Energy Rev. 2014, 34, 551–564. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia Response and Frequency Control Techniques for Renewable Energy Sources: A Review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Singarao, V.Y.; Rao, V.S. Frequency Responsive Services by Wind Generation Resources in United States. Renew. Sustain. Energy Rev. 2016, 55, 1097–1108. [Google Scholar] [CrossRef]
- Xu, L.; Yao, L.; Sasse, C. Grid Integration of Large DFIG-Based Wind Farms Using VSC Transmission. IEEE Trans. Power Syst. 2007, 22, 976–984. [Google Scholar] [CrossRef]
- Asad, M.; Martinez, S.; Sanchez-Fernandez, J.A. Diesel Governor Tuning for Isolated Hybrid Power Systems. Electronics 2023, 12, 2487. [Google Scholar] [CrossRef]
- Martínez-Lucas, G.; Sarasúa, J.I.; Sánchez-Fernández, J.Á. Eigen Analysis of Wind–Hydro Joint Frequency Regulation in an Isolated Power System. Int. J. Electr. Power Energy Syst. 2018, 103, 511–524. [Google Scholar] [CrossRef]
- Jones, D.I.; Mansoor, S.P.; Aris, F.C.; Jones, G.R.; Bradley, D.A.; King, D.J. A Standard Method for Specifying the Response of Hydroelectric Plant in Frequency-Control Mode. Electr. Power Syst. Res. 2004, 68, 19–32. [Google Scholar] [CrossRef]
- GE Energy. 1.5 MW Wind Turbine. Available online: https://geosci.uchicago.edu/~moyer/GEOS24705/Readings/GEA14954C15-MW-Broch.pdf (accessed on 10 January 2024).






| Symbol | Parameters | Values |
|---|---|---|
| Model of diesel engine | CAT-3512 DITA | |
| f | Frequency | 60 Hz |
| S | Capacity | 813 KVA |
| HT | Constant of inertia | 0.4208 s |
| Ns | Synchronous speed | 1200 RPM |
| Prated | Rated power | 650 kW |
| Vout | Output voltage | 480 V ± 5% |
| Tmax/Tmin | Torque max/min | 1.1 p.u./0 p.u. |
| t1/t2/t3 | Time constants | 0.024 s/0.1 s/0.01 s |
| Symbols | Parameters | Values |
|---|---|---|
| Pbase | Base power | 800 kW |
| Pg | Generator power min/max | 0.04 p.u./1 p.u. |
| dβ/dt, min/max | Rate of pitch angle min/max | −2°/s/+2°/s |
| Kopt | Optimization constant | 0.6728 |
| D | Diameter of the VSWT rotor | 59 m |
| fnom | Nominal frequency of the generator | 50 Hz |
| Hi | Constant of inertia | 4.18 |
| Kppc/Kipc | Gains of the PI pitch controller | 150/25 |
| ωmin, ω0, ω1, ωmax | Speed limits of MPPT | 0.5 p.u., 0.51 p.u., 1.09 p.u., 1.1 p.u. |
| n1, n2, n3, n4, n5, n6 | Constants of MPPT curve | 0.5176, 116, 0.4, 5, 21, 0.0068 |
| τp | Servo-motor time constant | 0.3 s |
| Ρ | Air density | 1.225 kgm−3 |
| τc | Time constant of the generator and electronics convertor | 20 ms |
| ⍵g,base | Base speed of the generator | 157.08 rad/s |
| ⍵t,base | Turbine base speed | 2.3 rad/s |
| Vw,nom | Nominal wind speed | 10 ms−1 |
| Kpsc/Kisc | Gain parameters of the speed controller min/max | 0.3/8 |
| Tem,min/max | Electromagnetic torque min/max | 0.08 p.u./0.91 p.u. |
| Case | Diesel Governor Controller Gain Parameters | Modified Synthetic Inertial Control | ||
|---|---|---|---|---|
| Kp_d | Ki_d | Kdn | Kpn | |
| Base | 2.294 | 1.458 | 0 | 0 |
| T | 10.13 | 13.35 | 0 | 0 |
| U | 10.13 | 13.35 | 0.15 | 7.45 |
| V | 10.13 | 13.35 | 0 | 1.92 |
| W | 10.13 | 13.35 | 0.004 | 0 |
| X | 30.76 | 32.76 | 0.26 | 18.18 |
| Y | 24.65 | 29.55 | 0 | 23.43 |
| Z | 23 | 31 | 0.02 | 0 |
| Case | Parameters | Values |
|---|---|---|
| Kpc/Kic | Pitch compensation controller parameters | 0/150 |
| Kppc/Kipc | Blade pitch controller gain parameters | 1300/150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asad, M.; Sanchez-Fernandez, J.A. Enhancing Frequency Regulation Support through Several Synthetic Inertial Approaches for WDPS. Electronics 2024, 13, 852. https://doi.org/10.3390/electronics13050852
Asad M, Sanchez-Fernandez JA. Enhancing Frequency Regulation Support through Several Synthetic Inertial Approaches for WDPS. Electronics. 2024; 13(5):852. https://doi.org/10.3390/electronics13050852
Chicago/Turabian StyleAsad, Muhammad, and Jose Angel Sanchez-Fernandez. 2024. "Enhancing Frequency Regulation Support through Several Synthetic Inertial Approaches for WDPS" Electronics 13, no. 5: 852. https://doi.org/10.3390/electronics13050852
APA StyleAsad, M., & Sanchez-Fernandez, J. A. (2024). Enhancing Frequency Regulation Support through Several Synthetic Inertial Approaches for WDPS. Electronics, 13(5), 852. https://doi.org/10.3390/electronics13050852







