Elastic and Inelastic Cross Sections for Low-Energy Electron Collisions with ClF Molecule Using the R-Matrix Method
Abstract
:1. Introduction
2. R-Matrix Method
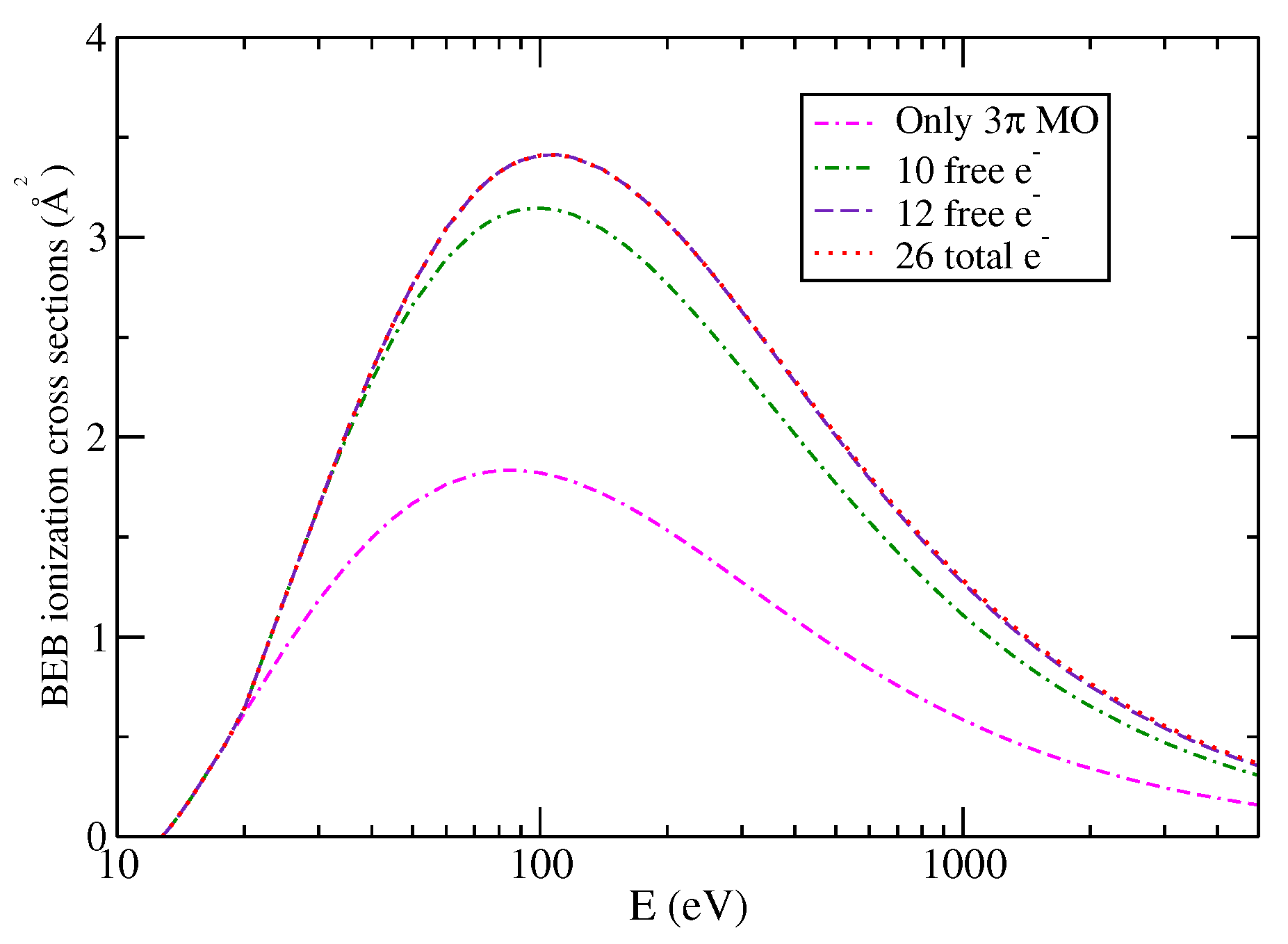
3. Target Description and Computational Details
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEB | Binary-encounter-Bethe |
| HF | Hartree–Fock |
| SE | Static-Exchange |
| SEP | Static-Exchange-polarisation |
| CI | Configuration Interaction |
| CC | Close Coupling |
| CASCI | Complete Active Space Configuration Interaction |
| CSF | Configuration State Functions |
| DCS | Differential Cross Sections |
| TICS | Total Ionization Cross Sections |
| MO | Molecular Orbitals |
| eV | Electron Volt |
| au | Atomic Unit |
| SCF | Self-Consistent Field |
References
- Ewig, C.S.; Sur, A.; Banna, M.S. A theoretical study of core and valence ionization in ClF. J. Chem. Phys. 1981, 75, 5002. [Google Scholar] [CrossRef]
- Law, C.K.; Chien, S.H.; Li, W.K. Thermochemistry of Chlorine Fluorides ClFn, n = 1–7, and Their Singly Charged Cations and Anions: A Gaussian-3 and Gaussian-3X Study . J. Phys. Chem. A 2002, 106, 11271. [Google Scholar] [CrossRef]
- Eden, J.G.; Dlabal, M.L.; Hutchison, S.B. The interhalogens IF and ICl as Visible Oscillators or Amplifiers. IEEE J. Quantum Electron. 1981, 17, 1085. [Google Scholar] [CrossRef]
- Diegelmann, M.; Hohla, K.; Rebentrost, F.; Kompa, K.L. Diatomic interhalogen laser molecules: Fluorescence spectroscopy and reaction kinetics. J. Chem. Phys. 1982, 76, 1233. [Google Scholar] [CrossRef]
- Diegelmann, M.; Proch, D.; Zhensheng, Z. Discharge pumped ClF laser at 285 nm. Appl. Phys. B 1986, 40, 49. [Google Scholar] [CrossRef]
- Naulin, C.; Bougon, R. Photochemistry of the chlorine monofluoride, ClF. Thermal and photochemical reactions with sulfur tetrafluoride SF4. J. Chem. Phys. 1980, 72, 2155. [Google Scholar] [CrossRef]
- Ibbotson, D.E.; Mucha, J.A.; Flamm, D.L. Plasmaless dry etching of silicon with fluorine-containing compounds. J. Appl. Phys. 1984, 56, 2939. [Google Scholar] [CrossRef]
- Takahashi, Y.; Kato, K.; Habuka, H. Development of SiC Etching by Chlorine Fluoride Gas. Mater. Sci. Forum 2020, 1004, 731. [Google Scholar] [CrossRef]
- Bargainer, M.; Dietrich, P.; Schwentner, N. Spectroscopy and photodissociation of ClF in rare gas solids. J. Chem. Phys. 2001, 115, 149. [Google Scholar]
- Naulin, C.; Lambard, J.; Bougon, R. Vibrational spectra of the chlorine monofluoride ClF in cryogenic solutions. J. Chem. Phys. 1982, 76, 3371. [Google Scholar] [CrossRef]
- Krogh, O.D.; Pimentel, G.C. Chemical Lasers from the Reactions of ClF and ClF3 with H2 and CH4: A Possible Chain-Branching Chemical Laser. J. Chem. Phys. 1972, 56, 969. [Google Scholar] [CrossRef]
- Krogh, O.D.; Pimentel, G.C. ClFx-H2 chemical lasers (x = 1, 3, 5): Vibration–rotation emission by HF from states with high rotational excitation. J. Chem. Phys. 1977, 67, 2993. [Google Scholar] [CrossRef]
- Cuellar, E.; Pimentel, G.C. Rotational laser emission by HF in the ClF-H2 chemical laser. J. Chem. Phys. 1979, 71, 1385. [Google Scholar] [CrossRef]
- Pimentel, G.C.; Krogh, O.D. Vibrational emission by HCl from the ClF-H2 chemical laser. J. Chem. Phys. 1980, 73, 120. [Google Scholar] [CrossRef]
- Alekseyev, A.B.; Liebermann, H.P.; Buenker, R.J.; Kokh, D.B. Relativistic configuration interaction study of the ClF molecule and its emission spectra from O+ ion-pair states. J. Chem. Phys. 2000, 112, 2274. [Google Scholar] [CrossRef]
- Li, S.; Chen, S.J.; Zhu, D.S.; Wei, J.J. Structure and Potential Energy Function of ClF− Molecular Ion. Acta Phys.-Chim. Sin. 2013, 29, 737. [Google Scholar]
- Horny, L.; Sattelmeyer, K.W.; Schaefer, H.L. Elusive electron affinity of ClF. J. Chem. Phys. 2003, 119, 11615. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Ha, T.K. Abinttio calculation of the ionization potentials and hyperfine splitting constants of the radical anions FClXXX and Cl. Chem. Phys. Lett. 1987, 136, 413. [Google Scholar] [CrossRef]
- Van Huis, T.J.; Galbraith, J.M.; Schaefer, H.F. The monochlorine fluorides (ClFn) and their anions (ClF) n = 1–7: Structures and energetics. Mol. Phys. 1996, 89, 607. [Google Scholar] [CrossRef]
- McDermid, I.S. Potential-energy curves, Franck-Condon factors and laser excitation spectrum for the B3Π(O+)-X1Σ+ system of chlorine monofluoride. J. Chem. Soc. Faraday Trans. II 1981, 77, 519. [Google Scholar] [CrossRef]
- de Jong, W.A.; Styszynski, J.; Visscher, L.; Nieuwpoort, W.C. Relativistic and correlation effects on molecular properties: The interhalogens ClF, BrF, BrCl, IF, ICl, and IBr. J. Chem. Phys. 1998, 108, 5177. [Google Scholar] [CrossRef] [Green Version]
- Kaur, S.; Baluja, K.L.; Tennyson, J. Electron-impact study of NeF using the R-matrix method. Phys. Rev. A 2008, 77, 032718. [Google Scholar] [CrossRef]
- Wang, F.; Liu, J.B.; Sinibaldi, J.; Brophy, C.; Kuthi, A.; Jiang, C.; Ronney, P.; Gundersen, M.A. Transient plasma ignition of quiescent and flowing air/fuel mixtures. IEEE Trans. Plasma Sci. 2005, 33, 844. [Google Scholar] [CrossRef]
- Nguyen-Kuok, S. Theory of Low-Temperature Plasma Physics; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Chu, P.K.; Lu, X.P. (Eds.) Low Temperature Plasma Technology: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Wiens, J.P.; Sawyer, J.C.; Miller, T.M.; Shuman, N.S.; Viggiano, A.A.; Khamesian, M.; Kokoouline, V.; Fabrikant, I.I. Electron attachment to the interhalogen compounds ClF, ICl, and IBr. Phys. Rev. A 2016, 93, 032706. [Google Scholar] [CrossRef] [Green Version]
- Tennyson, J. Electron–molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Baluja, K.L.; Burke, P.G.; Morgan, L.A. R-matrix propagation program for solving coupled second-order differential equations. Comput. Phys. Commun. 1982, 27, 299. [Google Scholar] [CrossRef]
- Masin, Z.; Benda, J.; Harvey, A.G.; Gorfinkiel, J.D.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comp. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef] [Green Version]
- Masin, Z.; Benda, J.; Harvey, A.G.; Al-Refaie, A.; Gorfinkiel, J.D.; Tennyson, J. UKRmol+: UKRMol-in (Version 3.0); Zenodo: Genève, Switzerland, 2019. [Google Scholar] [CrossRef]
- Johnson, R.D., III (Ed.) Computational Chemistry Comparison and Benchmark Database, Number 101, Release 21, August 2020. Available online: http://cccbdb.nist.gov (accessed on 21 December 2021).
- Faure, A.; Gorfinkiel, J.D.; Morgan, L.A.; Tennyson, J. GTOBAS: Fitting continuum functions with Gaussian-type orbitals. Comput. Phys. Commun. 2002, 144, 224. [Google Scholar] [CrossRef] [Green Version]
- Fabrikant, I.I. Long-range effects in electron scattering by polar molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 222005. [Google Scholar] [CrossRef]
- Bassi, M.; Bharadvaja, A.; Baluja, K.L. A study of electron scattering from 1-1 C2H2F2 from 0.1 eV to 5 keV. Eur. Phys. J. D 2020, 74, 232. [Google Scholar] [CrossRef]
- Ewing, J.J.; Tigelaar, H.L.; Flygare, W.H. Molecular Zeeman Effect, Magnetic Properties, and Electric Quadrupole Moments in ClF, BrF, ClCN, BrCN, and ICN J. Chem. Phys. 1972, 56, 1957. [Google Scholar] [CrossRef]
- Vassilakis, A.A.; Kalemos, A.; Mavridis, A. Accurate first principles calculations on chlorine fluoride ClF and its ions ClF±. Theor. Chem. Acc. 2014, 133, 1436. [Google Scholar] [CrossRef]
- Quintero-Monsebaiz, R.; Perea-Ram<i>ι</i>rez, L.I.; Piris, M.; Vela, A. Spectroscopic properties of open shell diatomic molecules using Piris natural orbital functionals. Phys. Chem. Chem. Phys. 2021, 23, 2953. [Google Scholar] [CrossRef] [PubMed]
- Darvesh, K.V.; Boyd, R.J.; Peyerimhoff, S.D. Electronically excited states of chlorine monofluoride: A multi-reference configuration interaction study. Chem. Phys. 1988, 121, 361. [Google Scholar] [CrossRef]
- Tennyson, J.; Noble, C.J. RESON-A program for the detection and fitting of Breit-Wigner resonances. Comput. Phys. Commun. 1984, 33, 421. [Google Scholar] [CrossRef]
- Sahgal, V.; Bharadvaja, A.; Baluja, K.L. Positron-induced scattering of acetone from 0.1 eV to 5 keV. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 075202. [Google Scholar] [CrossRef]
- Cooper, B.; Tudorovskaya, M.; Mohr, S.; O’Hare, A.; Hanicinec, M.; Dzarasova, A.; Gorfinkiel, J.D.; Benda, J.; Mašín, Z.; Al-Refaie, A.F.; et al. Quantemol Electron Collision: An expert system for performing UKRmol+ electron molecule collision calculations. Atoms 2019, 7, 97. [Google Scholar] [CrossRef] [Green Version]
- Itikawa, Y. Molecular Processes in Plasmas; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bharadvaja, A.; Kaur, S.; Baluja, K.L. Electron-impact cross sections of SiH2 using the R-matrix method at low energy. Phys. Rev. A 2015, 91, 032701. [Google Scholar] [CrossRef]
- Bharadvaja, A.; Kaur, S.; Baluja, K.L. Low-energy electron impact cross-sections and rate constants of NH2. Pramana-J. Phys. 2017, 89, 30. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Jain, A. The theory of electron scattering from polyatomic molecules. Phys. Rep. 1986, 143, 347. [Google Scholar] [CrossRef]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142. [Google Scholar] [CrossRef]
- Sarma, G.; Saha, A.K.; Bishwakarma, C.K.; Scheidsbach, R.; Yang, C.H.; Parker, D.; Wiesenfeld, L.; Buck, U.; Mavridis, L.; Marinakis, S. Collision energy dependence of state-to-state differential cross sections for rotationally inelastic scattering of H2O by He. Phys. Chem. Chem. Phys. 2017, 19, 4678. [Google Scholar] [CrossRef]
- Kaur, S.; Bharadvaja, A.; Baluja, K.L. Electron-impact study of S3 using the R-matrix method. Phys. Rev. A 2011, 27, 062707. [Google Scholar] [CrossRef]
- Itikawa, Y. Effective collision frequency of electrons in atmospheric gases. Planet. Space Sci. 1971, 19, 993. [Google Scholar] [CrossRef]
- Baille, P.; Chang, J.S.; Claude, A.; Hobson, R.M.; Ogram, G.L.; Yau, A.W. Effective collision frequency of electrons in noble gases. J. Phys B At. Mol. Phys. 1981, 14, 1485. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef] [PubMed] [Green Version]

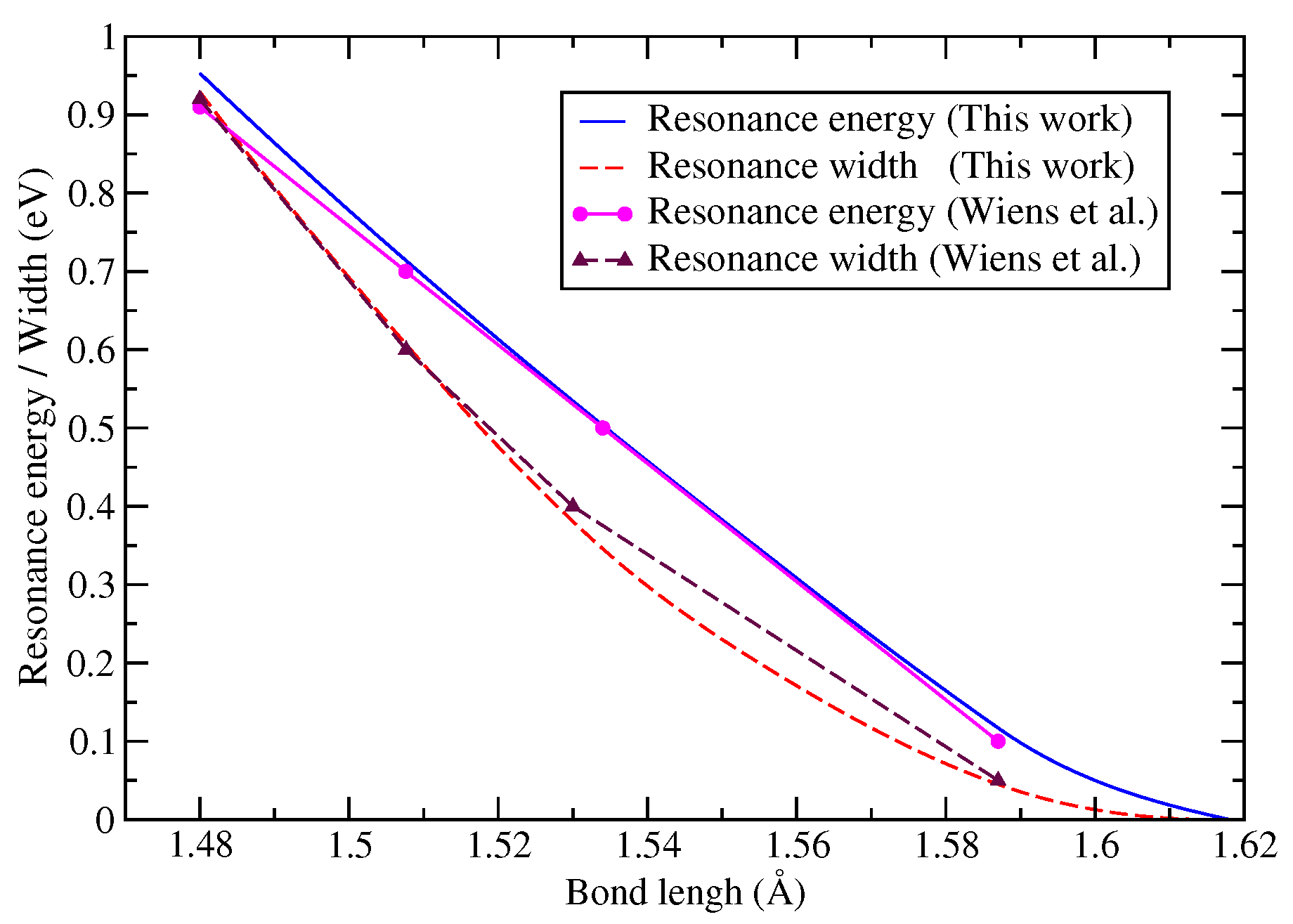

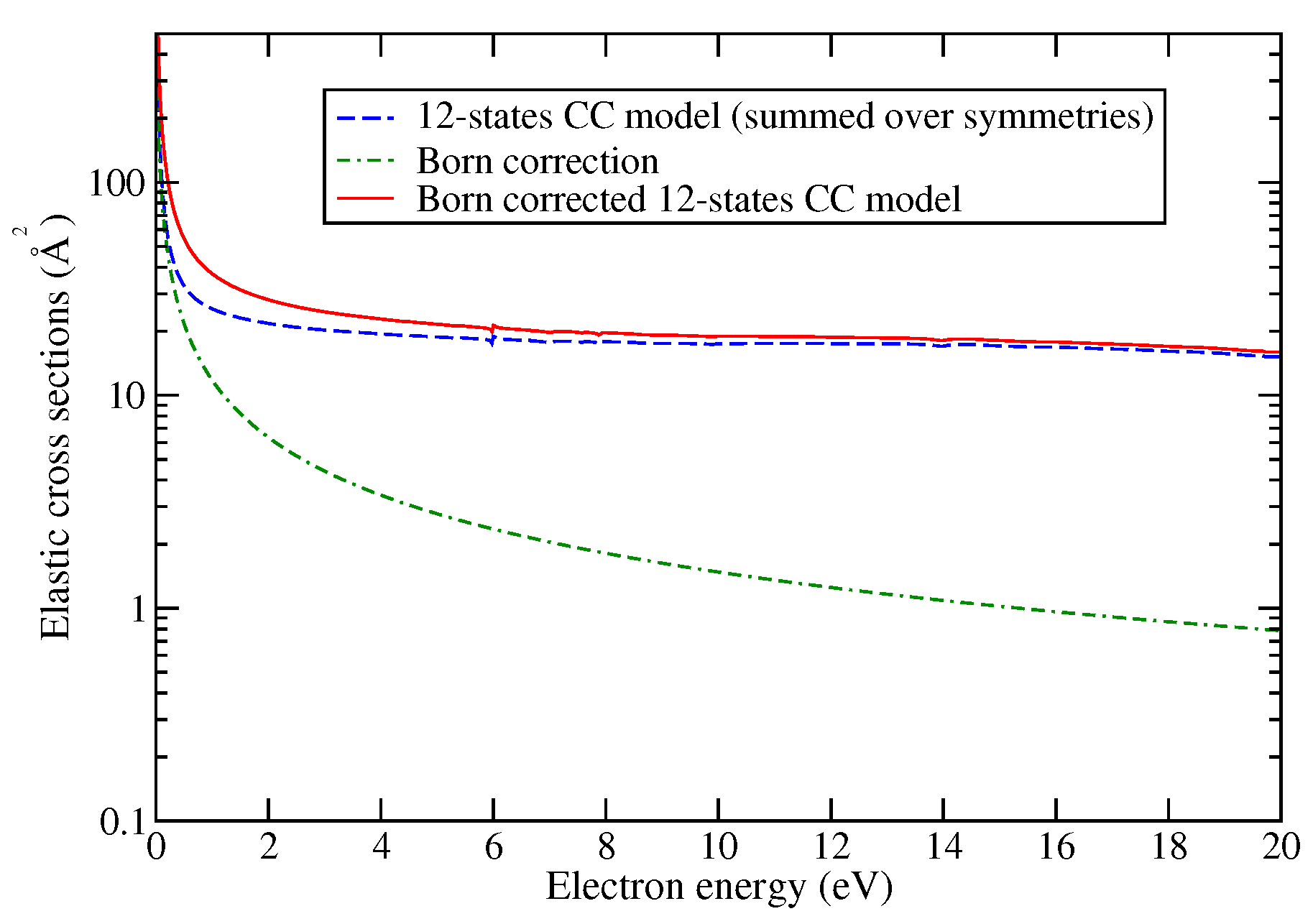
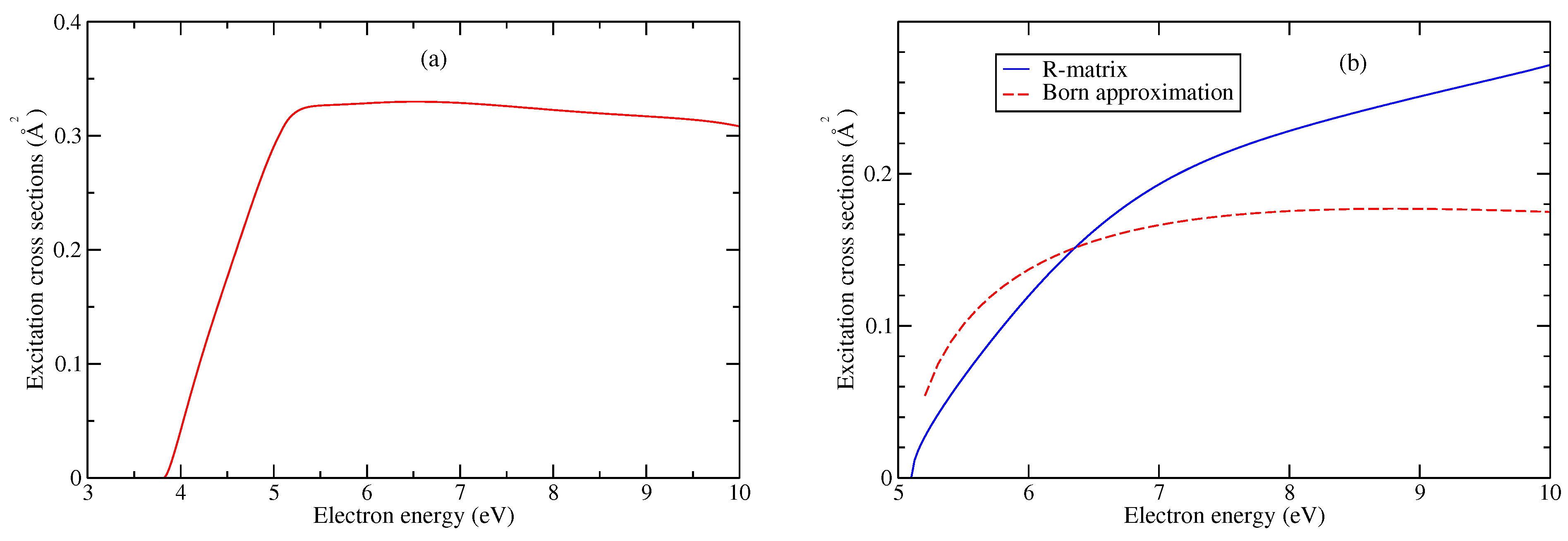
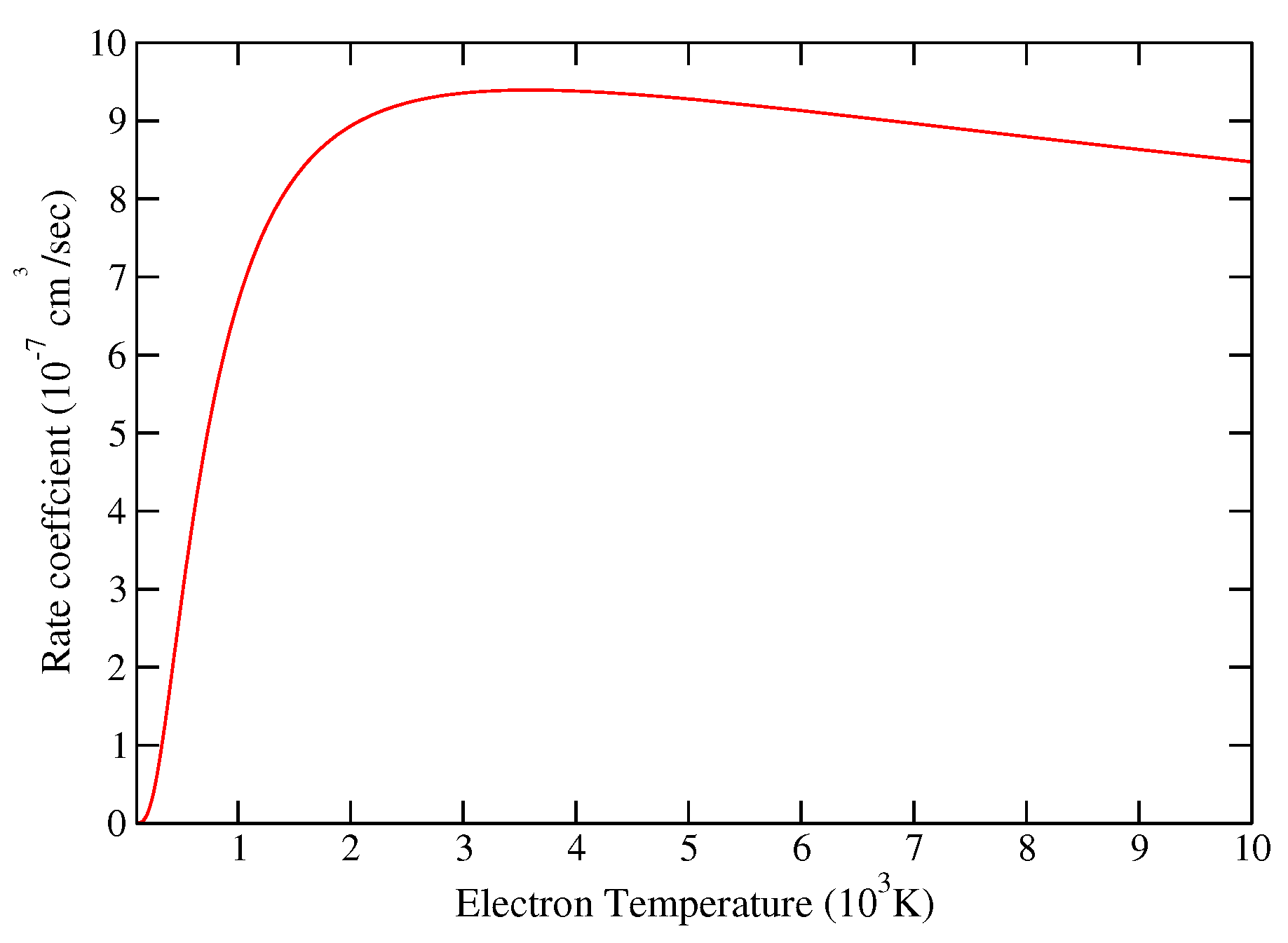



| Model | Energy | Dipole Moment | Quadrupole Moment |
|---|---|---|---|
| (au) | (au) | (Q) (au) | |
| HF | −558.8667 | 0.5545 | 0.9398 |
| 12-states CI | −558.9011 | 0.4363 (0.353 * [32]) | 1.0045 (1.0 * [36]) |
| Target State | Present Work | Other Works |
|---|---|---|
| 3.84 | 2.33 (Expt) [37] | |
| 3.10 (CASSCF) [38] | ||
| 5.10 | 4.63 (MRD-CI) [39] | |
| 4.34 (CI) [39] | ||
| 8.33 | - | |
| ) | 8.64 | - |
| ) | 8.80 | - |
| 9.01 | 9.08 (MRD-CI) [39] | |
| 8.19 (CI) [39] | ||
| ) | 9.45 | 10.54 (MRD-CI) [39] |
| 10.27 (CI) [39] |
| Scattering | ||
|---|---|---|
| Model | (eV) | (eV) |
| SE | 0.94 | 0.75 |
| SEP | 0.31 | 0.18 |
| 1-state | 0.79 | 0.62 |
| 5-states | 0.40 | 0.24 |
| 12-states | Bound | - |
| Molecular Orbital | |B| ( eV) | U ( eV) | N |
|---|---|---|---|
| 1σ () | 2855.47 | 3731.21 | 2 |
| 2σ () | 717.01 | 1013.66 | 2 |
| 3σ () | 289.97 | 593.89 | 2 |
| 1π () | 221.94 | 562.46 | 4 (2,2) |
| 4σ () | 221.10 | 560.52 | 2 |
| 5σ () | 44.69 | 101.877 | 2 |
| 6σ () | 30.14 | 91.28 | 2 |
| 2π () | 19.76 | 81.61 | 4 (2,2) |
| 7σ () | 19.00 | 79.52 | 2 |
| 3 () | 13.44 | 72.43 | 4 (2,2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassi, M.; Bharadvaja, A.; Baluja, K.L. Elastic and Inelastic Cross Sections for Low-Energy Electron Collisions with ClF Molecule Using the R-Matrix Method. Atoms 2022, 10, 8. https://doi.org/10.3390/atoms10010008
Bassi M, Bharadvaja A, Baluja KL. Elastic and Inelastic Cross Sections for Low-Energy Electron Collisions with ClF Molecule Using the R-Matrix Method. Atoms. 2022; 10(1):8. https://doi.org/10.3390/atoms10010008
Chicago/Turabian StyleBassi, Monika, Anand Bharadvaja, and Kasturi Lal Baluja. 2022. "Elastic and Inelastic Cross Sections for Low-Energy Electron Collisions with ClF Molecule Using the R-Matrix Method" Atoms 10, no. 1: 8. https://doi.org/10.3390/atoms10010008
APA StyleBassi, M., Bharadvaja, A., & Baluja, K. L. (2022). Elastic and Inelastic Cross Sections for Low-Energy Electron Collisions with ClF Molecule Using the R-Matrix Method. Atoms, 10(1), 8. https://doi.org/10.3390/atoms10010008






