Variational Bayesian Network with Information Interpretability Filtering for Air Quality Forecasting
Abstract
:1. Introduction
2. Related Works
2.1. PM2.5 Forecasting Method Based on Traditional Methods
2.2. PM2.5 Forecasting Method Based on Deep Learning
2.3. Multi-Factor PM2.5 Forecasting Method Based on Variable Screening
2.4. PM2.5 Forecasting Method for Noise Problems
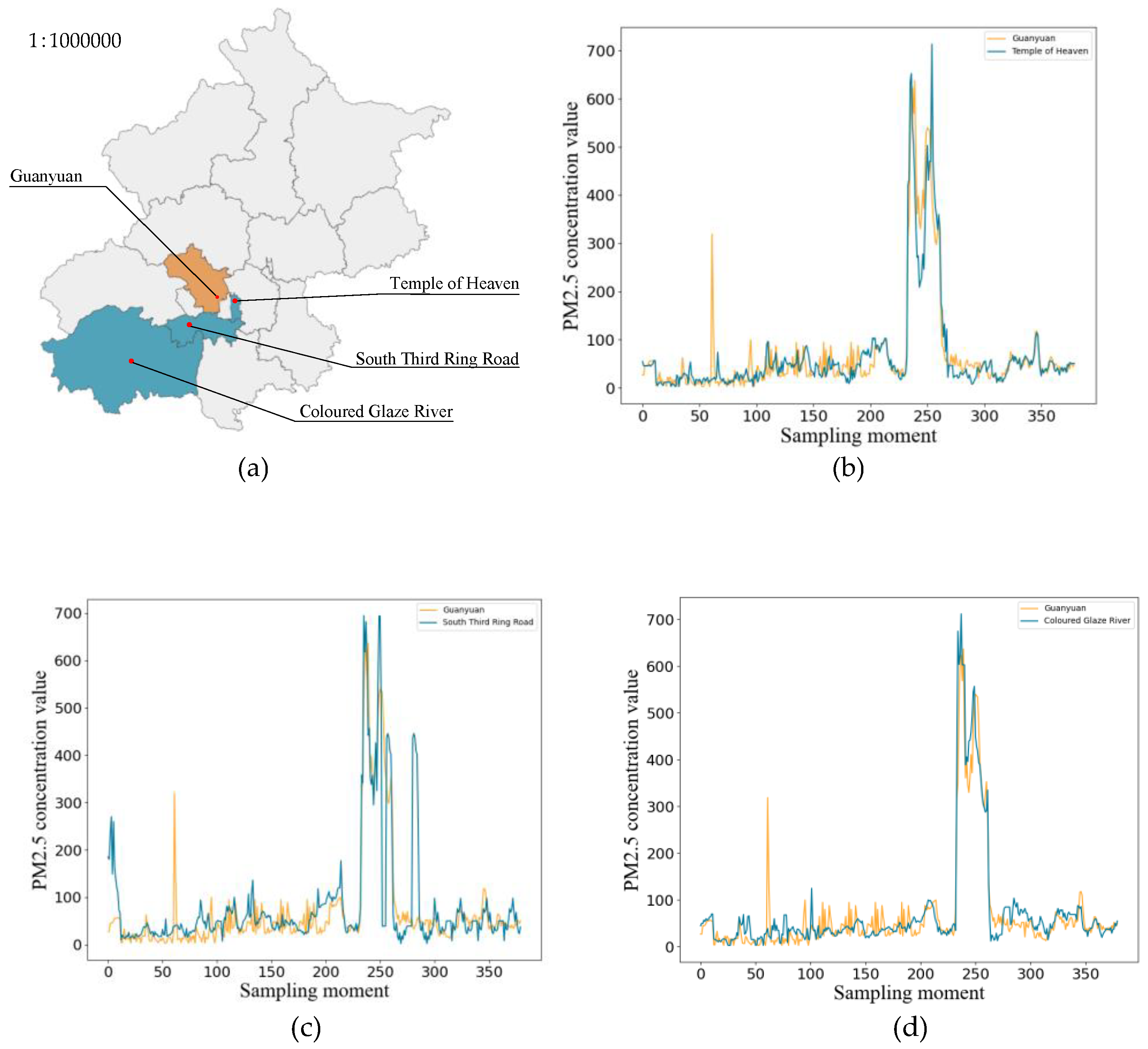
3. Data Set and Spatial Correlation Analysis
3.1. Data Set
3.2. Spatial Correlation Analysis
4. Information Interpretable Filtering
5. Deep Forecasting Network
6. Experiments
6.1. Experiment Setup and Evaluation Indicators
6.2. Numerical Experiment and Analysis of PM2.5 in Different Regions
6.3. Numerical Experiment and Analysis of Meteorological Factors
6.4. Interpretability Analysis
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, X.B.; Wang, Z.Y.; Kong, J.L.; Bai, Y.T.; Su, T.L.; Ma, H.J.; Chakrabarti, P. Deep Spatio-Temporal Graph Network with Self-Optimization for Air Quality Prediction. Entropy 2023, 25, 247. [Google Scholar] [CrossRef]
- Menares, C.; Perez, P.; Parraguez, S. Forecasting PM2.5 levels in santiago de chile using deep learning neural networks. Urban Clim. 2021, 38, 100906. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Wang, K. Atmospheric PM2.5 concentration prediction based on time series and interactive multiple model approach. Adv. Meteorol. 2019, 2019, 1279565. [Google Scholar] [CrossRef]
- Lee, C.M.; Ko, C.N. Short-term load forecasting using lifting scheme and ARIMA models. Expert Syst. Appl. 2011, 38, 5902–5911. [Google Scholar] [CrossRef]
- Ding, F.; Shi, Y.; Chen, T. Performance analysis of estimation algorithms of non-stationary ARMA processes. IEEE Trans. Signal Process. 2006, 54, 1041–1053. [Google Scholar] [CrossRef]
- D’Amico, A.; Ciulla, G. An intelligent way to predict the building thermal needs: ANNs and optimization. Expert Syst. Appl. 2022, 191, 116293. [Google Scholar] [CrossRef]
- Liu, W.; Liang, S.; Yu, Q. PM2.5 concentration prediction based on pseudo-F statistic feature selection algorithm and support vector regression. IOP Conf. Ser. Earth Environ. Sci. 2020, 569, 012039. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, H.; Li, C. Prediction of PM2.5 hourly concentrations in Beijing based on machine learning algorithm and ground-based LiDAR. Arch. Environ. Prot. 2021, 47, 98–107. [Google Scholar]
- Li, M.H.; Liu, X.M. Maximum likelihood hierarchical least squares-based iterative identification for dual-rate stochastic systems. Int. J. Adapt. Control Signal Process. 2021, 35, 240–261. [Google Scholar] [CrossRef]
- Li, M.H.; Liu, X.M. Iterative identification methods for a class of bilinear systems by using the particle filtering technique. Int. J. Adapt. Control Signal Process. 2021, 35, 2056–2074. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Combined parameter and output estimation of dual-rate systems using an auxiliary model. Automatica 2004, 40, 1739–1748. [Google Scholar] [CrossRef]
- Ding, F. Coupled-least-squares identification for multivariable systems. IET Control Theory Appl. 2013, 7, 68–79. [Google Scholar] [CrossRef]
- Xu, L. Separable Newton recursive estimation method through system responses based on dynamically discrete measurements with increasing data length. Int. J. Control Autom. Syst. 2022, 20, 432–443. [Google Scholar] [CrossRef]
- Xu, L. Separable multi-innovation Newton iterative modeling algorithm for multi-frequency signals based on the sliding measurement window. Circuits Syst. Signal Process. 2022, 41, 805–830. [Google Scholar] [CrossRef]
- Xu, L. Separable synchronous multi-innovation gradient-based iterative signal modeling from on-line measurements. IEEE Trans. Instrum. Meas. 2022, 71, 6501313. [Google Scholar] [CrossRef]
- Ding, F.; Liu, G.; Liu, X.P. Partially coupled stochastic gradient identification methods for non-uniformly sampled systems. IEEE Trans. Autom. Control 2010, 55, 1976–1981. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Parameter estimation of dual-rate stochastic systems by using an output error method. IEEE Trans. Autom. Control 2005, 50, 1436–1441. [Google Scholar] [CrossRef]
- Connor, J.T.; Martin, R.D.; Atlas, L.E. Recurrent neural networks and robust time series prediction. IEEE Trans. Neural Netw. 1994, 5, 240–254. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, K.; Li, J. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Pan, C.; Tan, J.; Feng, D. Prediction intervals estimation of solar generation based on gated recurrent unit and kernel density estimation. Neurocomputing 2020, 453, 552–562. [Google Scholar] [CrossRef]
- Wang, J.; Song, G. A Deep Spatial-temporal ensemble model for air quality prediction. Neurocomputing 2018, 314, 198–206. [Google Scholar] [CrossRef]
- Wang, G.; Awad, O.I.; Liu, S. NOx emissions prediction based on mutual information and back propagation neural network using correlation quantitative analysis. Energy 2020, 198, 117286. [Google Scholar] [CrossRef]
- Song, H.Y.; Park, S. An Analysis of correlation between personality and visiting place using spearman’s rank correlation coefficient. KSII Trans. Internet Inf. Syst. (TIIS) 2020, 14, 1951–1966. [Google Scholar]
- Jin, X.B.; Gong, W.T.; Kong, J.L.; Bai, Y.T.; Su, T.L. A variational Bayesian deep network with data self-screening layer for massive time-series data prediction. Entropy 2022, 24, 335. [Google Scholar] [CrossRef]
- Wu, D.; Wang, X.; Wu, S. A hybrid method based on extreme learning machine and wavelet transform denoising for stock prediction. Entropy 2021, 23, 440. [Google Scholar] [CrossRef]
- Ruiz-Aguilar, J.J.; Turias, I.; González-Enrique, J. A permutation entropy-based EMD–ANN forecasting ensemble approach for wind speed prediction. Neural Comput. Appl. 2021, 33, 2369–2391. [Google Scholar] [CrossRef]
- Liu, T.; Alexis, K.H.; Lau, K.S. Time series forecasting of air quality based on regional numerical modeling in Hong Kong. J. Geophys. Res. Atmos. 2018, 123, 4175–4196. [Google Scholar] [CrossRef]
- Zeng, Y.; Daniel, A.; Jaffe, X.Q. Prediction of potentially high PM2.5 concentrations in Chengdu, China. Aerosol Air Qual. Res. 2020, 20, 956–965. [Google Scholar] [CrossRef]
- Wang, X.; Wang, B. Research on prediction of environmental aerosol and PM2.5 based on artificial neural network. Neural Comput. Appl. 2018, 31, 8217–8227. [Google Scholar] [CrossRef]
- Chang, F.J.; Chang, L.C.; Kang, C.C. Explore spatio-temporal PM2.5 features in northern Taiwan using machine learning techniques. Sci. Total Environ. 2020, 736, 139656. [Google Scholar] [CrossRef]
- Shahriar, S.A.; Kayes, I.; Hasan, K. Potential of ARIMA-ANN, ARIMA-SVM, DT and CatBoost for atmospheric PM2.5 forecasting in Bangladesh. Atmosphere 2021, 12, 100. [Google Scholar] [CrossRef]
- Carreno, G.; Lopez-Cortes, X.A.; Marchant, C. Machine learning models to forecasting critical episodes of environmental pollution for PM2.5 and PM10 in Talca, Chile. Mathematics 2022, 10, 373. [Google Scholar] [CrossRef]
- Sun, K.; Tang, L.; Qian, J.S. A deep learning-based pm2.5 concentration estimator. Displays 2021, 69, 102072. [Google Scholar] [CrossRef]
- Shi, P.; Fang, X.; Ni, J. An Improved attention-based integrated deep neural network for PM2.5 concentration prediction. Appl. Sci. 2021, 11, 4001. [Google Scholar] [CrossRef]
- Mengfan, T.; Siwei, L.; Lechao, D.; Senlin, H. Including the feature of appropriate adjacent sites improves the PM2.5 concentration prediction with long short-term memory neural network model. Sustain. Cities Soc. 2021, 76, 103427. [Google Scholar] [CrossRef]
- Wang, W.; Mao, W.; Tong, X. A novel recursive model based on a convolutional long short-term memory neural network for air pollution prediction. Remote Sens. 2021, 13, 1284. [Google Scholar] [CrossRef]
- Wang, B.; Kong, W.; Zhao, P. An air quality forecasting model based on improved convnet and RNN. Soft Comput. 2021, 25, 9209–9218. [Google Scholar] [CrossRef]
- Prihatno, A.T.; Nurcahyanto, H.; Ahmed, M.F.; Rahman, M.H.; Alam, M.M.; Jang, Y.M. Forecasting PM2.5 concentration using a single-dense layer BiLSTM method. Electronics 2021, 10, 1808. [Google Scholar] [CrossRef]
- Zhu, J.; Deng, F.; Zhao, J. Attention-based parallel networks (APNet) for PM2.5 spatiotemporal prediction. Sci. Total Environ. 2021, 769, 145082. [Google Scholar] [CrossRef]
- Pak, U.; Ma, J.; Ryu, U. Deep learning-based PM2.5 prediction considering the spatiotemporal correlations: A case study of Beijing, China. Sci. Total Environ. 2020, 699, 133561. [Google Scholar] [CrossRef]
- Cifuentes, F.; Gálvez, A.; González, C.M. Hourly ozone and PM2.5 prediction using meteorological data–alternatives for cities with limited pollutant information. Aerosol Air Qual. Res. 2021, 21, 200471. [Google Scholar] [CrossRef]
- Zhu, M.; Xie, J. Investigation of nearby monitoring station for hourly PM2.5 forecasting using parallel multi-input 1D-CNN-biLSTM. Expert Syst. Appl. 2022, 211, 118707. [Google Scholar] [CrossRef]
- Xing, G.; Zhao, E.; Zhang, C. A Decomposition-ensemble approach with denoising strategy for PM2.5 concentration forecasting. Discret. Dyn. Nat. Soc. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Jin, X.B.; Zhang, J.H.; Su, T.L. Modeling and analysis of data-driven systems through computational neuroscience wavelet-deep optimized model for nonlinear multicomponent data forecasting. Comput. Intell. Neurosci. 2021, 2021, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Samal, K.K.R.; Babu, K.S.; Das, S.K. Temporal convolutional denoising autoencoder network for air pollution prediction with missing values. Urban Clim. 2021, 38, 100872. [Google Scholar] [CrossRef]
- Cai, J.; Dai, X.; Hong, L. An air quality prediction model based on a noise reduction self-coding deep network. Math. Probl. Eng. 2020, 2020, 3507197. [Google Scholar] [CrossRef]
- Jin, X.-B.; Yang, N.-X.; Wang, X.-Y.; Bai, Y.-T.; Su, T.-L.; Kong, J.-L. Deep hybrid model based on EMD with classification by frequency characteristics for long-term air quality prediction. Mathematics 2020, 8, 214. [Google Scholar] [CrossRef]
- Ding, F.; Ma, H.; Pan, J.; Yang, E.F. Hierarchical gradient- and least squares-based iterative algorithms for input nonlinear output-error systems using the key term separation. J. Frankl. Inst. 2021, 358, 5113–5135. [Google Scholar] [CrossRef]
- Zhang, X. State estimation for bilinear systems through minimizing the covariance matrix of the state estimation errors. Int. J. Adapt. Control Signal Process. 2019, 33, 1157–1173. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhao, C. Influence of meteorological conditions on PM2.5 concentrations across China: A review of methodology and mechanism. Environ. Int. 2020, 139, 105558. [Google Scholar] [CrossRef]
- Liao, T.; Wang, S.; Ai, J. Heavy pollution episodes, transport pathways and potential sources of PM2.5 during the winter of 2013 in Chengdu (China). Sci. Total Environ. 2017, 584, 1056–1065. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.C.; Zhang, Y.; Lin, H. The washout effects of rainfall on atmospheric particulate pollution in two Chinese cities. Environ. Pollut. 2016, 215, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.B.; Zheng, W.Z.; Kong, J.L.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Lin, S. Deep-learning forecasting method for electric power load via attention-based encoder-decoder with Bayesian optimization. Energies 2021, 14, 1596. [Google Scholar] [CrossRef]
- Xu, L.; Yang, E.F. Auxiliary model multiinnovation stochastic gradient parameter estimation methods for nonlinear sandwich systems. Int. J. Robust Nonlinear Control 2021, 31, 148–165. [Google Scholar] [CrossRef]
- Wan, L.J. Decomposition- and gradient-based iterative identification algorithms for multivariable systems using the multi-innovation theory. Circuits Syst. Signal Process. 2019, 38, 2971–2991. [Google Scholar] [CrossRef]
- Xu, L.; Song, G.L. A recursive parameter estimation algorithm for modeling signals with multi-frequencies. Circuits Syst. Signal Process. 2020, 39, 4198–4224. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Performance analysis of multi-innovation gradient type identification methods. Automatica 2007, 43, 1–14. [Google Scholar] [CrossRef]
- Ding, F.; Liu, X.; Liu, G. Multiinnovation least squares identification for linear and pseudo-linear regression models. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2010, 40, 767–778. [Google Scholar] [CrossRef]
- Zhang, X. Hierarchical parameter and state estimation for bilinear systems. Int. J. Syst. Sci. 2020, 1, 275–290. [Google Scholar] [CrossRef]
- Liu, S.Y.; Hayat, T. Hierarchical principle-based iterative parameter estimation algorithm for dual-frequency signals. Circuits Syst. Signal Process. 2019, 38, 3251–3268. [Google Scholar] [CrossRef]
- Xu, L.; Hayat, T. Hierarchical recursive signal modeling for multi-frequency signals based on discrete measured data. Int. J. Adapt. Control Signal Process. 2021, 35, 676–693. [Google Scholar] [CrossRef]






| TOH | STRR | CGR | |
|---|---|---|---|
| MI | 0.71 | 0.56 | 0.43 |
| AID | 1.39 | 1.46 | 1.53 |
| Input Data | RMSE | MSE | MAE | Training Time (s) |
|---|---|---|---|---|
| GY PM2.5 (only GY’s PM2.5 data as input) | 26.83 ± 0.0012 | 720.09 ± 0.0712 | 19.44 ± 0.007 | 44.25 |
| (GY & TOH) PM2.5 (GY and TOH’s PM2.5 data together as input) | 27.21 ± 0.0054 | 740.42 ± 0.0616 | 19.76 ± 0.0032 | 48.44 |
| (GY & STRR) PM2.5 (GY and STRR’s PM2.5 data together as input) | 26.15 ± 0.0011 | 684.02 ± 0.0702 | 18.77 ± 0.0015 | 44.81 |
| (GY & CGR) PM2.5 (GY and CGR’s PM2.5 data together as input) | 27.42 ± 0.0089 | 752.90 ± 0.0811 | 20.00 ± 0.0033 | 46.35 |
| Source | SS | df | MS | F | F-Crit |
|---|---|---|---|---|---|
| Type | 13,019.67 | 3 | 4339.89 | 10.42 | 2.61 |
| Error | 8,753,742.65 | 21,020 | 416.45 | ||
| Total | 8,766,762.32 | 21,023 |
| Variables | Temperature | Wind Direction | Humidity |
|---|---|---|---|
| MI | 0.26 | 0.22 | 0.34 |
| AID | 1.70 | 1.64 | 1.69 |
| Data | RMSE | MSE | MAE | Training Time (s) |
|---|---|---|---|---|
| (GY & STRR) PM2.5 (GY & STRR’s PM2.5 data together as input) | 26.15 ± 0.0011 | 684.02 ± 0.0702 | 18.77 ± 0.0015 | 44.81 |
| (GY & STRR) PM2.5 & temperature (GY & STRR’s PM2.5 data and temperature together as input) | 26.74 ± 0.0015 | 714.94 ± 0.0757 | 19.57 ± 0.0022 | 45.62 |
| (GY & STRR) PM2.5 & wind direction (GY & STRR’s PM2.5 data and wind direction together as input) | 26.97 ± 0.0033 | 727.31 ± 0.0815 | 19.72 ± 0.0063 | 47.91 |
| (GY & STRR) PM2.5 & humidity (GY & STRR’s PM2.5 data and humidity together as input) | 25.44 ± 0.0021 | 647.17 ± 0.0603 | 17.95 ± 0.0027 | 45.21 |
| Source | SS | df | MS | F | F-Crit |
|---|---|---|---|---|---|
| Type | 6934.63 | 3 | 2311.54 | 5.75 | 2.61 |
| Error | 8,445,274.19 | 21,020 | 401.77 | ||
| Total | 8,452,208.81 | 21,023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.-B.; Wang, Z.-Y.; Gong, W.-T.; Kong, J.-L.; Bai, Y.-T.; Su, T.-L.; Ma, H.-J.; Chakrabarti, P. Variational Bayesian Network with Information Interpretability Filtering for Air Quality Forecasting. Mathematics 2023, 11, 837. https://doi.org/10.3390/math11040837
Jin X-B, Wang Z-Y, Gong W-T, Kong J-L, Bai Y-T, Su T-L, Ma H-J, Chakrabarti P. Variational Bayesian Network with Information Interpretability Filtering for Air Quality Forecasting. Mathematics. 2023; 11(4):837. https://doi.org/10.3390/math11040837
Chicago/Turabian StyleJin, Xue-Bo, Zhong-Yao Wang, Wen-Tao Gong, Jian-Lei Kong, Yu-Ting Bai, Ting-Li Su, Hui-Jun Ma, and Prasun Chakrabarti. 2023. "Variational Bayesian Network with Information Interpretability Filtering for Air Quality Forecasting" Mathematics 11, no. 4: 837. https://doi.org/10.3390/math11040837
APA StyleJin, X. -B., Wang, Z. -Y., Gong, W. -T., Kong, J. -L., Bai, Y. -T., Su, T. -L., Ma, H. -J., & Chakrabarti, P. (2023). Variational Bayesian Network with Information Interpretability Filtering for Air Quality Forecasting. Mathematics, 11(4), 837. https://doi.org/10.3390/math11040837









