Closed-Form Formula for the Conditional Moment-Generating Function Under a Regime-Switching, Nonlinear Drift CEV Process, with Applications to Option Pricing

Abstract

An analytical derivation of the conditional moment-generating function (MGF) for a regime-switching nonlinear drift constant elasticity of variance process is established. The proposed model incorporates both regime-switching mechanisms and nonlinear drift components to better capture market phenomena such as volatility smiles and leverage effects. Regime-switching models can match the tendency of financial markets to often change their behavior abruptly and the phenomenon that the new behavior of financial variables often persists for several periods after such a change. Closed-form formulas for the MGF under various conditions, which are then applied for option pricing, are also derived. The efficacy and accuracy of the results are validated through a discrete Markov chain simulation. The results obtained from the proposed formulas completely match with those from MC simulations, while requiring significantly less computational time.

1. Introduction

The study of stochastic differential equations (SDEs) has become a cornerstone in modeling financial markets, particularly in the context of asset pricing and derivative pricing. Traditional models such as the Black–Scholes–Merton framework, which assumes constant volatility, have been widely used due to their analytical tractability. However, these models often fail to capture observed market phenomena such as volatility smiles and the leverage effect, especially when financial markets change their behavior rapidly [1,2]. This has led to the development of more sophisticated models that incorporate stochastic volatility and regime-switching mechanisms. The constant elasticity of variance (CEV) model, introduced by Cox [3] and Cox and Ross [4], extends the Black–Scholes model by allowing the volatility of the underlying asset to change as a function of the asset price. This model is particularly adept at capturing the volatility smile observed in the options markets. The CEV model assumes that the volatility of the asset price follows a power-law relationship with the price itself, making it more realistic for modeling financial markets where volatility is higher when asset prices are lower and vice versa. The inclusion of the nonlinear term in the CEV model, governed by the elasticity parameter, enables the model to capture a range of behaviors, particularly in terms of the shape and dynamics of the implied volatility curve. The specific behavior exhibited by the model varies depending on the value of the elasticity parameter [5,6,7]. This process, which we refer to as the nonlinear drift CEV (NLD-CEV) process, was proposed by [8] and is capable of encompassing diverse dynamics. The given processes are the Ornstein–Uhlenbeck (OU) process, Cox–Ingersoll–Ross (CIR) process [9], geometric Brownian motion, which is similar to the Black–Scholes model [10], and the inverse Feller (IF) process, commonly known as the 3/2-stochastic volatility model (SVM).

Recent advancements in financial modeling have seen the integration of regime-switching mechanisms into stochastic models, allowing parameters such as volatility and drift to switch between different states, typically governed by a Markov chain. These models capture changes in market conditions or economic regimes, effectively reflecting the effects of macroeconomic factors and market anomalies, thus providing a more comprehensive framework for asset pricing. The foundational work by Hamilton laid the groundwork for regime-switching models, which have since been applied to various financial processes, including interest rates and stock returns [11]. By introducing a level of flexibility and realism that constant-parameter models lack, regime-switching models can capture different market regimes, such as bull and bear markets, and provide a better fit to historical data.

Regime-switching models are frequently employed in the pricing of financial derivatives, as they allow different pricing models under varying market conditions. For example, Buffington and Elliott [12] extended the Black–Scholes framework to include regime-switching mechanisms, where parameters such as interest rates, drift, and volatility depend on the state of the economy. They derived the characteristic function for occupation times and extended the Barone–Adesi–Whaley approximation for valuing American options under regime switching. This work significantly advanced the valuation of both European and American options in a regime-switching context. In another significant work, Zhu, Badran, and Lu [13] provided an analytical solution for European option pricing in a two-state regime-switching economy. By reducing the final form of the closed-form solution from a double integral to a single integral comprised of elementary functions, this model enhances computational efficiency and accuracy. Li [14] extended the optimal VIX futures trading problem in a regime-switching model, utilizing the CIR process with regime-switching to reflect market changes. By incorporating a finite-state Markov chain, the model allowed investors to adapt trading strategies based on regime changes. Optimal entry and exit strategies were developed by solving variational inequalities using numerical methods. Building on these advancements, Lin and He [15] investigated European option pricing under the fractional Black–Scholes model, capturing key characteristics of asset returns with regime-switching. They developed a two-step solution procedure for the coupled fractional partial differential equation (PDE) system and derived an exact pricing formula using the Fourier cosine series expansion, demonstrating rapid convergence and practical applicability. Indeed, there are additional models that incorporate regime-switching, for more details, see [16,17,18,19,20,21].

In addition, the conditional moment-generating function (MGF) is crucial in the context of financial derivative pricing. The MGF provides a convenient way to obtain the moments of a probability distribution, which can be directly calculated using the SDE transition probability density function (PDF) [22]. In derivative pricing, particularly for options, the conditional MGF allows the characterization of the asset price distribution under different market conditions or regimes. However, the conditional MGF cannot be derived directly using the transition PDF due to the regime-switching property in the process, which makes the transition PDFs unknown. Investigating the conditional MGF of these SDEs remains imperative and challenging. This is particularly important in models that incorporate regime switching, as the ability to compute the MGF for different states can significantly enhance the accuracy and efficiency of option pricing models. By transforming complex SDEs into more manageable forms, the MGF facilitates the derivation of closed-form solutions for derivative prices, making it a powerful tool in financial mathematics.

This work has three key contributions. First, we derive closed-form formulas for the conditional moment-generating functions of the asset price process described by the NLD-CEV model with two-state regime-switching. These formulas are presented for two scenarios: when the elasticity parameter is within the range $[0,2)$ and when it is greater than 2. Second, we apply these theoretical results to the practical problem of option pricing. Third, we validate our closed-form formulas through extensive Monte Carlo simulations by utilizing the Euler–Maruyama discretization method to simulate processes and approximate MGFs.

The rest of the paper is organized as follows: Section 2 describes the regime-switching NLD-CEV process, outlining the model’s dynamics and mathematical formulation. In Section 3, we derive the conditional MGFs for the model under different parameter conditions and present the theoretical results. Section 4 is dedicated to applying these results in European option pricing. Section 5 presents experimental validations based on Monte Carlo simulations to verify the accuracy and efficacy of the proposed results. Finally, Section 6 concludes the paper, with a summary of the findings.

2. The Regime-Switching NLD-CEV Process

Let $(\Omega ,\mathcal{F},\mathbb{Q})$ be a probability space with filtration ${\left({\mathcal{F}}_t\right)}_{t\ge 0}$ and a risk-neutral probability measure $\mathbb{Q}$. We begin by introducing the NLD-CEV model, which is assumed to follow the dynamics:

$$\begin{array}{c}\hfill d{R}_t=\kappa \left(\theta R_t^{-(1-\beta )}-R_t\right)dt+\sigma R_t^{{\displaystyle \frac{\beta }{2}}}d{W}_t^{\mathbb{Q}},\end{array}$$

with elasticity parameter $\beta \in [0,2)\cup (2,\infty )$, where κ, θ, σ are constant parameters and $W_t^{\mathbb{Q}}$ is a standard Wiener process. In order to perform with the process $R_t$ for some cases of $\beta$, we will assume some sufficient assumptions: $\kappa ,\theta$ and $\sigma$ are strictly greater than zero and $2\kappa \theta \ge {\sigma }^2$ for $\beta \in [0,2)$; while $-\kappa ,\theta$ and $-\sigma$ are strictly greater than zero for $\beta \in (2,\infty )$. By considering different values of $\beta$, the model can capture different dynamics: for $\beta =0$, the NLD-CEV model behaves like an Ornstein–Uhlenbeck (OU) process when $R_t$ is very large; for $\beta =1$, the process transforms into a Cox–Ingersoll–Ross (CIR) process, characterized by mean reversion; for $\beta =2$ and $\theta =0$, the model reduces to a geometric Brownian motion, akin to the Black–Scholes model; for $\beta =3$, it transitions into an inverse Feller (IF) process, also referred to as the 3/2-stochastic volatility model (SVM). Additionally, the NLD-CEV process can be found in the alternative form [23]. Incorporating regime-switching mechanisms into the NLD-CEV model enhances its ability to describe the dynamic behavior of financial markets under varying economic conditions. We present a regime-switching version of this model in which the constants $\theta$ and $\sigma$ are allowed to transition between different states following a Markov chain $X_t$; that is,

$$\begin{array}{c}\hfill d{R}_t=\kappa \left({\theta }_{X_t}{R}_t^{-(1-\beta )}-R_t\right)dt+{\sigma }_{X_t}{R}_t^{{\displaystyle \frac{\beta }{2}}}d{W}_t^{\mathbb{Q}}.\end{array}$$

(1)

When the economy is believed to be in state i, the continuous-time irreducible m-state Markov chain with generator $Q={\left(q_{ij}\right)}_{m\times m}$, which is independent of $W_t^{\mathbb{Q}}$, is defined as follows:

$$\begin{array}{c}\hfill \mathbb{P}(X_{t+\delta }=j\mid X_t=i)=\left\{\begin{array}{cc}{q}_{ij}\delta +o\left(\delta \right)\hfill & \mathrm{if}i\ne j,\hfill \\ 1+q_{ij}\delta +o\left(\delta \right)\hfill & \mathrm{if}i=j,\hfill \end{array}\right.\end{array}$$

where $\delta >0$ and if $i\ne j$, the transition rate from i to j satisfies $q_{ij}\ge 0$ and $q_{ii}=-{\sum }_{i\ne j}{q}_{ij}$. This Markov chain serves as a representation of the evolving financial market regime, exerting a substantial influence on the dynamics of the index. To take into consideration the effect of regime switching, for simplicity of derivation, we assume a two-state Markov chain; however, extending this to a scenario with an arbitrary but finite number of states is relatively straightforward. We propose two different cases according to $\beta$ with regime-switching model (1) as follows:

In the case of $\beta \in [0,2)$, we set $\beta ={\displaystyle \frac{2\alpha -1}{\alpha }}$ for $\alpha \ge {\displaystyle \frac{1}{2}}$, the regime-switching NLD-CEV process can be expressed as

$$\begin{array}{c}\hfill d{R}_t=\kappa \left({\theta }_{X_t}{R}_t^{{\displaystyle \frac{\alpha -1}{\alpha }}}-R_t\right)dt+{\sigma }_{X_t}{R}_t^{{\displaystyle \frac{2\alpha -1}{2\alpha }}}d{W}_t^{\mathbb{Q}}.\end{array}$$

(2)

Conversely, when $\beta \in (2,\infty )$, we set $\beta ={\displaystyle \frac{2\alpha +1}{\alpha }}$ for $\alpha >0$, the regime-switching NLD-CEV process is given by

$$\begin{array}{c}\hfill d{R}_t=\kappa \left({\theta }_{X_t}{R}_t^{{\displaystyle \frac{\alpha +1}{\alpha }}}-R_t\right)dt+{\sigma }_{X_t}{R}_t^{{\displaystyle \frac{2\alpha +1}{2\alpha }}}d{W}_t^{\mathbb{Q}}.\end{array}$$

(3)

It is noted by Sutthimat [24] that $\beta \to 2$ in (1) is equivalent to $\alpha \to \infty$ for both (2) and (3).

3. Conditional Moment-Generating Function

The derivation of the conditional MGF for the regime-switching NLD-CEV process is a complex yet crucial task in financial mathematics. This section focuses on the analytical computation of the conditional MGF depending on the range of the elasticity parameter $\beta$ for the processes (2) and (3), providing a foundation for further applications in option pricing. The key idea relies on the Feynman–Kac formula, which involves expressing the solution of the corresponding hybrid system of PDEs and solving for the coefficients to obtain the closed forms, for more motivation, see [25,26,27].

3.1. Conditional Moment-Generating Function of the Model When $\beta \in [0,2)$

In this subsection, we derive the conditional MGF for the regime-switching NLD-CEV process when the elasticity parameter $\beta$ is within the range $[0,2)$. The following theorem establishes the foundation by providing a closed-form expression for the conditional MGF.

Theorem 1.

Suppose that $R_t$ follows the system of SDEs (2) on $[0,T]$ with initial values $R_t=R$ and $X_t=i,i\in \{1,2\}$. Then, the conditional MGF is defined by the following:

$$\begin{array}{cc}\hfill V_{\alpha ,i}^{\langle \delta \rangle }(\tau ,R):& ={\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]\hfill \\ & =e^{{\mathbb{1}}_{\left\{1\right\}}\left(i\right)\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)+{\mathbb{1}}_{\left\{2\right\}}\left(i\right)\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)},\hfill \end{array}$$

(4)

where $\tau =T-t\ge 0$, $\mathbb{1}$ is the indicator function, $A_{\alpha ,\delta }^{\langle k\rangle }\left(\tau \right)$ and $B_{\alpha ,\delta }^{\langle k\rangle }\left(\tau \right)$ for $k=0,1$ can be solved by the system of Riccati differential equations:

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+\kappa {\displaystyle \frac{1}{\alpha }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\displaystyle \frac{1}{2}}{\sigma }_1^2{\displaystyle \frac{1}{{\alpha }^2}}{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2=0,\hfill \end{array}$$

(5)

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+\kappa {\displaystyle \frac{1}{\alpha }}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\displaystyle \frac{1}{2}}{\sigma }_2^2{\displaystyle \frac{1}{{\alpha }^2}}{\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2=0\hfill \end{array}$$

(6)

with the initial conditions $A_{\alpha ,\delta }^{\langle 1\rangle }\left(0\right)=B_{\alpha ,\delta }^{\langle 1\rangle }\left(0\right)=\delta$ and the system of nonlinear ordinary differential equations (ODEs), as follows:

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-{\gamma }_{\alpha ,1}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{12}-q_{12}{e}^{\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{{\displaystyle \frac{1}{\alpha }}}+\left(B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}=0,\hfill \end{array}$$

(7)

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{B}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-{\gamma }_{\alpha ,2}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{21}-q_{21}{e}^{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{{\displaystyle \frac{1}{\alpha }}}+\left(A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}=0\hfill \end{array}$$

(8)

with the initial conditions $A_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=B_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=0$, where ${\gamma }_{\alpha ,i}=\kappa {\theta }_i{\displaystyle \frac{1}{\alpha }}+{\displaystyle \frac{1}{2}}{\sigma }_i^2{\displaystyle \frac{1}{\alpha }}\left({\displaystyle \frac{1}{\alpha }}-1\right)$.

Proof. 

According to Yao et al. [28], the conditional MGF in (4) satisfies the PDEs, as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial V_{\alpha ,i}^{\langle \delta \rangle }}{\partial \tau }}-\kappa \left({\theta }_i{R}^{-(1-\beta )}-R\right){\displaystyle \frac{\partial V_{\alpha ,i}^{\langle \delta \rangle }}{\partial R}}-{\displaystyle \frac{1}{2}}{\sigma }_i^2{R}^{\beta }{\displaystyle \frac{{\partial }^2{V}_{\alpha ,i}^{\langle \delta \rangle }}{\partial R^2}}-\sum _{j\ne i}{q}_{ij}\left(V_{\alpha ,j}^{\langle \delta \rangle }-V_{\alpha ,i}^{\langle \delta \rangle }\right)=0\end{array}$$

(9)

with $\beta ={\displaystyle \frac{2\alpha -1}{\alpha }}$, where $(\tau ,R)\in [0,T]\times {\mathbb{R}}^{+}$ subject to the initial condition at $\tau =0$:

$$\begin{array}{c}\hfill V_{\alpha ,i}^{\langle \delta \rangle }(0,R)=e^{\delta R^{{\displaystyle \frac{1}{\alpha }}}}\mathrm{for}i=1,2.\end{array}$$

(10)

The demonstration is split into two cases contingent on the condition $X_t=i$, where $i=1,2$. For $i=1$, we compare the coefficients of (4) with (10) to obtain the initial conditions $A_{\alpha ,\delta }^{\langle 1\rangle }\left(0\right)=\delta$ and $A_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=0$. Substituting the partial derivatives, we have the following:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial V_{\alpha ,i}^{\langle \delta \rangle }}{\partial \tau }}& =\left({\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+{\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)e^{A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}\hfill \\ \hfill {\displaystyle \frac{\partial V_{\alpha ,i}^{\langle \delta \rangle }}{\partial R}}& ={\displaystyle \frac{1}{\alpha }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}-1}{e}^{A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}\hfill \\ \hfill {\displaystyle \frac{{\partial }^2{V}_{\alpha ,i}^{\langle \delta \rangle }}{\partial R^2}}& ={\displaystyle \frac{1}{{\alpha }^2}}{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2{R}^{{\displaystyle \frac{2}{\alpha }}-2}{e}^{A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}\hfill \\ & +{\displaystyle \frac{1}{\alpha }}\left({\displaystyle \frac{1}{\alpha }}-1\right)A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}-2}{e}^{A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}\hfill \end{array}$$

into (9). This implies the following simplified form:

$$\begin{array}{c}\hfill {\overline{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}{e}^{A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}+{\overline{A}}_{\alpha ,\delta }^{\langle 2\rangle }\left(\tau \right)e^{A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}=0,\end{array}$$

(11)

where

$$\begin{array}{cc}\hfill {\overline{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)& ={\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+\kappa {\displaystyle \frac{1}{\alpha }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\displaystyle \frac{1}{2}}{\sigma }_1^2{\displaystyle \frac{1}{{\alpha }^2}}{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2,\hfill \\ \hfill {\overline{A}}_{\alpha ,\delta }^{\langle 2\rangle }\left(\tau \right)& ={\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-\left(\kappa {\theta }_1{\displaystyle \frac{1}{\alpha }}+{\displaystyle \frac{1}{2}}{\sigma }_1^2{\displaystyle \frac{1}{\alpha }}\left({\displaystyle \frac{1}{\alpha }}-1\right)\right)A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{12}\hfill \end{array}$$

(12)

$$\begin{array}{cc}& -q_{12}{e}^{\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{{\displaystyle \frac{1}{\alpha }}}+\left(B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}.\hfill \end{array}$$

(13)

As a result, we can directly follow from the previous case to derive the state $i=2$, as follows:

$$\begin{array}{c}\hfill {\overline{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}{e}^{B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}+{\overline{B}}_{\alpha ,\delta }^{\langle 2\rangle }\left(\tau \right)e^{B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}=0,\end{array}$$

(14)

where

$$\begin{array}{cc}\hfill {\overline{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)& ={\displaystyle \frac{d}{d\tau }}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+\kappa {\displaystyle \frac{1}{\alpha }}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\displaystyle \frac{1}{2}}{\sigma }_2^2{\displaystyle \frac{1}{{\alpha }^2}}{\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2,\hfill \\ \hfill {\overline{B}}_{\alpha ,\delta }^{\langle 2\rangle }\left(\tau \right)& ={\displaystyle \frac{d}{d\tau }}{B}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-\left(\kappa {\theta }_2{\displaystyle \frac{1}{\alpha }}+{\displaystyle \frac{1}{2}}{\sigma }_2^2{\displaystyle \frac{1}{\alpha }}\left({\displaystyle \frac{1}{\alpha }}-1\right)\right)B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{21}\hfill \end{array}$$

(15)

$$\begin{array}{cc}& -q_{21}{e}^{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{{\displaystyle \frac{1}{\alpha }}}+\left(A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}\hfill \end{array}$$

(16)

with the initial conditions $B_{\alpha ,\delta }^{\langle 1\rangle }\left(0\right)=\delta$ and $B_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=0$. We conclude from (11)–(16) to complete the proof.    □

A simple form of the MGF can be obtained as shown in the following corollary, making the results more tractable.

Corollary 1.

Keeping the notations as in Theorem 1, the moment-generating function (4) can be rewritten in the following form:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]={\mathbb{1}}_{\left\{1\right\}}\left(i\right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }{e}^{{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}}+{\mathbb{1}}_{\left\{2\right\}}\left(i\right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }{e}^{{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}},\end{array}$$

(17)

where ${\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)$ and ${\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)$ can be solved by the system of ODEs:

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-\left({\gamma }_{\alpha ,1}{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-q_{12}\right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-q_{12}D\left(\tau \right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)=0,\hfill \end{array}$$

(18)

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-\left({\gamma }_{\alpha ,2}{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-q_{21}\right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-q_{21}{D}^{-1}\left(\tau \right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)=0\hfill \end{array}$$

(19)

with the initial conditions ${\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)={\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=1$ and $D\left(\tau \right)=e^{\left({\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{{\displaystyle \frac{1}{\alpha }}}}$,

$$\begin{array}{c}\hfill {\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)={\displaystyle \frac{2\alpha \delta \kappa }{\delta {\sigma }_1^2+\left(2\alpha \kappa -\delta {\sigma }_1^2\right)e^{\frac{\kappa \tau }{\alpha }}}}and{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)={\displaystyle \frac{2\alpha \delta \kappa }{\delta {\sigma }_2^2+\left(2\alpha \kappa -\delta {\sigma }_2^2\right)e^{\frac{\kappa \tau }{\alpha }}}}.\end{array}$$

(20)

Proof. 

The solutions $A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)$ and $B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)$ from the Riccati Equations (5) and (6) can be solved by using the substitution technique to obtain ${\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)$ and ${\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)$ as defined in (20), respectively. For the transformed system of ODEs (7) and (8), we let ${\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)=e^{A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}$ and ${\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)=e^{B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)}$ to obtain (18) and (19) with the initial conditions ${\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)={\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=1$. Then, the conditional MGF (4) can be written as follows:

$$\begin{array}{cc}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]& =e^{{\mathbb{1}}_{\left\{1\right\}}\left(i\right)\left({\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)+{\mathbb{1}}_{\left\{2\right\}}\left(i\right)\left({\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}+B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}\hfill \\ & ={\mathbb{1}}_{\left\{1\right\}}\left(i\right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }{e}^{{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}}+{\mathbb{1}}_{\left\{2\right\}}\left(i\right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }{e}^{{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}}.\hfill \end{array}$$

This proof is complete.    □

The following corollary addresses the specific condition corresponding to the case when there is no switching regime, i.e., by using the same parameters of both states.

Corollary 2.

Keeping the notation as in Corollary 1 with ${\theta }_1={\theta }_2=\theta$ and ${\sigma }_1={\sigma }_2=\sigma$, then the moment-generating function (17) can be expressed in the following form:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]=e^{{\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)+C_{\alpha ,\delta }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}},\end{array}$$

(21)

where ${\gamma }_{\alpha }={\gamma }_{\alpha ,1}={\gamma }_{\alpha ,2}$,

$$\begin{array}{cc}\hfill C_{\alpha ,\delta }\left(\tau \right)& ={\displaystyle \frac{2\alpha \delta \kappa }{\delta {\sigma }^2+\left(2\alpha \kappa -\delta {\sigma }^2\right)e^{\frac{\kappa \tau }{\alpha }}}}and\hfill \\ \hfill {\tilde{C}}_{\alpha ,\delta }\left(\tau \right)& ={\displaystyle \frac{2\alpha }{{\sigma }^2}}\left(\kappa \tau +\alpha ln\left({\displaystyle \frac{2\alpha \kappa }{\delta {\sigma }^2+\left(2\alpha \kappa -\delta {\sigma }^2\right)e^{\frac{\kappa \tau }{\alpha }}}}\right)\right).\hfill \end{array}$$

Proof. 

The system of ODEs (18) and (19) can be written in the matrix differential equation, as follows:

$$\begin{array}{c}\hfill {\mathbf{u}}_{\alpha ,\delta }^{\prime }\left(\tau \right)={\mathbf{P}}_{\alpha ,\delta }\left(\tau \right){\mathbf{u}}_{\alpha ,\delta }\left(\tau \right)\mathrm{with}\mathrm{initial}\mathrm{conditions}{\mathbf{u}}_{\alpha ,\delta }\left(0\right)={[1,1]}^{\top },\end{array}$$

(22)

where

$$\begin{array}{cc}\hfill {\mathbf{u}}_{\alpha ,\delta }^{\prime }\left(\tau \right)& ={\left[{\displaystyle \frac{d}{d\tau }}{\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right),{\displaystyle \frac{d}{d\tau }}{\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right]}^{\top },{\mathbf{u}}_{\alpha ,\delta }\left(\tau \right)={\left[{\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right),{\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right]}^{\top },\hfill \\ \hfill {\mathbf{P}}_{\alpha ,\delta }\left(\tau \right)& =\left[\begin{array}{cc}{\gamma }_{\alpha ,1}{C}_{\alpha ,\delta }\left(\tau \right)-q_{12}& q_{12}\\ q_{21}& {\gamma }_{\alpha ,1}{C}_{\alpha ,\delta }\left(\tau \right)-q_{21}\end{array}\right].\hfill \end{array}$$

Then, the solution of the homogeneous problem (22) can be solved as follows:

$$\begin{array}{c}\hfill {\mathbf{u}}_{\alpha ,\delta }\left(\tau \right)=e^{{\tilde{\mathbf{P}}}_{\alpha ,\delta }\left(\tau \right)}{\mathbf{u}}_{\alpha ,\delta }\left(0\right),\end{array}$$

(23)

where

$$\begin{array}{cc}\hfill {\tilde{\mathbf{P}}}_{\alpha ,\delta }\left(\tau \right)& ={\int }_0^{\tau }{\mathbf{P}}_{\alpha ,\delta }\left(\xi \right)d\xi =\left[\begin{array}{cc}{\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)-q_{12}\tau & q_{12}\tau \\ q_{21}\tau & {\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)-q_{21}\tau \end{array}\right],\hfill \\ \hfill {\tilde{C}}_{\alpha ,\delta }\left(\tau \right)& ={\int }_0^{\tau }{C}_{\alpha ,\delta }\left(\xi \right)d\xi ,\mathrm{and}{\gamma }_{\alpha }={\gamma }_{\alpha ,1}={\gamma }_{\alpha ,2}.\hfill \end{array}$$

To obtain the result in the form of (21), we write the solution (23) using eigenvalue-eigenvectors of ${\tilde{\mathbf{P}}}_{\alpha ,\delta }\left(\tau \right)$. It is easy to verify that the eigenvalues of ${\tilde{\mathbf{P}}}_{\alpha ,\delta }\left(\tau \right)$ are ${\lambda }_1\left(\tau \right)={\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)$ and ${\lambda }_2\left(\tau \right)={\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)-(q_{12}+q_{21})\tau$ and correspond to the eigenvectors, respectively ${\mathbf{v}}_1={[1,1]}^{\top }$ and ${\mathbf{v}}_2={[-q_{12},q_{21}]}^{\top }$. Let $S=[{\mathbf{v}}_{\mathbf{1}},{\mathbf{v}}_{\mathbf{2}}]$ and ${\Lambda }_{\alpha }=\mathrm{diag}\left\{{\lambda }_1\left(\tau \right),{\lambda }_2\left(\tau \right)\right\}$. Consequently, the solution (23) can be expressed as follows:

$$\begin{array}{c}\hfill {\mathbf{u}}_{\alpha ,\delta }\left(\tau \right)=S{e}^{{\Lambda }_{\alpha }}{S}^{-1}{\mathbf{u}}_{\alpha ,\delta }\left(0\right)={\left[e^{{\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)},e^{{\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)}\right]}^{\top }.\end{array}$$

(24)

We conclude from (17) and (24) and complete the proof.    □

The following corollary provides a method to calculate the conditional moments of the asset price distribution using the complete exponential Bell polynomials, offering a straightforward way to obtain higher-order moments from the conditional MGF.

Corollary 3.

According to Corollary 2, the conditional ${\displaystyle \frac{n}{\alpha }}$-moment for $n\in {\mathbb{Z}}_0^{+}$ satisfies the complete exponential Bell polynomial, as follows:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[R_T^{{\displaystyle \frac{n}{\alpha }}}|R_t=R,X_t=i\right]=n!\sum _{j_1+2j_2+\cdots +n{j}_n=n}\prod _{\ell =1}^n{\displaystyle \frac{1}{\left(j_{\ell }\right)!}}{\left({\displaystyle \frac{1}{\ell !}}{\displaystyle \frac{{\partial }^{\ell }H}{\partial {\delta }^{\ell }}}{|}_{\delta =0}\right)}^{j_{\ell }}=:{\mathbf{B}}_{\alpha ,i}^{\langle n\rangle }(\tau ,R)\end{array}$$

where $H(\tau ,R,\delta ,\alpha ,i)={\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)+C_{\alpha ,\delta }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}$ and $j_1,j_2,\dots ,j_n$ are non-negative integers.

Proof. 

The conditional ${\displaystyle \frac{n}{\alpha }}$-moment is obtained by calculating the derivatives of the MGF (21) with respect to $\delta$ evaluated at $\delta =0$, which satisfies the complete exponential Bell polynomial as follows:

$$\begin{array}{cc}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[R_T^{{\displaystyle \frac{n}{\alpha }}}|R_t=R,X_t=i\right]& =\sum _{j=1}^n{\mathbf{B}}_{n,j}\left({\displaystyle \frac{\partial H}{\partial \delta }}{|}_{\delta =0},{\displaystyle \frac{{\partial }^{2}H}{\partial {\delta }^2}}{|}_{\delta =0}\dots ,{\displaystyle \frac{{\partial }^{n-j+1}H}{\partial {\delta }^{n-j+1}}}{|}_{\delta =0}\right)\hfill \\ & =\sum _{j=1}^n\sum _{\begin{array}{c}{j}_1+j_2+\cdots +j_{n-j+1}=j\\ j_1+2j_2+\cdots +(n-j+1)j_{n-j+1}=n\end{array}}{\displaystyle \frac{n!}{j_1!j_2!\cdots j_{n-j+1}!}}{\left({\displaystyle \frac{1}{1!}}{\displaystyle \frac{\partial H}{\partial \delta }}{|}_{\delta =0}\right)}^{j_1}\hfill \\ & {\left({\displaystyle \frac{1}{2!}}{\displaystyle \frac{{\partial }^{2}H}{\partial {\delta }^2}}{|}_{\delta =0}\right)}^{j_2}\cdots {\left({\displaystyle \frac{1}{(n-j+1)!}}{\displaystyle \frac{{\partial }^{n-j+1}H}{\partial {\delta }^{n-j+1}}}{|}_{\delta =0}\right)}^{j_{n-j+1}}\hfill \\ & =n!\sum _{j=1}^n\sum _{\begin{array}{c}{j}_1+j_2+\cdots +j_{n-j+1}=j\\ j_1+2j_2+\cdots +(n-j+1)j_{n-j+1}=n\end{array}}\prod _{\ell =1}^{n-j+1}{\displaystyle \frac{1}{\left(j_{\ell }\right)!}}{\left({\displaystyle \frac{1}{\ell !}}{\displaystyle \frac{{\partial }^{\ell }H}{\partial {\delta }^{\ell }}}{|}_{\delta =0}\right)}^{j_{\ell }}\hfill \\ & =n!\sum _{\begin{array}{c}{j}_1+2j_2+\cdots +n{j}_n=n\end{array}}\prod _{\ell =1}^n{\displaystyle \frac{1}{\left(j_{\ell }\right)!}}{\left({\displaystyle \frac{1}{\ell !}}{\displaystyle \frac{{\partial }^{\ell }H}{\partial {\delta }^{\ell }}}{|}_{\delta =0}\right)}^{j_{\ell }},\hfill \end{array}$$

where the second equality is obtained by applying Faà Bruno’s formula [29].    □

In order to illustrate the computation of conditional moments in Corollary 3, we provide some cases in the following example.

Example 1.

By utilizing Corollary 3, we obtain the ${\displaystyle \frac{n}{\alpha }}$-moment when $n=1$ and $n=2$, respectively.

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\alpha ,i}^{\langle 1\rangle }(\tau ,R)& =-{\displaystyle \frac{\alpha {\gamma }_{\alpha }{e}^{-\frac{\kappa \tau }{\alpha }}}{\kappa }}+{\displaystyle \frac{\alpha {\gamma }_{\alpha }}{\kappa }}+R^{{\displaystyle \frac{1}{\alpha }}}{e}^{-{\displaystyle \frac{\kappa \tau }{\alpha }}},\hfill \\ \hfill {\mathbf{B}}_{\alpha ,i}^{\langle 2\rangle }(\tau ,R)& ={\displaystyle \frac{{\alpha }^2{\gamma }^2{e}^{-\frac{2\kappa \tau }{\alpha }}}{{\kappa }^2}}-{\displaystyle \frac{2{\alpha }^2{\gamma }^2{e}^{-\frac{\kappa \tau }{\alpha }}}{{\kappa }^2}}+{\displaystyle \frac{{\alpha }^2{\gamma }^2}{{\kappa }^2}}+{\displaystyle \frac{\gamma {\sigma }^2{e}^{-\frac{2\kappa \tau }{\alpha }}}{2{\kappa }^2}}-{\displaystyle \frac{\gamma {\sigma }^2{e}^{-\frac{\kappa \tau }{\alpha }}}{{\kappa }^2}}+{\displaystyle \frac{\gamma {\sigma }^2}{2{\kappa }^2}}\hfill \\ & +R^{{\displaystyle \frac{2}{\alpha }}}{e}^{-{\displaystyle \frac{2\kappa \tau }{\alpha }}}-{\displaystyle \frac{2\alpha \gamma R^{\frac{1}{\alpha }}{e}^{-\frac{2\kappa \tau }{\alpha }}}{\kappa }}+{\displaystyle \frac{2\alpha \gamma R^{\frac{1}{\alpha }}{e}^{-\frac{\kappa \tau }{\alpha }}}{\kappa }}-{\displaystyle \frac{{\sigma }^2{R}^{\frac{1}{\alpha }}{e}^{-\frac{2\kappa \tau }{\alpha }}}{\alpha \kappa }}+{\displaystyle \frac{{\sigma }^2{R}^{\frac{1}{\alpha }}{e}^{-\frac{\kappa \tau }{\alpha }}}{\alpha \kappa }}.\hfill \end{array}$$

This example shows the specific conditional moments based on the process (2), where $\alpha \ge {\displaystyle \frac{1}{2}}$, which is derived from conditional MGF. For $n=1$, $\alpha =1$ provides the first conditional moment of the CIR process, while $\alpha ={\displaystyle \frac{1}{2}}$ yields the second conditional moment of the OU process. For $n=2$, $\alpha =1$ gives the second conditional moment of the CIR process, and $\alpha ={\displaystyle \frac{1}{2}}$ results in the fourth conditional moment of the OU process.

3.2. Conditional Moment-Generating Function of the Model When $\beta \in (2,\infty )$

This subsection focuses on deriving the conditional MGF for the regime-switching NLD-CEV process when the elasticity parameter $\beta$ lies within the range $(2,\infty )$. The following theorem lays the groundwork by presenting a closed-form expression for the conditional MGF.

Theorem 2.

Suppose that $R_t$ follows the system of SDEs (3) on $[0,T]$ with initial values $R_t=R$ and $X_t=i,i\in \{1,2\}$. The conditional moment-generating function is defined by the following:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{-{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]=e^{{\mathbb{1}}_{\left\{1\right\}}\left(i\right)\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{-{\displaystyle \frac{1}{\alpha }}}+A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)+{\mathbb{1}}_{\left\{2\right\}}\left(i\right)\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{-{\displaystyle \frac{1}{\alpha }}}+B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)},\end{array}$$

(25)

where $\tau =T-t\ge 0$, $\mathbb{1}$ is the indicator function, and $A_{\alpha }^{\langle k\rangle }$ and $B_{\alpha }^{\langle k\rangle }$ for $k=0,1$ can be solved by the system of recursive nonlinear differential equations, as follows:

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-\kappa {\displaystyle \frac{1}{\alpha }}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\displaystyle \frac{1}{2}}{\sigma }_1^2{\displaystyle \frac{1}{{\alpha }^2}}{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2=0,\hfill \\ & {\displaystyle \frac{d}{d\tau }}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-\kappa {\displaystyle \frac{1}{\alpha }}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\displaystyle \frac{1}{2}}{\sigma }_1^2{\displaystyle \frac{1}{{\alpha }^2}}{\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)}^2=0\hfill \end{array}$$

with the initial conditions $A_{\alpha ,\delta }^{\langle 1\rangle }\left(0\right)=B_{\alpha ,\delta }^{\langle 1\rangle }\left(0\right)=\delta$ and

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{A}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)+{\overline{\gamma }}_{\alpha ,1}{A}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{12}-q_{12}{e}^{\left(B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{-{\displaystyle \frac{1}{\alpha }}}+\left(B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}=0,\hfill \\ & {\displaystyle \frac{d}{d\tau }}{B}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)+{\overline{\gamma }}_{\alpha ,2}{B}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{21}-q_{21}{e}^{\left(A_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-B_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{-{\displaystyle \frac{1}{\alpha }}}+\left(A_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-B_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)\right)}=0\hfill \end{array}$$

with the initial conditions $A_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=B_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=0$, where ${\overline{\gamma }}_{\alpha ,i}=\kappa {\theta }_i{\displaystyle \frac{1}{\alpha }}-{\displaystyle \frac{1}{2}}{\sigma }_i^2{\displaystyle \frac{1}{\alpha }}\left({\displaystyle \frac{1}{\alpha }}+1\right)$.

Proof. 

The proof is similar to Theorem 1 and is omitted.    □

Corollary 4 makes the expression derived in Theorem 2 more tractable by simplifying it through the resolution of the system of recursive nonlinear differential equations.

Corollary 4.

Keeping the notations as in Theorem 2, the moment-generating function (25) can be rewritten as follows:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{-{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]={\mathbb{1}}_{\left\{1\right\}}\left(i\right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }{e}^{{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{-{\displaystyle \frac{1}{\alpha }}}}+{\mathbb{1}}_{\left\{2\right\}}\left(i\right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }{e}^{{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)R^{-{\displaystyle \frac{1}{\alpha }}}},\end{array}$$

(26)

where $A\left(\tau \right)$ and $B\left(\tau \right)$ can be solved by the following system of ODEs:

$$\begin{array}{cc}& {\displaystyle \frac{d}{d\tau }}{\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)+\left({\overline{\gamma }}_{\alpha ,1}{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{12}\right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-q_{12}D\left(\tau \right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)=0\hfill \\ & {\displaystyle \frac{d}{d\tau }}{\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)+\left({\overline{\gamma }}_{\alpha ,2}{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)+q_{21}\right){\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)-q_{21}{D}^{-1}\left(\tau \right){\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(\tau \right)=0\hfill \end{array}$$

with the initial conditions ${\tilde{A}}_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)={\tilde{B}}_{\alpha ,\delta }^{\langle 0\rangle }\left(0\right)=1$ such that $D\left(\tau \right)=e^{\left({\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)-{\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)\right)R^{-{\displaystyle \frac{1}{\alpha }}}}$,

$$\begin{array}{c}\hfill {\tilde{A}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)={\displaystyle \frac{-2\alpha \delta \kappa }{\delta {\sigma }_1^2-\left(2\alpha \kappa +\delta {\sigma }_1^2\right)e^{-\frac{\kappa \tau }{\alpha }}}}and{\tilde{B}}_{\alpha ,\delta }^{\langle 1\rangle }\left(\tau \right)={\displaystyle \frac{-2\alpha \delta \kappa }{\delta {\sigma }_2^2-\left(2\alpha \kappa +\delta {\sigma }_2^2\right)e^{-\frac{\kappa \tau }{\alpha }}}}.\end{array}$$

Proof. 

The proof is analogous to that of Corollary 1 and is omitted.    □

The following corollary builds on the results of Corollary 4 by applying them to the case where the parameters of both states are similar, resulting in a more streamlined form of the conditional MGF.

Corollary 5.

Keeping the notation as in Corollary 4 with ${\theta }_1={\theta }_2=\theta$ and ${\sigma }_1={\sigma }_2=\sigma$, then the moment-generating function (26) can be expressed in the following form:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[e^{\delta R_T^{-{\displaystyle \frac{1}{\alpha }}}}|R_t=R,X_t=i\right]=e^{-{\overline{\gamma }}_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)+C_{\alpha ,\delta }\left(\tau \right)R^{-{\displaystyle \frac{1}{\alpha }}}},\end{array}$$

where ${\overline{\gamma }}_{\alpha }={\overline{\gamma }}_{\alpha ,1}={\overline{\gamma }}_{\alpha ,2}$,

$$\begin{array}{cc}\hfill C_{\alpha ,\delta }\left(\tau \right)& ={\displaystyle \frac{-2\alpha \delta \kappa }{\delta {\sigma }^2-\left(2\alpha \kappa +\delta {\sigma }^2\right)e^{-\frac{\kappa \tau }{\alpha }}}}and\hfill \\ \hfill {\tilde{C}}_{\alpha ,\delta }\left(\tau \right)& ={\displaystyle \frac{2{\alpha }^2}{{\sigma }^2}}ln\left({\displaystyle \frac{2\alpha \kappa }{2\alpha \kappa -\delta {\sigma }^2\left(e^{\frac{\kappa \tau }{\alpha }}-1\right)}}\right).\hfill \end{array}$$

Proof. 

The proof is essentially the same as the proof of Corollary 2, so it is omitted.    □

Corollary 6 presents a technique for computing the conditional moments of the asset price distribution utilizing the findings of the conditional MGF.

Corollary 6.

According to Corollary 5, the conditional ${\displaystyle \frac{n}{\alpha }}$-moment for $n\in {\mathbb{Z}}_0^{-}$ satisfies the complete exponential Bell polynomial, as follows:

$$\begin{array}{c}\hfill {\mathbf{E}}^{\mathbb{Q}}\left[R_T^{{\displaystyle \frac{n}{\alpha }}}|R_t=R,X_t=i\right]=\left|n\right|!\sum _{j_1+2j_2+\cdots +\left|n\right|j_{\left|n\right|}=\left|n\right|}\prod _{\ell =1}^{\left|n\right|}{\displaystyle \frac{1}{\left(j_{\ell }\right)!}}{\left({\displaystyle \frac{1}{\ell !}}{\displaystyle \frac{{\partial }^{\ell }H}{\partial {\delta }^{\ell }}}{|}_{\delta =0}\right)}^{j_{\ell }}=:{\mathbf{B}}_{\alpha ,i}^{\langle n\rangle }(\tau ,R),\end{array}$$

where $H(\tau ,R,\delta ,\alpha ,i)={\gamma }_{\alpha }{\tilde{C}}_{\alpha ,\delta }\left(\tau \right)+C_{\alpha ,\delta }\left(\tau \right)R^{{\displaystyle \frac{1}{\alpha }}}$ and $j_1,j_2,\dots ,j_{\left|n\right|}$ are non-negative integers.

It is important to note that these moments can be directly calculated using the transition PDF, which is often unknown or not available in closed form. Additionally, the formulas for the conditional moments of the SDE may also be unavailable in closed form, making practical applications, such as the valuation of volatility swaps, particularly challenging, especially when half-moments are required. In such cases, Corollaries 3 and 5 can be directly applied to compute the values of volatility swaps when $\alpha =2$, see also [22].

To demonstrate the calculation of conditional moments in Corollary 6, we present some instances in the following example.

Example 2.

Applying Corollary 6, we can calculate the ${\displaystyle \frac{n}{\alpha }}$-moment for the cases where $n=-1$ and $n=-2$, respectively, as follows:

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\alpha ,i}^{\langle -1\rangle }(\tau ,R)& =-{\displaystyle \frac{\alpha \overline{\gamma }{e}^{\frac{\kappa \tau }{\alpha }}}{\kappa }}+{\displaystyle \frac{\alpha \overline{\gamma }}{\kappa }}+R^{-{\displaystyle \frac{1}{\alpha }}}{e}^{{\displaystyle \frac{\kappa \tau }{\alpha }}},\hfill \\ \hfill {\mathbf{B}}_{\alpha ,i}^{\langle -2\rangle }(\tau ,R)& =-{\displaystyle \frac{2{\alpha }^2{\overline{\gamma }}^2{e}^{\frac{\kappa \tau }{\alpha }}}{{\kappa }^2}}+{\displaystyle \frac{{\alpha }^2{\overline{\gamma }}^2{e}^{\frac{2\kappa \tau }{\alpha }}}{{\kappa }^2}}+{\displaystyle \frac{{\alpha }^2{\overline{\gamma }}^2}{{\kappa }^2}}+{\displaystyle \frac{\overline{\gamma }{\sigma }^2{e}^{\frac{\kappa \tau }{\alpha }}}{{\kappa }^2}}-{\displaystyle \frac{\overline{\gamma }{\sigma }^2{e}^{\frac{2\kappa \tau }{\alpha }}}{2{\kappa }^2}}-{\displaystyle \frac{\overline{\gamma }{\sigma }^2}{2{\kappa }^2}}\hfill \\ & +{\displaystyle \frac{2\alpha \overline{\gamma }{R}^{-\frac{1}{\alpha }}{e}^{\frac{\kappa \tau }{\alpha }}}{\kappa }}-{\displaystyle \frac{2\alpha \overline{\gamma }{R}^{-\frac{1}{\alpha }}{e}^{\frac{2\kappa \tau }{\alpha }}}{\kappa }}-{\displaystyle \frac{{\sigma }^2{R}^{-\frac{1}{\alpha }}{e}^{\frac{\kappa \tau }{\alpha }}}{\alpha \kappa }}+{\displaystyle \frac{{\sigma }^2{R}^{-\frac{1}{\alpha }}{e}^{\frac{2\kappa \tau }{\alpha }}}{\alpha \kappa }}+R^{-{\displaystyle \frac{2}{\alpha }}}{e}^{{\displaystyle \frac{2\kappa \tau }{\alpha }}}.\hfill \end{array}$$

This example shows the specific conditional moments based on the process (3) where $\alpha >0$, which is derived from the conditional MGF. For $n=-1$ and $n=-2$ with $\alpha =1$, we obtain the first and the second inverse conditional moment of the IF process, respectively.

4. Integral Representation for European Options

Based on the formulas derived in the previous section for the conditional MGFs of the asset price governed by the regime-switching NLD-CEV processes (2), we can employ the Fourier transform method to compute the option price. In the following Lemma, we utilize the Fourier transform technique proposed by Andersen and Piterbarg [30].

Lemma 1.

Let ξ be a random variable with a moment-generating function defined by $M_{\xi }\left(t\right)$. Then, for $k\in \mathbb{R}$, we have the following:

$${\displaystyle \mathbf{E}\left[{(\xi -k)}^{+}\right]=\frac{d{M}_{\xi }\left(t\right)}{dt}{|}_{t=0}-k+\frac{1}{\pi }{\int }_0^{\infty }\mathbb{R}\left(\frac{e^{-k(-\lambda +i\omega )}{M}_{\xi }(-\lambda +i\omega )}{{(-\lambda +i\omega )}^2}\right)d\omega ,}$$

(27)

for any $\lambda >0$ for which the right-hand side exists.

Then, we can express the closed-form formula of the European call option price as follows:

Theorem 3.

Suppose that the underlying asset price $R_t$ follows the NLD-CEV process in (2) with positive integer α. Let $C(t,R,i)$ be the value European call option price on an underlying asset spot price R at time t with state $i(i=1,2)$, and with a strike price K and an expiration date T. The fair value of the European call option is represented in the following integral form:

$$\begin{array}{cc}\hfill C(\tau ,R,i)& =e^{-r\tau }{\mathbf{E}}^{\mathbb{Q}}\left[{(R_T-K)}^{+}|R_t=R,X_t=i\right]\hfill \\ \hfill & =e^{-r\tau }\left[{\displaystyle \frac{d^{\alpha }}{d{\delta }^{\alpha }}{V}_{\alpha ,i}^{\langle \delta \rangle }(\tau ,R){|}_{\delta =0}-K+\frac{1}{\pi }{\int }_0^{\infty }\mathbb{R}\left(\frac{e^{-K(-\lambda +i\omega )}{V}_{\alpha ,i}^{\langle -\lambda +i\omega \rangle }(\tau ,R)}{{(-\lambda +i\omega )}^2}\right)d\omega }\right],\hfill \end{array}$$

(28)

where $V_{\alpha ,i}^{\langle ·\rangle }(\tau ,R)$ is defined in (4) and $\tau =T-t\ge 0$.

Proof. 

Lemma 1 can be utilized to directly implement option pricing.    □

The important benefit of our conditional MGF formula is its direct application to option pricing. The option price is calculated by performing optimized numerical integration once the conditional MGFs are determined. By employing advanced numerical methods, the computational complexity of the integration process is reduced, enabling faster and more precise calculations. This efficiency makes our approach highly suitable for real-time financial applications. This reduction in computational burden also allows for the handling of more complex financial instruments with greater accuracy.

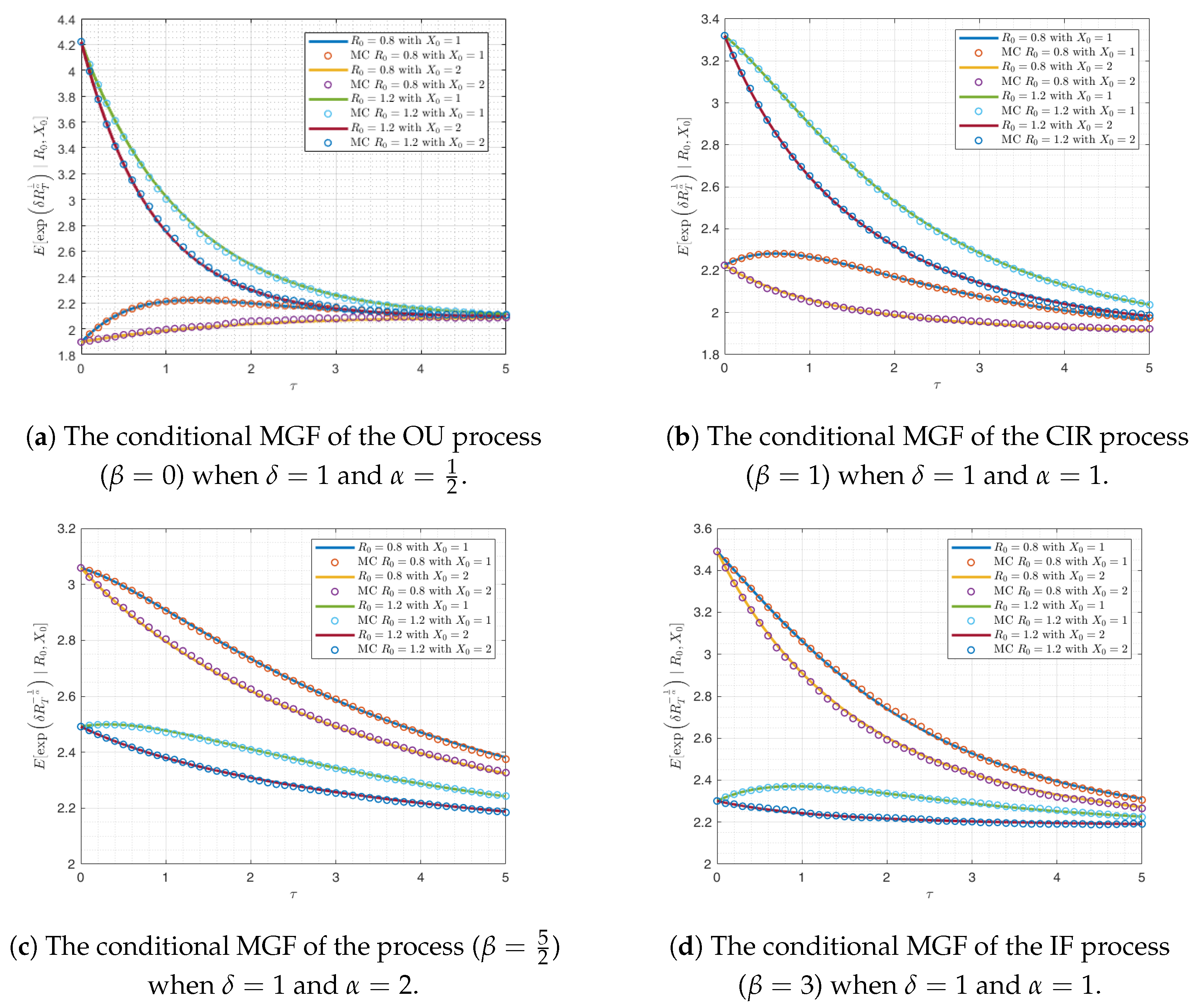
5. Experimental Validations

Let $X_t$ be a homogeneous continuous-time Markov chain defined on a finite state space $\{1,2\}$. The generator matrix of $X_t$, denoted as $Q={\left(q_{ij}\right)}_{2\times 2}$, is defined such that $q_{ij}\ge 0$ if $i\ne j$ and $q_{ii}=-{\sum }_{i\ne j}{q}_{ij}$, for all $i,j\in \{1,2\}$. Assuming that the transition probabilities from a state $i\in \{1,2\}$ at time t toward a state $j\in \{1,2\}$ at time $t+h$ are stationary, we define $P\left(h\right)$ as the matrix of transition probabilities, with $P_{ij}\left(h\right)=\mathbb{P}\left(X_h=j\mid X_0=i\right)$, for all $i,j\in \{1,2\}$. Then, the following relation holds:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{P}_{ij}\left(h\right)}{dh}}=Q_{ij}\end{array}$$

for all $i,j\in \{1,2\}$. Note that this relation implies that $P_{ij}\left(h\right)={\left(e^{Qh}\right)}_{ij}$.

To simulate the discrete Markov chain $\left\{X_k,k=0,1,\dots \right\}$, we define $X_{t_k}:=X_k=X\left(kh\right)$ for $k\ge 0$ as follows:

• Calculate the one-step transition probability matrix, $P\left(h\right)=e^{hQ}$.
• Set the initial state $X_0=i_0$. Generate a uniformly distributed random number $\omega$ on $[0,1]$ to determine the next state according to the following:

  $$\begin{array}{c}\hfill X_k=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\omega \le P_{i_{k}1},\hfill \\ 2,\hfill & \mathrm{if}{P}_{i_{k}1}<\omega \le P_{i_{k}1}+P_{i_{k}2}.\hfill \end{array}\right.\end{array}$$

  Then, update $i_{k+1}=X_{k+1}$.
• Repeat the second step until reaching $k^{*}$ such that $h{k}^{*}$ equals the final time, thus completing the discrete Markov chain $\{X_k,k=0,1,2,\cdots ,k^{*}\}$.

We utilize the EM discretization method directly with the discrete Markov chain $\{X_k,k=0,1,2,\cdots ,k^{*}\}$ to simulate the processes (2) and (3) and approximate the MGF. Let $\widehat{R}$ represent a time-discretized approximation to R, with ${\widehat{R}}_k=\widehat{R}\left(t_k\right),{\widehat{R}}_0=R_{t_0},{\xi }_0=i_0$ and $h=t_{k+1}-t_k$. The EM approximation of (1) is defined by the following:

$$\begin{array}{c}\hfill {\widehat{R}}_{k+1}={\widehat{R}}_k+\kappa \left({\theta }_{X_k}{\widehat{R}}_k^{-(1-\beta )}-{\widehat{R}}_k\right)h+{\sigma }_{X_k}{\widehat{R}}_t^{{\displaystyle \frac{\beta }{2}}}\sqrt{h}{Z}_k\end{array}$$

(29)

where $Z_k$ is the standard normal distribution; see also Algorithm 1.

Next, we validate the closed-from formula for the MGF in Theorem (1) and (2) based on the process (2) and (3), respectively. In this validation, we parameterize the process (2) as follows: $\kappa =0.5,{\theta }_1=1,{\theta }_2=0.5,{\sigma }_1=0.01$, and ${\sigma }_2=0.3$. Similarly, for the process (3), the parameter values are $\kappa =-0.5,{\theta }_1=1,{\theta }_2=0.5,{\sigma }_1=-0.01$, and ${\sigma }_2=-0.3$. MC simulations are implemented to generate 10,000 sample paths of $R_t$, where each path consists of 10,000 time steps over the time interval $[0,5]$. The results of these simulations are illustrated in Figure 1.

Algorithm 1 Simulation of the continuous-time Markov chain and EM approximation

Input: Generator matrix Q, time step h, terminal time T, initial state $i_0$, initial value $R_{t_0}$,    parameters $\kappa$, ${\theta }_{X_k}$, ${\sigma }_{X_k}$ and $\beta$ Output: Simulated discrete Markov chain $\{X_k,k=0,1,\cdots ,k^{*}\}$ and ${\widehat{R}}_k$   1: Calculate the one-step transition probability matrix $P\left(h\right)=e^{hQ}$   2: Set $t_0=0$ and $k=0$   3: Set $X_0=i_0$ and ${\widehat{R}}_0=R_{t_0}$   4: while  $t_k\le T$  do   5:      Generate a uniformly distributed random number $\omega \in [0,1]$   6:      if $\omega \le P_{i_{k}1}$ then   7:          $X_{k+1}=1$   8:      else   9:          $X_{k+1}=2$ 10:      end if 11:      Compute ${\widehat{R}}_{k+1}={\widehat{R}}_k+\kappa \left({\theta }_{X_k}{\widehat{R}}_k^{-(1-\beta )}-{\widehat{R}}_k\right)h+{\sigma }_{X_k}{\widehat{R}}_k^{{\displaystyle \frac{\beta }{2}}}\sqrt{h}{Z}_k$ 12:      Update $i_{k+1}=X_{k+1}$ 13:      Update $t_{k+1}=t_k+h$ 14:      Update $k=k+1$ 15: end while 16: return Simulated discrete Markov chain $\{X_k,k=0,1,\cdots ,k^{*}\}$ and ${\widehat{R}}_k$

In

Table 1. The MADs between our closed-form Formula (4) and MC simulations of the conditional MGF of OU process with parameters $\delta =1$, $\alpha ={\displaystyle \frac{1}{2}}$ and initial value $R_0=0.8$.

${\mathit{X}}_0$	No. of Paths	$\mathit{\tau }$
		1	5	10	15
1	5000	8.756 $\times {10}^{-4}$	2.789 $\times {10}^{-3}$	4.204 $\times {10}^{-3}$	4.041 $\times {10}^{-3}$
	10,000	6.379 $\times {10}^{-4}$	1.596 $\times {10}^{-3}$	2.043 $\times {10}^{-3}$	3.746 $\times {10}^{-3}$
	20,000	4.224 $\times {10}^{-4}$	6.450 $\times {10}^{-4}$	5.622 $\times {10}^{-4}$	2.373 $\times {10}^{-4}$
	40,000	2.652 $\times {10}^{-4}$	8.463 $\times {10}^{-4}$	6.305 $\times {10}^{-4}$	2.466 $\times {10}^{-4}$
2	5000	2.599 $\times {10}^{-3}$	3.562 $\times {10}^{-3}$	8.097 $\times {10}^{-3}$	7.673 $\times {10}^{-3}$
	10,000	5.147 $\times {10}^{-4}$	2.672 $\times {10}^{-3}$	6.019 $\times {10}^{-3}$	4.853 $\times {10}^{-3}$
	20,000	2.780 $\times {10}^{-4}$	1.753 $\times {10}^{-3}$	2.390 $\times {10}^{-3}$	3.165 $\times {10}^{-3}$
	40,000	2.573 $\times {10}^{-4}$	8.578 $\times {10}^{-4}$	1.759 $\times {10}^{-3}$	2.405 $\times {10}^{-3}$

, we present a comparison between a closed-form Formula (4) and Monte Carlo (MC) simulations for the conditional moment-generating function (MGF) of an Ornstein–Uhlenbeck (OU) process. The comparison is quantified by using the mean absolute deviations (MADs). The OU process parameters are set to $\delta =1$, $\alpha ={\displaystyle \frac{1}{2}}$, with an initial value $R_0=0.8$. The table explores two initial states ($X_0=1,2$) and four-time points (τ = 1, 5, 15, and 15). For each combination, MC simulations are run with increasing numbers of paths (5000, $10,000$, $20,000$, and $40,000$) to assess convergence. We can see that the closed-form formulas and the MC simulations provide highly accurate results, thus verifying the formula’s reliability and resilience. Furthermore, the accuracy of the MC simulations improves as the number of paths increases, although this comes at the expense of a longer computing time.

6. Conclusions and Discussion

This work investigates the MGFs for asset price processes that are governed by the NLD-CEV model with regime-switching. The objective of our investigation was to generate closed-form formulations for these MGFs under a variety of parameter conditions and to apply these findings to option pricing. The key contributions of our work are summarized as follows. Firstly, we derived closed-form formulas for the conditional MGFs of the asset price process under the NLD-CEV model with two-state regime-switching. These formulas were developed for two scenarios: when the elasticity parameter $\beta$ is within the range $(0,2]$ and when it is greater than 2. Figure 1 demonstrates that the results obtained from the proposed formulas completely match those from MC simulations, while also requiring significantly less computational time.

This significant achievement provides a robust framework for comprehending the behavior of asset prices under different market conditions and regimes, thus enhancing the understanding of financial market dynamics. Secondly, we applied the derived MGFs to the practical problem of option pricing using previously established methods. This approach not only demonstrated the applicability of our theoretical results but also showcased how MGFs can facilitate efficient and accurate option pricing. By transforming complex SDEs into more manageable forms, MGFs enable the derivation of closed-form solutions for derivative prices. This is a crucial advance as it simplifies the complex mathematical procedures involved in pricing financial derivatives. Thirdly, we validated our closed-form formulas through extensive numerical simulations. Utilizing the EM discretization method, we simulated the processes and approximated the MGFs. The validation involved generating multiple sample paths and time steps to ensure the robustness and accuracy of our results. These simulations confirmed that our theoretical findings are consistent with empirical observations, reinforcing our models’ reliability and practical relevance.

The findings of this study have substantial implications for financial mathematics, particularly in derivative pricing. The ability to derive closed-form MGFs under the NLD-CEV model with regime-switching offers enhanced accuracy, efficiency, and a more precise representation of asset price distributions, reducing reliance on computationally intensive numerical methods. The flexibility in modeling market conditions allows for better capture of dynamic market behaviors, making the model applicable across various conditions. Additionally, the broader applicability of our findings extends beyond European option pricing to other financial derivatives, benefiting a wider audience. Future research could explore multi-state regime-switching processes and the impact of different elasticity parameters, further enhancing the robustness and applicability of financial models.