On Spatial Systems of Bars Spherically Jointed at Their Ends and Having One Common End
Abstract
:1. Introduction
- -
- -
- -
- The equations used for the study. Generally, the authors use the equations of mechanics and/or strength of materials (for simple systems) [16,17], equations of multibody systems (whose disadvantage is the great number of unknowns) [18,19], Lagrange’s equations (for mobile systems with a few degrees of freedom) [20,21], or screw coordinates (which reduce the order of the matrices) [22].
- -
- Goal of the study. In most cases this is to determine the deformation of the system of bars and their motion.
- -
- The absence of a general method of study and, consequently, the use of particular methods, which are good for certain systems. Using a particular method adapted for a certain system, one may determine the unknowns of the problem.
- -
- Complicated forms for the equations. In these situations, it is known [22] that the numerical methods have small radii of convergence; that is, one has to know a good approximation of the exact solutions. We used solutions instead of solution because such a system may have more than one solution.
- -
- The situation of bars with fabrication errors (some bars are longer and some bars are shorter in our study).
2. Mathematical Model
3. Optimizations
- (i)
- the minimum displacement of the point along the direction; that is, one asks for the minimization of ;
- (ii)
- the minimum displacement of the point along the direction; that is, one asks for the minimization of ;
- (iii)
- the minimum displacement of the point along the direction; that is, one asks for the minimization of ;
- (iv)
- the minimum displacement of the point ; that is, one asks for the minimization of ;
- (v)
- the minimum tension in a certain bar; that is, one asks for the minimization of .
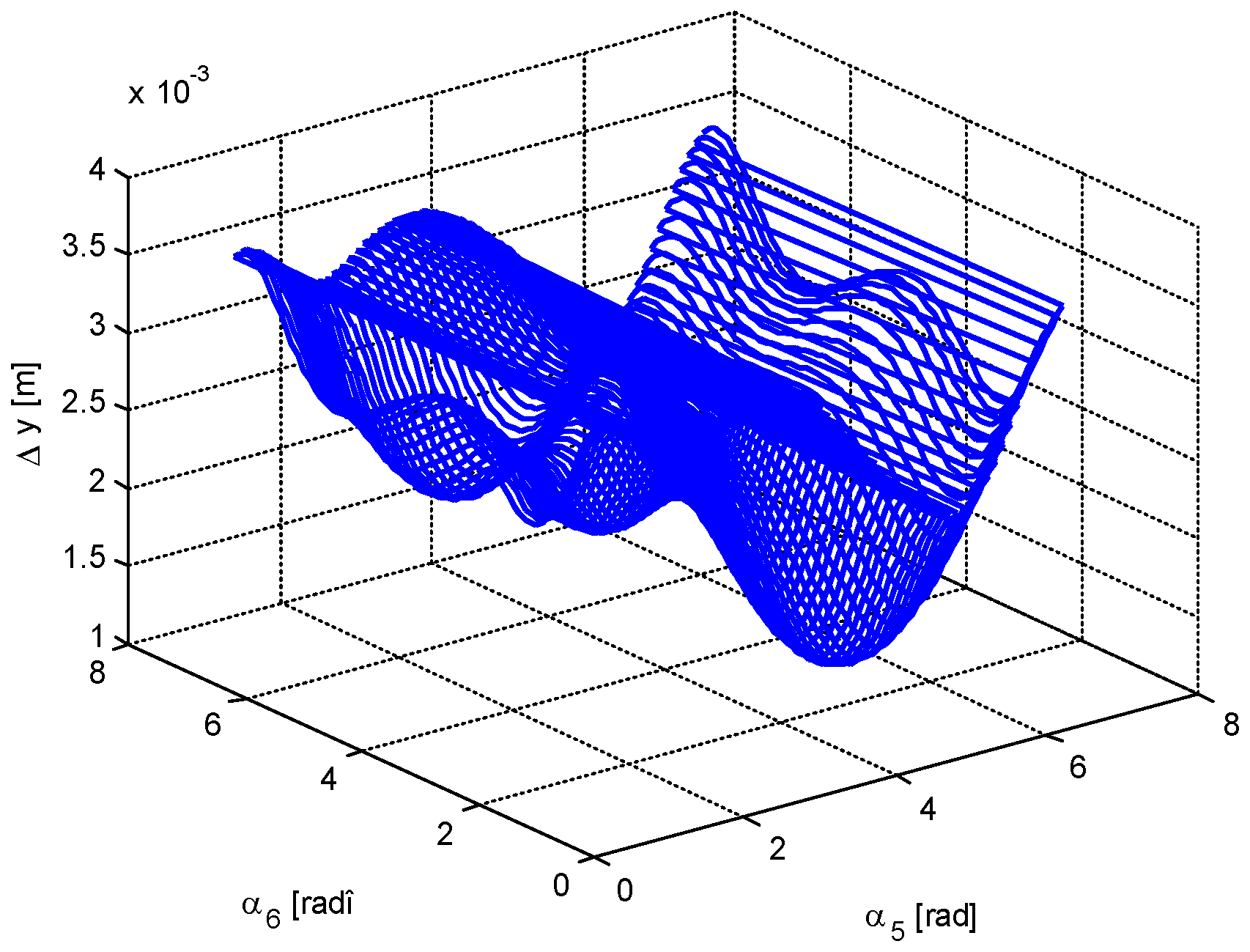
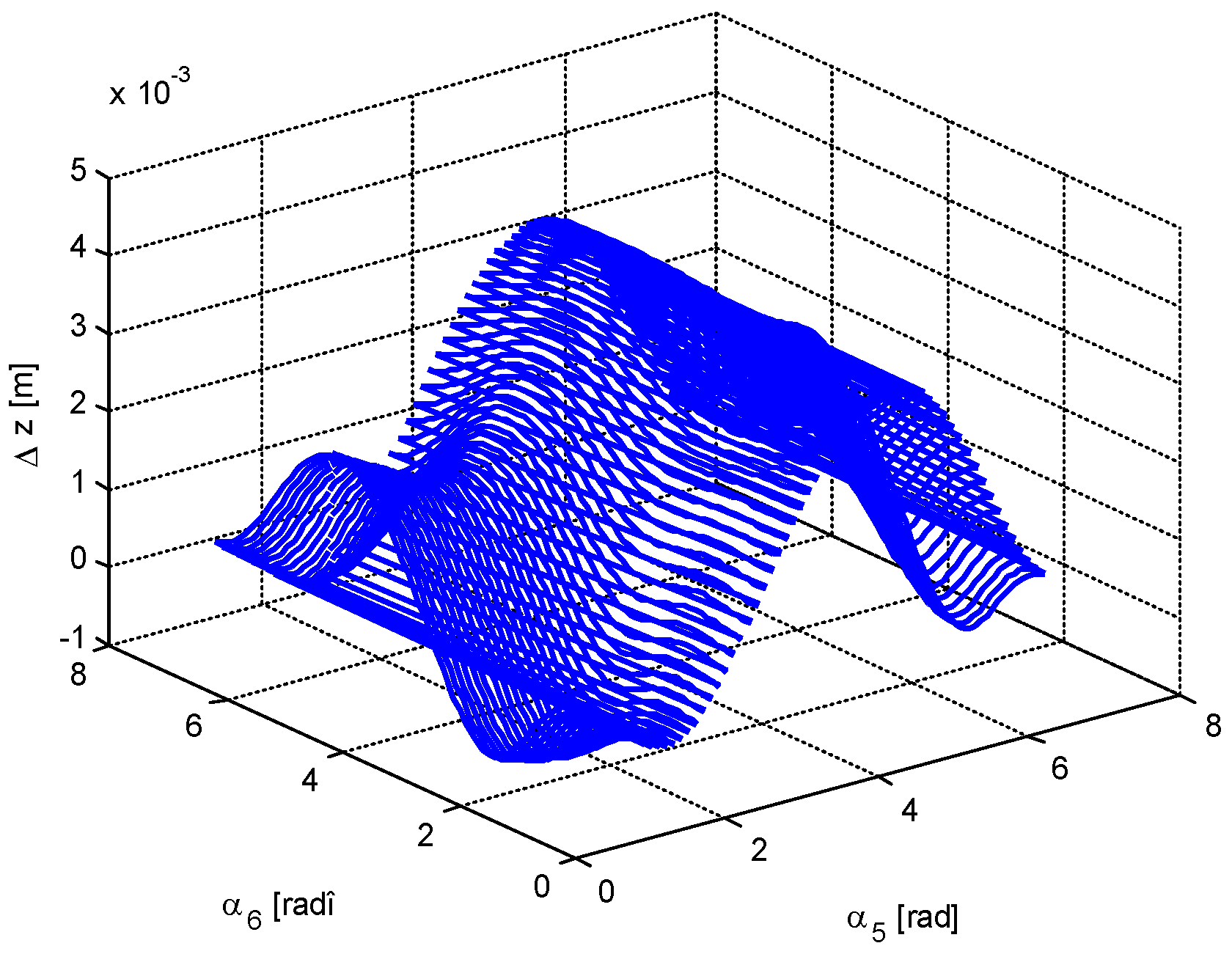
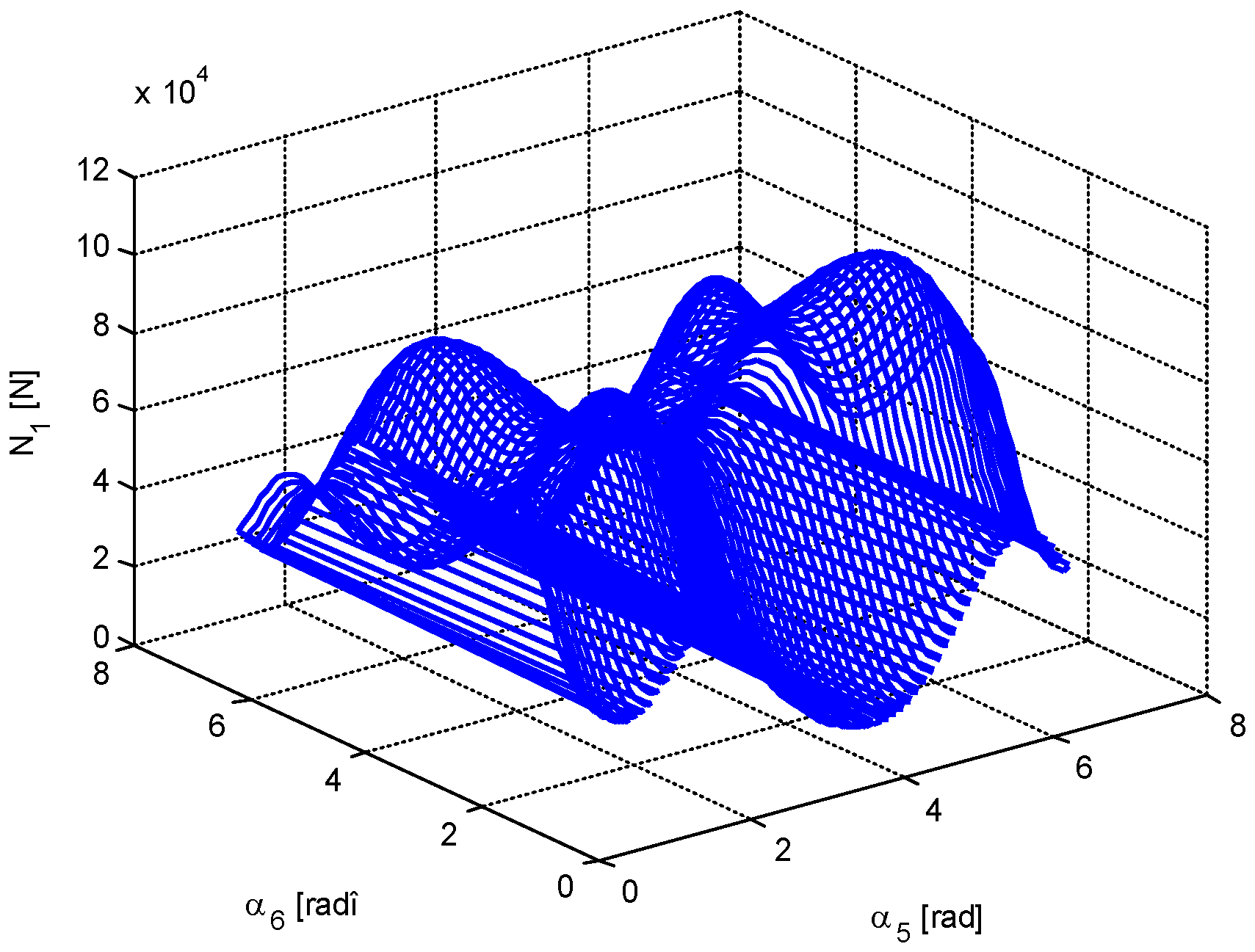
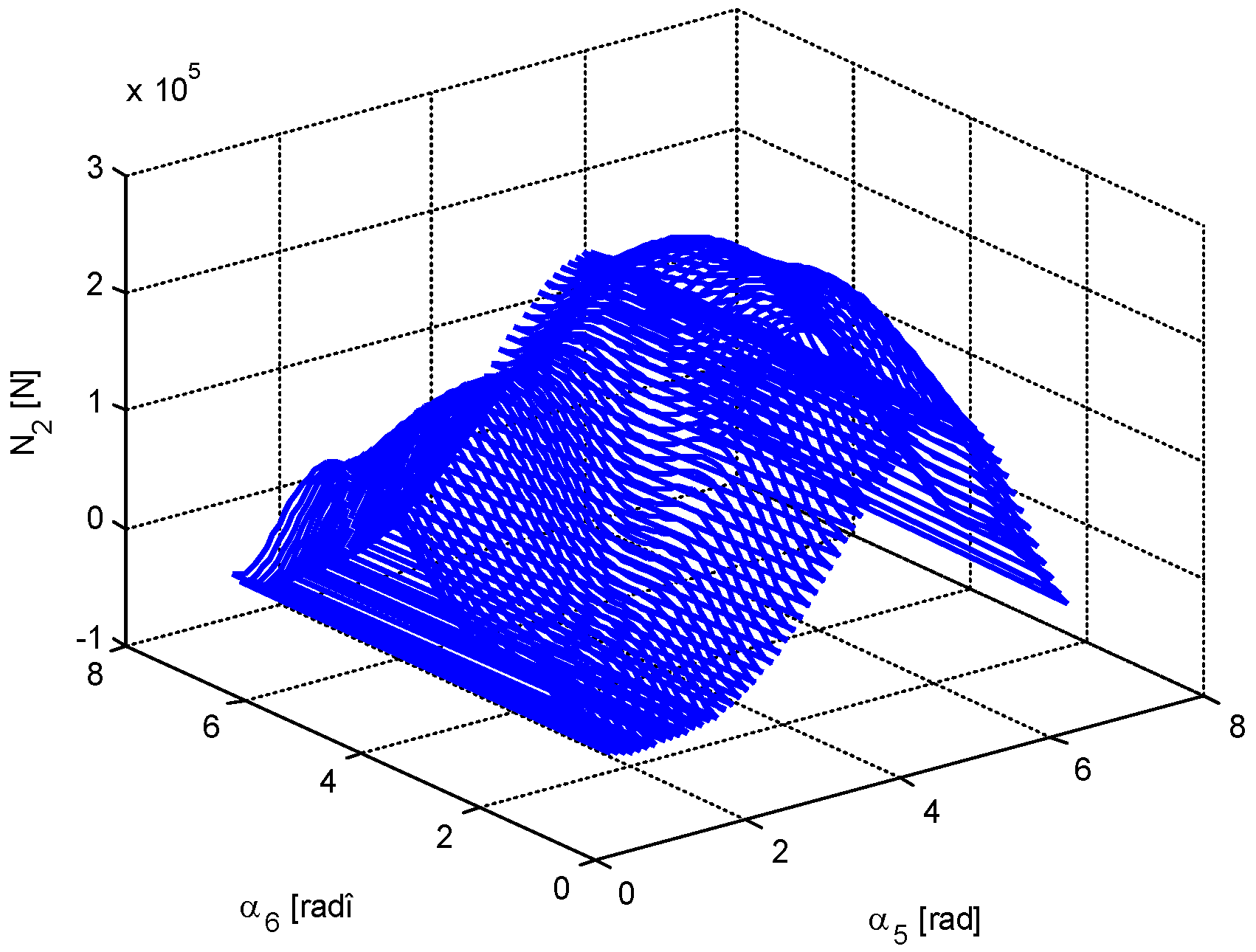
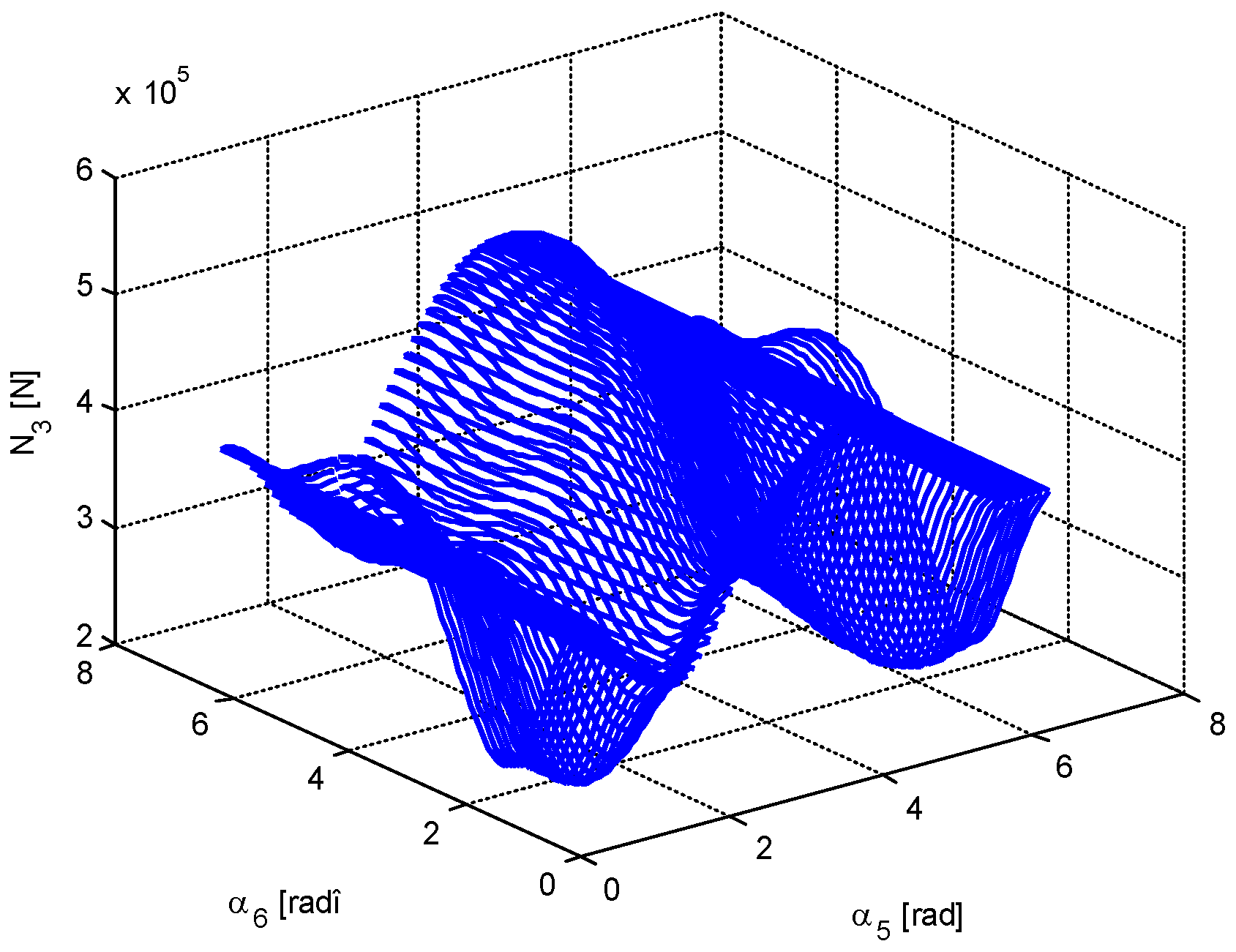
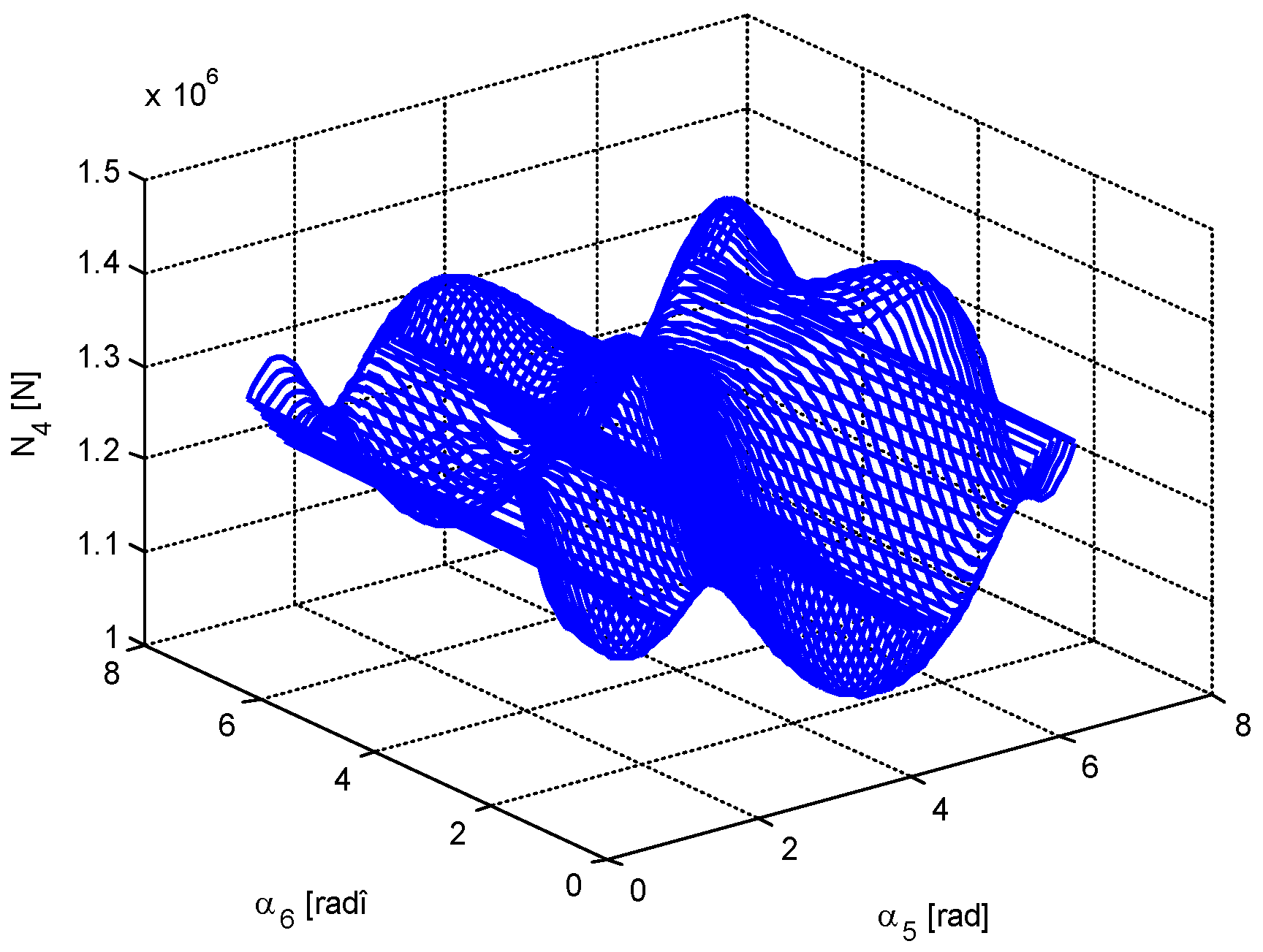
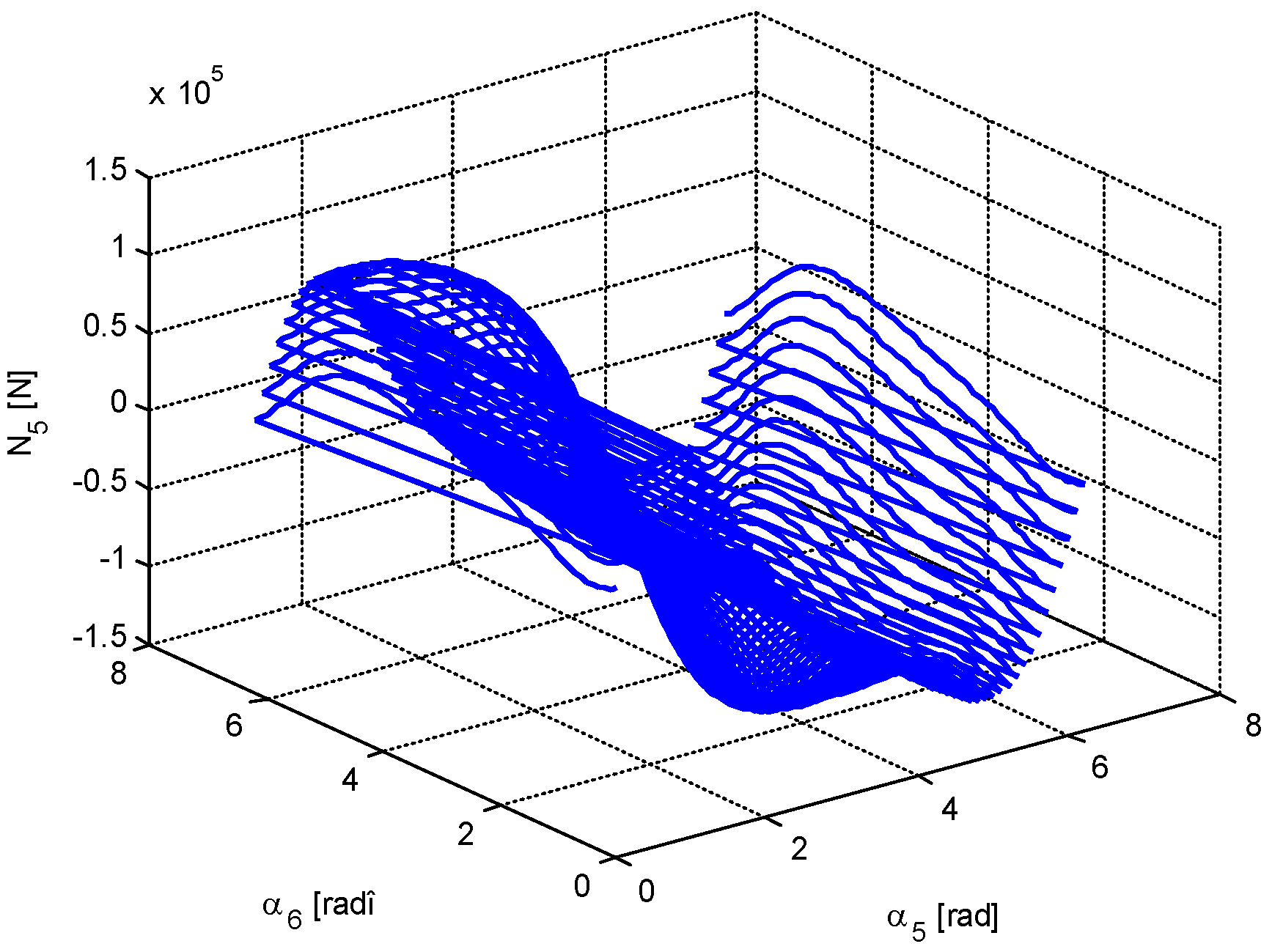
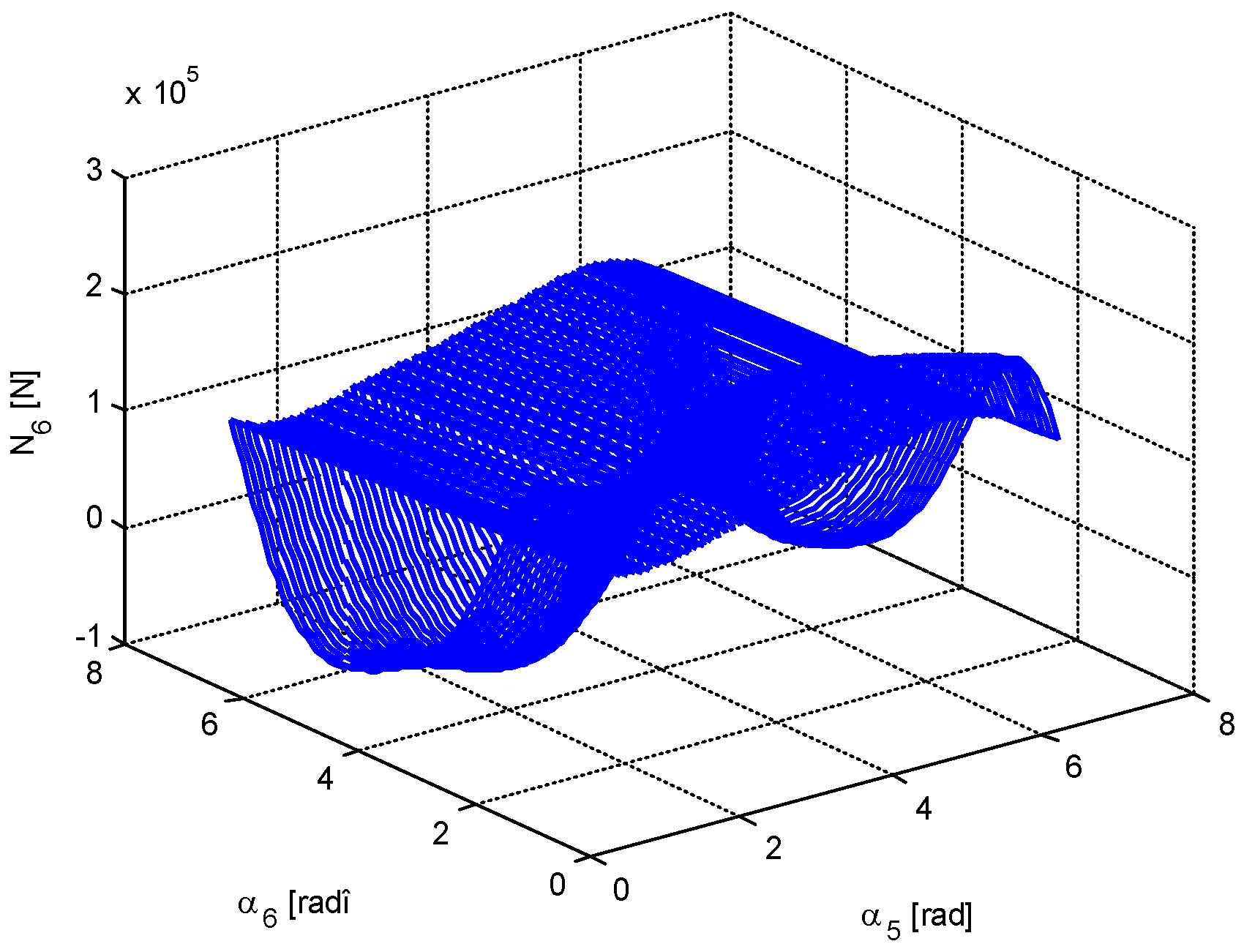
4. Numerical Simulation
- -
- The minimum value of the force in bar 5 is very close to 0; that is, there are two positions in which the bar 5 is useless. The same conclusion, but for one position, is valid for bar 6.
- -
- It is possible to obtain a very small value for the force in bar 1; that is, in a certain configuration, bar 1 may be eliminated.
- -
- There are not equal numbers of positions for which different parameters are minimized (there are one, two, three, or four positions of minimum value for a certain parameter).
- -
- Based on a certain criterion, one obtains some values for the optimization parameters, values which do not coincide to those obtained using another optimization criterion.
- -
- The displacements may be positive or negative. There is no rule to determine the sign of a certain displacement.
- -
- The forces in the bars may be also positive and negative and, again, there is no rule for the determination of the sign.
- -
- Generally speaking, the diagrams of variation for different parameters cannot be obtained by analytical calculation.
- -
- The calculation is valid only for small deformations of the bars (the statement holds true for the cases considered in this paper).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Răcășan, V.; Pandrea, N.; Stănescu, N.-D. On the rigid hung by elastic bars subjected to axial forces. In Proceedings of the 29th International Congress on Sound and Vibration, Prague, Czech Republic, 9–13 July 2023. [Google Scholar]
- Hwang, Y.-L. Dynamic recursive decoupling method for closed-loop flexible mechanical systems. Int. J. Non-Linear Mech. 2006, 41, 1181–1190. [Google Scholar] [CrossRef]
- Marques, F.; Roupa, I.; Silva, M.T.; Flores, P.; Lankarani, H.M. Examination and comparison of different methods to model closed loop kinematic chains using Lagrangian formulation with cut joint, clearance joint constraint and elastic joint approaches. Mech. Mach. Theory 2021, 160, 104294. [Google Scholar] [CrossRef]
- Sorgonà, O.; Cirelli, M.; Giannini, O.; Verotti, M. Comparison of flexibility models for the multibody simulation of compliant mechanisms. Multibody Syst. Dyn. 2024; online. [Google Scholar]
- Chen, J.; Chen, Q.; Liang, D.; Mo, J. Solution of geometrico-static problems and motion experiments for a suspended under-constrained parallel mechanism driven by two flexible cables. J. Mech. Sci. Technol. 2024, 38, 4365–4376. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J. Jerk distribution of a 6-3 Gough-Stewart platform. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2013, 217, 77–84. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, Y.; Li, B.; Wu, M.; Yu, J.; Chen, H. Position-Singularity Analysis of a Class of the 3/6-Gough-Stewart Manipulators based on Singularity-Equivalent-Mechanism. Int. J. Adv. Robot. Syst. 2012, 9, 1–9. [Google Scholar] [CrossRef]
- Ding, X.; Isaksson, M. Quantitative analysis of decoupling and spatial isotropy of a generalised rotation-symmetric 6-DOF Stewart platform. Mech. Mach. Theory 2023, 180, 105156. [Google Scholar] [CrossRef]
- Šika, Z.; Krivošej, J.; Vyhlídal, T. Three dimensional delayed resonator of Stewart platform type for entire absorption of fully spatial vibration. J. Sound Vib. 2024, 571, 118154. [Google Scholar] [CrossRef]
- Hajimirzaallan, H.; Ferraresi, C.; Moosavi, H.; Massah, M. An analytical method for the inverse dynamic analysis of the Stewart platform with asymmetric-adjustable payload. Proc. Int. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2013, 227, 162–171. [Google Scholar] [CrossRef]
- Leonov, G.A.; Zegzhda, S.A.; Zuev, S.M.; Ershov, B.A.; Kazunin, D.V.; Kostygova, D.M.; Kuznetsov, N.V.; Tovstik, P.E.; Tovstik, T.P.; Yushkov, M.P. Dynamics and Control of the Stewart platform. Dokl. Phys. 2014, 59, 405–410. [Google Scholar] [CrossRef]
- Korkealaakso, P.; Mikkola, A.; Rantalainen, T.; Rouvinen, A. Description of joint constraints in the floating frame of reference formulation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2009, 223, 133–145. [Google Scholar] [CrossRef]
- Bouzgarrou, B.C.; Ray, P.; Gogu, G. New approach for dynamic modeling of flexible manipulators. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2005, 219, 285–298. [Google Scholar]
- Huang, Z.; Zhao, Y.; Liu, J. Kinetostatic Analysis of 4-R (CRR) Parallel Manipulator with Overconstraints via Reciprocal-Screw Theory. Adv. Mech. Eng. 2010, 2, 404960. [Google Scholar] [CrossRef]
- Stan, A.-F.; Pandrea, N.; Stănescu, N.-D.; Munteanu, L.; Chiroiu, V. On the vibrations of a Rigid Solid Hung by Kinematic Chains. Symmetry 2022, 14, 770. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, H.; Wang, K.; Fang, Y.; Ma, C. Analytical analysis of vibration isolation characteristics of quasi-zero stiffness suspension backpack. Int. J. Dyn. Control, 2024; online. [Google Scholar]
- Chen, W.; Wang, S.; Li, J.; Lin, C.; Yang, Y.; Ren, A.; Li, W.; Zhao, X.; Zhang, W.; Guo, W.; et al. An ADRC-based triple-loop control strategy of ship-mounted Stewart platform for six-DOF wave compensation. Mech. Mach. Theory 2023, 184, 105289. [Google Scholar] [CrossRef]
- Yang, S.; Xu, P.; Li, B. Design and rigid-flexible dynamic analysis of a morphing wing eight-bar mechanism. Nonlinear Dyn. 2024, 112, 15025–15060. [Google Scholar] [CrossRef]
- Chen, G.; Rui, X.; Abbas, L.K.; Wang, G.; Yang, F.; Zhu, W. A novel method for the dynamic modeling of Stewart parallel mechanism. Mech. Mach. Theory 2018, 126, 397–412. [Google Scholar] [CrossRef]
- Xu, A.; Xu, Z.; Zhang, H.; He, S.; Wang, L. Novel coarse and fine stage parallel vibration isolation pointing platform for space optics payload. Mech. Syst. Signal Process. 2024, 213, 111359. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiao, H.; Yang, G.; Guo, H.; Liu, R.; Deng, Z. Study on transient dynamics of the pyrotechnic-driven large flexible expansion mechanism. Nonlinear Dyn. 2024, 112, 15917–15932. [Google Scholar] [CrossRef]
- Pandrea, N. Elements of Mechanics of Rigid Solids in Plűckerian Coordinates; The Romanian Academy Publishing House: Bucharest, Romania, 2000. [Google Scholar]
- Răcășan, V.; Stănescu, N.-D. Minimization of the small deformations for a planar system of concurrent bars jointed at their ends. In Proceedings of the 30th International Congress on Sound and Vibration, Amsterdam, The Netherlands, 8–11 July 2024. [Google Scholar]
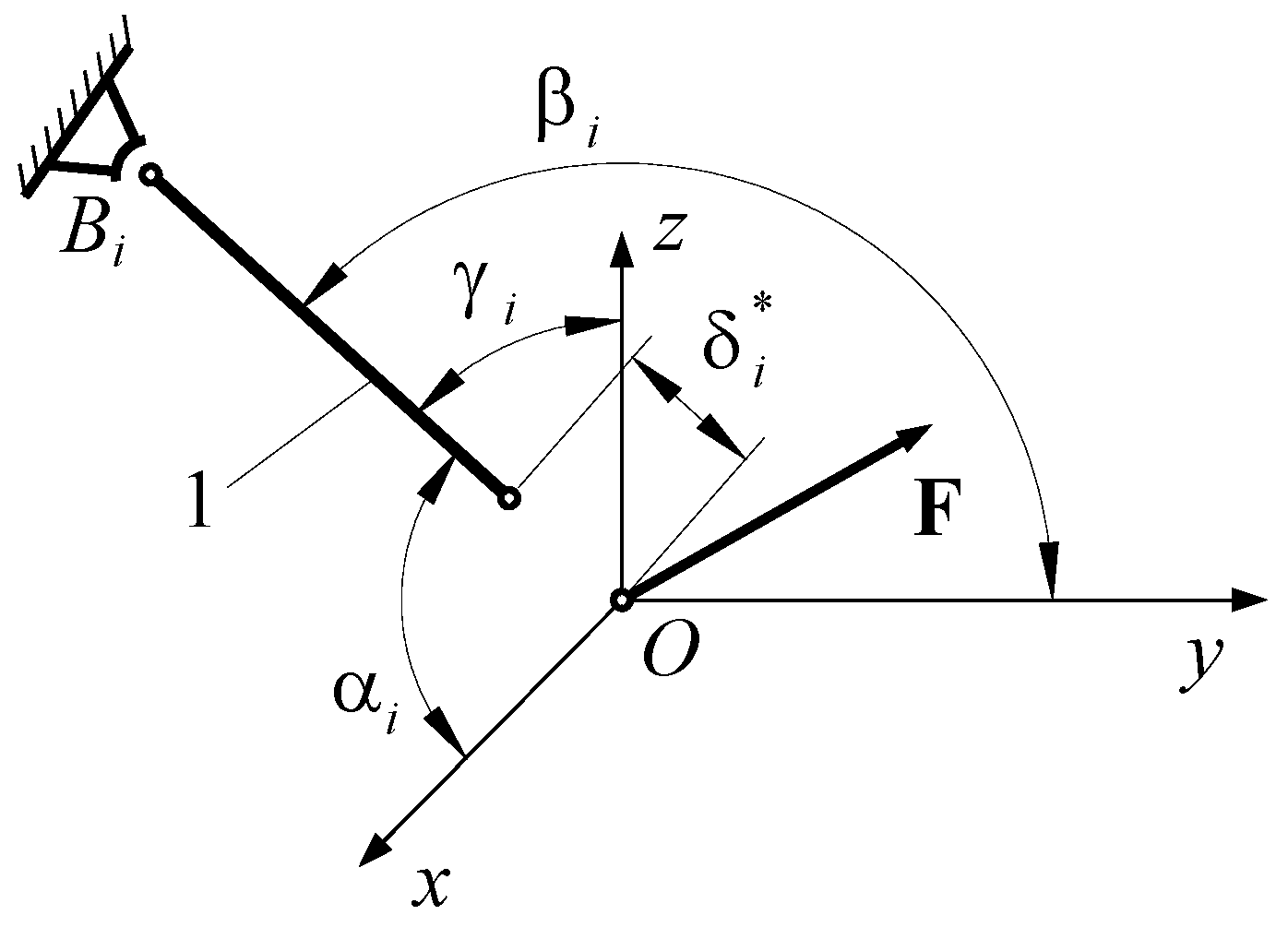

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Răcășan, V.; Stănescu, N.-D. On Spatial Systems of Bars Spherically Jointed at Their Ends and Having One Common End. Mathematics 2024, 12, 2680. https://doi.org/10.3390/math12172680
Răcășan V, Stănescu N-D. On Spatial Systems of Bars Spherically Jointed at Their Ends and Having One Common End. Mathematics. 2024; 12(17):2680. https://doi.org/10.3390/math12172680
Chicago/Turabian StyleRăcășan, Valentin, and Nicolae-Doru Stănescu. 2024. "On Spatial Systems of Bars Spherically Jointed at Their Ends and Having One Common End" Mathematics 12, no. 17: 2680. https://doi.org/10.3390/math12172680




