Dynamics of Activation and Regulation of the Immune Response to Attack by Viral Pathogens Using Mathematical Modeling

Abstract

In this paper, a mathematical model is developed to simulate the activation of regulatory T lymphocytes dynamics. The model considers the adaptive immune response and consists of epithelial cells, infected cells, free virus particles, helper and cytotoxic T lymphocytes, B lymphocytes, and regulatory T lymphocytes. A mathematical analysis was carried out to discuss the conditions of existence and stability of equilibrium solutions in terms of the basic reproductive number. In addition, the definitions and properties necessary to preserve the positivity and stability of the model are shown. The precision of these mathematical models can be affected by numerous sources of uncertainty, partly due to the balance between the complexity of the model and its predictive capacity to depict the biological process accurately. Nevertheless, these models can provide remarkably perspectives on the dynamics of infection and assist in identification specific immunological traits that improve our comprehension of immune mechanisms. The theoretical results are validated by numerical simulations using data reported in the literature. The construction, analysis, and simulation of the developed models demonstrate that the increased induced regulatory T lymphocytes effectively suppress the inflammatory response in contrast to similar cells at lower contents, playing a key role in maintaining self-tolerance and immune homeostasis.

1. Introduction

In December 2019, an outbreak of coronavirus pneumonia (COVID-19) was reported in Wuhan, China [1,2,3,4,5], showing on 13 April 2023 more than 761 million confirmed cases and more than 7 million deaths worldwide, due to severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), which is an enveloped, unsegmented, positive-sense RNA virus belonging to the genus betacoronavirus [6,7].

SARS-CoV-2 has undergone more than ten thousand unique mutations recorded compared to the reference genome [8,9]. The rapid spread and global transmission of COVID-19 provides the virus with substantial opportunities for the continued mutation of SARS-CoV-2 that generates multiple variants, but most of them have the same features [10,11,12,13,14,15].

Taking into account the global emergence evidenced [16], it is necessary to build in-host mathematical models involving the most recent advances in the knowledge of the immune response to the virus, showing in detail the interaction among SARS-CoV-2 with the immune response.

It should be noted that even in the case of the non-productive interaction of the virus with the cell, SARS-CoV-2 signaling can regulate the cellular activity, and this leads us to talk about the infection of T lymphocytes with SARS-CoV-2 [17,18,19] since this is accompanied by significant changes in the functioning of the immune system and its potential ability to infect T lymphocytes [18,20].

The regulatory T lymphocytes (Tregs) subpopulation plays a key role in the maintenance of self-tolerance and immune homeostasis. Natural Tregs (nTregs) mature in the thymus, and their primary task is to suppress the immune response to self-antigens, whereas inducible Tregs (iTregs) are formed in the later stages of any immune response, and they are designed to limit excessive inflammation, thus preventing tissue damage by products.

Several studies point to Tregs lymphocytes as a possible target for SARS-CoV-2 [20,21]. Therefore, this paper presents a new mathematical model of Tregs lymphocytes activation, which shows that the expansion of induced Tregs lymphocytes effectively suppresses the inflammatory response, playing a key role in maintaining self-tolerance and immune homeostasis. Furthermore, a new contribution is demonstrated, focusing on mathematical models representing infection within the human host, in which the existence and stability conditions for equilibrium solutions in terms of the basic reproductive number are established. The theoretical results are validated by numerical simulations using data reported in the literature.

The rest of the study is organized as follows: Section 2 presents the mathematical model, while Section 3 focuses on the mathematical analysis of the model and the discussion of the numerical results. Section 4 presents the conclusions drawn from the main results obtained and, finally, Appendix A, Appendix B and Appendix C describes the mathematical context related to the study problem.

2. Methods

Model

In this section, we present the mathematical modeling related to the activation of the immune system, variables and parameters in the dynamics of viral infection, and cellular immune response to SARS-CoV-2 virus. The main consideration is the activation of regulatory T lymphocytes leading to the homeostasis of the organism. The initial dynamics of the problem is represented by System (1), for which quotients are incorporated to control the maximal stimulus of infected cells (I) on Helper T lymphocytes (H), thus evidencing a decrease in infected cells.

On the other hand, where referring to an instant t, $E=E\left(t\right)$ is the number of epithelial cells (susceptible) [cells], $I=I\left(t\right)$ is the number of infected cells [cells] activated by the virus to initiate viral replication, and $V=V\left(t\right)$ is the number of free viral particles $[copies/ml]$. There is a presentation of previously phagocytosed antigens by cells of the reticuloendothelial system to specific H lymphocytes, which multiply and achieve clonal expansion. These Helper T lymphocytes release cytokines that direct a cellular and humoral response for the elimination of SARS-CoV-2 [22].

At least 20 different antigens have been identified among the virus proteins; however, approximately one-fifth are capable of generating an effective cellular and neutralizing the antibody response [23,24].

In addition, the activation of cytotoxic T lymphocytes (C) results in their clonal expansion and subsequent targeting of infected cells to induce programmed cell death or apoptosis. This process halts the release of new virions and eliminates existing virions within the infected cell (I), thus preventing their release into the extracellular environment. Furthermore, the activation of B lymphocytes leads to the production and secretion of antibodies that block viral entry into cells and enhance the virus’s elimination through phagocytosis. While both immune responses are crucial for controlling the infection, the cellular response is considered more decisive due to the strictly intracellular nature of the viral replication [25]. Thus, the described biological behavior is modeled in System (1) using a set of ordinary differential equations (ODEs):

$$\left\{\begin{array}{c}{E}^{\prime }=g_E-\left(d_E+{\tau }_E{\displaystyle \frac{V}{V+{\zeta }_{VE}}}\right)E,\hfill \\ I^{\prime }={\tau }_E{\displaystyle \frac{VE}{V+{\zeta }_{VE}}}-\left(d_I+{\tau }_I{\displaystyle \frac{C}{C+{\zeta }_{CI}}}\right)I,\hfill \\ V^{\prime }=\nu I-\left(d_V+{\tau }_V{\displaystyle \frac{B}{B+{\zeta }_{BV}}}\right)V,\hfill \\ H^{\prime }=g_H-\left(d_H-{\tau }_H{\displaystyle \frac{I}{I+{\zeta }_{IH}}}\right)H,\hfill \\ C^{\prime }=g_C-\left(d_C-{\tau }_C{\displaystyle \frac{H}{H+{\zeta }_{HC}}}\right)C,\hfill \\ B^{\prime }=g_B-\left(d_B-{\tau }_B{\displaystyle \frac{H}{H+{\zeta }_{HB}}}\right)B.\hfill \end{array}\right.$$

(1)

The definitions of the initial model variables and parameters, along with their biological interpretations, are given in

Table 1. Description of the variables and parameters of System (1).

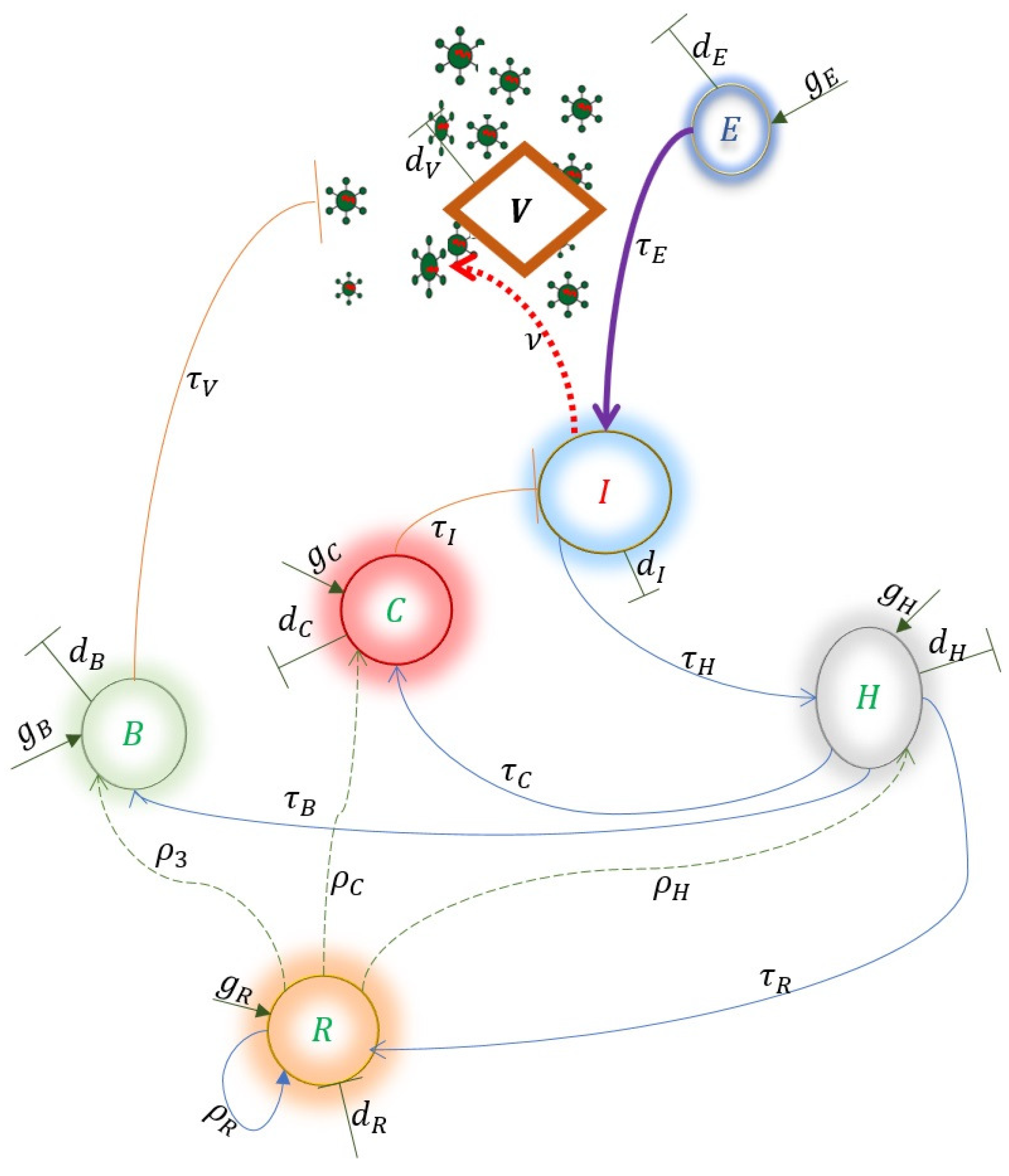
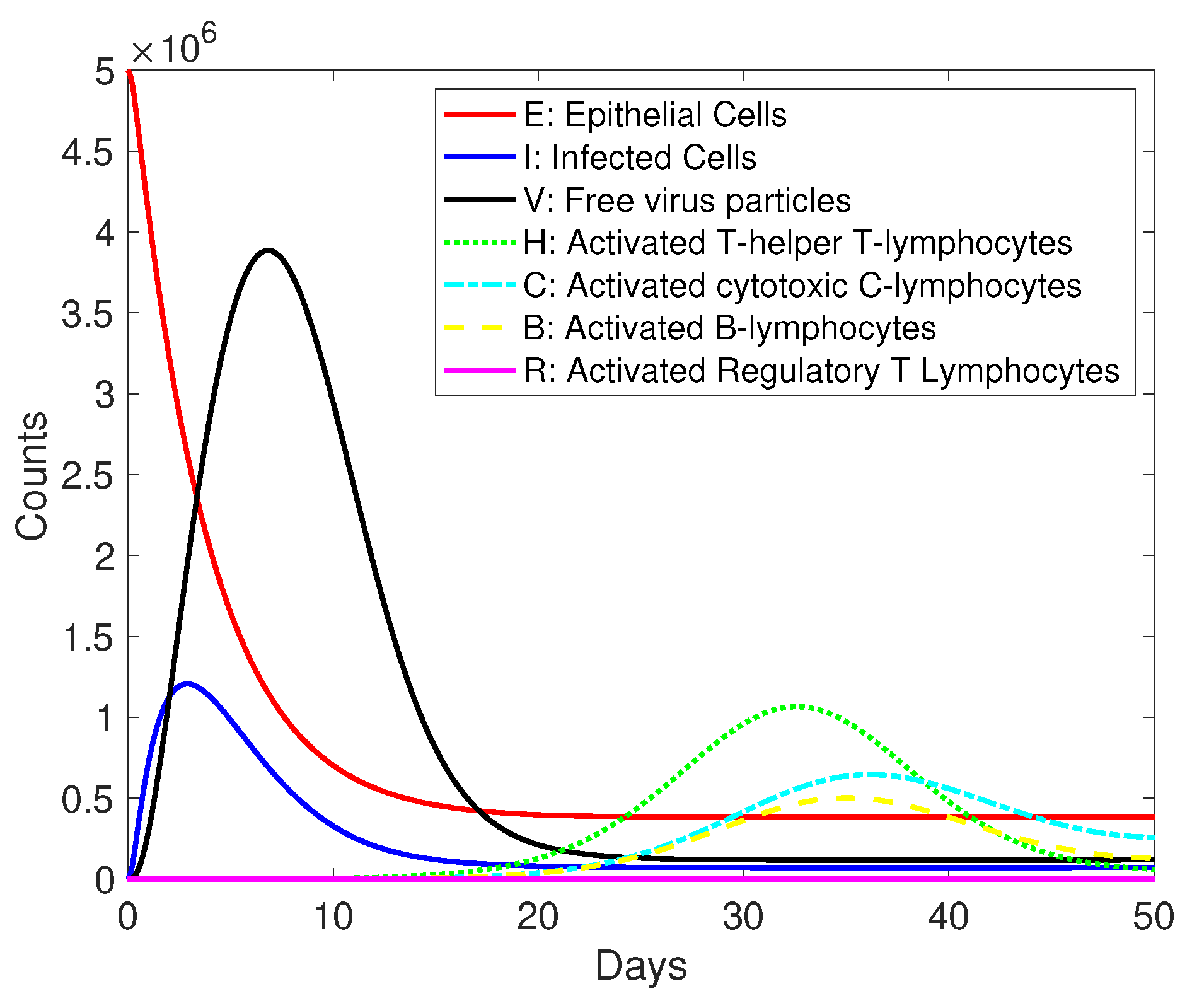
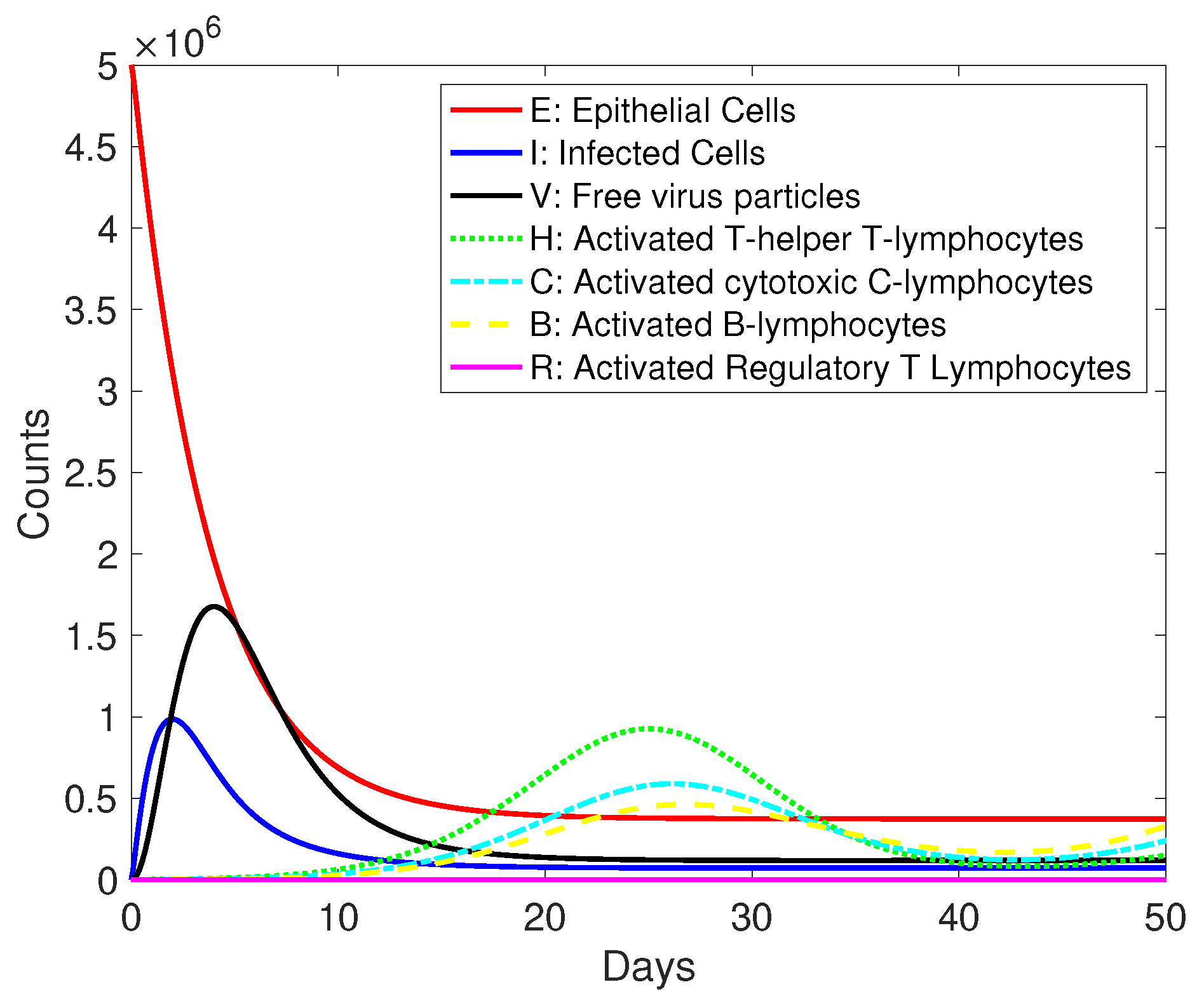
Variables	Description
E	Epithelial cells
I	Infected cells
V	Free viral particles
H	Helper T lymphocytes
C	Cytotoxic T lymphocytes
B	B lymphocytes
Parameters	Description
$d_E$	Epithelial cell death rates
$d_I$	Infected cell death rates
$d_V$	Degradation rate of free viral particles
$d_H$	Helper T lymphocytes death rate
$d_C$	Cytotoxic T lymphocytes death rate
$d_B$	B lymphocytes death rate
$g_E$	Epithelial cell generation rate
$g_H$	Helper T lymphocytes production rate
$g_C$	Cytotoxic T lymphocytes production rate
$g_B$	B lymphocytes production rate
$\nu$	Replication rate of viral particles free of infected cells
${\tau }_E$	Probability of epithelial cell infection per viral particle
${\tau }_I$	Lysis effect on infected cells
${\tau }_V$	Neutralization effect on free viral particles
${\tau }_H$	Activation effect on helper T lymphocytes
${\tau }_C$	Activation effect on cytotoxic T lymphocytes
${\tau }_B$	Activation effect on B lymphocytes
${\zeta }_{VE}$	Amount of virus at which half of the maximum infection rate is reached.
${\zeta }_{CI}$	Number of cytotoxic T lymphocytes at which half of the maximum clearance rate is reached
${\zeta }_{BV}$	Number of B lymphocytes at which half of the maximum neutralization rate is achieved.
${\zeta }_{IH}$	Number of infected cells at which half of the maximum activation rate is reached
${\zeta }_{HC}$	Number of helper T lymphocytes at which half of the maximum proliferation rate is reached
${\zeta }_{HB}$	Number of helper T lymphocytes at which half of the maximum proliferation rate is reached

.

Since maintaining self-tolerance and immune homeostasis requires effective suppression of the inflammatory response against similar cells with lower content, the activation of regulatory T lymphocytes (R), an important subpopulation of T cells that exert immunosuppressive effects is considered.

Recent studies have shown that the number of R lymphocytes is significantly reduced in patients with COVID-19, affecting several aspects, such as weakening the effect of inflammatory inhibition, causing an imbalance in the Treg/Th17 ratio, and increasing the risk of respiratory failure [8,17,26,27].

A better understanding of the role of R lymphocytes will allow advances in symptom management and the possibility of delaying or preventing disease progression in patients with COVID-19. These cells are made up of several subpopulations of T lymphocytes delimited by their expression of markers (CD4+, CD8+, etc.), ensuring immune homeostasis by substantially suppressing CD4+ cells, as well as playing a role in reducing the immune response after the infection has ended [17,27]. Therefore, the behavior of regulatory T lymphocytes is modeled within a robust mathematical framework that is both predictive and explanatory. The importance of including this variable in System (1) is described as follows:

• Helper and cytotoxic T lymphocytes and B lymphocytes curves do not achieve a sufficiently rapid decline in the simulations. In the immune response to infection, there is a more rapid decline in the number of active lymphocytes after antigen clearance is achieved.
• There is an over-dependence on cell turnover parameters $d_H,d_C$ and $d_B$. It is not possible to adjust cell turnover parameters to achieve a further decline in lymphocyte populations after infection. We have the restriction that ${\tau }_H,{\tau }_C$ and ${\tau }_B$ do not exceed deaths to avoid explosive growth.

Therefore, it is considered necessary to include an additional variable reflecting the role of regulatory T lymphocytes in the regulation of the immune system as shown in System (2):

$$\left\{\begin{array}{c}{E}^{\prime }=g_E-\left(d_E+{\tau }_E{\displaystyle \frac{V}{V+{\zeta }_{VE}}}\right)E,\hfill \\ I^{\prime }={\tau }_E{\displaystyle \frac{VE}{V+{\zeta }_{VE}}}-\left(d_I+{\tau }_I{\displaystyle \frac{C}{C+{\zeta }_{CI}}}\right)I,\hfill \\ V^{\prime }=\nu I-\left(d_V+{\tau }_V{\displaystyle \frac{B}{B+{\zeta }_{BV}}}\right)V,\hfill \\ H^{\prime }=g_H-\left(d_H-\alpha {\displaystyle \frac{I}{I+d}}+{\rho }_{H}R\right)H,\hfill \\ C^{\prime }=g_C-\left(d_C-\tau {\displaystyle \frac{H}{H+l}}+{\rho }_{C}R\right)C,\hfill \\ B^{\prime }=g_B-\left(d_B-\beta {\displaystyle \frac{H}{H+l}}+{\rho }_{B}R\right)B,\hfill \\ R^{\prime }=g_R-(d_R-{\tau }_{R}H)R,\hfill \end{array}\right.$$

(2)

where parameters ${\rho }_H$, ${\rho }_C$, and ${\rho }_B$ are numbers of R lymphocytes that inhibit the effect of other lymphocytes per unit of time.

Note that in System (3), quotients are included in the state variables $H,C,B$ and R to control the number of lymphocytes at which the maximum rate of each of their various effector functions is reached. This behavior is illustrated in a schematic diagram shown in Figure 1:

$$\left\{\begin{array}{c}{E}^{\prime }=g_E-\left(d_E+{\tau }_E{\displaystyle \frac{V}{V+{\zeta }_{VE}}}\right)E,\hfill \\ I^{\prime }={\tau }_E{\displaystyle \frac{VE}{V+{\zeta }_{VE}}}-\left(d_I+{\tau }_I{\displaystyle \frac{C}{C+{\zeta }_{CI}}}\right)I,\hfill \\ V^{\prime }=\nu I-\left(d_V+{\tau }_V{\displaystyle \frac{B}{B+{\zeta }_{BV}}}\right)V,\hfill \\ H^{\prime }=g_H-\left(d_H-{\tau }_H{\displaystyle \frac{I}{I+{\zeta }_{IH}}}+{\rho }_H{\displaystyle \frac{R}{R+{\zeta }_{RH}}}\right)H,\hfill \\ C^{\prime }=g_C-\left(d_C-{\tau }_C{\displaystyle \frac{H}{H+{\zeta }_{HC}}}+{\rho }_C{\displaystyle \frac{R}{R+{\zeta }_{RC}}}\right)C,\hfill \\ B^{\prime }=g_B-\left(d_B-{\tau }_B{\displaystyle \frac{H}{H+{\zeta }_{HB}}}+{\rho }_B{\displaystyle \frac{R}{R+{\zeta }_{RB}}}\right)B,\hfill \\ R^{\prime }=g_R-\left(d_R-{\tau }_R{\displaystyle \frac{H}{H+{\zeta }_{HR}}}+{\rho }_R\right)R.\hfill \end{array}\right.$$

(3)

3. Results and Discussion

We present a mathematical immunology model during the activation of the immune system, involving epithelial cells and their interaction with free SARS-CoV-2 virus particles. Tracking the functioning of different lymphocytes allows us to identify their behavior over time after symptom onset. In particular, the model suggests that activation of regulatory T lymphocytes enhances the inhibition of effector functions of the immune system, ensuring homeostasis. Our analysis is consistent with experimental data indicating that approximately 5 to 15 days after symptom onset is the peak of the immune response when there is an interaction between the SARS-CoV-2 virus and the immune System [28,29,30,31,32,33,34,35,36,37].

Figure 2, Figure 3, Figure 4 and Figure 5 reflect what happens to an individual who is in homeostasis. That is, the initial condition starts for the variables $E,H,C,B$ and R in the infection-free equilibrium. Note that, in the trajectories, the number of epithelial cells starts from its homeostatic value $g_E/d_E$, then decreases according to the intensity of the infection, and then recovers its value.

At the first moment of the first viral load in System (3), i.e., $V\left(0\right)>0$, without infected cells $I\left(0\right)=0$, then, the disease has a chance to take off (settle) as

$$I^{\prime }\left(0\right)={\tau }_E{\displaystyle \frac{V\left(0\right)}{V\left(0\right)+{\zeta }_{VE}}}{\displaystyle \frac{g_E}{d_E}}>0.$$

This also indicates that if the initial viral load is very large, then $I^{\prime }\left(0\right)={\tau }_E{g}_E/d_E$, the maximum number of epithelial cells that can be infected per unit time.

Figure 2 illustrates the biological behavior observed once free virus particles (V) enter the organism through the nasal cavity and interact with epithelial cells (E), facilitating their entry via cellular receptors, leading to infected cells (I). Thus, we can envision a set of epithelial cells undergoing cellular turnover depending on their generation rate ($g_E$) and death rate ($d_E$), the latter being a result of apoptosis that begins after completing their life cycle.

In addition, Figure 2 shows that around the third day, epithelial cells (E) decrease, leading to an increase in infected cells as symptoms begin. This, in turn, triggers the activation of H lymphocytes, which subsequently activate B and C lymphocytes. Additionally, the figure demonstrates that the activation of R lymphocytes helps the system achieve homeostasis after approximately 35 to 45 days, consistent with experimental data reported in the literature [28,29,30,31,32,33,34,35,38,39,40,41].

From the above, it is highlighted that taking into account relevant literature [28,29,30,31,32,33,34,35,36,41,42,43,44], suppression by R lymphocytes should occur between 25 and 35 days after the onset of infection. For this purpose, an adjustment was made to the value of the parameters, achieving a closer approximation to the expected biological process related to the immune response as shown in Figure 4.

Furthermore, it is ensured that the behavior of the R lymphocytes in Figure 2 and Figure 4 conforms to the expected; this is observed under a scale adjustment as shown in Figure 3 and Figure 5.

The curves represented in Figure 2 and Figure 4 compare the dynamics with different generation rates of H lymphocytes, C lymphocytes, and B lymphocytes, according to the values of parameters $g_H,g_B$, and $g_C$ and the same occurs in the elimination of these lymphocytes in relation to the parameters $d_H,d_B$ and $d_C$, proving that an increase in both the different generations and elimination of the mentioned lymphocytes leads to an early response of the immune response, as well as remaining within the established days to obtain an activation response in the established interval.

Thus, it is observed that the dynamics of regulatory T lymphocytes activation (${\tau }_R$) leads to the regulation of effector functions of the lymphocytes that are acting in System (3), and an increase in regulatory T lymphocytes implies the early neutralization of these functions, which leads to the establishment of homeostasis within the organism, without leaving aside that these are still in the ranges established by the literature [33,34,35,36,43,44]

Figure 4 shows that the increased cytotoxic response in infected cells tends to decrease the amount of free viral particles, resulting in fewer infected epithelial cells. When there is increased neutralization of free viral particles, it leads to an increased antibody response of the organism, resulting in an early immune response.

In other modeling work, different criteria are selected to define the severity of viral infection, such as the fraction of infected cells [2,32,37,45,46,47,48,49], cumulative tissue damage [22,23,50,51,52], damage-associated molecular patterns and pathogen-associated molecular patterns [23,29,38,50,53]. In our results, we demonstrate that individuals with an increased induced Treg effectively suppress the inflammatory response in contrast to similar cells of lower content, which is consistent with modeling studies indicating how Tregs help regulate the immune system, while activated H lymphocytes, C lymphocytes, and B lymphocytes enter a memory phase with latent capacity to respond more rapidly to the reintroduction of the same pathogen [54,55,56].

Basic Reproductive Number

The reproductive number for cell models, usually denoted by $R_0$, is defined as the number of new infected cells generated from a first infected cell when the virus is introduced into a population of susceptible cells (E) [38].

If $R_0<1$, it is assumed that the infection is eliminated, i.e., the virus is not able to reproduce, resulting in a viral load that tends to zero. Therefore, each virus-infected cell produces, on average, less than one new infected cell. It is then predicted that the infection will disappear from the population or that the virus will be eliminated from the individual; therefore, the infection cannot spread, and the system returns to the uninfected state.

If $R_0>1$, the infection progresses and the virus can invade the susceptible cell population (E).

To derive the expression of the reproductive number of System (3), the next generation matrix method [57] is used as follows:

$$R_0={\displaystyle \frac{g_E(g_B+d_B{\zeta }_{BV})(g_C+d_C{\zeta }_{CI})\nu {\tau }_E}{d_E(d_I(g_C+d_C{\zeta }_{CI})+g_C{\tau }_I)(d_V(g_B+d_B{\zeta }_{BV})+g_B{\tau }_V){\zeta }_{VE}}}.$$

(4)

Remark. 

It is specified that in an organism without the disease, that is, $V\left(0\right)=0$ and $I\left(0\right)=0$, this is a case where $E^{\prime }=g_E-d_{E}E$; this implies $E\left(t\right)\to g_E/d_E$.

We are aware that our mathematical analysis is an initial attempt to examine the activation of the immune response and may not fully account for the associated intertwined cellular communication pathways. Nevertheless, it serves as a hypothesis-building and hypothesis-provoking process that should encourage the integrated analysis of SARS-CoV-2 pathogenesis. Future experimental data examining the interrelationships between SARS-CoV-2 and the immune response will allow us to further refine our model and implement realistic parameters in the rates of systems of equations.

4. Conclusions

This paper formulated a seven-compartment mathematical model to simulate the dynamics of activation and regulation of the immune response to viral pathogens. The model includes the following state variables: epithelial cells, infected cells, free viral particles, helper T lymphocytes, cytotoxic T lymphocytes, B lymphocytes and regulatory T lymphocytes. This type of cell-mediated immune response is relevant in respiratory diseases caused by viruses such as measles and influenza, among others. The study demonstrated the positivity of the proposed model solutions, ensuring that the state variables remain positive as long as there is an initial presence of virus and infected cells in the system. In addition, an analysis of the local stability of the homogeneous system was performed, which provided essential insight into the dynamics of the state variables of the model. The results indicated that solutions tend to stabilize around an equilibrium point, which biologically implies the neutralization of viral particles and the elimination of infected cells.

Finally, the theoretical results were validated by numerical simulations using data reported in the literature on the SARS-CoV-2 virus. These simulations showed an approximation of biological behavior and provided an appropriate fit to the timing of virus transmissibility, symptom onset, antibody levels, and lymphocyte response, thus improving the understanding of the dynamics of viral infection.