Fuzzy Stress and Strength Reliability Based on the Generalized Mixture Exponential Distribution
Abstract
:1. Introduction
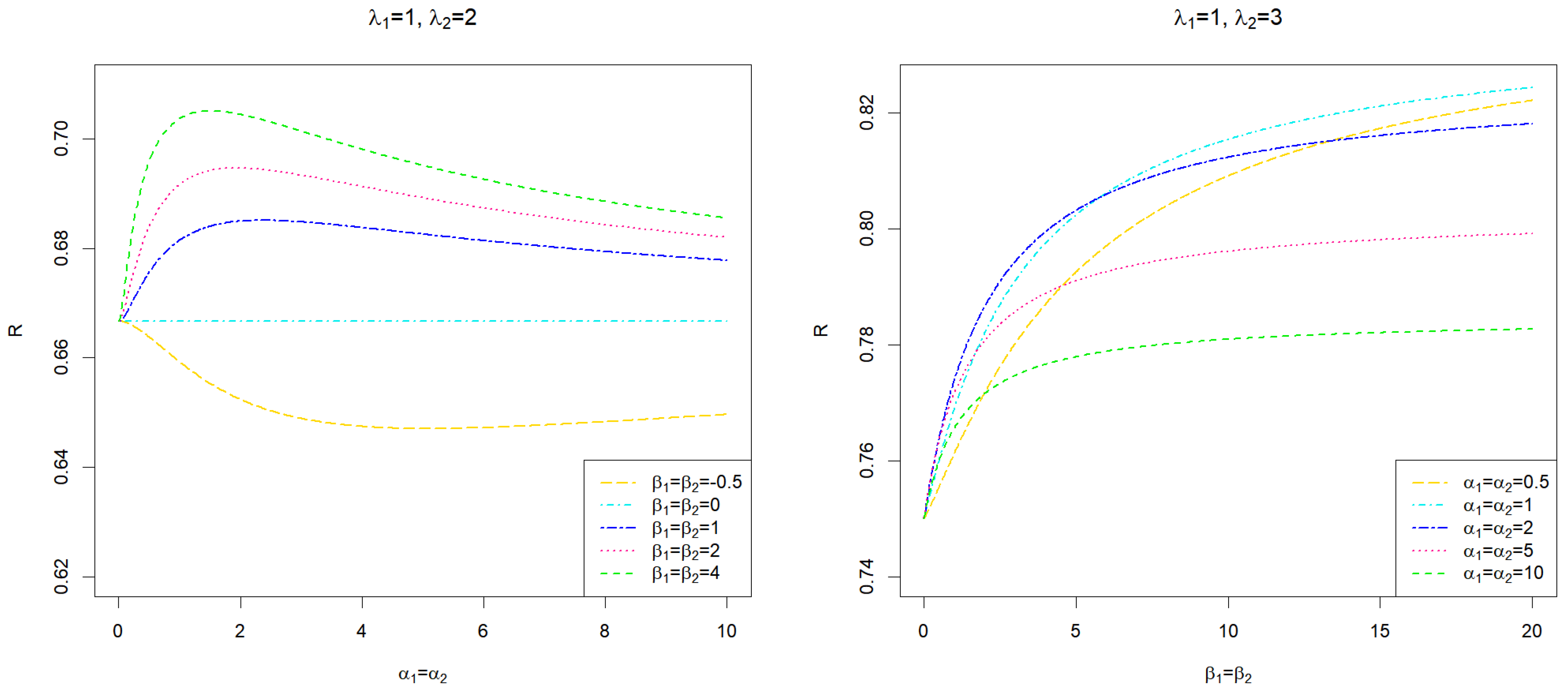
2. Stress and Strength Reliability
- (i)
- For ,
- (ii)
- For and ,
- (iii)
- For ,
- (iv)
- For , , and , we have
- (i)
- For ,
- (ii)
- For ,
3. Methods of Estimation
3.1. Maximum Likelihood Estimator
3.2. Percentile Estimator
3.3. Weighted Least-Square Estimator
4. Simulation Studies
5. Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kelley, G.D.; Kelley, J.A.; Schucany, W.R. Efficient estimation of P(Y<X) in the exponential case. Technometrics 1976, 18, 359–360. [Google Scholar]
- Tong, H. A note on the estimation of P(Y<X) in the exponential case. Technometrics 1974, 16, 625. [Google Scholar]
- Tong, H. On The Estimation of Pr(Y≤X) for Exponential Families. IEEE Trans. Reliab. 1977, 26, 54–56. [Google Scholar] [CrossRef]
- Awad, A.M.; Azzam, M.M.; Hamdan, M.A. Some inference results on P(Y<X) in the bivariate exponential model. Commun.-Stat.-Theory Methods 1981, 10, 2515–2525. [Google Scholar]
- Kundu, D.; Gupta, R.D. Estimation of P[Y<X] for generalized exponential distribution. Metrika 2005, 61, 291–308. [Google Scholar]
- Saraçoğlu, B.; Kinaci, I.; Kundu, D. On estimation of R=P(Y<X) for exponential distribution under progressive type-II censoring. J. Stat. Comput. Simul. 2012, 82, 729–744. [Google Scholar]
- Jafari, A.A.; Bafekri, S. Inference on stress-strength reliability for the two-parameter exponential distribution based on generalized order statistics. Math. Popul. Stud. 2021, 28, 201–227. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Elbatal, I.; Almetwally, E.M. Bayesian and Non-Bayesian Reliability Estimation of Stress-Strength Model for Power-Modified Lindley Distribution. Comput. Intell. Neurosci. 2022, 2022, 1154705. [Google Scholar] [CrossRef]
- Liu, Y.; Khan, M.; Anwar, S.M.; Rasheed, Z.; Feroze, N. Stress-Strength Reliability and Randomly Censored Model of Two-Parameter Power Function Distribution. Math. Probl. Eng. 2022, 2022, 5509684. [Google Scholar] [CrossRef]
- Kumari, R.; Lodhi, C.; Tripathi, Y.M.; Sinha, R.K. Estimation of stress–strength reliability for inverse exponentiated distributions with application. Int. J. Qual. Reliab. Manag. 2023, 40, 1036–1056. [Google Scholar] [CrossRef]
- Ma, J.G.; Wang, L.; Tripathi, Y.M.; Rastogi, M.K. Reliability inference for stress-strength model based on inverted exponential Rayleigh distribution under progressive Type-II censored data. Commun.-Stat.-Simul. Comput. 2023, 52, 2388–2407. [Google Scholar] [CrossRef]
- Sultana, F.; Çetinkaya, Ç.; Kundu, D. Estimation of the stress-strength parameter under two-sample balanced progressive censoring scheme. J. Stat. Comput. Simul. 2024, 94, 1269–1299. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Huang, H.Z. Reliability analysis method in the presence of fuzziness attached to operating time. Microelectron. Reliab. 1995, 35, 1483–1487. [Google Scholar] [CrossRef]
- Cai, K.Y. System failure engineering and fuzzy methodology an introductory overview. Fuzzy Sets Syst. 1996, 83, 113–133. [Google Scholar] [CrossRef]
- Huang, H.Z.; Zuo, M.J.; Sun, Z.Q. Bayesian reliability analysis for fuzzy lifetime data. Fuzzy Sets Syst. 2006, 157, 1674–1686. [Google Scholar] [CrossRef]
- Li, Z.; Kapur, K.C. Some perspectives to define and model reliability using fuzzy sets. Qual. Eng. 2013, 25, 136–150. [Google Scholar] [CrossRef]
- Eryilmaz, S.; TütTxuxncTxux, G.Y. Stress strength reliability in the presence of fuzziness. J. Comput. Appl. Math. 2015, 282, 262–267. [Google Scholar] [CrossRef]
- Yazgan, E.; Gürler, S.; Esemen, M.; Sevinc, B. Fuzzy stress-strength reliability for weighted exponential distribution. Qual. Reliab. Eng. Int. 2022, 38, 550–559. [Google Scholar] [CrossRef]
- Hassan, M.K.; Muse, A.H. Fuzzy Stress-Strength Model and Mean Remaining Strength for Lindley Distribution: Estimation and Application in Cancer of Benign Endocrine. Comput. Math. Methods Med. 2023, 2023, 8952946. [Google Scholar] [CrossRef]
- Milošević, B.; Stanojevixcx, J. On the estimation of fuzzy stress–strength reliability parameter. J. Comput. Appl. Math. 2024, 438, 115536. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, W.; Tong, T. Generalized mixtures of exponential distribution and associated inference. Mathematics 2021, 9, 1371. [Google Scholar] [CrossRef]
- Chesneau, C.; Kumar, V.; Khetan, M.; Arshad, M. On a modified weighted exponential distribution with applications. Math. Comput. Appl. 2022, 27, 17. [Google Scholar] [CrossRef]
- Bean, N.G.; O’Reilly, M.M.; Palmowski, Z. Matrix-analytic methods for the analysis of stochastic fluid-fluid models. Stoch. Model. 2022, 38, 416–461. [Google Scholar] [CrossRef]
- Hussam, E.; Sabry, M.A.; Abd El-Raouf, M.M.; Almetwally, E.M. Fuzzy vs. traditional reliability model for inverse Weibull distribution. Axioms 2023, 12, 582. [Google Scholar] [CrossRef]
- Swain, J.J.; Venkatraman, S.; Wilson, J.R. Least-squares estimation of distribution functions in Johnson’s translation system. J. Stat. Comput. Simul. 1988, 29, 271–297. [Google Scholar] [CrossRef]
- Xia, Z.P.; Yu, J.Y.; Cheng, L.D.; Liu, L.F.; Wang, W.M. Study on the breaking strength of jute fibres using modified Weibull distribution. Compos. Part Appl. Sci. Manuf. 2009, 40, 54–59. [Google Scholar] [CrossRef]

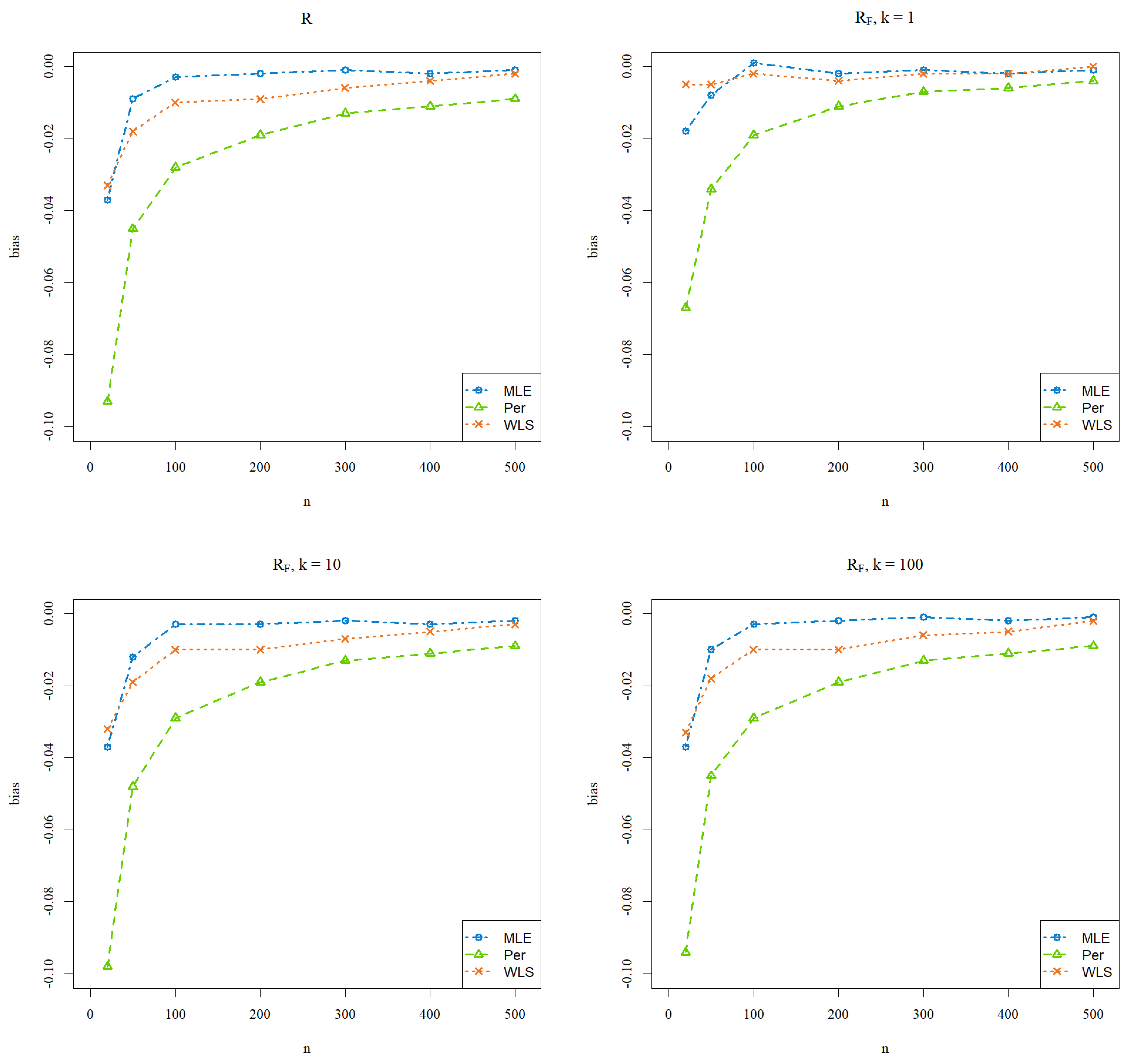
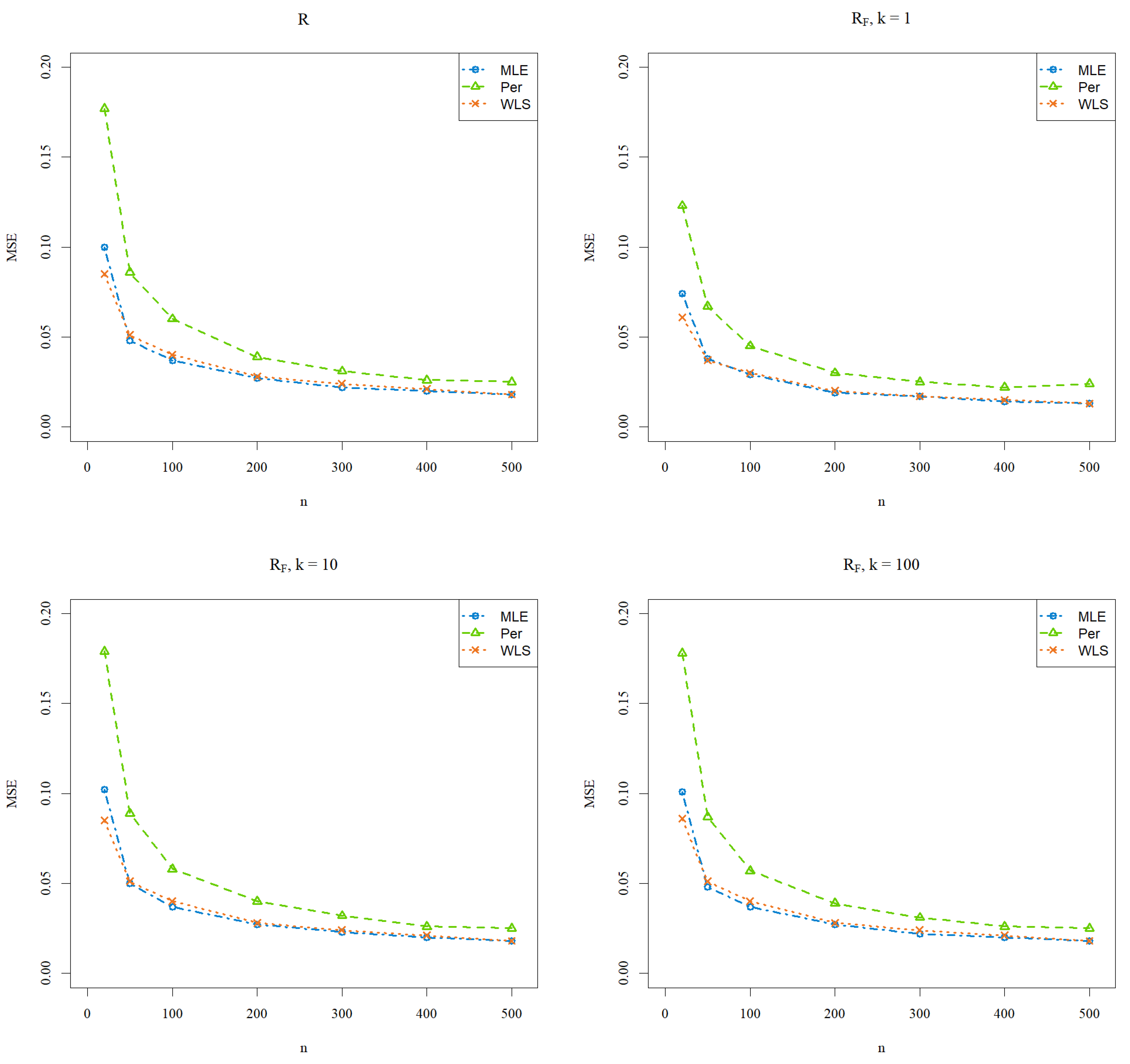
| Sample Size | Method | R | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | |||||||||||||||||
| Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | ||
| MLE | 0.512 | 0.094 | −0.037 | 0.100 | 0.247 | 0.072 | −0.018 | 0.074 | 0.454 | 0.095 | −0.037 | 0.102 | 0.505 | 0.095 | −0.037 | 0.101 | |
| PE | 0.456 | 0.151 | −0.093 | 0.177 | 0.198 | 0.104 | −0.067 | 0.123 | 0.394 | 0.150 | −0.098 | 0.179 | 0.448 | 0.151 | −0.094 | 0.178 | |
| WLE | 0.516 | 0.079 | −0.033 | 0.085 | 0.260 | 0.061 | −0.005 | 0.061 | 0.460 | 0.079 | −0.032 | 0.085 | 0.509 | 0.079 | −0.033 | 0.086 | |
| MLE | 0.540 | 0.048 | −0.009 | 0.048 | 0.257 | 0.037 | −0.008 | 0.038 | 0.480 | 0.048 | −0.012 | 0.050 | 0.533 | 0.048 | −0.010 | 0.048 | |
| Per | 0.504 | 0.074 | −0.045 | 0.086 | 0.231 | 0.058 | −0.034 | 0.067 | 0.444 | 0.075 | −0.048 | 0.089 | 0.497 | 0.074 | −0.045 | 0.087 | |
| WLE | 0.531 | 0.048 | −0.018 | 0.051 | 0.260 | 0.037 | −0.005 | 0.037 | 0.473 | 0.048 | −0.019 | 0.051 | 0.524 | 0.048 | −0.018 | 0.051 | |
| MLE | 0.546 | 0.037 | −0.003 | 0.037 | 0.266 | 0.029 | 0.001 | 0.029 | 0.489 | 0.037 | −0.003 | 0.037 | 0.540 | 0.037 | −0.003 | 0.037 | |
| PE | 0.521 | 0.049 | −0.028 | 0.060 | 0.246 | 0.041 | −0.019 | 0.045 | 0.462 | 0.051 | −0.029 | 0.058 | 0.514 | 0.050 | −0.029 | 0.057 | |
| WLE | 0.539 | 0.039 | −0.010 | 0.040 | 0.263 | 0.030 | −0.002 | 0.030 | 0.481 | 0.039 | −0.010 | 0.040 | 0.532 | 0.039 | −0.010 | 0.040 | |
| MLE | 0.547 | 0.027 | −0.002 | 0.027 | 0.263 | 0.019 | −0.002 | 0.019 | 0.489 | 0.027 | −0.003 | 0.027 | 0.540 | 0.027 | −0.002 | 0.027 | |
| PE | 0.530 | 0.034 | −0.019 | 0.039 | 0.254 | 0.028 | −0.011 | 0.030 | 0.472 | 0.035 | −0.019 | 0.040 | 0.523 | 0.034 | −0.019 | 0.039 | |
| WLE | 0.540 | 0.026 | −0.009 | 0.028 | 0.261 | 0.019 | −0.004 | 0.020 | 0.482 | 0.026 | −0.010 | 0.028 | 0.532 | 0.026 | −0.010 | 0.028 | |
| MLE | 0.548 | 0.022 | −0.001 | 0.022 | 0.264 | 0.017 | −0.001 | 0.017 | 0.450 | 0.023 | −0.002 | 0.023 | 0.541 | 0.022 | −0.001 | 0.022 | |
| PE | 0.536 | 0.029 | −0.013 | 0.031 | 0.258 | 0.024 | −0.007 | 0.025 | 0.478 | 0.029 | −0.013 | 0.032 | 0.529 | 0.027 | −0.013 | 0.031 | |
| WLE | 0.543 | 0.023 | −0.006 | 0.024 | 0.263 | 0.017 | −0.002 | 0.017 | 0.485 | 0.023 | −0.007 | 0.024 | 0.536 | 0.023 | −0.006 | 0.024 | |
| MLE | 0.547 | 0.020 | −0.002 | 0.020 | 0.263 | 0.014 | −0.002 | 0.014 | 0.489 | 0.020 | −0.003 | 0.020 | 0.540 | 0.020 | −0.002 | 0.020 | |
| PE | 0.538 | 0.023 | −0.011 | 0.026 | 0.259 | 0.021 | −0.006 | 0.022 | 0.480 | 0.024 | −0.011 | 0.026 | 0.531 | 0.023 | −0.011 | 0.026 | |
| WLE | 0.545 | 0.020 | −0.004 | 0.021 | 0.263 | 0.015 | −0.002 | 0.015 | 0.487 | 0.020 | −0.005 | 0.021 | 0.538 | 0.020 | −0.005 | 0.021 | |
| MLE | 0.548 | 0.018 | −0.001 | 0.018 | 0.264 | 0.013 | −0.001 | 0.013 | 0.490 | 0.018 | −0.002 | 0.018 | 0.541 | 0.018 | −0.001 | 0.018 | |
| PE | 0.540 | 0.024 | −0.009 | 0.025 | 0.261 | 0.024 | −0.004 | 0.024 | 0.482 | 0.024 | −0.009 | 0.025 | 0.533 | 0.024 | −0.009 | 0.025 | |
| WLE | 0.547 | 0.018 | −0.002 | 0.018 | 0.265 | 0.013 | 0.000 | 0.013 | 0.489 | 0.017 | −0.003 | 0.018 | 0.540 | 0.018 | −0.002 | 0.018 | |
| Sample Size | Method | R | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | |||||||||||||||||
| Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | ||
| MLE | 0.640 | 0.085 | −0.028 | 0.089 | 0.297 | 0.070 | −0.023 | 0.073 | 0.563 | 0.090 | −0.033 | 0.094 | 0.631 | 0.086 | −0.029 | 0.090 | |
| PE | 0.631 | 0.154 | −0.121 | 0.193 | 0.214 | 0.101 | −0.106 | 0.144 | 0.460 | 0.154 | −0.136 | 0.203 | 0.537 | 0.156 | −0.124 | 0.196 | |
| WLE | 0.645 | 0.066 | −0.024 | 0.069 | 0.312 | 0.051 | −0.008 | 0.051 | 0.568 | 0.066 | −0.029 | 0.071 | 0.635 | 0.066 | −0.025 | 0.070 | |
| MLE | 0.648 | 0.047 | −0.021 | 0.051 | 0.311 | 0.040 | −0.008 | 0.040 | 0.576 | 0.049 | −0.020 | 0.053 | 0.640 | 0.048 | −0.021 | 0.052 | |
| PE | 0.643 | 0.057 | −0.026 | 0.062 | 0.289 | 0.056 | −0.030 | 0.063 | 0.562 | 0.062 | −0.034 | 0.070 | 0.633 | 0.058 | −0.027 | 0.063 | |
| WLE | 0.643 | 0.050 | −0.026 | 0.055 | 0.305 | 0.040 | −0.015 | 0.042 | 0.567 | 0.051 | −0.029 | 0.058 | 0.634 | 0.050 | −0.026 | 0.056 | |
| MLE | 0.662 | 0.039 | −0.007 | 0.039 | 0.317 | 0.031 | −0.002 | 0.031 | 0.589 | 0.041 | −0.007 | 0.042 | 0.654 | 0.039 | −0.007 | 0.040 | |
| PE | 0.638 | 0.038 | −0.031 | 0.049 | 0.287 | 0.040 | −0.032 | 0.051 | 0.559 | 0.042 | −0.037 | 0.056 | 0.629 | 0.039 | −0.032 | 0.050 | |
| WLE | 0.663 | 0.031 | −0.006 | 0.031 | 0.321 | 0.026 | 0.001 | 0.026 | 0.590 | 0.032 | −0.007 | 0.032 | 0.654 | 0.031 | −0.006 | 0.031 | |
| MLE | 0.666 | 0.027 | −0.003 | 0.027 | 0.317 | 0.024 | −0.002 | 0.024 | 0.592 | 0.029 | −0.004 | 0.029 | 0.657 | 0.028 | −0.004 | 0.028 | |
| PE | 0.660 | 0.032 | −0.009 | 0.033 | 0.313 | 0.027 | −0.006 | 0.028 | 0.585 | 0.033 | −0.011 | 0.035 | 0.651 | 0.032 | −0.009 | 0.033 | |
| WLE | 0.663 | 0.020 | −0.006 | 0.021 | 0.318 | 0.018 | −0.002 | 0.018 | 0.589 | 0.021 | −0.008 | 0.022 | 0.654 | 0.020 | −0.007 | 0.021 | |
| MLE | 0.667 | 0.021 | −0.002 | 0.021 | 0.318 | 0.017 | −0.001 | 0.017 | 0.594 | 0.022 | −0.002 | 0.022 | 0.659 | 0.021 | −0.002 | 0.021 | |
| PE | 0.659 | 0.024 | −0.010 | 0.026 | 0.312 | 0.023 | −0.008 | 0.024 | 0.584 | 0.0255 | −0.012 | 0.028 | 0.650 | 0.024 | −0.010 | 0.026 | |
| WLE | 0.664 | 0.018 | −0.005 | 0.019 | 0.317 | 0.017 | −0.003 | 0.017 | 0.588 | 0.020 | −0.008 | 0.021 | 0.655 | 0.019 | −0.006 | 0.019 | |
| MLE | 0.667 | 0.018 | −0.002 | 0.019 | 0.317 | 0.015 | −0.003 | 0.016 | 0.593 | 0.019 | −0.003 | 0.020 | 0.658 | 0.019 | −0.002 | 0.019 | |
| PE | 0.663 | 0.023 | −0.006 | 0.024 | 0.316 | 0.020 | −0.003 | 0.020 | 0.589 | 0.024 | −0.007 | 0.025 | 0.654 | 0.024 | −0.006 | 0.024 | |
| WLE | 0.667 | 0.019 | −0.002 | 0.019 | 0.318 | 0.017 | −0.002 | 0.017 | 0.593 | 0.020 | −0.004 | 0.020 | 0.658 | 0.019 | −0.003 | 0.019 | |
| MLE | 0.667 | 0.017 | −0.002 | 0.017 | 0.317 | 0.013 | −0.002 | 0.014 | 0.593 | 0.018 | −0.003 | 0.018 | 0.658 | 0.017 | −0.002 | 0.017 | |
| PE | 0.664 | 0.023 | −0.005 | 0.024 | 0.317 | 0.020 | −0.003 | 0.020 | 0.590 | 0.024 | −0.006 | 0.025 | 0.655 | 0.024 | −0.005 | 0.024 | |
| WLE | 0.663 | 0.016 | −0.006 | 0.017 | 0.314 | 0.011 | −0.006 | 0.012 | 0.588 | 0.016 | −0.008 | 0.017 | 0.654 | 0.016 | −0.007 | 0.017 | |
| Sample Size | Method | R | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | |||||||||||||||||
| Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | Mean | SD | Bias | MSE | ||
| MLE | 0.626 | 0.067 | −0.024 | 0.069 | 0.220 | 0.042 | −0.019 | 0.044 | 0.532 | 0.065 | −0.029 | 0.069 | 0.615 | 0.067 | −0.025 | 0.069 | |
| PE | 0.667 | 0.027 | 0.018 | 0.030 | 0.240 | 0.032 | 0.001 | 0.029 | 0.571 | 0.032 | 0.009 | 0.030 | 0.657 | 0.027 | 0.017 | 0.029 | |
| WLE | 0.655 | 0.093 | 0.005 | 0.088 | 0.247 | 0.066 | 0.008 | 0.062 | 0.566 | 0.094 | 0.005 | 0.089 | 0.645 | 0.093 | 0.005 | 0.088 | |
| MLE | 0.642 | 0.056 | −0.008 | 0.055 | 0.239 | 0.045 | −0.000 | 0.044 | 0.553 | 0.060 | −0.008 | 0.059 | 0.632 | 0.056 | −0.008 | 0.056 | |
| PE | 0.635 | 0.073 | −0.015 | 0.072 | 0.239 | 0.045 | 0.000 | 0.043 | 0.550 | 0.072 | −0.012 | 0.071 | 0.626 | 0.073 | −0.014 | 0.072 | |
| WLE | 0.657 | 0.041 | 0.007 | 0.041 | 0.248 | 0.025 | 0.008 | 0.026 | 0.569 | 0.040 | 0.007 | 0.026 | 0.569 | 0.041 | 0.007 | 0.041 | |
| MLE | 0.646 | 0.033 | −0.003 | 0.032 | 0.240 | 0.026 | 0.001 | 0.026 | 0.558 | 0.035 | −0.003 | 0.034 | 0.637 | 0.033 | −0.003 | 0.033 | |
| PE | 0.645 | 0.051 | −0.004 | 0.051 | 0.240 | 0.037 | 0.001 | 0.036 | 0.556 | 0.053 | −0.005 | 0.052 | 0.635 | 0.052 | −0.005 | 0.051 | |
| WLE | 0.658 | 0.041 | 0.009 | 0.042 | 0.250 | 0.030 | 0.011 | 0.032 | 0.571 | 0.043 | 0.009 | 0.044 | 0.649 | 0.042 | 0.009 | 0.042 | |
| MLE | 0.645 | 0.027 | −0.004 | 0.027 | 0.238 | 0.018 | −0.001 | 0.018 | 0.557 | 0.027 | −0.004 | 0.027 | 0.636 | 0.027 | −0.004 | 0.027 | |
| PE | 0.651 | 0.034 | 0.001 | 0.034 | 0.246 | 0.024 | 0.007 | 0.024 | 0.564 | 0.035 | 0.003 | 0.034 | 0.641 | 0.034 | 0.001 | 0.034 | |
| WLE | 0.651 | 0.022 | 0.002 | 0.022 | 0.242 | 0.016 | 0.003 | 0.017 | 0.563 | 0.023 | 0.002 | 0.023 | 0.642 | 0.022 | 0.002 | 0.022 | |
| MLE | 0.648 | 0.022 | −0.002 | 0.022 | 0.238 | 0.016 | −0.001 | 0.015 | 0.559 | 0.023 | −0.002 | 0.023 | 0.659 | 0.022 | −0.002 | 0.022 | |
| PE | 0.659 | 0.065 | 0.009 | 0.065 | 0.251 | 0.038 | 0.012 | 0.040 | 0.572 | 0.065 | 0.011 | 0.066 | 0.650 | 0.065 | 0.010 | 0.066 | |
| WLE | 0.650 | 0.021 | 0.001 | 0.021 | 0.241 | 0.015 | 0.002 | 0.015 | 0.562 | 0.022 | 0.000 | 0.022 | 0.641 | 0.021 | 0.001 | 0.021 | |
| MLE | 0.649 | 0.018 | −0.001 | 0.018 | 0.239 | 0.012 | 0.000 | 0.012 | 0.560 | 0.018 | −0.001 | 0.018 | 0.649 | 0.018 | −0.001 | 0.018 | |
| PE | 0.653 | 0.020 | 0.004 | 0.020 | 0.244 | 0.014 | 0.006 | 0.015 | 0.565 | 0.020 | 0.004 | 0.020 | 0.644 | 0.020 | 0.004 | 0.020 | |
| WLE | 0.650 | 0.019 | 0.001 | 0.019 | 0.241 | 0.013 | 0.002 | 0.013 | 0.562 | 0.019 | 0.001 | 0.019 | 0.641 | 0.019 | 0.001 | 0.019 | |
| MLE | 0.650 | 0.017 | 0.001 | 0.017 | 0.240 | 0.011 | 0.001 | 0.011 | 0.562 | 0.017 | 0.001 | 0.017 | 0.641 | 0.017 | 0.001 | 0.017 | |
| PE | 0.654 | 0.020 | 0.004 | 0.020 | 0.247 | 0.014 | 0.008 | 0.016 | 0.567 | 0.020 | 0.005 | 0.021 | 0.644 | 0.020 | 0.004 | 0.020 | |
| WLE | 0.652 | 0.017 | 0.002 | 0.017 | 0.241 | 0.011 | 0.002 | 0.011 | 0.563 | 0.017 | 0.002 | 0.017 | 0.642 | 0.017 | 0.002 | 0.017 | |
| No. | 10 mm (X) | 20 mm (Y) | No. | 10 mm (X) | 20 mm (Y) | No. | 10 mm (X) | 20 mm (Y) |
|---|---|---|---|---|---|---|---|---|
| 1 | 693.73 | 71.46 | 11 | 671.49 | 578.62 | 21 | 262.90 | 547.44 |
| 2 | 704.66 | 419.02 | 12 | 183.16 | 756.70 | 22 | 353.24 | 116.99 |
| 3 | 323.83 | 284.64 | 13 | 257.44 | 594.29 | 23 | 422.11 | 375.81 |
| 4 | 778.17 | 585.57 | 14 | 727.23 | 166.49 | 24 | 43.93 | 581.60 |
| 5 | 123.06 | 456.60 | 15 | 291.27 | 99.72 | 25 | 590.48 | 119.86 |
| 6 | 637.66 | 113.85 | 16 | 101.15 | 707.36 | 26 | 212.13 | 48.01 |
| 7 | 383.43 | 187.85 | 17 | 376.42 | 765.14 | 27 | 303.90 | 200.16 |
| 8 | 151.48 | 688.16 | 18 | 163.40 | 187.13 | 28 | 506.60 | 36.75 |
| 9 | 108.94 | 662.66 | 19 | 141.38 | 145.96 | 29 | 530.55 | 244.53 |
| 10 | 50.16 | 45.58 | 20 | 700.74 | 350.70 | 30 | 177.25 | 83.55 |
| X | Y | |
|---|---|---|
| AD value | 0.692 | 0.572 |
| AD* value | 0.711 | 0.587 |
| p-value | 0.064 | 0.126 |
| Method | R | |||
|---|---|---|---|---|
| MLE | 0.514 | 0.512 | 0.513 | 0.514 |
| PE | 0.538 | 0.537 | 0.538 | 0.538 |
| WLE | 0.525 | 0.524 | 0.525 | 0.525 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Tian, C.; Li, S.; Zhang, Y.; Han, J. Fuzzy Stress and Strength Reliability Based on the Generalized Mixture Exponential Distribution. Mathematics 2024, 12, 2684. https://doi.org/10.3390/math12172684
Tian W, Tian C, Li S, Zhang Y, Han J. Fuzzy Stress and Strength Reliability Based on the Generalized Mixture Exponential Distribution. Mathematics. 2024; 12(17):2684. https://doi.org/10.3390/math12172684
Chicago/Turabian StyleTian, Weizhong, Chengliang Tian, Sha Li, Yunchu Zhang, and Jiayi Han. 2024. "Fuzzy Stress and Strength Reliability Based on the Generalized Mixture Exponential Distribution" Mathematics 12, no. 17: 2684. https://doi.org/10.3390/math12172684







