A Novel Optimized Link-State Routing Scheme with Greedy and Perimeter Forwarding Capability in Flying Ad Hoc Networks
Abstract
:1. Introduction
- In OLSR+GPSR, a fuzzy system is provided to regulate the time period for broadcasting hello messages based on the two inputs, namely velocity and position prediction error. This fuzzy system causes the adaptability of the proposed method to FANET so that high-speed UAVs employ a shorter time interval to propagate hello messages, and low-speed UAVs apply a longer time period to disseminate hello messages in the network.
- In OLSR+GPSR, unlike OLSR, MPR nodes are determined based on several metrics, including neighbor degree, node stability (based on velocity, direction, and distance), the occupied buffer capacity, and residual energy. This increases the stability of MPRs, improves energy efficiency, and decreases delay and communication overhead in FANET.
- In OLSR+GPSR, two phases, namely TC message dissemination and route calculation in OLSR, have been deleted to reduce the overhead. Then, after the broadcast of hello messages and the selection of MPRs, the greedy and perimeter forwarding phase is started to find routing paths through MPR nodes, and data packets are sent to the destination.
2. Related Works
3. Basic Concepts
3.1. OLSR
- Phase (1) Obtaining neighboring information: This phase is carried out through the periodic exchange of hello messages. According to this phase, each node obtains information about its one-hop and two-hop neighbors and records this information in a neighbor table.
- Phase (2) Selecting multi-point relays: This phase presents an MPR selection algorithm to choose some one-hop and symmetric neighboring nodes of each node as its MPRs. These nodes are responsible for transmitting control messages and data packets in the network. When selecting these MPRs, this algorithm must meet a condition so that the MPR nodes corresponding to each node can access all of its two-hop neighbors.
- Phase (3) Broadcasting topology control messages: This phase is related to the regular exchange of TC messages to get the global network topology.
- Phase (4) Calculating routing paths: In this phase, communication paths between all nodes are made based on hop counts. Each node maintains a routing table that contains information about routes. This routing table is regularly updated through the periodic dissemination of TC messages in the network.
3.2. GPSR
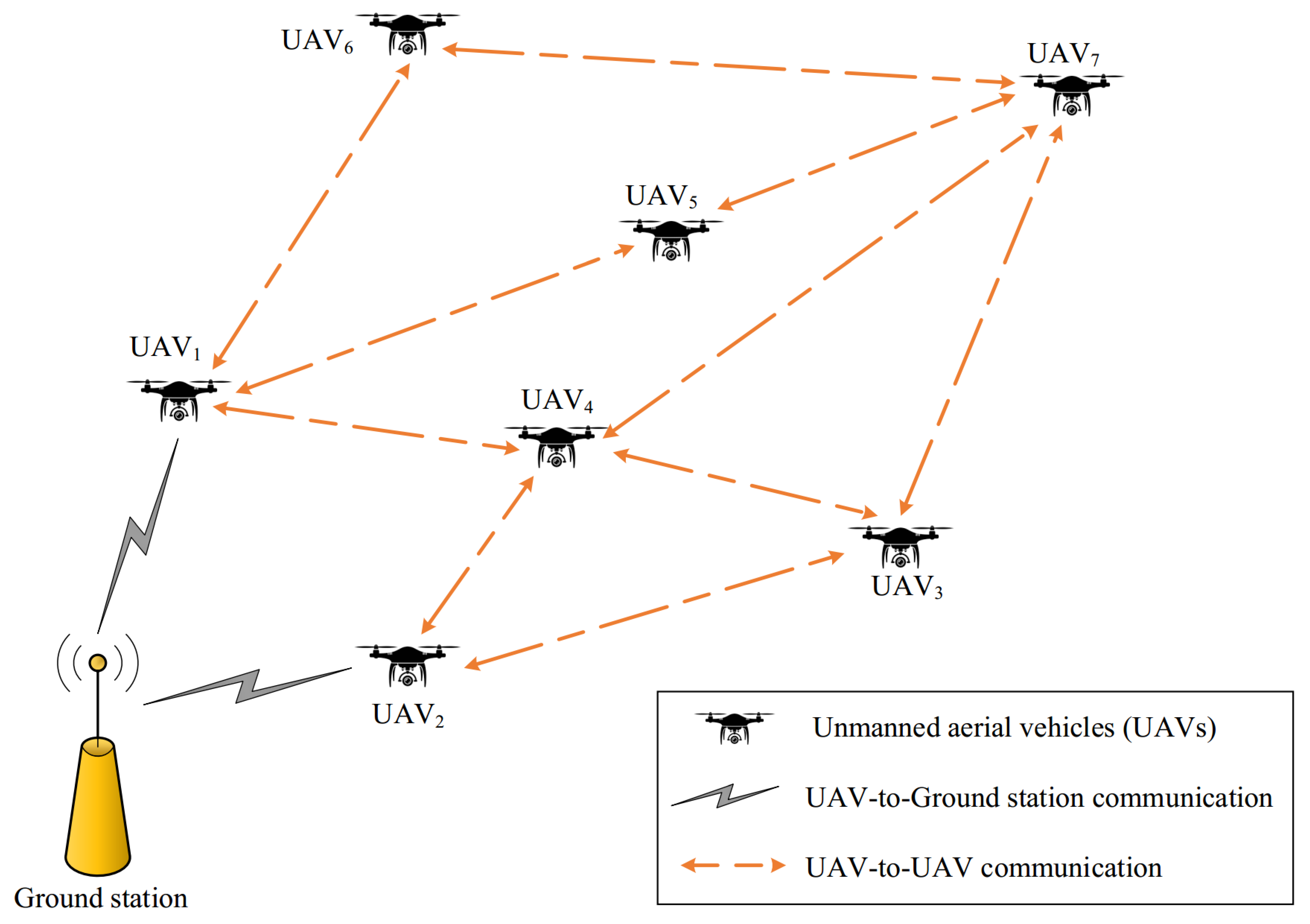
4. Network Model
5. Proposed Method
- Propagating hello messages based on a fuzzy system;
- Selecting MPR nodes;
- Greedy and perimeter forwarding techniques.
5.1. Propagating Hello Messages Based on a Fuzzy System
- The propagation range of the hello message is local. Hence, this message should not be broadcast in the entire network.
- Compared with OLSR, the hello message in OLSR+GPSR includes four additional fields, i.e., geographic location (yellow field), remaining energy (pink field), occupied buffer capacity (green field), and velocity (blue field). See the format of this message in Figure 3.
- The hello propagation process is repeated periodically at a specific time interval so that the information of the neighbor table is always up to date. In OLSR+GPSR, each UAV adjusts its propagation interval according to a fuzzy system. Note that fuzzy logic is a useful tool for presenting mathematical sentences and reasoning propositions. Fuzzy logic moves from the absolute truth to partial truth and follows fuzzy set theory, which is a generalized version of classical set theory [31]. To achieve this fuzzy system, the initial propagation interval of hello messages in OLSR+GPSR is equal to one second. Then, the proposed fuzzy system decides whether to decrease, increase, or fix this interval. This fuzzy system follows the structure of the Mamdani fuzzy control system [32] and includes two input elements, one output, and a rule base.
5.1.1. Fuzzy Inputs
- Velocity (): The time interval associated with hello messages and the velocity of are inversely related to each other. Therefore, if has a high velocity, then it should propagate its hello messages in a shorter time period to update its status information in a timely manner because its communication links are highly unstable, whereas if has a low velocity, it considers a longer time period for broadcasting the hello message due to more stable communication links. Note that is connected to the positioning system and consequently can access its velocity vector at any moment. Therefore, its velocity length () is calculated through Equation (1).Additionally, a normalization operation is performed on using Equation (2) to limit this value to .so that and are the highest and lowest allowed velocity of in the network, respectively. Furthermore, represents the normalized value of .
- Position prediction error (): The propagation interval of hello messages and have an opposite relationship with each other, so if estimates its future position with a large error, it should shorten its hello propagation interval to reduce the position prediction error. Note that has access to its real position through the positioning device. Additionally, it uses the movement equation to estimate its new position. In OLSR+GPSR, each assumes that its velocity vector is fixed in the time period between two consecutive hello messages. As a result, can calculate its future position in the next hello message based on its previous position and its current velocity vector .where is the estimated spatial coordinates of when receiving the next hello message, and expresses the hello propagation interval.Now, the error value () between the actual position, i.e., , and the estimated position, i.e., , is obtained from Equation (6).Finally, is normalized according to Equation (7) to limit this value to .where is the maximum error of the estimated position in the network, and represents the normalized value of . Now, must convert into a fuzzy parameter according to the membership diagram presented in Figure 5. According to Figure 5, this fuzzy parameter involves three states, i.e., low, medium, and high.
5.1.2. Fuzzy Output
5.1.3. Rule Base
| Algorithm 1 Hello message broadcast |
| Input: : |
| : Default period of time for propagating hello messages in . |
| : Simulation time |
| : The number of adjacent drones of . |
| Output: : The period of time for propagating hello messages in . |
| Begin |
| 1: repeat |
| 2: if then |
| 3: : Connect to a positioning system such as GPS; |
| 4: : Get the next position and its velocity from GPS; |
| 5: : Record its position, velocity, energy, and occupied buffer capacity in the hello message; |
| 6: : Propagate this hello message for adjacent UAVs; |
| 7: : Obtain the size of its velocity, i.e., according to Equation (1); |
| 8: : Get the normalized (i.e., ) based on Equation (2); |
| 9: : Transform into a fuzzy variable in accordance with the membership graph in Figure 4; |
| 10: : Approximate the next position based on Equations (3)–(5); |
| 11: : Compute the error value () between and based on Equation (6); |
| 12: : Obtain the normalized error value () in accordance with Equation (7); |
| 13: : Transform into a fuzzy variable in accordance with the membership graph in Figure 5; |
| 14: : Get the broadcast period change rate () based on Figure 6 and the rule base in Table 1; |
| 15: : Obtain ; |
| 16: end if |
| 17: for to do |
| 18: if gets a new hello message from then |
| 19: : Record the information of in its neighbor table; |
| 20: end if |
| 21: end for |
| 22: ; |
| 23: until |
| End |
5.2. Selecting MPR Nodes
- Calculating the score of one-hop neighboring nodes;
- MPR selection algorithm.
5.2.1. Calculating the Score of One-Hop Neighboring Nodes
- Neighbor degree (): In OLSR+GPSR, similar to OLSR, pays attention to the neighbor degree of (i.e., ), which is equal to the number of its one-hop neighbor to determine . is obtained from its neighbor table. This component represents the number two-hop neighboring UAVs of that covers in the network. Thus, can choose suitable one-hop neighbors such as as because with high has more communication links with other nodes and creates stable paths in the network. This decreases routing overhead. and are directly related to each other. Therefore, increases the score of , which has a higher so that gets a higher priority to be selected as . uses Equation (8) to perform a normalization operation on corresponding to (where ) so that this element is limited to .Here, is the normalized value of , and is equal to the maximum degree of the one-hop neighbors in (i.e., ).
- Node stability (): In OLSR+GPSR, measures the stability of (i.e., ) based on the effective distance, relative velocity, and movement direction of to determine the most stable in . is calculated according to Equation (9).Here, and , , and are the weight coefficients to determine the effect of each component (i.e., effective distance, relative velocity, and movement direction) on . In OLSR+GPSR, the effect of all three parameters, including effective distance (), relative velocity (), and movement direction (), on is the same (i.e., ). These three parameters are explained below.
- –
- Effective distance (): The distance between and has an important effect on node stability. If this distance is close to the effective area of , is a stable neighbor. Otherwise, it is not suitable to choose this node as the MPR. In Figure 7, the white area shows the effective area of .In general, the stability of and its effective distance have a direct relationship with each other. Hence, if the distance between and is very short (i.e., ), the selection of as is not a useful option because plays the role of the next-hop node in the routing process, and its proximity to will cause an excessive increase in the number of hops in the route. In Figure 7, the distance between and is less than . Thus, should not be selected as an MPR node. On the other hand, if the distance between and is very long (i.e., ), the selection of as is not appropriate because it may go out of the communication range of very quickly. In Figure 7, the distance between and is more than . Thus, should not be selected as an MPR node, whereas if the distance between and is in the effective range (i.e., ), the selection of as is a very good option. In Figure 7, the distance between and is between and . Thus, is a stable neighbor and can be selected as an MPR node. This issue is stated in Equation (10).where R is the communication radius of UAVs, and is the Euclidean distance between and obtained from Equation (11).
- –
- Relative velocity (): The relative velocity of with regard to is an important factor in determining node stability. This factor determines whether these two UAVs (i.e., and ) fly at a relatively similar velocity. If this factor approaches zero, then the velocities of and are similar. Therefore, they do not leave the neighboring area of each other quickly. In this case, is a stable one-hop neighbor, which can create stable paths and decrease the number of path failures. Now, if the relative velocity is large, has weak stability. The length of the relative velocity of with regard to (i.e., ) is calculated according to Equation (12).where and are the velocity vectors of and , respectively.is normalized through Equation (13).Here, is the normalized value of . is the maximum relative velocity of one-hop neighbors in , i.e., .
- –
- Movement direction (): The direction of relative to (i.e., ) is an effective factor to evaluate the stability of . If moves in the opposite direction to , is known as an unstable node, and vice versa. is calculated based on Equation (14).where and are the velocity vectors of and , respectively.Now, is normalized based on Equation (15).So is the normalized value of in .
- Occupied buffer capacity (): In OLSR+GPSR, the occupied buffer capacity of (i.e., ) is used to determine in . is calculated based on the ratio of the number of data packets in the buffer queue to the size of the buffer. This parameter is exchanged through hello messages. There is an inverse relationship between and because if is a large value, it shows the presence of congestion and high traffic in . This congestion decreases energy efficiency and network lifetime. As a result, gives a lower score to with a higher so that has a lower priority to be selected as . uses Equation (16) to perform a normalization operation on corresponding to () to limit this element to .Here, is the normalized value of , and is equal to the maximum occupied buffer capacity of one-hop neighbors in (i.e., ).
- Residual energy (): In OLSR+GPSR, applies the remaining energy of (i.e., ) to determine in . When deciding on MPRs, this component is really vital for calculating the score of because each MPR node such as experiences higher routing overhead than other nodes. Hence, its energy consumption is high. is obtained from the neighbor table, and there is a direct relationship between and . If is high, is more stable and has priority to be selected as . normalizes corresponding to () through Equation (17) so that this parameter is limited to .Here, is the normalized value of , and is equal to the maximum remaining energy in (i.e., ).
5.2.2. MPR Selection Algorithm
- sorts the members of (i.e., so that ) based on .
- If some of have the same score, those with a higher neighbor degree have a higher priority.
- chooses a with the highest score (the first member of , i.e., ) and inserts it as into .
- removes determined as from .
- All IDs of two-hop neighbors (such as ) that have at least one communication path to through MPRs in are removed from .
| Algorithm 2 The selection process of multi-point relays (MPRs) |
| Input: : |
| : Default period of time for propagating hello messages in . |
| : |
| : A one-hop neighbor of . |
| : The score of . |
| Output: |
| Begin |
| 1: for to P do |
| 2: : Obtain corresponding to from its neighbor table; |
| 3: : Normalized according to Equation (8); |
| 4: : Gain corresponding to based on Equation (9); |
| 5: : Extract corresponding to from its neighbor table; |
| 6: : Calculate the normalized (i.e., ) based on Equation (16); |
| 7: : Obtain corresponding to from its neighbor table; |
| 8: : Get the normalized (i.e., ) in accordance with Equation (17); |
| 9: : Compute the score () related to according to Equation (18); |
| 10: end for |
| 11: : Consider an empty set to record the selected MPRs; |
| 12: for to Q do |
| 13: for to P do |
| 14: if in has then |
| 15: : Determine this as a member of ; |
| 16: : Delete this from ; |
| 17: : Remove the 2-hop neighbors () covered by from ; |
| 18: else if there is a in covered only by then |
| 19: : Determine this as a member of ; |
| 20: : Eliminate this from ; |
| 21: : Delete the 2-hop neighbors () covered by from ; |
| 22: end if |
| 23: end for |
| 24: end for |
| 25: while do |
| 26: : Sort the members of based on their ; |
| 27: if two one-hop neighbor have the same then |
| 28: : Prioritize these one-hop neighbors based on their ; |
| 29: end if |
| 30: : Select the first member of as ; |
| 31: : Eliminate this from ; |
| 32: : Delete the 2-hop neighbors () covered by from ; |
| 33: end while |
| End |
5.3. Greedy and Perimeter Forwarding Techniques
| Algorithm 3 Routing process |
| Input: : |
| Output: Routing path between source and destination. |
| Begin |
| 1: repeat |
| 2: if find the nearest to the destination then |
| 3: : Choose this as the next-hop node; |
| 4: : Forward the data packet to this using the greedy forwarding mode in GPSR; |
| 5: else if there is no close to the destination compared the current node then |
| 6: : Select the next-hop node using the perimeter forwarding mode in GPSR; |
| 7: : Forward the data packet to the next-hop node; |
| 8: end if |
| 9: until the data packet reaches the destination |
| End |
6. Simulation and Evaluation of Results
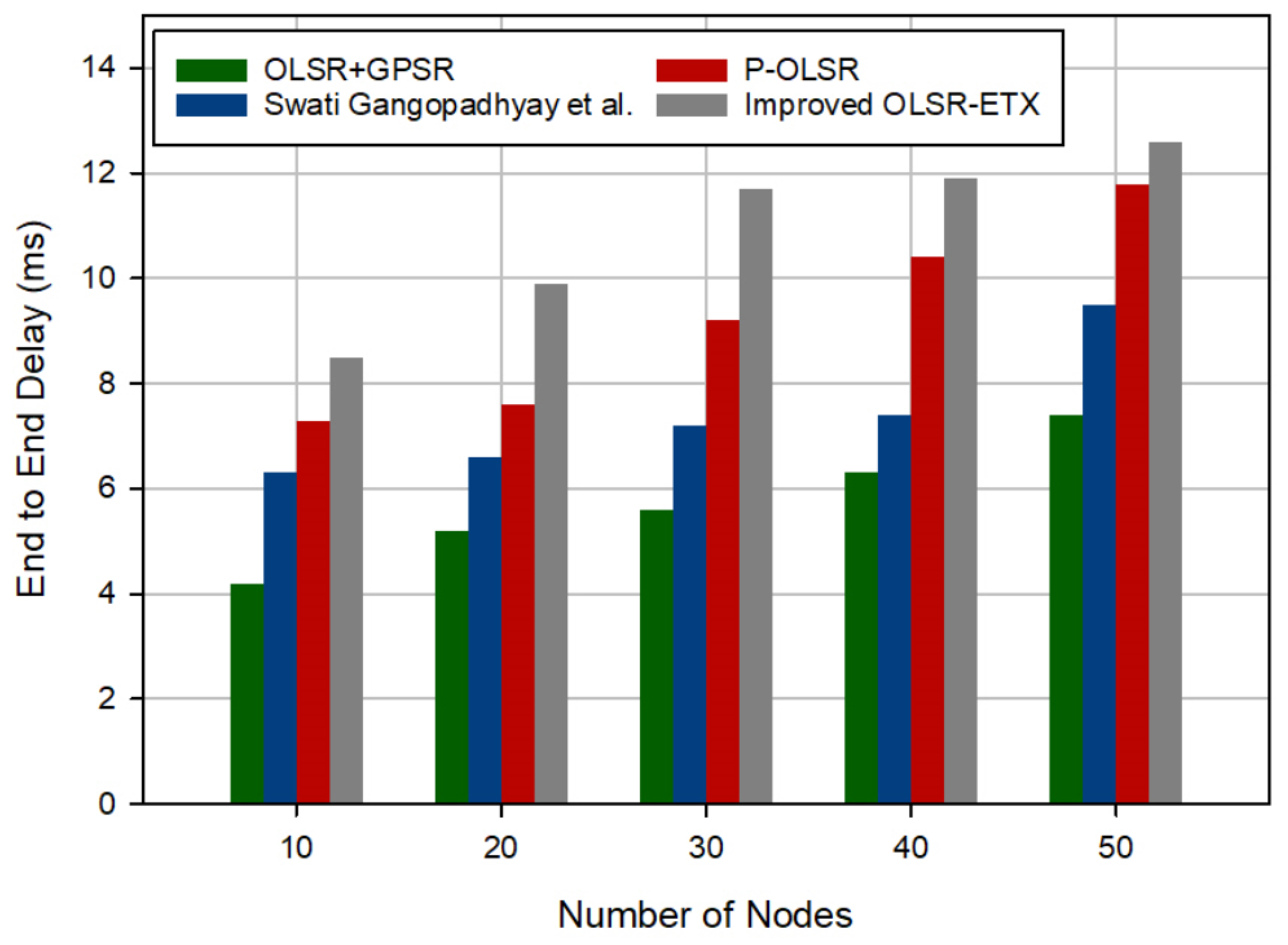
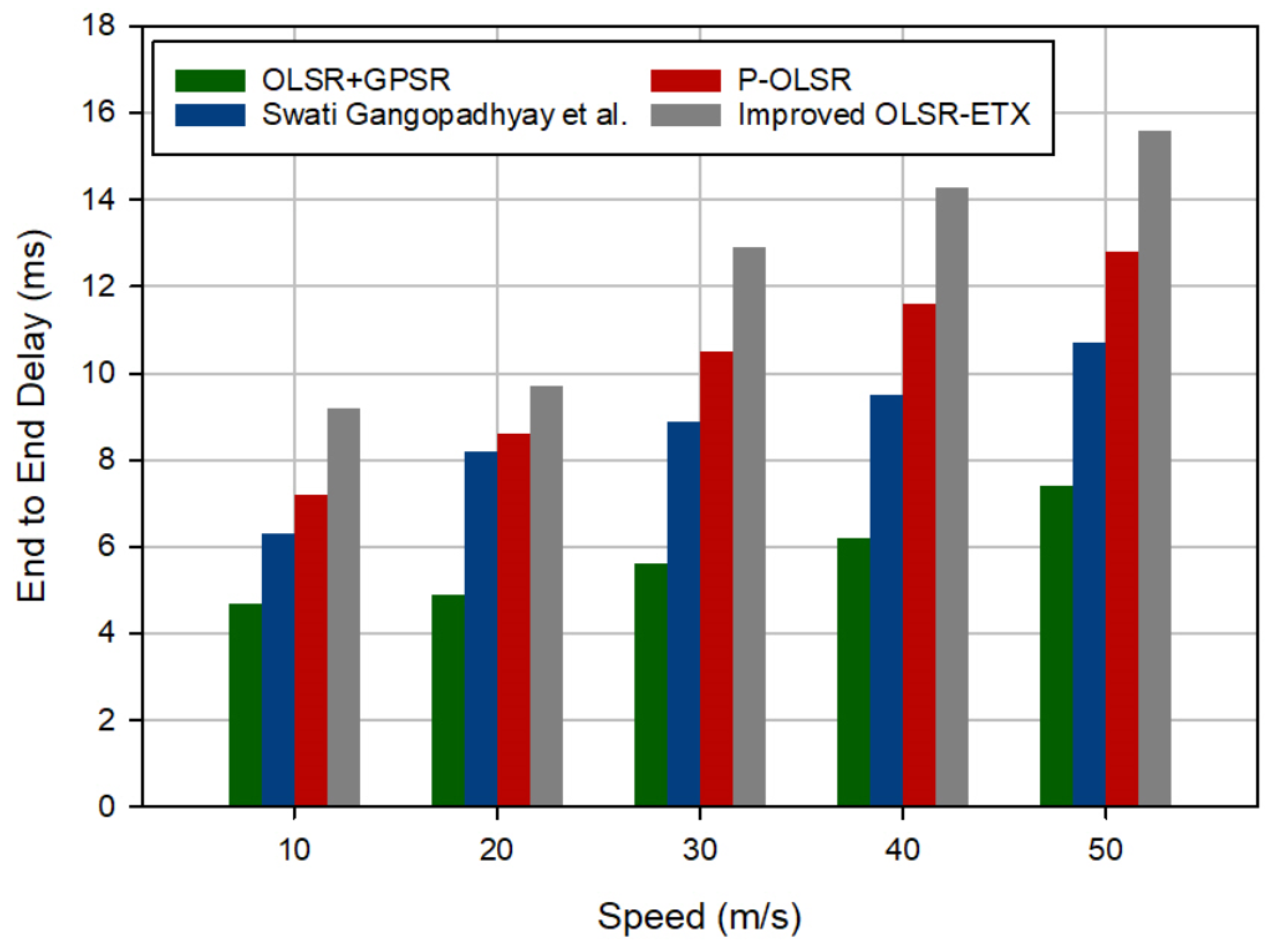
6.1. End-to-End Delay (EED)
6.2. Packet Delivery Rate (PDR)
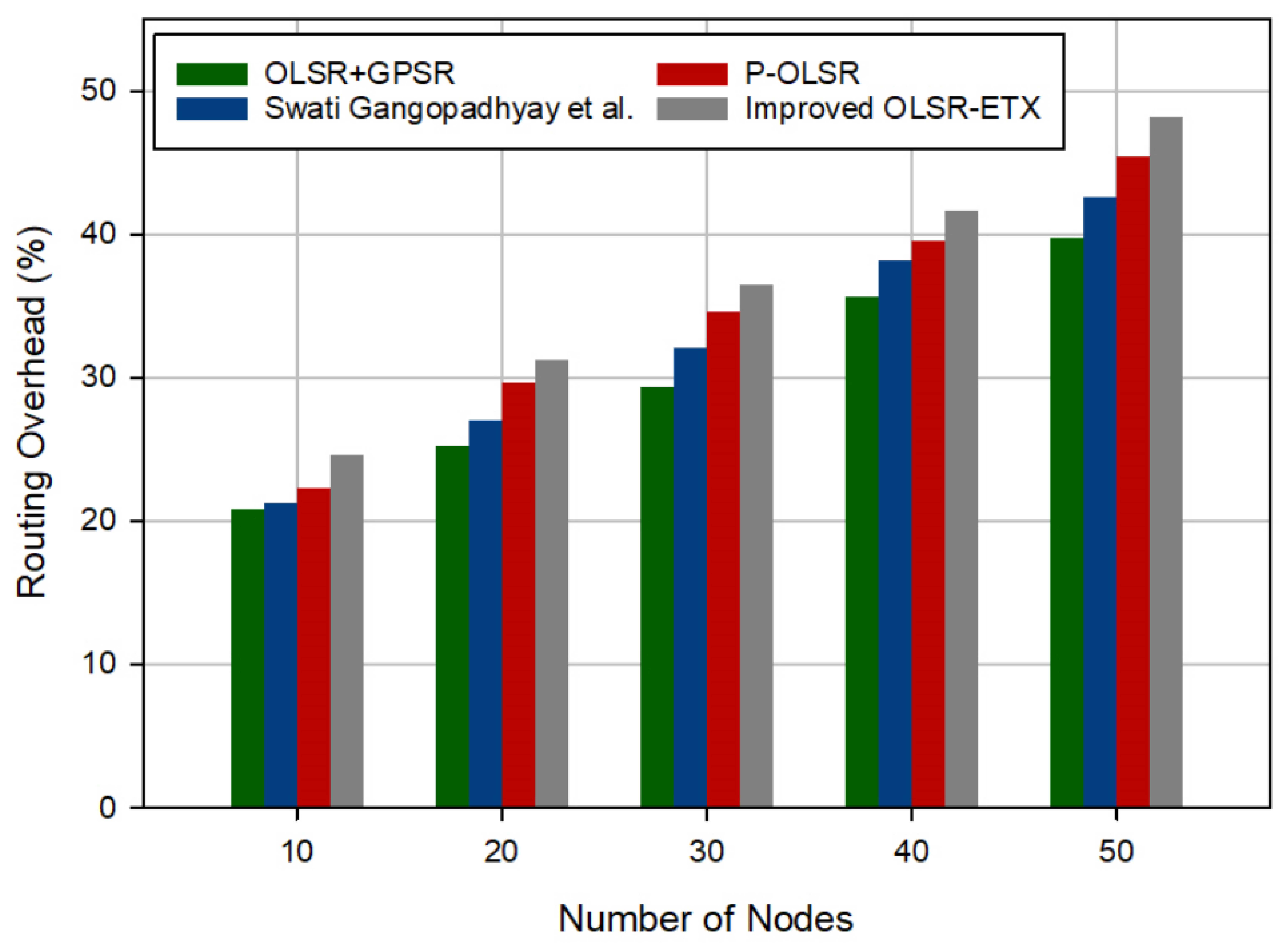
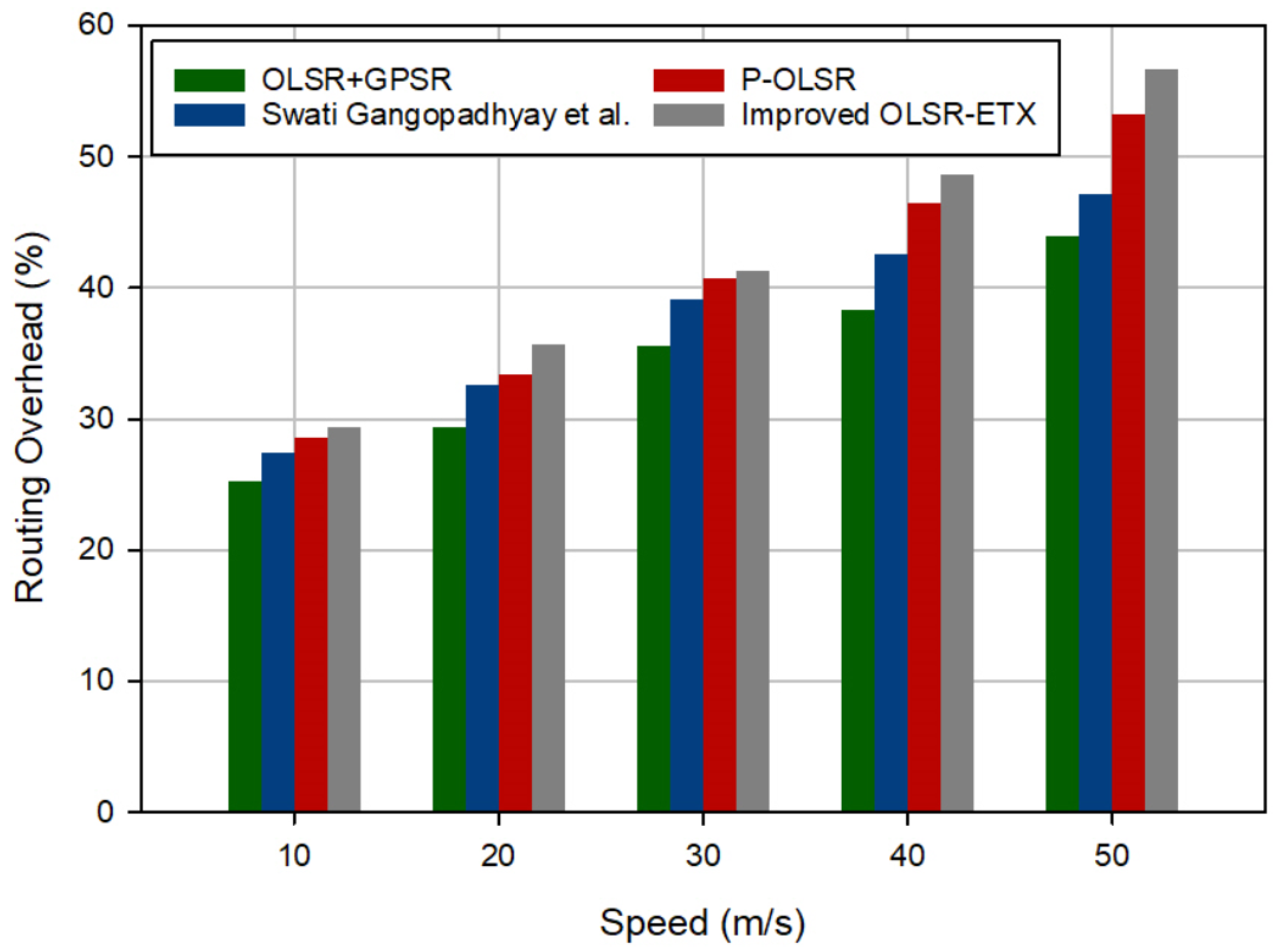
6.3. Routing Overhead
6.4. Throughput
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swain, S.; Khilar, P.M.; Senapati, B.R. A reinforcement learning-based cluster routing scheme with dynamic path planning for mutli-uav network. Veh. Commun. 2023, 3, 100605. [Google Scholar] [CrossRef]
- Gharib, M.; Afghah, F.; Bentley, E.S. LB-OPAR: Load balanced optimized predictive and adaptive routing for cooperative UAV networks. Ad Hoc Netw. 2022, 3, 102878. [Google Scholar] [CrossRef]
- Yang, J.; Sun, K.; He, H.; Jiang, X.; Chen, S. Dynamic virtual topology aided networking and routing for aeronautical ad hoc networks. IEEE Trans. Commun. 2022, 3, 4702–4716. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, C.; Yang, P.; Tao, T.; Wu, Q.; Quek, T.Q. Adaptive routing design for flying ad hoc networks. IEEE Commun. Lett. 2022, 3, 1438–1442. [Google Scholar] [CrossRef]
- Kumar, S.; Raw, R.S.; Bansal, A. LoCaL: Link-oriented cone-assisted location routing in flying ad hoc networks. Int. J. Commun. Syst. 2023, 36, e5375. [Google Scholar] [CrossRef]
- Oubbati, O.S.; Lakas, A.; Zhou, F.; Güneş, M.; Yagoubi, M.B. A survey on position-based routing protocols for flying ad hoc networks (FANETs). Veh. Commun. 2017, 10, 29–56. [Google Scholar] [CrossRef]
- Messaoudi, K.; Oubbati, O.S.; Rachedi, A.; Lakas, A.; Bendouma, T.; Chaib, N. A survey of UAV-based data collection: Challenges, solutions and future perspectives. J. Netw. Comput. Appl. 2023, 216, 103670. [Google Scholar] [CrossRef]
- Kumar, S.; Raw, R.S.; Bansal, A.; Singh, P. UF-GPSR: Modified geographical routing protocol for flying ad hoc networks. Trans. Emerg. Telecommun. Technol. 2023, 34, e4813. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Tanveer, J.; Rahmani, A.M.; Aurangzeb, K.; Yousefpoor, E.; Yousefpoor, M.S.; Darwesh, A.; Lee, S.W.; Fazlali, M. A Q-learning-based smart clustering routing method in flying Ad Hoc networks. J. King Saud-Univ.-Comput. Inf. Sci. 2024, 3, 101894. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Mohammed, A.H.; Alenizi, F.A.; Malik, M.H.; Yousefpoor, E.; Yousefpoor, M.S.; Ahmed, O.H.; Rahmani, A.M.; Tightiz, L. A Novel Fuzzy Trust-based Secure Routing Scheme in Flying Ad Hoc Networks. Veh. Commun. 2023, 44, 100665. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Ali, S.; Mohammed, A.H.; Lansky, J.; Mildeova, S.; Yousefpoor, M.S.; Yousefpoor, E.; Ahmed, O.H.; Rahmani, A.M.; Mehmood, A. An energy-aware routing scheme based on a virtual relay tunnel in flying ad hoc networks. Alex. Eng. J. 2024, 91, 249–260. [Google Scholar] [CrossRef]
- Singh, V.; Sharma, K.P.; Verma, H.K. ABNT: Adaptive beaconing and neighbor timeout for geographical routing in UAV networks. Peer-Peer Netw. Appl. 2022, 3, 2079–2100. [Google Scholar] [CrossRef]
- Ren, Z.; Hussain, K.; Faheem, M. K-means online-learning routing protocol (K-MORP) for unmanned aerial vehicles (UAV) adhoc networks. Ad Hoc Netw. 2024, 3, 103354. [Google Scholar] [CrossRef]
- Zhang, H.; Lv, X.; Liu, Y.; Zou, X. Hedge transfer learning routing for dynamic searching and reconnoitering applications in 3D multimedia FANETs. Multimed. Tools Appl. 2024, 3, 7505–7539. [Google Scholar] [CrossRef] [PubMed]
- Shokrollahi, S.; Dehghan, M. TGRV: A trust-based geographic routing protocol for VANETs. Ad Hoc Netw. 2023, 3, 103062. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; Jain, V.K. A Position-based modified OLSR Routing Protocol for Flying Ad Hoc Networks. IEEE Trans. Veh. Technol. 2023, 72, 12087–12098. [Google Scholar] [CrossRef]
- Rosati, S.; Krużelecki, K.; Heitz, G.; Floreano, D.; Rimoldi, B. Dynamic routing for flying ad hoc networks. IEEE Trans. Veh. Technol. 2015, 3, 1690–1700. [Google Scholar] [CrossRef]
- Xie, P. An enhanced OLSR routing protocol based on node link expiration time and residual energy in ocean FANETS. In Proceedings of the 2018 24th Asia-Pacific Conference on Communications (APCC), Ningbo, China, 12–14 November 2018; pp. 598–603. [Google Scholar] [CrossRef]
- Khedr, A.M.; Salim, A.; PV, P.R.; Osamy, W. MWCRSF: Mobility-based weighted cluster routing scheme for FANETs. Veh. Commun. 2023, 3, 100603. [Google Scholar] [CrossRef]
- Zheng, B.; Zhuo, K.; Zhang, H.; Wu, H.X. A novel airborne greedy geographic routing protocol for flying Ad hoc networks. Wirel. Netw. 2022, 1–15. [Google Scholar] [CrossRef]
- Rahmani, A.M.; Ali, S.; Yousefpoor, E.; Yousefpoor, M.S.; Javaheri, D.; Lalbakhsh, P.; Ahmed, O.H.; Hosseinzadeh, M.; Lee, S.W. OLSR+: A new routing method based on fuzzy logic in flying ad hoc networks (FANETs). Veh. Commun. 2022, 3, 100489. [Google Scholar] [CrossRef]
- Lee, S.W.; Ali, S.; Yousefpoor, M.S.; Yousefpoor, E.; Lalbakhsh, P.; Javaheri, D.; Rahmani, A.M.; Hosseinzadeh, M. An energy-aware and predictive fuzzy logic-based routing scheme in flying ad hoc networks (fanets). IEEE Access 2021, 3, 129977–130005. [Google Scholar] [CrossRef]
- Lansky, J.; Rahmani, A.M.; Malik, M.H.; Yousefpoor, E.; Yousefpoor, M.S.; Khan, M.U.; Hosseinzadeh, M. An energy-aware routing method using firefly algorithm for flying ad hoc networks. Sci. Rep. 2023, 3, 1323. [Google Scholar] [CrossRef] [PubMed]
- Clausen, T.; Jacquet, P. (Eds.) RFC3626: Optimized Link State Routing Protocol (OLSR); The Internet Society: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Parihar, A.S.; Chakraborty, S.K.; Sharma, A.; Saini, M. A comparative study and proposal of a novel distributed mutual exclusion in UAV assisted flying ad hoc network using density-based clustering scheme. Wirel. Netw. 2023, 3, 2635–2648. [Google Scholar] [CrossRef]
- Xie, H.; Zheng, J.; He, T.; Wei, S.; Hu, C. A blockchain-based ubiquitous entity authentication and management scheme with homomorphic encryption for FANET. Peer-Peer Netw. Appl. 2024, 1–16. [Google Scholar] [CrossRef]
- Wang, X.; Shi, S.; Xue, J.; Wu, C. Controller placement in software defined FANET. Wirel. Netw. 2023, 1–14. [Google Scholar] [CrossRef]
- Parihar, A.S.; Chakraborty, S.K. Flying ad hoc network (fanet): Opportunities, trending applications and simulators. In Proceedings of the 2022 IEEE Pune Section International Conference (PuneCon), Pune, India, 15–17 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Gupta, A.; Barthwal, A.; Vardhan, H.; Kakria, S.; Kumar, S.; Parihar, A.S. Evolutionary study of distributed authentication protocols and its integration to UAV-assisted FANET. Multimed. Tools Appl. 2023, 3, 42311–42330. [Google Scholar] [CrossRef]
- Karp, B.; Kung, H.T. GPSR: Greedy perimeter stateless routing for wireless networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 243–254. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, T.; Hong, J.; Zhang, H.; Zhao, Q.; Meng, Z. Research on driving control strategy and Fuzzy logic optimization of a novel mechatronics-electro-hydraulic power coupling electric vehicle. Energy 2021, 3, 121221. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy control systems: Past, present and future. IEEE Comput. Intell. Mag. 2019, 3, 56–68. [Google Scholar] [CrossRef]
- Manzoor, S.; Manzoor, M.; Manzoor, H.; Adan, D.E.; Kayani, M.A. Which Simulator to Choose for Next Generation Wireless Network Simulations? NS-3 or OMNeT++. Eng. Proc. 2023, 3, 36. [Google Scholar] [CrossRef]
- Gomez, J.; Kfoury, E.F.; Crichigno, J.; Srivastava, G. A survey on network simulators, emulators, and testbeds used for research and education. Comput. Netw. 2023, 3, 110054. [Google Scholar] [CrossRef]
- Ergun, S.; Sammour, I.; Chalhoub, G. A survey on how network simulators serve reinforcement learning in wireless networks. Comput. Netw. 2023, 234, 109934. [Google Scholar] [CrossRef]
- Alqahtani, M.; Hu, M. Dynamic energy scheduling and routing of multiple electric vehicles using deep reinforcement learning. Energy 2022, 3, 122626. [Google Scholar] [CrossRef]
- Xie, J.; Wan, Y.; Kim, J.H.; Fu, S.; Namuduri, K. A survey and analysis of mobility models for airborne networks. IEEE Commun. Surv. Tutor. 2013, 3, 1221–1238. [Google Scholar] [CrossRef]






| Technique | Strengths | Weaknesses |
|---|---|---|
| [16] | Improving various quality of services (QoS) requirements such as PDR, delay, throughput and energy consumption, suitable for the FANET environment, high link stability, managing routing overhead, high reliability | Low scalability |
| P-OLSR [17] | Improving various QoS requirements such as PLR, throughput, and delay, increasing link stability | Low scalability, low adaptability to FANET because of not calculating an adaptive hello period |
| OLSR-ETX [18] | Improving various QoS requirements such as PLR, throughput, delay, and energy consumption | Low scalability, lack of adaptability to the FANET environment, low reliability, low link stability |
| MWCRSF [19] | Improving various QoS requirements such as throughput, delay, energy consumption, and PDR, increasing network scalability, rapid cluster construction, high cluster stability | High time complexity, not calculating an adaptive hello period |
| AGGR [20] | Improving various QoS requirements such as PDR, throughput, delay, and energy consumption, decreasing routing overhead, high adaptability to FANET | Low scalability, not solving local optimization issue, dealing with routing loops |
| OLSR+ [21] | Improving various QoS requirements such as PLR, throughput, and energy consumption, high adaptability to FANET, increasing reliability | High routing overhead, low scalability |
| [22] | Improving various QoS requirements such as PDR, throughput, delay, and energy consumption, increasing reliability | High routing overhead, low scalability, low adaptability to FANET |
| [23] | Improving various QoS requirements such as PDR, throughput, energy consumption, and delay, enhancing reliability | High routing overhead, low scalability, not calculating an adaptive hello period |
| Number | Fuzzy Inputs | Fuzzy Output | |
|---|---|---|---|
| 1 | Slow | Low | Increment |
| 2 | Slow | Medium | Changeless |
| 3 | Slow | High | Low decrement |
| 4 | Medium | Low | Changeless |
| 5 | Medium | Medium | Low decrement |
| 6 | Medium | High | Decrement |
| 7 | Fast | Low | Low decrement |
| 8 | Fast | Medium | Decrement |
| 9 | Fast | High | High decrement |
| Parameter | Value |
|---|---|
| Simulation tool | NS3 |
| Network environment | m3 |
| Number of UAVs | 10–50 |
| Velocity of UAVs | 10–50 m/s |
| Communication range of UAVs | 500 m |
| Initial energy of UAVs | 100 J |
| Execution time | 500 s |
| Packet size | 512 bytes |
| Traffic type | CBR |
| Mobility model | 3D GM |
| Mac protocol | IEEE 802. 11b |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsalami, O.M.; Yousefpoor, E.; Hosseinzadeh, M.; Lansky, J. A Novel Optimized Link-State Routing Scheme with Greedy and Perimeter Forwarding Capability in Flying Ad Hoc Networks. Mathematics 2024, 12, 1016. https://doi.org/10.3390/math12071016
Alsalami OM, Yousefpoor E, Hosseinzadeh M, Lansky J. A Novel Optimized Link-State Routing Scheme with Greedy and Perimeter Forwarding Capability in Flying Ad Hoc Networks. Mathematics. 2024; 12(7):1016. https://doi.org/10.3390/math12071016
Chicago/Turabian StyleAlsalami, Omar Mutab, Efat Yousefpoor, Mehdi Hosseinzadeh, and Jan Lansky. 2024. "A Novel Optimized Link-State Routing Scheme with Greedy and Perimeter Forwarding Capability in Flying Ad Hoc Networks" Mathematics 12, no. 7: 1016. https://doi.org/10.3390/math12071016
APA StyleAlsalami, O. M., Yousefpoor, E., Hosseinzadeh, M., & Lansky, J. (2024). A Novel Optimized Link-State Routing Scheme with Greedy and Perimeter Forwarding Capability in Flying Ad Hoc Networks. Mathematics, 12(7), 1016. https://doi.org/10.3390/math12071016







