A New Radial Basis Function Approach Based on Hermite Expansion with Respect to the Shape Parameter
Abstract
:1. Introduction
1.1. Changing the Interpolant
1.2. Changing the Basis
1.3. Current Work
2. The Radial Basis Function Method
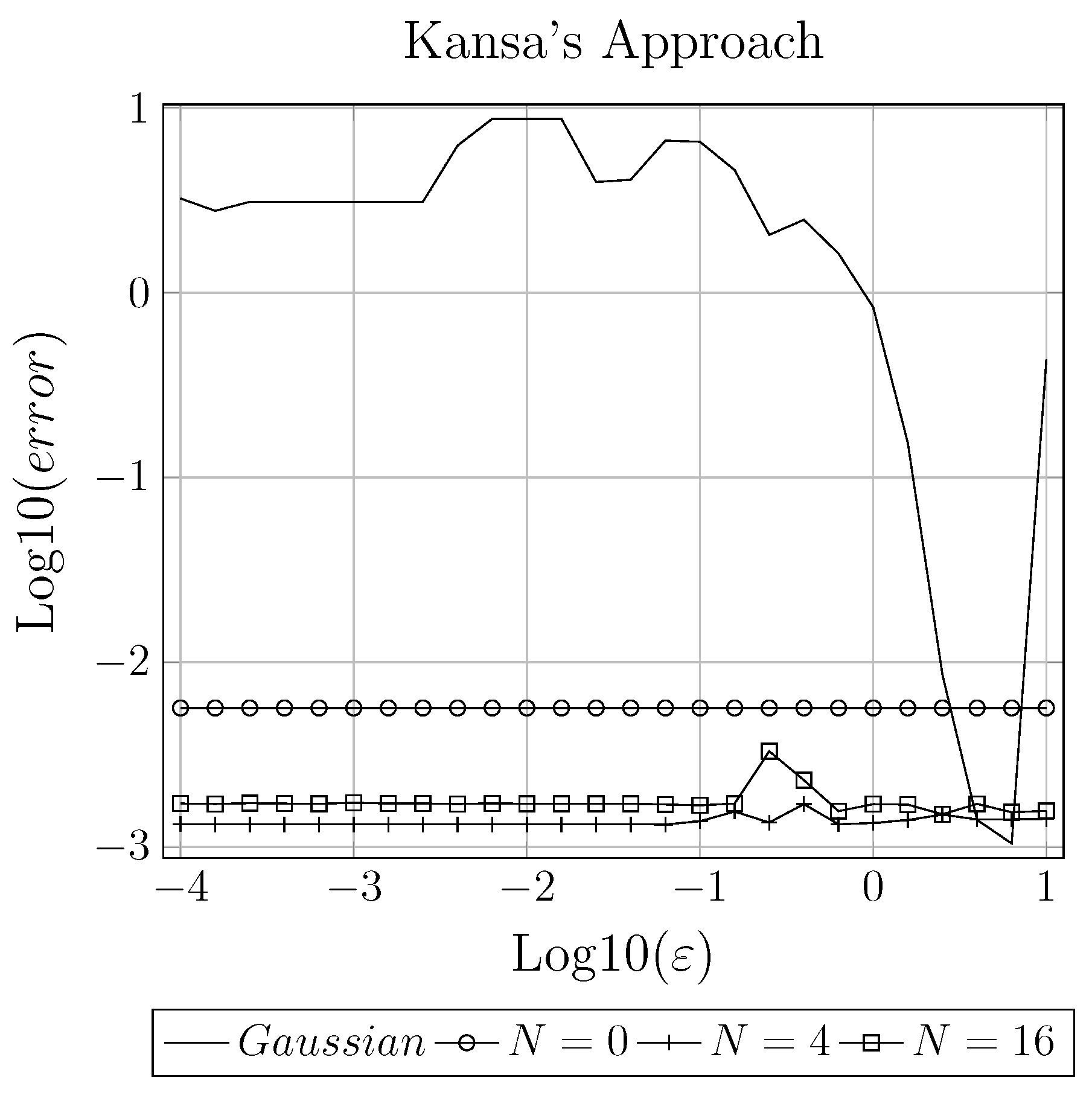
2.1. Kansa’s Approach
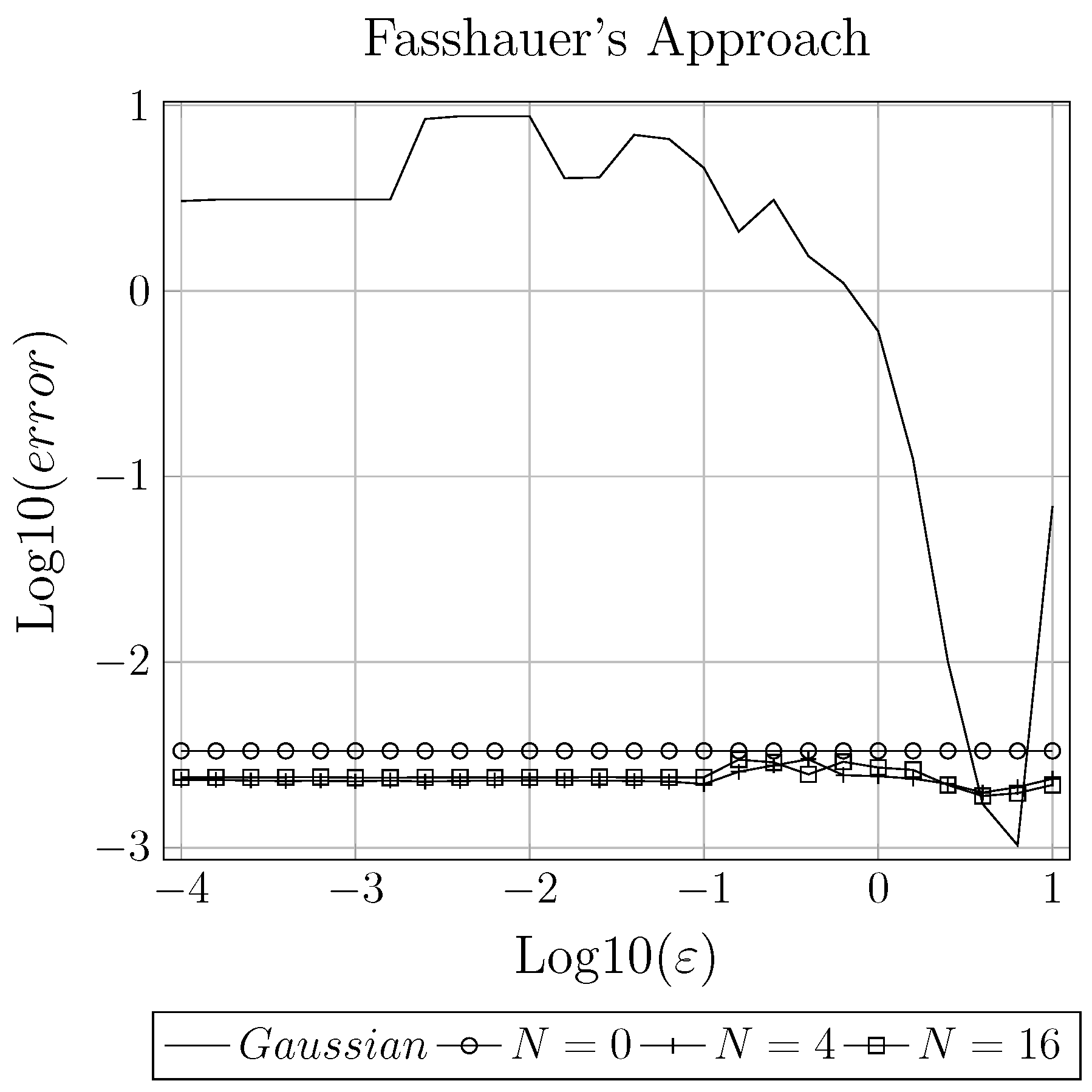
2.2. Fasshauer’s Approach
2.3. Time Integration
3. The Hermite Expansion of the Radial Basis Function
3.1. Direct Evaluation
3.2. Recursive Relations
4. Results and Discussion
4.1. General Comparison
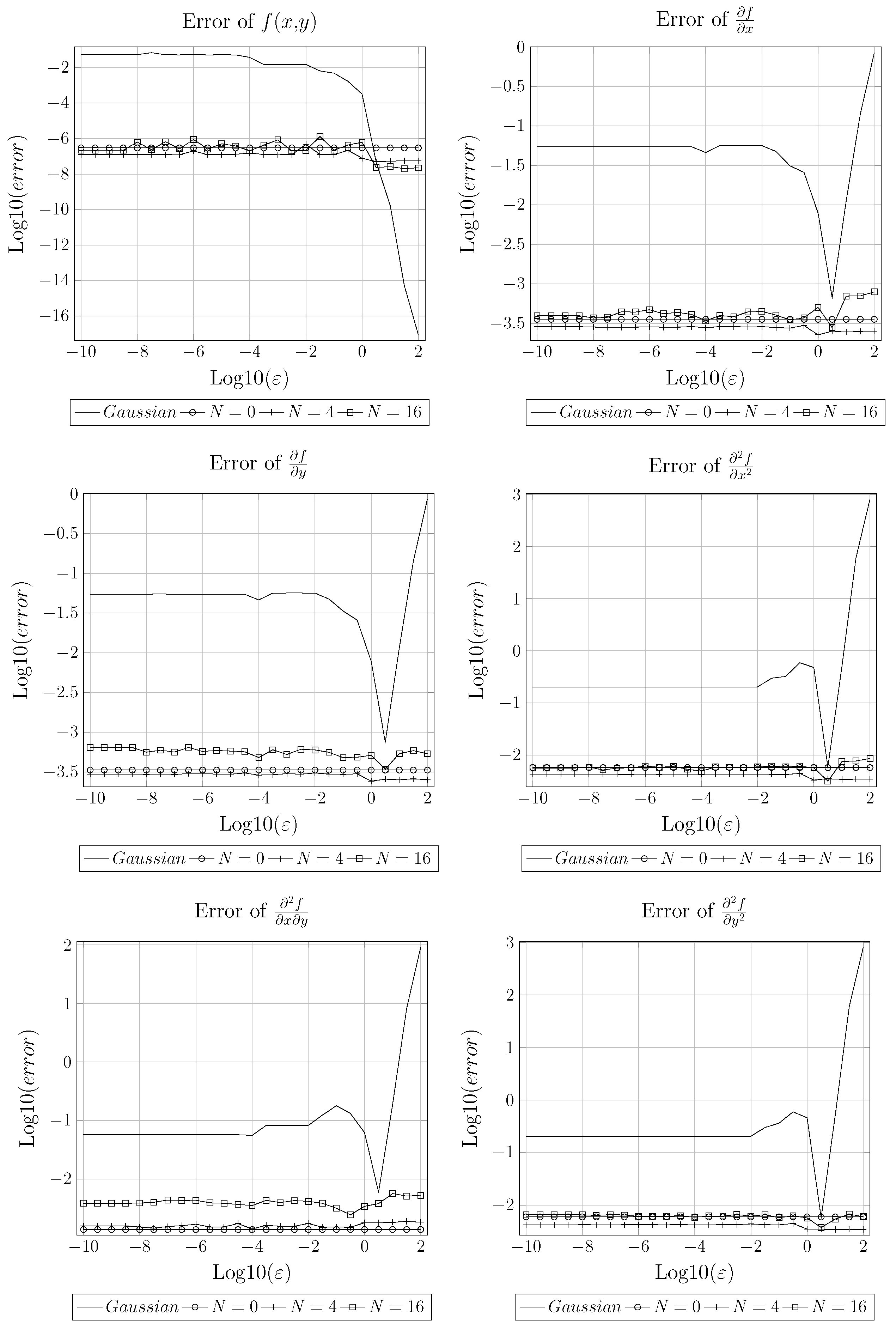
4.2. Fixing the Mesh Size and Varying
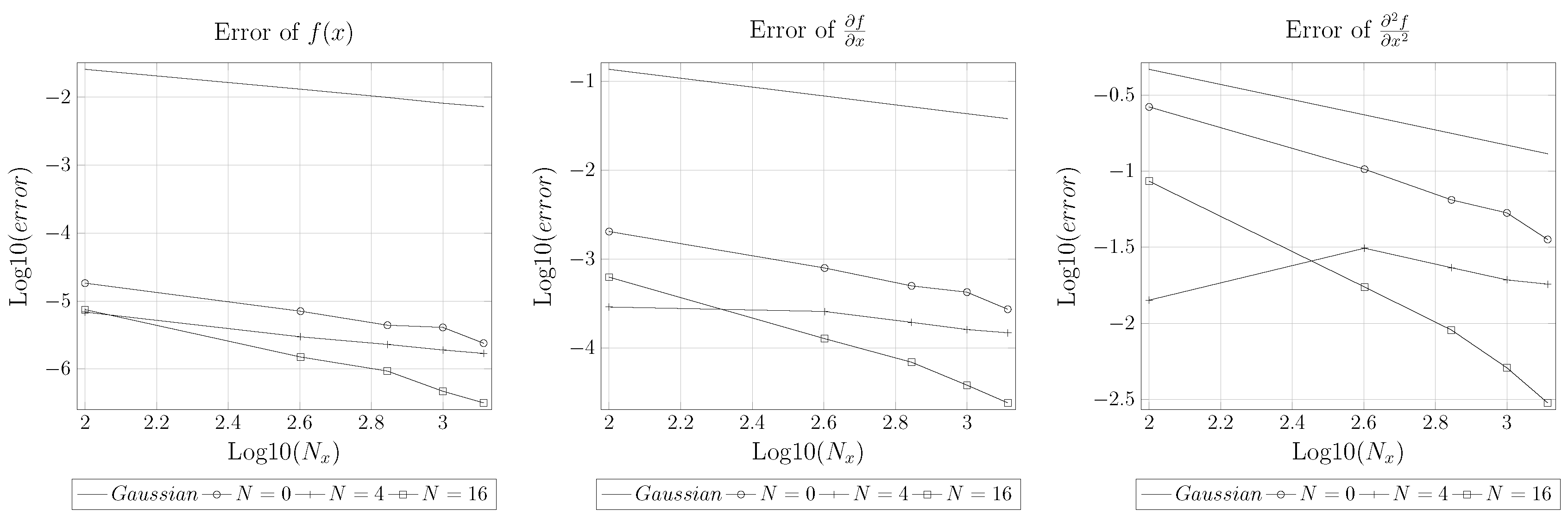
4.3. Varying the Mesh Size and Fixing (Convergence)
4.4. Comparison between the Direct and Recursive Approaches
4.5. The Advection Equation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kansa, E.J. Multiquadrics A scattered data approximation scheme with applications to computational fluid-dynamics—I surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics A scattered data approximation scheme with applications to computational fluid-dynamics—II solutions to parabolic, hyperbolic and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Solving Partial Differential Equations by Collocation with Radial Basis Functions. In Proceedings of Chamonix; Vanderbilt University Press: Nashville, TN, USA, 1996; Volume 1997, pp. 1–8. [Google Scholar]
- Jumarhon, B.; Amini, S.; Chen, K. The Hermite collocation method using radial basis functions. Eng. Anal. Bound. Elem. 2000, 24, 607–611. [Google Scholar] [CrossRef]
- Zhang, X.; Song, K.; Lu, M.; Liu, X. Meshless methods based on collocation with radial basis functions. Comput. Mech. 2000, 26, 333–343. [Google Scholar] [CrossRef]
- Power, H.; Barraco, V. A comparison analysis between unsymmetric and symmetric radial basis function collocation methods for the numerical solution of partial differential equations. Comput. Math. Appl. 2002, 43, 551–583. [Google Scholar] [CrossRef] [Green Version]
- Fasshauer, G.E. RBF collocation methods as pseudospectral methods. WIT Trans. Model. Simul. 2005, 39, 47–56. [Google Scholar]
- La Rocca, A.; Rosales, A.H.; Power, H. Radial basis function Hermite collocation approach for the solution of time dependent convection–diffusion problems. Eng. Anal. Bound. Elem. 2005, 29, 359–370. [Google Scholar] [CrossRef]
- Wright, G.B.; Fornberg, B. Scattered node compact finite difference-type formulas generated from radial basis functions. J. Comput. Phys. 2006, 212, 99–123. [Google Scholar] [CrossRef]
- Sanyasiraju, Y.; Satyanarayana, C. Local Hermite-RBF based grid-free scheme with a variable (optimal) shape parameter for steady convection-diffusion equations. Int. J. Numer. Anal. Model. Ser. B 2013, 4, 382–393. [Google Scholar]
- Rocca, A.L.; Power, H. A double boundary collocation Hermitian approach for the solution of steady state convection–diffusion problems. Comput. Math. Appl. 2008, 55, 1950–1960. [Google Scholar] [CrossRef]
- Stevens, D.; Power, H.; Lees, M.; Morvan, H. The use of PDE centres in the local RBF Hermitian method for 3D convective-diffusion problems. J. Comput. Phys. 2009, 228, 4606–4624. [Google Scholar] [CrossRef]
- La Rocca, A.; Power, H.; La Rocca, V.; Morale, M. A meshless approach based upon radial basis function hermite collocation method for predicting the cooling and the freezing times of foods. CMC Tech Sci. Press 2005, 2, 239. [Google Scholar]
- Gutierrez, G.; Baquero, O.; Valencia, J.; Florez, W. Extending the local radial basis function collocation methods for solving semi-linear partial differential equations. WIT Trans. Model. Simul. 2009, 49, 117–128. [Google Scholar] [Green Version]
- Stevens, D.; LaRocca, A.; Power, H.; LaRocca, V. A Generalised RBF Finite Difference Approach to Solve Nonlinear Heat Conduction Problems on Unstructured Datasets. In Convection and Conduction Heat Transfer; InTech Open: London, UK, 2011. [Google Scholar] [Green Version]
- Bustamante Chaverra, C.A.; Power, H.; Florez Escobar, W.F.; Hill Betancourt, A.F. Two-Dimensional Meshless Solution of the Non-Linear Convection-Diffusion-Reaction Equation by the Local Hermitian Interpolation Method. Ing. Cienc. 2013, 9, 21–51. [Google Scholar] [CrossRef]
- Libre, N.; Emdadi, A.; Kansa, E.; Rahimian, M.; Shekarchi, M. Stable PDE solution methods for large multiquadric shape parameters. CMES Comput. Model. Eng. Sci. 2008, 25, 23–41. [Google Scholar]
- Beatson, R.K.; Levesley, J.; Mouat, C. Better bases for radial basis function interpolation problems. J. Comput. Appl. Math. 2011, 236, 434–446. [Google Scholar] [CrossRef] [Green Version]
- De Marchi, S.; Santin, G. A new stable basis for radial basis function interpolation. J. Comput. Appl. Math. 2013, 253, 1–13. [Google Scholar] [CrossRef]
- Rashidinia, J.; Fasshauer, G.; Khasi, M. A stable method for the evaluation of Gaussian radial basis function solutions of interpolation and collocation problems. Comput. Math. Appl. 2016, 72, 178–193. [Google Scholar] [CrossRef]
- Yurova, A.; Kormann, K. Stable evaluation of Gaussian radial basis functions using Hermite polynomials. arXiv, 2017; arXiv:1709.02164. [Google Scholar]
- Cavoretto, R.; De Rossi, A.; Perracchione, E. RBF-PU Interpolation with Variable Subdomain Sizes and Shape Parameters. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2016; Volume 1776, p. 070003. [Google Scholar]
- Cavoretto, R.; De Marchi, S.; De Rossi, A.; Perracchione, E.; Santin, G. Partition of unity interpolation using stable kernel-based techniques. Appl. Numer. Math. 2017, 116, 95–107. [Google Scholar] [CrossRef] [Green Version]
- Fornberg, B.; Piret, C. A stable algorithm for flat radial basis functions on a sphere. SIAM J. Sci. Comput. 2007, 30, 60–80. [Google Scholar] [CrossRef]
- Fornberg, B.; Larsson, E.; Flyer, N. Stable Computations with Gaussian Radial Basis Functions in 2-D; Technical Report 2009-020; Uppsala University, Division of Scientific Computing: Uppsala, Sweden, 2009. [Google Scholar]
- Fornberg, B.; Larsson, E.; Flyer, N. Stable computations with Gaussian radial basis functions. SIAM J. Sci. Comput. 2011, 33, 869–892. [Google Scholar] [CrossRef]
- Larsson, E.; Lehto, E.; Heryudono, A.; Fornberg, B. Stable computation of differentiation matrices and scattered node stencils based on gaussian radial basis functions. SIAM J. Sci. Comput. 2013, 35, A2096–A2119. [Google Scholar] [CrossRef]
- Fornberg, B.; Lehto, E.; Powell, C. Stable calculation of Gaussian-based RBF-FD stencils. Comput. Math. Appl. 2013, 65, 627–637. [Google Scholar] [CrossRef]
- Gonnet, P.; Pachón, R.; Trefethen, L.N. Robust rational interpolation and least-squares. Electron. Trans. Numer. Anal. 2011, 38, 146–167. [Google Scholar]
- Wright, G.B.; Fornberg, B. Stable computations with flat radial basis functions using vector-valued rational approximations. J. Comput. Phys. 2017, 331, 137–156. [Google Scholar] [CrossRef] [Green Version]
- Fasshauer, G.E. Meshfree Approximation Methods with MATLAB; World Scientific: Singapore, 2007. [Google Scholar] [CrossRef]
- Lebedev, N.N. The Special Functions and Their Applications; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Sarra, S.A.; Kansa, E.J. Multiquadric Radial Basis Function Approximation Methods for the Numerical Solution of Partial Differential Equations. In Advances in Computational Mechanics; Tech Science Press: Henderson, NV, USA, 2009; Volume 2. [Google Scholar]




| n | |||||
|---|---|---|---|---|---|
| 0 | |||||
| 2 | |||||
| 4 | |||||
| 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bawazeer, S.A.; Baakeem, S.S.; Mohamad, A. A New Radial Basis Function Approach Based on Hermite Expansion with Respect to the Shape Parameter. Mathematics 2019, 7, 979. https://doi.org/10.3390/math7100979
Bawazeer SA, Baakeem SS, Mohamad A. A New Radial Basis Function Approach Based on Hermite Expansion with Respect to the Shape Parameter. Mathematics. 2019; 7(10):979. https://doi.org/10.3390/math7100979
Chicago/Turabian StyleBawazeer, Saleh Abobakur, Saleh Saeed Baakeem, and Abdulmajeed Mohamad. 2019. "A New Radial Basis Function Approach Based on Hermite Expansion with Respect to the Shape Parameter" Mathematics 7, no. 10: 979. https://doi.org/10.3390/math7100979
APA StyleBawazeer, S. A., Baakeem, S. S., & Mohamad, A. (2019). A New Radial Basis Function Approach Based on Hermite Expansion with Respect to the Shape Parameter. Mathematics, 7(10), 979. https://doi.org/10.3390/math7100979






