Convergence Theorems for Modified Inertial Viscosity Splitting Methods in Banach Spaces
Abstract
:1. Introduction
2. Preliminaries
- (i)
- ,
- (ii)
- ,
- (iii)
- implies for any subsequence .
3. Main Results
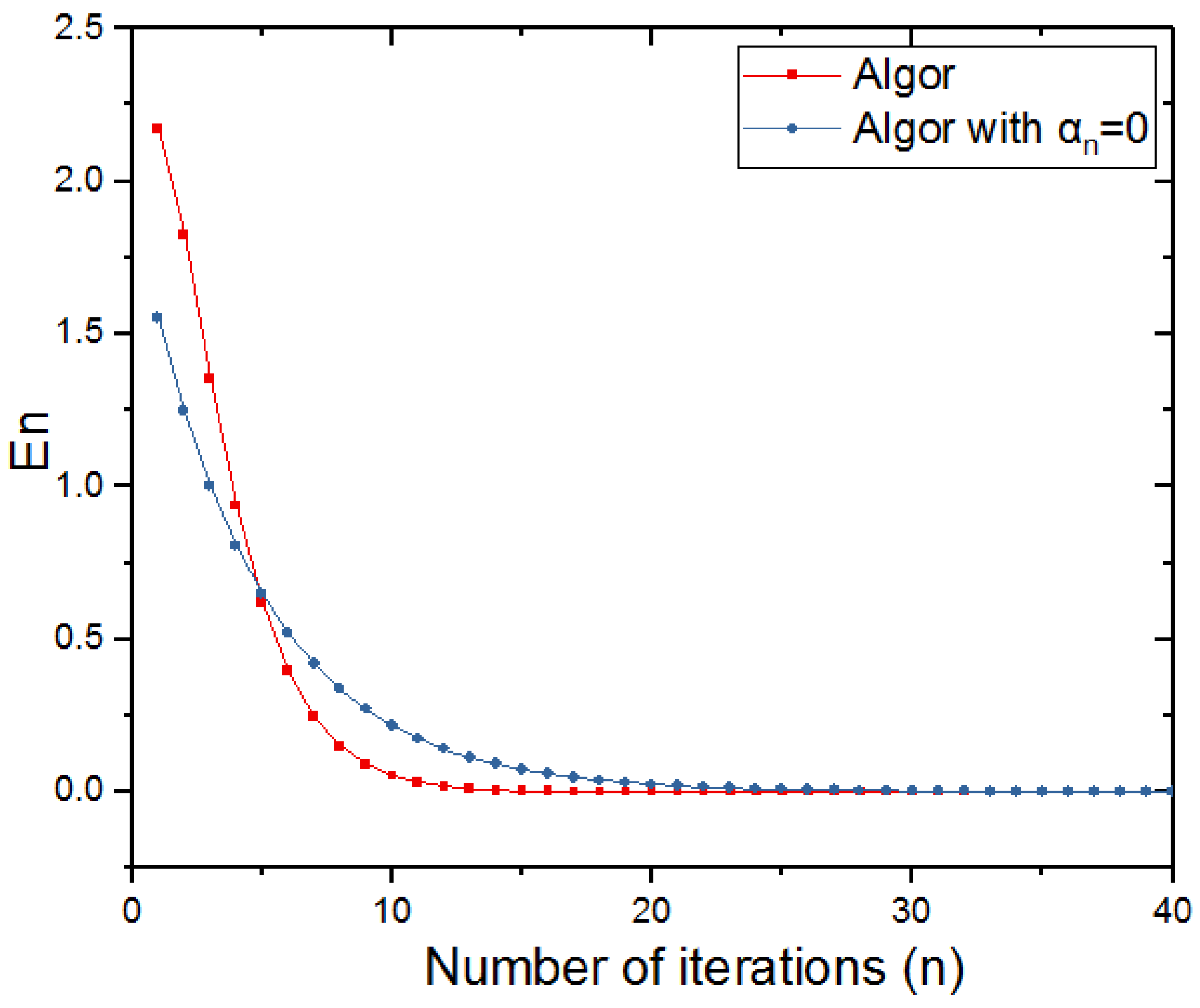
4. Applications and Numerical Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yao, Y.; Shahzad, N. Strong convergence of a proximal point algorithm with general errors. Optim. Lett. 2012, 6, 621–628. [Google Scholar] [CrossRef]
- Zhu, J.H.; University, Y. Approximation of solutions to finite family of variational inclusion and the set of common fixed point for finite family of λ-strict pseudocontraction mapping in Banach spaces. Math. Pract. Theory 2013, 43, 207–217. [Google Scholar]
- Yao, Y.H.; Chen, R.D.; Xu, H.K. Schemes for finding minimum-norm solutions of variational inequalities. Nonlinear Anal. 2010, 72, 3447–3456. [Google Scholar] [CrossRef]
- Attouch, H.; Peypouquet, J.; Redont, P. Backward–forward algorithms for structured monotone inclusions in hilbert spaces. J. Math. Anal. Appl. 2016, 457, 1095–1117. [Google Scholar] [CrossRef]
- Bagarello, F.; Cinà, M.; Gargano, F. Projector operators in clustering. Math. Methods Appl. Sci. 2016, arXiv:1605.03093. [Google Scholar] [CrossRef]
- Zegeye, H.; Shahzad, N.; Yao, Y. Minimum-norm solution of variational inequality and fixed point problem in banach spaces. Optimization 2015, 64, 453–471. [Google Scholar] [CrossRef]
- Czarnecki, M.O.; Noun, N.; Peypouquet, J. Splitting forward-backward penalty scheme for constrained variational problems. arXiv, 2014; arXiv:1408.0974. [Google Scholar]
- Takahashi, W.; Wong, N.C.; Yao, J.C. Two generalized strong convergence theorems of Halpern’s type in Hilbert spaces and applications. Taiwan. J. Math. 2012, 16, 1151–1172. [Google Scholar] [CrossRef]
- López, G.; Martínmárquez, V.; Wang, F.; Xu, H.K. Forward-Backward splitting methods for accretive operators in Banach spaces. Soc. Ind. Appl. Math. 2012, 2012, 933–947. [Google Scholar] [CrossRef]
- Pholasa, N.; Cholamjiak, P.; Cho, Y.J. Modified forward-backward splitting methods for accretive operators in Banach spaces. J. Nonlinear Sci. Appl. 2016, 9, 2766–2778. [Google Scholar] [CrossRef]
- Alvarez, F.; Attouch, H. An inertial proximal method for monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Bot, R.I.; Csetnek, E.R.; Hendrich, C. Inertial douglas–rachford splitting for monotone inclusion problems. Appl. Math. d Comput. 2015, 256, 472–487. [Google Scholar] [CrossRef]
- Suantai, S.; Pholasa, N.; Cholamjiak, P. The modified inertial relaxed cq algorithm for solving the split feasibility problems. J. Ind. Manag. Optim. 2017, 13, 1–21. [Google Scholar] [CrossRef]
- Chan, R.H.; Ma, S.; Yang, J.F. Inertial proximal ADMM for linearly constrained separable convex optimization. SIAM J. Imaging Sci. 2015, 8, 2239–2267. [Google Scholar] [CrossRef]
- Bot, R.I.; Csetnek, E.R. An inertial alternating direction method of multipliers. Mathematics 2000, arXiv:1404.4582. [Google Scholar]
- Dong, Q.L.; Cho, Y.J.; Zhong, L.L.; Rassias, T.M. Inertial projection and contraction algorithms for variational inequalities. J. Glob. Optim. 2018, 70, 687–704. [Google Scholar] [CrossRef]
- Vong, S.; Liu, D. An inertial mann algorithm for nonexpansive mappings. J. Fixed Point Theory Appl. 2018, 20, 102. [Google Scholar] [CrossRef]
- Moudafi, A.; Oliny, M. Convergence of a splitting inertial proximal method for monotone operators. J. Comput. Appl. Math. 2003, 155, 447–454. [Google Scholar] [CrossRef]
- Lorenz, D.; Pock, T. An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 2015, 51, 311–325. [Google Scholar] [CrossRef]
- Cholamjiak, W.; Cholamjiak, P.; Suantai, S. An inertial forward–backward splitting method for solving inclusion problems in Hilbert spaces. J. Fixed Point Theory Appl. 2018, 20, 42. [Google Scholar] [CrossRef]
- Xu, H.K. Viscosity approximation methods for nonexpansive mappings. J. Math. Anal. Appl. 2004, 298, 279–291. [Google Scholar] [CrossRef]
- Cioranescu, I. Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems; Band 62 von Mathematics and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Matsushita, S.; Takahashi, W. Weak and strong convergence theorems for relatively nonexpansive mappings in Banach spaces. Fixed Point Theory Appl. 2004, 2004, 829453. [Google Scholar] [CrossRef]
- Wang, Y.H.; Pan, C.J. The modified viscosity implicit rules for uniformly L-Lipschitzian asymptotically pseudocontractive mappings in Banach spaces. J. Nonlinear Sci. Appl. 2017, 10, 1582–1592. [Google Scholar] [CrossRef]
- He, S.; Yang, C. Solving the variational inequality problem defined on intersection of finite level sets. SAbstr. Appl. Anal. 2013, 2013, 942315. [Google Scholar] [CrossRef]
- Shehu, Y.; Cai, G. Strong convergence result of forward-backward splitting methods for accretive operators in banach spaces with applications. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A Matemáticas 2018, 112, 71–87. [Google Scholar] [CrossRef]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
| n | ||
|---|---|---|
| 1 | 2.1732179 | |
| 10 | ||
| 20 | ||
| 30 | ||
| 40 | ||
| 50 | ||
| 60 | ||
| 70 | ||
| 80 | ||
| 90 | ||
| 100 | ||
| 200 | ||
| 300 | ||
| 400 | ||
| 500 | ||
| 600 |
| n | ||
|---|---|---|
| 1 | 1.9308196 | |
| 10 | ||
| 20 | ||
| 30 | ||
| 40 | ||
| 50 | ||
| 60 | ||
| 70 | ||
| 80 | ||
| 90 | ||
| 100 | ||
| 200 | ||
| 300 | ||
| 400 | ||
| 500 | ||
| 600 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.; Wang, Y. Convergence Theorems for Modified Inertial Viscosity Splitting Methods in Banach Spaces. Mathematics 2019, 7, 156. https://doi.org/10.3390/math7020156
Pan C, Wang Y. Convergence Theorems for Modified Inertial Viscosity Splitting Methods in Banach Spaces. Mathematics. 2019; 7(2):156. https://doi.org/10.3390/math7020156
Chicago/Turabian StylePan, Chanjuan, and Yuanheng Wang. 2019. "Convergence Theorems for Modified Inertial Viscosity Splitting Methods in Banach Spaces" Mathematics 7, no. 2: 156. https://doi.org/10.3390/math7020156
APA StylePan, C., & Wang, Y. (2019). Convergence Theorems for Modified Inertial Viscosity Splitting Methods in Banach Spaces. Mathematics, 7(2), 156. https://doi.org/10.3390/math7020156





