Research on the Damage Model of Cold Recycled Mixtures with Asphalt Emulsion under Freeze-Thaw Cycles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Mixture Design and Preparation of the Samples
2.2.1. Mixture Design
2.2.2. Preparation of the Samples
2.3. Experimental Methods
2.3.1. Freezing and Thawing Test
- (1)
- Dry condition, namely 0% water saturation condition. The cured samples were directly covered with plastic preservative film.
- (2)
- Complete water saturation condition, namely 100% water saturation condition. Firstly, the cured samples were vacuumed for 15 min in water. The vacuum pressure was 98.3~98.7 kPa. Secondly, the vacuumed samples were kept in normal pressure water for longer than 2 h until absorbing water completely. Thirdly, the surface of vacuum saturated samples was dried through the wet cloth and covered with plastic preservative film.
- (3)
- Half water-saturation condition, namely 50% water saturation condition. The cured samples were weighed. The weighted samples were vacuum saturated according to (2). The weight of the vacuum-saturated sample was measured. The environmental furnace then reduced the weight of water absorption by half. Finally, the surface of the half water-saturated specimens was covered with plastic preservative film and placed in an indoor environment for more than 12 h.
2.3.2. Uniaxial Penetration Test
2.3.3. Indirect Tensile Test
2.4. Modeling Method
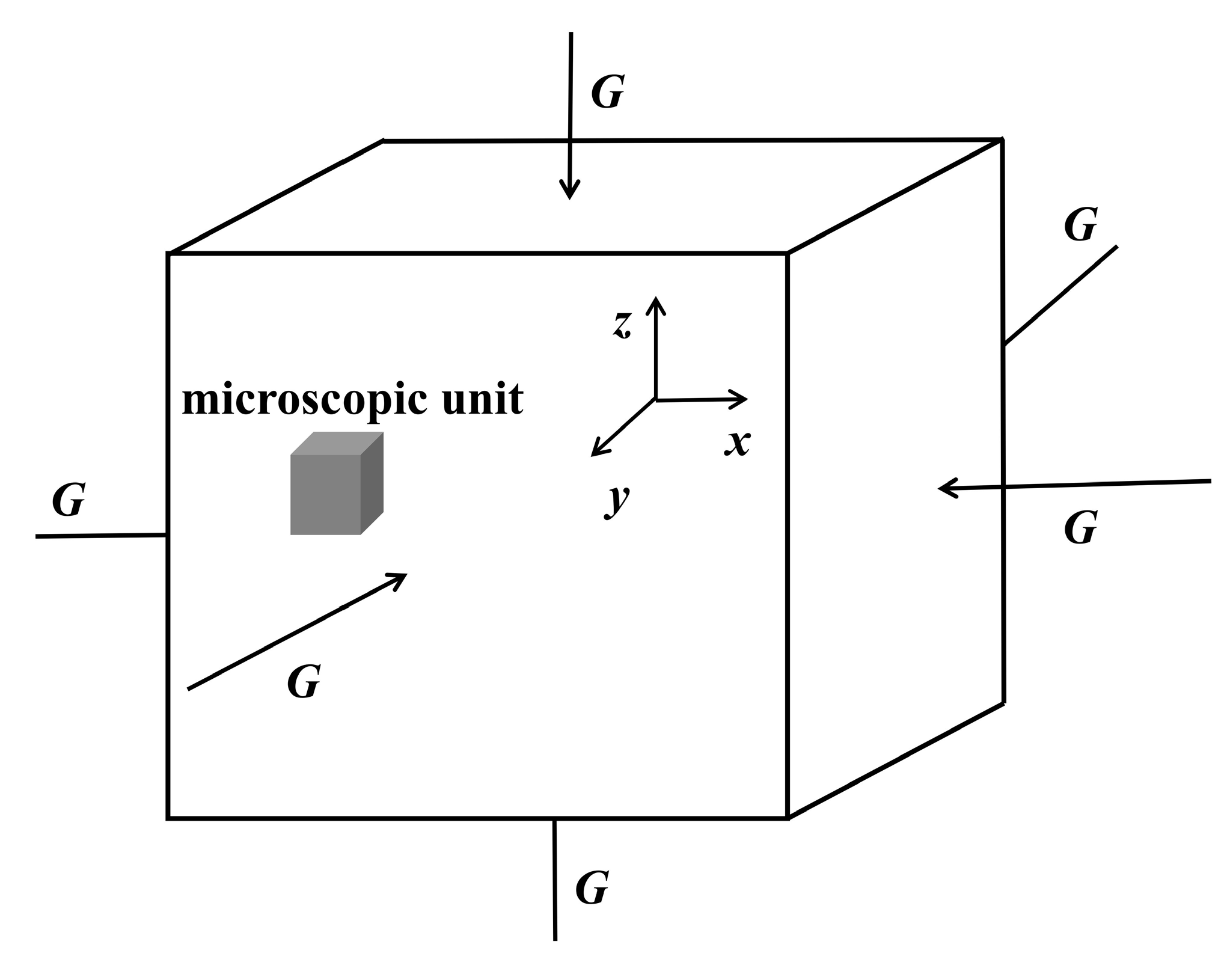
2.4.1. Basic Model Assumptions
2.4.2. Model Derivation
2.4.3. Numerical Algorithm of Damage Evolution
3. Results and Discussions
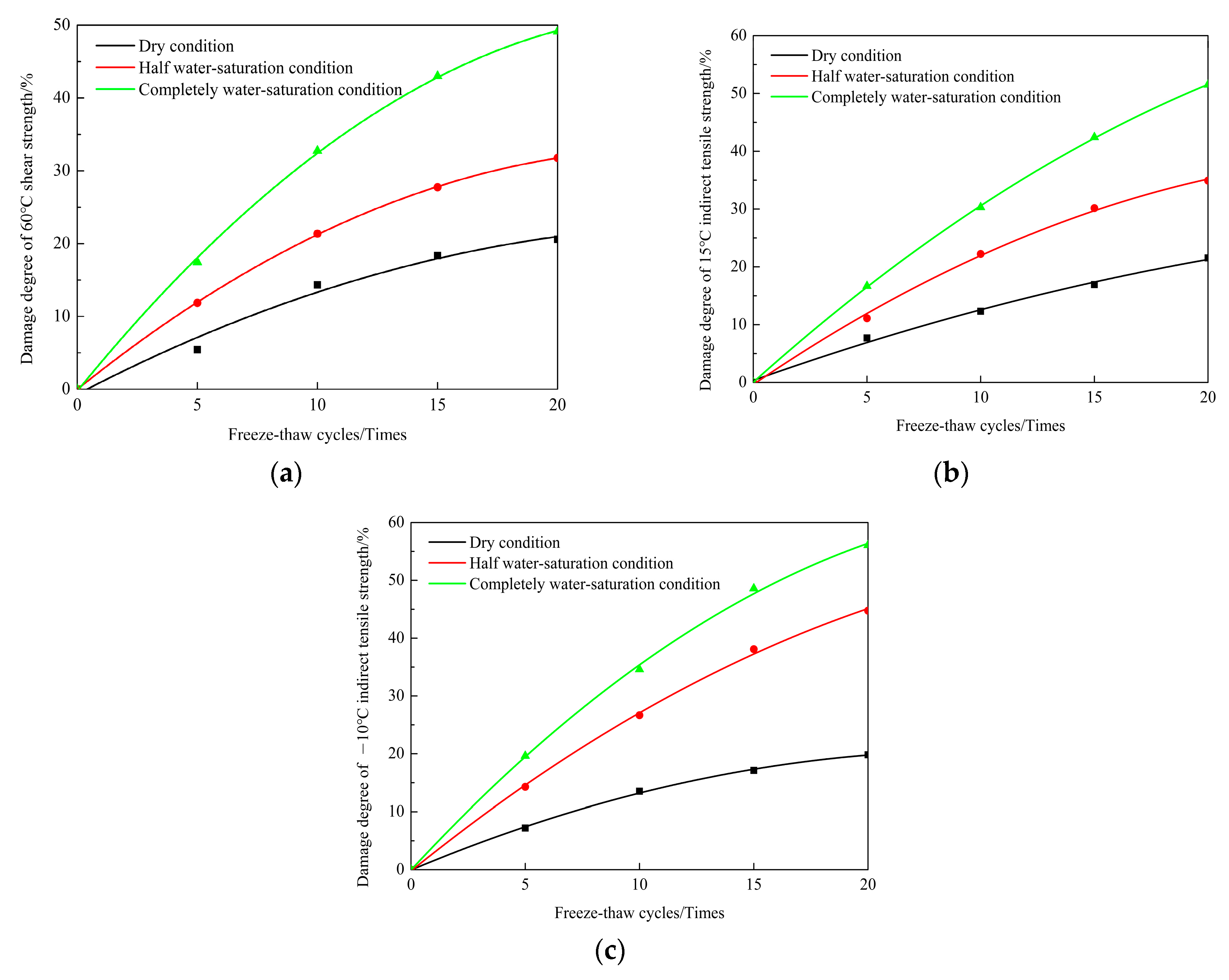
3.1. Experimental Results
3.2. Damage Models
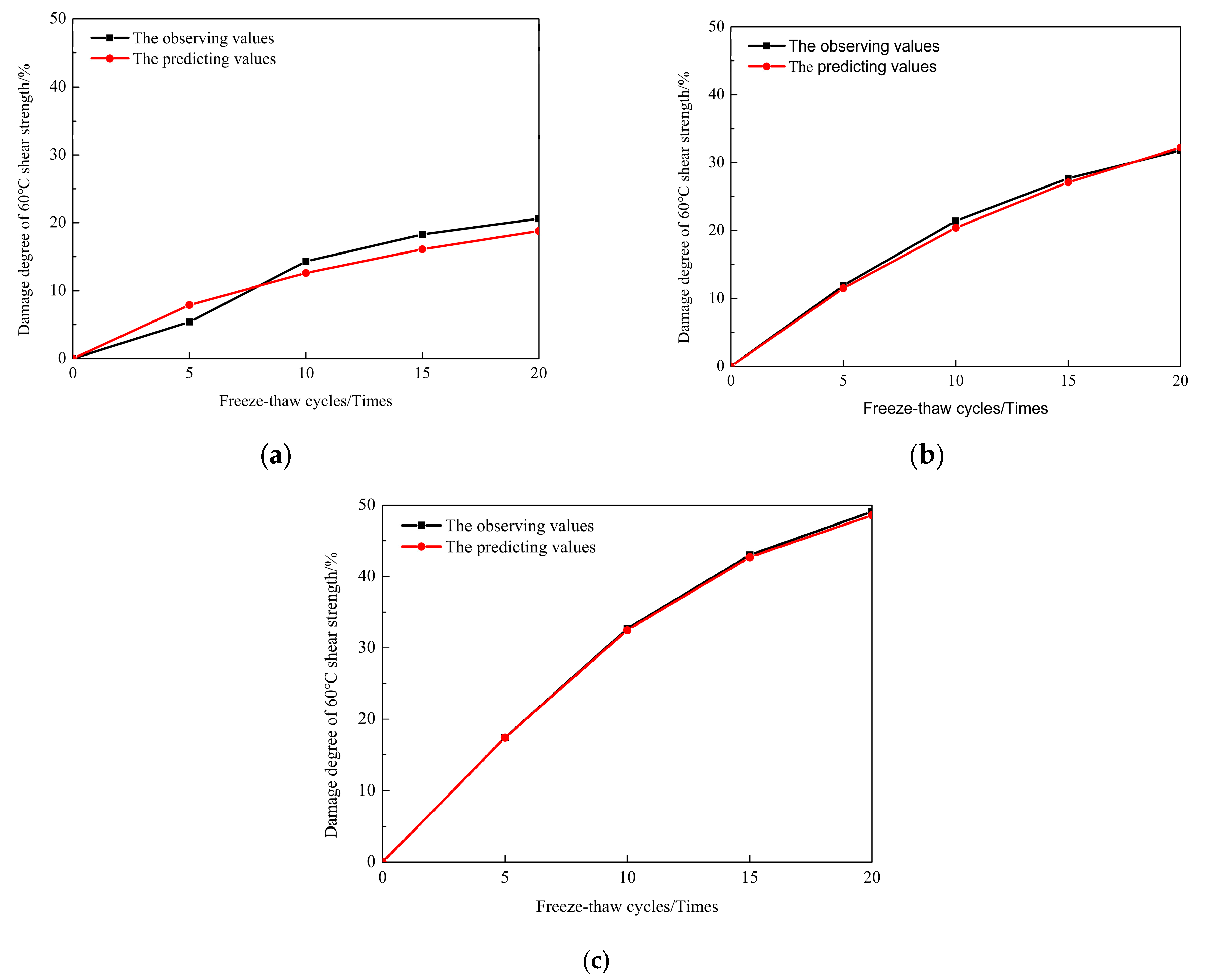
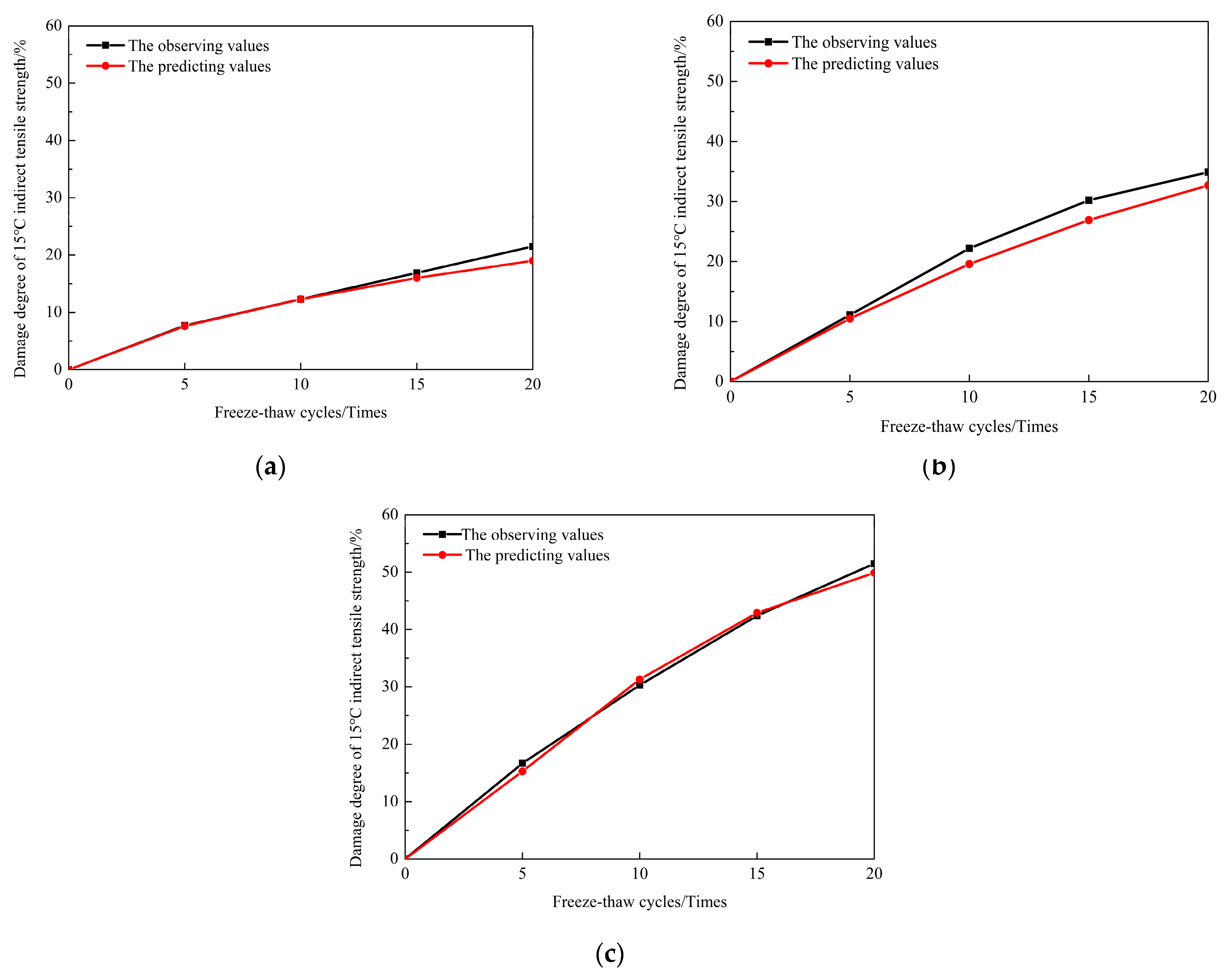
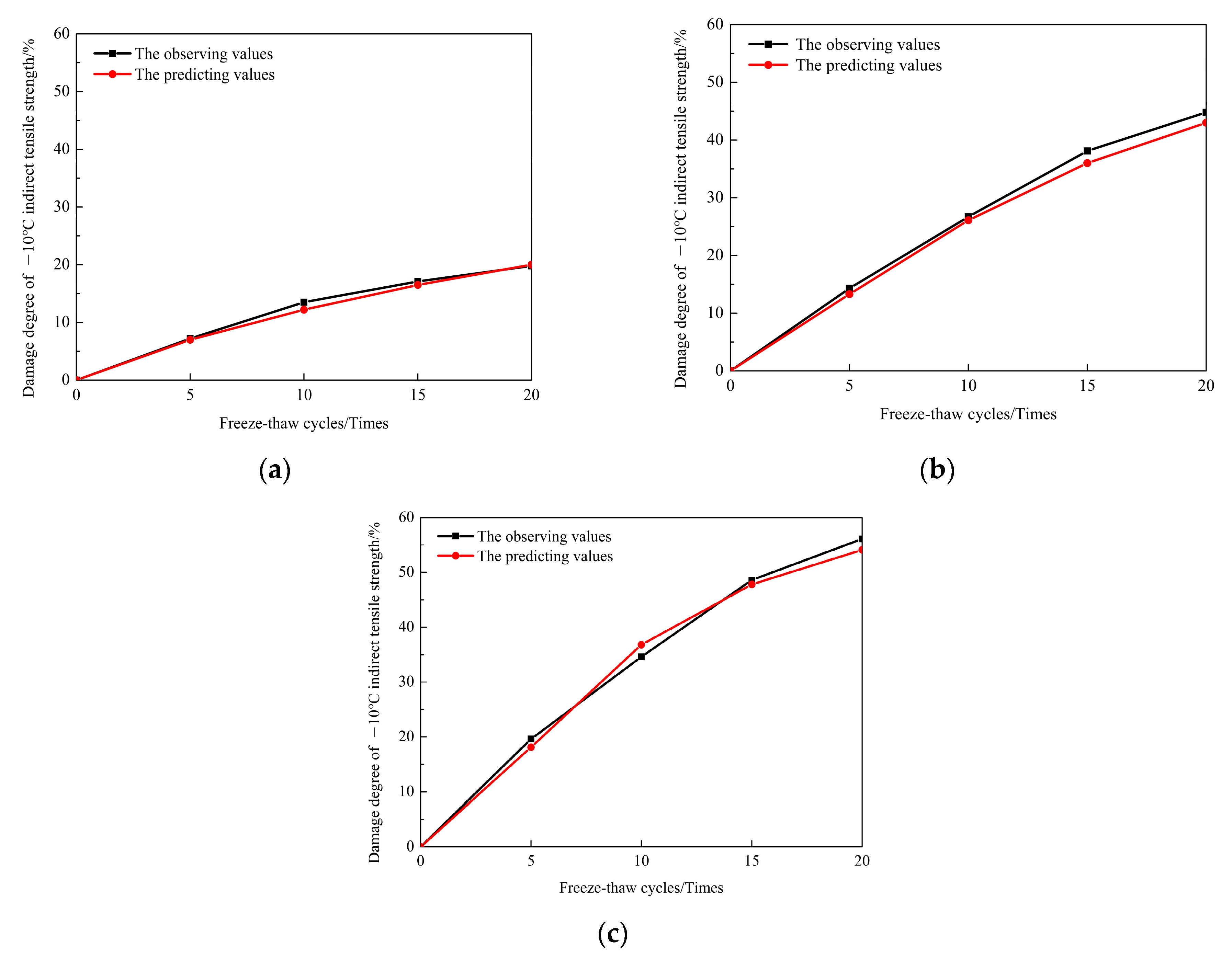
3.3. Parameter Analysis of Damage Model
4. Conclusions
- The damage degree of 60 °C shear strength and −10 °C and 15 °C indirect tensile strength of the CRME increases with the freezing and thawing cycles increasing. As the water content increases, the damage degree of performance increases significantly under freezing and thawing cycles.
- The fitting accuracy of the damage evolution model of CRME was good under freezing and thawing cycles, and the correlation coefficients were greater than 0.98.
- The shape factor and gradient factor of 60 °C shear strength and −10 °C and 15 °C indirect tensile strength gradually increased with the increasing degree of saturation. On the contrary, the scale factors gradually decreased with the increase in saturation degree.
- With the water content increasing, the generation of new voids and the interconnection of voids occurred. The homogeneity of the CRME became worse, resulting in a significant decrease in performance under freezing and thawing cycles with different water contents.
- Based on the results of the present study and other studies on the CRME subjected to freezing–thawing cycles with various water contents, it is recommended that future studies examine the fatigue performance, dynamic characteristic, and cracking behaviors and establish a multi-scale model to reflect damage mechanisms.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, W.; Cao, M.; Xiao, L.; Li, J.; Zhu, M. Experimental study on the fatigue performance of emulsified asphalt cold recycled mixtures. Constr. Build. Mater. 2023, 369, 130607. [Google Scholar] [CrossRef]
- Ji, J.; Li, J.; Wang, J.; Suo, Z.; Li, H.; Yao, H. Early strength of cold recycled emulsified asphalt mixtures. J. Mater. Civ. Eng. 2023, 35, 04023088. [Google Scholar] [CrossRef]
- Hu, G.; Yang, Q.; Qiu, X.; Zhang, D.; Zhang, W.; Xiao, S.; Xu, J. Use of DIC and AE for investigating fracture behaviors of cold recycled asphalt emulsion mixtures with 100% RAP. Constr. Build. Mater. 2022, 344, 128278. [Google Scholar] [CrossRef]
- Han, D.; Liu, G.; Xi, Y.; Zhao, Y. Research on long-term strength formation and performance evolution with curing in cold recycled asphalt mixture. Case Stud. Constr. Mater. 2023, 18, e01757. [Google Scholar] [CrossRef]
- Zhao, Z.; Ni, F.; Zheng, J.; Cheng, Z.; Xie, S. Evaluation of curing effects on bitumen emulsion-based cold in-place recycling mixture considering field-water evaporation and heat-transfer conditions. Coatings 2023, 13, 1204. [Google Scholar] [CrossRef]
- Xia, Y.; Lin, J.; Chen, Z.; Cai, J.; Hong, J.; Zhu, X. Fatigue cracking evolution and model of cold recycled asphalt mixtures during different curing times. Materials 2022, 15, 4476. [Google Scholar] [CrossRef]
- Xiao, F.; Yao, S.; Wang, J.; Li, X.; Amirkhanian, S. A literature review on cold recycling technology of asphalt pavement. Constr. Build. Mater. 2018, 180, 579–604. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, M.; Xing, X.; Pei, J.; Zhang, J.; Li, H.; Xu, P.; Wang, D. Investigation on the designing method of asphalt emulsion cold recycled mixture based on one-time compaction. J. Clean. Prod. 2021, 286, 124958. [Google Scholar] [CrossRef]
- Han, Z.; Liu, Z.; Jiang, Y.; Wu, P.; Li, S.; Sun, G.; Zhang, L. Engineering properties and air void characteristics of cold recycled mixtures with different compaction methods. J. Build. Eng. 2023, 77, 107430. [Google Scholar] [CrossRef]
- Chen, T.; Luan, Y.; Ma, T.; Zhu, J.; Ma, S. Mechanical and microstructural characteristics of different interfaces in cold recycled mixture containing cement and asphalt emulsion. J. Clean. Prod. 2020, 258, 120674. [Google Scholar] [CrossRef]
- Gao, L.; Ni, F.; Luo, H.; Charmot, S. Characterization of air voids in cold in-place recycling mixtures using X-ray computed tomography. Constr. Build. Mater. 2015, 84, 429–436. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, H.D. Performance evaluation of Cold In-Place Recycling mixtures using emulsified asphalt based on dynamic modulus, flow number, flow time, and raveling loss. KSCE J. Civ. Eng. 2012, 16, 586–593. [Google Scholar] [CrossRef]
- Jiang, J.; Ni, F.; Zheng, J.; Han, Y.; Zhao, X. Improving the high-temperature performance of cold recycled mixtures by polymer-modified asphalt emulsion. J. Pavement Eng. 2018, 21, 41–48. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, M.; Pei, J.; Zhang, J.; Li, R. Research on low temperature performance of emulsified asphalt cold recycled mixture and improvement measures based on fracture energy. Materials 2020, 13, 3176. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Leng, Z.; Li, F.; Zhu, H.; Bao, S. Early-age strength and long-term performance of asphalt emulsion cold recycled mixes with various cement contents. Constr. Build. Mater. 2017, 137, 153–159. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Qian, B. Performance and microstructure of cold recycled mixes using asphalt emulsion with different contents of cement. Materials 2019, 12, 2548. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Wang, D.; Hao, P.; Zhang, Q.; Bi, J.; Chen, W. Quantitative assessment and mechanism analysis of modification approaches for cold recycled mixtures with asphalt emulsion. J. Clean. Prod. 2021, 323, 129163. [Google Scholar] [CrossRef]
- Du, S. Effect of different fibres on the performance properties of cold recycled mixture with asphalt emulsion. J. Pavement Eng. 2021, 23, 1–10. [Google Scholar] [CrossRef]
- Xu, S.; Ruan, P.; Lu, Z.; Liang, L.; Han, B.; Hong, B. Effects of the high temperature and heavy load on the rutting resistance of cold-mix emulsified asphalt mixture. Constr. Build. Mater. 2021, 298, 123831. [Google Scholar] [CrossRef]
- Azadgoleh, M.A.; Modarres, A.; Ayar, P. Effect of polymer modified bitumen emulsion production method on the durability of recycled asphalt mixture in the presence of deicing agents. Constr. Build. Mater. 2021, 307, 124958. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, L.; Cui, H.; Yang, Y. Simulation and evaluation of fatigue damage of cold recycled mixtures with bitumen emulsion. Constr. Build. Mater. 2023, 364, 129976. [Google Scholar] [CrossRef]
- Lin, J.; Hong, J.; Xiao, Y. Dynamic characteristics of 100% cold recycled asphalt mixture using asphalt emulsion and cement. J. Clean. Prod. 2017, 156, 337–344. [Google Scholar] [CrossRef]
- Guo, W.; Guo, X.; Chen, W.; Li, Y.; Sun, M.; Dai, M. Laboratory assessment of deteriorating performance of nano hydrophobic silane silica modified asphalt in spring-thaw season. Appl. Sci. 2019, 9, 2305. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, Z.; Yang, Y.; Yue, L.; Chen, G. Effects of freeze–thaw cycles on performance and microstructure of cold recycled mixtures with asphalt emulsion. Coatings 2022, 12, 802. [Google Scholar] [CrossRef]
- Lachance-Tremblay, E.; Perraton, D.; Vaillancourt, M.; Benedetto, H. Effect of hydrated lime on linear viscoelastic properties of asphalt mixtures with glass aggregates subjected to freeze-thaw cycles. Constr. Build. Mater. 2018, 184, 58–67. [Google Scholar] [CrossRef]
- You, L.; You, Z.; Dai, Q.; Guo, S.; Wang, J.; Schultz, M. Characteristics of water-foamed asphalt mixture under multiple freeze-thaw cycles, Laboratory evaluation. J. Mater. Civ. Eng. 2018, 30, 04018270. [Google Scholar] [CrossRef]
- Fan, Z.; Xu, H.; Xiao, J.; Tan, Y. Effects of freeze-thaw cycles on fatigue performance of asphalt mixture and development of fatigue-freeze-thaw (FFT) uniform equation. Constr. Build. Mater. 2020, 242, 118043. [Google Scholar] [CrossRef]
- Fu, L.; Zhou, H.; Yuan, P.; An, W.; Chen, X. Damage fracture characterization of asphalt mixtures considering freeze-thaw cycling and aging effects based on acoustic emission monitoring. Materials 2021, 14, 5930. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y.; Zhu, C.; Liu, H.; Ma, C.; Wang, X.; Qu, T. High- and low-temperature fracture behavior of pervious asphalt mixtures under different freeze–thaw cycles based on acoustic emission technique. Arab. J. Geosci. 2022, 15, 1542. [Google Scholar] [CrossRef]
- Ud Din, I.M.; Mir, M.S.; Farooq, M.A. Effect of freeze-thaw cycles on the properties of asphalt pavements in cold regions: A Review. Transp. Res. Procedia 2020, 48, 3634–3641. [Google Scholar] [CrossRef]
- Xu, H.; Guo, W.; Tan, Y. Internal structure evolution of asphalt mixtures during freeze-thaw cycles. Mater. Des. 2015, 86, 436–446. [Google Scholar] [CrossRef]
- Xu, H.; Shi, H.; Zhang, H.; Li, H.; Leng, Z.; Tan, Y. Evolution of dynamic flow behavior in asphalt mixtures exposed to freeze-thaw cycles. Constr. Build. Mater. 2020, 255, 119320. [Google Scholar] [CrossRef]
- Wang, J.; Yu, X.; Ding, G.; Si, J.; Xing, M.; Xie, R. Strength and toughness attenuation mechanism of biobased cold-mixed epoxy asphalt under freeze–thaw cycles. Int. J. Pavement Eng. 2022, 1–9. [Google Scholar] [CrossRef]
- Jin, D.; Yin, L.; Xin, K.; You, Z. Comparison of asphalt emulsion-based chip seal and hot rubber asphalt-based chip seal. Case Stud. Constr. Mater. 2023, 18, e02175. [Google Scholar] [CrossRef]
- Zhao, H.; Ren, J.; Chen, Z.; Luan, H.; Yi, J. Freeze and thaw field investigation of foamed asphalt cold recycling mixture in cold region. Case Stud. Constr. Mater. 2021, 15, e00710. [Google Scholar] [CrossRef]
- Lövqvist, L.; Balieu, R.; Kringos, N. Multiscale model for predicting freeze-thaw damage in asphalt mixtures. Int. J. Pavement Eng. 2022, 23, 5048–5065. [Google Scholar] [CrossRef]
- Cheng, Y.; Yu, D.; Tan, G.; Zhu, C. Low-temperature performance and damage constitutive model of eco-friendly basalt fiber–diatomite-modified asphalt mixture under freeze–thaw cycles. Materials 2018, 11, 2148. [Google Scholar] [CrossRef]
- Yang, Y.; Cui, H.; Yang, Y.; Zhang, H.; Liu, H. Effect of freeze-thaw cycle on performance of unsaturated emulsified asphalt cold recycled mixture. J. Jilin Univ. Eng. Technol. Ed. 2022, 52, 2352–2359. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Yang, Y. Characterization of air voids in cold recycled mixtures with emulsified asphalt under freeze-thaw cycles. Mater. Rev. 2022, 36, 69–75. [Google Scholar]
- JTG T5521-2019; Technical Specifications for Highway Asphalt Pavement Recycling. China Communications Press: Beijing, China, 2019.
- JTG F40-2004; Technical Specifications for Construction of Highway Asphalt Pavements. China Communications Press: Beijing, China, 2004.
- JTG E40-2007; Test Methods of Soils for Highway Engineering. China Communications Press: Beijing, China, 2007.
- Duojie, C.; Si, W.; Ma, B.; Hu, Y.; Xue, L.; Wang, X. Assessment of freeze-thaw cycles impact on flexural tensile characteristics of asphalt mixture in cold regions. Math. Probl. Eng. 2021, 2021, 6697693. [Google Scholar] [CrossRef]
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. China Communications Press: Beijing, China, 2017.
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. China Communications Press: Beijing, China, 2011.
- Tan, Y.; Zhao, L.; Lan, B.; Liang, M. Research on freeze-thaw damage model and life prediction of asphalt mixture. J. Highw. Transp. Res. Dev. 2011, 28, 1–7. [Google Scholar]
- Chen, Y.; Yu, D.; Tan, G.; Wang, W.; Zhang, P. Evolution on freeze-thaw damage of basalt fiber asphalt mixture. J. Harbin Eng. Univ. 2019, 40, 518–524. [Google Scholar]


| Characteristic | Requirements | Results |
|---|---|---|
| Demulsification speed | Slow-cracking | Slow-cracking |
| Particle charge | Cation (+) | Cation (+) |
| Remained content on 1.18 mm/wt% | ≤0.1 | 0.021 |
| Solid content/wt% | >60 | 63.6 |
| Penetration (25 °C, 100 g, 5 s)/0.1 mm | 50~130 | 69.5 |
| Softening point/°C | — | 45.6 |
| Ductility (15 °C)/cm | ≥40 | 76.5 |
| Solubility in trichloroethylene/wt% | ≥97.5 | 99.1 |
| Storage stability at 1 d/wt% | ≤1 | 0.4 |
| Storage stability at 5 d/wt% | ≤5 | 2.6 |
| Size/mm | 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Passing rate/% | RAP (68.95%) | 100 | 100 | 88.8 | 78.7 | 63.5 | 38.1 | 22.8 | 13.7 | 7.6 | 4.1 | 2.0 | 1.0 |
| New Aggregate (29.55%) | 100 | 93.9 | 88.8 | 78.7 | 63.5 | 38.1 | 22.8 | 13.7 | 7.6 | 4.1 | 2.0 | 1.0 | |
| Freeze-Thaw Cycles/Times | 60 °C Shear Strength/MPa | 15 °C Indirect Tensile Strength/MPa | −10 °C Indirect Tensile Strength/MPa | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dry Condition | Half Water Saturation Condition | Complete Water Saturation Condition | Dry Condition | Half Water Saturation Condition | Complete Water Saturation Condition | Dry Condition | Half Water Saturation Condition | Complete Water Saturation Condition | |
| 0 | 0.573 (0.041) | 0.548 (0.040) | 0.556 (0.039) | 0.65 (0.023) | 0.63 (0.015) | 0.66 (0.003) | 1.11 (0.008) | 1.05 (0.012) | 1.07 (0.019) |
| 5 | 0.542 (0.024) | 0.483 (0.033) | 0.459 (0.057) | 0.60 (0.016) | 0.56 (0.011) | 0.55 (0.003) | 1.03 (0.023) | 0.90 (0.018) | 0.86 (0.010) |
| 10 | 0.491 (0.015) | 0.431 (0.018) | 0.374 (0.020) | 0.57 (0.011) | 0.49 (0.007) | 0.46 (0.008) | 0.96 (0.031) | 0.77 (0.026) | 0.70 (0.009) |
| 15 | 0.468 (0.029) | 0.396 (0.022) | 0.317 (0.012) | 0.54 (0.005) | 0.44 (0.012) | 0.38 (0.007) | 0.92 (0.014) | 0.65 (0.009) | 0.55 (0.011) |
| 20 | 0.455 (0.038) | 0.374 (0.031) | 0.283 (0.019) | 0.51 (0.017) | 0.41 (0.006) | 0.32 (0.008) | 0.86 (0.014) | 0.58 (0.006) | 0.47 (0.007) |
| Freeze-Thaw Cycles/Times | Damage Degree of 60 °C Shear Strength/% | Damage Degree of 15 °C Indirect Tensile Strength/% | Damage Degree of −10 °C Indirect Tensile Strength/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Dry Condition | Half Water Saturation Condition | Complete Water Saturation Condition | Dry Condition | Half Water Saturation Condition | Complete Water Saturation Condition | Dry Condition | Half Water Saturation Condition | Complete Water Saturation Condition | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 7.7 | 11.1 | 16.7 | 5.4 | 11.9 | 17.4 | 7.2 | 14.3 | 19.6 |
| 10 | 12.3 | 22.2 | 30.3 | 14.3 | 21.4 | 32.7 | 13.5 | 26.7 | 34.6 |
| 15 | 16.9 | 30.2 | 42.4 | 18.3 | 27.7 | 43.0 | 17.1 | 38.1 | 48.6 |
| 20 | 21.5 | 34.9 | 51.5 | 20.6 | 31.8 | 49.1 | 19.8 | 44.8 | 56.1 |
| Performance | Water-Saturated Condition | Correlation Coefficient | Parameters of Damage Model | ||
|---|---|---|---|---|---|
| The Shape Factor α | The Scale Factor λ | The Gradient Factor v | |||
| 15 °C indirect tensile strength | Dry condition | 0.995 | 0.7873 | 0.0208 | 0.0197 |
| Half water saturation condition | 0.997 | 1.0427 | 0.0455 | 0.0451 | |
| Complete water saturation condition | 0.996 | 1.3223 | 0.0838 | 0.0831 | |
| 60 °C shear strength | Dry condition | 0.985 | 0.7821 | 0.0252 | 0.0218 |
| Half water saturation condition | 0.998 | 0.9898 | 0.0488 | 0.0466 | |
| Complete water saturation condition | 0.999 | 1.2009 | 0.0875 | 0.0871 | |
| −10 °C indirect tensile strength | Dry condition | 0.994 | 0.9115 | 0.0265 | 0.0234 |
| Half water saturation condition | 0.999 | 1.2011 | 0.0675 | 0.0668 | |
| Complete water saturation condition | 0.988 | 1.4273 | 0.1046 | 0.0988 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Sun, Z.; Yang, Y.; Wang, C.; Qi, L. Research on the Damage Model of Cold Recycled Mixtures with Asphalt Emulsion under Freeze-Thaw Cycles. Processes 2023, 11, 3031. https://doi.org/10.3390/pr11103031
Yang Y, Sun Z, Yang Y, Wang C, Qi L. Research on the Damage Model of Cold Recycled Mixtures with Asphalt Emulsion under Freeze-Thaw Cycles. Processes. 2023; 11(10):3031. https://doi.org/10.3390/pr11103031
Chicago/Turabian StyleYang, Ye, Zongguang Sun, Yanhai Yang, Chonghua Wang, and Lin Qi. 2023. "Research on the Damage Model of Cold Recycled Mixtures with Asphalt Emulsion under Freeze-Thaw Cycles" Processes 11, no. 10: 3031. https://doi.org/10.3390/pr11103031
APA StyleYang, Y., Sun, Z., Yang, Y., Wang, C., & Qi, L. (2023). Research on the Damage Model of Cold Recycled Mixtures with Asphalt Emulsion under Freeze-Thaw Cycles. Processes, 11(10), 3031. https://doi.org/10.3390/pr11103031








