Iterative Tomographic Image Reconstruction Algorithm Based on Extended Power Divergence by Dynamic Parameter Tuning
Abstract
1. Introduction
2. Proposed Method
2.1. Definition and Properties of EPD
2.2. Iterative Reconstruction Algorithm by Dynamic Parameter Tuning
| Algorithm 1 Procedure of PXEM algorithm |
Require: , , , , ,
|
| Algorithm 2 Procedure of PDEM algorithm |
Require: , , , , ,
|
2.3. Practical Strategy for Dynamic Parameter Tuning Using Reduced-Size System
| Algorithm 3 Procedure of PREM algorithm |
Require: , , , , , , , ,
|
3. Experiment
3.1. Experimental Method
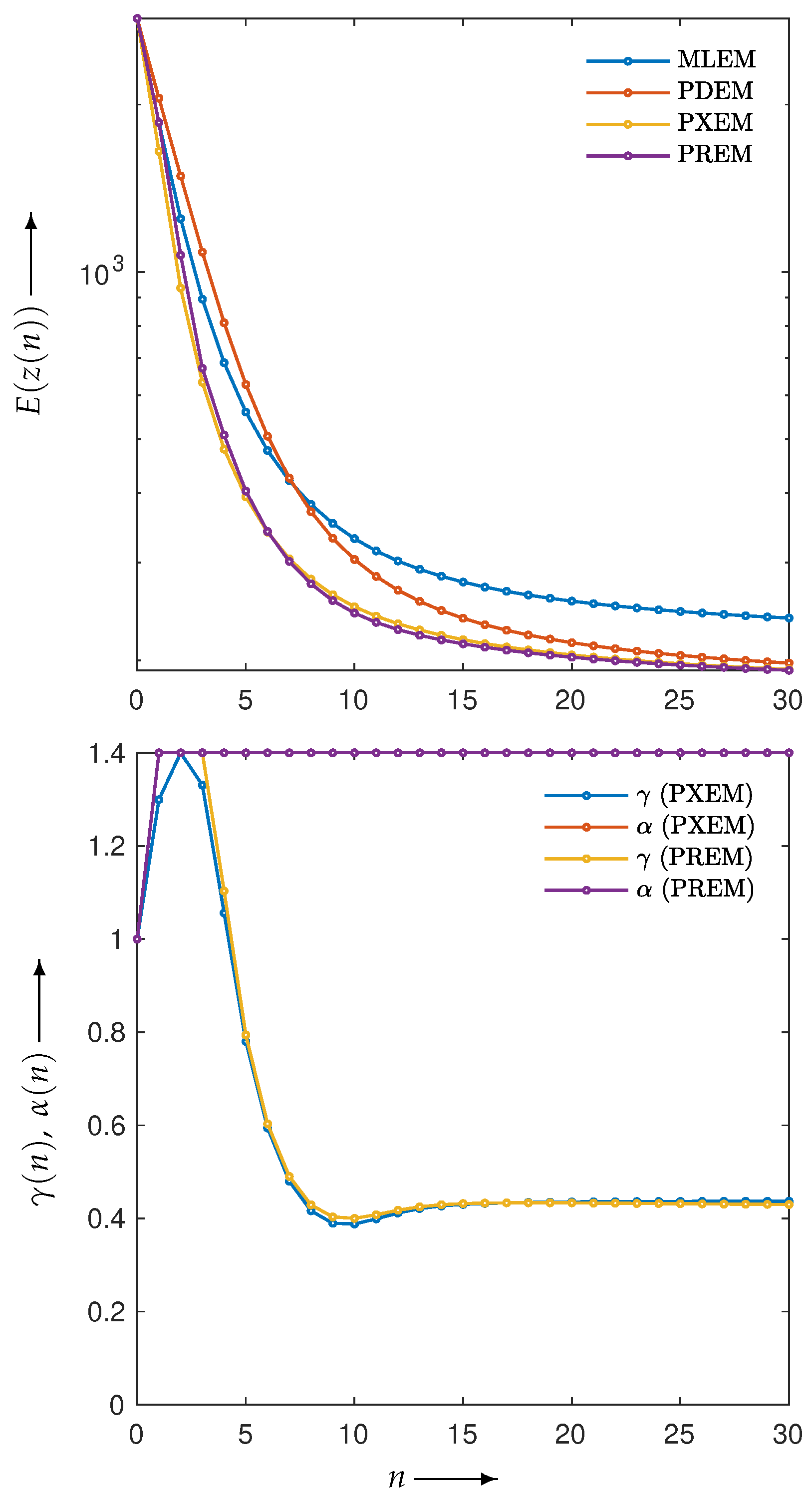
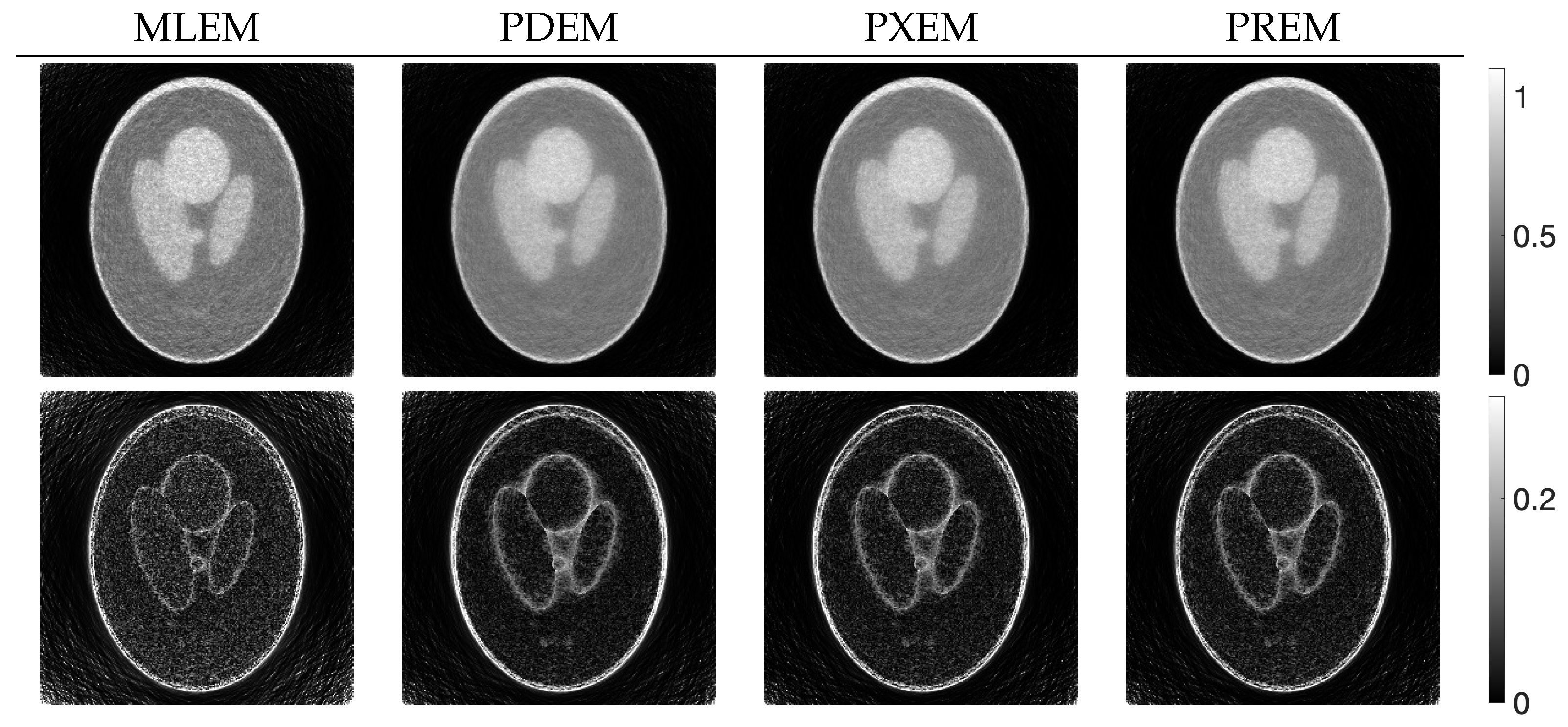
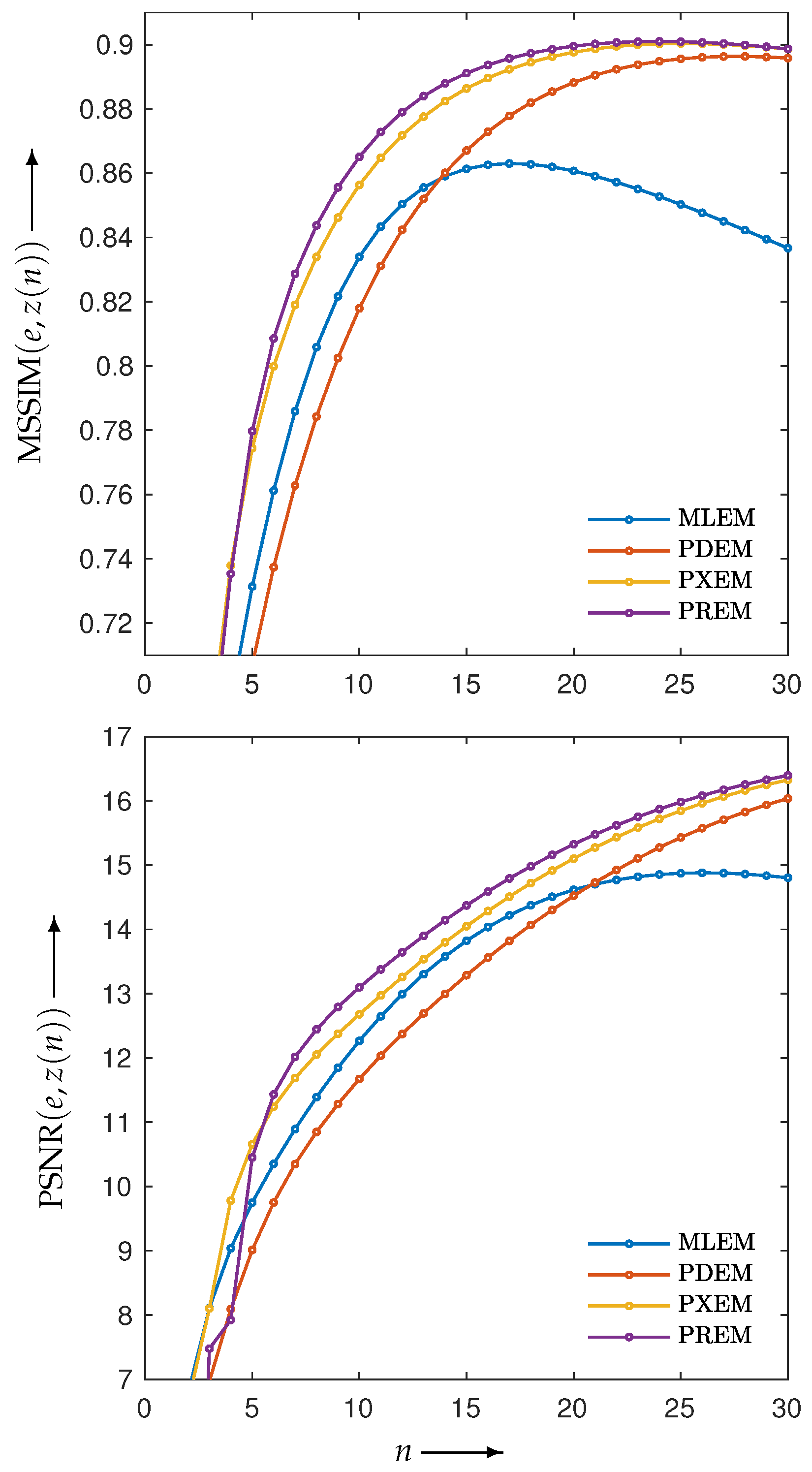
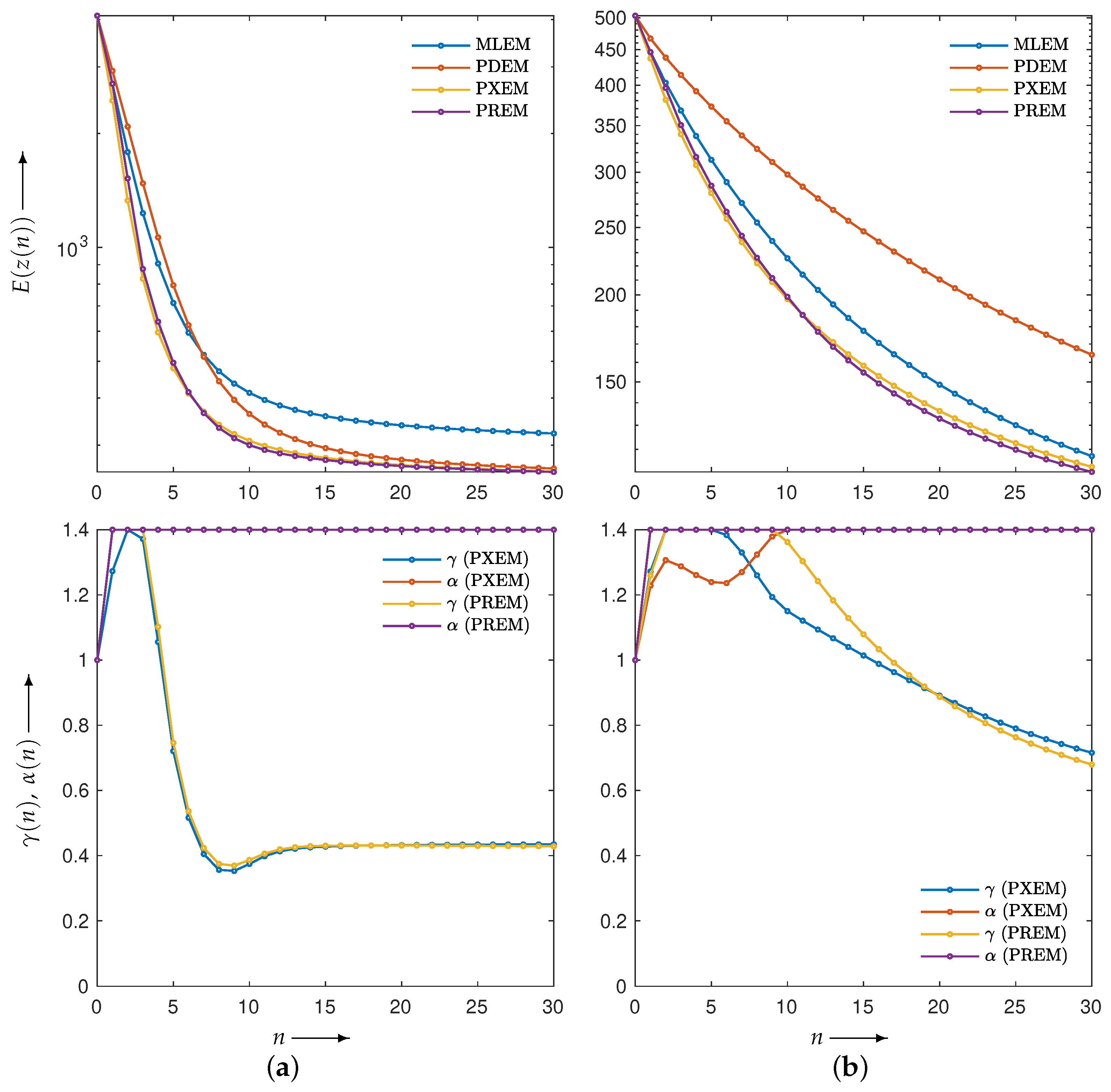
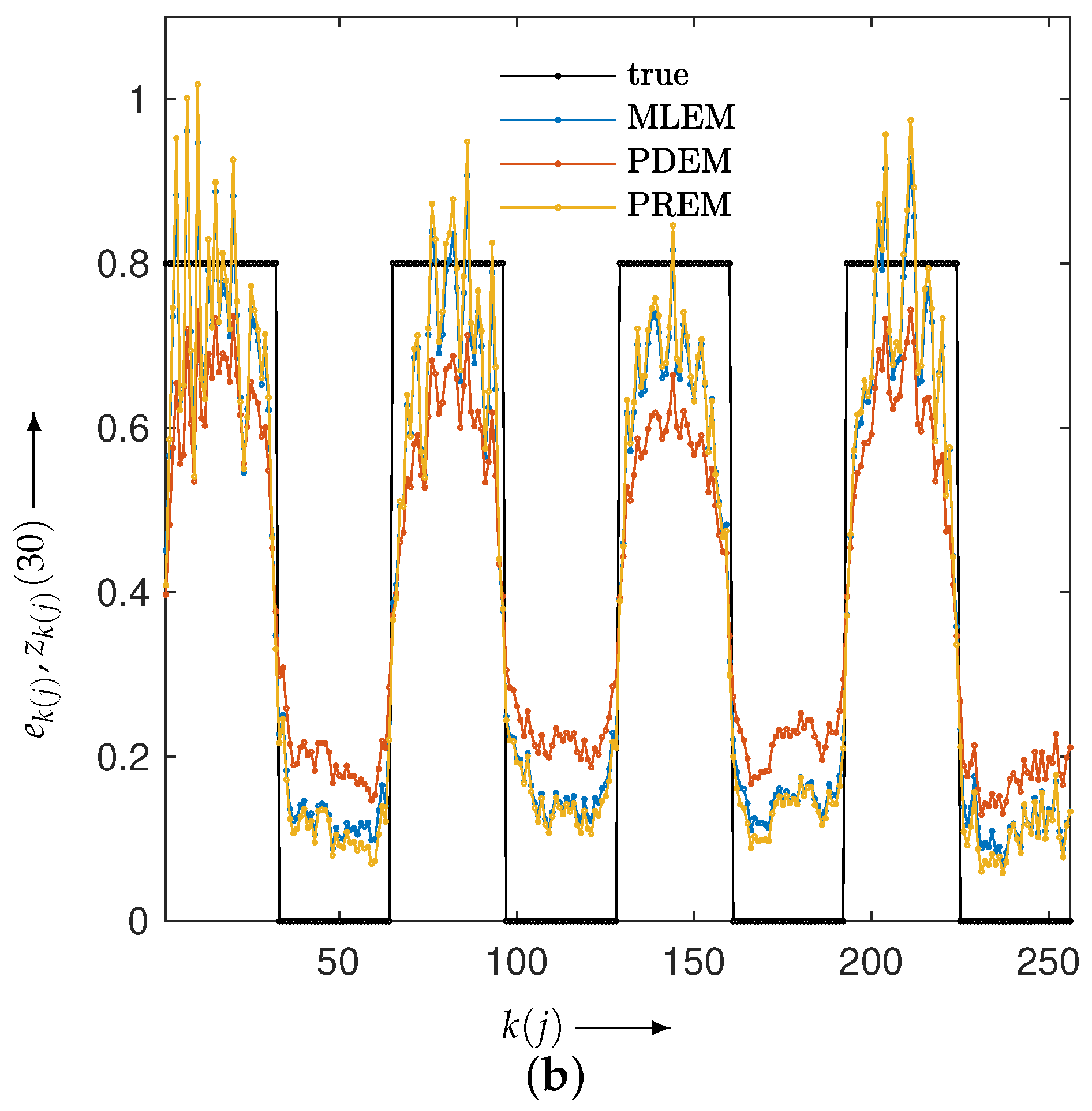
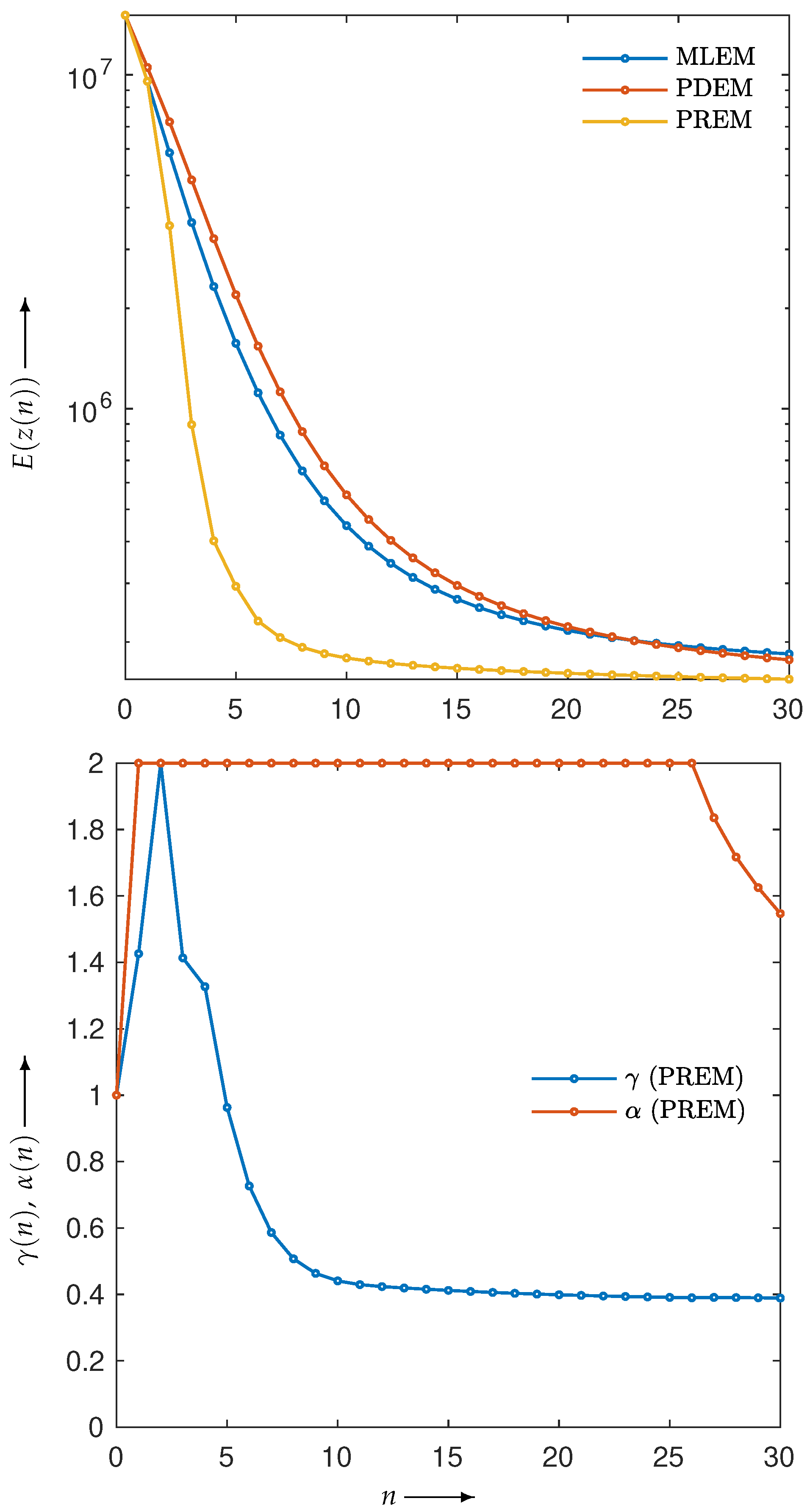
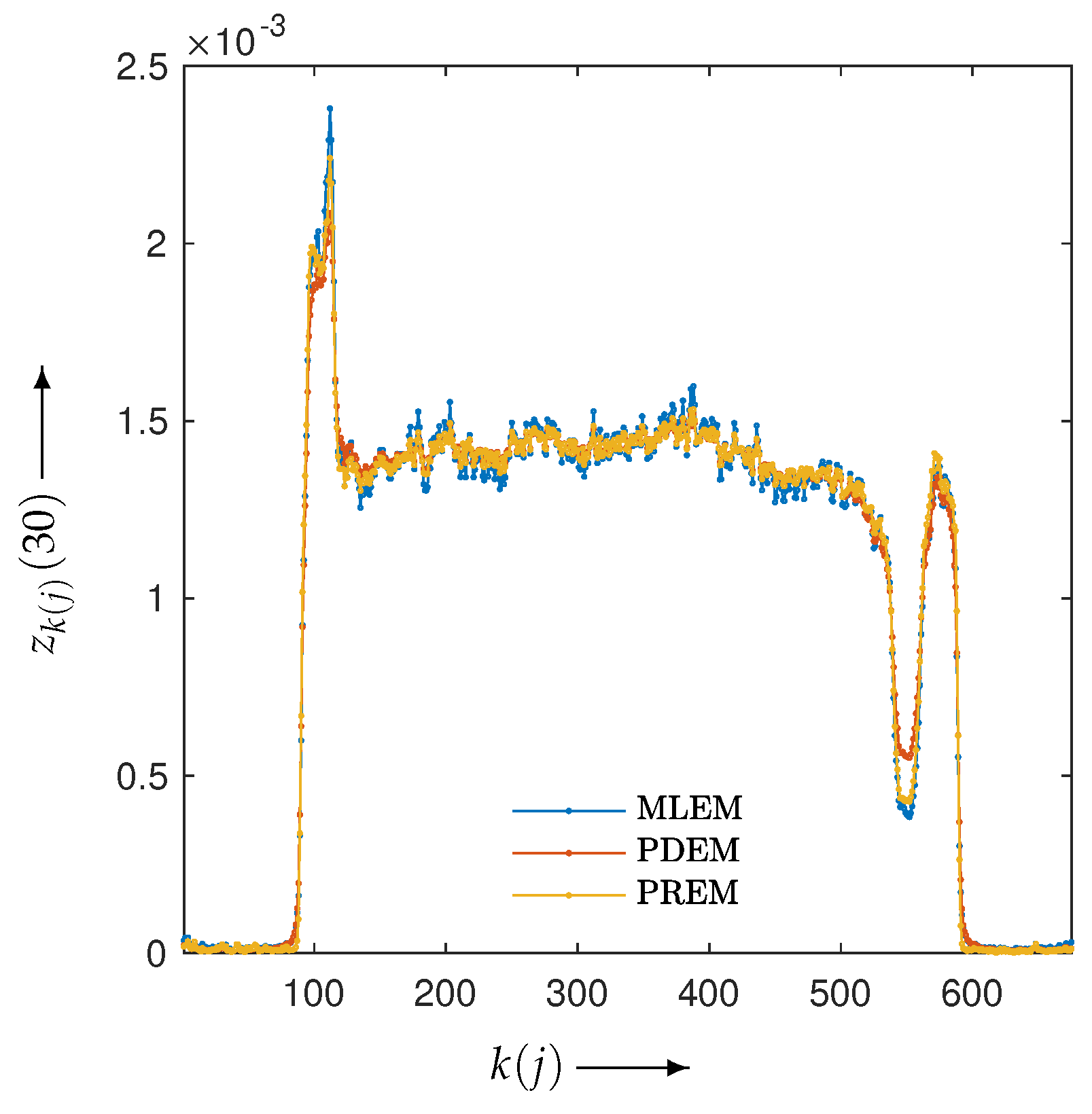
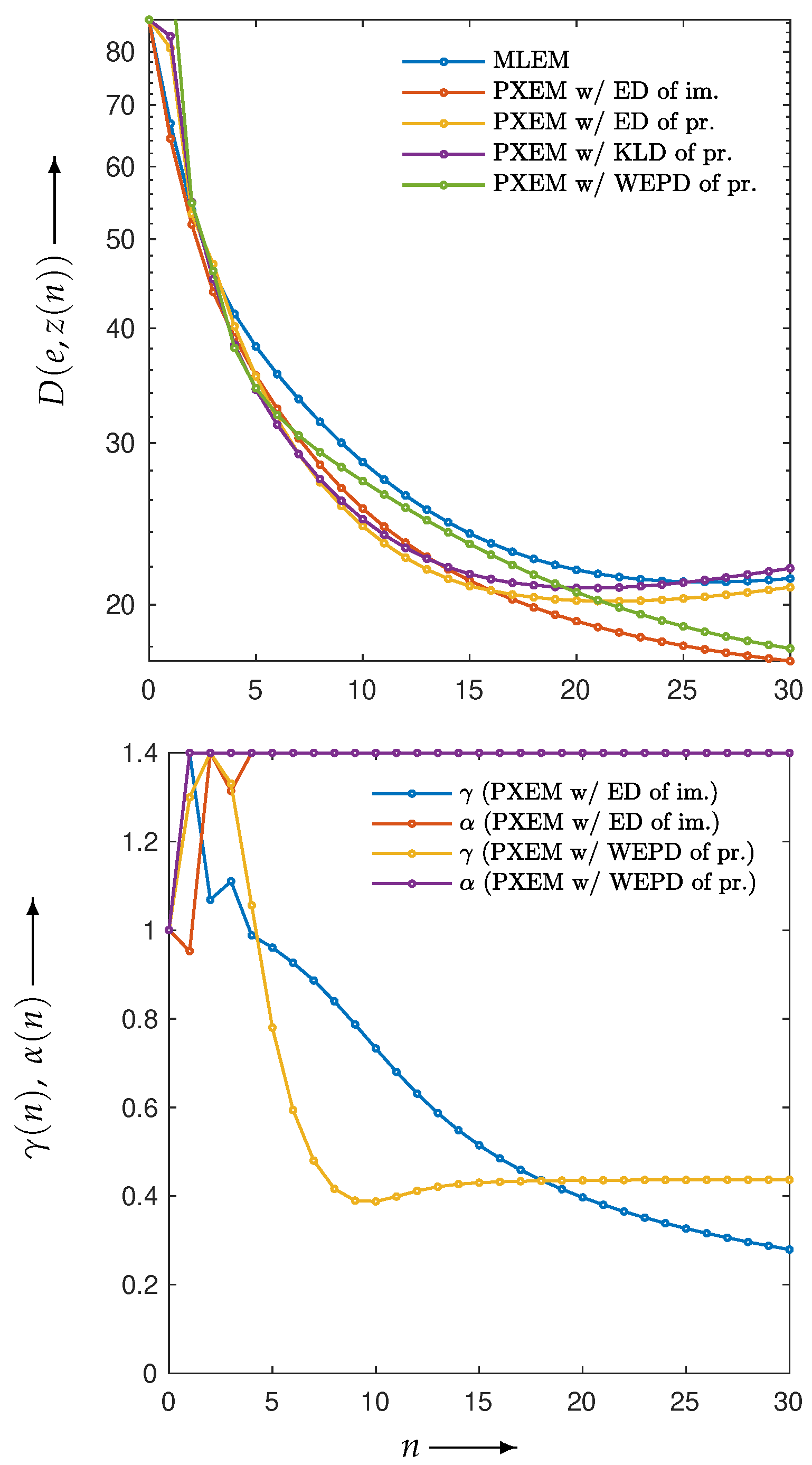
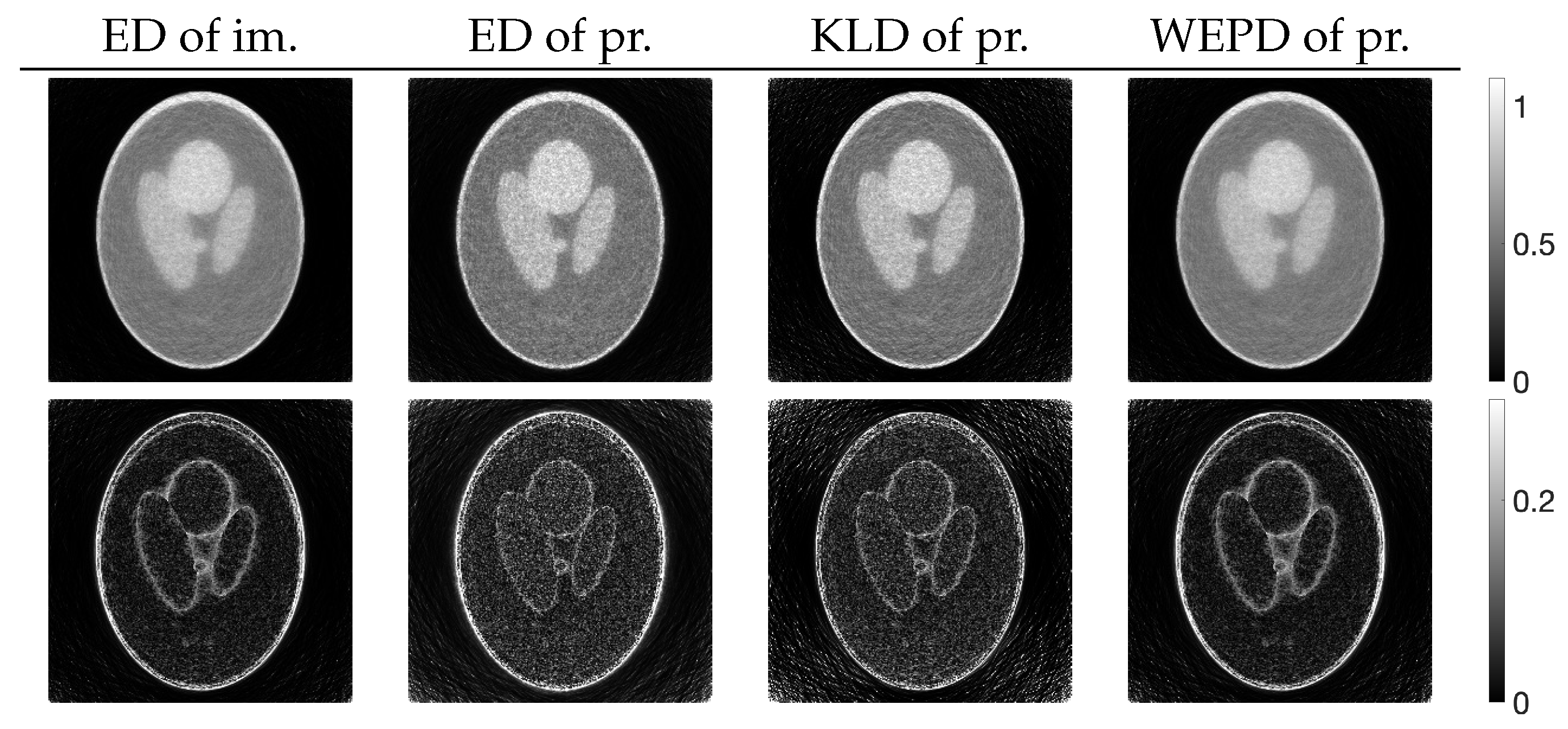
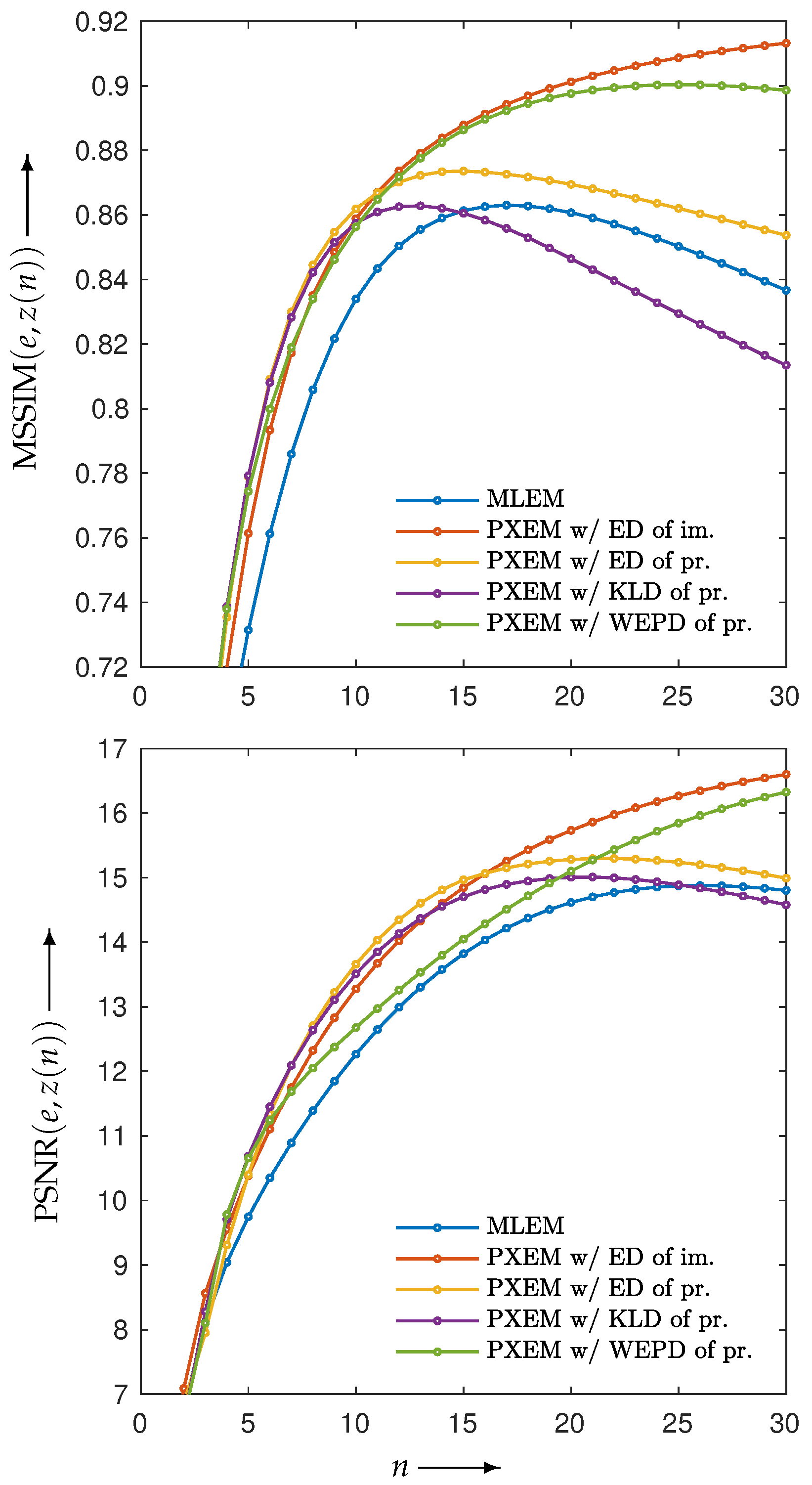
3.2. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kak, A.C.; Slaney, M. Principles of Computerized Tomographic Imaging; IEEE Press: Piscataway, NJ, USA, 1988. [Google Scholar]
- Stark, H. Image Recovery: Theory and Application; Academic Press: Orlando, FL, USA, 1987. [Google Scholar] [CrossRef]
- Herman, G. Image Reconstruction from Projections. Fundamentals of Computerized Tomography; Advances in Computer Vision and Pattern Recognition; Springer: London, UK, 1980. [Google Scholar] [CrossRef]
- Seeram, E. Computed Tomography: Physical Principles, Clinical Applications, and Quality Control, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Gordon, R.; Bender, R.; Herman, G. Algebraic Reconstruction Techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef] [PubMed]
- Badea, C.; Gordon, R. Experiments with the nonlinear and chaotic behaviour of the multiplicative algebraic reconstruction technique (MART) algorithm for computed tomography. Phys. Med. Biol. 2004, 49, 1455–1474. [Google Scholar] [CrossRef] [PubMed]
- Seibert, J.A. Iterative reconstruction: How it works, how to apply it. Pediatr. Radiol. 2014, 44, 431–439. [Google Scholar] [CrossRef] [PubMed]
- Geyer, L.L.; Schoepf, U.J.; Meinel, F.G.; Nance, J.W.; Bastarrika, G.; Leipsic, J.A.; Paul, N.S.; Rengo, M.; Laghi, A.; De Cecco, C.N. State of the Art: Iterative CT Reconstruction Techniques. Radiology 2015, 276, 339–357. [Google Scholar] [CrossRef] [PubMed]
- Qiu, D.; Seeram, E. Does Iterative Reconstruction Improve Image Quality and Reduce Dose in Computed Tomography? Radiology 2016, 1, 42–54. [Google Scholar] [CrossRef]
- Shepp, L.; Vardi, Y. Maximum Likelihood Reconstruction for Emission Tomography. IEEE Trans. Med. Imaging 1982, 1, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Byrne, C.L. Block-iterative methods for image reconstruction from projections. IEEE Trans. Image Process. 1996, 5, 792–794. [Google Scholar] [CrossRef]
- Darroch, J.N.; Ratcliff, D. Generalized Iterative Scaling for Log-Linear Models. Ann. Math. Stat. 1972, 43, 1470–1480. [Google Scholar] [CrossRef]
- Katsekpor, T. Convergence of the Multiplicative Algebraic Reconstruction Technique for the Inconsistent System of Equations. Oper. Res. Forum 2023, 4, 88. [Google Scholar] [CrossRef]
- Mohammadinejad, P.; Mileto, A.; Yu, L.; Leng, S.; Guimaraes, L.S.; Missert, A.D.; Jensen, C.T.; Gong, H.; McCollough, C.H.; Fletcher, J.G. CT Noise-Reduction Methods for Lower-Dose Scanning: Strengths and Weaknesses of Iterative Reconstruction Algorithms and New Techniques. RadioGraphics 2021, 41, 1493–1508. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Baek, J. Iterative reconstruction for limited-angle CT using implicit neural representation. Phys. Med. Biol. 2024, 69, 105008. [Google Scholar] [CrossRef]
- Zhang, M.; Gu, S.; Shi, Y. The use of deep learning methods in low-dose computed tomography image reconstruction: A systematic review. Complex Intell. Syst. 2022, 8, 5545–5561. [Google Scholar] [CrossRef]
- Koetzier, L.R.; Mastrodicasa, D.; Szczykutowicz, T.P.; van der Werf, N.R.; Wang, A.S.; Sandfort, V.; van der Molen, A.J.; Fleischmann, D.; Willemink, M.J. Deep Learning Image Reconstruction for CT: Technical Principles and Clinical Prospects. Radiology 2023, 306, e221257. [Google Scholar] [CrossRef] [PubMed]
- Byrne, C.L. A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl. 2004, 20, 103–120. [Google Scholar] [CrossRef]
- Byrne, C.L. Block-Iterative Algorithms. Int. Trans. Oper. Res. 2009, 16, 427–463. [Google Scholar] [CrossRef]
- Beister, M.; Kolditz, D.; Kalender, W.A. Iterative reconstruction methods in X-ray CT. Phys. Medica 2012, 28, 94–108. [Google Scholar] [CrossRef] [PubMed]
- Kasai, R.; Yamaguchi, Y.; Kojima, T.; Yoshinaga, T. Tomographic Image Reconstruction Based on Minimization of Symmetrized Kullback-Leibler Divergence. Math. Probl. Eng. 2018, 9, 8973131. [Google Scholar] [CrossRef]
- Kasai, R.; Yamaguchi, Y.; Kojima, T.; Abou Al-Ola, O.M.; Yoshinaga, T. Noise-Robust Image Reconstruction Based on Minimizing Extended Class of Power-Divergence Measures. Entropy 2021, 23, 1005. [Google Scholar] [CrossRef] [PubMed]
- Kojima, T.; Yoshinaga, T. Iterative Image Reconstruction Algorithm with Parameter Estimation by Neural Network for Computed Tomography. Algorithms 2023, 16, 60. [Google Scholar] [CrossRef]
- Lu, W.; Yin, F. Adaptive algebraic reconstruction technique. Med. Phys. 2004, 31, 3222–3230. [Google Scholar] [CrossRef]
- Lin, C.; Zang, J.; Qing, A. Algebraic reconstruction technique with adaptive relaxation parameter based on hyperplane distance and data noise level. In Proceedings of the 2016 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Beijing, China, 27–29 July 2016. [Google Scholar] [CrossRef]
- Oliveira, N.; Mota, A.; Matela, N.; Janeiro, L.; Almeida, P. Dynamic relaxation in algebraic reconstruction technique (ART) for breast tomosynthesis imaging. Comput. Methods Programs Biomed. 2016, 132, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Abou Al-Ola, O.M.; Fujimoto, K.; Yoshinaga, T. Common Lyapunov Function Based on Kullback–Leibler Divergence for a Switched Nonlinear System. Math. Probl. Eng. 2011, 2011, 723509. [Google Scholar] [CrossRef]
- Tateishi, K.; Yamaguchi, Y.; Abou Al-Ola, O.M.; Yoshinaga, T. Continuous Analog of Accelerated OS-EM Algorithm for Computed Tomography. Math. Probl. Eng. 2017, 2017, 1564123. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Shepp, L.; Logan, B.F. The Fourier reconstruction of a head section. IEEE Trans. Nucl. Sci. 1974, 21, 21–43. [Google Scholar] [CrossRef]
- Kagaku, K. CT Whole Body Phantom PBU-60. Available online: https://www.kyotokagaku.com/en/products_data/ph-2b/ (accessed on 1 June 2024).
- Beran, R. Minimum Hellinger Distance Estimates for Parametric Models. Ann. Stat. 1977, 5, 445–463. [Google Scholar] [CrossRef]
- Beran, R. An Efficient and Robust Adaptive Estimator of Location. Ann. Stat. 1978, 6, 292–313. [Google Scholar] [CrossRef]
- Ishikawa, K.; Yamaguchi, Y.; Abou Al-Ola, O.M.; Kojima, T.; Yoshinaga, T. Block-Iterative Reconstruction from Dynamically Selected Sparse Projection Views Using Extended Power-Divergence Measure. Entropy 2022, 24, 740. [Google Scholar] [CrossRef]




| MLEM | PDEM | PXEM | PREM | |
|---|---|---|---|---|
| std. dev. | 0.083 | 0.056 | 0.056 | 0.057 |
| contrast | 0.532 | 0.418 | 0.544 | 0.550 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yabuki, R.; Yamaguchi, Y.; Abou Al-Ola, O.M.; Kojima, T.; Yoshinaga, T. Iterative Tomographic Image Reconstruction Algorithm Based on Extended Power Divergence by Dynamic Parameter Tuning. J. Imaging 2024, 10, 178. https://doi.org/10.3390/jimaging10080178
Yabuki R, Yamaguchi Y, Abou Al-Ola OM, Kojima T, Yoshinaga T. Iterative Tomographic Image Reconstruction Algorithm Based on Extended Power Divergence by Dynamic Parameter Tuning. Journal of Imaging. 2024; 10(8):178. https://doi.org/10.3390/jimaging10080178
Chicago/Turabian StyleYabuki, Ryuto, Yusaku Yamaguchi, Omar M. Abou Al-Ola, Takeshi Kojima, and Tetsuya Yoshinaga. 2024. "Iterative Tomographic Image Reconstruction Algorithm Based on Extended Power Divergence by Dynamic Parameter Tuning" Journal of Imaging 10, no. 8: 178. https://doi.org/10.3390/jimaging10080178
APA StyleYabuki, R., Yamaguchi, Y., Abou Al-Ola, O. M., Kojima, T., & Yoshinaga, T. (2024). Iterative Tomographic Image Reconstruction Algorithm Based on Extended Power Divergence by Dynamic Parameter Tuning. Journal of Imaging, 10(8), 178. https://doi.org/10.3390/jimaging10080178






