Freight Operations Modelling for Urban Delivery and Pickup with Flexible Routing: Cluster Transport Modelling Incorporating Discrete-Event Simulation and GIS
Abstract
:1. Introduction
2. Literature Review on Urban Pickup and Delivery with Flexible Routing
2.1. Conventional Vehicle Routing Problems (VPRs)
2.2. GIS
2.3. Computer Simulation Methods
2.4. Gaps
3. Method
3.1. Research Objective
3.2. Approach
4. Results
4.1. Identification of Main Suburbs
4.2. Discrete-Event Simulation Model
4.2.1. Freight Operations Modelling
4.2.2. Transport Modelling
4.3. Simple Suburb Cluster Network with DES with an Average Speed
4.4. Intersection-Based Network with Specified Speeds
4.5. Case Study
4.5.1. Description
4.5.2. ArcGIS Models
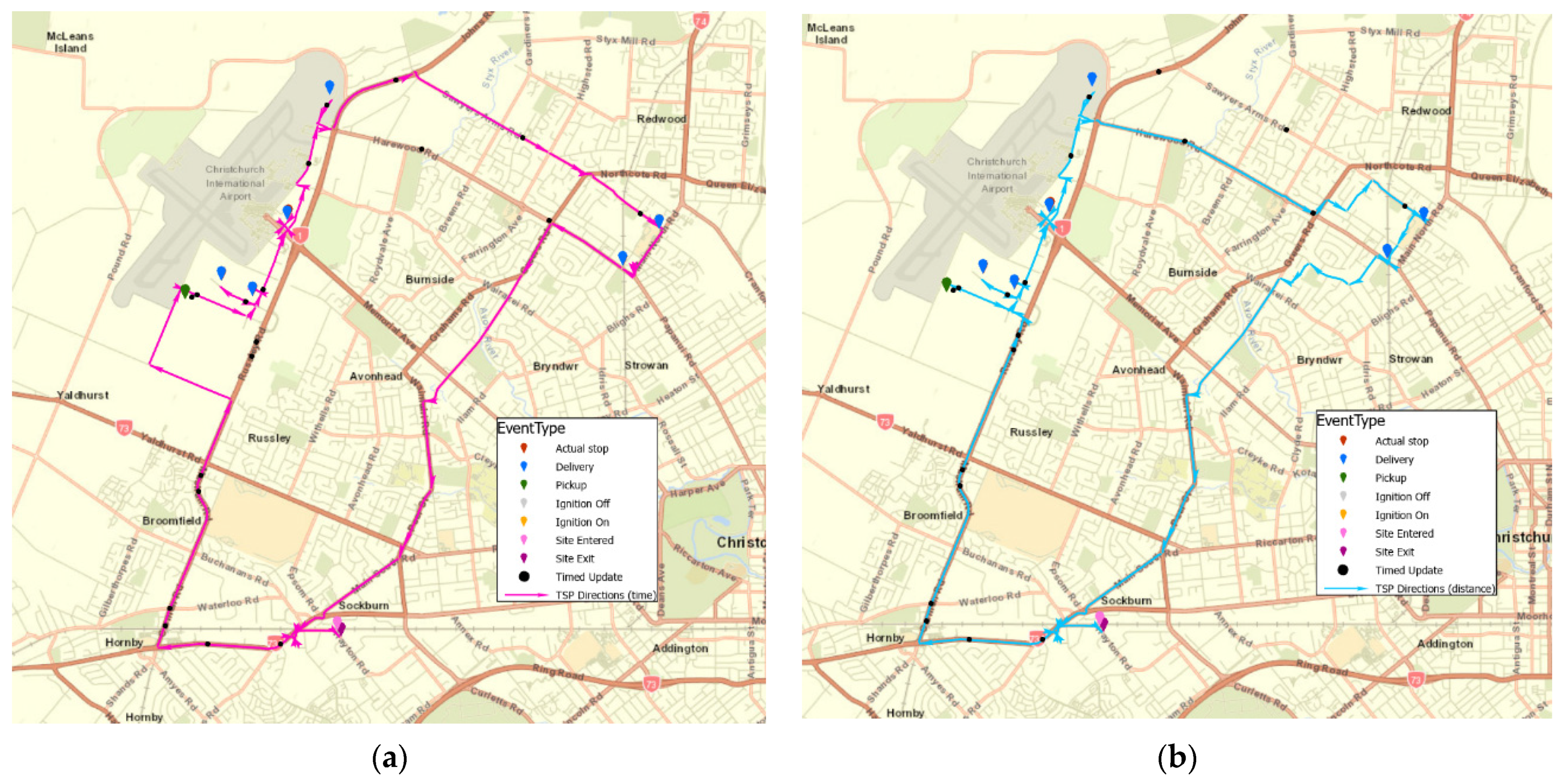
4.5.3. Model Validation and Result Comparison
5. Discussion
5.1. Advantages and Disadvantages of Logistics Simulation Models
5.1.1. Pure GIS Models
5.1.2. GIS + DES Models
5.2. Limitations
5.3. Implications
5.4. Opportunities for Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Asuncion, J.; Rendall, S.; Murray, R.; Krumdieck, S. New Zealand Intermodal Freight Network and the Potential for Mode Shifting. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2012. Available online: http://hdl.handle.net/10092/8825 (accessed on 10 December 2021).
- Kim, H.-C.; Nicholson, A.; Kusumastuti, D. Freight Transport Mode Choice and Mode Shift in New Zealand: Findings of a Revealed Preference Survey; Sustainable Logistics (Transport and Sustainability, Vol. 6); Emerald Group Publishing Limited: Bingley, UK, 2014; Volume 6, pp. 165–192. [Google Scholar]
- Patil, G.R.; Thadoju, S.; Sahu, P.K.; Mondal, A.; Bajpai, V. Data Collection and Modeling of Restaurants’ Freight Trip Generation for Indian Cities. Transp. Dev. Econ. 2021, 7, 9. [Google Scholar] [CrossRef]
- Szander, N.; Albert, G. The Competitive Position Of Hungarian Hauling Companies In The Road Freight Transportation Sector. Bus. Logist. Mod. Manag. 2021, 21, 277–293. [Google Scholar]
- Amaya, J.; Delgado-Lindeman, M.; Arellana, J.; Allen, J. Urban freight logistics: What do citizens perceive? Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102390. [Google Scholar] [CrossRef]
- Hopkins, D.; McCarthy, A. Change trends in urban freight delivery: A qualitative inquiry. Geoforum 2016, 74, 158–170. [Google Scholar] [CrossRef] [Green Version]
- Dulebenets, M.A. A comprehensive multi-objective optimization model for the vessel scheduling problem in liner shipping. Int. J. Prod. Econ. 2018, 196, 293–318. [Google Scholar] [CrossRef]
- Taylor, G.D. Logistics Engineering Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Ghiani, G.; Laporte, G.; Musmanno, R. Introduction to Logistics Systems Planning and Control; J. Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Elbert, R.; Knigge, J.-K.; Friedrich, A. Analysis of decentral platoon planning possibilities in road freight transport using an agent-based simulation model. J. Simul. 2020, 14, 64–75. [Google Scholar] [CrossRef]
- Silva, B.C.H.; Fernandes, I.F.C.; Goldbarg, M.C.; Goldbarg, E.F.G. Quota travelling salesman problem with passengers, incomplete ride and collection time optimization by ant-based algorithms. Comput. Oper. Res. 2020, 120. [Google Scholar] [CrossRef]
- Marinov, M.; Viegas, J. A mesoscopic simulation modelling methodology for analyzing and evaluating freight train operations in a rail network. Simul. Model. Pract. Theory 2011, 19, 516–539. [Google Scholar] [CrossRef]
- Robinson, S. Successful Simulation: A Practical Approach to Simulation Projects; McGraw-Hill: London, UK; New York, NY, USA, 1994. [Google Scholar]
- Rahimi, A.M.; Dulebenets, M.A.; Mazaheri, A. Evaluation of Microsimulation Models for Roadway Segments with Different Functional Classifications in Northern Iran. Infrastructures 2021, 6, 46. [Google Scholar] [CrossRef]
- Aliahmadi, S.Z.; Barzinpour, F.; Pishvaee, M.S. A fuzzy optimization approach to the capacitated node-routing problem for municipal solid waste collection with multiple tours: A case study. Waste Manag. Res. 2020, 38, 279–290. [Google Scholar] [CrossRef] [PubMed]
- Salazar-Aguilar, M.A.; Langevin, A.; Laporte, G. The synchronized arc and node routing problem: Application to road marking. Comput. Oper. Res. 2013, 40, 1708–1715. [Google Scholar] [CrossRef]
- Kumar, A. Improved Genetic Algorithm to Solve Small Scale Travelling Salesman Problem. In Proceedings of the 2020 International Conference on Intelligent Computing and Control Systems, ICICCS 2020, Madurai, India, 13–15 May 2020; pp. 516–520. [Google Scholar]
- Agrawal, M.; Jain, V. Applying Improved Genetic Algorithm to Solve Travelling Salesman Problem. In Proceedings of the 2nd International Conference on Inventive Research in Computing Applications, ICIRCA 2020, Coimbatore, India, 15–17 July 2020; pp. 1194–1197. [Google Scholar]
- Zbib, H.; Laporte, G. The commodity-split multi-compartment capacitated arc routing problem. Comput. Oper. Res. 2020, 122. [Google Scholar] [CrossRef]
- Amini, A.; Tavakkoli-Moghaddam, R.; Ebrahimnejad, S. A bi-objective transportation-location arc routing problem. Transp. Lett. 2020, 12, 623–637. [Google Scholar] [CrossRef]
- Padungwech, W.; Thompson, J.; Lewis, R. Effects of update frequencies in a dynamic capacitated arc routing problem. Networks 2020, 76, 522–538. [Google Scholar] [CrossRef]
- Campbell, J.F.; Corberan, A.; Plana, I.; Sanchis, J.M.; Segura, P. Solving the length constrained K-drones rural postman problem. Eur. J. Oper. Res. 2021, 292, 60–72. [Google Scholar] [CrossRef]
- Benavent, E.; Corberan, A.; Lagana, D.; Vocaturo, F. The periodic rural postman problem with irregular services on mixed graphs. Eur. J. Oper. Res. 2019, 276, 826–839. [Google Scholar] [CrossRef]
- Afanasev, V.A.; van Bevern, R.; Tsidulko, O.Y. The Hierarchical Chinese Postman Problem: The slightest disorder makes it hard, yet disconnectedness is manageable. Oper. Res. Lett. 2021, 49, 270–277. [Google Scholar] [CrossRef]
- Siloi, I.; Carnevali, V.; Pokharel, B.; Fornari, M.; Di Felice, R. Investigating the Chinese postman problem on a quantum annealer. Quantum Mach. Intell. 2021, 3. [Google Scholar] [CrossRef]
- Majumder, S.; Kar, S.; Pal, T. Uncertain multi-objective Chinese postman problem. Soft Comput. 2019, 23, 11557–11572. [Google Scholar] [CrossRef]
- Barkaoui, M.; Gendreau, M. An adaptive evolutionary approach for real-time vehicle routing and dispatching. Comput. Oper. Res. 2013, 40, 1766–1776. [Google Scholar] [CrossRef]
- Schmidt, L.; Gazmuri, P. Online simulation for a real-time route dispatching problem. J. Oper. Res. Soc. 2012, 63, 1492–1498. [Google Scholar] [CrossRef]
- Bertsimas, D.; Jaillet, P.; Martin, S. Online vehicle routing: The edge of optimization in large-scale applications. Oper. Res. 2019, 67, 143–162. [Google Scholar] [CrossRef]
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef] [Green Version]
- Keenan, P. Modelling vehicle routing in GIS. Oper. Res. 2008, 8, 201. [Google Scholar] [CrossRef]
- Meersman, H.; Ben-Akiva, M.E.; Van De Voorde, E.; Ben-Akiva, M.E. Freight Transport Modelling; Emerald Publishing Limited: Bingley, UK, 2013. [Google Scholar]
- Akay, A.E.; Wing, M.G.; Sivrikaya, F.; Sakar, D. A GIS-based decision support system for determining the shortest and safest route to forest fires: A case study in Mediterranean Region of Turkey. Environ. Monit. Assess. 2012, 184, 1391–1407. [Google Scholar] [CrossRef]
- Vu, H.L.; Ng, K.T.W.; Fallah, B.; Richter, A.; Kabir, G. Interactions of residential waste composition and collection truck compartment design on GIS route optimization. Waste Manag. 2020, 102, 613–623. [Google Scholar] [CrossRef]
- Hemidat, S.; Oelgemöller, D.; Nassour, A.; Nelles, M. Evaluation of Key Indicators of Waste Collection Using GIS Techniques as a Planning and Control Tool for Route Optimization. Waste Biomass Valorization 2017, 8, 1533–1554. [Google Scholar] [CrossRef]
- Jwad, Z.A.; Hasson, S.T. An Optimization Approach for Waste Collection Routes Based on GIS in Hillah-Iraq. In Proceedings of the 2018 International Conference on Advanced Science and Engineering, ICOASE 2018, Duhok, Kurdistan Region, Iraq, 9–11 October 2018; pp. 60–63. [Google Scholar]
- Vu, H.L.; Bolingbroke, D.; Ng, K.T.W.; Fallah, B. Assessment of waste characteristics and their impact on GIS vehicle collection route optimization using ANN waste forecasts. Waste Manag. 2019, 88, 118–130. [Google Scholar] [CrossRef]
- Dao-Tuan, A.; Nguyen-Thi-Ngoc, A.; Nguyen-Trong, K.; Bui-Tuan, A.; Dinh-Thi-Hai, V. Optimizing vehicle routing with path and carbon dioxide emission for municipal solid waste collection in Ha Giang, Vietnam. In Proceedings of the 3rd International Conference on Industrial Networksand Intelligent Systems, INISCOM 2017, Ho Chi Minh City, Vietnam, 4 September 2017; pp. 212–227. [Google Scholar]
- Pamučar, D.; Gigović, L.; Ćirović, G.; Regodić, M. Transport spatial model for the definition of green routes for city logistics centers. Environ. Impact Assess. Rev. 2016, 56, 72–87. [Google Scholar] [CrossRef]
- Zsigraiova, Z.; Semiao, V.; Beijoco, F. Operation costs and pollutant emissions reduction by definition of new collection scheduling and optimization of MSW collection routes using GIS. The case study of Barreiro, Portugal. Waste Manag. 2013, 33, 793–806. [Google Scholar] [CrossRef]
- Couclelis, H. The Certainty of Uncertainty: GIS and the Limits of Geographic Knowledge. Trans. GIS 2003, 7, 165–175. [Google Scholar] [CrossRef]
- Mommens, K.; Lebeau, P.; Verlinde, S.; van Lier, T.; Macharis, C. Evaluating the impact of off-hour deliveries: An application of the TRansport Agent-BAsed model. Transp. Res. Part D Transp. Environ. 2018, 62, 102–111. [Google Scholar] [CrossRef]
- Lu, S.; Xin, B.; Zhang, H.; Chen, J. Agent-based Self-organized Constructive Heuristics for Travelling Salesman Problem. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020; pp. 1164–1169. [Google Scholar] [CrossRef]
- Blamah, N.V.; Oluyinka, A.A.; Wajiga, G.; Baha, Y.B. MAPSOFT: A Multi-Agent based Particle Swarm Optimization Framework for Travelling Salesman Problem. J. Intell. Syst. 2021, 30, 413–428. [Google Scholar] [CrossRef]
- Viana, J.; Ziener, V.M.; Holhjem, M.S.; Ponton, I.G.; Thogersen, L.J.; Simonsen, T.B. Optimizing home hospital health service delivery in norway using a combined geographical information system, agent based, discrete event simulation model. In Proceedings of the 2017 Winter Simulation Conference, WSC 2017, Las Vegas, NV, USA, 3–6 December 2017; pp. 1658–1669. [Google Scholar]
- Kogler, C.; Rauch, P. Discrete event simulation of multimodal and unimodal transportation in the wood supply chain: A literature review. Silva Fenn. 2018, 52, 9984. [Google Scholar] [CrossRef]
- Abbott, D.; Marinov, M.V. An event based simulation model to evaluate the design of a rail interchange yard, which provides service to high speed and conventional railways. Simul. Model. Pract. Theory 2015, 52, 15–39. [Google Scholar] [CrossRef] [Green Version]
- Motraghi, A.; Marinov, M.V. Analysis of urban freight by rail using event based simulation. Simul. Model. Pract. Theory 2012, 25, 73–89. [Google Scholar] [CrossRef]
- Wu, B.; Liu, Z.; Liu, B. The Model and Simulation of Utilization Optimization of Railway Passenger Waiting Compartment Based on Arena. In Proceedings of the 2013 International Conference on Computational and Information Sciences, Shiyang, China, 21–23 June 2013; pp. 1216–1219. [Google Scholar]
- Zhao, Y.; Ioannou, P.A.; Dessouky, M.M. Dynamic Multimodal Freight Routing Using a Co-Simulation Optimization Approach. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2657–2667. [Google Scholar] [CrossRef]
- Li, L.; Qiu, M.; Wu, B.; Wang, X. Simulation Research on Road Transport in Container Port Based on Arena. In Proceedings of the ICLEM 2010: ICLEM 2010: Logistics For Sustained Economic Development: Infrastructure, Information, Integration, Chengdu, China, 8–10 October 2010; pp. 1880–1888. [Google Scholar] [CrossRef]
- Jaoua, A.; Riopel, D.; Gamache, M. A simulation framework for real-time fleet management in internal transport systems. Simul. Model. Pract. Theory 2012, 21, 78–90. [Google Scholar] [CrossRef]
- Wu, W.; Shen, L.; Ji, X.; Jin, W. Analysis of freeway service patrol with discrete event-based simulation. Simul. Model. Pract. Theory 2014, 47, 141–151. [Google Scholar] [CrossRef]
- Sun, L.; Sun, Y.; Zheng, W. The stochastic and dynamic vehicle routing problem with crowdshipping. In Proceedings of the 17th COTA International Conference of Transportation Professionals: Transportation Reform and Change-Equity, Inclusiveness, Sharing, and Innovation, CICTP 2017, Shanghai, China, 7–9 July 2017; pp. 1500–1510. [Google Scholar]
- Herazo-Padilla, N.; Montoya-Torres, J.R.; Nieto Isaza, S.; Alvarado-Valencia, J. Simulation-optimization approach for the stochastic location-routing problem. J. Simul. 2015, 9, 296–311. [Google Scholar] [CrossRef]
- Mayer, T.; Uhlig, T.; Rose, O. An open-source discrete event simulator for rich vehicle routing problems. In Proceedings of the 19th IEEE International Conference on Intelligent Transportation Systems, ITSC 2016, Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1305–1310. [Google Scholar]
- Outalha, A.; Lakhal, Y.; Baghli, F.Z.; Kzaiber, F. The efficiency of discrete event systems for the general pickup and delivery problem with electric vehicles. In Proceedings of the 3rd International Conference of Computer Science and Renewable Energies, ICCSRE 2020, Agadir, Morocco, 22–24 December 2020. [Google Scholar]
- Sun, Z.; Guan, Z. Vehicle routing problem based on object-oriented discrete event simulation. In Proceedings of the 2nd IEEE International Conference on Advanced Computer Control, ICACC, Shenyang, China, 27–29 March 2010; pp. 638–643. [Google Scholar]











| Problems | Explanation |
|---|---|
| Node routing problem (NRP) [15,16] | No need for arcs and edges |
| Travelling salesman problem [9,17,18] | One circuit is finished by one vehicle in NRP, Including the asymmetric travelling salesman problem and the symmetric travelling salesman problem |
| Arc routing problem (ARP) [19,20,21] | No need for vertices |
| Rural postman problem (RPP) [22,23] | One circuit finished by one vehicle in ARP |
| Chinese postman problem (CPP) [24,25,26] | Each arc and edge needs to be serviced in RPP |
| Real-time vehicle routing and dispatching problem [27,28,29] | GIS, GPS, vehicle allocation could be involved. Considerations include quick response, denied or deferred service, congestion and system dynamism [7] |
| Suburb | Percentage |
|---|---|
| PAPANUI | 50.84% |
| BURNSIDE | 10.30% |
| CHRISTCHURCH AIRPORT | 7.88% |
| HAREWOOD | 7.53% |
| BISHOPDALE | 7.47% |
| ST ALBANS | 3.38% |
| YALDHURST | 3.06% |
| NORTHCOTE | 2.62% |
| AVONHEAD | 2.29% |
| NORTHLANDS | 1.88% |
| BRYNDWR | 0.44% |
| MAIREHAU | 0.38% |
| WIGRAM | 0.32% |
| CHRISTCHURCH CENTRAL | 0.32% |
| HORNBY | 0.24% |
| REDWOOD | 0.21% |
| RICHMOND | 0.21% |
| HALSWELL | 0.18% |
| SOCKBURN | 0.09% |
| RUSSLEY | 0.09% |
| ADDINGTON | 0.06% |
| STROWAN | 0.03% |
| FENDALTON | 0.03% |
| SYDENHAM | 0.03% |
| CHRISTCHURCH | 0.03% |
| BELFAST | 0.03% |
| MIDDLETON | 0.03% |
| ILAM | 0.03% |
| Road Type | Average Speed (km/h) |
|---|---|
| All roads | 30.633 |
| Open road | 56.140 |
| Urban road | 23.279 |
| Sequence | Suburb Cluster |
|---|---|
| 1 | Yaldhurst |
| 2 | Christchurch airport |
| 3 | Burnside |
| 4 | Harewood |
| 5 | Bishopdale |
| 6 | Papanui |
| 7 | ST Albans |
| 8 | Backhaul pickup |
| Delivery Suburb | Consignment Number |
|---|---|
| Airport | 1 |
| Harewood | 1 |
| Yaldhurst | 2 |
| Papanui | 2 |
| Models | Input Variables | Key Assumption | Travel Time (min) | Travel Distance (km) | Output Average Speed (km/h) | Delivery Sequence | Pickup |
|---|---|---|---|---|---|---|---|
| ArcGIS estimated by time measurement | Addresses by sequence | Historical traffic data | 47.018 | 39.675 | 50.630 | Set sequence | Backhaul |
| ArcGIS estimated by distance measurement | Addresses by sequence | Historical traffic data | 49.545 | 38.755 | 46.933 | Set sequence | Backhaul |
| Simple suburb model | Customer suburb clusters, truck average speed | Customer locations | 70.44 | 35.950 | 30.622 | Arena determined sequence with predefined priority | Backhaul |
| Intersection-based model | Customer suburb clusters, truck average speed and speed factors | Customer locations | 77.97 | 36.450 | 28.049 | Arena determined sequence with predefined priority | Backhaul |
| Ground truth-GPS actual | 73.267 | 39.200 | 32.102 | Backhaul |
| Advantages | Disadvantages | |
|---|---|---|
| GIS models on their own for PUD |
|
|
| DES models on their own for PUD |
|
|
| GIS + DES combined models for PUD |
|
|
| Advantages | Disadvantages | |
|---|---|---|
| Simple cluster suburb model |
|
|
| Intersection-based model |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Z.; Pons, D.; Zhang, Y.; Ji, Z. Freight Operations Modelling for Urban Delivery and Pickup with Flexible Routing: Cluster Transport Modelling Incorporating Discrete-Event Simulation and GIS. Infrastructures 2021, 6, 180. https://doi.org/10.3390/infrastructures6120180
Lyu Z, Pons D, Zhang Y, Ji Z. Freight Operations Modelling for Urban Delivery and Pickup with Flexible Routing: Cluster Transport Modelling Incorporating Discrete-Event Simulation and GIS. Infrastructures. 2021; 6(12):180. https://doi.org/10.3390/infrastructures6120180
Chicago/Turabian StyleLyu, Zichong, Dirk Pons, Yilei Zhang, and Zuzhen Ji. 2021. "Freight Operations Modelling for Urban Delivery and Pickup with Flexible Routing: Cluster Transport Modelling Incorporating Discrete-Event Simulation and GIS" Infrastructures 6, no. 12: 180. https://doi.org/10.3390/infrastructures6120180
APA StyleLyu, Z., Pons, D., Zhang, Y., & Ji, Z. (2021). Freight Operations Modelling for Urban Delivery and Pickup with Flexible Routing: Cluster Transport Modelling Incorporating Discrete-Event Simulation and GIS. Infrastructures, 6(12), 180. https://doi.org/10.3390/infrastructures6120180








