Backstepping Control with a Fractional-Order Command Filter and Disturbance Observer for Unmanned Surface Vehicles

Abstract

In the paper, a backstepping control strategy based on a fractional-order finite-time command filter and a fractional-order finite-time disturbance observer is proposed for the trajectory tracking control of an unmanned surface vehicle. A fractional-order finite-time command filter is presented to estimate the derivatives of the intermediate control, which cannot be directly calculated, thereby reducing the chattering generated by the integer-order command filter. The fractional-order finite-time disturbance observer is presented to approximate and compensate for the model uncertainty and unknown external disturbances in the system. Subsequently, the globally asymptotically stable nature of the closed-loop system is proved based on the Lyapunov method. The effectiveness of the method is proven by simulation experiments on unmanned surface vehicles.

1. Introduction

Recently, with the increase of marine activities, such as resource exploration, maritime rescue, and environmental monitoring, unmanned surface vehicles (USVs) with low failure rates and high reliability have received more and more attention [1,2,3]. To promote a variety of applications of USVs, trajectory tracking is the core problem of USVs for marine operations. However, due to the complexity of the marine environment and the uncertainty in the modeling process, the control of USVs faces great challenges. Hence, it has important, realistic meaning to research the trajectory tracking control of USVs in complex environments.

At present, there are some control methods used in USVs, such as model predictive control (MPC) [4], sliding mode control (SMC) [5], backstepping control (BC) [6], and optimum control [7]. Among them, backstepping control is one of the most effective design tools for USV nonlinear systems. By continuously constructing Lyapunov functions, the intermediate control laws of each subsystem can be given, and the control inputs of the system can be obtained [8]. Nevertheless, the repeated derivation of the intermediate control law in the backstepping control will cause a complexity explosion. The first-order filter applied to dynamic surface control technology is the first effective solution to avoid the complexity explosion problem [9]. Although this method avoids the complexity explosion, it ignores the influence of compensation error, which also increases the difficulty of proving the stability of the controller. Nowadays, the command filter is the preferred choice to avoid the issue that the intermediate control law cannot be derived directly [10]. The backstepping control technology based on command filtering, which is proposed in [11], avoids the problem of direct derivation of intermediate control laws and eliminates the impact of command filtering errors by designing the auxiliary signal. In addition, most of the backstepping control is based on the infinite-time stability theory, which has the problem of slow convergence time. The finite-time command filter proposed in [12] adopts the error compensation mechanism to eliminate the filtering error, which not only ensures the finite-time stability of the system, but also avoids the direct derivation problem of the intermediate control law of the system. However, adding auxiliary signals to the command filter will lead to more complexity in controller design and a slower convergence time for the filter. Properly increasing the gain can optimize these problems but also lead to higher actual control input or aggravate system chattering.

The modeling uncertainties and the external disturbances (winds, waves, and currents, etc.) caused by the complex environment of the USVs can be estimated and compensated by constructing a disturbance observer [13,14,15]. The adaptive sliding mode control system proposed by [15] uses the radial basis function neural network approximator to approach the modeling uncertainty and constructs the disturbance observer to estimate the influence of environmental disturbances while ensuring the stability of the unmanned underwater vehicle system. In [16], the fuzzy logic system (FLS) is used to approximate the uncertainty in the nonlinear USV model, and a disturbance observer with a learning factor is proposed to compensate for external disturbances, effectively improving the accuracy and speed of trajectory tracking. In [17], an adaptive control law based on a finite-time disturbance observer and neural network is proposed for USV containment with external environmental disturbances and obstacles. Consequently, the disturbance observer is used to accurately observe the unknown disturbances, and the cascade analysis and Lyapunov method are combined to guarantee the globally asymptotical stability of the unmanned submersible system. For all that, the above literature ignores the problem that the disturbance observer faces: excessive control input and the input chattering phenomenon.

Fractional calculus [18,19,20] is an extension of integer calculus. Then, fractional-order systems can also be regarded as an extension of integer-order systems. Fractional calculus has non-locality and a long memory, which makes it especially suitable for describing the development of system functions with historical dependence. Some scholars have added fractional calculus to traditional control method, such as fractional-order optimal control [21], fractional-order proportional-integral-derivative (FOPID) control [22,23], fractional-order sliding mode control (FOSMC) [24], fractional-order adaptive fuzzy control [25], and so on. The results show that the controller designed by fractional calculus has a better effect than the integer one on the steady-state and transient responses of the closed-loop system, as well as its robustness and immunity to uncertainty.

Based on the above statements, this paper combines fractional calculus with a disturbance observer and a command filter. A backstepping control scheme for unmanned submersibles based on a fractional-order disturbance observer and command filter is designed. The major contributions are listed as follows:

(1)

The fractional-order finite-time command filter is proposed, which is proved to be finite-time stable. It can track the derivatives of the intermediate control well without adding additional compensation signals, and the direct derivation issue is avoided when designing a controller.

(2)

A fractional-order finite-time disturbance observer is designed to compensate for unknown environmental disturbances and model uncertainty, which can improve the transient and steady-state performances of the USVs system.

(3)

The controller in the paper can ensure the globally asymptotical stability of the closed-loop system. Thus, good control performance can be achieved. In addition, using the fractional-order command filter and disturbance observer can reduce chattering caused by the finite-time differentiator, which facilitates the application in practice.

2. Preliminaries and Problem Formulation

2.1. Fractional Calculus

It is necessary to have an understanding of basic fractional order concepts and properties, the model of the USVs system, and the control objectives before the main body of this paper.

Definition 1 ([26]). 

The $\gamma -order$ fractional integral of the given function $f(t):(0,\infty )\to R$ is defined as

$${}_{t_0}I_t^{\gamma }f(t)=\frac{1}{\mathsf{\Gamma }(\gamma )}{\displaystyle {\int }_{t_0}^t\frac{f(\tau )}{{(t-\tau )}^{1-\gamma }}}d\tau$$

(1)

where $\mathsf{\Gamma }\left(\gamma \right)={\displaystyle {\int }_0^{\infty }{t}^{\gamma -1}{e}^{-t}}dt$ is the Gamma function, and $\gamma >0$.

Definition 2 ([27]). 

The Caputo-type fractional differential of the function $f(t):(0,\infty )\to R$ is defined as

$${}_{t_0}{}^{C}D_t^{\gamma }f(t)=\frac{1}{\mathsf{\Gamma }(m-\gamma )}{\displaystyle {\int }_{t_0}^t\frac{f^m(\tau )}{{(t-\tau )}^{-m+\gamma +1}}}d\tau$$

(2)

where $m-1<\gamma <m$ and $m\in N$, and $\gamma >0$.

Property 1 ([28]). 

The Caputo-type fractional differentiation satisfies the linearity property:

$${}_{t_0}{}^{C}D_t^{\gamma }[{\lambda }_{1}f(t)+{\lambda }_{2}g(t)]={\lambda }_1({}_{t_0}{}^{C}D_t^{\gamma }f(t))+{\lambda }_2{}_{t_0}{}^{C}D_t^{\gamma }g((t))$$

(3)

where ${\lambda }_1$ and ${\lambda }_2$ are real numbers.

Property 2 ([28]). 

For the Caputo-type fractional derivative, if the function $f(t)\in C[0,t]$ and $t>0$, the following relation holds:

$${}_{t_0}{}^{C}D_t^{\gamma }({}_{t_0}{}^{C}D_t^{\beta }f(t))={}_{t_0}{}^{C}D_t^{\gamma +\beta }f(t)$$

(4)

where $\gamma ,\beta \in R^{+}$, and $\gamma +\beta \le 1$.

According to basic fractional order concepts and properties, the lemmas are obtained as follows.

Lemma 1 ([29]). 

The problem of solving the Caputo-type fractional-order equation ${}_{t_0}{}^{C}D{}_t^{\gamma }x(t)=f(t,x)$ can be converted to solving the homologous integer-order equation. The initial value issue of the fractional equation is presented as

$${}_{t_0}{}^{C}D{}_t^{\gamma }(x(t)-x_0)=f(t,x),\&x_0=x(0)$$

(5)

where $0<\gamma <1$, and $f(t,x)\in C([0,T]\times R,R)$.

Lemma 2 ([29]). 

Assume that $f(t,x)\in C(R_I,R)$, where $R_I=[(t,x):0\le t\le c\&\left|x-x_0\right|\le d]$ and $\left|f(t,x)\right|\le M$ on $R_I$. There is at least a solution for fractional-order Equation (5) on $0\le t\le \delta$, where $\delta =\min (\mathrm{c},[\frac{d}{M}\mathsf{\Gamma }(\gamma +1){]}^{1/\gamma })$ and $0<\gamma <1$. Then, a solution of the problem (5) is obtained by $x(t)=x^{*}(\frac{t^{\gamma }}{\mathsf{\Gamma }(\gamma +1)})$, and $x^{*}(\upsilon )$ is the solution of the corresponding integer-order equation $\frac{d(x^{*}(\upsilon ))}{d\upsilon }=g(\upsilon ,x^{*}(\upsilon ))=f(t-{(t^{\gamma }-\upsilon \mathsf{\Gamma }(\gamma +1))}^{1/\gamma },x(t-{(t^{\gamma }-\upsilon \mathsf{\Gamma }(\gamma +1))}^{1/\gamma }))$, with the original condition $x_0=x^{*}(0)$.

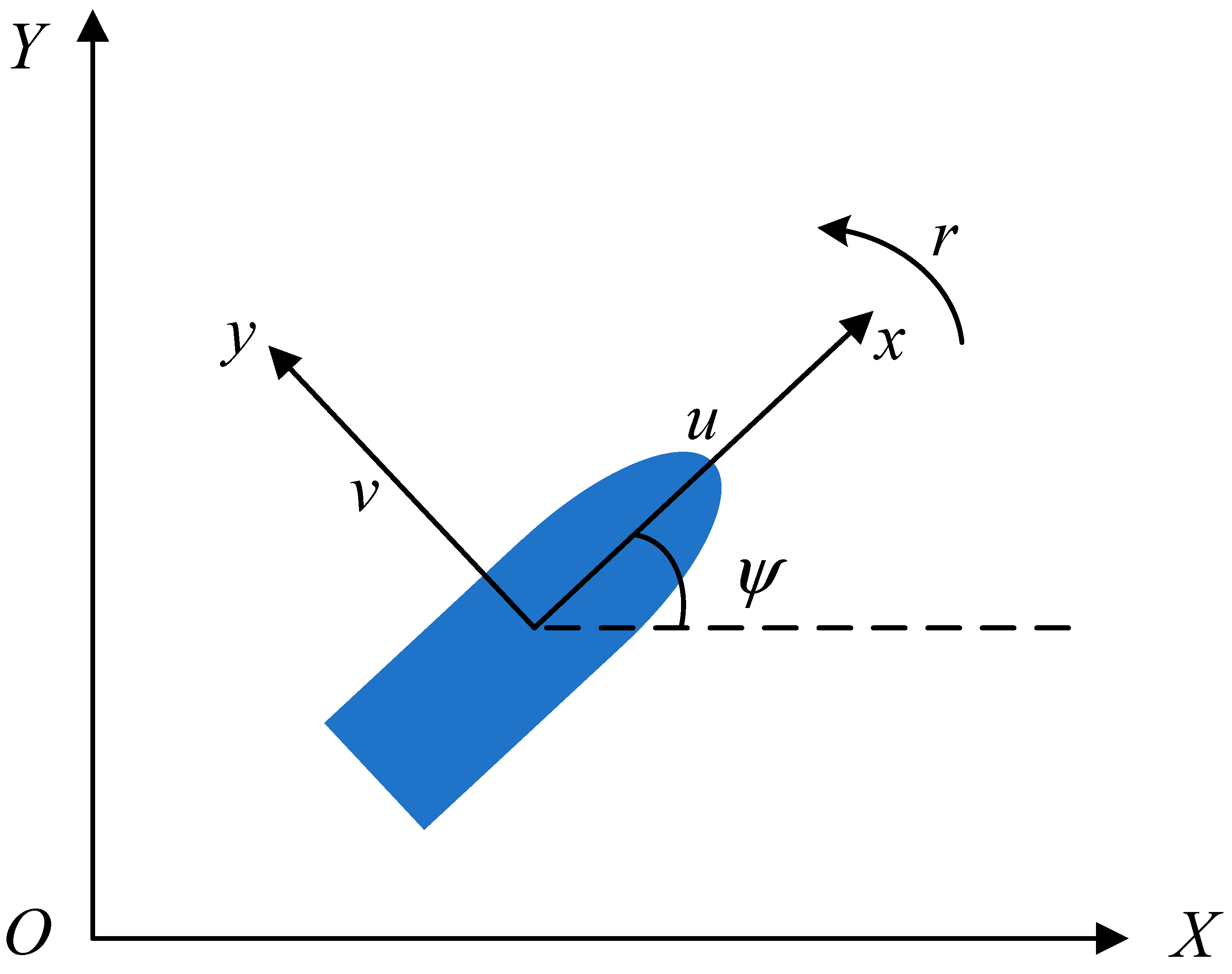
2.2. Problem Formulation

To describe the motion process of the USVs and simplify the design of the controller as much as possible, the three degrees of freedom model coordinate frames of the USV is shown in Figure 1.

The kinematic equation of the USV is described as [30].

$$\{\begin{array}{l}\dot{x}=u\cos \psi -v\sin \psi \hfill \\ \dot{y}=u\sin \psi +v\cos \psi \hfill \\ \dot{\psi }=r\hfill \end{array}$$

(6)

where $\eta ={[x,y,\psi ]}^T$ consists of the position coordinates and the yaw angle in the ground coordinate system. $\nu ={[u,v,r]}^T$ is composed of the surge, sway, and yaw velocity of the USV in the vehicle body coordinate system.

The dynamic equation of the USV with unknown external disturbances and model uncertainties is described as [31].

$$\{\begin{array}{l}\dot{u}=\frac{{\tau }_u}{m_u}+\frac{m_{v}vr-X_{u}u-f_u(\nu )}{m_u}+\frac{{\omega }_u(t)}{m_u}\hfill \\ \dot{v}=\frac{-m_{u}ur-Y_{v}v-f_v(\nu )}{m_v}+\frac{{\omega }_v(t)}{m_v}\hfill \\ \dot{r}=\frac{{\tau }_r}{m_r}+\frac{(m_u-m_v)uv-N_{r}r-f_r(\nu )}{m_r}+\frac{{\omega }_r(t)}{m_r}\hfill \end{array}$$

(7)

where $m_u$, $m_v$ denote the additional mass and $m_r$ represents the moment of inertia. ${\tau }_u$, ${\tau }_r$ denote the surge force and the yaw moment of the actual control inputs, respectively. ${\omega }_u(t)$, ${\omega }_v(t)$ and ${\omega }_r(t)$ represent the environmental disturbances by the winds, waves, and currents. $f_u(\nu )$, $f_v(\nu )$, and $f_r(\nu )$ are uncertain hydrodynamic damping effects; this part will be explained in the simulation.

Remark 1: 

The unmanned surface vehicles have only two control inputs, but have three control outputs, which is a typical underactuated system. At the same time, the USV model contains unknown uncertainty terms $f_i(\nu )(i=u,v,r)$ and unmeasurable external disturbances. These factors bring difficulties to the design of the actual controller.

2.3. Control Objective

Let ${\eta }_d={[x_d,y_d,{\psi }_d]}^T$ be the desired trajectory without a dynamic loop (7), which can be generated by

$$\{\begin{array}{l}{\dot{x}}_d=u_d\cos {\psi }_d\hfill \\ {\dot{y}}_d=u_d\sin {\psi }_d\hfill \\ {\dot{\psi }}_d=r_d\hfill \end{array}$$

(8)

where ${\nu }_d={[u_d,0,r_d]}^T$ represents the reference speed velocity. The control target is to construct a controller such that the system output $\eta$ is capable of tracking the reference trajectory ${\eta }_d$ while ensuring all closed loop signals are global asymptotically stable. Assumptions are presented as follows.

Assumption 1. 

The expected position coordinates $x_d$, $y_d$ and the reference yaw angle ${\psi }_d$ are bounded, differentiable and available.

Assumption 2. 

The marine disturbances ${\omega }_i(t),i=u,v,r$ are bounded and differentiable. Moreover, ${\dot{\omega }}_i(t),i=u,v,r$ is bounded, and there exists ${\iota }_i>0$ satisfying $\left|{\dot{\omega }}_i(t)\right|\le {\iota }_i,i=u,v,r$.

3. Results Analysis

The controller will be designed for the USVs in this section. The errors of the system are provided as

$$\{\begin{array}{l}{x}_e=(x-x_d)\cos \psi +(y-y_d)\sin \psi \hfill \\ y_e=-(x-x_d)\sin \psi +(y-y_d)\cos \psi \hfill \\ {\psi }_e=\psi -{\psi }_d\hfill \end{array}$$

(9)

The time differentiation of (9) is obtained as

$$\{\begin{array}{l}{\dot{x}}_e=u-u_d\cos {\psi }_e+y_{e}r\hfill \\ {\dot{y}}_e=v+u_d\sin {\psi }_e-x_{e}r\hfill \\ {\dot{\psi }}_e=r-r_d\hfill \end{array}$$

(10)

where ${\eta }_e={[x_e,y_e,{\psi }_e]}^T$ is the deviation between the actual trajectory and the expected trajectory.

3.1. Fractional-Order Finite-Time Command Filter

The integer-order command filter is defined as [32]

$$\begin{array}{l}{\dot{z}}_{i,1}=z_{i,2},\\ z_{i,2}=-{\zeta }_{i1}{\left|z_{i,1}-{\alpha }_i(t)\right|}^{1/2}\mathrm{sgn}(z_{i,1}-{\alpha }_i(t))+{\overline{z}}_{i,2},\\ {\dot{\overline{z}}}_{i,2}=-{\zeta }_{i2}\mathrm{sgn}({\overline{z}}_{i,2}-z_{i,2}).\end{array}$$

(11)

where $z_{i,1}$, $z_{i,2}$, and ${\overline{z}}_{i,2}$ represent the state variables of the system. The measurable locally bound function ${\alpha }_i(t),t\in [0,+\infty )$ is the intermediate control signal. There is a differential with Lipschitz’s constant $\zeta >0$. ${\zeta }_{i1}$, ${\zeta }_{i2}>\zeta$ are the adjustable positive real number. The sign function is defined as $\mathrm{sgn}(\theta )=\{\begin{array}{cc}-1& \theta <0\\ 1& \theta \ge 0\end{array}$.

Lemma 4 [33]: 

It can be obtained that there is ${\zeta }_{i2}>\zeta >0$, $0<\frac{2({\zeta }_{i2}+\zeta )}{{\zeta }_{i1}^2({\zeta }_{i2}-\zeta )}<1$ and a sufficiently large ${\zeta }_{i1}>0$, such that $z_{i,2}$, ${\dot{z}}_{i,1}$ converge to ${\dot{\alpha }}_i$ and $z_{i,1}$ converges to ${\alpha }_i$ in the finite time.

According to Lemma 4, it is known that the second-order command filter (11) is finite-time stable without additional compensation signals. However, using the integer-order command filter for nonlinear systems (9) and (10) will lead to the chattering phenomenon, which will affect the practical application effect.

The n-order integer-order nonlinear system corresponding to the fractional-order command filter is presented as [34]

$$\begin{array}{l}{\dot{z}}_{j,1}=z_{j,2},\\ z_{j,2}=-{\zeta }_{j1}{\left|z_{j,1}-{\alpha }_j\right|}^{n/n+1}\mathrm{sgn}(z_{j,1}-{\alpha }_j)+{\overline{z}}_{j,2},\\ {\dot{\overline{z}}}_{j,2}=-{\zeta }_{j2}{\left|{\overline{z}}_{j,2}-{\dot{z}}_{j,1}\right|}^{n-1/n}\mathrm{sgn}({\overline{z}}_{j,2}-{\dot{z}}_{j,1})+{\overline{z}}_{j,3},\\ {\dot{\overline{z}}}_{j,3}=-{\zeta }_{j3}{\left|{\overline{z}}_{j,3}-{\dot{\overline{z}}}_{j,2}\right|}^{n-2/n-1}\mathrm{sgn}({\overline{z}}_{j,3}-{\dot{\overline{z}}}_{j,2})+{\overline{z}}_{j,4},\\ ⋮\\ {\dot{\overline{z}}}_{j,n+1}=-{\zeta }_{j,n+1}\mathrm{sgn}({\overline{z}}_{j,n+1}-{\dot{\overline{z}}}_{j,n}),j=1,2,\dots ,n(n\in Z^{+}).\end{array}$$

(12)

where $z_{j,1},{\overline{z}}_{j,2},\dots {\overline{z}}_{j,n+1},j=1,2,\dots ,n$ represent the USV state variables, ${\zeta }_{j1},{\zeta }_{j2},\dots {\zeta }_{j,n+1},j=1,2,\dots ,n$ denote the positive real number.

Lemma 5 [34]: 

If the appropriate parameters are selected, the following equation is correct in the case of a finite-time transient process without input noises.

$$\begin{array}{l}{z}_{j,1}={\alpha }_{j,0}(t),\\ {\overline{z}}_{j,k}={\alpha }_{j,0}^{(k)}(t),j=1,2,\dots ,n\&k=2,3,\dots ,n(n\in Z^{+}).\end{array}$$

(13)

Therefore, the solutions of the system are finite-time stable.

Based on the integer-order system (12), the fractional-order finite-time command filter can be obtained as

$$\begin{array}{l}{}_{t_0}{}^{C}D_t^{1/n}{z}_{j,1}=z_{j,2},\\ z_{j,2}=-{\zeta }_{j1}{\left|z_{j,1}-{\alpha }_j\right|}^{n/n+1}\mathrm{sgn}(z_{j,1}-{\alpha }_j)+{\overline{z}}_{j,2},\\ {}_{t_0}{}^{C}D_t^{1/n}{\overline{z}}_{j,2}=z_{j,3},\\ z_{j,3}=-{\zeta }_{j2}{\left|{\overline{z}}_{j,2}-z_{j,2}\right|}^{n-1/n}\mathrm{sgn}({\overline{z}}_{j,2}-z_{j,2})+{\overline{z}}_{j,3},\\ {}_{t_0}{}^{C}D_t^{1/n}{\overline{z}}_{j,3}=z_{j,4},\\ z_{j,4}=-{\zeta }_{j3}{\left|{\overline{z}}_{j,3}-z_{j,3}\right|}^{n-2/n-1}\mathrm{sgn}({\overline{z}}_{j,3}-z_{j,3})+{\overline{z}}_{j,4},\\ ⋮\\ {}_{t_0}{}^{C}D_t^{1/n}{\overline{z}}_{j,n+1}=-{\zeta }_{j,n+1}\mathrm{sgn}({\overline{z}}_{j,n+1}-z_{j,n}),j=1,2,\dots ,n(n\in Z^{+}).\end{array}$$

(14)

Theorem 1: 

There is finite time $t_s$ for any initial condition $z_{j,1}(0),{\overline{z}}_{j,2}(0),\cdots ,{\overline{z}}_{j,n+1}(0)$; there are parameters ${\zeta }_{j1},{\zeta }_{j2},\dots ,{\zeta }_{j,n+1}$, such that $z_{j,1},{\overline{z}}_{j,2},\dots ,{\overline{z}}_{j,n+1}$ are able to converge to zero in the finite time $t_s$.

Proof. 

Motivated by Lemma 2, the integer-order system corresponding to Equation (14) is expressed as

$$\begin{array}{l}{\dot{z}}_{j,1}^{\ast }(\upsilon )=z_{j,2}^{\ast }(\upsilon ),\\ z_{j,2}^{\ast }(\upsilon )=-{\zeta }_{j1}{\left|z_{j,1}^{\ast }(\upsilon )-{\alpha }_j\right|}^{n/n+1}\mathrm{sgn}(z_{j,1}^{\ast }(\upsilon )-{\alpha }_j)+{\overline{z}}_{j,2}^{\ast }(\upsilon ),\\ {\dot{\overline{z}}}_{j,2}^{\ast }(\upsilon )=-{\zeta }_{j2}{\left|{\overline{z}}_{j,2}^{\ast }(\upsilon )-{\dot{z}}_{j,1}^{\ast }(\upsilon )\right|}^{n-1/n}\mathrm{sgn}({\overline{z}}_{j,2}^{\ast }(\upsilon )-{\dot{z}}_{j,1}^{\ast }(\upsilon ))+{\overline{z}}_{j,3}^{\ast }(\upsilon ),\\ {\dot{\overline{z}}}_{j,3}^{\ast }(\upsilon )=-{\zeta }_{j3}{\left|{\overline{z}}_{j,3}^{\ast }(\upsilon )-{\dot{\overline{z}}}_{j,2}^{\ast }(\upsilon )\right|}^{n-2/n-1}\mathrm{sgn}({\overline{z}}_{j,3}^{\ast }(\upsilon )-{\dot{\overline{z}}}_{j,2}^{\ast }(\upsilon ))+{\overline{z}}_{j,4}^{\ast }(\upsilon ),\\ ⋮\\ {\dot{\overline{z}}}_{j,n+1}^{\ast }(\upsilon )=-{\zeta }_{j,n+1}\mathrm{sgn}({\overline{z}}_{j,n+1}^{\ast }(\upsilon )-{\dot{\overline{z}}}_{j,n}^{\ast }(\upsilon )),j=1,2,\dots ,n(n\in Z^{+}).\end{array}$$

(15)

where $\upsilon$ denotes the time scale, and $z_{j,1}^{\ast }(0)=z_{j,1}(0),{\overline{z}}_{j,2}^{\ast }(0)={\overline{z}}_{j,2}(0),\dots ,{\overline{z}}_{j,n+1}^{\ast }(0)={\overline{z}}_{j,n+1}(0)$ are the initial conditions. Motivated by Lemma 5, the stability of Equation (15) can be proved by the solutions of the integer-order Equation (12). □

Motivated by Lemma 2, the solutions of Equation (15) can be given as

$$\begin{array}{l}{z}_{j,1}(t)=z_{j,1}^{\ast }(t)(\frac{t^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}),\\ {\overline{z}}_{j,k}(t)=z_{j,k}^{\ast }(t)(\frac{t^{\gamma }}{\mathsf{\Gamma }(\gamma +1)}),j=1,2,\dots ,n\&k=2,3,\dots ,n(n\in Z^{+}).\end{array}$$

(16)

For $\alpha =t-{(t^{\gamma }-\upsilon \mathsf{\Gamma }(\gamma +1))}^{1/\gamma }$ of Lemma 2, $t_s=t_s-{(t_s^{\gamma }-{\upsilon }_s\mathsf{\Gamma }(\gamma +1))}^{1/\gamma }$ with the time scale ${\upsilon }_s$ being able to be maintained in a steady state. Thus, there is a corresponding relationship between the convergence time $t_s$ of $z_{j,1}(t),{\overline{z}}_{j,2}(t),\dots ,{\overline{z}}_{j,n}(t),j=1,2,\dots ,n$ and the integer-order command-filter convergence time ${\upsilon }_s$.□

Remark 2: 

The fractional-order command filter (14) avoids the problem that the derivative of the intermediate control law cannot be calculated directly in the process of designing a controller. It can track the derivative of the intermediate control without adding an additional compensation signal because it is finite-time stable. In addition, the fractional-order command filter can suppress the chattering phenomenon well.

3.2. Fractional-Order Finite-Time Disturbance Observer

According to Theorem 1, the n-order fractional-order disturbance observer can be given as follows:

$$\begin{array}{l}{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,1}=-{\varsigma }_{j1}{\left|{\vartheta }_{j,1}-{\nu }_j(t)\right|}^{n+1/n+2}\mathrm{sgn}({\vartheta }_{j,1}-{\nu }_j(t))+{\vartheta }_{i,2},\\ {}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,2}=-{\varsigma }_{j2}{\left|{\vartheta }_{j,2}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,1}\right|}^{n/n+1}\mathrm{sgn}({\vartheta }_{j,2}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,1})+{\vartheta }_{j,3},\\ ⋮\\ {}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n}=-{\varsigma }_{j,n}{\left|{\vartheta }_{j,n}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n-1}\right|}^{2/3}\mathrm{sgn}({\vartheta }_{j,n}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n-1})+{\vartheta }_{j,n+1}+g_j(\nu )+{\tau }_j,\\ ⋮\\ {}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n+2}=-{\varsigma }_{j,n+2}\mathrm{sgn}({\vartheta }_{j,n+2}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n+1}),\\ {\widehat{\omega }}_j=-{\varsigma }_{j,n}{\left|{\vartheta }_{j,n}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n-1}\right|}^{2/3}\mathrm{sgn}({\vartheta }_{j,n}-{}_{t_0}{}^{C}D_t^{1/n}{\vartheta }_{j,n-1})+{\vartheta }_{j,n+1},j=1,2,\cdots ,n(n\in Z^{+}).\end{array}$$

(17)

where ${\vartheta }_{j,1},{\vartheta }_{j,2},\dots ,{\vartheta }_{j,n+2},j=1,2,\dots ,n$ represent the variables of the disturbance observer, and ${\varsigma }_{j1},{\varsigma }_{j2},\dots ,{\varsigma }_{j,n+2},j=1,2,\dots ,n$ represent the adjustable positive real number. ${\tau }_j$ and $g_j(\nu )$ represent the actual control input and known modeling error, respectively. ${\nu }_j(t)$ denotes the speed velocity of the dynamic model. ${\widehat{\omega }}_j$ is the output of disturbance observer and represents the estimated value of the system disturbances and unknown model uncertainties.

Theorem 2: 

There is a time  $t_r$ for any original conditions ${\vartheta }_{j,1}(0),{\vartheta }_{j,2}(0),\dots ,{\vartheta }_{j,n+2}(0)$; there are parameters ${\varsigma }_{j1},{\varsigma }_{j2},\dots ,{\varsigma }_{j,n+2}$, such that ${\vartheta }_{j,1},{\vartheta }_{j,2},\cdots ,{\vartheta }_{j,n+2}$ are able to converge to zero in finite time $t_r$.

Proof. 

According to the similar proof method of Theorem 1, it can be concluded that Theorem 2 holds. □

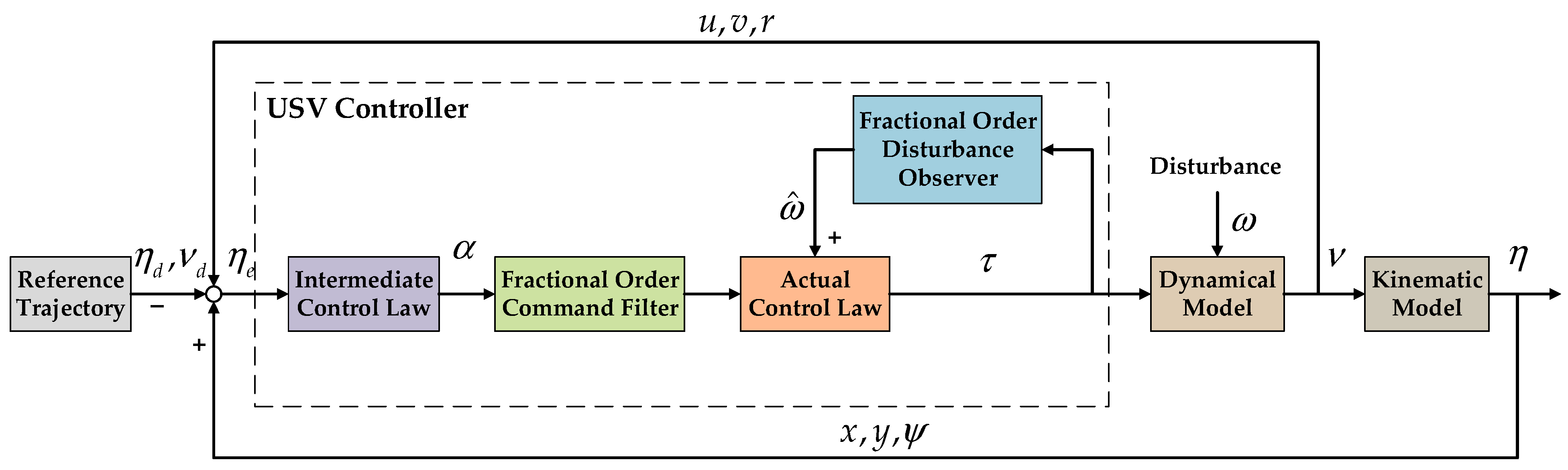
3.3. Controller Design

On the basis of the above section, the fractional-order backstepping controller block diagram is shown in Figure 2.

The conversion of coordinates is defined as follows:

$$u_e=u-{\alpha }_u,{\overline{\psi }}_e={\psi }_e-{\alpha }_{\psi },r_e=r-{\alpha }_r.$$

(18)

The system intermediate control signals ${\alpha }_u,{\alpha }_{\psi },{\alpha }_r$ are defined as

$$\begin{array}{l}{\alpha }_u=-c_x{x}_e+u_d\cos {\psi }_e-y_{e}r,\\ {\alpha }_{\psi }=\frac{1}{u_d}(-c_y{y}_e-v+x_{e}r),\\ {\alpha }_r=-c_{\psi }{\overline{\psi }}_e+r_d+z_{\psi ,n+1}-y_e{u}_d.\end{array}$$

(19)

where $c_x,c_y,c_{\psi }$ are positive real numbers.

The actual control inputs ${\tau }_u,{\tau }_r$ are designed as

$$\begin{array}{l}{\tau }_u=m_u(-c_u{u}_e-x_e+z_{u,n+1}-\frac{m_{v}vr-X_{u}u}{m_u}-\frac{{\widehat{\omega }}_u}{m_u}),\\ {\tau }_r=m_r(-c_r{r}_e-{\overline{\psi }}_e+z_{r,n+1}-\frac{(m_u-m_v)uv-X_{r}r}{m_r}-\frac{{\widehat{\omega }}_r}{m_r}).\end{array}$$

(20)

where $c_u,c_r\in R^{+}$.

3.4. Stability Analysis

Consider the Lyapunov function as

$$V=V_x+V_y+V_{\psi }+V_u+V_r$$

(21)

and

$$\begin{array}{l}{V}_x=\frac{1}{2}{x}_e^2,V_y=\frac{1}{2}{y}_e^2,V_{\psi }=\frac{1}{2}{\psi }_e^2,\\ V_u=\frac{1}{2}{u}_e^2,V_r=\frac{1}{2}{r}_e^2.\end{array}$$

(22)

The differential of (21) can be written as

$$\dot{V}={\dot{V}}_x+{\dot{V}}_y+{\dot{V}}_{\psi }+{\dot{V}}_u+{\dot{V}}_r$$

(23)

Combining (10) and (22), the differential of the Lyapunov function $V_x$ is expressed as

$${\dot{V}}_x=x_e{\dot{x}}_e=x_e(u-u_d\cos {\psi }_e+y_{e}r)$$

(24)

According to Lemma 5, Theorem 1, (18), and (19), adding (14) to the Lyapunov function, where $z_{u,1}={\alpha }_u$, (24) can then be simplified as

$${\dot{V}}_x=x_e(u_e+{\alpha }_u-u_d\cos {\psi }_e+y_{e}r)=-c_x{x}_e^2+x_e{u}_e$$

(25)

Based on (11) and (22), the differential of the Lyapunov candidate $V_y$ is given as

$${\dot{V}}_y=y_e{\dot{y}}_e=y_e(v+u_d\sin {\psi }_e-x_{e}r)$$

(26)

According to Lemma 5, Theorem 1, (14), (18), and (19), there is $z_{\psi ,1}={\alpha }_{\psi }$; then, (26) can be simplified as

$${\dot{V}}_y=y_e(v+u_d({\overline{\psi }}_e+{\alpha }_{\psi })-x_{e}r)=-c_y{y}_e^2+u_d{y}_e{\overline{\psi }}_e$$

(27)

From Formulas (10) and (22), the differentiation of the Lyapunov candidate $V_{\psi }$ is rewritten as

$${\dot{V}}_{\psi }={\overline{\psi }}_e{\dot{\overline{\psi }}}_e={\overline{\psi }}_e({\dot{\psi }}_e-{\dot{\alpha }}_{\psi })={\overline{\psi }}_e(r-r_d-{\dot{\alpha }}_{\psi })$$

(28)

Combining (14), (18), (19), Lemma 5, and Theorem 1, we can obtain $z_{r,1}={\alpha }_r$ and ${}_{t_0}{}^{C}D_t^{1/n}{\overline{z}}_{\psi ,n}=z_{\psi ,n+1}={\dot{\alpha }}_{\psi }$. Thus, (28) can be simplified as

$${\dot{V}}_{\psi }={\overline{\psi }}_e((r_e+{\alpha }_r)-r_d-{\dot{\alpha }}_{\psi })=-c_{\psi }{\overline{\psi }}_e^2+{\overline{\psi }}_e{r}_e$$

(29)

According to Lemma 5, Theorem 1, and Formula (14), there are ${}_{t_0}{}^{C}D_t^{1/n}{\overline{z}}_{u,n}=z_{u,n+1}={\dot{\alpha }}_u$ and ${}_{t_0}{}^{C}D_t^{1/n}{\overline{z}}_{r,n}=z_{r,n+1}={\dot{\alpha }}_r$. Based on Theorem 2, there is a finite time $t_r$ such that $t>t_r$ has ${\widehat{\omega }}_u(t)={\omega }_u(t)-f_u(\nu )$ and ${\widehat{\omega }}_r(t)={\omega }_r(t)-f_r(\nu )$. Therefore, the time derivatives of the Lyapunov candidates $V_u$ and $V_r$ are expressed as

$$\begin{array}{ll}{\dot{V}}_u& =u_e{\dot{u}}_e=u_e(\dot{u}-{\dot{\alpha }}_u)\\ & =u_e(\frac{{\tau }_u}{m_u}+\frac{m_{v}vr-X_{u}u-f_u(\nu )}{m_u}+\frac{{\omega }_u(t)}{m_u}-{\dot{\alpha }}_u)\\ & =-c_u{u}_e^2-u_e{x}_e\end{array}$$

(30)

and

$$\begin{array}{ll}{\dot{V}}_r& =r_e{\dot{r}}_e=r_e(\dot{r}-{\dot{\alpha }}_r)\\ & =r_e(\frac{{\tau }_r}{m_r}+\frac{(m_u-m_v)uv-N_{r}r-f_r(\nu )}{m_r}+\frac{{\omega }_r(t)}{m_r}-{\dot{\alpha }}_r)\\ & =-c_r{r}_e^2-{\overline{\psi }}_e{r}_e\end{array}$$

(31)

Substituting (25), (27), and (29)–(31) into (23), we obtain

$$\dot{V}=-c_x{x}_e^2-c_y{y}_e^2-c_{\psi }{\overline{\psi }}_e^2-c_u{u}_e^2-c_r{r}_e^2$$

(32)

The Lyapunov function $V=V_x+V_y+V_{\psi }+V_u+V_r$ satisfies the relation

$$\begin{array}{ll}\dot{V}& =-c_x{x}_e^2-c_y{y}_e^2-c_{\psi }{\overline{\psi }}_e^2-c_u{u}_e^2-c_r{r}_e^2\\ & <-CV\end{array}$$

(33)

where $C=\min (2*(c_x,c_y,c_{\psi },c_u,c_r))$.

Theorem 3: 

For the USVs (6) and (7) with Assumptions 1 and 2, the reference signals are given as (8), the fractional-order finite-time command filter is denoted by (14), the fractional-order finite-time disturbance observer is provided as (17), the intermediate control signals are represented by (19), and the actual control inputs are designed as (20). By choosing appropriate positive parameters $c_x,c_y,c_{\psi },c_u,c_r$, ${\varsigma }_{j1},{\varsigma }_{j2},\dots ,{\varsigma }_{j,n+2}$, and ${\zeta }_{j1},{\zeta }_{j2},\dots ,{\zeta }_{j,n+1}$, the solutions of the closed-loop nonlinear system are globally asymptotically stable in nature, and satisfy $\eta ={\eta }_d$ when $t\to \infty$.

Proof. 

According to formula (33), when $V=V_x+V_y+V_{\psi }+V_u+V_r>0$, there is $\dot{V}<-CV$, then the closed-loop systems (6) and (7) are global asymptotically stable. Since the USV system satisfies the globally asymptotic stability, if the appropriate system parameters $c_x,c_y,c_{\psi },c_u,c_r$, ${\varsigma }_{j1},{\varsigma }_{j2},\dots ,{\varsigma }_{j,n+2}$, and ${\zeta }_{j1},{\zeta }_{j2},\dots ,{\zeta }_{j,n+1}$ are selected, it is obvious that $\underset{t\to \infty }{\lim }\left|\eta -{\eta }_d\right|\to 0$. □

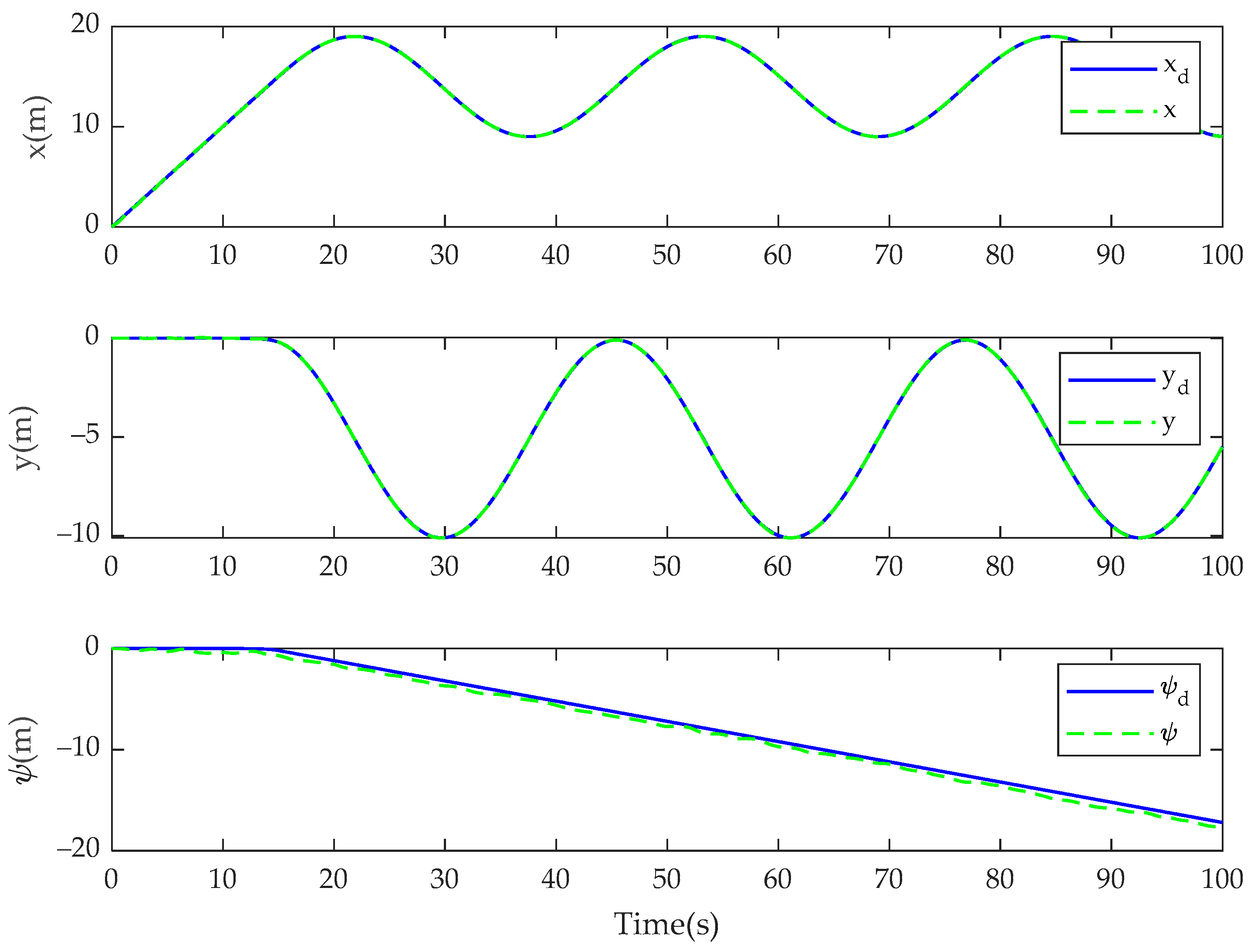
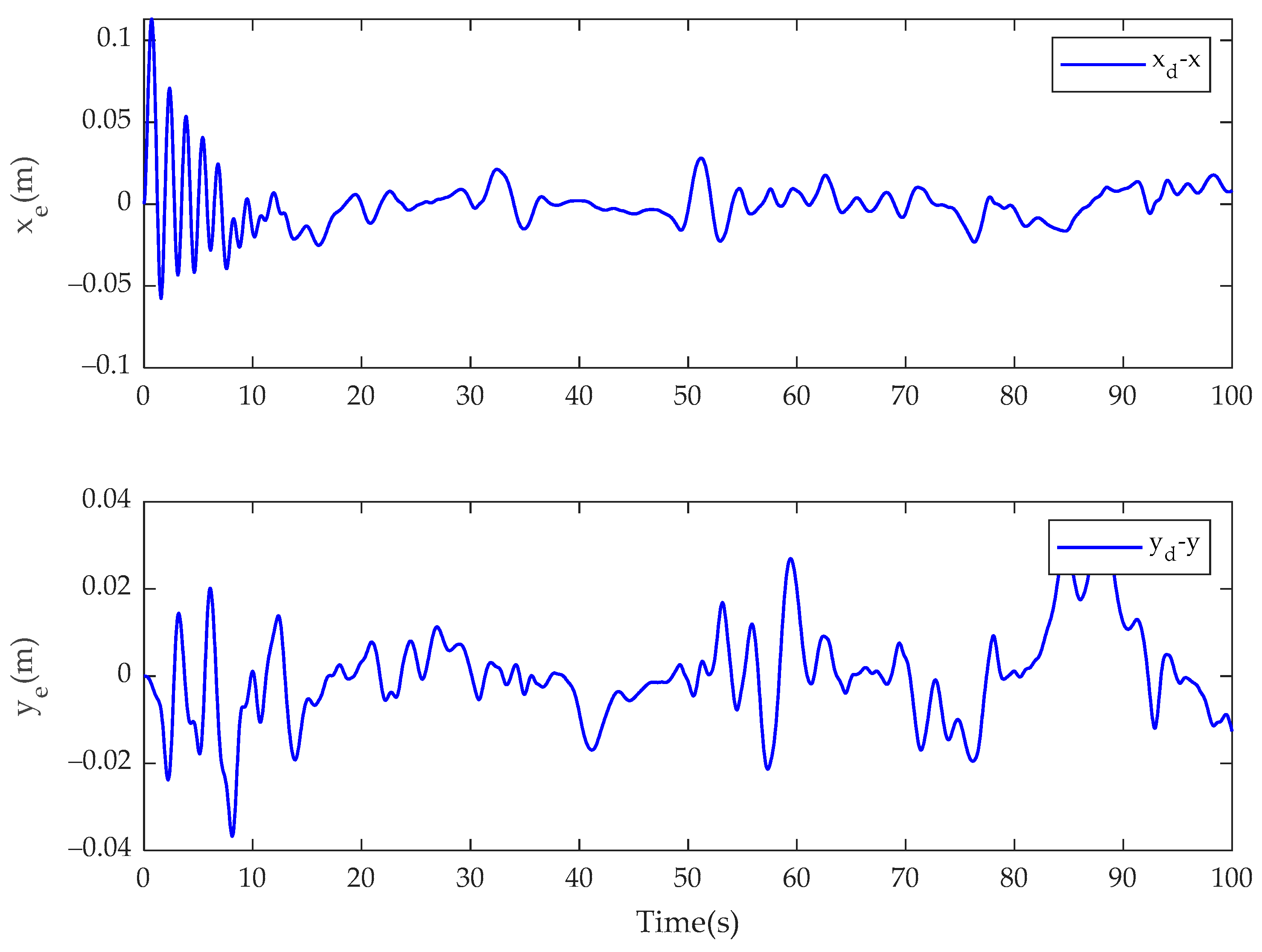
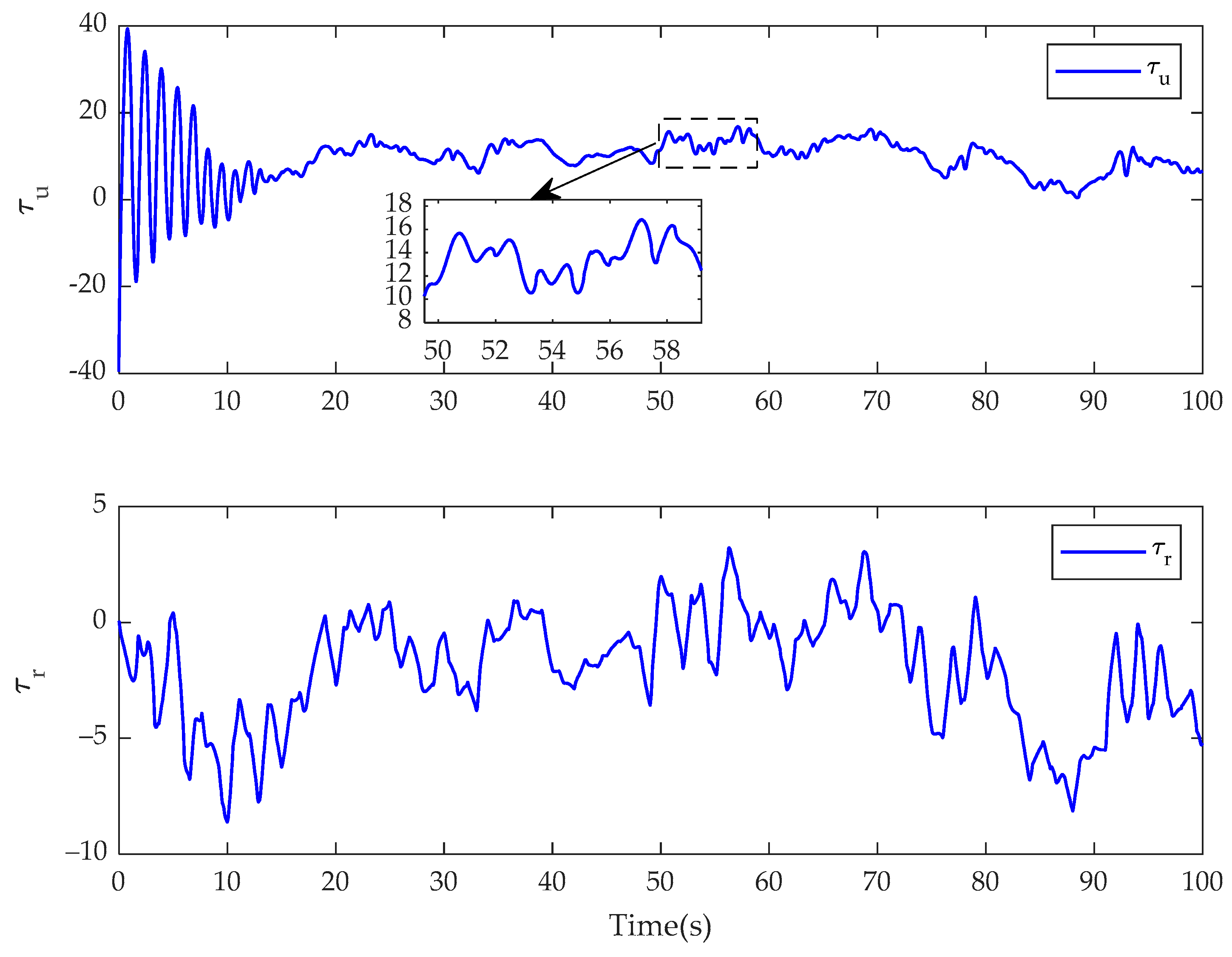
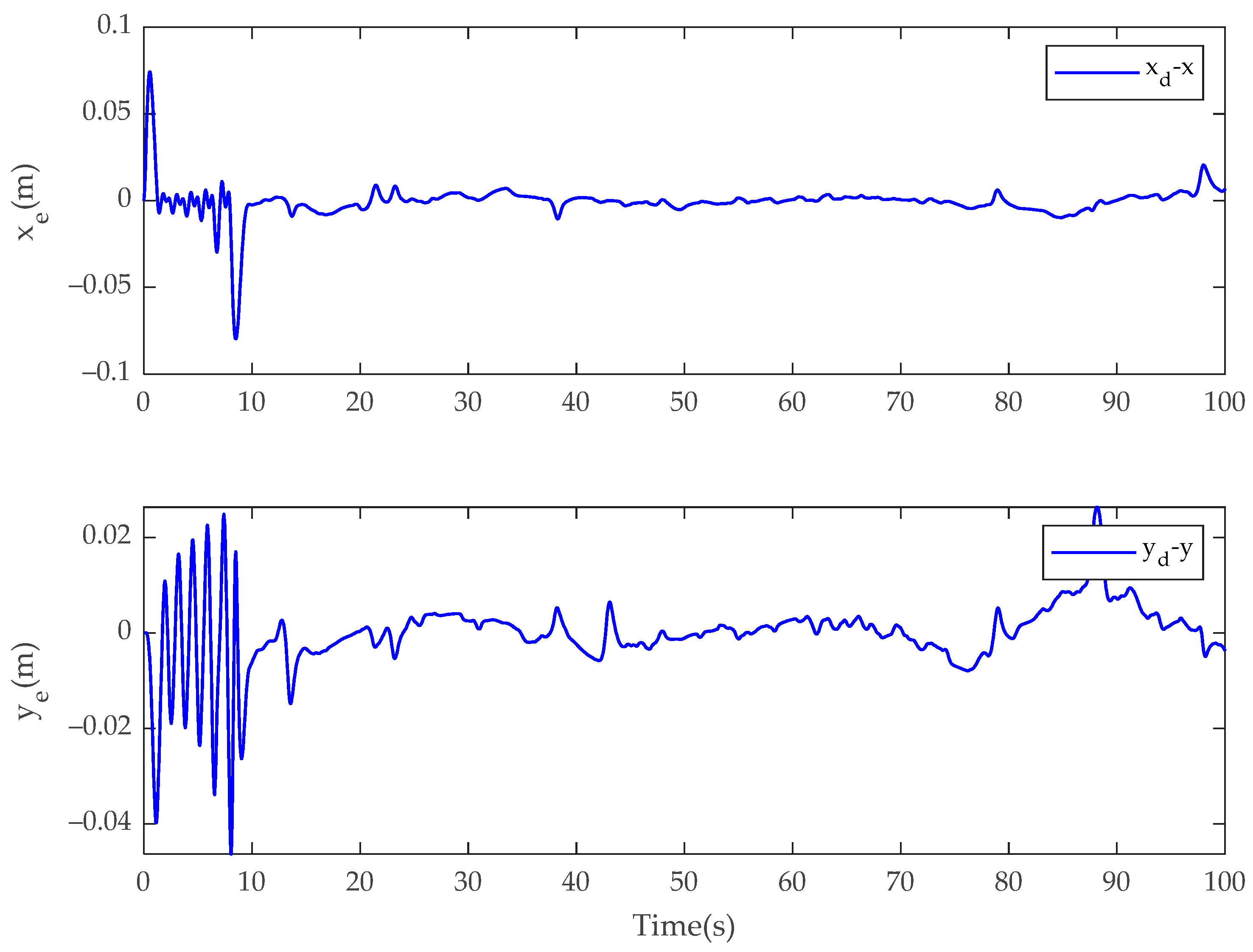
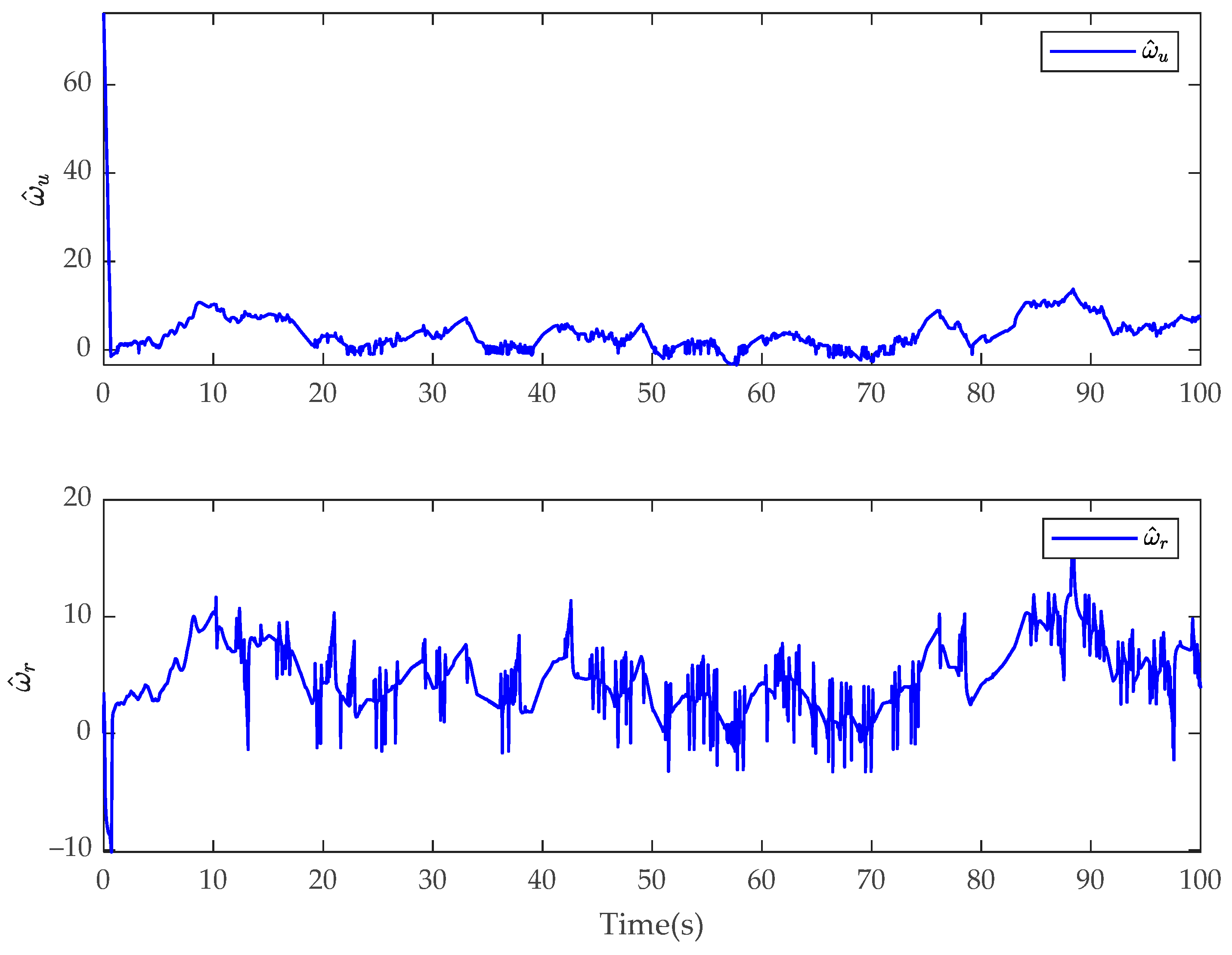
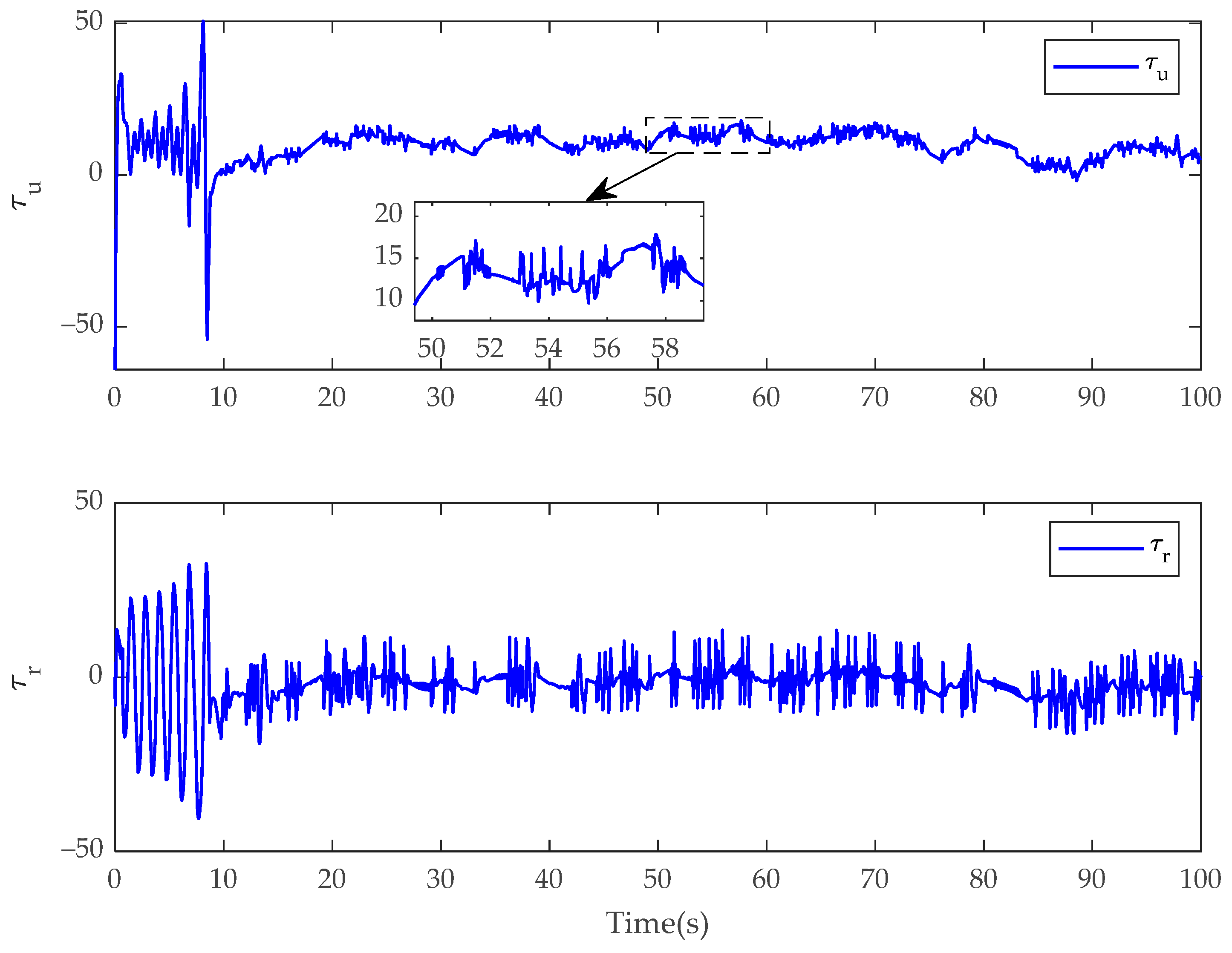
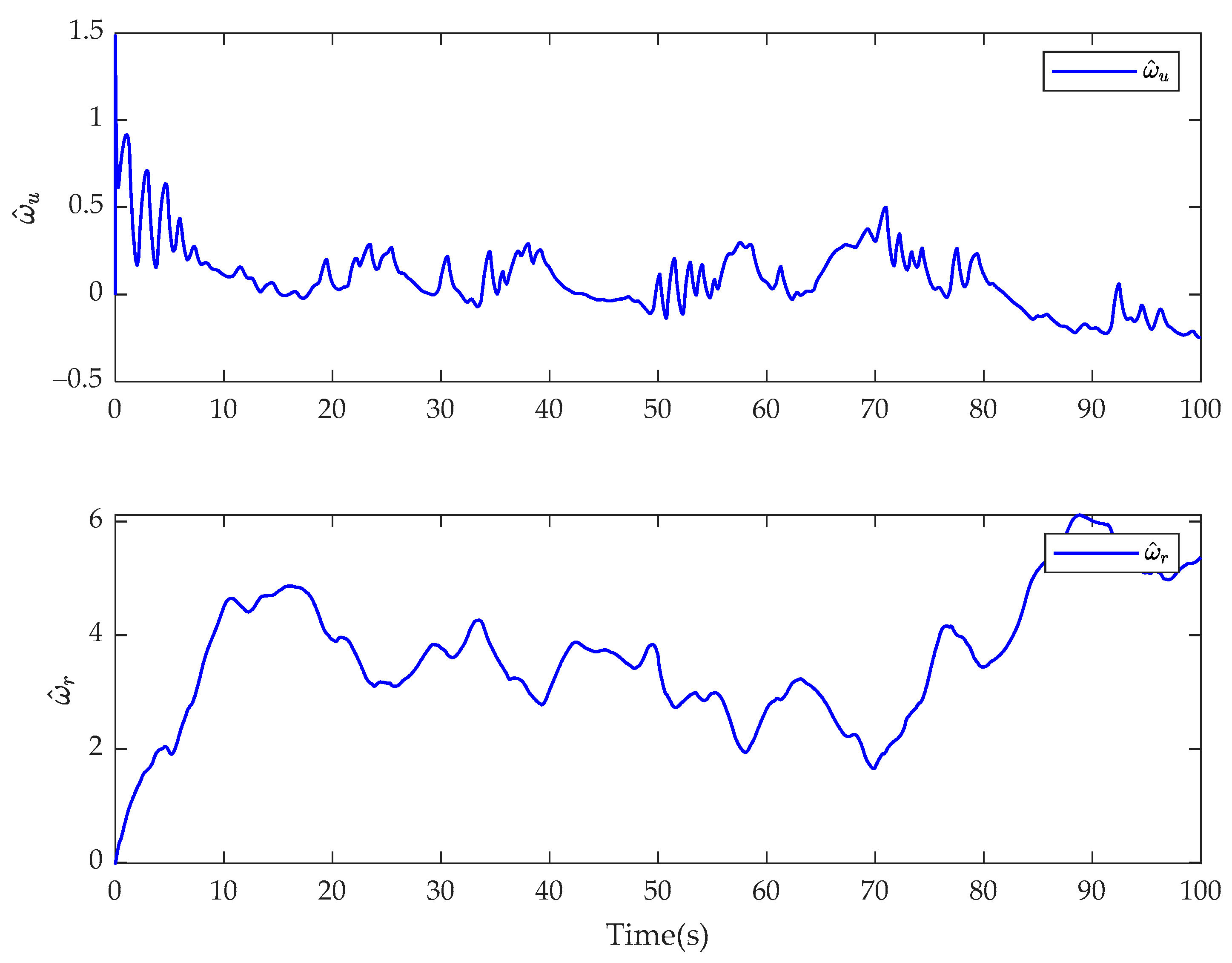
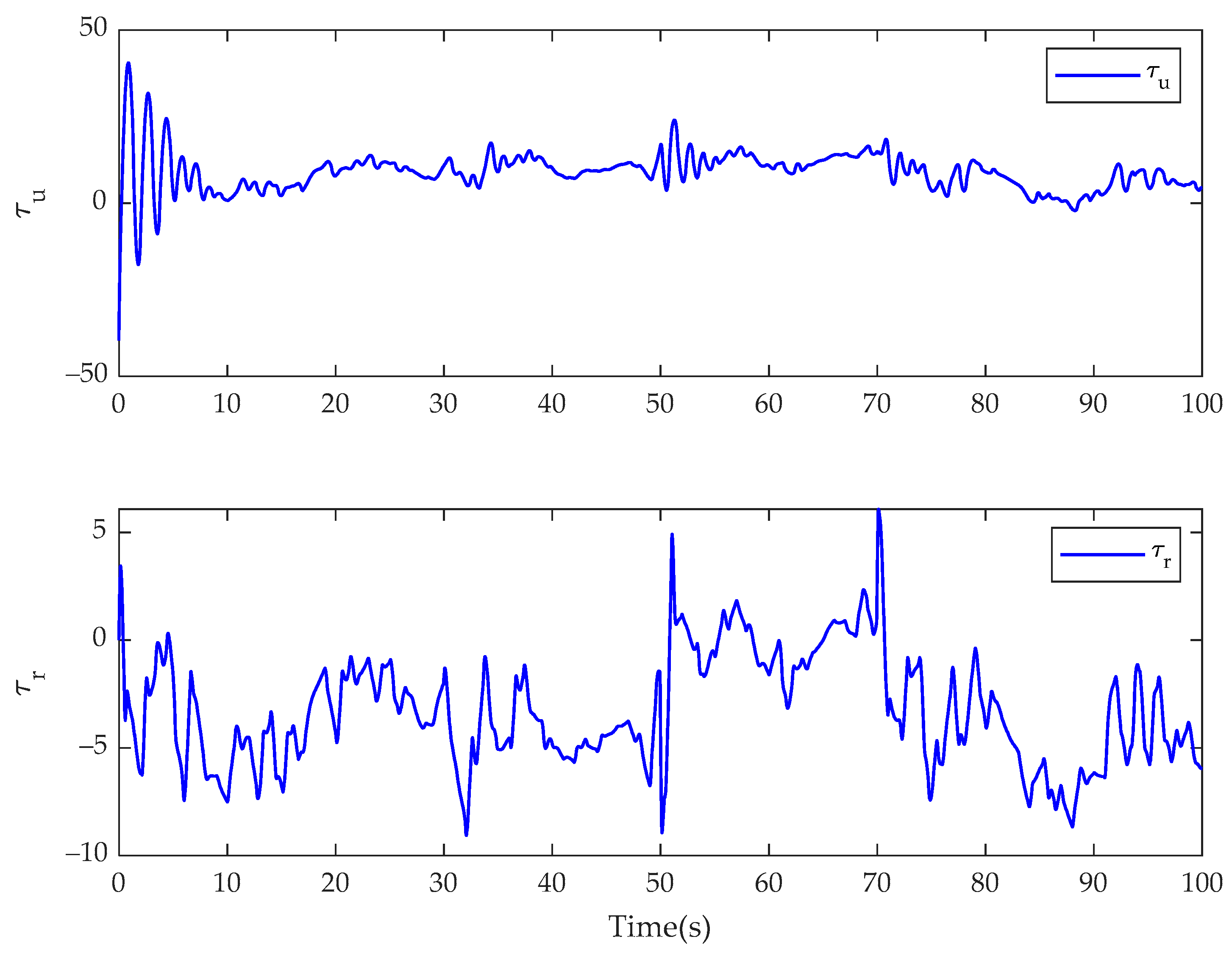
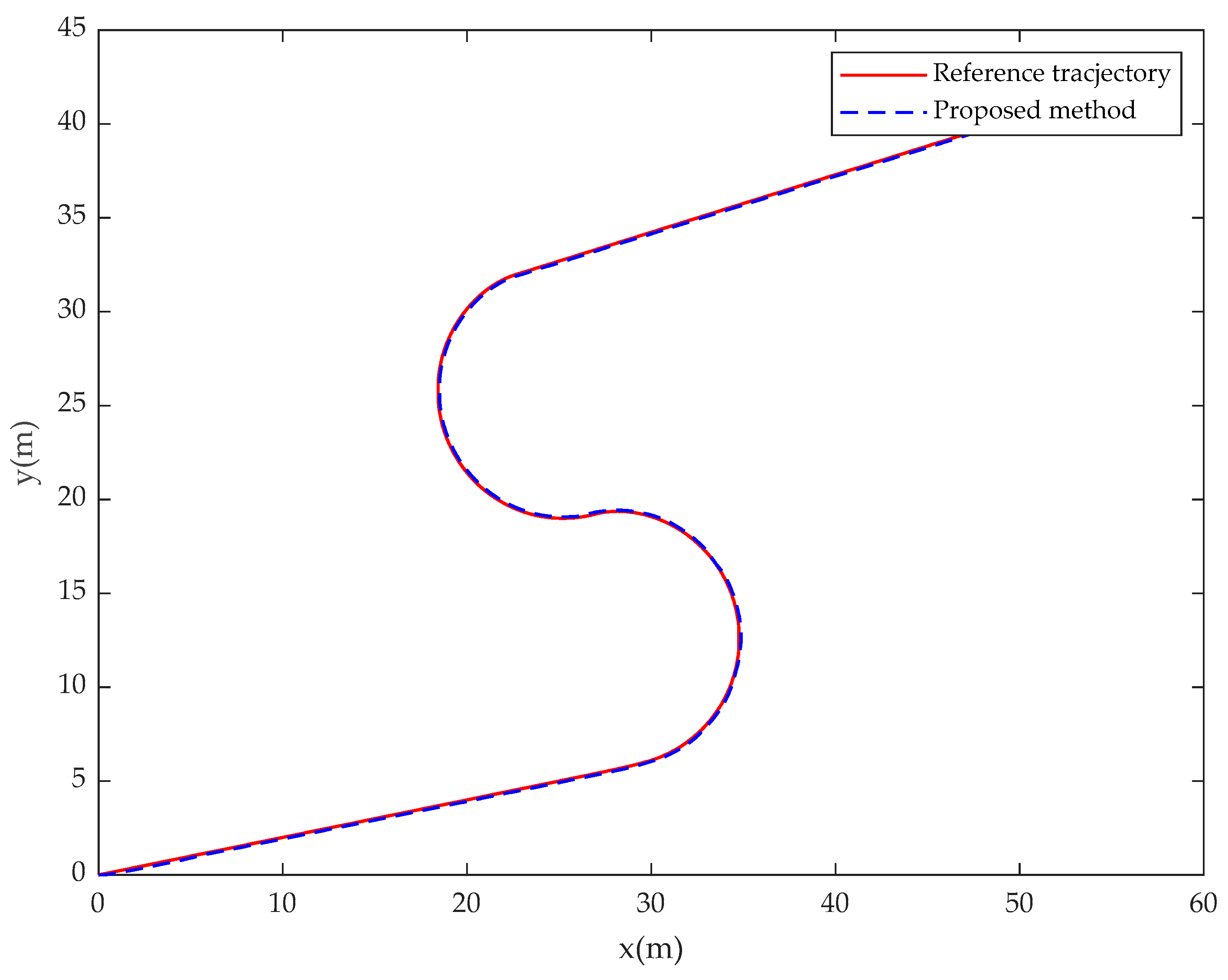
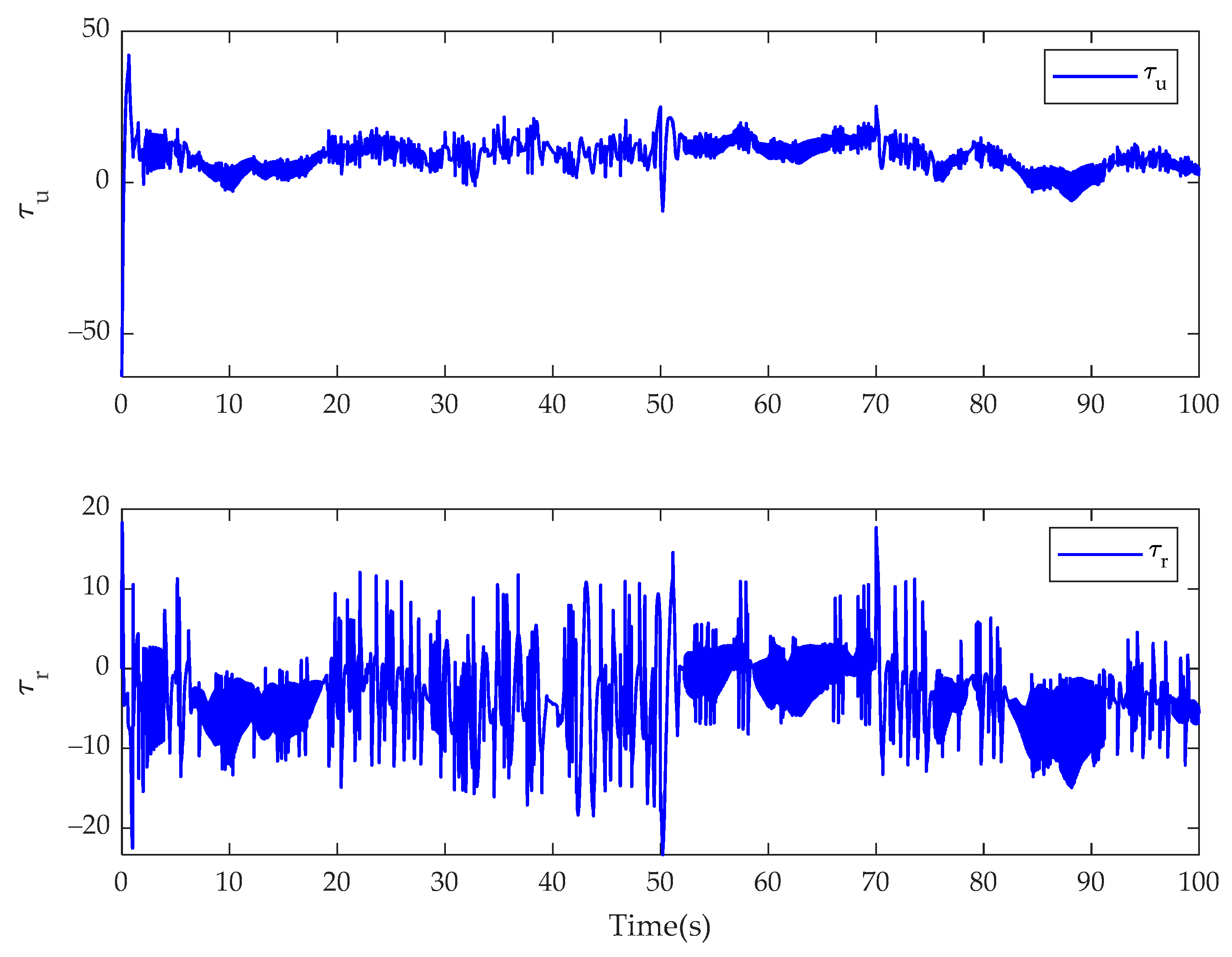
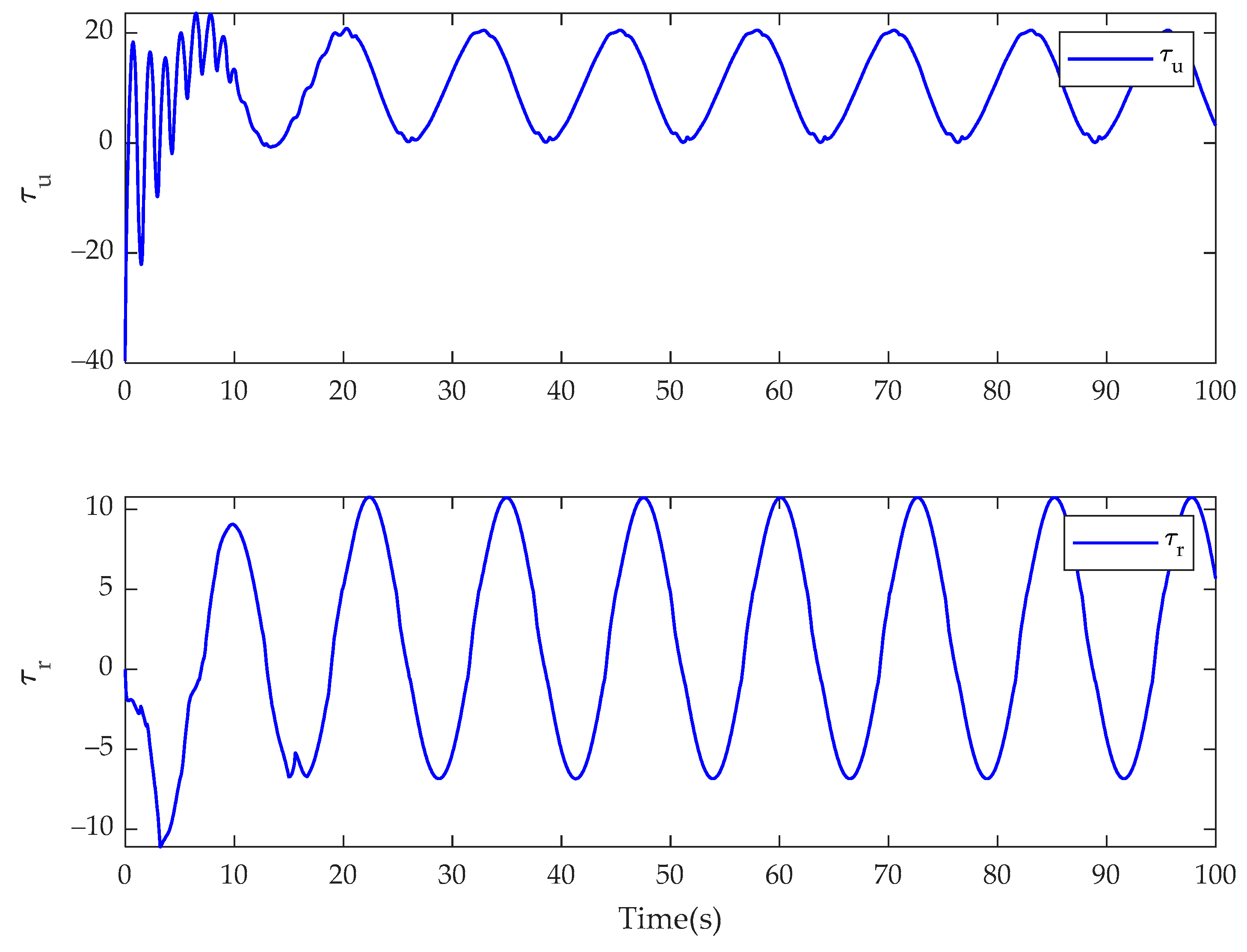
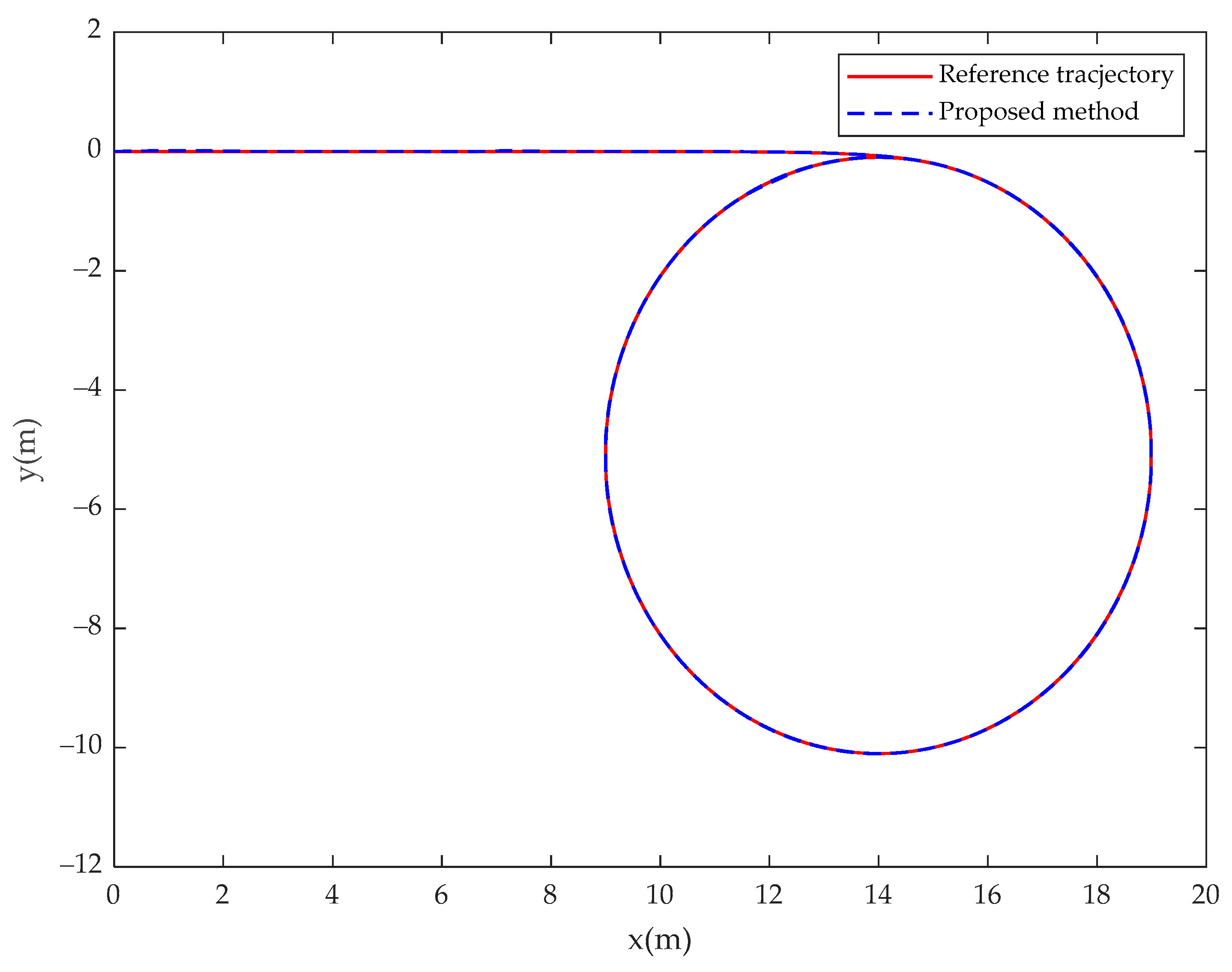
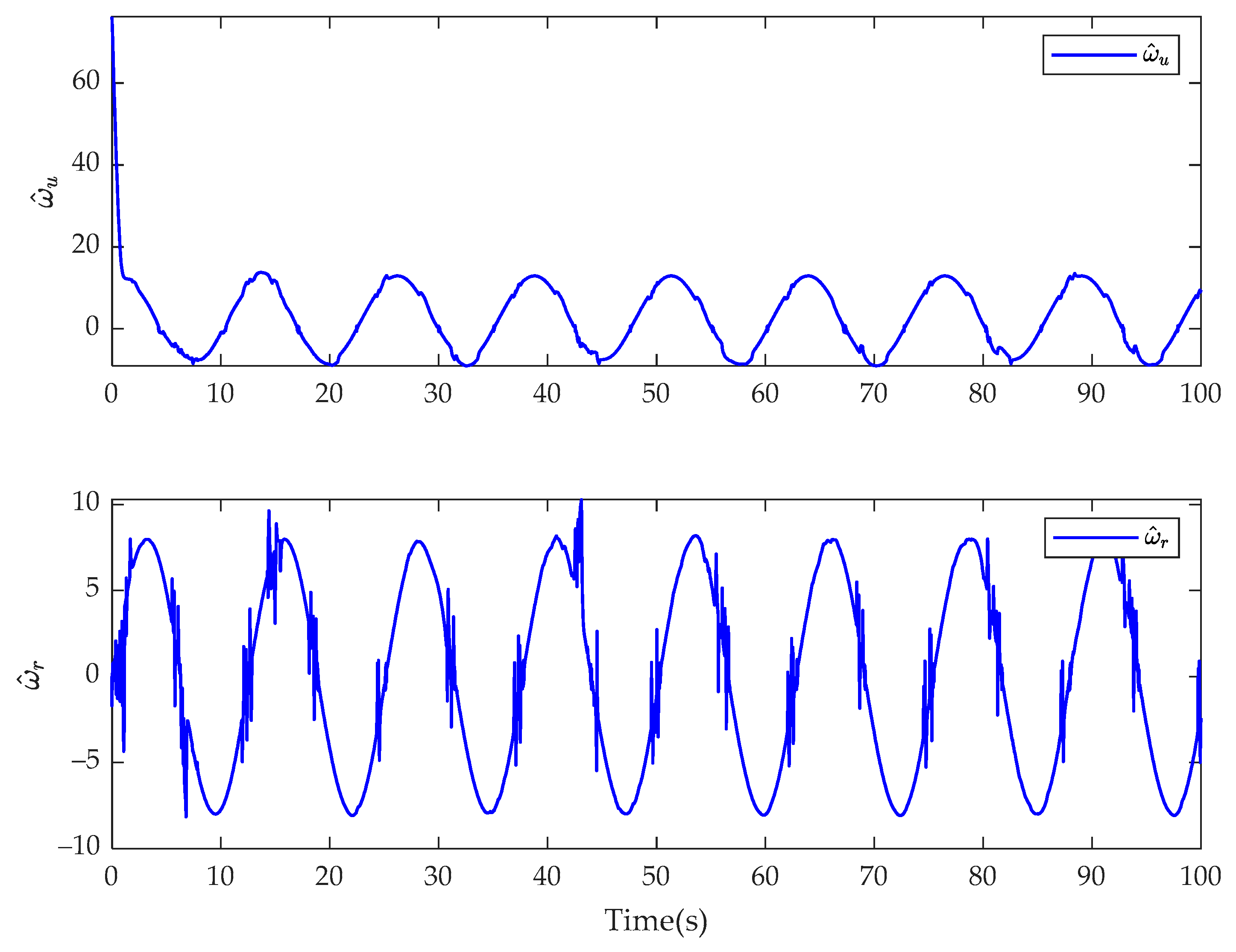
4. Simulation Results

To prove the effectiveness and superiority of the fractional-order backstepping controller, simulation experiments based on the USV model are proposed in this section. The same reference trajectory and system model are used for comparison experiments. The initial value of USV is defined as ${\eta }_0={[0\mathrm{m},0\mathrm{m},0\mathrm{rad}]}^T$, ${\nu }_0={[1\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s},0\mathrm{rad}/\mathrm{s}]}^T$. The hydrodynamic coefficients effects are assumed as $f_u(\nu )=X_{\left|u\right|u}\left|u\right|u$, $f_v(\nu )=Y_{\left|v\right|v}\left|v\right|v$, and $f_r(\nu )=N_{\left|r\right|r}\left|r\right|r$. The system parameters are denoted as $m_u=25.8\mathrm{kg}$, $m_v=33.8\mathrm{kg}$, $m_r=2.76\mathrm{kg}\cdot {\mathrm{m}}^2$, $X_u=12\mathrm{N}$, $X_v=17\mathrm{N}$, $X_r=0.5\mathrm{N}\cdot \mathrm{m}$, $X_{\left|u\right|u}=2.5$, $Y_{\left|v\right|v}=4.5$, and $N_{\left|r\right|r}=0.1$.

Case 1: The unknown external disturbances are defined as ${\dot{\omega }}_u=-0.01{\omega }_u+3\mathrm{rand}$, ${\dot{\omega }}_v=-0.01{\omega }_v+2\mathrm{rand}$, ${\dot{\omega }}_r=-0.01{\omega }_r+2.5\mathrm{rand}$, where $\mathrm{rand}$ is a random number with a mean value of 0, a variance of 0.5, and a sampling time of 1. The USV reference trajectory are given as $u_d=1\mathrm{m}/\mathrm{s}$, $v_d=0\mathrm{m}/\mathrm{s}$ for $0\le t\le 100\mathrm{s}$. $r_d=-0.2e^{-(15-t)}\mathrm{rad}/\mathrm{s}$ for $0\le t\le 15\mathrm{s}$, and $r_d=-0.2\mathrm{rad}/\mathrm{s}$ for $15<t\le 100\mathrm{s}$.

(1) For the fractional-order backstepping controller, the fractional-order command filter is (14), and the fractional-order disturbance observer is (18). When $n=2$, the control parameters are selected as $c_x=20$, $c_y=10$, $c_{\psi }=1$, $c_u=1$, $c_r=30$, ${\zeta }_{\psi 1}={\zeta }_{u1}={\zeta }_{r1}=1$, ${\zeta }_{\psi 2}={\zeta }_{u2}={\zeta }_{r2}=0.1$, ${\zeta }_{\psi 3}=0.01$, ${\zeta }_{r3}=0.01$, ${\zeta }_{u3}=0.001$, ${\varsigma }_{u1}={\varsigma }_{r1}=5$, ${\varsigma }_{u2}=0.1$, ${\varsigma }_{r2}=1$, ${\varsigma }_{u3}={\varsigma }_{r3}=0.1$, ${\varsigma }_{u4}={\varsigma }_{r4}=0.001$.

(2) For the integer-order backstepping controller, the command filter is given as (11), and the integer-order disturbance observer is defined as

$$\begin{array}{l}{\dot{\vartheta }}_{i,1}=-{\varsigma }_{i1}{\left|{\vartheta }_{i,1}-{\nu }_i(t)\right|}^{1/2}\mathrm{sgn}({\vartheta }_{i,1}-{\nu }_i(t))+{\vartheta }_{i,2}+g_i(\nu )+{\tau }_i,\\ {\dot{\vartheta }}_{i,2}=-{\varsigma }_{i2}\mathrm{sgn}({\vartheta }_{i,2}-{\dot{\vartheta }}_{i,1}),\\ {\widehat{\omega }}_i=-{\varsigma }_{i1}{\left|{\vartheta }_{i,1}-{\nu }_i(t)\right|}^{1/2}\mathrm{sgn}({\vartheta }_{i,1}-{\nu }_i(t))+{\vartheta }_{i,2}.\end{array}$$

(34)

where ${\vartheta }_{i,2}$ and ${\vartheta }_{i,1}$ represent the state variables of the disturbance observer, ${\varsigma }_{i1}$, ${\varsigma }_{i2}$ are the adjustable positive constants, ${\nu }_i(t)$ denotes the output of the dynamic equation, ${\tau }_i$ and $g_i(\nu )$ represent the actual control input and known modeling error, respectively. ${\widehat{\omega }}_i$ is the output of the disturbance observer and represents the estimated value of the system disturbances and uncertainties.

Then, the control parameters are selected as $c_x=c_y=c_{\psi }=c_u=c_r=4$, ${\zeta }_{\psi 1}={\zeta }_{u1}={\zeta }_{r1}=10$, ${\zeta }_{\psi 2}={\zeta }_{u2}={\zeta }_{r2}=0.001$, ${\varsigma }_{u1}={\varsigma }_{r1}=15$, ${\varsigma }_{u2}={\varsigma }_{r2}=0.01$.

In Case 1, the simulation results of the USV system with model uncertainty and external environmental disturbance are presented in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. Figure 3, Figure 4 and Figure 5 present the trajectory tracking diagram and error diagram of the proposed fractional-order backstepping controller, and Figure 8, Figure 9 and Figure 10 present the trajectory tracking of the integer-order controller. It can be seen from Figure 3 and Figure 8 that the tracking error of the proposed controller is basically the same as that of the comparison controller; that is, the trajectory tracking effect of both is basically the same. Random numbers are used as disturbance sources in this paper. Figure 6 shows the disturbance observations of the fractional-order backstepping controller. It is clear that the original observation value of the observer of the fractional-order backstepping controller is small, and there is no chattering. Figure 11 presents the disturbance observations of the integer-order backstepping controller. It can be seen that the observed initial value of the integer-order controller is large, and chattering is always present during trajectory tracking. Figure 7 represents the actual control inputs of the fractional-order backstepping controller, and there is no chattering in the control inputs. Figure 12 denotes the actual control inputs of the integer-order controller, and it can be seen that the chattering phenomenon of the control inputs is severe. Combined with the local amplification view, it is clear that the control input chattering of the controller proposed in this paper is significantly improved compared with the integer-order controller under the condition that the trajectory tracking effect is basically the same.

Case 2: Comparative experiment of Case 1. Modify the reference trajectory of Case 1 without changing other conditions. The USV reference trajectory are given as $u_d=1\mathrm{m}/\mathrm{s}$, $v_d=0.2\mathrm{m}/\mathrm{s}$ for $0\le t\le 100\mathrm{s}$. $r_d=-0.1e^{-(30-t)}\mathrm{rad}/\mathrm{s}$ for $0\le t\le 30\mathrm{s}$, $r_d=0.15+0.1e^{-(50-t)}\mathrm{rad}/\mathrm{s}$ for $30\le t\le 50\mathrm{s}$, $r_d=-(0.15+0.1e^{-(70-t)})\mathrm{rad}/\mathrm{s}$ for $50\le t\le 70\mathrm{s}$, and $r_d=-0.1e^{-(100-t)}\mathrm{rad}/\mathrm{s}$ for $70<t\le 100\mathrm{s}$.

(1) For fractional-order backstepping controller, when $n=2$, the control parameters of USV system are selected as $c_x=15$, $c_y=20$, $c_{\psi }=1$, $c_u=1$, $c_r=15$, ${\zeta }_{\psi 1}={\zeta }_{u1}={\zeta }_{r1}=1$, ${\zeta }_{\psi 2}={\zeta }_{u2}={\zeta }_{r2}=0.1$, ${\zeta }_{\psi 3}=0.01$, ${\zeta }_{r3}=0.01$, ${\zeta }_{u3}=0.001$, ${\varsigma }_{u1}={\varsigma }_{r1}=5$, ${\varsigma }_{u2}=0.1$, ${\varsigma }_{r2}=1$, ${\varsigma }_{u3}={\varsigma }_{r3}=0.1$, ${\varsigma }_{u4}={\varsigma }_{r4}=0.001$.

(2) For integer-order backstepping controller, the control parameters of USV are selected as $c_x=c_y=c_{\psi }=c_u=c_r=2$, ${\zeta }_{\psi 1}={\zeta }_{u1}={\zeta }_{r1}=10$, ${\zeta }_{\psi 2}={\zeta }_{u2}={\zeta }_{r2}=0.001$, ${\varsigma }_{u1}={\varsigma }_{r1}=15$, ${\varsigma }_{u2}={\varsigma }_{r2}=0.01$.

In Case 2, the simulation results of the USV system with model uncertainty and external environmental disturbance are presented in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. Figure 13 and Figure 16 are the reference trajectory tracking plans of the fractional-order controller and the integer-order controller after changing the desired trajectory, respectively. Figure 14 and Figure 17 are the disturbance observed values of the disturbance for the fractional-order controller and integer-order controller, respectively. Figure 15 and Figure 18 are the actual control input values of the fractional-order controller and the integer-order controller after changing the desired trajectory, respectively. By comparing Figure 13 and Figure 16, it can be seen that the proposed controller and the integer-order controller have the same trajectory tracking effect. It can be seen from the comparison between Figure 14 and Figure 15 and Figure 17 and Figure 18 that the disturbance observation value and control input chattering of the controller proposed in this paper are significantly improved compared with the integer-order controller. Comparing the experimental results with Case 1, it shows that the fractional-order controller is not sensitive to the motion reference trajectory of the USV.

Case 3: Comparative experiment with Case 1. Modify the disturbances in Case 1 without changing other conditions. The unknown external disturbances are defined as ${\omega }_u=5+10\sin (0.5t+\pi /3)$, ${\omega }_v=5\sin (0.5t+2\pi /3)$, ${\omega }_r=48\sin (0.5t)$.

(1) For fractional-order backstepping controller, when $n=2$, the control parameters of USV system are given as $c_x=21$, $c_y=10$, $c_{\psi }=1$, $c_u=1$, $c_r=30$, ${\zeta }_{\psi 1}={\zeta }_{u1}={\zeta }_{r1}=1$, ${\zeta }_{\psi 2}={\zeta }_{u2}={\zeta }_{r2}=0.1$, ${\zeta }_{\psi 3}=0.01$, ${\zeta }_{r3}=0.01$, ${\zeta }_{u3}=0.001$, ${\varsigma }_{u1}={\varsigma }_{r1}=5$, ${\varsigma }_{u2}=0.1$, ${\varsigma }_{r2}=1$, ${\varsigma }_{u3}={\varsigma }_{r3}=0.1$, ${\varsigma }_{u4}={\varsigma }_{r4}=0.001$.

(2) For integer-order backstepping controller, the control parameters of system are given as $c_x=c_y=c_{\psi }=c_u=c_r=3$, ${\zeta }_{\psi 1}={\zeta }_{u1}={\zeta }_{r1}=10$, ${\zeta }_{\psi 2}={\zeta }_{u2}={\zeta }_{r2}=0.001$, ${\varsigma }_{u1}={\varsigma }_{r1}=15$, ${\varsigma }_{u2}={\varsigma }_{r2}=0.01$.

In Case 3, the simulation results of the USV system with model uncertainty and external environmental disturbance are presented in Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24. Figure 19 and Figure 22 are the reference trajectory tracking plane diagrams of the fractional-order controller and the integer-order controller, respectively. The comparison between the two shows that the proposed controller and the integer-order controller have basically the same trajectory tracking effect. Figure 20 and Figure 23 are the disturbance observations of the fractional-order controller and the integer-order controller after changing the disturbance, respectively. It can be seen that the fractional-order disturbance observer has a greater improvement in the chattering of the disturbance observation value than the integer-order disturbance observer. Figure 21 and Figure 24 are the actual control input values of the fractional-order controller and the integer-order controller, respectively. It is obvious from the diagram that the controller proposed in this paper eliminates the input chattering of the integer-order controller. Therefore, when the trajectory tracking effect is basically the same, the fractional-order controller can improve the chattering phenomenon of the actual control input of the integer-order controller. Comparing the experimental results with Case 1, it can be seen that the fractional-order controller can improve the chattering of the control input when changing the system disturbance, indicating that the controller proposed in this paper is insensitive to the disturbance type.

5. Conclusions

The backstepping control strategy, which combines a fractional-order command filter and a fractional-order finite-time disturbance observer, is presented for the trajectory tracking control of the USV with model uncertainty and unknown environmental disturbances in the paper. The fractional-order command filter is used to replace the original integer-order command filter, which reduces the chattering phenomenon of the integer-order command filter and avoids the problem that the controller cannot be directly derived. The fractional-order disturbance observer is adopted to compensate for the model uncertainty and environmental disturbances of the USV system. The simulation examples demonstrate that the fractional-order controller is capable of reducing the chattering phenomenon of the actual control inputs of the integer-order controller under the condition of consistent performance. At the same time, the controller proposed in this paper is not sensitive to the desired trajectory and disturbance type.