Probing Light Mediators and Neutrino Electromagnetic Moments with Atomic Radiative Emission of Neutrino Pairs †
Abstract
:1. Introduction
2. Atomic Radiative Emission of Neutrino Pairs
3. Non-Standard Interactions with Light Mediators
3.1. Vector Mediators
3.2. Scalar Mediator
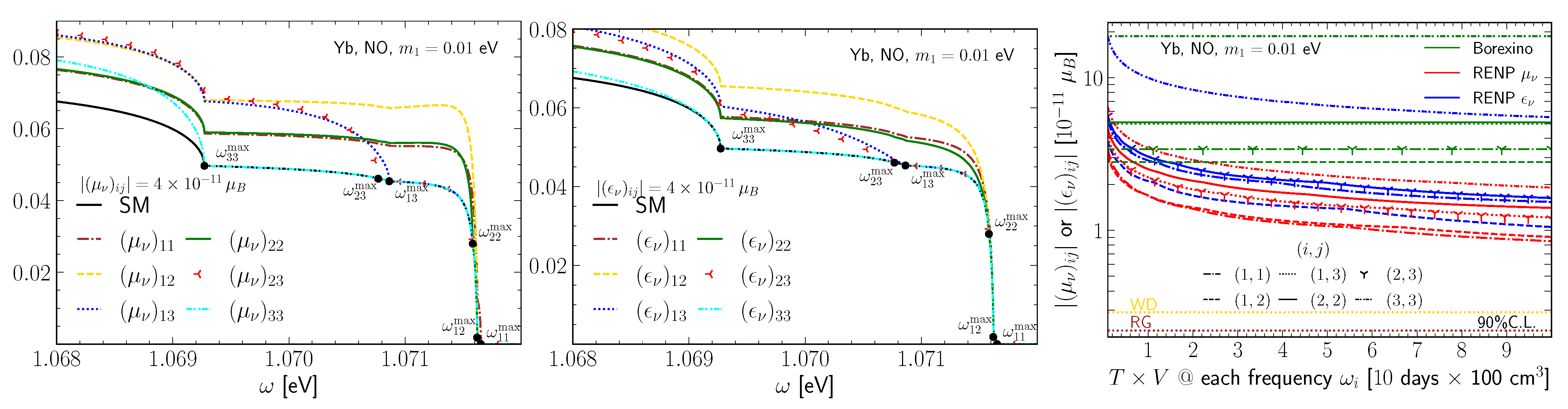
4. Neutrino Electromagnetic Moments
5. Conclusions
6. Notes Added
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farzan, Y.; Tortola, M. Neutrino oscillations and Non-Standard Interactions. Front. Phys. 2018, 6, 10. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Babu, K.S.; Denton, P.B.; Machado, P.A.N.; Argüelles, C.A.; Barrow, J.L.; Chatterjee, S.S.; Chen, M.C.; de Gouvêa, A.; Dutta, B.; et al. Neutrino Non-Standard Interactions: A Status Report. SciPost Phys. Proc. 2019, 2, 001. [Google Scholar] [CrossRef]
- Smirnov, A.Y.; Xu, X.J. Wolfenstein potentials for neutrinos induced by ultra-light mediators. J. High Energy Phys. 2019, 12, 046. [Google Scholar] [CrossRef]
- Babu, K.S.; Chauhan, G.; Bhupal Dev, P.S. Neutrino nonstandard interactions via light scalars in the Earth, Sun, supernovae, and the early Universe. Phys. Rev. D 2020, 101, 095029. [Google Scholar] [CrossRef]
- Yoshimura, M. Neutrino Pair Emission from Excited Atoms. Phys. Rev. D 2007, 75, 113007. [Google Scholar] [CrossRef]
- Fukumi, A.; Kuma, S.; Miyamoto, Y.; Nakajima, K.; Nakano, I.; Nanjo, H.; Ohae, C.; Sasao, N.; Tanaka, M.; Taniguchi, T.; et al. Neutrino Spectroscopy with Atoms and Molecules. Prog. Theor. Exp. Phys. 2012, 2012, 04D002. [Google Scholar] [CrossRef]
- Hiraki, T.; Hara, H.; Miyamoto, Y.; Imamura, K.; Masuda, T.; Sasao, N.; Uetake, S.; Yoshimi, A.; Yoshimura, K.; Yoshimura, M. Coherent two-photon emission from hydrogen molecules excited by counter-propagating laser pulses. J. Phys. B 2019, 52, 045401. [Google Scholar] [CrossRef]
- Tashiro, M.; Das, B.P.; Ekman, J.; Jönsson, P.; Sasao, N.; Yoshimura, M. Macro-coherent radiative emission of neutrino pair between parity-even atomic states. Eur. Phys. J. C 2019, 79, 907. [Google Scholar] [CrossRef]
- Ge, S.F.; Pasquini, P. Probing light mediators in the radiative emission of neutrino pair. Eur. Phys. J. C 2022, 82, 208. [Google Scholar] [CrossRef]
- Ge, S.F.; Pasquini, P. Unique Probe of Neutrino Electromagnetic Moments with Radiative Pair Emission. Phys. Lett. B 2023, 841, 137911. [Google Scholar] [CrossRef]
- Yoshimura, M. Solitons and Precision Neutrino Mass Spectroscopy. Phys. Lett. B 2011, 699, 123–128. [Google Scholar] [CrossRef]
- Yoshimura, M.; Sasao, N.; Tanaka, M. Dynamics of paired superradiance. Phys. Rev. A 2012, 86, 013812. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Dinh, D.N.; Petcov, S.T.; Sasao, N.; Tanaka, M.; Yoshimura, M. Observables in Neutrino Mass Spectroscopy Using Atoms. Phys. Lett. B 2013, 719, 154–163. [Google Scholar] [CrossRef]
- Song, N.; Garcia, R.B.; Gomez-Cadenas, J.J.; Gonzalez-Garcia, M.C.; Conde, A.P.; Taron, J. Conditions for Statistical Determination of the Neutrino Mass Spectrum in Radiative Emission of Neutrino Pairs in Atoms. Phys. Rev. D 2016, 93, 013020. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, S. Improved Statistical Determination of Absolute Neutrino Masses via Radiative Emission of Neutrino Pairs from Atoms. Phys. Rev. D 2016, 93, 113020. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Giunti, C.; Studenikin, A. Neutrino electromagnetic interactions: A window to new physics. Rev. Mod. Phys. 2015, 87, 531. [Google Scholar] [CrossRef]
- Beda, A.G.; Brudanin, V.B.; Egorov, V.G.; Medvedev, D.V.; Pogosov, V.S.; Shevchik, E.A.; Shirchenko, M.V.; Starostin, A.S.; Zhitnikov, I.V. Gemma experiment: The results of neutrino magnetic moment search. Phys. Part. Nucl. Lett. 2013, 10, 139–143. [Google Scholar] [CrossRef]
- Agostini, M.; Altenmüller, K.; Appel, S.; Atroshchenko, V.; Bagdasarian, Z.; Basilico, D.; Bellini, G.; Benziger, J.; Bick, D.; Bonfini, G.; et al. Limiting neutrino magnetic moments with Borexino Phase-II solar neutrino data. Phys. Rev. D 2017, 96, 091103. [Google Scholar] [CrossRef]
- Díaz, S.A.; Schröder, K.P.; Zuber, K.; Jack, D.; Barrios, E.E.B. Constraint on the axion-electron coupling constant and the neutrino magnetic dipole moment by using the tip-RGB luminosity of fifty globular clusters. arXiv 2019, arXiv:1910.10568. [Google Scholar]
- Córsico, A.H.; Althaus, L.G.; Bertolami, M.M.M.; Kepler, S.O.; García-Berro, E. Constraining the neutrino magnetic dipole moment from white dwarf pulsations. J. Cosmol. Astropart. Phys. 2014, 8, 054. [Google Scholar] [CrossRef]
- Bertolami, M.M.M. Limits on the neutrino magnetic dipole moment from the luminosity function of hot white dwarfs. Astron. Astrophys. 2014, 562, A123. [Google Scholar] [CrossRef]
- Hansen, B.M.S.; Richer, H.; Kalirai, J.; Goldsbury, R.; Frewen, S.; Heyl, J. Constraining Neutrino Cooling using the Hot White Dwarf Luminosity Function in the Globular Cluster 47 Tucanae. Astrophys. J. 2015, 809, 141. [Google Scholar] [CrossRef]
- Stancliffe, R.J.; Fossati, L.; Passy, J.-C.; Schneider, F.R.N. Confronting uncertainties in stellar physics. II. Exploring differences in main-sequence stellar evolution tracks. Astron. Astrophys. 2016, 586, A119. [Google Scholar] [CrossRef]
- Sierra, D.A.; Miranda, O.G.; Papoulias, D.K.; Garcia, G.S. Neutrino magnetic and electric dipole moments: From measurements to parameter space. Phys. Rev. D 2022, 105, 035027. [Google Scholar] [CrossRef]
- Ge, S.F.; Pasquini, P. Disentangle Neutrino Electromagnetic Properties with Atomic Radiative Pair Emission. arXiv 2023, arXiv:2306.12953. [Google Scholar]
- Khan, A.N. Light new physics and neutrino electromagnetic interactions in XENONnT. Phys. Lett. B 2023, 837, 137650. [Google Scholar] [CrossRef]
- Khan, A.N. Neutrino millicharge and other electromagnetic interactions with COHERENT-2021 data. Nucl. Phys. B 2023, 986, 116064. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, S.-F.; Pasquini, P. Probing Light Mediators and Neutrino Electromagnetic Moments with Atomic Radiative Emission of Neutrino Pairs. Phys. Sci. Forum 2023, 8, 51. https://doi.org/10.3390/psf2023008051
Ge S-F, Pasquini P. Probing Light Mediators and Neutrino Electromagnetic Moments with Atomic Radiative Emission of Neutrino Pairs. Physical Sciences Forum. 2023; 8(1):51. https://doi.org/10.3390/psf2023008051
Chicago/Turabian StyleGe, Shao-Feng, and Pedro Pasquini. 2023. "Probing Light Mediators and Neutrino Electromagnetic Moments with Atomic Radiative Emission of Neutrino Pairs" Physical Sciences Forum 8, no. 1: 51. https://doi.org/10.3390/psf2023008051
APA StyleGe, S. -F., & Pasquini, P. (2023). Probing Light Mediators and Neutrino Electromagnetic Moments with Atomic Radiative Emission of Neutrino Pairs. Physical Sciences Forum, 8(1), 51. https://doi.org/10.3390/psf2023008051





