Tip Pressure on Semicircular Specimens in Tapping Mode Atomic Force Microscopy in Viscous Fluid Environments
Abstract
:1. Introduction
2. Methods
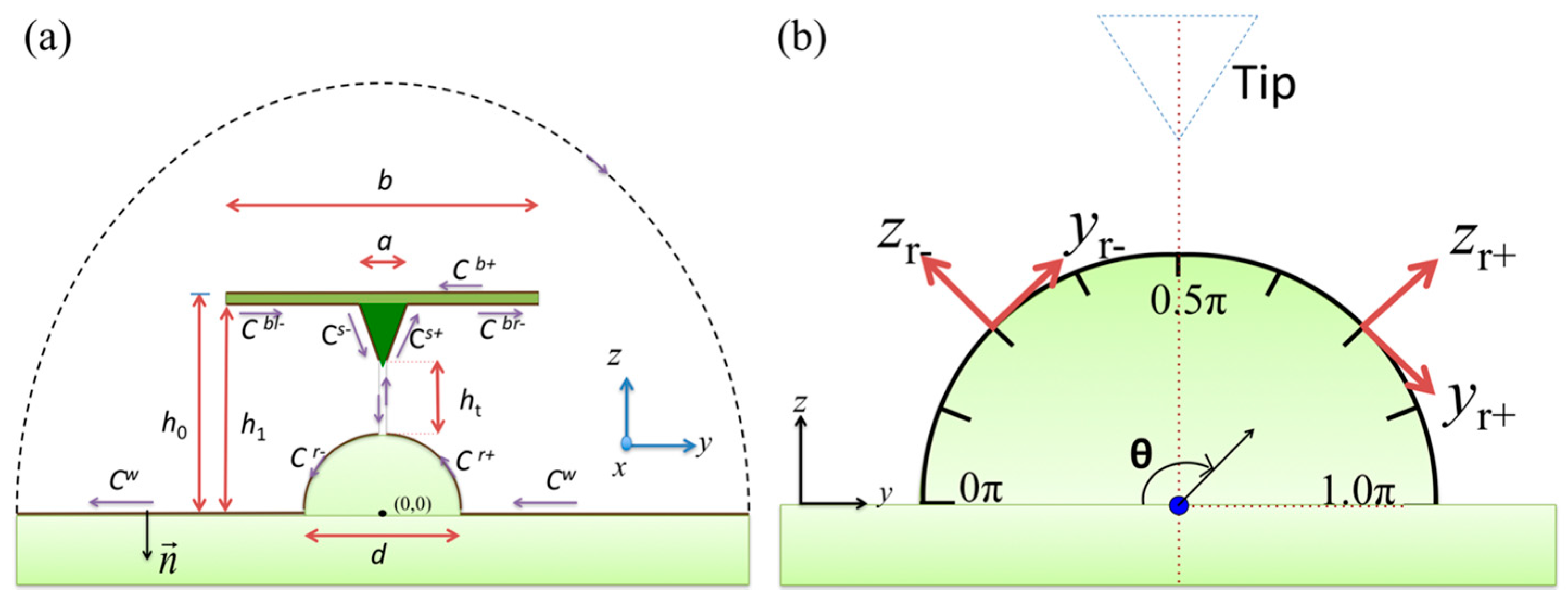
2.1. Mathematical Model
2.2. Numerical Calculation
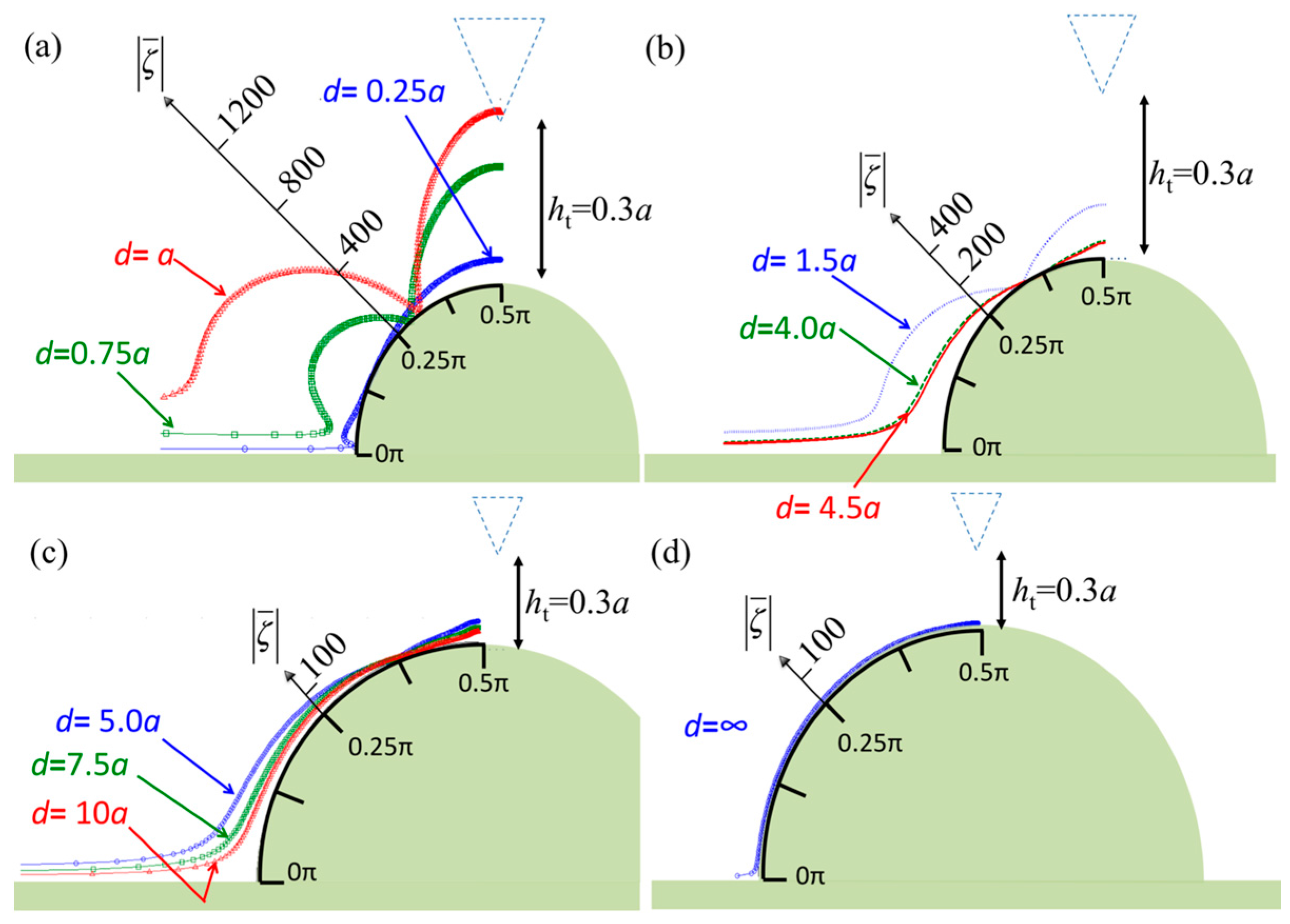
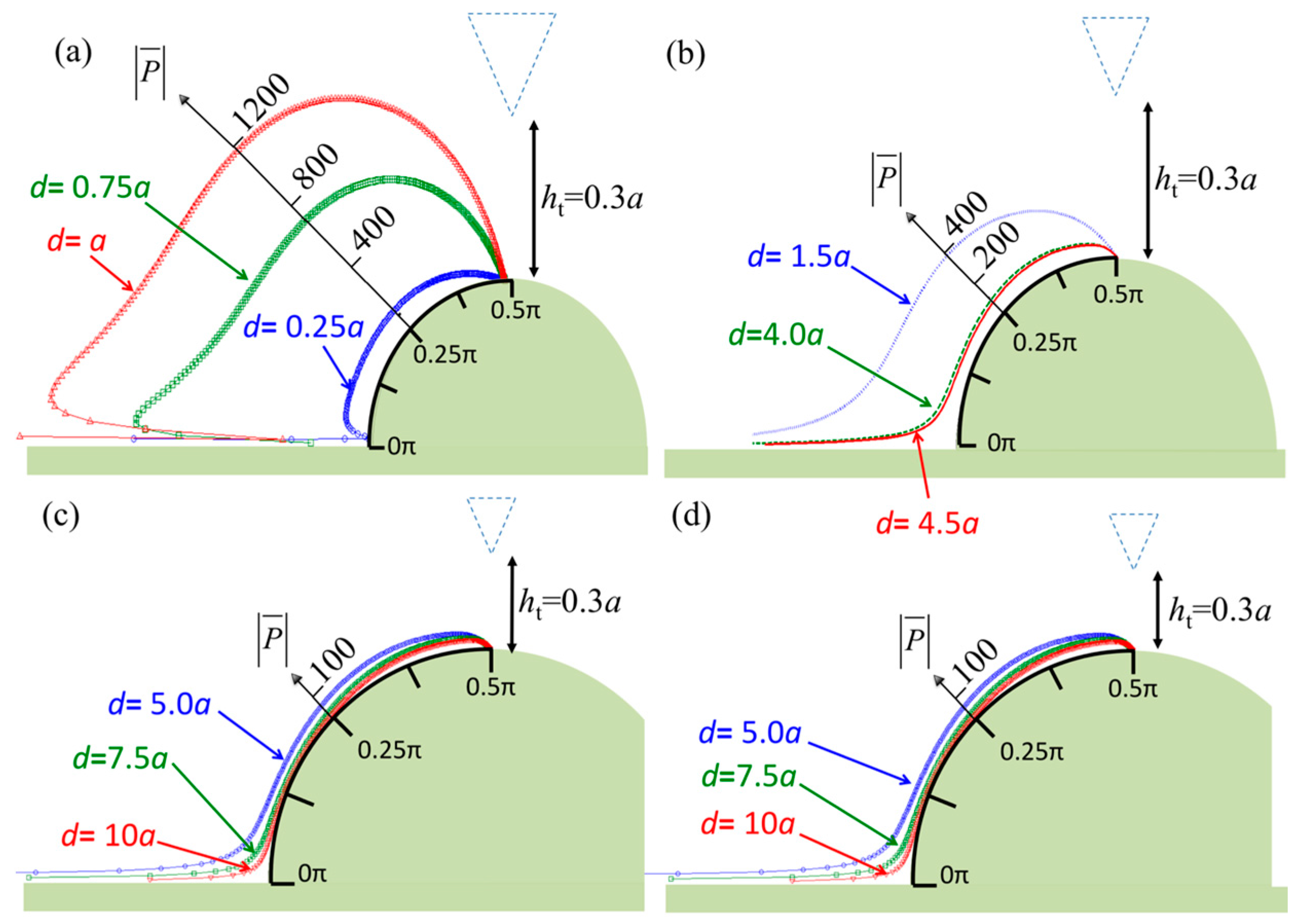
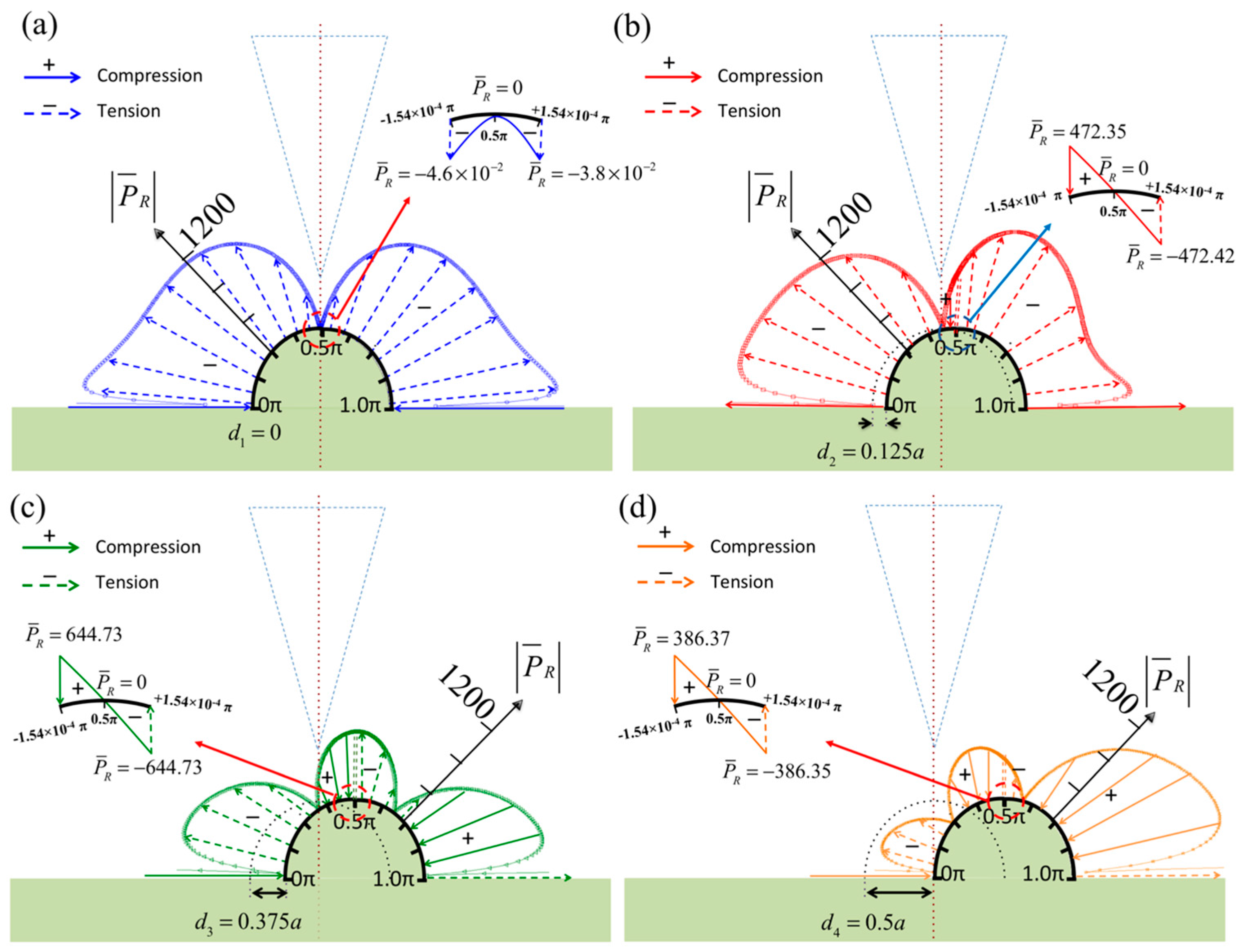
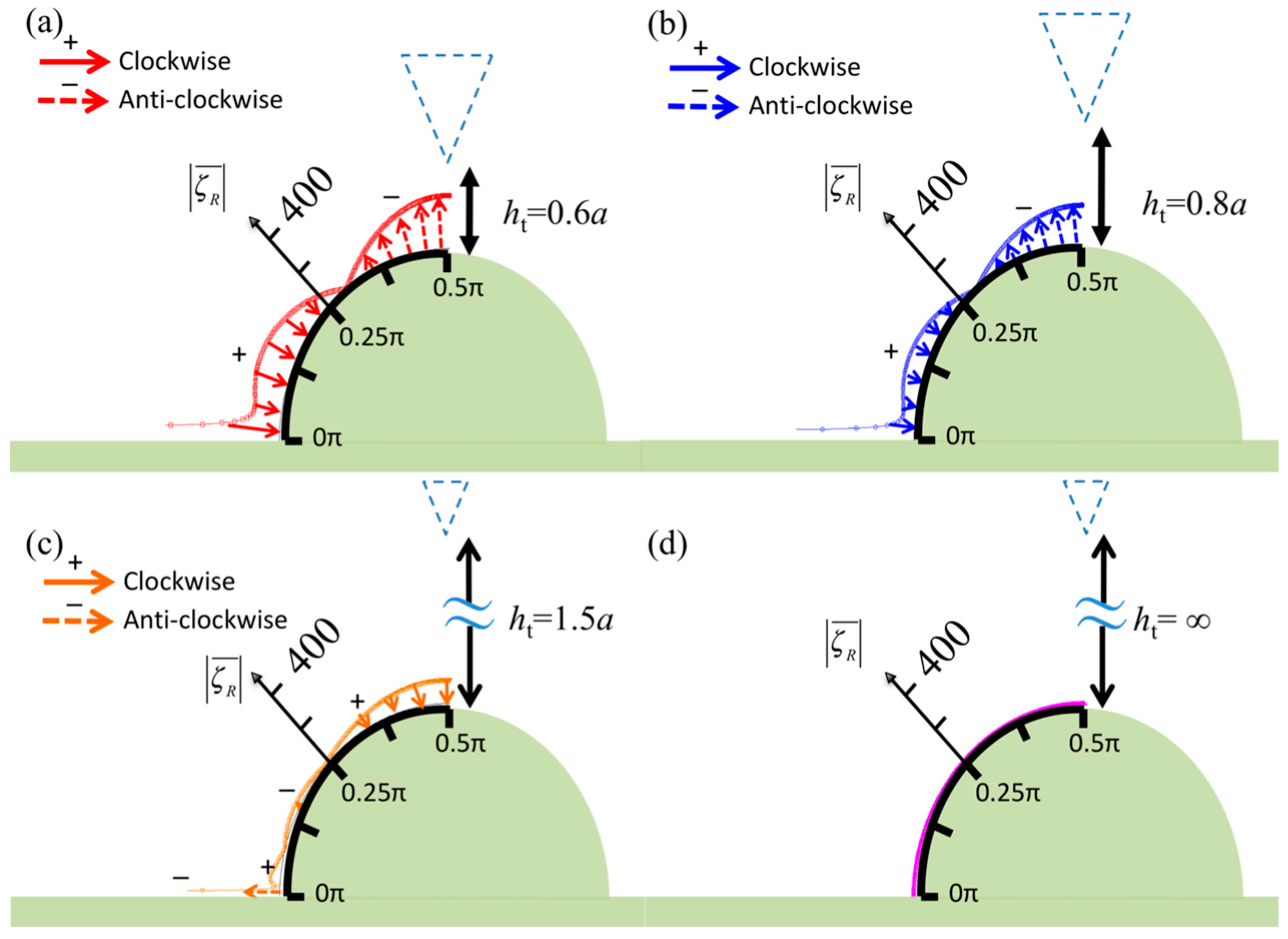
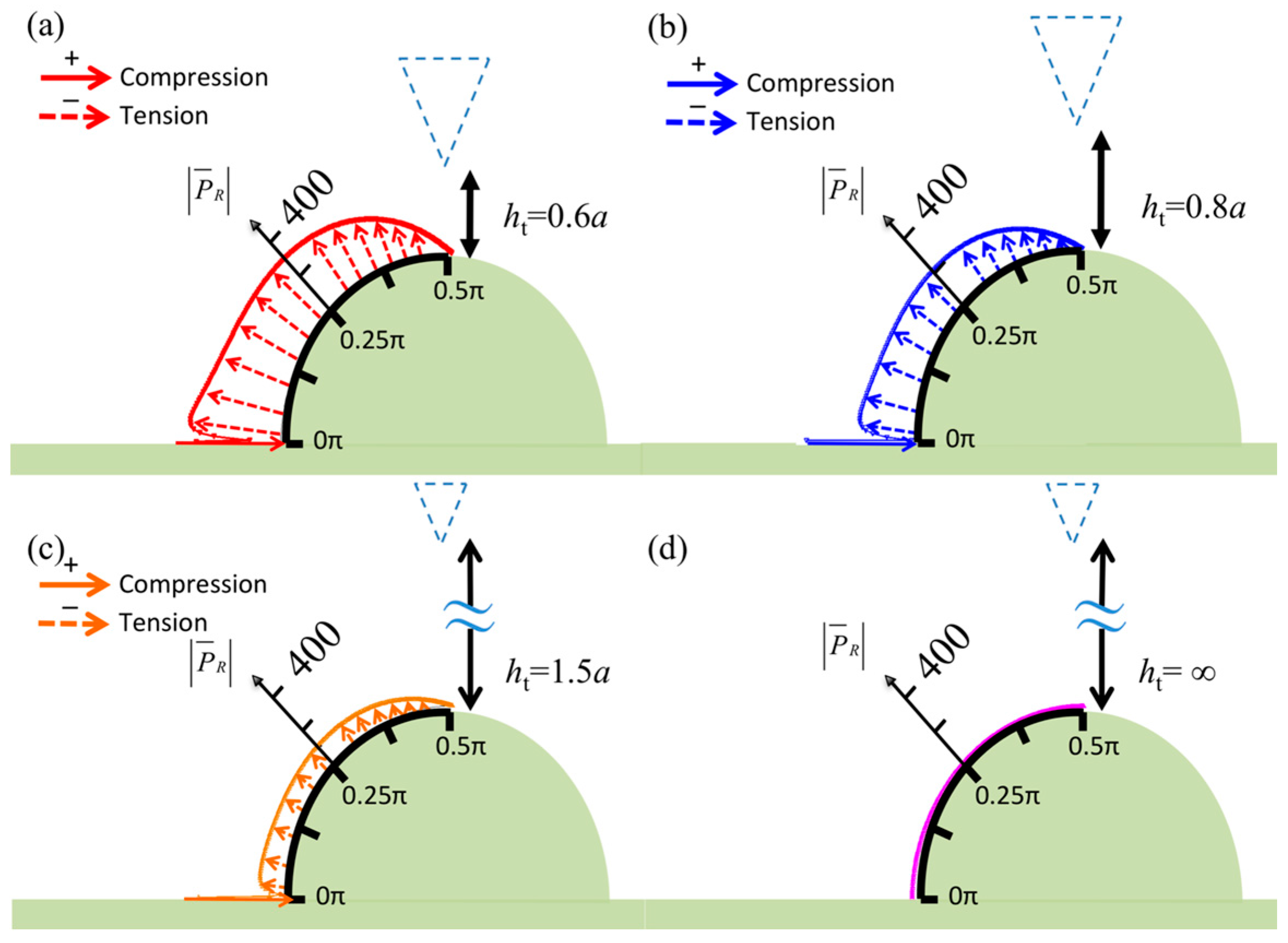
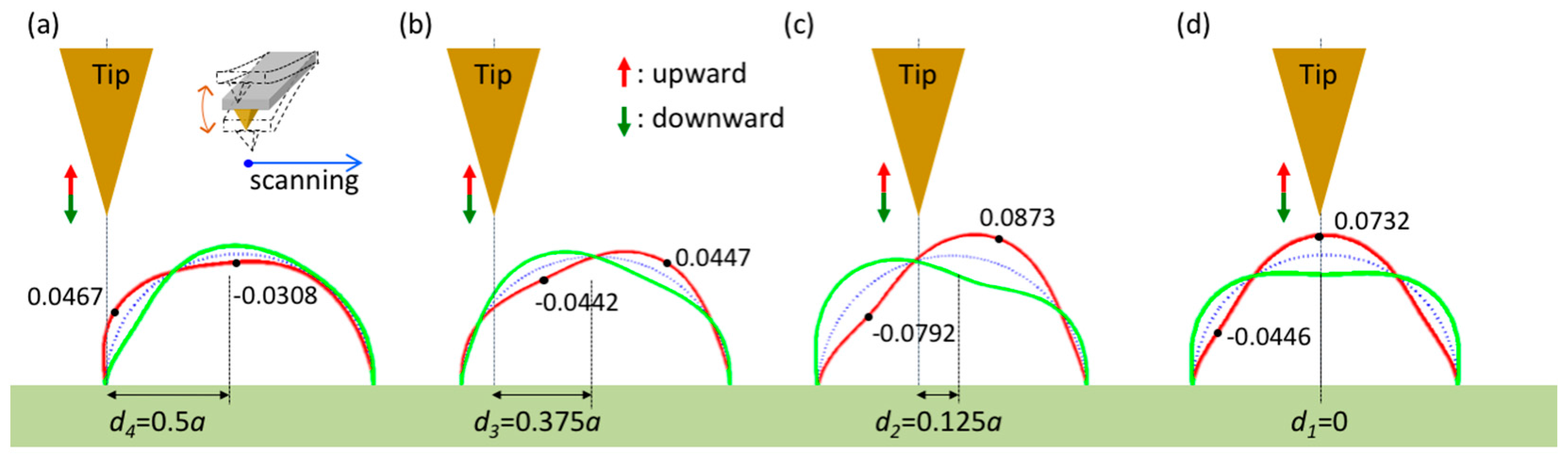
3. Numerical Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Wall | Specimen | Beam | Tip | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cw+ | Cw− | Cr+ | Cr− | Cb+ | Cbl− | Cbr− | Cs+ | Cs− | |
| Y | y′ | y′ | y’ | y’ | y’ | ||||
| Z | 0 | 0 | ×sin β | ×sin (γ-90°) | h0 | h1 | h1 | ×sin θ | ×sin (α-90°) |
Appendix B
References
- Basak, S.; Raman, A.; Garimella, S.V. Hydrodynamic loading of microcantilevers vibrating in viscous fluids. J. Appl. Phys. 2006, 99, 114906. [Google Scholar]
- Woolley, A.T.; Cheung, C.L.; Hafner, J.H.; Lieber, C.M. Structure biology with carbon nanotube AFM probes. Cell Chem. Biol. 2000, 7, R193–R204. [Google Scholar]
- Xu, X.; Carrasco, C.; de Pablo, P.J.; Gomez-Herrero, J.; Raman, A. Unmasking imaging forces on soft biological samples in liquids when using dynamic atomic force microscopy: A case study on viral capsids. Biophys. J. 2008, 95, 2520–2528. [Google Scholar]
- Li, L.X.; Liu, R.P.; Xu, Z.; Xu, Y.; Wang, W.K.; Fan, C.Z. Distorted surface topography observed by atomic force microscopy. Measurement 2006, 39, 12–15. [Google Scholar]
- Shih, P.J. Frequency function in atomic force microscopy applied to a liquid environment. Sensors 2014, 14, 9369–9379. [Google Scholar] [CrossRef] [PubMed]
- Green, C.P.; Sader, J.E. Small amplitude oscillations of a thin beam immersed in a viscous fluid near a solid surface. Phys. Fluids 2005, 17. [Google Scholar] [CrossRef]
- Tung, R.C.; Jana, A.; Raman, A. Hydrodynamic loading of microcantilevers oscillating near rigid walls. J. Appl. Phys. 2008, 104. [Google Scholar] [CrossRef]
- Janovjak, H.; Struckmeier, J.; Muller, D.J. Hydrodynamic effects in fast AFM single-molecule force measurements. Eur. Biophys. J. 2005, 34, 91–96. [Google Scholar]
- Shih, H.J.; Shih, P.J. Tip effect of the tapping mode of atomic force microscope in viscous fluid environments. Sensors 2015, 15, 18381–18401. [Google Scholar]
- Walczyk, W.; Hain, N.; Schonherr, H. Hydrodynamic effects of the tip movement on surface nanobubbles: A combined tapping mode, lift mode and force volume mode AFM study. Soft Matter 2014, 10, 5945–5954. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kang, S.K.; Choi, I.; Lee, J.; Yi, J. Dependence of image distortion in a liquid-cell atomic force microscope on fluidic properties. Appl. Phys. Lett. 2006, 88, 173121. [Google Scholar] [CrossRef]
- Guzman, H.V.; Perrino, A.P.; Garcia, R. Peak forces in high-resolution imaging of soft matter in liquid. ACS Nano 2013, 7, 3198–3204. [Google Scholar] [CrossRef] [PubMed]
- Moller, C.; Allen, M.; Elings, V.; Engel, A.; Muller, D.J. Tapping-mode atomic force microscopy produces faithful high-resolution images of protein surfaces. Biophys. J. 1999, 77, 1150–1158. [Google Scholar] [CrossRef]
- Medalsy, I.D.; Muller, D.J. Nanomechanical properties of proteins and membranes depend on loading rate and electrostatic interactions. ACS Nano 2013, 7, 2642–2650. [Google Scholar] [CrossRef] [PubMed]
- Vichare, S.; Inamdar, M.M.; Sen, S. Influence of cell spreading and contractility on stiffness measurements using AFM. Soft Matter 2012, 8, 10464–10471. [Google Scholar] [CrossRef]
- Li, Q.S.; Lee, G.Y.; Ong, C.N.; Lim, C.T. AFM indentation study of breast cancer cells. Biochem. Biophys. Res. Commun. 2008, 374, 609–613. [Google Scholar] [CrossRef]
- Tuck, E.O. Calculation of unsteady flows due to small motions of cylinders in a viscous fluid. J. Eng. Math. 1969, 3, 29–44. [Google Scholar] [CrossRef]
- Sader, J.E.; Green, P. Small amplitude oscillations of a thin beam immersed in a viscous fluid near a solid surface. AIP Phys. Fluids 2005, 17, 073102. [Google Scholar]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64. [Google Scholar] [CrossRef]
- Sader, J.E.; Chon, J.W.M. Calibration of rectangular atomic force microscope cantilevers. Rev. Sci. Instrum. 1999, 70, 3967. [Google Scholar] [CrossRef] [Green Version]
- Green, C.P.; Sader, J.E. Torsional frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 2002, 92, 6262–6274. [Google Scholar] [CrossRef]
- Green, C.P.; Lioe, H.; Cleveland, J.P.; Proksch, R.; Mulvaney, P.; Sader, J.E. Normal and torsional spring constants of atomic force microscope cantilevers. Rev. Sci. Instrum. 2004, 75, 1988–1996. [Google Scholar] [CrossRef]
- Chung, K.H.; Lee, Y.H.; Kim, D.E. Characteristics of fracture during the approach process and wear mechanism of a silicon AFM tip. Ultramicroscopy 2005, 102, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsova, T.G.; Starodubtseva, M.N.; Yegorenkov, N.I.; Chizhik, S.A.; Zhdanov, R.I. Atomic force microscopy probing of cell elasticity. Micron 2007, 38, 824–833. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shih, H.-J.; Dai, C.-L.; Shih, P.-J. Tip Pressure on Semicircular Specimens in Tapping Mode Atomic Force Microscopy in Viscous Fluid Environments. Sensors 2017, 17, 2182. https://doi.org/10.3390/s17102182
Shih H-J, Dai C-L, Shih P-J. Tip Pressure on Semicircular Specimens in Tapping Mode Atomic Force Microscopy in Viscous Fluid Environments. Sensors. 2017; 17(10):2182. https://doi.org/10.3390/s17102182
Chicago/Turabian StyleShih, Hua-Ju, Ching-Liang Dai, and Po-Jen Shih. 2017. "Tip Pressure on Semicircular Specimens in Tapping Mode Atomic Force Microscopy in Viscous Fluid Environments" Sensors 17, no. 10: 2182. https://doi.org/10.3390/s17102182




