A Fast Algorithm for 2D DOA Estimation Using an Omnidirectional Sensor Array
Abstract
:1. Introduction
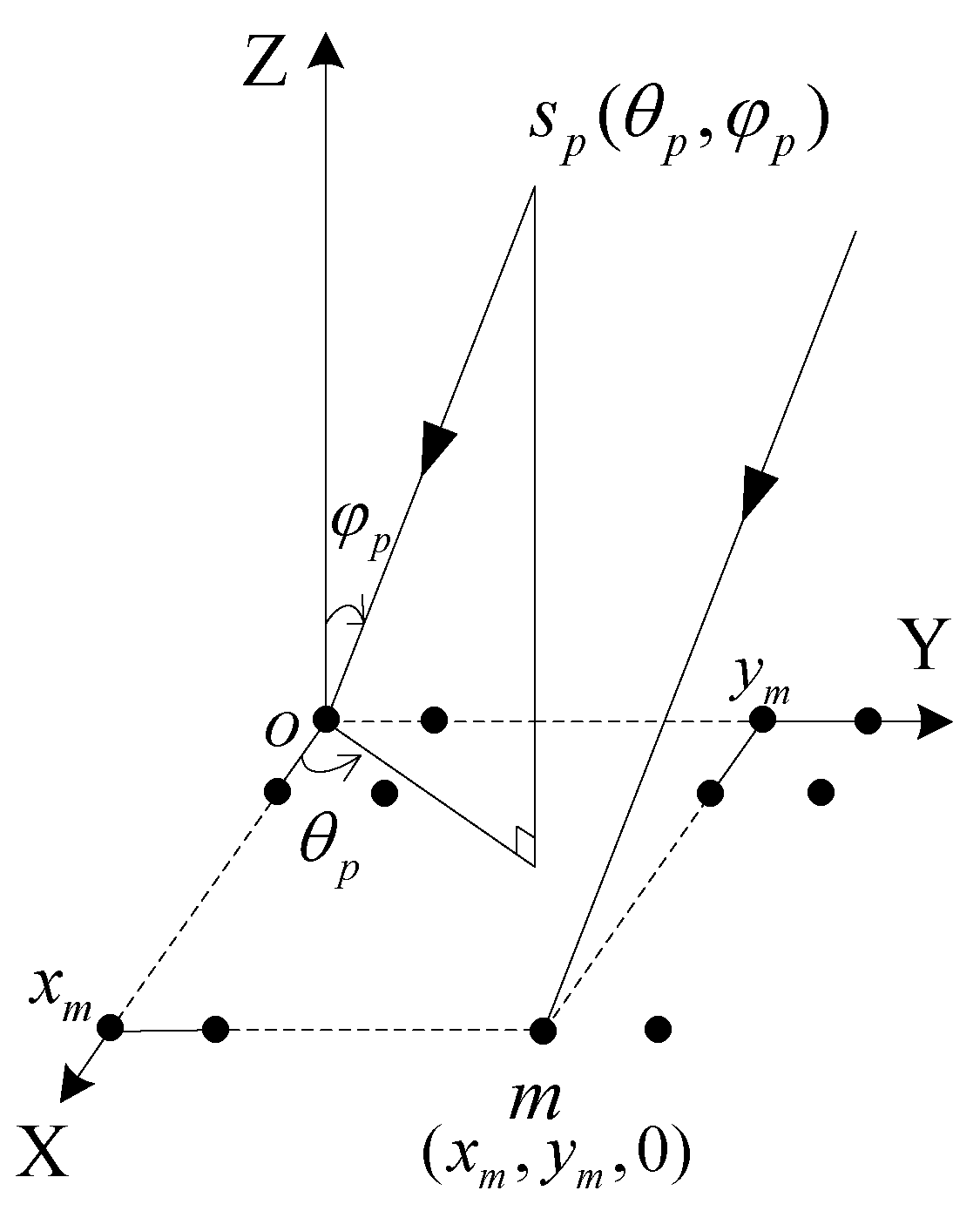
2. Problem Formulation
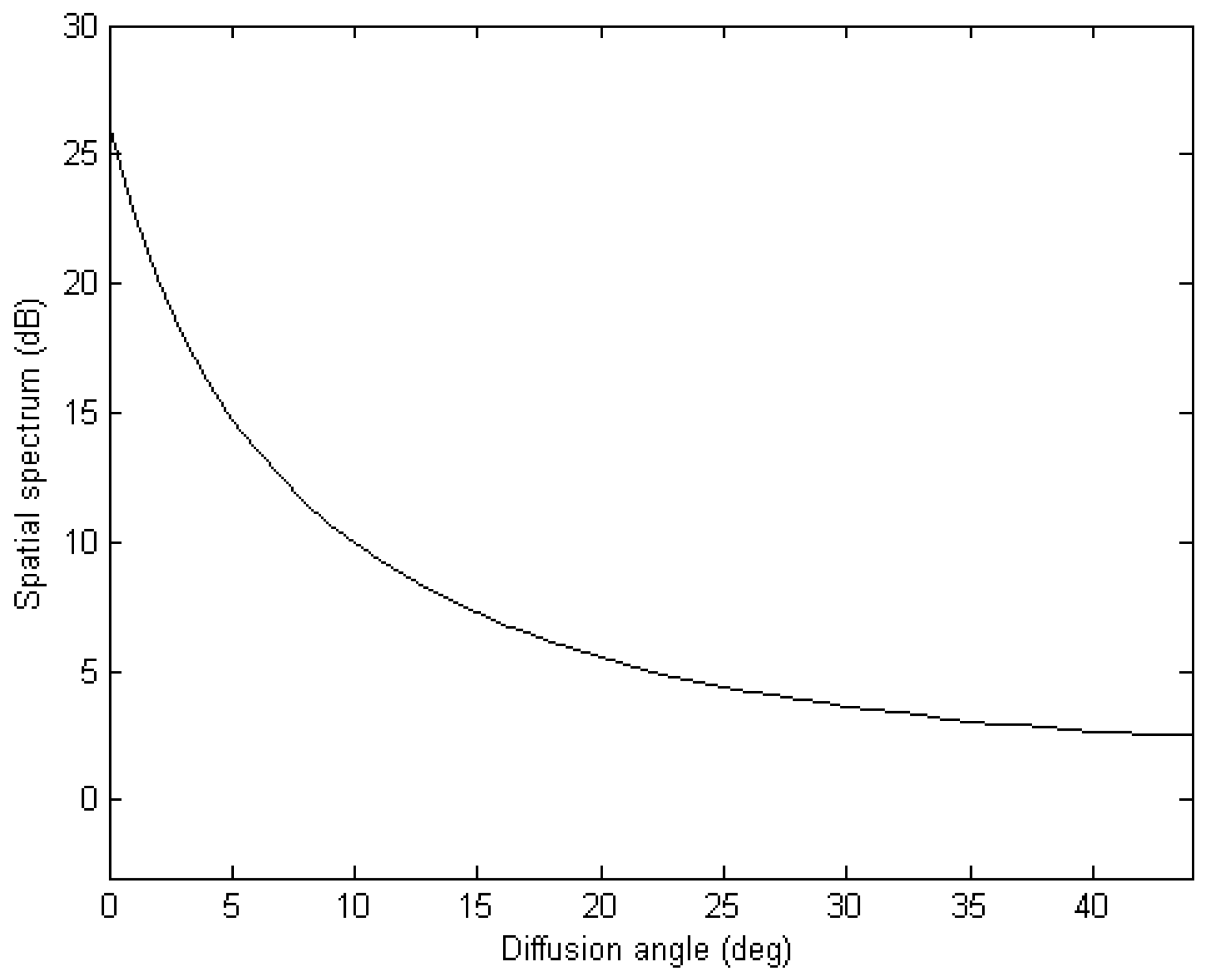
3. Spectrum Peak Diffusion Effect
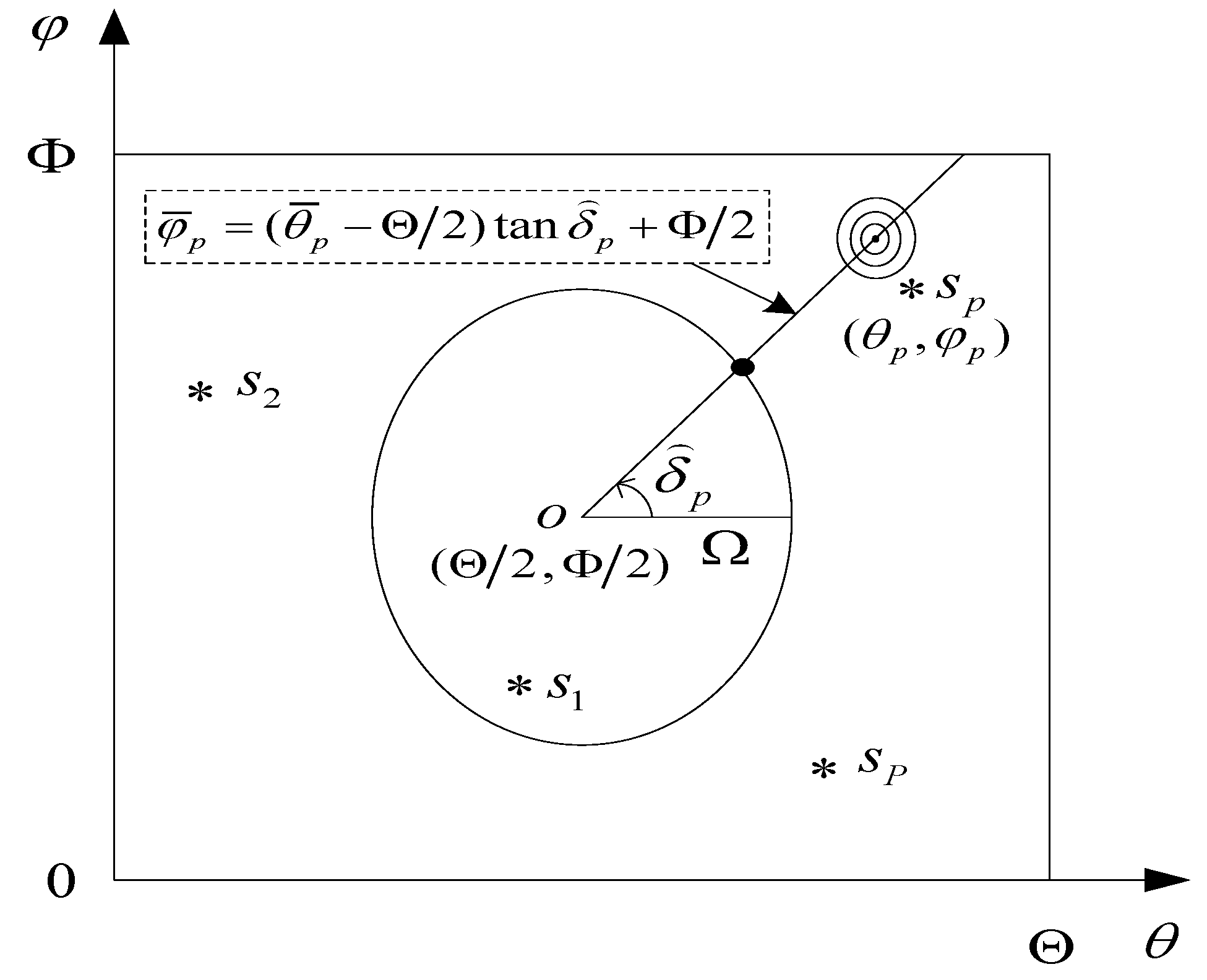
4. Proposed Fast Algorithm
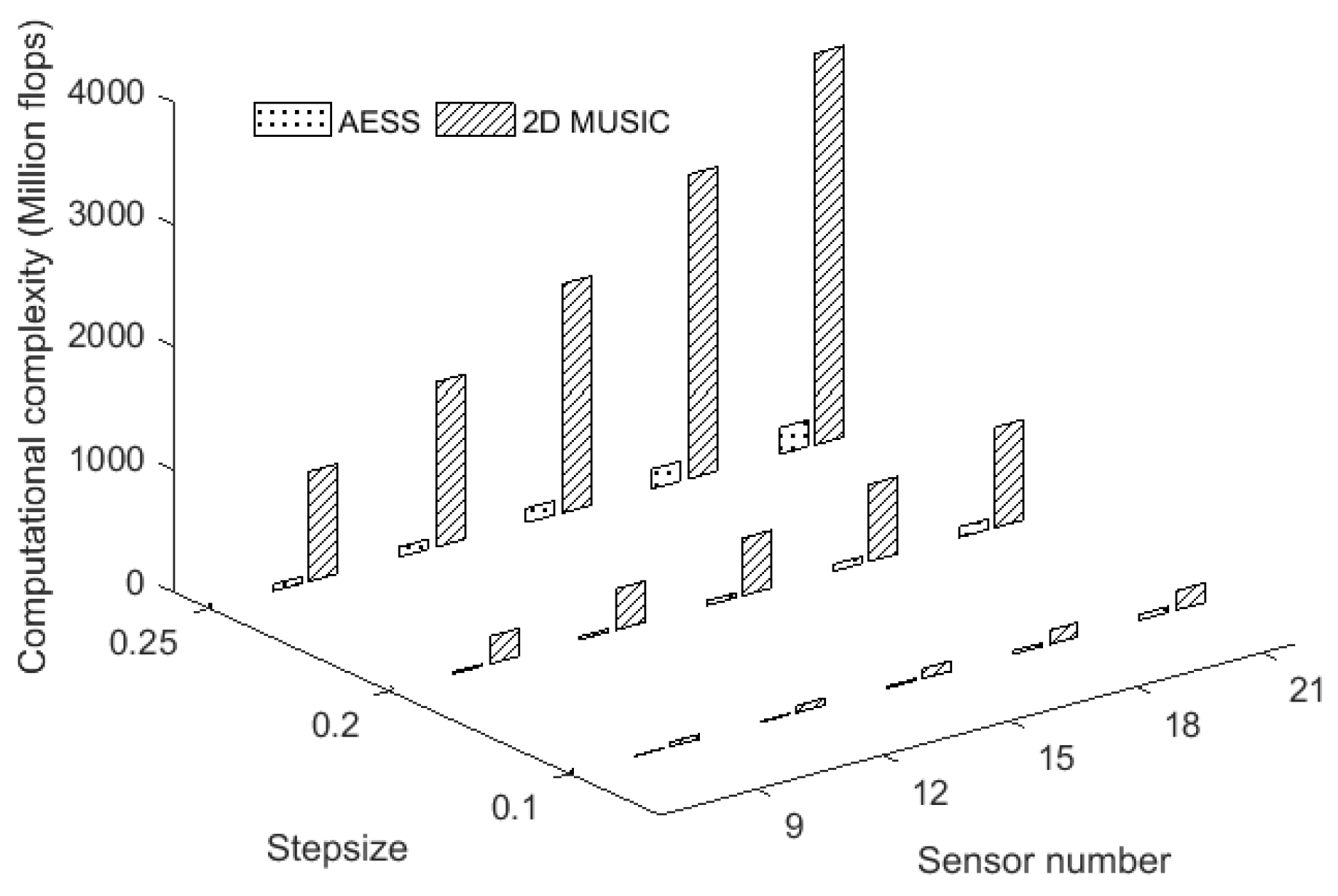
5. Computational Complexity Analysis
6. Simulation Results
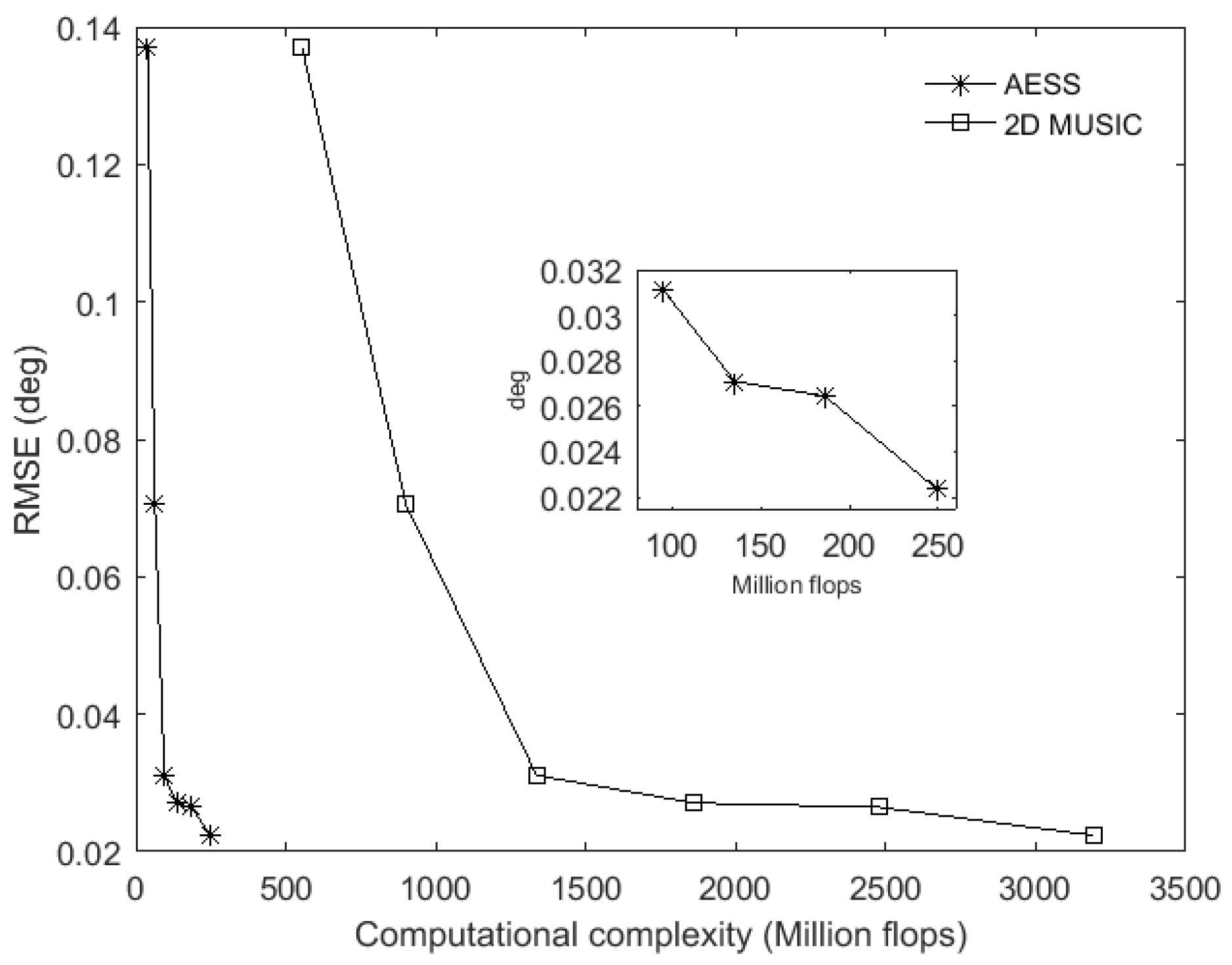
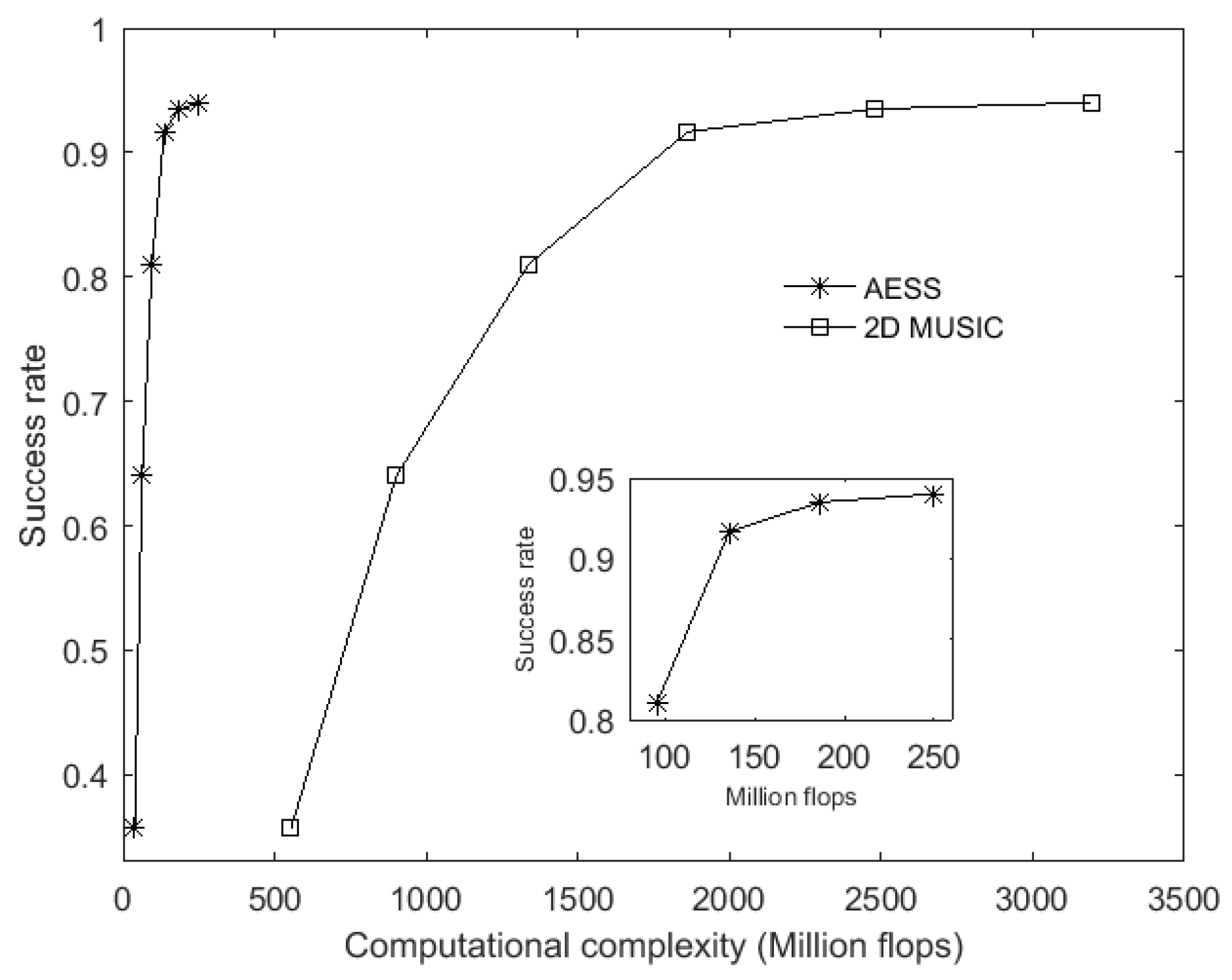
6.1. RMSE and Estimation Success Rate versus Computational Complexity
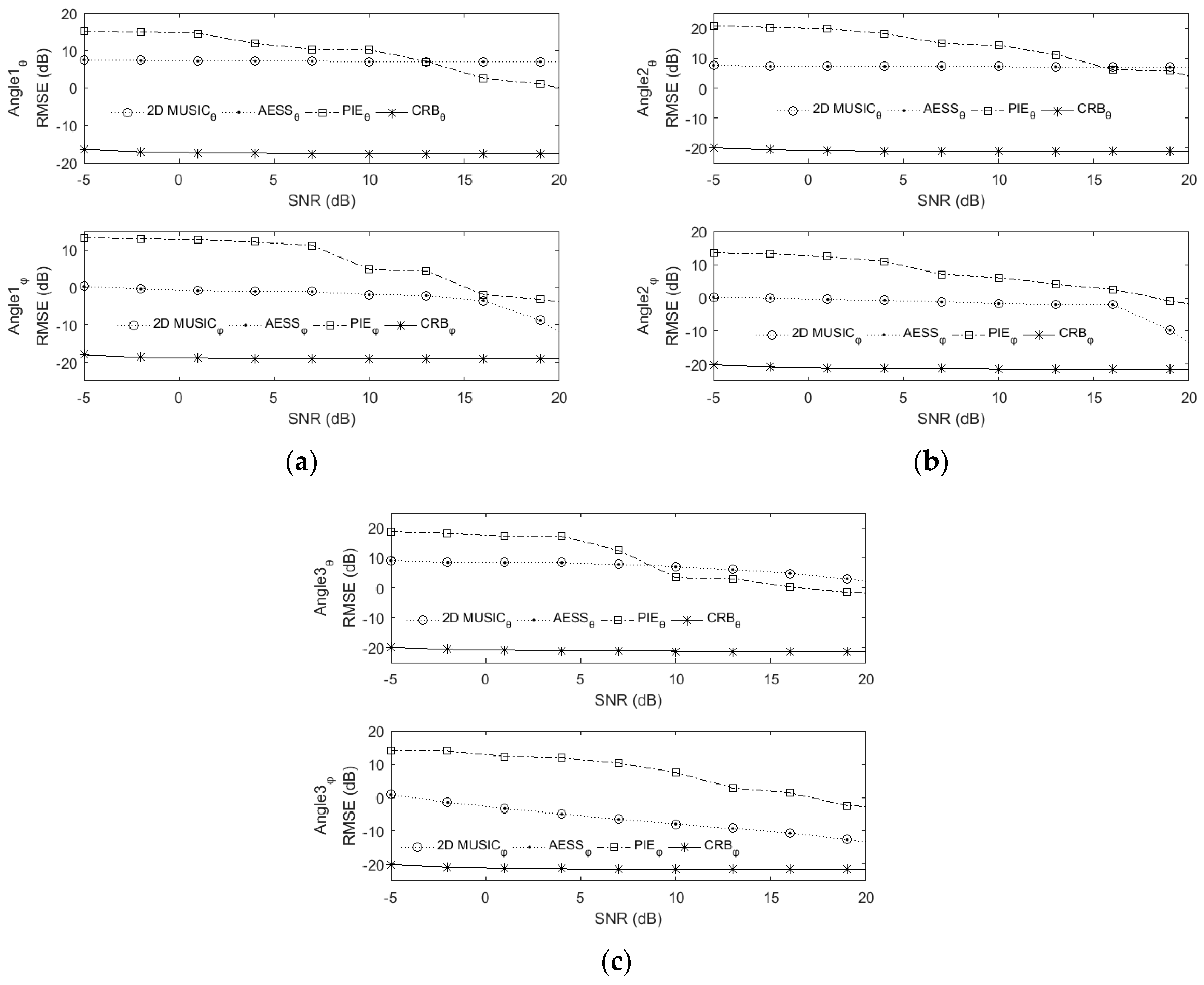
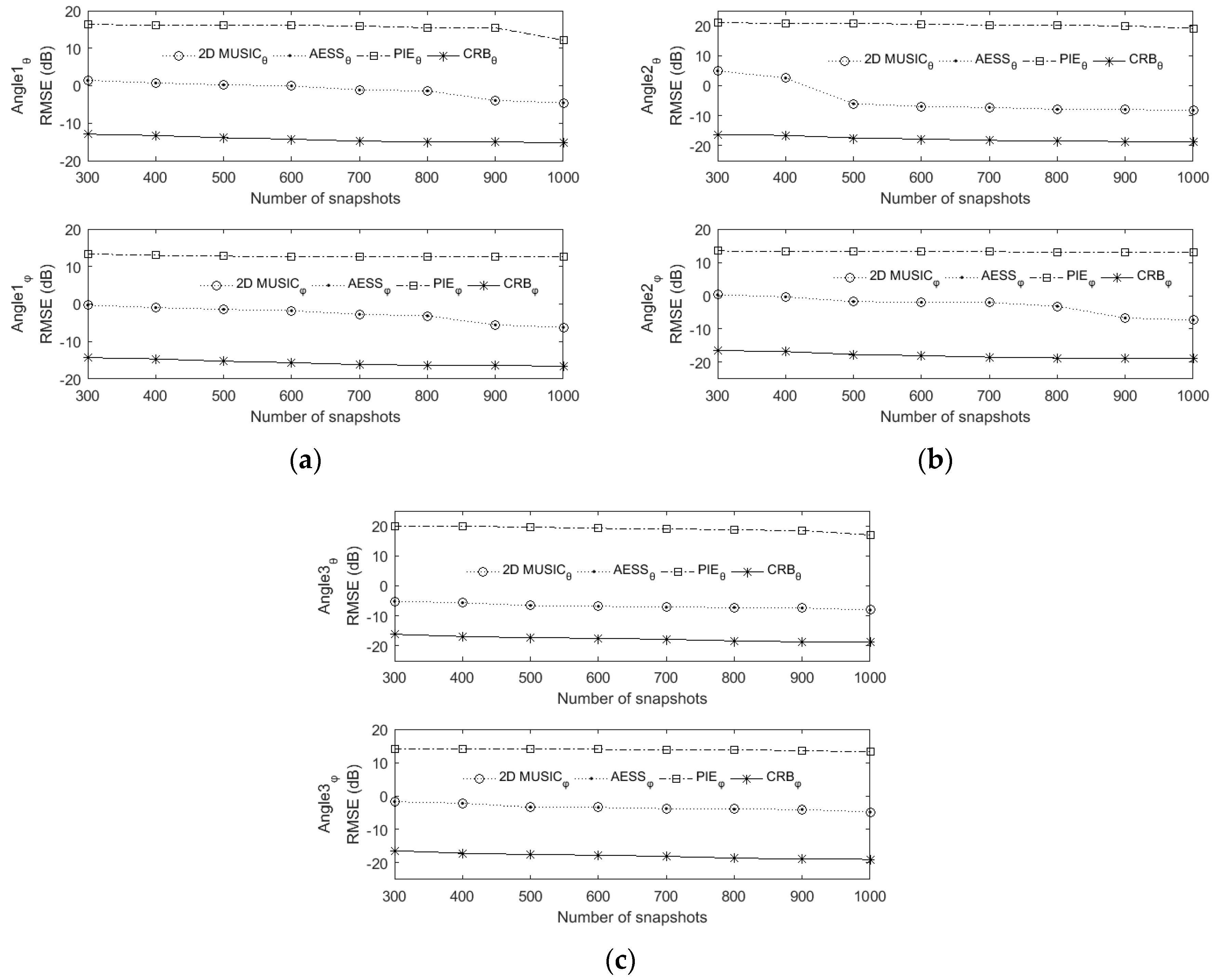
6.2. RMSE versus SNR and Snapshot
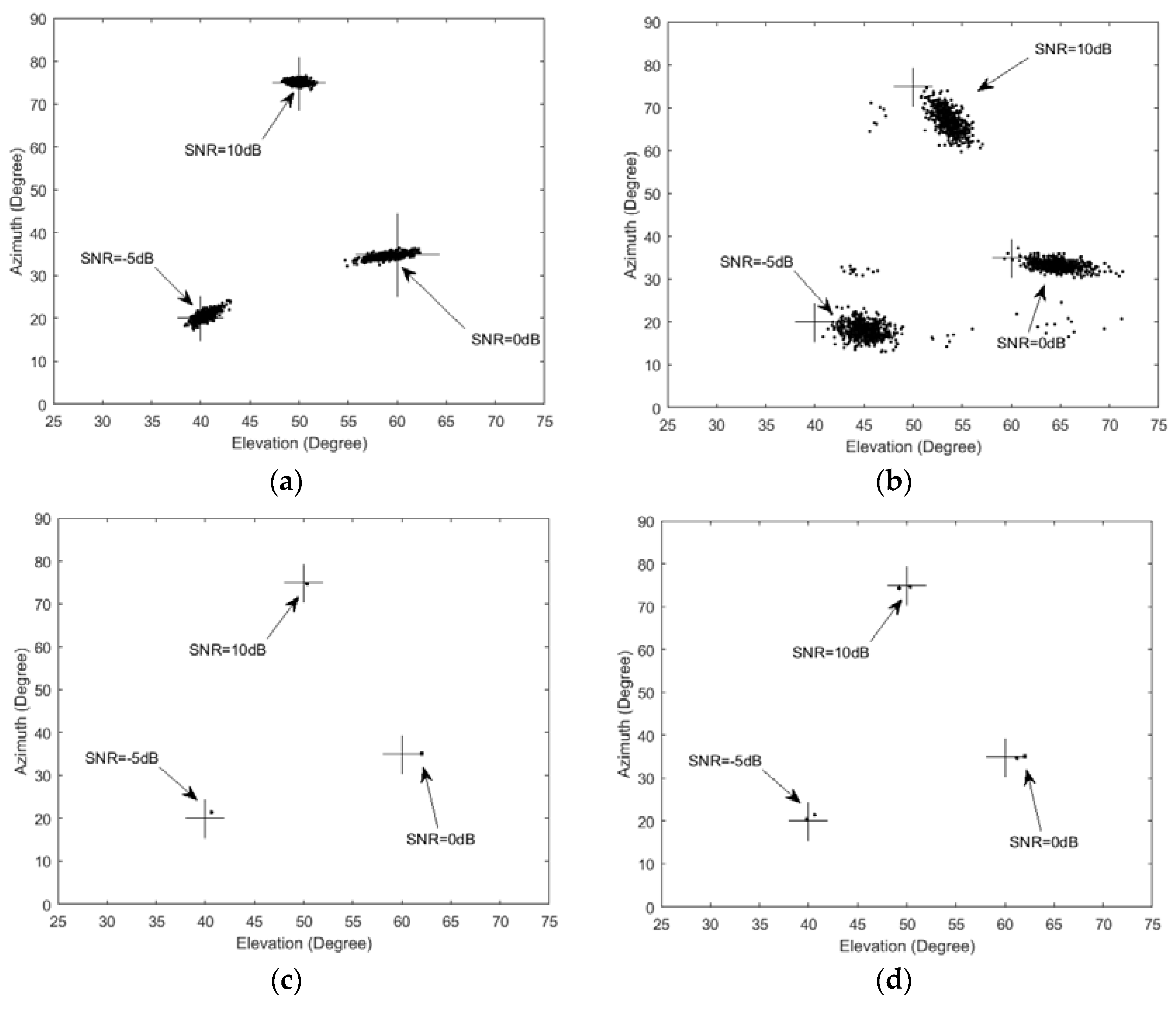
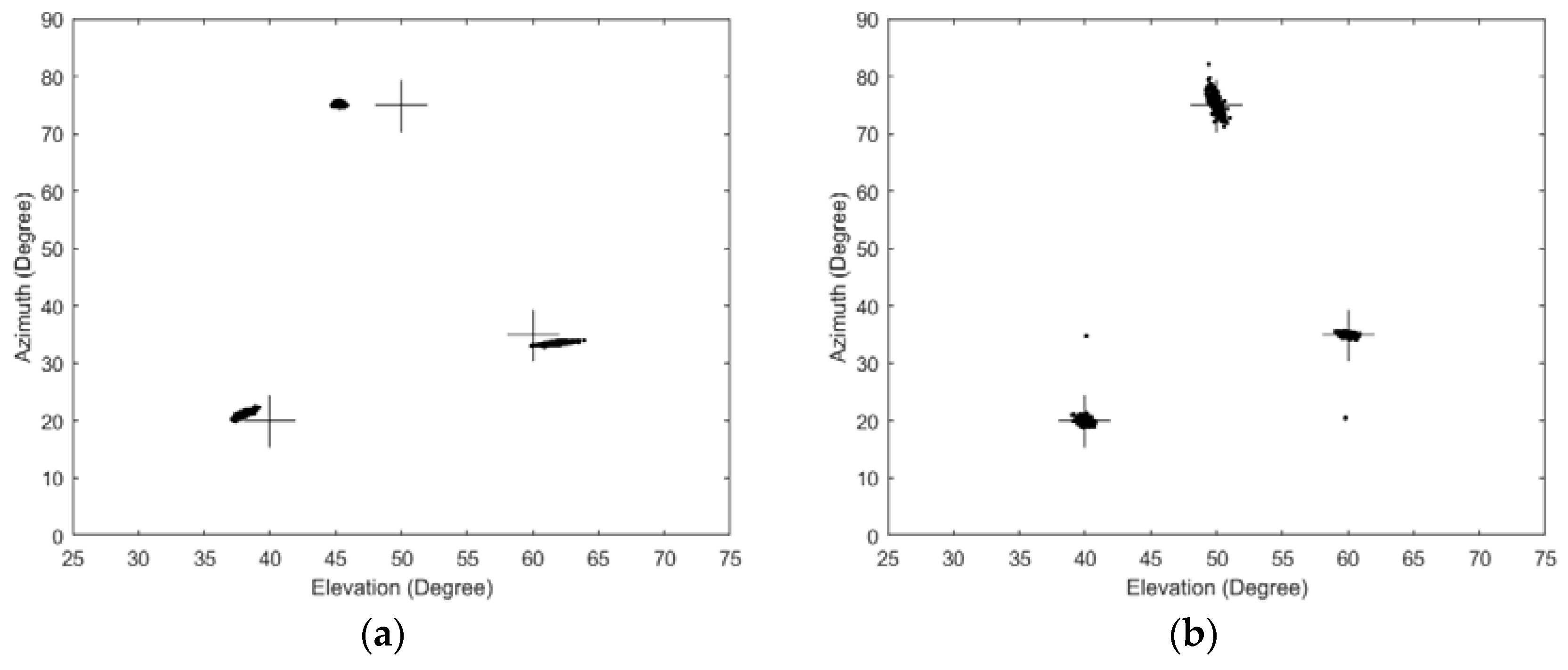
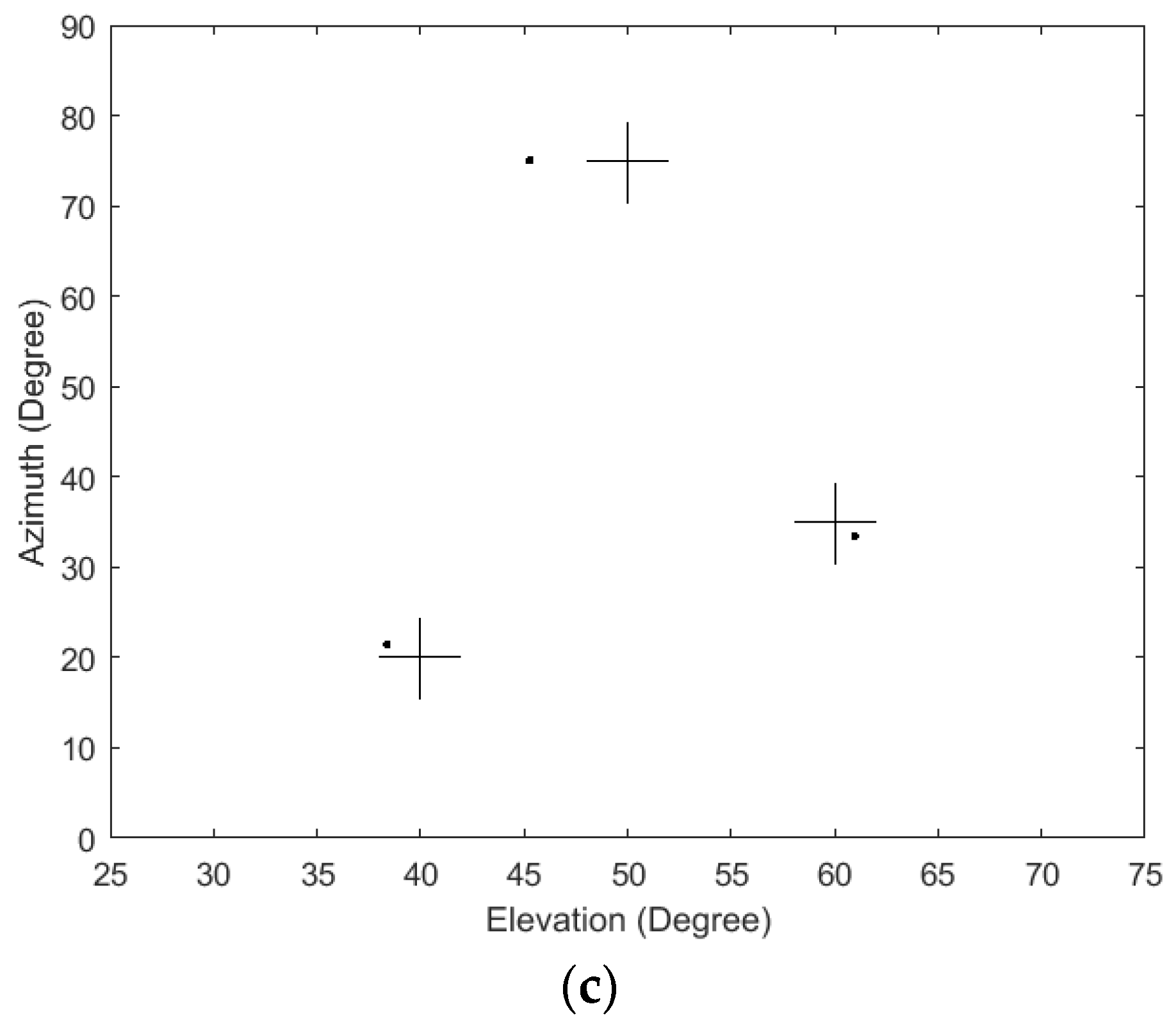
6.3. Comparison Scatter Plots of Estimated 2D Angles in Different SNR
6.4. CPU Time Comparison
6.5. RMSE and CRB versus Source Separation δ
6.6. Performance in the Presence of Mutual Coupling
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Basikolo, T.; Arai, H. APRD-MUSIC algorithm DOA estimation for reactance based uniform circular array. IEEE Trans. Antennas Propag. 2016, 64, 4415–4422. [Google Scholar] [CrossRef]
- Huang, W.; Yang, X.; Liu, D.; Chen, S. Diffusion LMS with component-wise variable step-size over sensor networks. IET Signal Process. 2016, 10, 37–45. [Google Scholar] [CrossRef]
- Ni, J.; Yang, J. Variable step-size diffusion least mean fourth algorithm for distributed estimation. Signal Process. 2015, 122, 93–97. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, Z.; Gu, Y.; Shen, X. DECOM: DOA estimation with combined MUSIC for coprime array. In Proceedings of the IEEE International Conference on Wireless Communications and Signal Processing, Hangzhou, China, 24–26 October 2013; pp. 1–5.
- Wang, Y.Y.; Lee, L.C.; Yang, S.J.; Chen, J.T. A tree structure one-dimensional based algorithm for estimating the two-dimensional direction of arrivals and its performance analysis. IEEE Trans. Antennas Propag. 2008, 56, 178–188. [Google Scholar] [CrossRef]
- Karthikeyan, B.R.; Kadambi, G.R.; Vershinin, Y.A. A formulation of 1-D search technique for 2-D DOA estimation using orthogonally polarized components of linear array. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 1117–1120. [Google Scholar] [CrossRef]
- Kikuchi, S.; Tsuji, H.; Sano, A. Pair-matching method for estimating 2-D angle of arrival with a cross-correlation matrix. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 35–40. [Google Scholar] [CrossRef]
- Gershman, A.B.; Rübsamen, M.; Pesavento, M. One- and two dimensional direction-of-arrival estimation: An overview of search-free techniques. Signal Process. 2010, 90, 1338–1349. [Google Scholar] [CrossRef]
- Han, F.M.; Zhang, X.D. An ESPRIT-like algorithm for coherent DOA estimation. IEEE Antennas Wirel. Propag. Lett. 2005, 4, 443–446. [Google Scholar] [CrossRef]
- Chen, F.J.; Kwong, S.; Kok, C.W. ESPRIT-Like Two-Dimensional DOA Estimation for Coherent Signals. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1477–1484. [Google Scholar] [CrossRef]
- Chen, F.J.; Fung, C.C.; Kok, C.W.; Kwong, S. Estimation of 2-Dimensional Frequencies Using Modified Matrix Pencil Method. In Proceedings of the IEEE 6th Workshop on Signal Processing Advances in Wireless Communications, New York, NY, USA, 5–8 June 2005; pp. 718–724.
- Barabell, A.J. Improving the resolution performance of eigenstructure-based direction-finding algorithms. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Boston, MA, USA, 14–16 April 1983; pp. 336–339.
- Qian, C.; Huang, L.; So, H.C. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling. IEEE Signal Process. Lett. 2014, 21, 140–144. [Google Scholar] [CrossRef]
- Costa, M.; Richter, A.; Koivunen, V. DoA and polarization estimation for arbitrary array configurations. IEEE Trans. Signal Process. 2012, 60, 2330–2343. [Google Scholar] [CrossRef]
- Weiss, A.; Friedlander, B. Direction finding for diversely polarized signal using polynomial rooting. IEEE Trans. Signal Process. 1993, 41, 1893–1905. [Google Scholar] [CrossRef]
- Wong, K.; Li, L.; Zoltowski, M. Root-MUSIC-based direction finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 129–132. [Google Scholar] [CrossRef]
- Goossens, R.; Rogier, H. A hybrid UCA-RARE/Root-MUSIC approach for 2-D direction of arrival estimation in uniform circular array in the presence of mutual coupling. IEEE Trans. Antennas Propag. 2007, 55, 841–849. [Google Scholar] [CrossRef]
- Ye, Z.F.; Liu, C. 2-D DOA estimation in the presence of mutual coupling. IEEE Trans. Antennas Propag. 2008, 56, 3150–3158. [Google Scholar] [CrossRef]
- Filik, T.; Tuncer, T.E. A fast and automatically paired 2-D direction-of-arrival estimation with and without estimating the mutual coupling coefficients. Radio Sci. 2010, 45, 428–451. [Google Scholar] [CrossRef]
- Ren, S.W.; Ma, X.C.; Yan, S.F.; Hao, C.P. 2-D unitary ESPRIT-Like direction-of-arrival (DOA) estimation for coherent signals with a uniform rectangular array. Sensors 2013, 13, 4272–4288. [Google Scholar] [CrossRef] [PubMed]
- Haardt, M.; Nossek, J.A. Unitary ESPRIT: How to obtain increased estimation accuracy with a reduced computational burden. IEEE Trans. Signal Process. 1995, 43, 1232–1242. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Haardt, M.; Mathews, C.P. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT. IEEE Trans. Signal Process. 1996, 44, 316–328. [Google Scholar] [CrossRef]
- Perez-Neira, A.I.; Lagunas, M.; Kirlin, R.L. Cross-coupled DOA trackers. IEEE Trans. Signal Process. 1997, 45, 2560–2565. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, D.Z.; Liu, J.Q. A novel algorithm for two-dimension frequency estimation. Signal Process. 2007, 87, 1–12. [Google Scholar] [CrossRef]

| Configuration | Ss 0.1° | Ss 0.1° | Ss 0.25° | Ss 0.25° | Ss 0.5° | Ss 0.5° | |
|---|---|---|---|---|---|---|---|
| Row × Column | AESS | MUSIC | AESS | MUSIC | AESS | MUSIC | PIE |
| 3 × 3 | 2.4032 | 41.9570 | 0.4205 | 6.6706 | 0.1228 | 1.7263 | 0.0043 |
| 3 × 4 | 2.4063 | 41.9736 | 0.4221 | 6.7262 | 0.1236 | 1.7394 | 0.0050 |
| 3 × 5 | 2.4176 | 43.4240 | 0.4228 | 6.8137 | 0.1238 | 1.7728 | 0.0052 |
| 3 × 6 | 2.4221 | 43.9129 | 0.4248 | 6.9126 | 0.1241 | 1.7955 | 0.0078 |
| 3 × 7 | 2.4399 | 44.8107 | 0.4398 | 7.0829 | 0.1351 | 1.8056 | 0.0089 |
| 3 × 8 | 2.5659 | 45.4299 | 0.4553 | 7.7317 | 0.1525 | 1.8943 | 0.0095 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, W.; Xu, K.; Feng, D.; Wu, C.Q.; Hou, A.; Yin, X. A Fast Algorithm for 2D DOA Estimation Using an Omnidirectional Sensor Array. Sensors 2017, 17, 515. https://doi.org/10.3390/s17030515
Nie W, Xu K, Feng D, Wu CQ, Hou A, Yin X. A Fast Algorithm for 2D DOA Estimation Using an Omnidirectional Sensor Array. Sensors. 2017; 17(3):515. https://doi.org/10.3390/s17030515
Chicago/Turabian StyleNie, Weike, Kaijie Xu, Dazheng Feng, Chase Qishi Wu, Aiqin Hou, and Xiaoyan Yin. 2017. "A Fast Algorithm for 2D DOA Estimation Using an Omnidirectional Sensor Array" Sensors 17, no. 3: 515. https://doi.org/10.3390/s17030515






