An Improved Particle Filter for Target Tracking in Sensor Systems
Abstract
:1. Introduction
2. Target Motion and Observation Model of Sensor Systems
3. Principle of the PF-RBF Algorithm
3.1. Generic Particle Filter
3.2. Trajectory Approximation with RBFN
3.3. Improved PF Algorithm Combined with RBFN
| Algorithm 1. |
| Algorithm 1 |
|
4. Experimental Results
4.1. Experiment Setup
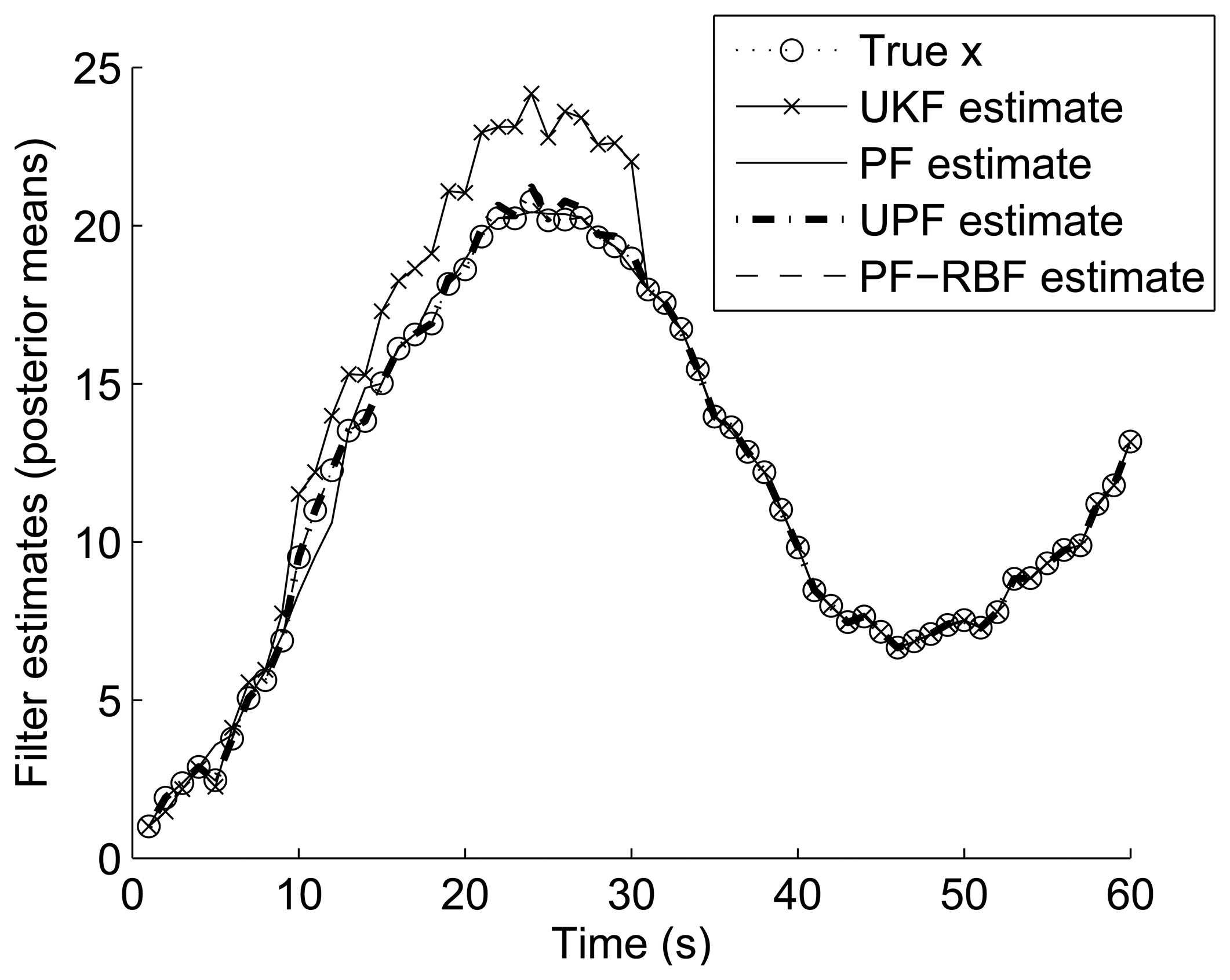
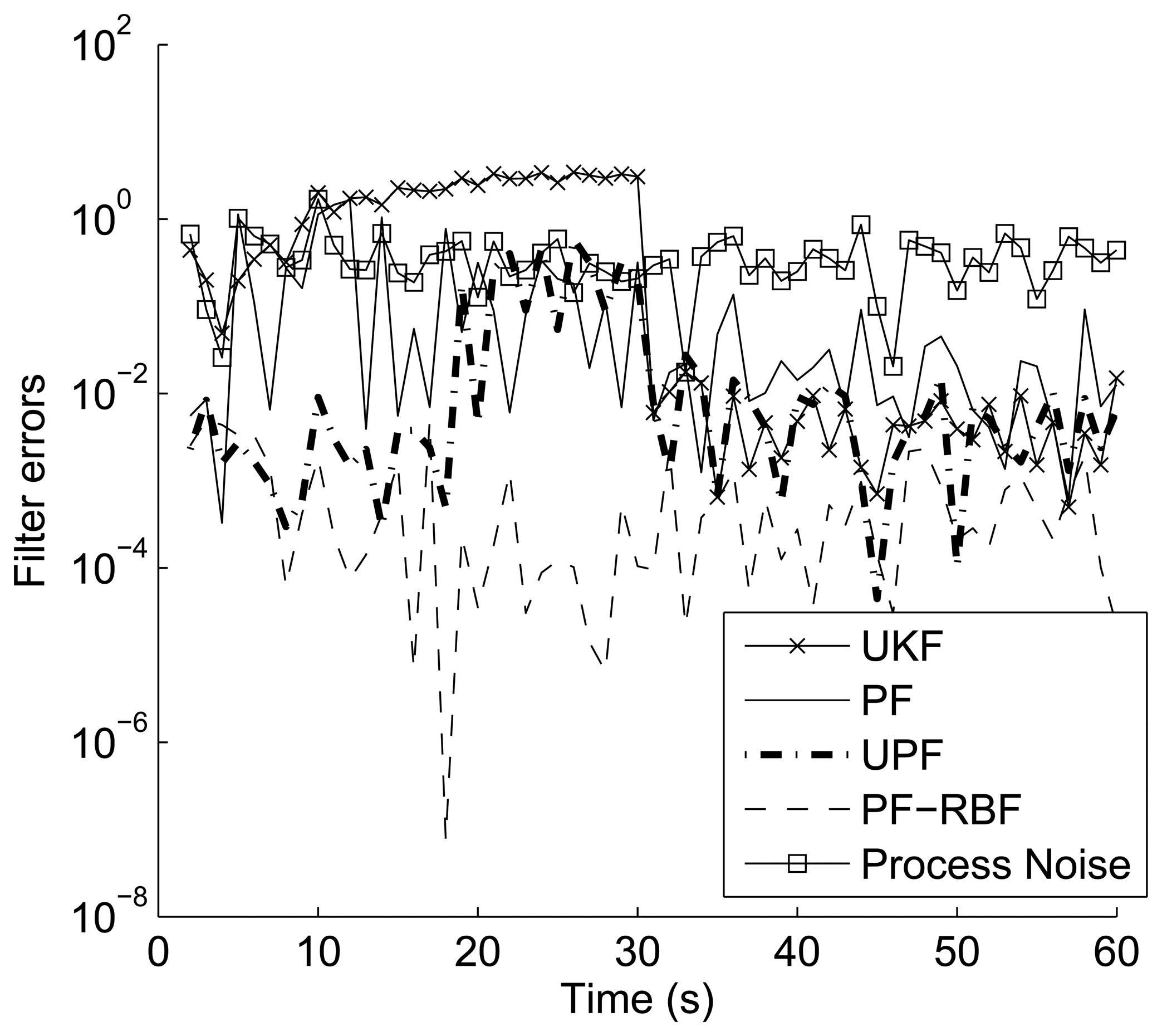
4.2. Tracking results
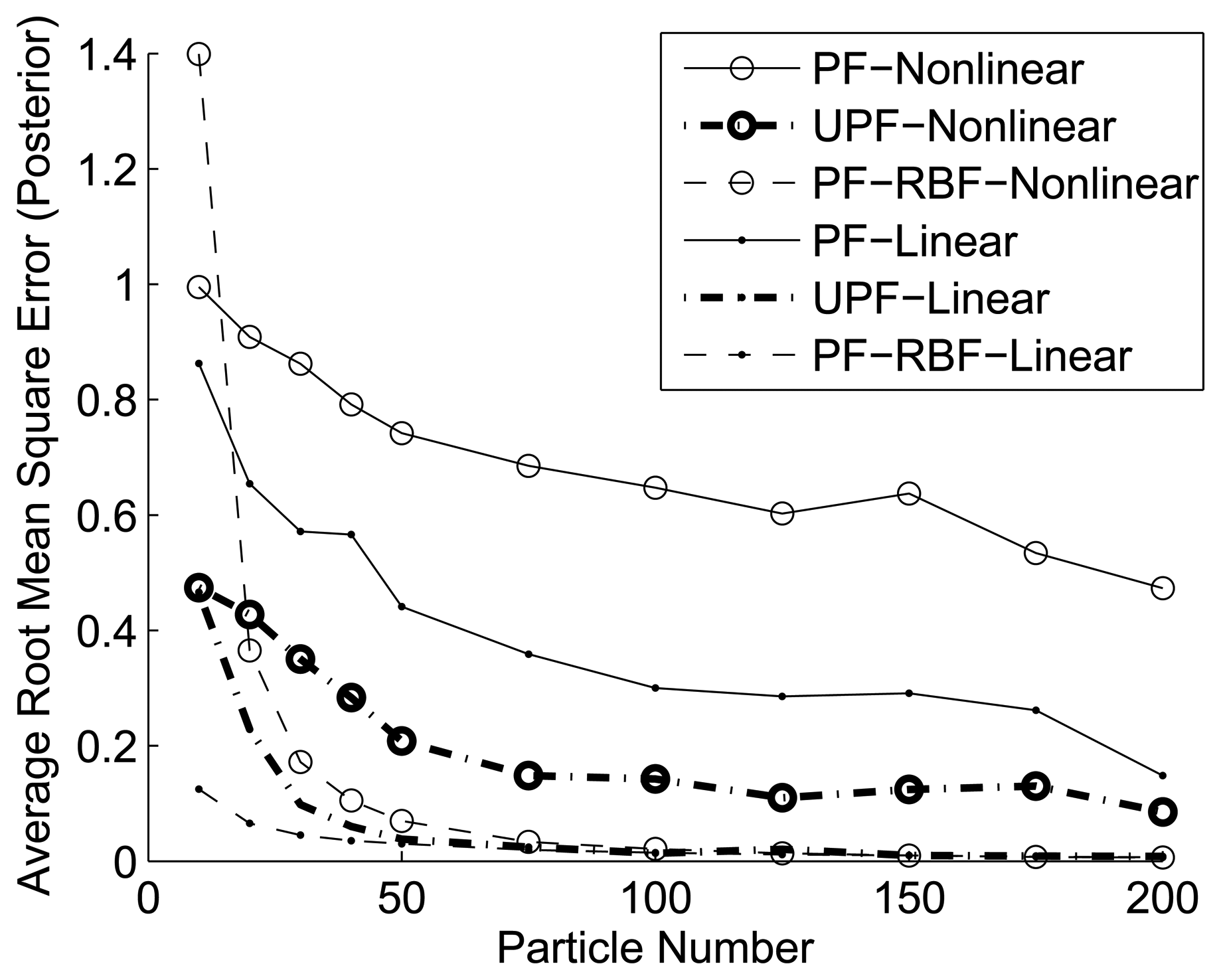
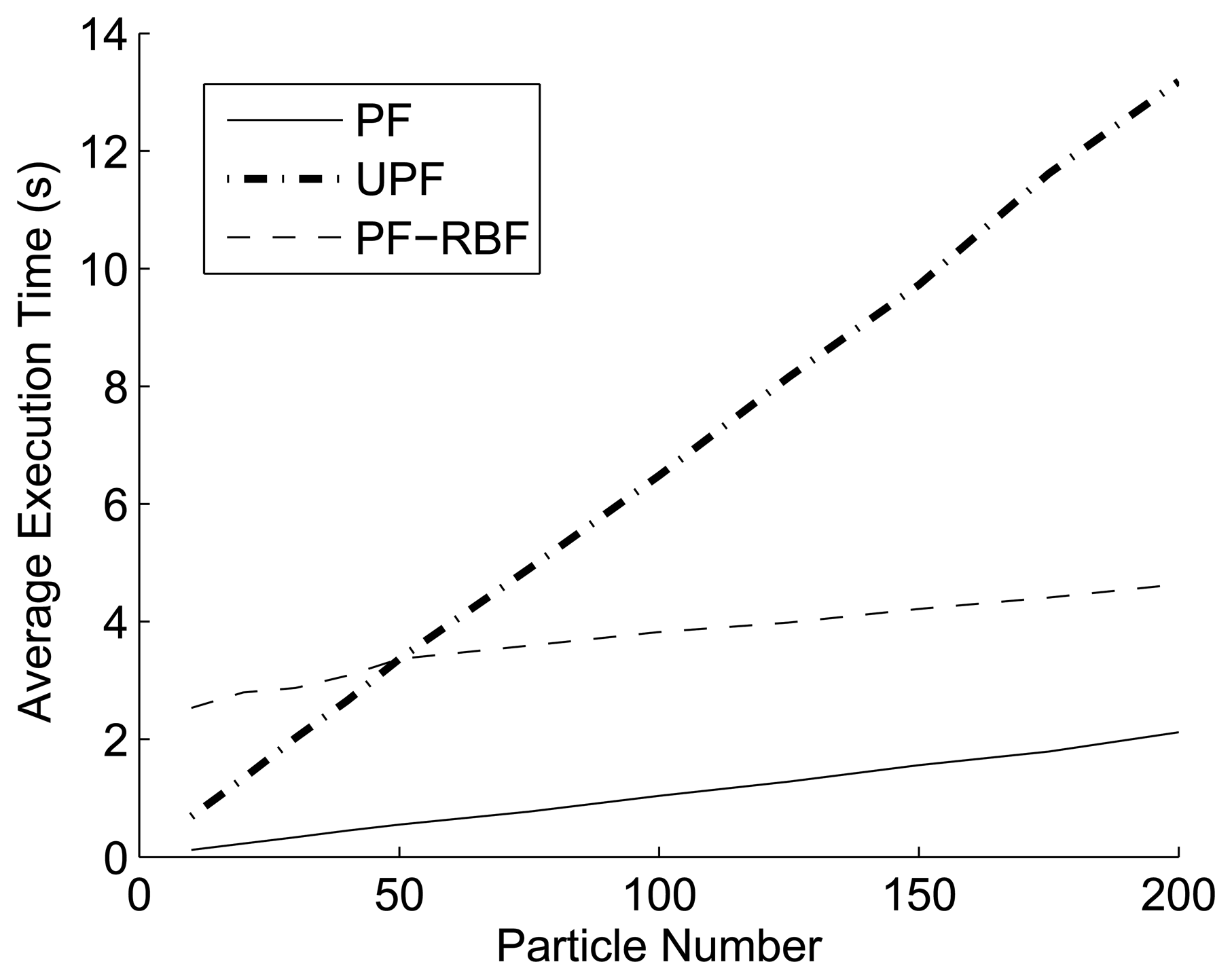
4.3. Execution time and accuracy
5. Conclusions
Acknowledgments
References and Notes
- Duh, F.; Lin, C. Tracking a maneuvering target using neural fuzzy network. IEEE Trans. Sys. Man, Cyber. 2004, 34, 16–33. [Google Scholar]
- Van der Merwe, R.; Doucet, A.; de Freitas, N.; Wan, E. The unscented particle filter. In Technical Report CUED/ F-INPENG/TR 380; Department of Engineering, Cambridge University: Cambridge, UK, 2000. [Google Scholar]
- Anderson, B. D.; Moore, J. B. Optimal Filtering; Prentice Hall: NJ, U.S.A., 1979. [Google Scholar]
- Julier, S.; Uhlmann, J.K. A general method for approximating nonlinear transformations of probability distributions. In Technical Report, Department of Engineering Science; Oxford University: Oxford, UK, 1996. [Google Scholar]
- Doucet, A. On sequential simulation-based methods for Bayesian filtering. In Techical Report, CUED/F-INFENG/TR 310; Department of Engineering, Cambridge University: Cambridge, UK, 1998. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to non-linear/non-Gaussian Bayesian state estimation. Proc. Inst. Elect. Eng. F 1993, 140, 107–113. [Google Scholar]
- Doucet, A.; Godsill, S.; Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar]
- Chan, Y.T.; Hu, A.G.C.; Plant, J.B. A Kalman filter based tracking scheme with input estimation. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 237–244. [Google Scholar]
- Bar-Shalom, Y.; Birmiwal, K. Variable dimension filter for maneuvering target tracking. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 621–629. [Google Scholar]
- Hong, S.; Bolić, M.; Djurić, P.M. An efficient fixed-point implementation of residual resampling scheme for high-speed particle filters. IEEE Sig. Process. Lett. 2004, 11, 482–485. [Google Scholar]
- Cheng, C.; Ansari, R. Kernel particle filter for visual tracking. IEEE Sig. Process. Lett. 2005, 12, 42–245. [Google Scholar]
- Haykin, S. Neural Networks: a Comprehensive Foundation; Prentice Hall: NJ, U.S.A., 1999. [Google Scholar]
- Yang, N.; Tian, W.; Jin, Z. An interacting multiple model particle filter for maneuvering target location. Meas. Sci. Tech. 2006, 17, 1307–1311. [Google Scholar]
- Bar-Shalom, Y.; Chen, H. IMM estimator with out-of-sequence measurements. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 90–98. [Google Scholar]
- Angelova, D.; Mihaylova, L. Joint target tracking and classification with particle filtering and mixture Kalman filtering using kinematic radar information. Dig. Sig. Process. 2006, 16, 180–204. [Google Scholar]
- Yu, Y.; Cheng, Q. Particle filters for maneuvering target tracking problem. Sig. Process. 2006, 86, 195–203. [Google Scholar]
- Morelande, M.R.; Challa, S. Manoeuvring target tracking in clutter using particle filters. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 252–270. [Google Scholar]
- Arulampalam, M.S.; Ristic, B.; Gordon, N.; Mansell, T. Bearings-only tracking of maneuvering targets using particle filters. EURASIP J. Appl. Sig. Process. 2004, 15, 2351–2365. [Google Scholar]
- Orr., Mark J. L. Introduction to radial basis function networks. Technical Report; Centre for Cognitive Science, University of Edinburgh: Edinburgh, 1996. [Google Scholar]
- Huang, G. B.; Saratchandran, P.; Sundararajan, S. A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation. IEEE Trans. Neural Net. 2005, 16, 57–67. [Google Scholar]
| Algorithm | Mean of RMSEs | |
|---|---|---|
| Nonlinear | Linear | |
| UKF | 0.58461 | 0.0067026 |
| Generic PF | 0.47292 | 0.1485 |
| UPF | 0.085445 | 0.0080179 |
| PF-RBF | 0.0187598 | 0.0066431 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Wang, X.; Wang, S.; Ma, J.-J. An Improved Particle Filter for Target Tracking in Sensor Systems. Sensors 2007, 7, 144-156. https://doi.org/10.3390/s7010144
Wang X, Wang S, Ma J-J. An Improved Particle Filter for Target Tracking in Sensor Systems. Sensors. 2007; 7(1):144-156. https://doi.org/10.3390/s7010144
Chicago/Turabian StyleWang, Xue, Sheng Wang, and Jun-Jie Ma. 2007. "An Improved Particle Filter for Target Tracking in Sensor Systems" Sensors 7, no. 1: 144-156. https://doi.org/10.3390/s7010144




