Adaptive Unscented Kalman Filter for Target Tracking in the Presence of Nonlinear Systems Involving Model Mismatches

Abstract

In order to improve filtering precision and restrain divergence caused by sensor faults or model mismatches for target tracking, a new adaptive unscented Kalman filter (N-AUKF) algorithm is proposed. First of all, the unscented Kalman filter (UKF) problem to be solved for systems involving model mismatches is described, after that, the necessary and sufficient condition with third order accuracy of the standard UKF is given and proven by using the matrix theory. In the filtering process of N-AUKF, an adaptive matrix gene is introduced to the standard UKF to adjust the covariance matrixes of the state vector and innovation vector in real time, which makes full use of normal innovations. Then, a covariance matching criterion is designed to judge the filtering divergence. On this basis, an adaptive weighted coefficient is applied to restrain the divergence. Compared with the standard UKF and existing adaptive UKF, the proposed UKF algorithm improves the filtering accuracy, rapidity and numerical stability remarkably, moreover, it has a good adaptive capability to deal with sensor faults or model mismatches. The performance and effectiveness of the proposed UKF is verified in a target tracking mission.

1. Introduction

Target Tracking is an essential technology in both military and civil fields, and it is critical to the success of many tasks, such as target recognition and attack [1,2,3,4,5]. The main mission of target tracking is to show the value of current state estimation and latter state prediction by using sensor measurements. In this sense, target tracking is essentially a filtering problem. To perform perfect target tracking tasks with valuable state estimation, real-time filtering algorithms with high performance are needed [6]. However, traditional filtering algorithms are greatly limited in applications for the complexity of the motion states and maneuvering characteristics for missiles and aircraft, thus leading to growing difficulties in target tracking. Therefore, it must be resolved as to how to design an effective, adaptive and stable filtering algorithm for target tracking within complicated environments.

The Kalman filter (KF) algorithm has been proven effective in dealing with theoretical and practical estimation problems since it was first proposed for Project Apollo in 1960 [7,8,9], but it can only get optimal estimation in Gaussian-Linear models, making KF quite limited in the scope of target tracking applications. In order to improve the performance of the Kalman filter on nonlinear systems, the extended Kalman filter (EKF) algorithm has been developed [10,11], which replaces the state transition and the measurement equations by Taylor series expansions. However, there are also two main shortcomings of EKF: (1) Jacobi matrices of nonlinear functions are hard to compute and it is easy to make errors; (2) high order truncation errors exist. Therefore, EKF will encounter low accuracy problems when it is applied to strongly nonlinear systems. The particle filter (PF) algorithm, also known as sequential Monte Carlo for online filtering and prediction of nonlinear and non-Gaussian state space models, has extremely good performance in the aspect of filtering precision, unfortunately, poor samples and large calculation problems exist [12,13].

Recently, the unscented Kalman filter (UKF) algorithm based on the unscented transformation has gradually become one of the most popular filtering approaches for nonlinear systems [14,15]. The standard UKF passes the first and second moment of random variables through nonlinear functions and can capture the posterior mean and covariance of the state of any Gaussian and nonlinear systems with third order accuracy. It can also avoid the cumbersome evaluation of Jacobian matrices. Therefore, UKF has advantages of higher filtering precision compared with EKF and lower computation complexity than PF, which makes the algorithm easier to implement. At present, UKF has been widely used in various fields such as signal processing [16], navigation [17], target tracking [18], fault detection [19], and power sources [20].

Although UKF holds unique advantages for solving nonlinear filtering problems, similarly to EKF, it requires valuable prior knowledge of the characteristics of system models and noises. However, various limitations and factors always exist in practical engineering applications. For example, sensor faults will produce inaccurate system models and noise statistical properties. Standard UKF have no adaptive abilities for external and internal uncertainties of system models, and large filtering errors, even filtering divergence, may occur. The adaptive UKF algorithm is considered an effective method to resist the influence on the filtering solution of the inaccurate statistics of system noises [21,22,23,24], but there are still some shortcomings: (1) the algorithm considers just the noise problem but no systems involving model mismatches [21]; (2) new limitations are introduced, for example, not enough origin state errors [16]; (3) the algorithm structure is too complicated to be applicable to the practical target tracking in real-time performance [19].

In the presence of sensor faults and systems involving model mismatches, the state estimation results will deviate from the true values seriously, if standard UKF and previous adaptive UKF are used. To deal with this problem, Gao et al. uses a principle of variance inflation based on standard UKF, and proposes an adaptive UKF algorithm by introducing adaptive genes, which improves the filtering accuracy greatly [25,26]. Soken et al. puts forward a robust UKF to accomplish the satellite attitude estimation in the presence of measurement faults [27]. However, one main deficiency of the above suggested algorithms is that it can only apply to the system in which the process equation is nonlinear while the measurement equation is linear, because the derivation and proof of the algorithms are completely based on linear measurement equations. Furthermore, the filtering divergence is not solved in the literature.

A new adaptive UKF (N-AUKF) algorithm for nonlinear systems involving model mismatches is proposed. In current research, the nonlinear measurement equation is considered, and filtering divergence can be judged and restrained. First, the filter problem to be solved is described and, for the UKF algorithm, the third order accuracy conditions of the standard UKF algorithm is proposed and proven. On this basis, an adaptive matrix gene is introduced to the standard UKF to adjust the covariance matrixes of the state vector and innovation vector in real time. Moreover, the possible filtering divergence is judged by using the covariance matching method, and an adaptive weighted coefficient is introduced to correct covariance matrices of prediction errors to further guarantee the stability of the adaptive UKF. Simulation results of different conditions show that the proposed algorithm can significantly increase the filtering precision and improve the stability due to the strongly adaptive ability to model mismatches.

2. Problem Description

To design the new adaptive UKF algorithm, the filtering problem to be solved in the presence of nonlinear systems involving model mismatches is described thusly.

2.1. System Model Formulation for Target Tracking

For target tracking, regard the general mathematical model of nonlinear discrete stochastic system of the target as [1,3]

$$\{\begin{array}{l}{\mathit{X}}_k=\mathit{f}[{\mathit{X}}_{k-1},k-1]+{\Gamma }_{k-1}{W}_{k-1}\\ {\mathit{Z}}_k=\mathit{h}[{\mathit{X}}_k,k]+V_k\end{array}$$

(1)

Similarly, view the mathematical model of nonlinear discrete stochastic system of the target involving model mismatches as [25,27]

$$\{\begin{array}{l}{\mathit{X}}_k=\mathit{f}[{\mathit{X}}_{k-1},k-1]+{\Gamma }_{k-1}{W}_{k-1}\\ {\mathit{Z}}_k=\mathit{h}[{\mathit{X}}_k,k]+V_k+\delta {\mathit{h}}_{out,k}\end{array}$$

(2)

Especially, when measurement equations of the models shown in Equations (1) and (2) are linear equations, Equations (1) and (2) respectively, can be rewritten as

$$\{\begin{array}{l}{\mathit{X}}_k=\mathit{f}[{\mathit{X}}_{k-1},k-1]+{\Gamma }_{k-1}{W}_{k-1}\\ {\mathit{Z}}_k={\mathit{A}}_k{\mathit{X}}_k+V_k\end{array}$$

(3)

$$\{\begin{array}{l}{\mathit{X}}_k=\mathit{f}[{\mathit{X}}_{k-1},k-1]+{\Gamma }_{k-1}{W}_{k-1}\\ {\mathit{Z}}_k={\mathit{A}}_k{\mathit{X}}_k+V_k+\delta {\mathit{A}}_{out,k}\end{array}$$

(4)

where ${\mathit{X}}_k$ and ${\mathit{X}}_{k-1}$ denote, respectively, the system state vector at time step $k$ and $k-1$; ${\Gamma }_{k-1}$ is the process noise gain matrix with appropriate dimension; ${\mathit{Z}}_k$ denotes the measurement vector; $W_{k-1}$ and $V_k$ represent, respectively, the process noise and the measurement noise; $\mathit{f}[•]$ is a nonlinear vector function of process equations with $n$ dimension; $\mathit{h}[•]$ is a nonlinear vector function of measurement equations with $m$ dimension; ${\mathit{A}}_k$ is a coefficient matrix of linear measurement equations with $m\times n$ dimension; both $\delta {\mathit{h}}_{out,k}$ and $\delta {\mathit{A}}_{out,k}$ represent model mismatches involved in nonlinear systems.

Assumption 1.

$W_k$ and $V_k$ are white Gaussian noises, which meet

$$\{\begin{array}{l}\mathrm{E}[W_k]=\mathbf{0},\mathrm{Cov}[W_k,W_j]=\mathrm{E}[W_k{W}_j{}^{\mathrm{T}}]=Q_k{\delta }_{kj}\\ \mathrm{E}[V_k]=\mathbf{0},\mathrm{Cov}[V_k,V_j]=\mathrm{E}[V_k{V}_j{}^{\mathrm{T}}]=R_k{\delta }_{kj}\\ \mathrm{Cov}[W_k,V_j]=\mathrm{E}[W_k{V}_j{}^{\mathrm{T}}]=\mathbf{0}\end{array}$$

(5)

where ${\delta }_{kj}$ is a $\mathrm{Kronecker}-\delta$ function; $\mathrm{E}[]$ and $\mathrm{Cov}[]$ are, respectively, the expected value and covariance of the variable.

Assumption 2.

The origin value ${\mathit{X}}_0$ meets the following statistical properties:

$$\{\begin{array}{l}{\widehat{\mathit{X}}}_0=\mathrm{E}[{\mathit{X}}_0]\\ P_0=\mathrm{Cov}[{\mathit{X}}_0,{\mathit{X}}_0{}^{\mathrm{T}}]=\mathrm{E}[({\mathit{X}}_0-{\widehat{\mathit{X}}}_0){({\mathit{X}}_0-{\widehat{\mathit{X}}}_0)}^{\mathrm{T}}]\end{array}$$

(6)

2.2. Standard UKF

Nonlinear systems evaluated by Equations (1) and (3), with accurate statistics of models and noises, the standard UKF algorithm can be described as follows:

Step 1: Initialize the state estimate and error covariance matrix.

$$\{\begin{array}{l}{\widehat{\mathit{X}}}_0=\mathrm{E}[{\mathit{X}}_0]\\ P_0=\mathrm{E}[({\mathit{X}}_0-{\widehat{\mathit{X}}}_0){({\mathit{X}}_0-{\widehat{\mathit{X}}}_0)}^{\mathrm{T}}]\end{array}$$

(7)

For time step $k=1,2,3,\cdots$ implement Step 2.

Step 2: Calculate $2n+1$ Sigma points at $k-1$ moment:

$${\chi }_{k-1}^{(0)}={\mathit{X}}_{k-1}$$

(8)

$${\chi }_{k-1}^{(i)}={\mathit{X}}_{k-1}+\sqrt{n+\lambda }{(\sqrt{P_{k-1}})}_{(i)},i=1,2,\cdots ,n$$

(9)

$${\chi }_{k-1}^{(i)}={\mathit{X}}_{k-1}-\sqrt{n+\lambda }{(\sqrt{P_{k-1}})}_{(i-n)},i=n+1,n+2,\cdots ,2n$$

(10)

where $n$ is the dimension of the system state vector; $\lambda$ ($\lambda ={\alpha }^2(n+\kappa )-n$) denotes the scale factor of sampling; $\alpha$ is a small positive constant which is set to ${10}^{-4}\le \alpha \le 1$ normally; $\kappa$ is set to $0$ or $3-n$ [3].

Step 3: Compute the one step prediction value at $k$ moment:

$${\chi }_{k/k-1}^{(i)}=\mathit{f}[{\chi }_{k-1}^{(i)},k-1],i=0,1,2,\cdots ,2n$$

(11)

$${\widehat{\mathit{X}}}_{k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(m)}}{\chi }_{k/k-1}^{(i)}$$

(12)

$$P_{k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\chi }_{k/k-1}^{(i)}-{\widehat{\mathit{X}}}_{k/k-1}]{[{\chi }_{k/k-1}^{(i)}-{\widehat{X}}_{k/k-1}]}^{\mathrm{T}}+Q_{k-1}$$

(13)

where ${\widehat{\mathit{X}}}_{k/k-1}$ is the one step prediction output value; $P_{k/k-1}$ denotes the responding covariance matrix; both $W_i^{(m)}$ and $W_i^{(c)}$ represent weighted coefficients, which are set to

$$\{\begin{array}{l}{W}_0^{(m)}=\frac{\lambda }{n+\lambda }\\ W_0^{(c)}=\frac{\lambda }{n+\lambda }+(1-{\alpha }^2+\beta )\\ W_i^{(m)}=W_i^{(c)}=\frac{\lambda }{2(n+\lambda )},i=1,2,\cdots ,2n\end{array}$$

(14)

where $\beta$ includes the prior information of ${\mathit{X}}_k$ distribution, and $\beta =2$ is set up for Gaussian distribution.

Step 4: Calculate measurement values:

$${\gamma }_{k/k-1}^{(i)}=\mathit{h}[{\chi }_{k/k-1}^{(i)},k],i=0,1,2,\cdots ,2n$$

(15)

$${\widehat{\mathit{Z}}}_{k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(m)}{\gamma }_{k/k-1}^{(i)}}.$$

(16)

Step 5: Calculate $P_{(XZ)k/k-1}$ and $P_{(ZZ)k/k-1}$:

$$P_{(XZ)k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\chi }_{k/k-1}^{(i)}-{\widehat{\mathit{X}}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]}^{\mathrm{T}}$$

(17)

$$P_{(ZZ)k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]}^{\mathrm{T}}+R_k.$$

(18)

Step 6: Calculate gain matrices:

$$K_k=P_{(XZ)k/k-1}{(P_{(ZZ)k/k-1})}^{-1}.$$

(19)

Step 7: Calculate filtering solutions:

$${\widehat{\mathit{X}}}_k={\widehat{\mathit{X}}}_{k/k-1}+K_k({\mathit{Z}}_k-{\widehat{\mathit{Z}}}_{k/k-1})$$

(20)

$$P_k=P_{k/k-1}-K_k{P}_{(ZZ)k/k-1}{K}_k{}^{\mathrm{T}}.$$

(21)

2.3. Problem Description of the Filter for Systems Involving Model Mismatches

According to steps of the standard UKF algorithm, the actual calculated results of ${\chi }_{k/k-1}^{(i)}$ and ${\widehat{\mathit{X}}}_{k/k-1}$ are influenced through Equations (11) and (12), if the deviation between the initialized value and actual value of ${\widehat{\mathit{X}}}_0$ exists, and the affected ${\chi }_{k/k-1}^{(i)}$ and ${\widehat{\mathit{X}}}_{k/k-1}$ will lead to errors of innovation vectors forecasts ${\widehat{\mathit{Z}}}_{k/k-1}$ by Equation (15). What is more, uncertainties, such as $\delta {\mathit{h}}_{out,k}$ and $\delta {\mathit{A}}_{out,k}$, are affecting the calculated values of ${\widehat{\mathit{X}}}_{k/k-1}$, ${\widehat{\mathit{Z}}}_{k/k-1}$, and ${\widehat{\mathit{X}}}_k$ via Equations (15), (16) and (20), making standard UKF unsuitable for systems given by Equations (2) and (4) involving model mismatches.

The effective adaptive UKF algorithms for the system given by Equation (4) have been proposed [25,26,27]. Therefore, the filtering problem to be solved is described as an issue of how to design an effective adaptive UKF algorithm for systems given by Equation (2) based on the measurement ${\mathit{Z}}_k={[z{1}_k,z{2}_k,\cdots ,z{m}_k]}^{\mathrm{T}}$, when the model mismatches exist, namely the system model uncertainties $\delta {\mathit{h}}_{out,k}$ and $\delta {\mathit{A}}_{out,k}$.

3. Adaptive UKF Algorithm

For adaptive UKF, it is absolutely necessary to make full use of the information obtained in the filtering process for resisting the disturbance of system noise and model errors on system state estimation. In order to decrease the influence of the initial estimation value deviation and system model uncertainties on the filtering solution, the latest adaptive UKF algorithm is put forward [25,26,27], and is abbreviated as L-AUKF for simplicity.

3.1. L-AUKF Algorithm

L-AUKF inflates $P_{k/k-1}$, $P_{(XZ)k/k-1}$ and $P_{(ZZ)k/k-1}$ adaptively by using traditional thinking, which can balance the influence of system states and measurement information.

Rewrite the covariance matrices in Equations (17), (18) and (21) as

$${\overline{P}}_{(XZ)k/k-1}=\frac{1}{{\alpha }_k}{\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\chi }_{k/k-1}^{(i)}-{\widehat{\mathit{X}}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]}^{\mathrm{T}}$$

(22)

$${\overline{P}}_{(ZZ)k/k-1}=\frac{1}{{\alpha }_k}{\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]}^{\mathrm{T}}+R_k$$

(23)

$${\overline{P}}_k=\frac{1}{{\alpha }_k}{P}_{k/k-1}-K_k{P}_{(ZZ)k/k-1}{K}_k{}^{\mathrm{T}}$$

(24)

where ${\alpha }_k(0<{\alpha }_k\le 1)$ denotes an adaptive gene, which is set to

$${\alpha }_k=\{\begin{array}{ll}1\hfill & \mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}})\le \mathrm{tr}(P_{(ZZ)k/k-1})\hfill \\ \frac{\mathrm{tr}(P_{(ZZ)k/k-1})}{\mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}})}\hfill & \mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}})>\mathrm{tr}(P_{(ZZ)k/k-1})\hfill \end{array}$$

(25)

where $\mathrm{tr}(•)$ represents the trace of a matrix; ${\tilde{\mathit{Z}}}_{k/k-1}$ denotes the innovation residual vector, which satisfies

$${\tilde{\mathit{Z}}}_{k/k-1}={\mathit{Z}}_k-{\widehat{\mathit{Z}}}_{k/k-1}.$$

(26)

According to the concrete algorithm of L-AUKF and simulation results analyses, the L-AUKF algorithm can greatly improve the accuracy of filtering solutions for system given by Equation (4).

3.2. N-AUKF Algorithm

Motivated by L-AUKF, a new adaptive UKF algorithm, charged as N-AUKF, is designed for the system given by Equation (2) through setting adaptive matrix genes. To facilitate discussion, covariance matrices $P_{k/k-1}$, $P_{(XZ)k/k-1}$ and $P_{(ZZ)k/k-1}$ are rewritten as $P_{k/k-1}^e$, $P_{(XZ)k/k-1}^e$ and $P_{(ZZ)k/k-1}^e$, respectively, when the adaptive UKF is applied for the system given by Equations (2) and (4).

Theorem 1.

L-AUKF can only apply to the particular system given by Equation (4), but not to the general system given by Equation (2).

Proof. 

For the system given by Equation (4), the theoretical covariance matrix of ${\widehat{\mathit{X}}}_{k/k-1}$ should be amplified to [28,29]

$$P_{k/k-1}^g=\frac{1}{{\alpha }_k}{P}_{k/k-1}^e$$

(27)

where ${\alpha }_k$ denotes the adaptive gene, which is set to $0<{\alpha }_k\le 1$.

According to Equation (26), and rules of variance propagation for linear equations, the theoretical covariance matrix of ${\tilde{\mathit{Z}}}_{k/k-1}$ is obtained as

$$P_{(ZZ)k/k-1}^g={\mathit{A}}_k{P}_{k/k-1}^g{\mathit{A}}_k{}^{\mathrm{T}}+R^k.$$

(28)

After introducing the adaptive gene, the adaptive UKF algorithm must meet the following condition:

$$P_{(\tilde{Z}\tilde{Z})k/k-1}^e=P_{(ZZ)k/k-1}^g$$

(29)

where $P_{(\tilde{Z}\tilde{Z})k/k-1}^e$ denotes the covariance matrix of ${\tilde{\mathit{Z}}}_{k/k-1}$, and it is expressed as $P_{(\tilde{Z}\tilde{Z})k/k-1}^e={\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}}$.

For linear measurement equations, Equation (18) is rewritten as

$$P_{(ZZ)k/k-1}^e={\mathit{A}}_k{P}_{k/k-1}^e{\mathit{A}}_k{}^{\mathrm{T}}+R^k.$$

(30)

One can obtain the following from Equations (27)–(30):

$${\alpha }_k=\{\begin{array}{ll}1\hfill & \mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}})\le \mathrm{tr}(P_{(ZZ)k/k-1})\hfill \\ \frac{\mathrm{tr}(P_{(ZZ)k/k-1}^e-R_k)}{\mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}}-R_k)}\hfill & \mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}})>\mathrm{tr}(P_{(ZZ)k/k-1})\hfill \end{array}$$

(31)

where the relative small matrix $R^k$ in the numerator and denominator can be neglected, then the expression of ${\alpha }_k$ is approximated for Equation (25). Therefore, the adaptive UKF algorithm can meet the adaptive requirement of the system given by Equation (4), specifically, L-AUKF can apply to the system given by Equation (4), after the adaptive gene ${\alpha }_k$ is constructed as Equation (25) based on the standard UKF algorithm.

For the system given by Equation (2), the rules of error propagation for linear equations are invalid because the measurement equations are nonlinear, making the establishment false for Equations (28) and (30) of the derivation process. Therefore, Equation (31) can also not be deduced, which means that the adaptive gene ${\alpha }_k$ in Equation (25) cannot meet the adaptive requirement of a filter for the system given by Equation (2), specifically, L-AUKF cannot apply to the system given by Equation (2).

This completes the proof. ☐

Theorem 2.

To reach third order accuracy, the necessary and sufficient condition of the UKF algorithm designed for systems given by Equations (1) and (3) involving no model mismatches is

$${\mathit{P}}_{k/k-1}={\mathit{P}}_{(\tilde{X}\tilde{X})k/k-1}=\mathrm{E}[{\tilde{X}}_{k/k-1}{\tilde{X}}_{k/k-1}{}^{\mathrm{T}}]$$

(32)

$$P_{(XZ)k/k-1}=P_{(\tilde{X}\tilde{Z})k/k-1}=\mathrm{E}[{\tilde{X}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}}]$$

(33)

$$P_{(ZZ)k/k-1}=P_{(\tilde{Z}\tilde{Z})k/k-1}=\mathrm{E}[{\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}}]$$

(34)

where ${\tilde{X}}_{k/k-1}$ represents the prediction error vector, and ${\tilde{X}}_{k/k-1}={\mathit{X}}_k-{\widehat{\mathit{X}}}_{k/k-1}$.

Proof. 

Similar to ${\tilde{\mathit{Z}}}_{k/k-1}$ and ${\tilde{X}}_{k/k-1}$, the estimation error vector can be defined as

$${\tilde{X}}_k={\mathit{X}}_k-{\widehat{\mathit{X}}}_k.$$

(35)

For the system given by Equation (1), expanding ${\mathit{X}}_k$ via Taylor series, at stated points ${\widehat{\mathit{X}}}_{k-1}$ and ${\widehat{\mathit{X}}}_{k/k-1}$, respectively, for time step $k$, we have

$$\begin{array}{ll}{X}_k& =f[{\widehat{X}}_{k-1},k-1]+\frac{\partial f[{\mathit{X}}_{k-1},k-1]}{\partial {\mathit{X}}_{k-1}}{|}_{X_{k-1}={\widehat{X}}_{k-1}}(X_{k-1}-{\widehat{X}}_{k-1})+o^2(X_{k-1}-{\widehat{X}}_{k-1})+{\Gamma }_{k-1}{W}_{k-1}\\ & =f[{\widehat{X}}_{k-1},k-1]+{\Omega }_{k-1}{F}_{k-1}(X_{k-1}-{\widehat{X}}_{k-1})+{\Gamma }_{k-1}{W}_{k-1}\end{array}$$

(36)

$$\begin{array}{ll}{\mathit{Z}}_k& =\mathit{h}[{\widehat{\mathit{X}}}_{k/k-1},k]+\frac{\partial \mathit{h}[{\mathit{X}}_k,k]}{\partial {\mathit{X}}_k}{|}_{X_k={\widehat{\mathit{X}}}_{k/k-1}}(X_k-{\widehat{\mathit{X}}}_{k/k-1})+V_k\\ & =\mathit{h}[{\widehat{\mathit{X}}}_{k/k-1},k]+{\Xi }_k{H}_k(X_k-{\widehat{\mathit{X}}}_{k/k-1})+V_k\end{array}$$

(37)

where $F_{k-1}=\frac{\partial f[X_{k-1},k-1]}{\partial X_{k-1}}{|}_{{\mathit{X}}_{k-1}={\widehat{\mathit{X}}}_{k-1}}$, $H_k=\frac{\partial \mathit{h}[X_k,k]}{\partial X_k}{|}_{{\mathit{X}}_k={\widehat{\mathit{X}}}_{k/k-1}}$; ${\Omega }_{k-1}$ and ${\Xi }_k$ are introduced matrixes to decrease the first order approximation error.

Substitute, respectively, Equations (36) to (35), and Equations (37) to (26), the following Equations can be obtained:

$${\tilde{X}}_{k/k-1}={\Omega }_{k-1}{F}_{k-1}{\tilde{X}}_{k-1}+{\Gamma }_{k-1}{W}_{k-1}$$

(38)

$${\tilde{\mathit{Z}}}_{k/k-1}={\Xi }_k{H}_k{\tilde{\mathit{X}}}_{k/k-1}+V_k.$$

(39)

The result of substituting Equations (37) to (20) is

$$\begin{array}{ll}{\widehat{\mathit{X}}}_k& ={\widehat{\mathit{X}}}_{k/k-1}+K_k({\mathit{Z}}_k-{\widehat{Z}}_{k/k-1})\\ & ={\widehat{\mathit{X}}}_{k/k-1}+K_k{\Xi }_k{H}_k{\tilde{\mathit{X}}}_{k/k-1}+K_k{V}_k\end{array}.$$

(40)

Based on Equations (35) and (40), the predicted error in transmission equation is deduced by

$$\begin{array}{ll}{\tilde{X}}_k& =X_k-{\widehat{\mathit{X}}}_{k/k-1}-K_k{\Xi }_k{H}_k{\tilde{\mathit{X}}}_{k/k-1}-K_k{V}_k\\ & =(I-K_k{\Xi }_k{H}_k){\tilde{\mathit{X}}}_{k/k-1}-K_k{V}_k\end{array}.$$

(41)

It follows from Equations (38) and (41) that

$${\tilde{X}}_{k+1/k}={\Omega }_k{F}_k(I-K_k{\Xi }_k{H}_k){\tilde{\mathit{X}}}_{k/k-1}+{\Omega }_k{F}_k{K}_k{V}_k+{\Gamma }_k{W}_k.$$

(42)

Expanding Equation (42) to the general case, one can obtain

$$\begin{array}{ll}{\tilde{X}}_{k+i/k+i-1}=& {\displaystyle \prod _{j=1}^i[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1}){\tilde{\mathit{X}}}_{k/k-1}]}\\ & -{\displaystyle \sum _{l=1}^i{\displaystyle \prod _{j=1}^{i-l}[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]}}{\Omega }_{k+l-1}{F}_{k+l-1}{K}_{k+l-1}{V}_{k+l-1}\\ & +{\displaystyle \sum _{l=1}^i{\displaystyle \prod _{j=1}^{i-l}[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]W_{k+l-1}}}\end{array}.$$

(43)

For an innovation residual vector ${\tilde{\mathit{Z}}}_{k/k-1}$, define the covariance matrix $P_{(\tilde{Z}\tilde{Z})k/k-1}(i)$ as

$$\begin{array}{ll}{P}_{(\tilde{Z}\tilde{Z})k/k-1}(i)& =\mathrm{E}[{\tilde{Z}}_{k+i/k+i-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}}]\\ & =\mathrm{E}\left\{[{\Xi }_{k+i}{H}_{k+i}{\tilde{\mathit{X}}}_{k+i/k+i-1}+V_{k+i}]{[{\Xi }_k{H}_k{\tilde{\mathit{X}}}_{k/k-1}+V_k]}^{\mathrm{T}}\right\}\\ & ={\Xi }_{k+i}{H}_{k+i}{\displaystyle \prod _{j=1}^i[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]}\\ & •{\mathit{P}}_{k/k-1}{H}_{k+i}{}^{\mathrm{T}}{\Xi }_{k+i}{}^{\mathrm{T}}-{\Xi }_{k+i}{H}_{k+i}{\displaystyle \prod _{j=1}^{i-1}[{\Omega }_{k+j-1}{F}_{k+j-1}}\\ & •(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]{\Omega }_k{F}_k{K}_k{R}_k\\ & ={\Xi }_{k+i}{H}_{k+i}{\displaystyle \prod _{j=1}^i[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]}\\ & •{\Omega }_k{F}_k[{\mathit{P}}_{k/k-1}{H}_k{}^{\mathrm{T}}{\Xi }_k{}^{\mathrm{T}}-K_k({\Xi }_k{H}_k{P}_{k/k-1}{H}_k{}^{\mathrm{T}}{\Xi }_k{}^{\mathrm{T}}+R_k)\end{array}$$

(44)

where ${\mathit{P}}_{k/k-1}={\mathit{P}}_{(\tilde{X}\tilde{X})k/k-1}=\mathrm{E}[{\tilde{X}}_{k/k-1}{\tilde{X}}_{k/k-1}{}^{\mathrm{T}}]$.

Specifically, the covariance matrix of ${\tilde{\mathit{Z}}}_{k/k-1}$ will be

$$\begin{array}{ll}{P}_{(\tilde{Z}\tilde{Z})k/k-1}& =\mathrm{E}[{\tilde{Z}}_{k/k-1}{\tilde{Z}}_{k/k-1}{}^{\mathrm{T}}]\\ & ={\Xi }_k{H}_k{\mathit{P}}_{k/k-1}{H}_k{}^{\mathrm{T}}{\Xi }_k{}^{\mathrm{T}}+R_k\end{array}.$$

(45)

For ${\tilde{X}}_{k/k-1}$ and ${\tilde{\mathit{Z}}}_{k/k-1}$, the cross-covariance matrix is

$$\begin{array}{ll}{P}_{(\tilde{X}\tilde{Z})k/k-1}& =\mathrm{E}[{\tilde{X}}_{k/k-1}{\tilde{Z}}_{k/k-1}{}^{\mathrm{T}}]\\ & =\mathrm{E}[{\tilde{X}}_{k/k-1}{({\Xi }_k{H}_k{\tilde{\mathit{X}}}_{k/k-1}+V_k)}^{\mathrm{T}}]\\ & ={\mathit{P}}_{k/k-1}{H}_k{}^{\mathrm{T}}{\Xi }_k{}^{\mathrm{T}}\end{array}.$$

(46)

According to Equations (19) and (44) can be expressed as

$$\begin{array}{ll}{P}_{(\tilde{Z}\tilde{Z})k/k-1}(i)& ={\Xi }_{k+i}{H}_{k+i}{\displaystyle \prod _{j=1}^i[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]}\\ & •{\Omega }_k{F}_k[P_{(\tilde{X}\tilde{Z})k/k-1}-K_k{P}_{(\tilde{Z}\tilde{Z})k/k-1}]\\ & ={\Xi }_{k+i}{H}_{k+i}{\displaystyle \prod _{j=1}^i[{\Omega }_{k+j-1}{F}_{k+j-1}(I-K_{k+j-1}{\Xi }_{k+j-1}{H}_{k+j-1})]}\\ & •{\Omega }_k{F}_k{P}_{(\tilde{X}\tilde{Z})k/k-1}[I-P_{(ZZ)k/k-1}{}^{-1}{P}_{(\tilde{Z}\tilde{Z})k/k-1}]\end{array}.$$

(47)

According to the precision and optimization requirements of the standard UKF algorithm, if $P_{(\tilde{Z}\tilde{Z})k/k-1}(i)=0$, the result is

$$P_{(ZZ)k/k-1}=P_{(\tilde{Z}\tilde{Z})k/k-1}.$$

(48)

Equation (48) validates the establishment of Equation (34), similarly, Equations (32) and (33) can be validated.

This completes the proof. ☐

Remark 1.

Formulas given by Equations (32)–(34) always hold for systems given by Equations (1) and (3), because the third order accuracy conditions of the UKF algorithm are independent of ${\Omega }_{k+i}$ and ${\Xi }_{k+i}$. However, practical calculated values $P_{k/k-1}^e,P_{(XZ)k/k-1}^e,P_{(ZZ)k/k-1}^e$ $P_{k/k-1}^e,P_{(XZ)k/k-1}^e,P_{(ZZ)k/k-1}^e$ deviate from theoretical values $P_{k/k-1},P_{(XZ)k/k-1},P_{(ZZ)k/k-1}$ for systems given by Equations (2) and (4), which makes Equations (32)–(34) false, and it implies that the standard UKF algorithm cannot apply to systems given by Equations (2) and (4).

For common sensors, measurement components are supposed to be relatively independent, so a diagonal matrix gene can be introduced creating the following theorem:

Theorem 3.

Design a N-AUKF algorithm by constructing the adaptive diagonal matrix gene ${\Delta }_k=diag({\epsilon }_{1k}{\epsilon }_{2k}\cdots {\epsilon }_{mk})$, and let

$$P_{(ZZ)k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]}^{\mathrm{T}}+{\Delta }_k{R}_k$$

(49)

where ${\Delta }_k$ meets

$${\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]}^{\mathrm{T}}+{\Delta }_k{R}_k=P_{(\tilde{Z}\tilde{Z})k/k-1}.$$

(50)

Thus, the N-AUKF algorithm can apply to systems given by Equations (2) and (4).

Proof. 

For systems given by Equations (2) and (4), because the stated equation includes uncertainties and disturbances, according to Theorem 2, the result is

$$P_{k/k-1}^e={\mathit{P}}_{k/k-1}={\mathit{P}}_{(\tilde{X}\tilde{X})k/k-1}$$

(51)

$$P_{(XZ)k/k-1}^e=P_{(XZ)k/k-1}=P_{(\tilde{X}\tilde{Z})k/k-1}.$$

(52)

After constructing the adaptive diagonal matrix gene ${\Delta }_k$ given by Equation (49), one can obtain

$$P_{(ZZ)k/k-1}^e=P_{(ZZ)k/k-1}=P_{(\tilde{Z}\tilde{Z})k/k-1}.$$

(53)

Equations (49)–(53), show that the N-AUKF algorithm meets the necessary and sufficient condition with third order accuracy of the standard UKF algorithm according to Theorem 2. When sensor faults and uncertainties of measurement equations exist, the N-AUKF algorithm adjusts the covariance matrixes of the stated vector and innovation vector in real time, which improves the filter accuracy remarkably. Therefore, the N-AUKF algorithm can apply to systems given by Equations (2) and (4).

This completes the proof. ☐

From Equation (50), the following can be obtained:

$${\Delta }_k=\left\{P_{(\tilde{Z}\tilde{Z})k/k-1}-{\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]}^{\mathrm{T}}\right\}{R}_k{}^{-1}$$

(54)

where the practical calculated formula of $P_{(\tilde{Z}\tilde{Z})k/k-1}$ is

$$P_{(\tilde{Z}\tilde{Z})k/k-1}^p=\frac{1}{k-1}{\displaystyle \sum _{i=1}^k{\tilde{\mathit{Z}}}_{i/i-1}{\tilde{\mathit{Z}}}_{i/i-1}{}^{\mathrm{T}}}.$$

(55)

In the practical engineering application, if there are no sensor faults and no model mismatches for nonlinear systems, the value of ${\Delta }_k$ is

$${\Delta }_k=diag(\underset{m}{\underbrace{11\cdots 1}}).$$

(56)

In the presence of the situation shown by Equation (56), the N-AUKF algorithm is the same to the standard UKF algorithm. In N-AUKF, whether or not there are sensor faults depends on the innovation residual vector values and preset threshold values, which are set based on the types, characteristics, and measurement components of sensors. At every sample moment, if any one component of the innovation residual vector values is greater than the corresponding threshold value, the sensor fault is judged to exist; otherwise, the sensor is in normal working condition.

In summary, the value of ${\Delta }_k$ depends on the following steps:

Step 1: Set the threshold matrix $\Theta =[z_{0,1}{z}_{0,2}\cdots z_{0,m}]$ based on the characteristics of sensors;

Step 2: Let ${\tilde{\mathit{Z}}}_{k/k-1}=[z_{1k}{z}_{2k}\cdots z_{mk}]$, and use the mathematical method to judge the OR operations:

$$z_{1k}>z_{0,1}\left|\right|z_{2k}>z_{0,2}\left|\right|\cdots \left|\right|z_{mk}>z_{0,m}.$$

Step 3: If the judgment in step 2 is true, the sensor fault exists, thus one can obtain

$${\Delta }_k=\left\{P_{(\tilde{Z}\tilde{Z})k/k-1}-{\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{Z}}_{k/k-1}]}^{\mathrm{T}}\right\}{R}_k{}^{-1}$$

and if the judgment is false, the sensor fault does not exist, one can obtain

$${\Delta }_k=diag(\underset{m}{\underbrace{11\cdots 1}}).$$

3.3. Filtering Divergence Suppression of the N-AUKF Algorithm

Compared with the standard UKF, adaptive UKF algorithms are always easier to produce the filtering divergence, so it is necessary to restrain the filtering divergence for N-AUKF.

First of all, use the covariance matching criterion to judge

$$\mathrm{tr}({\tilde{\mathit{Z}}}_{k/k-1}{\tilde{\mathit{Z}}}_{k/k-1}{}^{\mathrm{T}})\le \Psi \cdot \mathrm{tr}(P_{(ZZ)k/k-1})$$

(57)

where $\Psi$ ($\Psi \ge 1$) is a preset adjustable coefficient. If Equation (57) holds, the filtering is convergent, and N-AUKF algorithm designed in Section 3.2 is used. If Equation (57) is not workable, the filtering divergence exists and an adaptive weighted coefficient ${\zeta }_k$ is introduced to N-AUKF. ${\zeta }_k$ can update ${\mathit{P}}_{k/k-1}$ in real time, which increases the contribution of the current measurement ${\mathit{Z}}_k$ on the filtering solution and restrains the filtering divergence.

${\mathit{P}}_{k/k-1}$, shown by Equation (13), changes to

$${\overline{P}}_{k/k-1}={\zeta }_k{\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\chi }_{k/k-1}^{(i)}-{\widehat{\mathit{X}}}_{k/k-1}]{[{\chi }_{k/k-1}^{(i)}-{\widehat{X}}_{k/k-1}]}^{\mathrm{T}}+Q_{k-1}$$

(58)

where ${\zeta }_k$ is determined by

$${\zeta }_k=\{\begin{array}{l}{\zeta }_0{\zeta }_0\ge 1\\ 1{\zeta }_0<1\end{array}$$

(59)

$${\zeta }_0=\frac{\mathrm{tr}(P_{(\tilde{Z}\tilde{Z})k/k-1}-R_k)}{\mathrm{tr}({\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\chi }_{k/k-1}^{(i)}-{\widehat{X}}_{k/k-1}]{[{\chi }_{k/k-1}^{(i)}-{\widehat{\mathit{X}}}_{k/k-1}]}^{\mathrm{T}})}.$$

(60)

3.4. Implementation Steps of N-AUKF Algorithm

Aimed at target tracking problems, the N-AUKF algorithm can realize the filtering function in the presence of sensor faults and systems involving model mismatches. The implementation steps of the N-AUKF algorithm are as follows:

Step 1: Original value selection and prediction updating.

Select the initial values ${\widehat{\mathit{X}}}_0$ and $P_0$, and calculate the covariance matrixes $P_{k/k-1},P_{(XZ)k/k-1},P_{(ZZ)k/k-1}$ based on the standard UKF, respectively.

Step 2: Adaptive matrix gene calculation and prediction error covariance matrixes correction.

Define the value of ${\Delta }_k$ according to Equations (54)–(56), and correct the value of $P_{(ZZ)k/k-1}$ based on Equation (49) by

$${\overline{P}}_{(ZZ)k/k-1}={\displaystyle \sum _{i=0}^{2n}{W}_i^{(c)}}[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]{[{\gamma }_{k/k-1}^{(i)}-{\widehat{\mathit{Z}}}_{k/k-1}]}^{\mathrm{T}}+{\Delta }_k{R}_k.$$

(61)

Step 3: Filtering divergence judgment and suppression.

Judge whether there is filtering divergence through Equation (57); if the divergence exists, update ${\mathit{P}}_{k/k-1}$ to ${\overline{\mathit{P}}}_{k/k-1}$ according to Equations (58)–(60); if the convergence exists, go straight to the next step.

Step 4: Measurement updating.

$$K_k=P_{(XZ)k/k-1}{({\overline{P}}_{(ZZ)k/k-1})}^{-1}$$

(62)

$${\widehat{\mathit{X}}}_k={\widehat{\mathit{X}}}_{k/k-1}+K_k({\mathit{Z}}_k-{\widehat{\mathit{Z}}}_{k/k-1})$$

(63)

$$P_k={\overline{P}}_{k/k-1}-K_k{\overline{P}}_{(ZZ)k/k-1}{K}_k{}^{\mathrm{T}}.$$

(64)

4. Experimental Results and Discussion

In order to validate the filtering performance of the proposed N-AUKF algorithm for target tracking applications, contrast simulations of the standard UKF [18], L-AUKF [25,27] and N-AUKF algorithms, respectively, are conducted in two simulation cases. In this study, all experiments are performed using MATLAB R2013a on an Intel i7 quad-core 2.40-GHz 64-bit machine with 8 GB RAM.

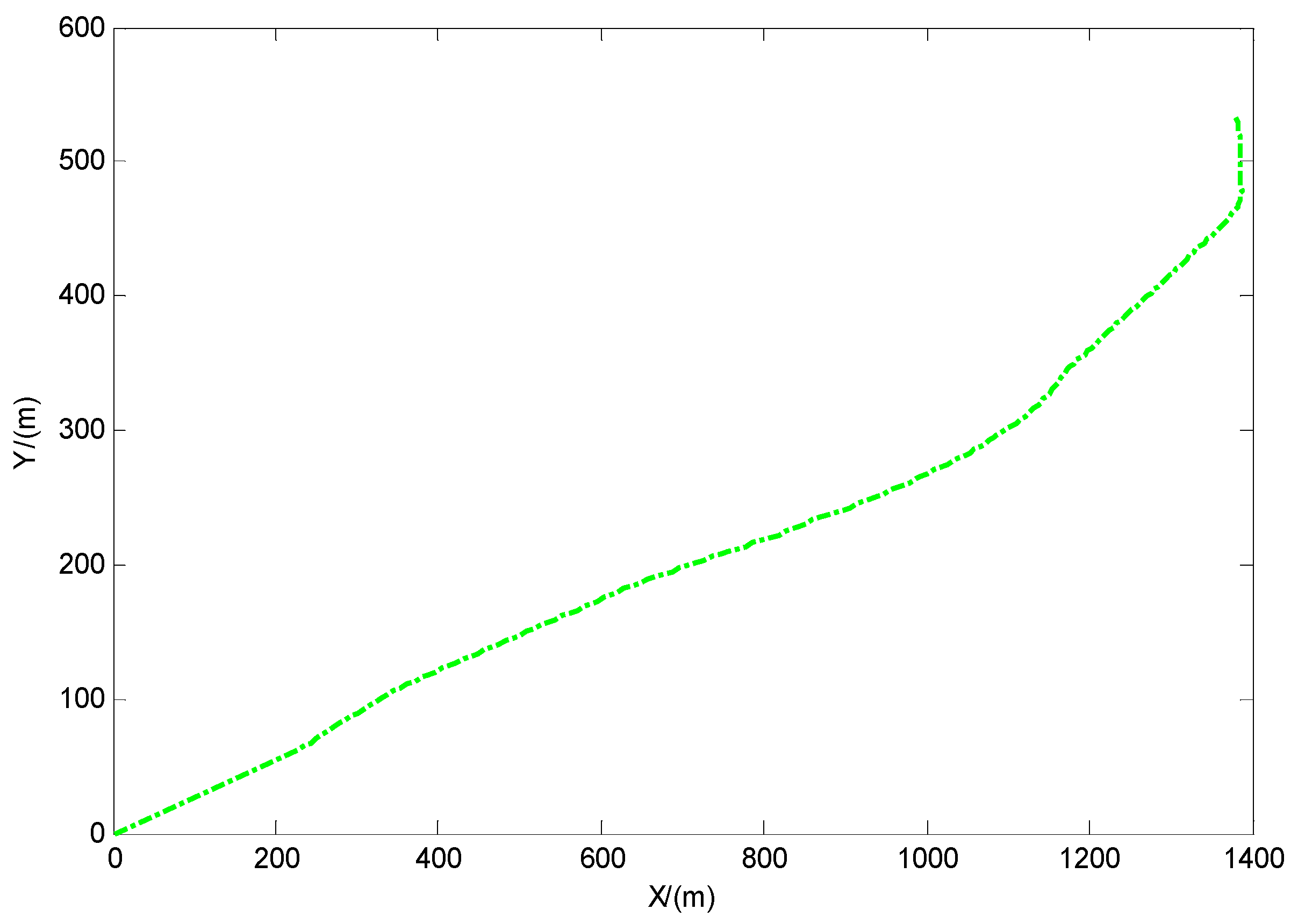
4.1. Simulation Cases

Suppose that the radar observation station is located in origin coordinates. The target makes an approximate uniform linear motion, then a turn movement in a two-dimensional plane.

Simulation Case 1: The radar is in normal working condition, which implies that there are no model mismatches, and the nonlinear system of the target can be depicted as

$$\{\begin{array}{l}{\mathit{X}}_k=\mathit{f}[{\mathit{X}}_{k-1},k-1]+W_{k-1}\\ {\mathit{Z}}_k=\left[\begin{array}{l}{r}_k\\ {\theta }_k\end{array}\right]=\left[\begin{array}{l}\sqrt{(x_k{}^2+y_k{}^2)}\\ {\tan }^{-1}(y_k/x_k)\end{array}\right]+V_k\end{array}.$$

(65)

Simulation Case 2: The radar fault exists, which implies that there are model mismatches, and the nonlinear system of the target can be depicted as

$$\{\begin{array}{l}{\mathit{X}}_k=\mathit{f}[{\mathit{X}}_{k-1},k-1]+W_{k-1}\\ {\mathit{Z}}_k=\left[\begin{array}{l}{r}_k\\ {\theta }_k\end{array}\right]=\left[\begin{array}{l}\sqrt{(x_k{}^2+y_k{}^2)}\\ {\tan }^{-1}(y_k/x_k)\end{array}\right]+V_k+\delta {\mathit{h}}_{out,k}\end{array}.$$

(66)

For Equations (65) and (66), the stated equation is as follows.

$${\mathit{X}}_k=\left[\begin{array}{cccc}1& 0& T& 0\\ 0& 1& 0& T\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]{\mathit{X}}_{k-1}+{\mathit{W}}_{k-1}.$$

In the above two cases, $\mathit{X}=[x,y,\dot{x},\dot{y}]$ is the stated vector, where $x$ and $y$ represent, respectively, components along the x-axis and y-axis of the position coordinates of the target; $\dot{x}$ and $\dot{y}$ represent, respectively, components along the x-axis and y-axis of the velocity of the target. ${\mathit{Z}}_k={\left[r_k{\theta }_k\right]}^{\mathrm{T}}$ denotes the measurement vector, where $r_k$ represents the slope distance between the radar and target, and ${\theta }_k$ represents the azimuth angle of the target relative to the radar. $W_{k-1}$ and $V_k$ are limited to be independent Gaussian noises with zero mean value. $\delta {\mathit{h}}_{out,k}={[\delta r_k\delta {\theta }_k]}^{\mathrm{T}}$ stands for the radar fault, where $\delta r_k$ is the measurement deviation and $\delta {\theta }_k$ is the drift rate. In the simulation process, $\delta r_k$ and $\delta {\theta }_k$ are both random variations with an interval value of $[-5\mathrm{m}5\mathrm{m}]$ and $[01.0\times {10}^{-2}\mathrm{rad}/\mathrm{s}]$ respectively. The initial value of the target is ${\mathit{X}}_0=[0\mathrm{m},0\mathrm{m},21\mathrm{m}/\mathrm{s},21\mathrm{m}/\mathrm{s}]$, and the variance matrix of the system noise is

$$Q={\sigma }_a^2\left[\begin{array}{cccc}\frac{T^4}{4}& 0& \frac{T^3}{2}& 0\\ 0& \frac{T^4}{4}& 0& \frac{T^3}{2}\\ \frac{T^3}{2}& 0& T^2& 0\\ 0& \frac{T^3}{2}& 0& T^2\end{array}\right]$$

(67)

where ${\sigma }_a=1$. The variance matrix of the system noise is $R=diag({\sigma }_w^2,{\sigma }_w^2)=diag(15,15)$. The observation time is $100\mathrm{s}$, and the sampling period is $1\mathrm{s}$.

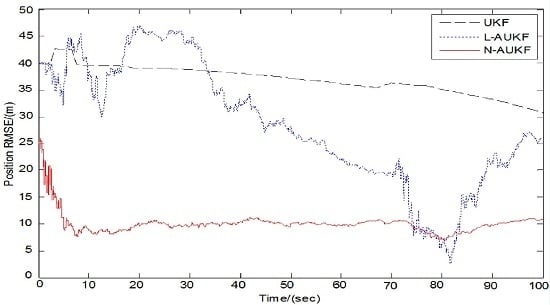
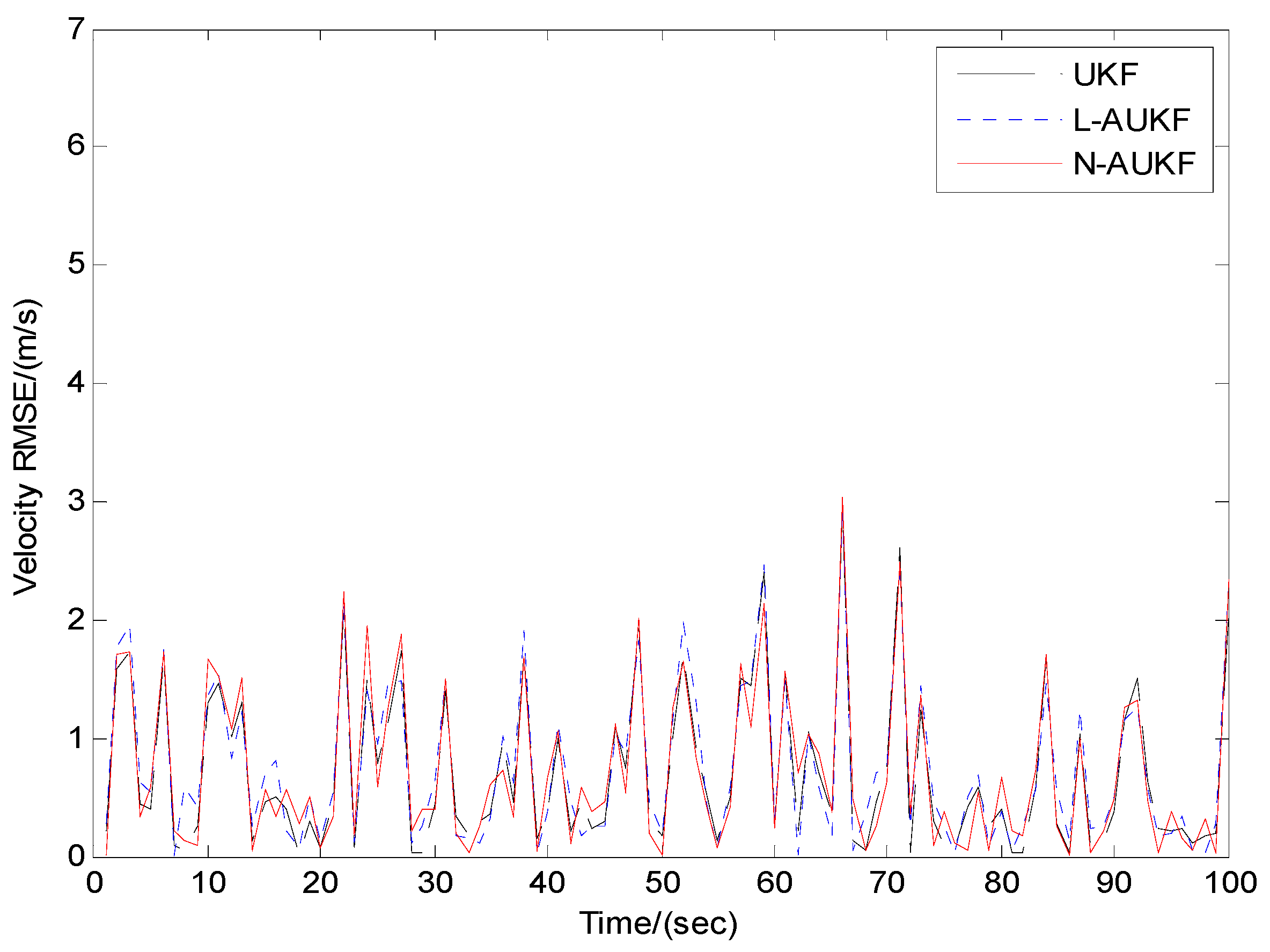
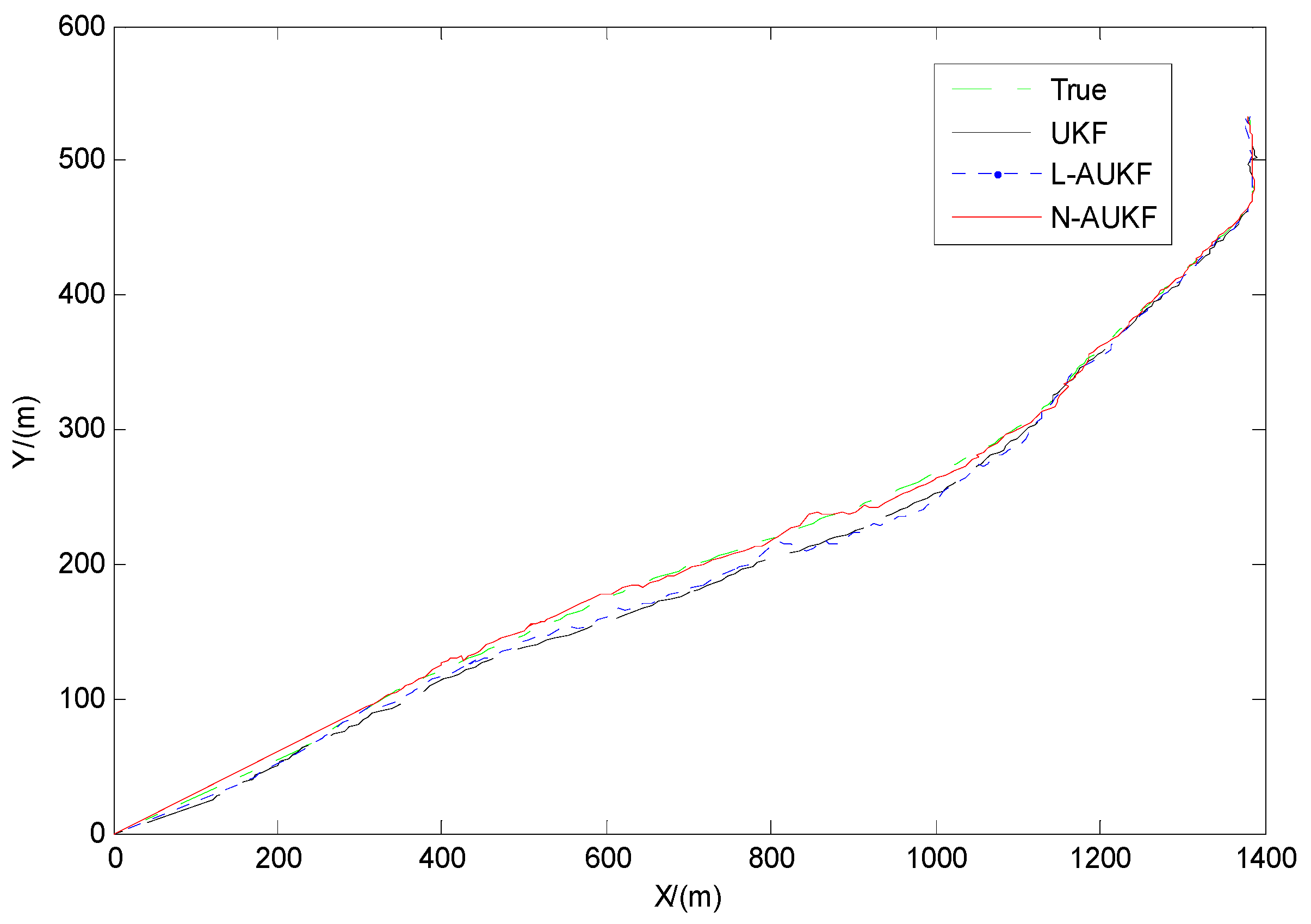
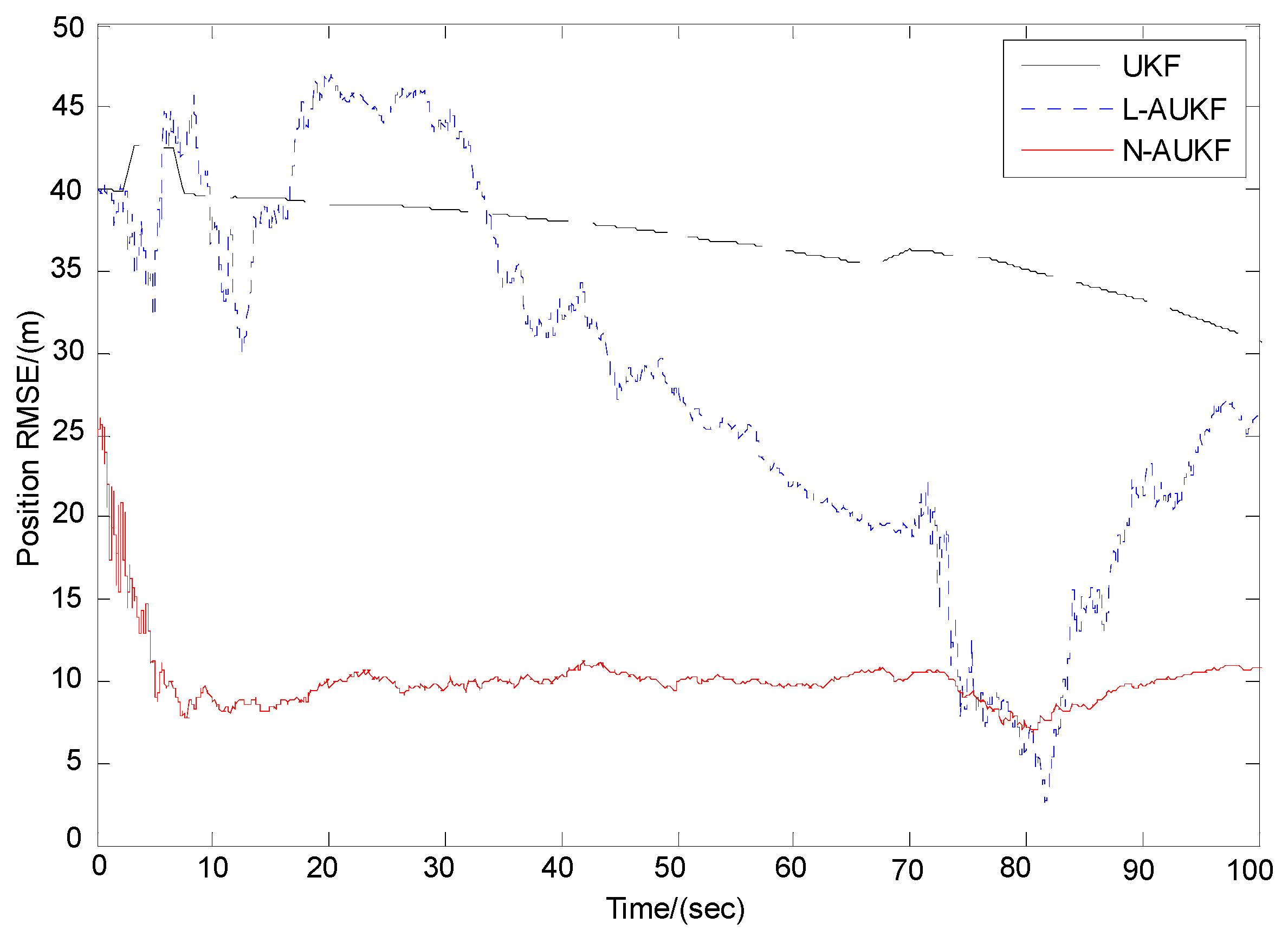
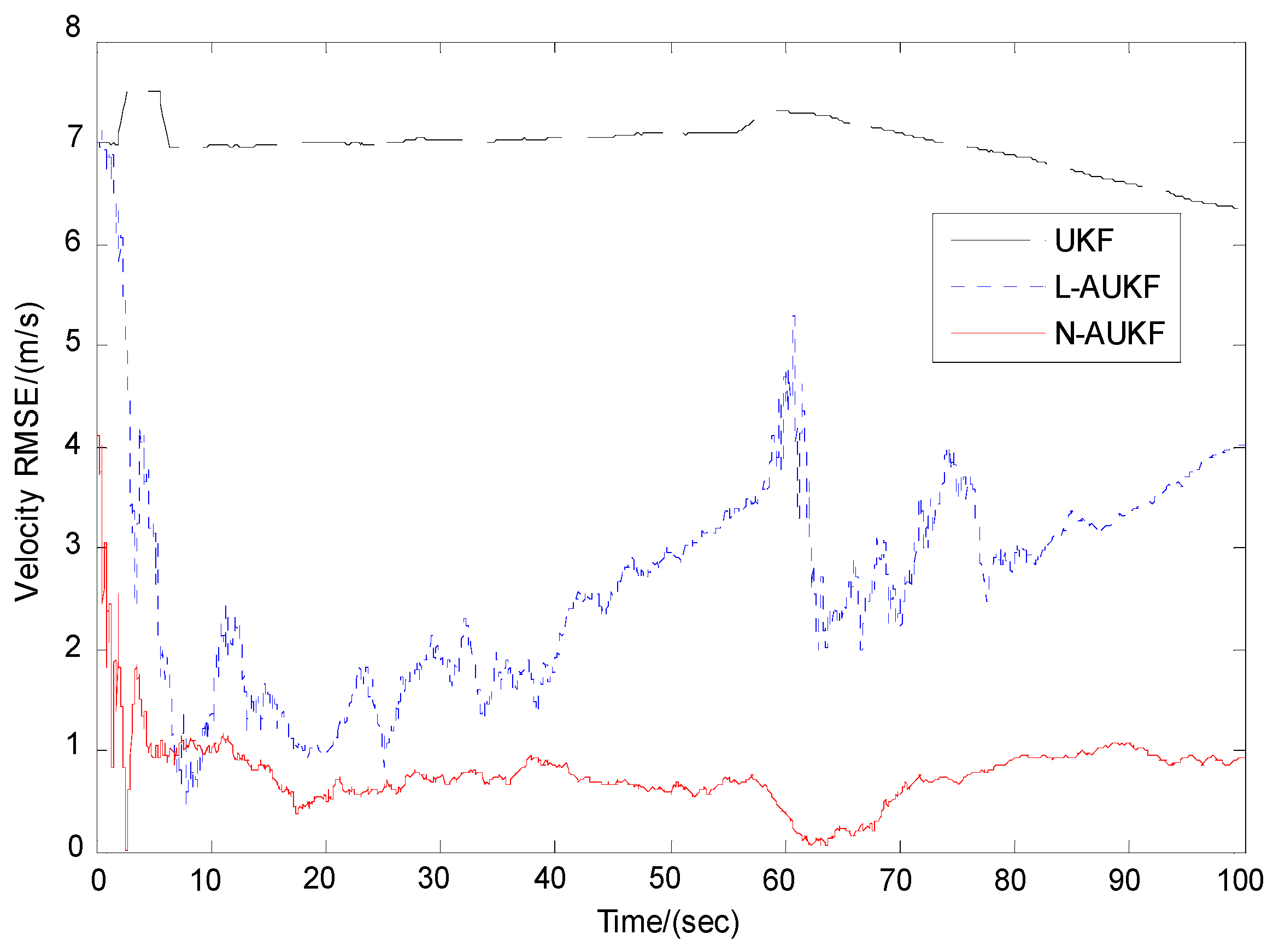
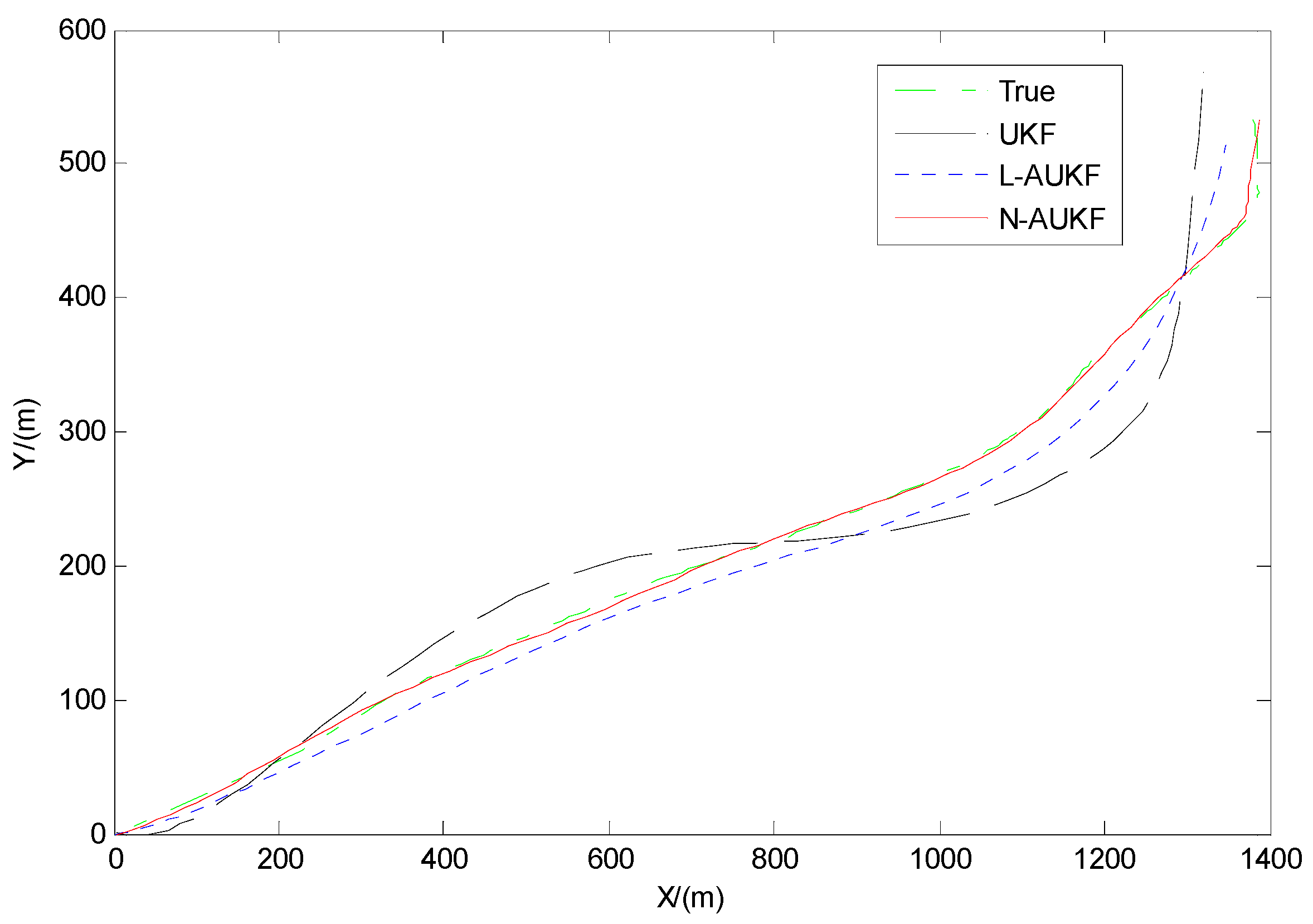
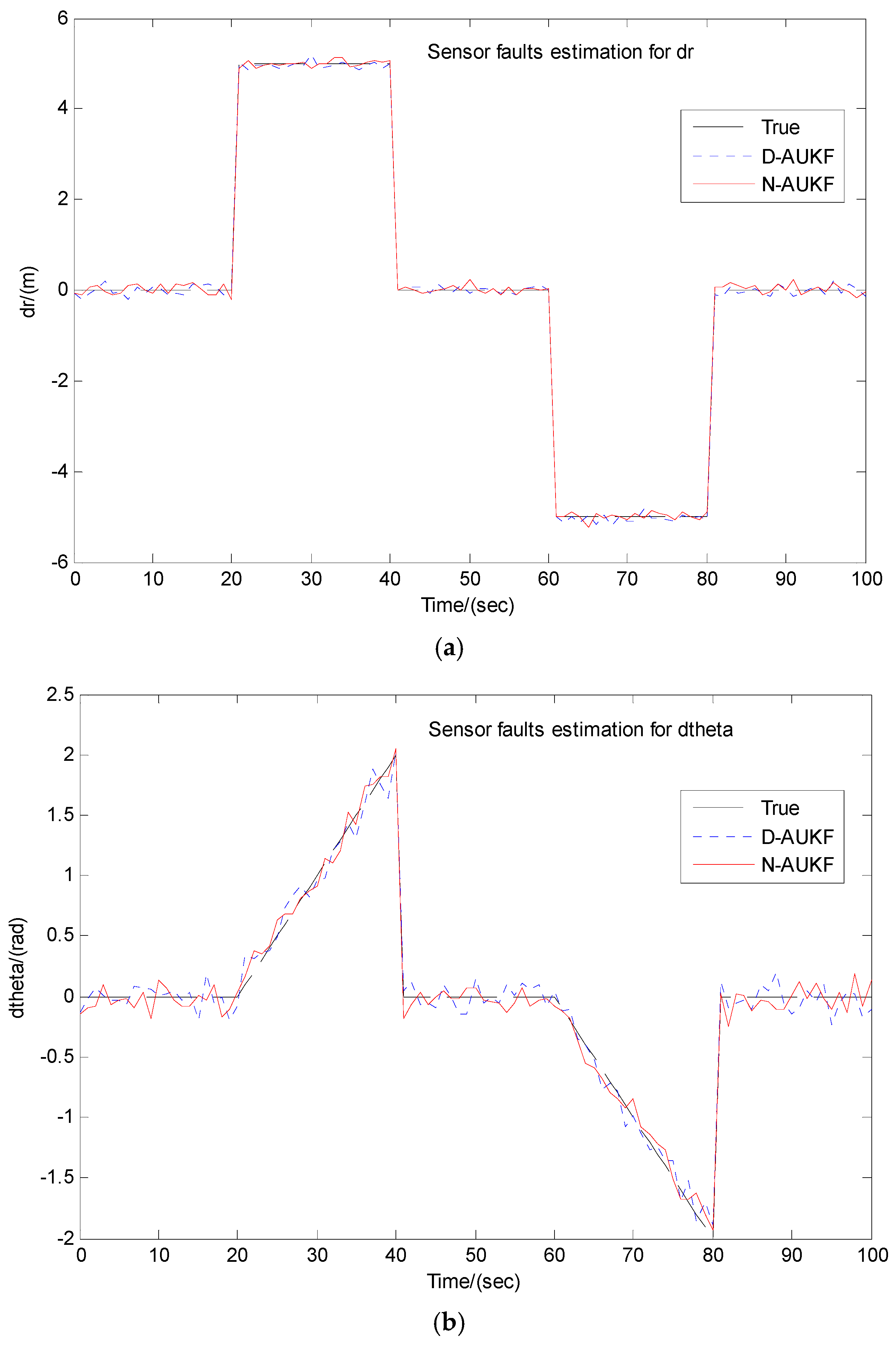
4.2. Simulation Results

The simulation is repeated 100 times using the Monte Carlo method in two cases, and the standard UKF, L-AUKF and N-AUKF algorithms through the root mean square error (RMSE) is assessed. RMSE is calculated by

$$E=\sqrt{\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N({\widehat{X}}^i-X^i){({\widehat{\mathit{X}}}^i-{\mathit{X}}^i)}^{\mathrm{T}}}\right)}$$

(68)

where $N$ is the simulation times, and $N=100$; ${\widehat{\mathit{X}}}^i$ and ${\mathit{X}}^i$ represent, respectively, the estimation and real value of the target state vector in the ith simulation. In an independent simulation experiment, the true motion path of the target is depicted in Figure 1.

For Case 1, the comparisons of RMSE curves of three filtering algorithms are depicted in Figure 2 and Figure 3, the true and estimated trajectories of the target are depicted in Figure 4, and the statistical data of RMSE are shown in

Table 1. Performance comparison of algorithms for Case 1.

Algorithm	Position Error (m)		Velocity Error (m/s)
	Mean	Variance	Mean	Variance
UKF	4.6438	2.9790	0.8750	0.7054
L-AUKF	4.2685	2.5421	0.8326	0.7247
N-AUKF	4.0533	2.2850	0.8821	0.6596

.

As shown in Figure 2, Figure 3 and Figure 4 and Table 1, the filtering precision and stability of the standard UKF, L-AUKF and N-AUKF are basically the same in Case 1, which demonstrates that the three algorithms are almost the same in respect to filtering effects when there are no sensor faults and no model mismatches for nonlinear systems.

For Case 2, the comparisons of RMSE curves of three filtering algorithms are depicted in Figure 5 and Figure 6, the true and estimated trajectories of the target are depicted in Figure 7, and the statistical data of RMSE are shown in

Table 2. Performance comparison of algorithms for Case 2.

Algorithm	Position Error (m)		Velocity Error (m/s)
	Mean	Variance	Mean	Variance
UKF	37.6647	6.2481	6.9442	5.2972
L-AUKF	26.5571	5.3244	2.7469	5.3367
N-AUKF	8.4256	1.0057	0.9015	0.7523

.

It can be seen that the filtering error of the standard UKF is too large, although the filtering convergence is good. L-AUKF increases the filtering precision to some extent, compared with the standard UKF, but it makes little contribution to filtering precision, furthermore, the convergence is poor since even L-AUKF will diverge as time goes on. For the N-AUKF algorithm, the filtering precision has been greatly improved, compared with the other two algorithms, moreover, the filtering convergence has been maintained.

Going a step further, the real-time performance of the standard UKF, L-AUKF and N-AUKF is studied for Case 2, and the computational cost curves are depicted in Figure 8.

Although the computational cost of N-AUKF is a little more than the standard UKF and L-AUKF, there are no big differences among them. The mean time of the standard UKF at every step is 6 ms, L-AUKF is 7 ms, and N-AUKF is 8.5 ms, which can ensure that the three algorithms all have good real-time results and are effective for engineering applications.

As is mentioned in Section 3.2, whether there are sensor faults or not can be judged. For Dual State-Parameter estimation approaches [27,30,31], charged as D-AUKF, sensor biases can also be estimated within the filter as an additional state. Therefore, contrast simulations of the D-AUKF [31] and N-AUKF are conducted for Case 2. For simplicity, only the sensor biases estimations and statistical data of RMSE are given. The radar faults estimation results are depicted in Figure 9 and the statistical data of RMSE for state estimation is shown in

Table 3. Performance comparison of D-AUKF and N-AUKF for Case 2.

Algorithm	Position Error (m)		Velocity Error (m/s)
	Mean	Variance	Mean	Variance
D-AUKF	18.2655	3.8917	2.1542	4.2263
N-AUKF	7.9632	0.9117	0.7854	0.6544

.

Figure 9 shows that both D-AUKF and N-AUKF have the ability to estimate the sensor faults as an additional state, and there are no big differences in sensor fault estimated performance for them. Stated estimation shown in Table 3, the D-AUKF is still significantly disturbed by the uncertainties of sensor faults, resulting in a decrease in filtering precision compared with N-AUKF. Thus, N-AUKF has better filtering performance than D-AUKF in respect to stated estimation.

4.3. Discussion

The nonlinear filtering problems for target tracking have been researched, and a new adaptive UKF algorithm has been proposed to deal with model mismatches involved in nonlinear systems caused by sensor faults. It can be seen from Figure 2, Figure 3 and Figure 4 and Table 1 that, the standard UKF, L-AUKF and N-AUKF algorithms have almost the same filtering performance, such as good filtering accuracy, when there are no sensor faults and no model mismatches for nonlinear systems. The reasons are that, the three methods are all UKF algorithms in essence, and they are all third-order accurate in Taylor series.

Sensor faults and model mismatches have a great influence on the filtering effect. As was shown in the experiment results in Figure 5, Figure 6 and Figure 7 and Table 2, when model mismatches exist, the standard UKF had poor filtering precision, which could lead to target misdetection. Although the standard UKF also could solve uncertainties, for example, noises, it could no longer meet the third order accuracy conditions when model mismatches were involved in nonlinear systems. Compared with the standard UKF, L-AUKF increased the filtering precision by constructing an adaptive gene, but it made little contribution to filtering precision due to the nonlinear characteristics of the measurement equation. On the other hand, because L-AUKF had no suppression strategies, there was a trend of divergence for L-AUKF.

Using N-AUKF, the filtering precision was greatly improved due to the introduction of the adaptive matrix gene compared with the other two algorithms, which was proven by the third order accuracy conditions. The filtering convergence was well maintained by using the covariance matching method and introducing an adaptive weighted coefficient. Therefore, although N-AUKF was proposed as a method for systems involving model mismatches caused by sensor faults, in most cases, it also performed well in nonlinear filtering problems, such as unknown statistics of noises. Furthermore, N-AUKF had a more complicated algorithm structure, but the computational cost had no difference from the standard UKF and L-AUKF, which was shown in Figure 8. Thus, N-AUKF also had a good real-time performance and can be effectively used for engineering applications. Meanwhile, the N-AUKF not only could estimate the state of the system, but also the sensor faults, which was shown in Figure 9 and Table 3.

In summary, the proposed N-AUKF algorithm greatly improves the filtering precision, rapidity and stability in the presence of sensor faults and systems involving model mismatches, compared with the standard UKF and existing adaptive UKF algorithms. Future research topics applying N-AUKF to other navigation systems with infrared sensors or laser sensors, and integrated navigation systems, can significantly broaden the application fields of N-AUKF.

5. Conclusions

In a target tracking process, the filtering precision will decrease and filtering divergence may appear for the standard and existing adaptive UKF, if there are sensor faults and systems involving model mismatches. For that reason, a new adaptive UKF algorithm named N-AUKF is proposed. In the N-AUKF, the covariance matrixes of the state vector and innovation vector can be adjusted in real time by introducing an adaptive matrix gene and the optimality with third order accuracy is guaranteed and proven theoretically. The filtering divergence is judged by using a covariance matching method, then, the filtering divergence is effectively restrained by introducing an adaptive weighted coefficient making the filtering precision, rapidity and stability of the filter greatly improved. Simulation results show that the proposed adaptive UKF algorithm has the advantage of high filtering performance, compared with the standard UKF and existing adaptive UKF algorithms. The research results will benefit practical missions of target tracking in the future. For future study, it is proposed to set up a simple, but surprisingly effective, framework for the detection, recognition and tracking of remote sensing images and moving targets based on the proposed UKF algorithm.