Contribution-Based Grouping under Noise

Abstract

Many real-world mechanisms are “noisy” or “fuzzy”, that is the institutions in place to implement them operate with non-negligible degrees of imprecision and error. This observation raises the more general question of whether mechanisms that work in theory are also robust to more realistic assumptions such as noise. In this paper, in the context of voluntary contribution games, we focus on a mechanism known as “contribution-based competitive grouping”. First, we analyze how the mechanism works under noise and what happens when other assumptions such as population homogeneity are relaxed. Second, we investigate the welfare properties of the mechanism, interpreting noise as a policy instrument, and we use logit dynamic simulations to formulate mechanism design recommendations.

1. Motivation

Typically, individual decisions in social-dilemma interactions are not perfectly observable in the real world. Applied mechanism designers should keep this in mind when implementing mechanisms, in particular in the context of interactions that have the strategic nature of voluntary contribution games where imperfect observability is ubiquitous.1 Real-world institutions are usually “noisy” or “fuzzy”, operating with non-negligible degree of imprecision. By contrast, theory investigations of mechanisms for the most part study perfect mechanisms. In this paper, as a first step towards performing robustness checks of mechanisms under relaxed assumptions more generally, we investigate the mechanism of contribution-based competitive grouping (as introduced by [5]): we relax some assumptions and investigate what happens when there is (i) noise, (ii) heterogeneity and (iii) different action spaces.

The paper is structured as follows. Next, we introduce our model. In Section 3, we first analyze how the existence of Nash equilibria depends on (iii) the strategy space of the game and on (ii) the underlying population homogeneity/heterogeneity in terms of contribution budgets. Then, we assess their robustness when we allow more and more (i) monitoring noise. In Section 4, we investigate how a social planner, interpreting monitoring noise and/or the other model characteristics as policy instruments, would trade-off efficiency and equality to maximize social welfare. Finally, we use agent-based simulations to study the logit dynamics of the game in order to quantify the effect of noisy monitoring.

Our results are summarized as follows. In terms of the existence of Nash equilibria, the zero-contribution outcome is always a Nash equilibrium and becomes the unique one under too much noise. High-contribution equilibria exist if three things come together: the rate of return of the underlying contribution game is high enough, grouping is sufficiently precise, and agent homogeneity is established (either in terms of budgets or via the strategy space). In terms of welfare, implementations with an intermediate level of noise/fuzziness, enabling high efficiency gains at low inequality costs, maximize welfare in most cases. The exception is the case of heterogeneous budgets and binary (all-or-nothing) contribution decisions, where less noise is unambiguously preferable. Finally, our logit-dynamics simulations indicate that high-contribution equilibria, when existent, tend to be more robust than the zero-contribution equilibrium, and we are able to identify an optimal level of mechanism noise/fuzziness as a function of the behavioral noise that is inherent under the logit-choice rule.

2. The Mechanism

2.1. The Model

Population $N=\{1,2,\dots ,n\}$ plays the following three-step game under common knowledge.

Step 1. Voluntary contributions:

Action Space 1. Binary: Each $i\in N$ simultaneously decides whether to set $c_i^{\prime }=0$ (i.e., to free-ride) or to set $c_i^{\prime }=1$ (i.e., to contribute).

Action Space 2. Continuous: Each $i\in N$ simultaneously decides on a proportional contribution $c_i^{\prime }\in [0,1]$ between free-ride ($c_i^{\prime }=0$) and contribute ($c_i^{\prime }=1$).

Each $i\in N$ has a budget of $B_i\in {\mathcal{R}}^{+}$, and his/her above action results in an effective contribution of $c_i=c_i^{\prime }·B_i$. The effective contributions yield a population contribution vector $\mathbf{c}={\left\{c_i\right\}}_{i\in N}$. Denote by ${\mathbf{c}}_{-i}$ the vector excluding i.

Budget 1. Homogeneity: $B_i=1$ for all i.

Budget 2. Heterogeneity: $B_i\ne B_j\forall i\ne j$ with (w.l.o.g.) $B_i<B_{i-1}$. We place a very mild constraint on how different endowments can be by imposing that $\exists X\in \Re s.t. B_i>B_{i-1}+X\forall i$ and any $X>0$.

Step 2. Fuzzy grouping based on a ‘noisy’ ranking of contributions:

Step 2.1. From ‘noisy’ rankings...: Instead of $c_i$, the authority observes $x_i=c_i+e_i$, where $e_i$ is some i.i.d. white noise with mean zero and variance ${\sigma }^2=\frac{1-\beta }{\beta }$ where $\beta \in \left(0,1\right]$. Based on the vector of observed contributions $\mathbf{x}$, players are ranked from highest to lowest.

$\beta$ takes the role of a “meritocracy” parameter in our setting: (i) under no meritocracy (when $\beta \to 0$), all rankings are equally likely, and all players have the same expected rank2; (ii) under full meritocracy (when $\beta =1$), only “perfect” rankings are possible, that is, players who contributed more have a higher rank than players who contributed less, and ties are randomly broken; (iii) under intermediate meritocracy (when $\beta \in (0,1)$), all rankings have positive probability, but on aggregate, depending on $\beta$, players who contributed more have a higher expected rank than players who contributed less. As $\beta$ increases, we move continuously from (i) to (ii).

Step 2.2. ...to fuzzy groupings: Groups form based on the noisy ranking such that g groups $\{S_1,S_2,\dots ,S_g\}$ of a fixed size $s<n$ form. The result is a partition $\rho$ of N (where $s=n/g>1$ for some $s,g\in {\mathbf{N}}^{+}$) with groups $S_p\in \rho$ (s.t. $p=1,2,\dots ,g$) where the s highest-ranked players form Group 1, the s second-highest players form Group 2, etc.3

(See Appendix B for implementation examples of fuzzy grouping.)

Step 3. Payoffs:

Step 3.1. Realized payoffs (ex post): Given $\mathbf{c}$ and $\rho$, total payoffs generated in each $S\in \rho$ are $s+(r-1){\sum }_{i\in S}{c}_i$, where r is the rate of return. Each $i\in N$ s.t.$i\in S\in \rho$ receives an individual payoff of:

$${\varphi }_i(c_i|c_{-i},\rho )=\underset{\mathrm{remainder} \mathrm{from} \mathrm{budget}}{\underbrace{(1-c_i)}}+\underset{\mathrm{return} \mathrm{from} \mathrm{the} \mathrm{public} \mathrm{good}}{\underbrace{(R)\ast \sum _{j\in S}{c}_j.}},$$

(1)

where $R:=\frac{r}{s}$ is the marginal per capita rate of return; it is standard to assume a ‘social dilemma’ character of the game by setting $R\in \left(\frac{1}{s},1\right)$.4 Let $\varphi ={\left\{{\varphi }_i\right\}}_{i\in N}$ denote the payoff vector.

Step 3.2. Expected payoffs (ex ante): Groups form in Step 2, and payoffs materialize in Step 3, both based on the sunk contribution decisions taken during Step 1. From expression (1), i’s expected payoff of contributing $c_i$, as evaluated during Step 1 given $c_{-i}$, is therefore:

$$\underset{\exp . \mathrm{return} \mathrm{from} c_i}{\underbrace{\mathbf{E}\left[{\varphi }_i(c_i|c_{-i})\right]}}=\underset{(i) \mathrm{budget}}{\underbrace{1}}-\underset{(ii) \mathrm{sure} \mathrm{loss} \mathrm{on} \mathrm{own} \mathrm{contribution}}{\underbrace{\left(1-R\right)\ast c_i}}+\underset{(iii) \exp .\mathrm{return} \mathrm{from} \mathrm{others} \mathrm{in} \mathrm{group}}{\underbrace{R\ast \mathbf{E}\left[(\sum _{j\ne i:j\in S}{c}_j) | c_i\right],}}$$

(2)

Note that Term $(iii)$, the expected return from others’ contributions, may depend on one’s own contribution if $\beta >0$.

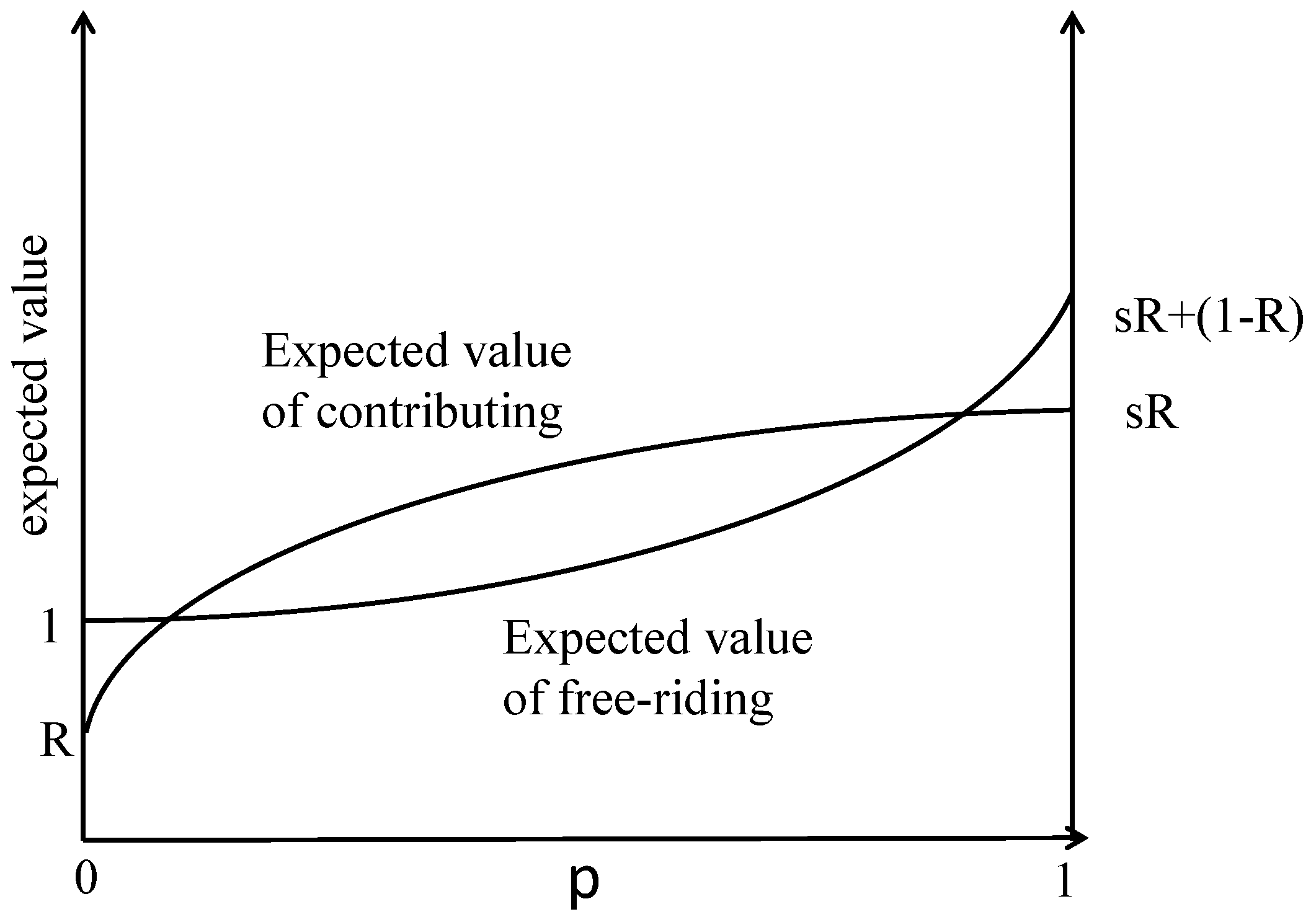
3. Nash Equilibria

Next, we analyze the Nash equilibria in terms of the ex ante decisions made in the games that we detailed in the previous section, where various games result from the different combinations of the chosen model ingredients. Figure 1 and Figure 2 summarize the models we shall consider and the results we obtain.

3.1. Game 1: ‘Baseline’

The following equilibrium structure results in the no-noise implementation with agent homogeneity and continuous action space (as in [5]). For this case, there always exists a Nash equilibrium with zero contributions; as in standard voluntary contribution games with a single group or with random grouping. We call this equilibrium the “non-contribution equilibrium”. However, non-contribution is not a dominant strategy, as it would be if groups were randomly assigned, because players may prefer to contribute when this gets them into high-contribution groups that promise higher payoffs. As a result, provided the marginal per capita rate of return R is high enough, [5] prove that there exist new asymmetric pure-strategy Nash equilibria where most players contribute and very few players free-ride.5 We call these equilibria “high-contribution equilibria”. We call the threshold for which these equilibria exist $mpcr$; note that this threshold is increasing in the relative group size $s/n$, which implies that it is, ceteris paribus, harder (easier) to satisfy for relatively large groups (populations).

High-contribution equilibria are particularly interesting, because several recent experimental studies provide support for them [5,19,20].6

3.2. Game 2: ‘Heterogeneity Extension’ (Extension 1)

3.2.1. Heterogeneity and Continuous Action Space

The first negative result is that under heterogeneity, non-contribution is the only existing equilibrium. A key property of high-contribution equilibria in the baseline case is that there exists a mixed group where both defectors and contributors are placed. In these equilibria, a contributor has a high-enough probability to be placed in a group filled only with contributors and a low enough probability to be placed in the mixed group so that it is, in expectation, not beneficial to free-ride and be placed with certainty in the low group instead.

However, in [22], it is proven that, under heterogeneity, there cannot exist an equilibrium where two or more players contribute the same amount. The reason is that, if two or more players contribute the same amount, then the one with the highest endowment would have a profitable deviation in contributing slightly more due to the existence of the mixed group: contributing only slightly more, and he/she is guaranteed not to be placed in a worse group. Conversely, if players in a higher group already contribute everything, then the wealthiest player could instead contribute slightly less and still be guaranteed to remain in the same group. Therefore, when players have access to a continuous action space and can thus reduce or increase their contributions by an infinitesimal amount, then there can be no high contribution equilibrium for heterogeneous endowments.

It is important to note that this result relies on players all having different endowments. Indeed, if players were to belong only to two endowment classes, Gunnthorsdottir et al. [23] prove that there might exist an equilibrium where every player contributes everything. This equilibrium, however, requires conditions that become harder to satisfy the more classes of endowments are introduced, eventually becoming impossible if there are as many levels of endowment as there are players.Interestingly, Gunnthorsdottir et al. [19,23] also find empirical support for the high-efficiency equilibria by showing that, when existing, near-efficient equilibria are re-preferred over the worst ones.

3.2.2. Binary Action Space

With a binary action space, the above argument about infinitesimal changes in contributions does not hold any more. Indeed, it can be shown (see Proposition A5 in Appendix A) that in the case of heterogeneous endowments and binary action space, there exists a threshold for the marginal rate of return such that contributive equilibria exist.

For this configuration, a maximum of g pure strategy Nash equilibria can coexist, depending on the value of r. Their structure is so that the $k·s$ ($0\le k<g$) poorest players defect and the $\left(g-k\right)·s$ richest players contribute. The non-contribution equilibrium ($k=0$) always exists, regardless of the value of the marginal rate of return. Interestingly, for the equilibrium with $k=1$ to exist, the marginal rate of return has to be higher than for the equilibrium with $k=2$ to exist, and so on, until the lowest threshold for R such that the only contributive equilibrium is the one were all but one group is filled with contributors7.

As a corollary of Proposition A5, there also exist high-contribution equilibria for homogeneous endowments and binary action space. In this case, all thresholds collapse and reduce to the same value as in the baseline case, and all the existing equilibria are such that there exists a mixed group of contributors and defectors, in analogy with the continuous action space case.

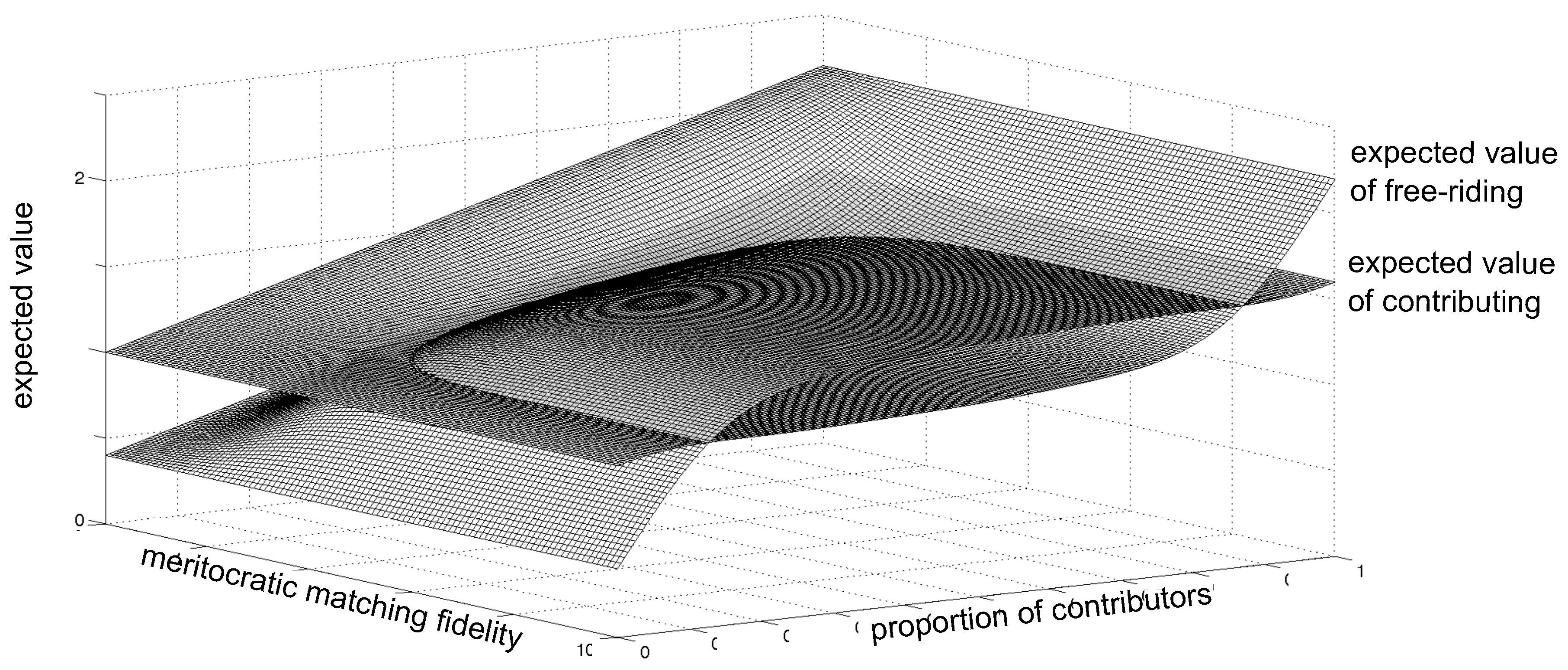
3.3. Game 3: ‘Noise Extension’ (Extension 2)

In the case of a noisy mechanism, the existence of Nash equilibria summarizes as follows.

Whenever the chosen model allows for high-contribution equilibria in perfect meritocracy, then there exists a noise/fuzziness level below which the same equilibria continue to exist: given any $R>mpcr$, there exists a $\beta <1$ such that the same high-contribution equilibria (possibly with more free-riders than under $\beta =1$, but $<s$) continue to exist as when $\beta =1$ (see Appendix A, Proposition A8). The minimum level of $\beta$, denoted by $\beta$, for which high-contribution equilibria exist, is an implicit function that is decreasing in R and increasing $s/n$.

Universal non-contribution is a Nash equilibrium for any $\beta$ (see Appendix A, Proposition A7). The reason for this is that the only incentive for an individual to contribute a positive amount under contribution-based grouping is to be grouped with others doing likewise. When no one else contributes, there is no such incentive.

3.4. Remark: Mixed-Strategy Nash Equilibria

With heterogeneous endowments, symmetric mixed-strategy NE do not exist, either because the only existing equilibrium is non-contribution by all or because of the structure of the high-efficient equilibria (see Proposition A5 in Appendix A and Theorem 2 in [22]).

Similarly, for heterogeneous endowments and continuous action space, mixed-strategy equilibria do not exist (see Appendix A, Corollary A14). When contribution decisions are restricted to coarse or binary action spaces, however, it is the case that, for every $\beta$, there exists a $R\in (mpcr,1)$ at which there exists one and above which there exist two mixed-strategy Nash equilibria of the form ‘contribute fully with p and free-ride with $1-p^{\prime }$, one with a high contribution probability $\overline{p}$ and one with a low p (see Appendix A, Proposition A10).8

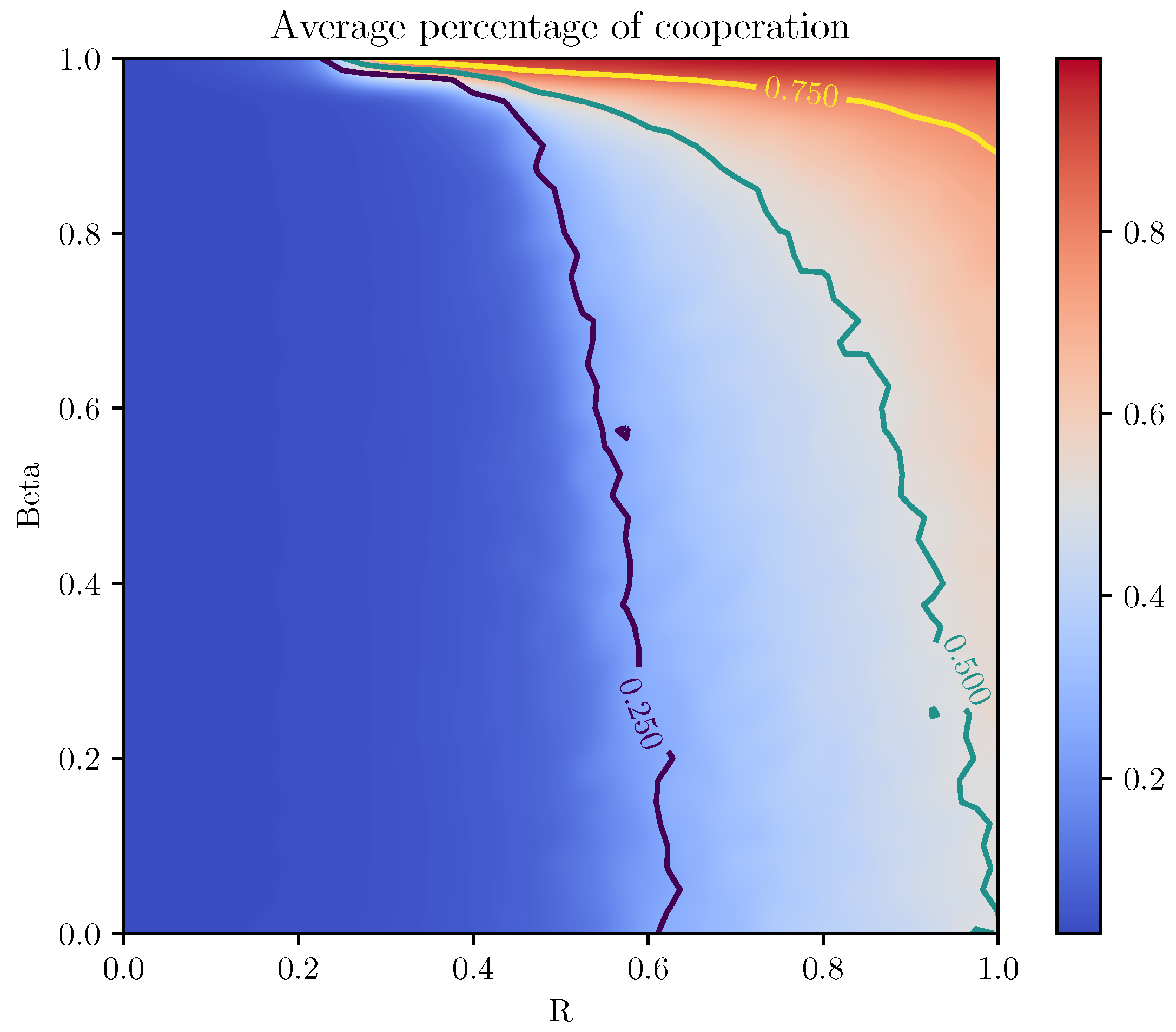
4. Welfare Comparison

You can’t have your cake and eat it, too, is a good candidate for the fundamental theorem of economic analysis. We can’t have our cake of market efficiency and share it equally.

[24], p. 1.

We now turn to the point of view of a social planner and analyze the welfare properties of equilibria in terms of realized payoffs $\varphi$.9 Ex post, in contrast to ex ante, it is not always the case that high-contribution equilibria are payoff-dominant.10 Hence, it is not obvious which equilibria a social planner who cares about equality will prefer. To evaluate welfare, we therefore use a variant of the social welfare function of [28], which has the advantage that, like the parameter $\beta$ governing meritocracy, a single parameter characterizes a continuous range of social planner preferences, spanning preferences across the entire equality-efficiency tradeoff.

Social welfare: Given outcome $(\rho ,\varphi )$, let $W_e(\varphi )$ be the social welfare function measuring its welfare given the inequality aversion parameter $e\in [0,\infty )$:

$$W_e(\varphi )=\frac{1}{n(1-e)}\sum _{i\in N}{\varphi }_i^{1-e}$$

(3)

(For $e=1$, expression (3) is defined by $W_1(\varphi )=\frac{1}{n}{\prod }_{i\in N}{\varphi }_i$, i.e., by the Nash product.) Expression (3) nests both the utilitarian (Bentham) and Rawlsian social welfare functions as special cases.11 When $e=0$, Expression (3) reduces to $W_0(\varphi )=\frac{1}{n}{\sum }_{i\in N}{\varphi }_i$, i.e., the utilitarian criterion measuring the state’s ‘efficiency’ (total payoffs) only. When $e\to \infty$, Expression (3) approaches $W_{\infty }(\varphi )=\min ({\varphi }_i)$, i.e., the Rawlsian criterion measuring the outcome’s welfare by the utility of the worst-off. Obviously, a utilitarian social planner prefers the high-contribution equilibria to the non-contribution equilibrium, because it is more efficient. A Rawlsian, however, would prefer the non-contribution equilibrium (with perfect equality of payoffs) if any player receives a lesser payoff in the high-contribution equilibria.

Which equilibrium is preferable in terms of social welfare for any given social welfare function depends on the game considered and on the social planner’s relative weights on efficiency and equality. Critical for this assessment is the inequality aversion e.

Welfare criterion: The social planner acts in order to maximize $\mathbf{E}\left[W_e(\varphi )\right]$, where $\varphi$ are evaluated according to the equilibrium selection criterion. Suppose that the social planner can set some of the rules of the game to achieve the above goal: Which conditions maximize the social welfare? Depending on the game, what is the value of $\beta \in \left[0,1\right]$ that maximizes $\mathbf{E}\left[W_e(\varphi )\right]$?

4.1. Homogeneous Endowments

In case of homogeneous endowments, there is a clear trade-off between efficiency and equality: the high gains in efficiency are obtained at the expense of the cooperative players placed in the group containing some defectors. These few players are worse off than in the case where everybody defects. A very inequality averse social planner might choose to increase the fuzziness in the observations in order to revert to the non-contribution equilibrium and thus improve the ex-post payoff of the worst off.

For an example, consider the economy illustrated in

Table 1. Stem-and-leaf plot of individual payoffs for the non-contribution equilibrium (valid for any $\beta \in [0,1]$) and for the high-contribution equilibrium (when evaluated at $\beta =1$). Parameter values are $n=16$, $s=4$, $r=1.6$ and $\beta =1$.

High-Contribution Equilibrium	Payoff	Non-Contribution Equilibrium
When ${\beta }=\mathbf{1}$		When $\mathit{\beta }=\mathbf{0}$
0	0.0	0
0	0.2	0
0	0.4	0
0	0.6	0
13 14 ($c_i=1$) 2	0.8	0
0	1.0	16 ($c_i=0$)  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
0	1.2	0
0	1.4	0
1 2 3 4 5 6 7 8 9 10 11 12 ($c_i=1$) 12	1.6	0
15 16 ($c_i=0$) 2	1.8	0
24.4	efficiency	16

The stem of the table comprises the payoffs. The leafs are the number of players receiving that payoff (with their contribution decision) and the individual ranks of players corresponding to payoffs in the two equilibria. At the bottom, the efficiencies of the two outcomes are calculated.

(with $n=16$, $s=4$ and $r=1.6$), and suppose a social planner considers moving from $\beta =0$ to $\beta =1$ (i.e., from completely random to fully-meritocratic ranking). At $\beta =0$, he/she considers the non-contribution equilibrium. At $\beta =1$, he/she considers the high-contribution equilibrium. To assess which one he/she prefers, he/she makes a $W_e$-comparison. For this numerical example, it turns out that for any $W_e$ with $e<10.3$ he/she prefers the high-contribution equilibria, while for a $W_e$ with $e\ge 10.3$, he/she prefers the non-contribution equilibrium.12 The following general statement about the welfare-optimal $\beta$ can be made.

Proposition 1.

For any $R>\max \{mpcr, 1/(s-1)\}$, there exists a population size $n < \infty$ such that $\mathbf{E}[W_e(\varphi );\beta ]>\mathbf{E}[W_e(\varphi );\beta ]$ for all $\beta \ne \beta$ given any parameter of inequality aversion e bounded away from ∞.

Proof. 

Below $\beta$, the high-contribution equilibrium does not exist. The non-contribution equilibrium cannot be welfare-maximizing for any $e < \infty$ as $n\to \infty$, because large efficiency gains (approaching infinity) would be foregone at virtually no inequality cost. Consider setting some $\overline{\beta }\in (\beta ,1)$ instead, for which the high-contribution equilibrium exists. Write $q_1^n$ for the probability of having more than one free-rider in any group for a realized outcome $(\rho ,\varphi )$ given $n<\infty$. Since the number of free-riders does not increase as n increases, $\partial q_1^n/\partial n<0$. Since contributors in groups with at most one free-rider receive a payoff strictly greater than one ($(s-1)R>1$), we have $\mathbf{E}[W_e(\varphi );\beta ]>(1-q_1^n)\times W_e({\varphi }_i=(s-1)R\forall i)$. Because, given any $\beta <1$, $\partial q_1^n/\partial n<0$, there therefore must exist a population size $n<\infty$ above which $\mathbf{E}\left[W_e(\varphi )\right]>W_e({\varphi }_i=1\forall i)$. Hence, $\beta$ is generally welfare-optimal for any $e<\infty$ as $n\to \infty$. ☐

Remark 2.

$\mathbf{E}[W_e(\varphi );\beta ]>\mathbf{E}[W_e(\varphi );\beta ]$ for all $\beta \ne \beta$ is also the case for n bounded away from infinity if $(a)e$ is set below some bound $e<\infty$ and/or $(b)$ R is set above some bound $R>1/(s-1)$.

4.2. Heterogeneous Endowments

In the case of heterogeneous endowments and binary action space13, there is no equilibrium in which some contributors are grouped together with some defectors. Hence, no player is worse off in the high-contributing equilibria compared to the non-contributing one. Indeed, every contributive equilibria Pareto dominates the non-contributing one. The equilibrium where all but the S poorest players contribute is ex-post payoff dominant.

Hence, regardless of the value of the social planner preference parameter e, a social planner will always prefer the least possible amount of noise in the observations (ideally $\beta =1$) in order to ensure the most efficient outcome.

Note however that this does not mean that inequality does not increase due to the agents playing the efficient equilibrium. The starting inequality due to the initial endowments is amplified by the fact that the poorest players are the ones in the non-contributing group and thus the ones that do not benefit from the common good. Indeed, if the social planner were to measure inequality based on statistical dispersion measures rather than looking at the worst off player, he/she would observe an increase in inequality. As an example, consider the Gini coefficient14, a standard measure of inequality in a population, for a population of 16 players with initial endowments distributed according to a normal distribution $\mathcal{N}\left(1,{0.1}^2\right)$: for a realization of the starting endowment resulting in a Gini coefficient of ∼0.09, the Gini coefficient for the realized payoff in the ex-post dominant equilibrium is ∼0.18. Hence, by this measure, the inequality in the population doubled after the game.

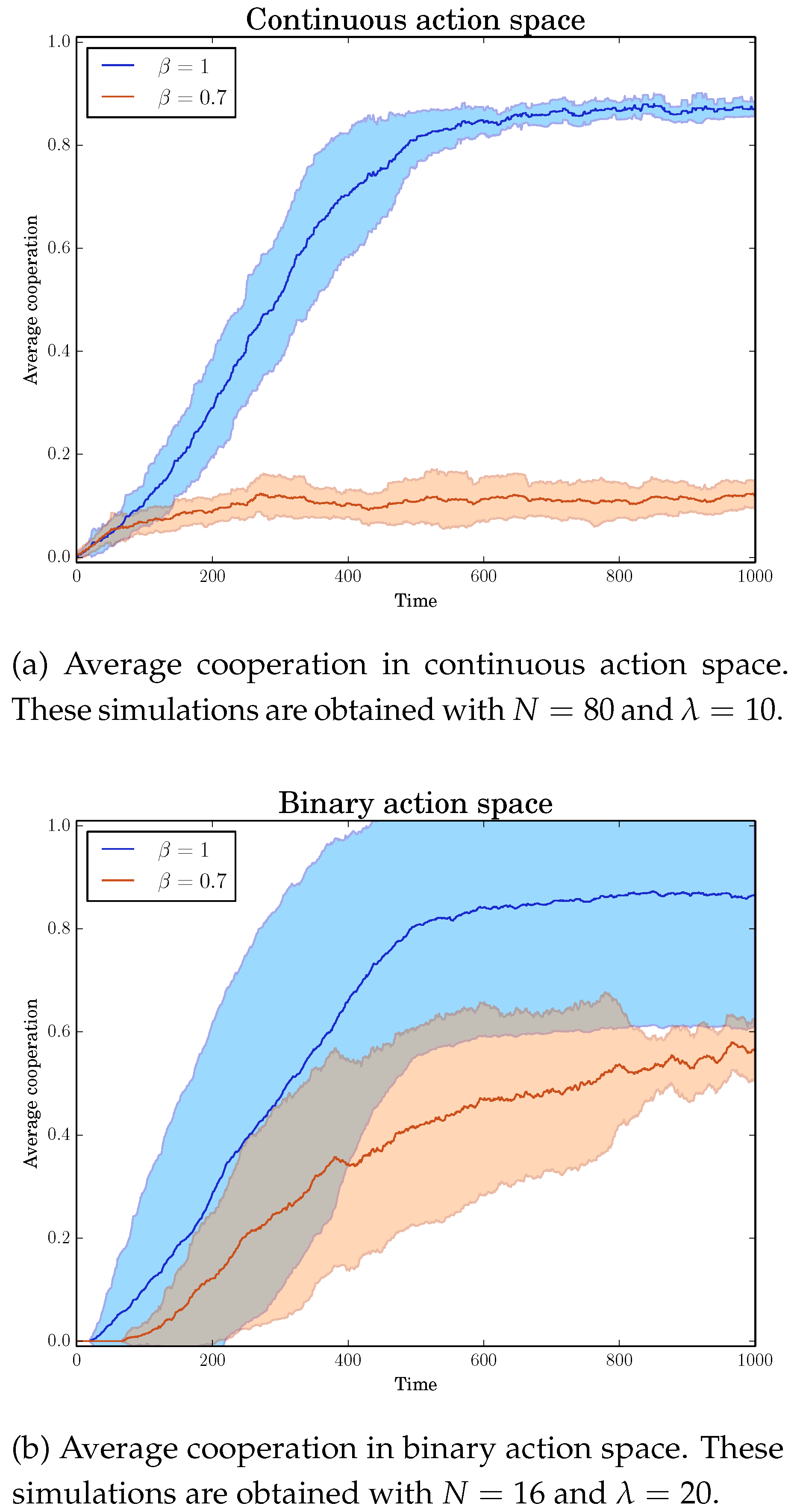
5. Logit Dynamics

In order to quantify the effect of noise, we simulate the above games with an agent-based model where players use logit-response [32,33] study the dynamics of the game. The following algorithm is used in these simulations:

Algorithm 1: Logit choice dynamics.
1	Initialization: Assign the initial endowments to each player sampling them from a Gaussian distribution with mean $W_0$ and standard deviation $\sigma$. If some endowments are zero or negative, the sampling is repeated.a
2	Initialization: Set initial strategy ${\alpha }_i$ to 0 $\forall i$ (start the simulation in the fully-defective stateb), and set time t to zero.
	repeat
	until $t<T$;

^a 

The standard deviation is chosen for this to be an unlikely event.

^b 

Different initial starting conditions have been explored, and they have been observed to have no effect on the final outcome of the simulation.

^c 

Inertia was added to ensure the convergence to the pure-strategy Nash equilibrium (if existing). Without inertia, the best-response dynamics could oscillate around such an equilibrium.

^d 

For a definition, see, e.g., [34].

After T rounds, the algorithm stops, and the population average of the strategies is computed. The procedure is repeated $EN$ times, and the ensemble average of the population average is obtained.

Figure 3 shows example results for homogeneous endowments in four different cases: perfect and imperfect observations for continuous and binary action spaces. When the matching mechanism is implemented perfectly, we observe a high level of contributions both in the binary and continuous action space (blue lines in Figure 3a,b). However, for an intermediate level of noise in the observed contributions, the results are quite different: in the binary case, we observe an intermediate level of average contributions (orange line in Figure 3b), while in the continuous case, we see very low amounts of cooperation (orange line in Figure 3a).

In Figure 4, we quantify how the percentage of contributions depends on the rate of return R and the level of noise in the matching mechanism $\beta$ for agents with homogeneous endowments in a strategy space with continuous action. As predicted, the average level of cooperation weakly increases with increasing R and $\beta$, and we observe almost complete cooperation when approaching one. Naturally, regardless of the value of $\beta$, we observe no cooperation for a value of $R\le \frac{1}{s}$. The contour lines indicate when the average contribution is above a certain threshold.

6. Summary

Our analysis aimed to achieve three things. First, we study how the existence of high-contributions Nash equilibria depends on the strategy space of the players and on the homogeneity/heterogeneity of their initial endowment Second, we allow noisy/fuzzy implementations of the mechanism everywhere between “no meritocracy” (completely random grouping) and “full meritocracy” (perfect contribution-based grouping). We found that the minimum meritocracy threshold that enables pure-strategy equilibria with high contributions decreases with the population size, the number of groups and with the rate of return. Where they exist, we established that, in the presence of some unconditional contributors, the high-contribution equilibria are selected rather than the non-contribution equilibrium. Mixed-strategy equilibria do not exist, unless the contribution space is binary (or very coarse).

Finally, we assessed the welfare properties of candidate equilibria to identify the welfare-maximizing regime, given varying degrees of inequality aversion of the regime. We found that setting meritocracy at the minimum meritocracy threshold that enables high-contribution equilibria maximizes welfare for general social welfare functionals as the population becomes infinitely large. An exception to this is in the case of coarse/binary action space and heterogeneous endowments where a mechanism with perfect matching is preferred regardless of how inequality averse the social planner is. For finite populations, the same result holds if (a) the inequality aversion is not extreme and (b) the rate of return is high.

More broadly, the mechanism we considered here belongs to a family of “grouping” mechanisms that enable high-contribution equilibria in voluntary contribution games.15 Their common feature is that they implement non-random, contribution-based grouping, but require no payoff transfers between players. Importantly, these mechanisms incentivize contributions even if most of the players are narrowly self-interested. Our paper therefore complements other research on cooperative phenomena that arise from other-regarding preferences [43,44], in particular in public goods games (e.g., [45]).16 We found that a fuzzy mechanism implementation could outperform a perfect implementation. It is an avenue for future research to consider fuzzy implementations of these alternative grouping mechanisms and of other mechanisms and to study other social dilemmas and games more generally under fuzzy mechanism design.