Casimir Energies for Isorefractive or Diaphanous Balls

Abstract

It is known that the Casimir self-energy of a homogeneous dielectric ball is divergent, although a finite self-energy can be extracted through second order in the deviation of the permittivity from the vacuum value. The exception occurs when the speed of light inside the spherical boundary is the same as that outside, so the self-energy of a perfectly conducting spherical shell is finite, as is the energy of a dielectric-diamagnetic sphere with $\epsilon \mu =1$, a so-called isorefractive or diaphanous ball. Here we re-examine that example and attempt to extend it to an electromagnetic $\delta$-function sphere, where the electric and magnetic couplings are equal and opposite. Unfortunately, although the energy expression is superficially ultraviolet finite, additional divergences appear that render it difficult to extract a meaningful result in general, but some limited results are presented.

1. Introduction

Although it is clear that Casimir energies between distinct rigid bodies are finite, even though they arise formally from a summation of changes in zero-point field energies by material bodies, that finiteness fails for the self-energy of a single body. For a detailed review, see [1]. However, for certain special cases, a unique finite self-energy can be extracted. The classic case is that of the perfectly conducting sphere of zero thickness, where a unique, finite, positive self-energy has been extracted by a variety of methods [2,3,4]:

$$E_B=\frac{0.04617\hslash c}{a}$$

(1)

where a is the radius of the sphere.

An obvious generalization of a perfecting conducting spherical shell is a dielectric ball, with a permittivity $ϵ$ within the spherical volume. This, however, immediately runs into problems [5]. Although it is possible to identify a finite self-energy in the dilute limit, that is, to order ${(ϵ-1)}^2$, unremovable divergences occur in higher order [6]. The weak-coupling limit coincides with the result obtained by summing the van der Waals forces between the molecules that make up the medium [7]:

$$E_{\mathrm{vdW}}=\frac{23\hslash c}{1536\pi a}{(ϵ-1)}^2$$

(2)

The divergence in order ${(ϵ-1)}^3$ was verified in heat kernel analyses [8], where the second heat kernel coefficient was shown to be nonzero in that order, resulting in a logarithmic divergence, making it impossible to extract a finite energy. Dispersion does not appear to be sufficient to resolve this problem.

A possible way out is to consider a ball having both electric permittivity $ϵ$ and magnetic permeability $\mu$. A general statement of this formulation was given in [9], where both the self-energy and the stress on the sphere were given, consistent with the principle of virtual work. However, much earlier, Brevik and collaborators realized that, in the special case $ϵ\mu =1$, that is, when the speed of light is the same both inside and outside the sphere, the divergences cancel, and a completely unique finite self-energy can be found [10,11,12,13,14,15,16]. We will refer to such a situation as a diaphanous ball. In [16], the result for the diaphanous ball was rather successfully extrapolated to a dilute dielectric ball. One could also note analogous results for diaphanous cylinders [17,18,19], which yield a vanishing energy in the dilute limit, in contrast to the nonvanishing energy of a diaphanous ball.

Another generalization was explored more recently—that of an electromagnetic $\delta$-function shell [20]. This was explored less completely in [1]. In that case there are, in general, two (transverse) coupling constants, electric and magnetic, and we indicated there that, although in general for finite couplings, the self-energy was divergent, in the special case where the two couplings were equal and opposite, the divergences apparently cancel. In this paper, we wish to explore this problem further. We will find that the modes brought in by the magnetic coupling contribute additional divergences that seem to render extraction of a finite self-energy problematic.

The outline of this paper is as follows. In Section 2, we re-analyze the dielectric-diamagnetic ball where the speed of light is the same inside and outside, $ϵ\mu =1$, and present accurate numerical results, which are slightly better than those given previously. In Section 3, we will examine the special case of the electromagnetic $\delta$-sphere, where the two couplings are equal and opposite, ${\lambda }_e=-{\lambda }_g$, and carry out the asymptotic analysis to higher order, and identify the difficulties. Concluding remarks are offered in Section 4.

We use natural units, with $\hslash =c=1$, and Heaviside–Lorentz electromagnetic units.

2. The Diaphanous Ball

What we shall call a diaphanous ball is a spherical volume of radius a, in vacuum, with both electric permittivity $ϵ$ and magnetic permeability $\mu$ such that $ϵ\mu =1$, so the speed of light is the same both inside and outside the sphere. Here we will ignore dispersion, which was considered in [13]. The Casimir energy is given by the formula:

$$E=-\frac{1}{4\pi a}{\int }_{-\infty }^{\infty }dy{e}^{iy\tilde{\tau }}\sum _{l=1}^{\infty }(2l+1)P_l\left(\cos \delta \right)x\frac{d}{dx}\ln \left(1-{\xi }^2{\left[{\left(e_l\left(x\right)s_l\left(x\right)\right)}^{\prime }\right]}^2\right),x=\left|y\right|=\left|\zeta \right|a$$

(3)

where $\zeta$ is the Euclidean frequency, and the modified spherical Bessel functions are:

$$s_l\left(x\right)={\left(\frac{\pi x}{2}\right)}^{1/2}{I}_{\nu }\left(x\right),e_l\left(x\right)={\left(\frac{2x}{\pi }\right)}^{1/2}{K}_{\nu }\left(x\right)$$

(4)

and $\nu =l+1/2$. Here,

$$\xi =\frac{\mu -{\mu }^{\prime }}{\mu +{\mu }^{\prime }}=-\frac{ϵ-{ϵ}^{\prime }}{ϵ+{ϵ}^{\prime }}$$

(5)

where $ϵ$, ${ϵ}^{\prime }$ are the exterior and interior values of the permittivity, and similarly for the permeability. Note that, when $\xi \to 1$, the familiar expression of the Casimir energy for a perfectly conducting spherical shell is recovered. Of particular note are the point-splitting regulator terms in Equation (3): $\tilde{\tau }=\tau /a$ is the dimensionless point-splitting parameter in Euclidean time, while $\delta$ represents point-splitting in the angular (transverse) directions. The regulator parameters are to be taken to zero at the end of the calculation.

This expression with $\xi =1$ was evaluated accurately first in [3,4] and has been reconfirmed several times since [21,22,23,24]. In [10,11], the uniform asymptotic expansion (UAE) for the Bessel functions was used to evaluate the leading term in the expansion of Equation (3) for small $\xi$:

$$E^{\left(2\right)}=\frac{3}{64a}{\xi }^2$$

(6)

(The superscript refers to the order in the UAE, not to the order in $\xi$). Some years later, Klich realized that the leading term in the $\xi$ expansion could be exactly computed by using the addition theorem for spherical Bessel functions [25]:

$$\sum _{l=0}^{\infty }(2l+1)s_l\left(x\right)e_l\left(y\right)P_l\left(\cos \theta \right)=\frac{xy}{\rho }{e}^{-\rho }$$

(7)

where $\rho =\sqrt{x^2+y^2-2xy\cos \theta }$. The exact $O\left({\xi }^2\right)$ result is only about 6% larger than the estimate (6):

$$E_2=\frac{5}{32\pi a}{\xi }^2$$

(8)

As Klich noted, even extrapolating this result to $\xi =1$ agrees within 8% with the Boyer energy! The extrapolation of Equation (6) to $\xi =1$ is good to 2%. (Incidentally, the same exact treatment can be given for the second-order coefficient for a dilute purely dielectric ball, Equation (2), first calculated numerically in [6], but analytically in [26]. Here, however, including even the first two terms in the UAE is still 15% too low).

In [16], the Casimir energy of a diaphanous sphere is calculated to a higher order in the UAE. The second-order term in the UAE is (keeping the ${\xi }^4$ term, which was not done in [16]):

$$E^{\left(4\right)}=\frac{9{\xi }^2}{2^{12}a}\left(\frac{{\pi }^2}{8}-1\right)(6-7{\xi }^2)$$

(9)

and at $\xi =1$ the sum of $E^{\left(2\right)}$ and $E^{\left(4\right)}$ is only about 0.5% high, while the coefficient of ${\xi }^2$ in the small $\xi$ expansion is high by about the same percentage. This suggests it may be sufficient to remove the first two terms in the UAE from the logarithm in (3) and then add the the corresponding approximants:

$$E=E^{\left(2\right)}+E^{\left(4\right)}+\sum _{l=1}^{\infty }{R}_l$$

(10)

where ($x=\nu z$, $\nu =l+1/2$, $t={(1+z^2)}^{-1/2}$).

$$\begin{array}{ccc}\hfill R_l& =& \frac{{\left(2\nu \right)}^2}{4\pi a}{\int }_0^{\infty }dz\{\ln [1-{\xi }^2{\left(e_l\left(\nu z\right)s_l\left(\nu z\right)\right)}^{\prime 2}]\hfill \\ & & +\frac{{\xi }^2{t}^6}{{\left(2\nu \right)}^2}+\frac{t^6{\xi }^2}{{\left(2\nu \right)}^4}\left(\frac{{\xi }^2}{2}{t}^6-(1-t^2)(2-25t^2+35t^4)\right)\}\hfill \end{array}$$

(11)

Because $R_l$ is finite, the cutoffs can now be dropped. Equation (10) is to be understood as an asymptotic expansion, in that only an optimal number of terms in the series are to be included. Only $R_1$ here makes a substantial contribution, as

Table 1. $E^{\left(2\right)}$, $E^{\left(4\right)}$, $R_1$, $R_2$, $R_3$, and the sum E for various values of $\xi$.

$\mathit{\xi }$	${\mathit{E}}^{\mathbf{\left(}\mathbf{2}\mathbf{\right)}}\mathit{a}$	${\mathit{E}}^{\mathbf{\left(}\mathbf{4}\mathbf{\right)}}\mathit{a}$	${\mathit{R}}_{\mathbf{1}}\mathit{a}$	${\mathit{R}}_{\mathbf{2}}\mathit{a}$	${\mathit{R}}_{\mathbf{3}}\mathit{a}$	$\mathit{Ea}$
1	$0.046875$	$-0.0005135$	$-0.0001517$	$-0.0000223$	$-6\times {10}^{-6}$	$0.04618$
$0.5$	$0.011719$	$0.0005456$	$-0.0000384$	$-6\times {10}^{-6}$	$-1.6\times {10}^{-6}$	$0.0122184$
$0.01$	$4.687\times {10}^{-6}$	$3.081\times {10}^{-7}$	$-1.793\times {10}^{-8}$	$-2.74\times {10}^{-9}$	$-7.53\times {10}^{-10}$	$4.974\times {10}^{-6}$

shows for various values of $\xi$.

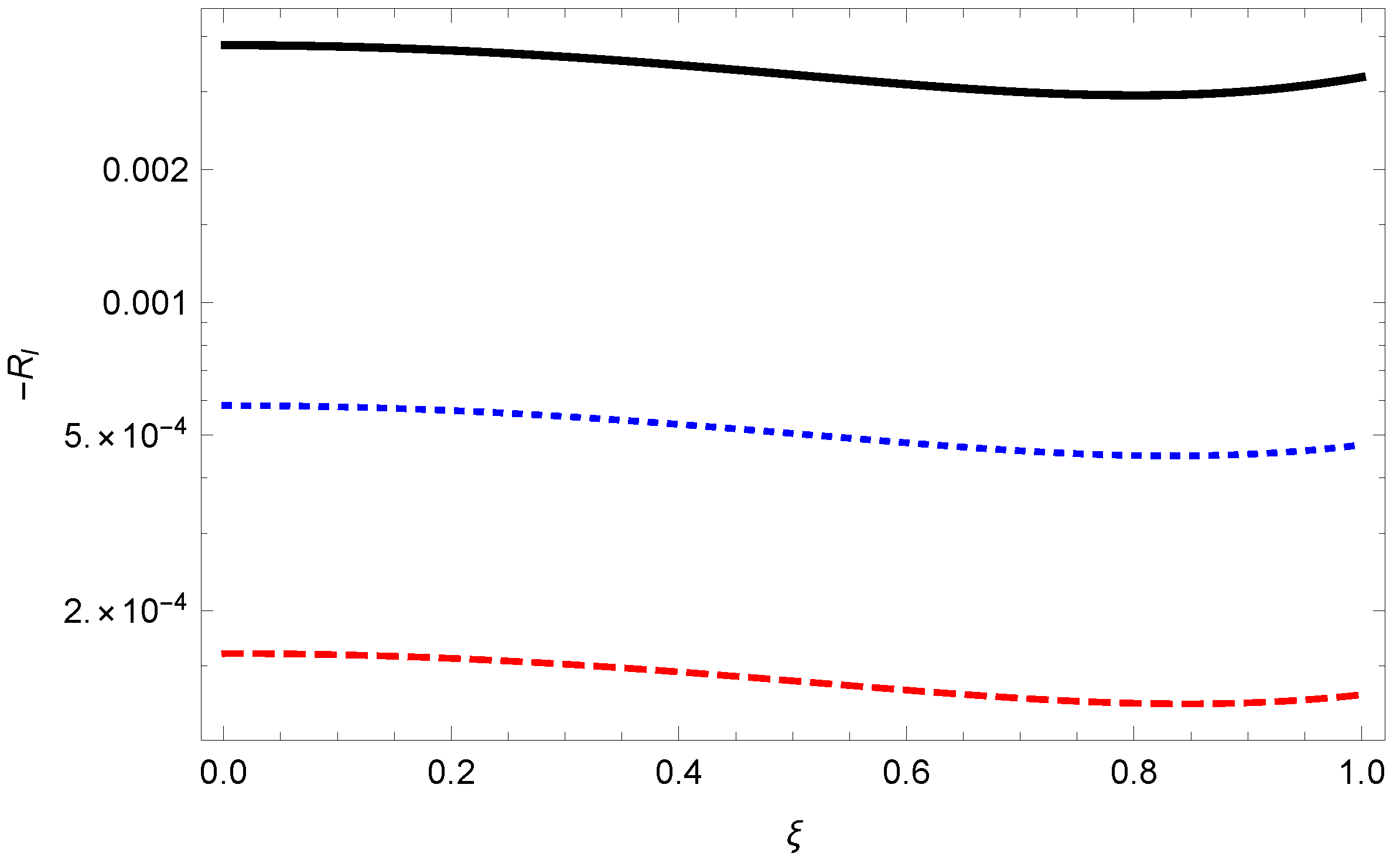
In Figure 1, we show how the remainders rapidly go to zero with l for all $\xi$.

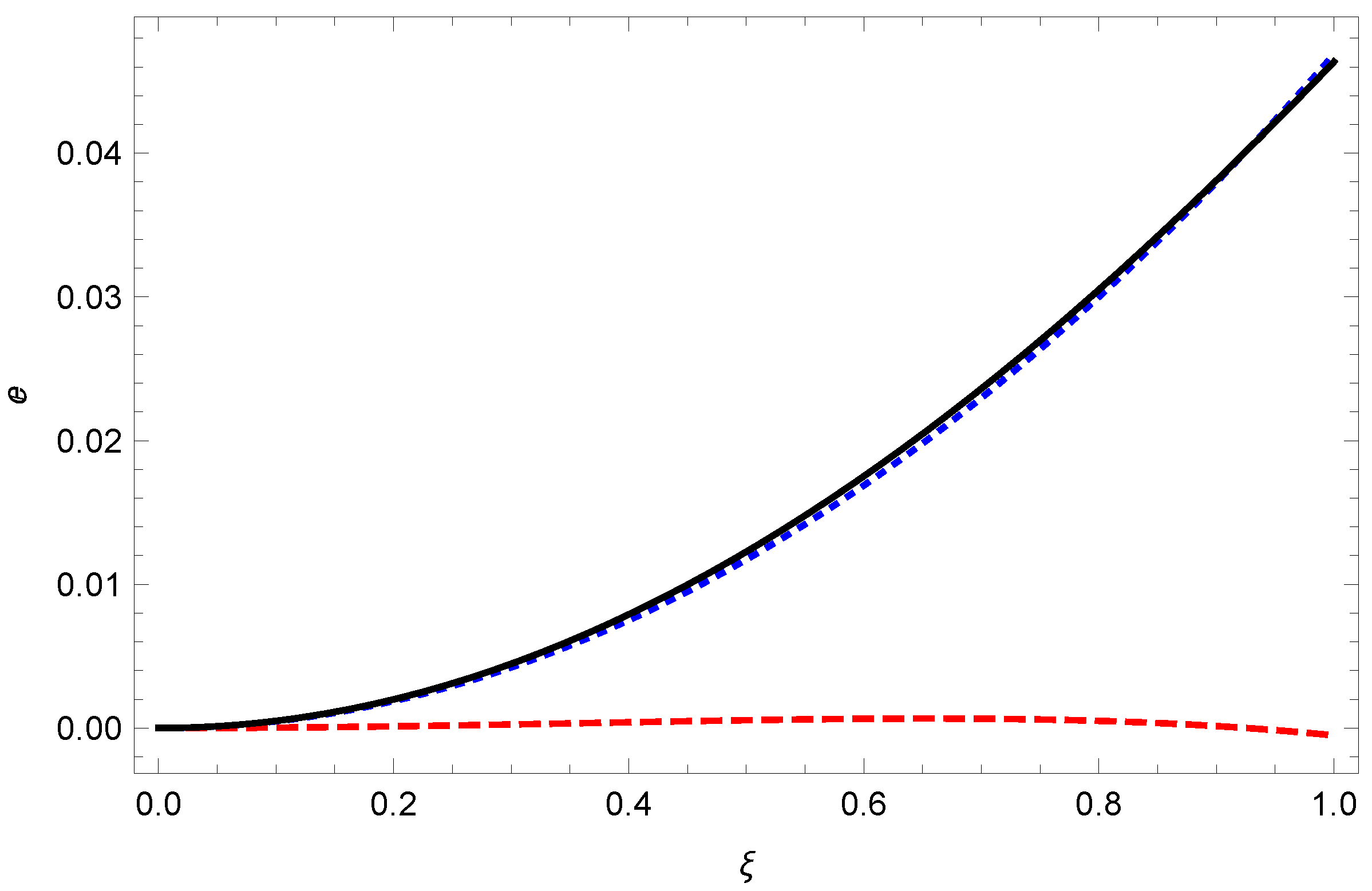
Since the corrections are so small, for all $\xi$, the lowest UAE contribution is all that is discernible in a graph of the energy (Figure 2).

Brevik and Kolbenstvedt [11] provide an analytic approximant to the Casimir energy engineered to be exact for strong coupling $\xi =1$, but it does not give the exact low-$\xi$ behavior. The same is true for the approximation given in [14]. Brevik and Einevoll [13] include dispersion in the coupling, but this leads to linearly divergent terms that are regulated by insertion of an arbitrary parameter. The direct mode sum given in [16] includes the first three terms in the UAE, and is accurate to almost $0.1\%$, not quite as accurate as the results reported here.

3. The Dual Electromagnetic $\mathit{\delta }$ Sphere

In general, Casimir self energies of bodies are divergent, so it is of interest to study examples where unambiguous finite self energies can be extracted. Such is the case of a perfectly conducting spherical shell, or the diaphanous ball discussed in the previous section, which reduces to the former in the $\xi \to 1$ limit. Another generalization of the spherical shell that would seem to admit finiteness is an electromagnetic $\delta$-function sphere, with equal and opposite electric and magnetic couplings; it was observed in [20] that then the catastrophic divergence in the third order in the coupling cancels, because only even powers in the coupling appear in the uniform asymptotic expansion of the energy integrand. It turns out, however, that this is a more subtle problem than we would have anticipated.

We follow the notation and formalism given in [20]. In this model, the couplings are modeled by a plasma-like dispersion relation, ${\lambda }_{e,g}={\zeta }_{p,m}/{\zeta }^2$, and the form of the Casimir energy, after the bulk vacuum energy is subtracted, is analogous to (3), except we have used a more general form of the frequency regulator:

$$E=-\frac{1}{4\pi }\sum _{l=1}^{\infty }(2l+1)P_l\left(\cos \delta \right){\int }_{-\infty }^{\infty }d\zeta \frac{e^{i\zeta \tau }-1}{i\zeta \tau }\zeta \frac{d}{d\zeta }\ln {\Delta }^E{\Delta }^H$$

(12)

where the TE and TM modes are given by:

$${\Delta }^{E,H}=1+{\zeta }^2\frac{{\lambda }_e{\lambda }_g}{4}+\left|\zeta \right|[{\lambda }_{e,g}{e}_l\left(x\right)s_l\left(x\right)-{\lambda }_{g,e}{e}_l^{\prime }\left(x\right)s_l^{\prime }\left(x\right)],x=\left|\zeta \right|a$$

(13)

In [20], we mostly considered the electric case where ${\lambda }_g=0$, but we did remark that interesting cancellations occur if ${\lambda }_e=-{\lambda }_g$. Here we will explore this further and define $\lambda ={\zeta }_{p}a=-{\zeta }_{m}a$. This leads to the following form for the quantities in the logarithm:

$${\Delta }^{E,H}=1-\frac{{\lambda }^2}{4x^2}\pm \frac{\lambda }{x}[e_l\left(x\right)s_l\left(x\right)+e_l^{\prime }\left(x\right)s_l^{\prime }\left(x\right)]$$

(14)

As we will see in Section 3.4, there is a difficulty with this model, in that singularities appear for finite imaginary frequency $\zeta$ arising from the $e_l^{\prime }{s}_l^{\prime }$ terms.

3.1. Uniform Asymptotic Expansion

To focus on the ultraviolet behavior, we will modify the UAE expansions by replacing, as suggested in [20], $1/z\to t$, which is correct for a high z. Doing so leads to the modified UAE expansion (recall $x=\nu z$, $\nu =l+1/2$, $t={(1+z^2)}^{-1/2}$):

$$\begin{array}{ccc}\hfill \ln {\Delta }^E{\Delta }^H& \sim & -{\lambda }^2\frac{t^2}{2{\nu }^2}-{\lambda }^4\frac{t^4}{16{\nu }^4}-{\lambda }^2\frac{t^6}{192{\nu }^6}[3{(1-6t^2+6t^4)}^2+2{\lambda }^4]\hfill \\ & & -{\lambda }^2\frac{t^8}{512{\nu }^8}[2(-1+t)(1+t)(1-6t^2+6t^4)(-13+275t^2-840t^4+630t^6)\hfill \\ & & +4{\lambda }^2{(1-6t^2+6t^4)}^2+{\lambda }^6]+O\left({\nu }^{-10}\right)\hfill \end{array}$$

(15)

In [20], we calculated the energies corresponding to the first two terms in this uniform expansion, which was just twice those from the ${\lambda }_e$ contribution. The $O\left({\nu }^{-2}\right)$ term in the UAE is in general sensitive to the regulator,

$$E^{\left(2\right)}=\frac{{\lambda }^2}{4a}\left(1-\frac{1}{\Delta }\right)$$

(16)

where $\Delta =\sqrt{{\delta }^2+{\tilde{\tau }}^2}$. The divergent term arises from the form of the temporal point splitting in Equation (12). Had we used a simple imaginary exponential instead, and set $\delta =0$, no divergence would have appeared, as we saw in Equation (6). However, the form of the divergence is that expected on general grounds, but it would seem it can be consistently removed. The fourth-order term is finite but was not explicitly given in [20]. It is twice the $O\left({\lambda }^4\right)$ term evaluated in Equation (4.14) in [27]:

$$E^{\left(4\right)}=-\frac{{\lambda }^4}{16a}\left(\frac{{\pi }^2}{8}-1\right)$$

(17)

3.2. First Approximation

Before we consider the general situation, let us see if we can extract some sort of reasonable approximation to the energy. We note that the leading terms in Equation (16) (the highest power of $\lambda$ in each order of $1/\nu$) can be readily summed:

$$\ln {\Delta }^E{\Delta }^H\sim -2\sum _{n=1}^{\infty }\frac{1}{n}{\left(\frac{\lambda t}{2\nu }\right)}^{2n}=2\ln \left(1-\frac{{\lambda }^2{t}^2}{{\left(2\nu \right)}^2}\right)$$

(18)

The terms we have summed here might be presumed to be the largest contributions, since, for a given power of ${\lambda }^2$, only the leading power of $1/{\nu }^2$ is kept. Then, if we subtract the leading, divergent term, we can write this contribution to the energy as:

$$\tilde{E}=E^{\left(2\right)}+{\tilde{E}}_R$$

(19)

where

$${\tilde{E}}_R=-\frac{{\lambda }^2}{\pi a}\sum _{l=1}^{\infty }f(2\nu /\lambda )$$

(20)

in terms of the function

$$f\left(x\right)={\int }_0^{1}dt{t}^2\sqrt{1-t^2}\frac{1}{x^2-t^2}=-\frac{\pi }{4}(1-2x^2+2x\sqrt{x^2-1})$$

(21)

which only exists if $x>1$. For a high x,

$$f\left(x\right)\sim \frac{\pi }{16x^2},x\gg 1$$

(22)

To improve convergence of the l sum, we can subtract the next term in the UAE, so:

$$\tilde{E}=E^{\left(2\right)}+E^{\left(4\right)}-\frac{{\lambda }^2}{\pi a}\sum _{l=1}^{\infty }\left[f\left(\frac{2\nu }{\lambda }\right)-\frac{\pi }{16}{\left(\frac{\lambda }{2\nu }\right)}^2\right]$$

(23)

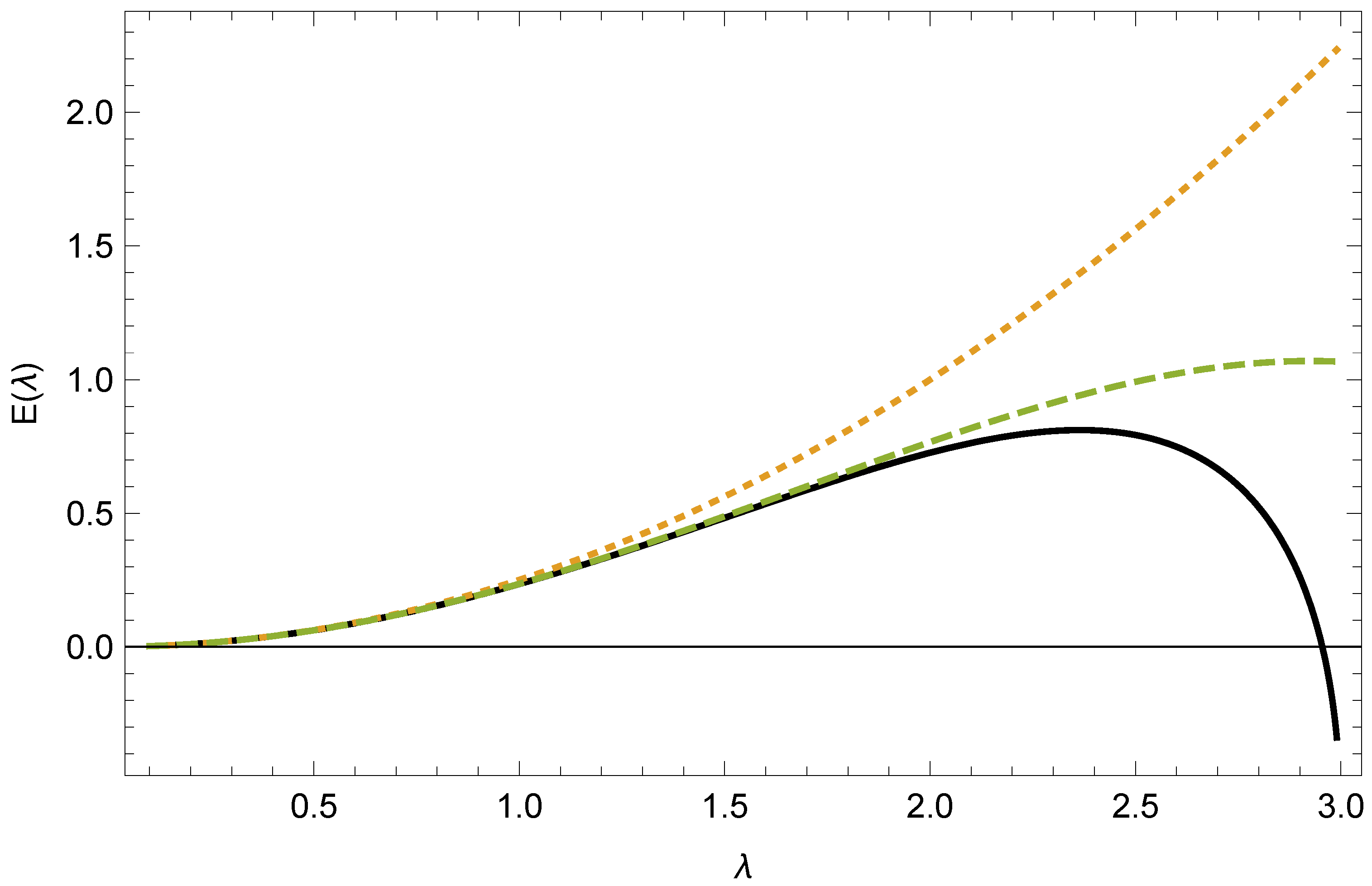
From this, we can readily obtain a numerical estimate, based on this leading approximation, valid for $\lambda <3$, shown in Figure 3.

The figure shows the first two UAE contributions, and the sum of all the leading terms as explained above, with the second-order divergence removed. It should be noted that the exact approximant is finite at $\lambda =3$, and $\tilde{E}(\lambda =3)=-0.686434/a$, but it is singular at that point, since the derivative becomes infinite here. Therefore, it is unclear how to analytically continue this approximant result to higher values of the coupling $\lambda$.

3.3. $O\left({\lambda }^2\right)$ Contribution

We can also, in principle, compute the exact order-${\lambda }^2$ contribution by doing the same angular momentum sum again using the addition theorem [25]. Indeed, the l-sum over the Bessel functions can thus be replaced by integrals over $w=2x\sqrt{2(1-\cos \delta )}$, for example,

$$\sum _{l=0}^{\infty }(2l+1)e_l^2\left(x\right)s_l^2\left(x\right)=\frac{x^2}{2}{\int }_0^{4x}\frac{dw}{w}{e}^{-w}$$

(24)

The divergence at $w=0$ here is irrelevant because of the derivative appearing in Equation (12). However, the terms involving derivatives of Bessel functions possess serious singularities when $\cos \delta =1$, which at present we do not know how to handle. Although these structures represent the infrared singularities of the derivatives of the modified Bessel function, because they result in divergences when the field-points overlap, they seem to represent ultraviolet singularities not captured by the UAE.

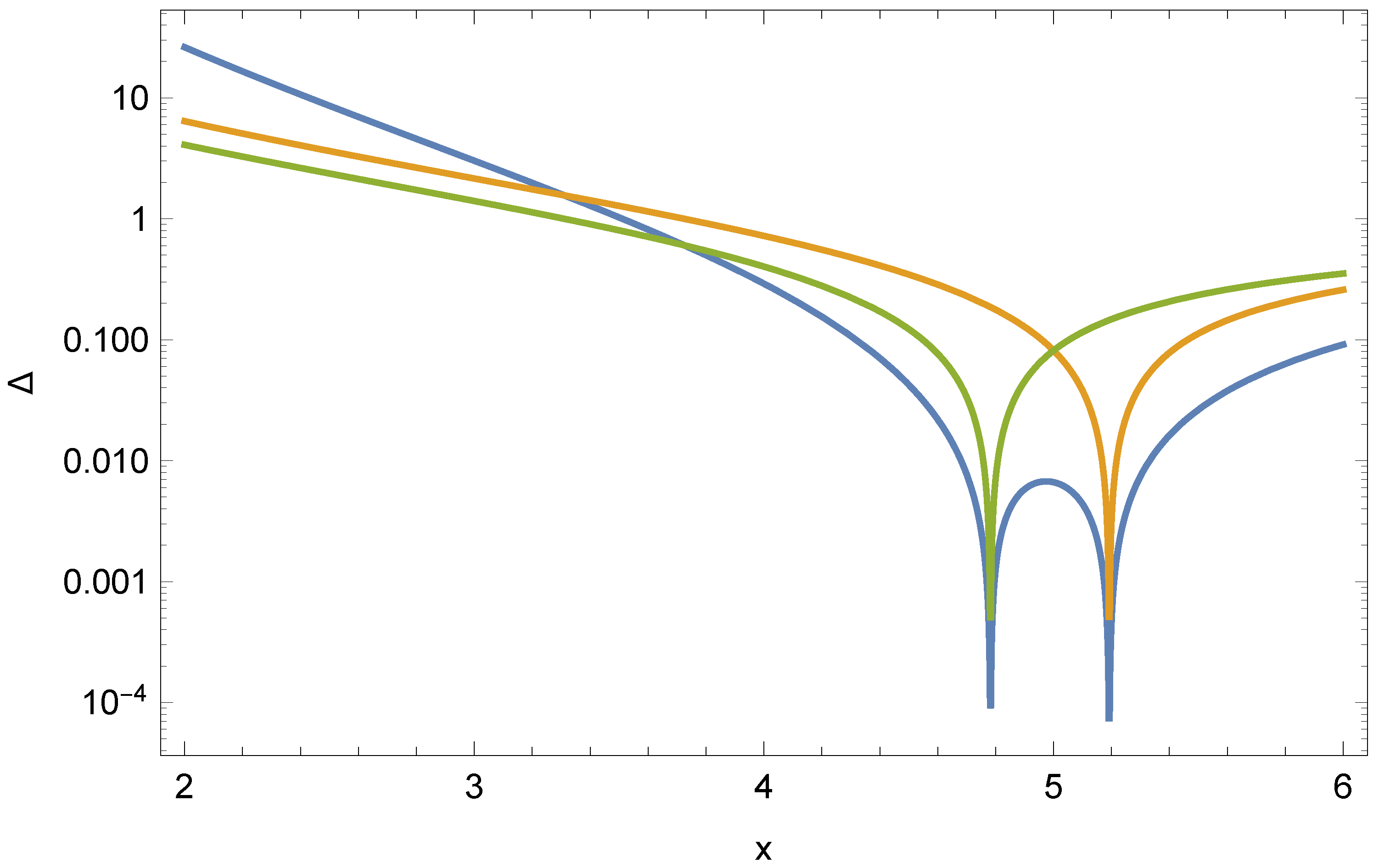
3.4. General Analysis

The difficulties we have encountered in $O\left({\lambda }^2\right)$ are symptomatic of a more general pathology. It is easy to see that ${\Delta }^E$ always has one zero for a finite positive x, and if $\lambda$ is large enough ${\Delta }^H$ does as well. (For $l=1$, the minimum value of $\lambda$ for ${\Delta }^H$ to develop a zero is ${\lambda }_1=8/3=2.666\dots$). For a high $\lambda$, both zeroes approach $\lambda /2$, as shown in Figure 4.

These zeroes translate into poles in the frequency integrand in Equation (12). This is rather surprising, since the point of doing the Euclidean rotation of the frequency to the imaginary axis, $\omega \to i\zeta$, is to avoid singularities along the real axis. However, this phenomenon by itself is not fatal, since we would think that the energy would be obtained by taking the real parts of Equations (12) and (14), that is, the principal values coming from these simple poles. However, numerically, this is slightly challenging.

Therefore, a better scheme would seem to consist in rotating back through $-\pi /4$, to a path of integration bisecting the first quadrant of the complex frequency plane. Removing the first two approximants coming from the UAE, we then obtain the following expression, which would seem amenable to numerical evaluation:

$$E=E^{\left(2\right)}+E^{\left(4\right)}-\frac{1}{4\pi a}\sum _{l=1}^{\infty }(2l+1)R_l\left(\lambda \right)$$

(25)

where the remainder is given by (the cutoff has been dropped, in the expectation that the remainder is finite):

$$R_l={\int }_0^{\infty }dx{w}_l(x,\lambda ),w_l(x,\lambda )=\Re (1-i)x\frac{d}{dx}{\left[\ln {\Delta }^E{\Delta }^h+\frac{{\lambda }^2{t}^2}{2{\nu }^2}+\frac{{\lambda }^4{t}^4}{{\left(2\nu \right)}^2}\right]}_{x\to x(1-i)}$$

(26)

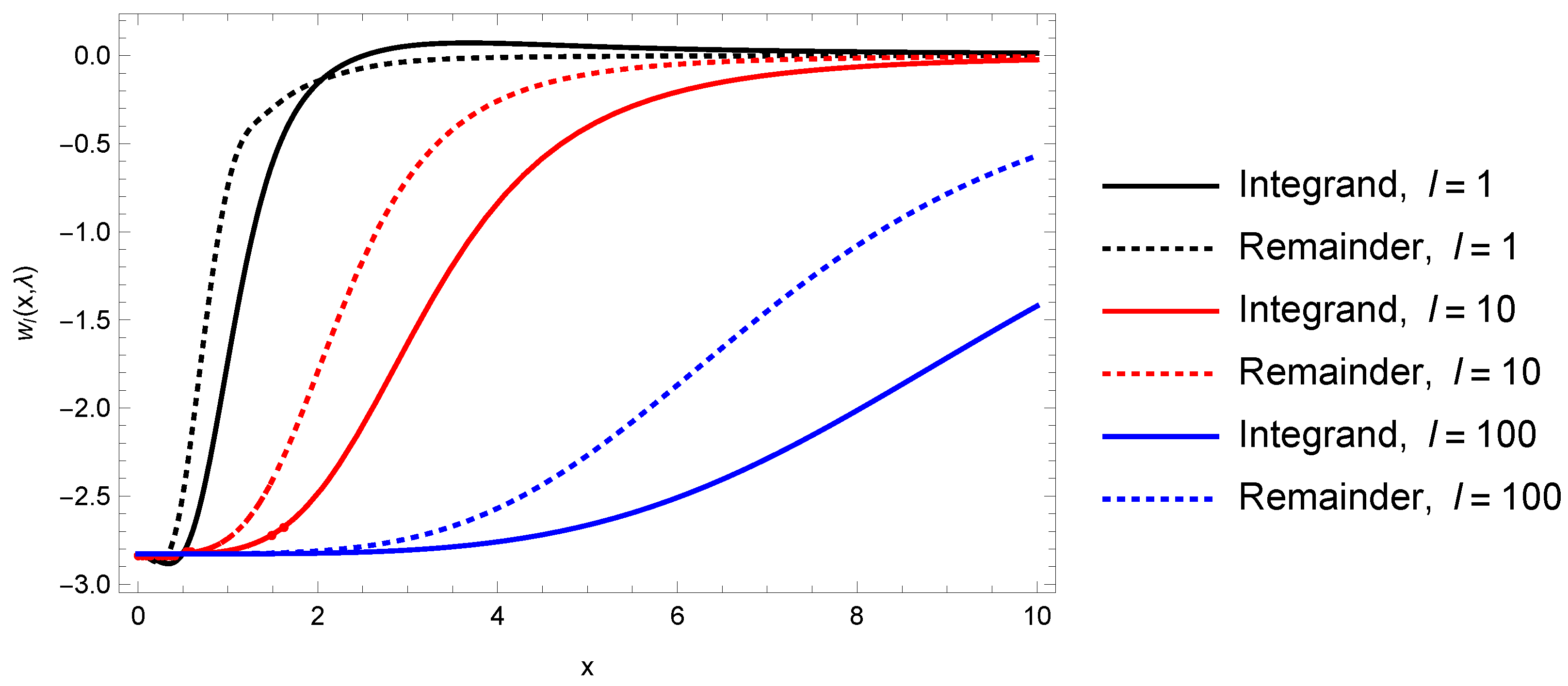
The integrand, computed numerically, is plotted in Figure 5.

It can be seen that subtraction of the leading UAE contributions greatly suppresses the large-x behavior, so the integrals are rapidly convergent. However, because of the small x singularities of the derivatives of the Bessel functions, there is a finite contribution at moderate x values, all the way down to $x=0$, which grows with l. Consequently, when this is integrated over x, the remainder $R_l$ grows with l. This growth appears to be cubic. When the $P_l\left(\cos \delta \right)$ convergence factor is inserted into the l summation, this translates into a divergence of order ${\delta }^{-5}$, a quintic divergence. We conclude that the UAE does not capture the real divergence of the self-energy for the isorefractive sphere. Because of numerical errors, and the likely appearance of a subleading logarithmic divergence, it appears infeasible to extract a finite remainder, even if the divergent terms can be “renormalized”.

4. Conclusions

We have re-examined two situations that extend the classic problem of the perfectly conducting sphere: the diaphanous dielectric-diamagnetic ball, where the speed of light is the same on both sides of the spherical surface, and the isorefractive $\delta$-function sphere, where the electric and magnetic couplings are equal and opposite. The former situation has been well studied, and is uniquely finite; here we extend the accuracy of the numerical calculations slightly. The latter situation, although apparently ultravioletly finite, possesses infrared sensitivity that translates into much more severe ultraviolet divergences than the divergences revealed by the UAE, which seem to make it practically impossible to extract a well-defined self-energy. This sensitivity manifests itself as poles on the imaginary frequency axis in the energy integrand. By truncating the theory, we are able to make estimates for small coupling $\lambda$. Further study of this surprisingly pathological model is warranted.

As with the diaphanous ball problem discussed in Section 2, we could also consider the cylindrical analog of the isorefractive $\delta$ sphere. This is a problem that has yet to be investigated, to our knowledge, but doing so might shed light on the difficulties we have encountered in the spherical problem. It should also be emphasized that we have only considered the static situation; another research direction would be to examine a time-varying $\delta$-function shell, which would generalize commonly discussed models of the “dynamical Casimir effect” with radially pulsating metallic walls [28].