An Adaptive Initial Alignment Algorithm Based on Variance Component Estimation for a Strapdown Inertial Navigation System for AUV
Abstract
:1. Introduction
2. Basic Knowledge
2.1. Principles of SINS Initial Alignment
2.2. Nonlinear Filter CKF
3. An Improved Initial Alignment Algorithm Based on Adaptive VCKF
3.1. Adaptive Filter Based on the VCE Method
3.2. An initial Alignment Algorithm Based on VCKF
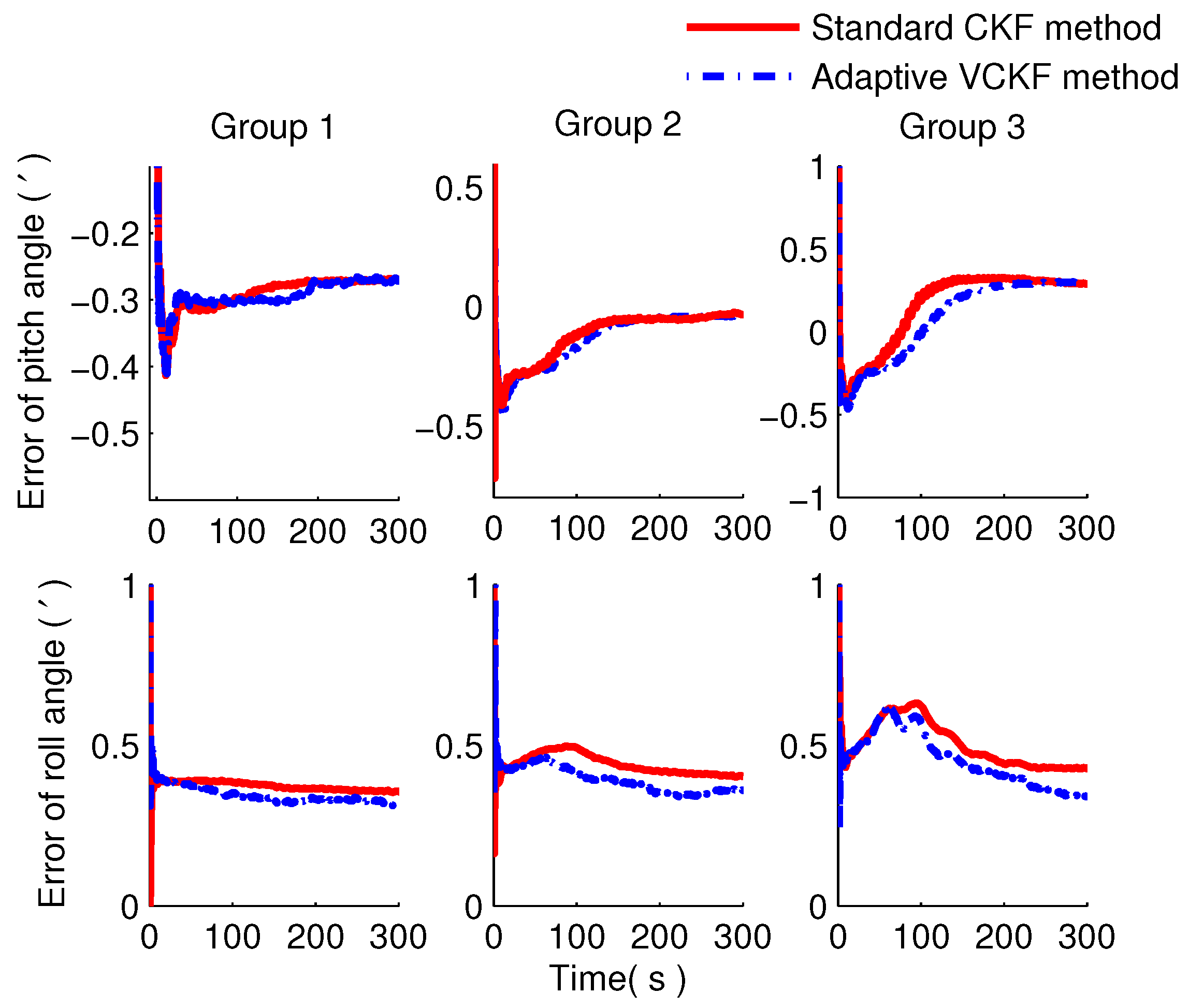
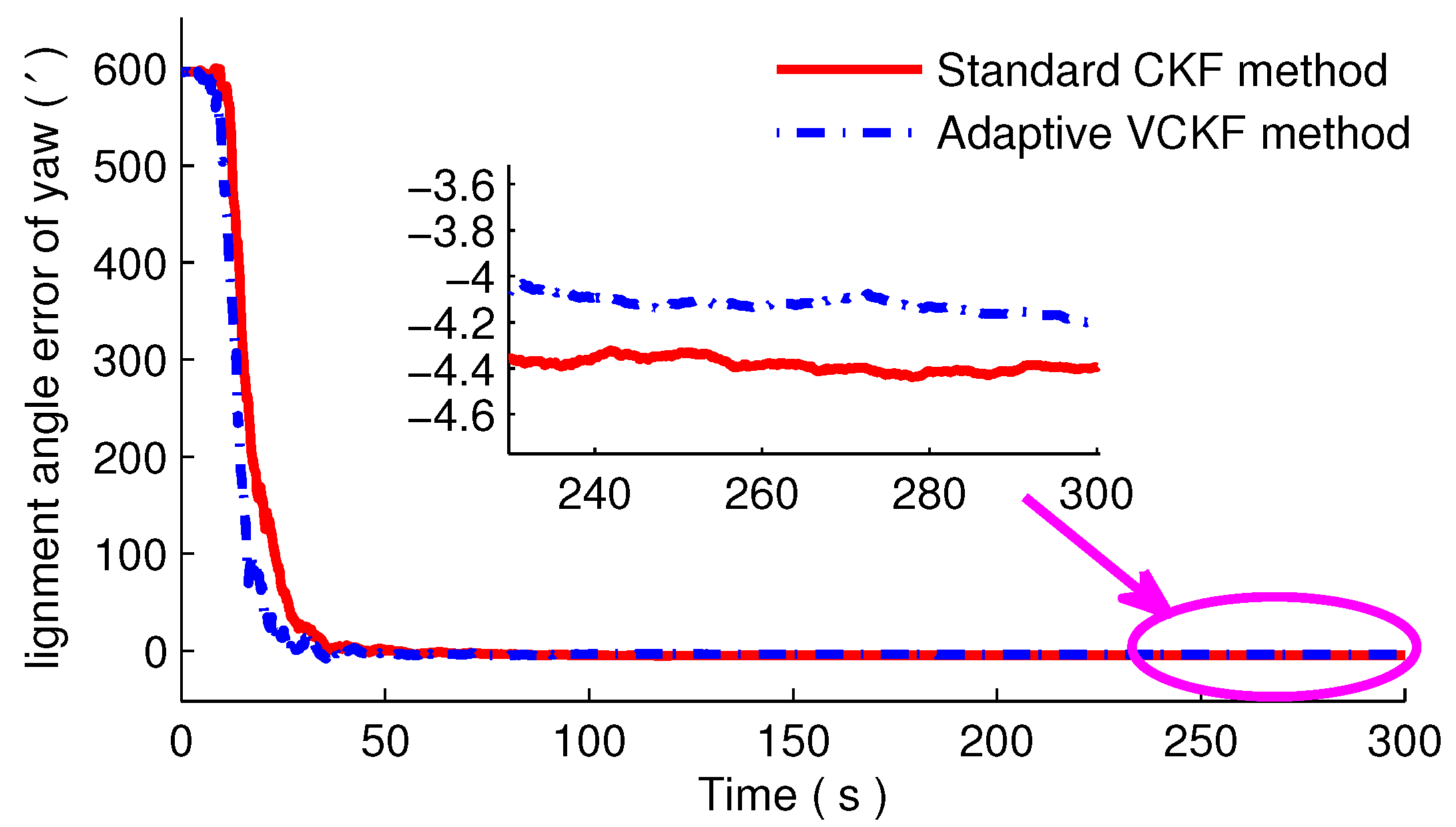
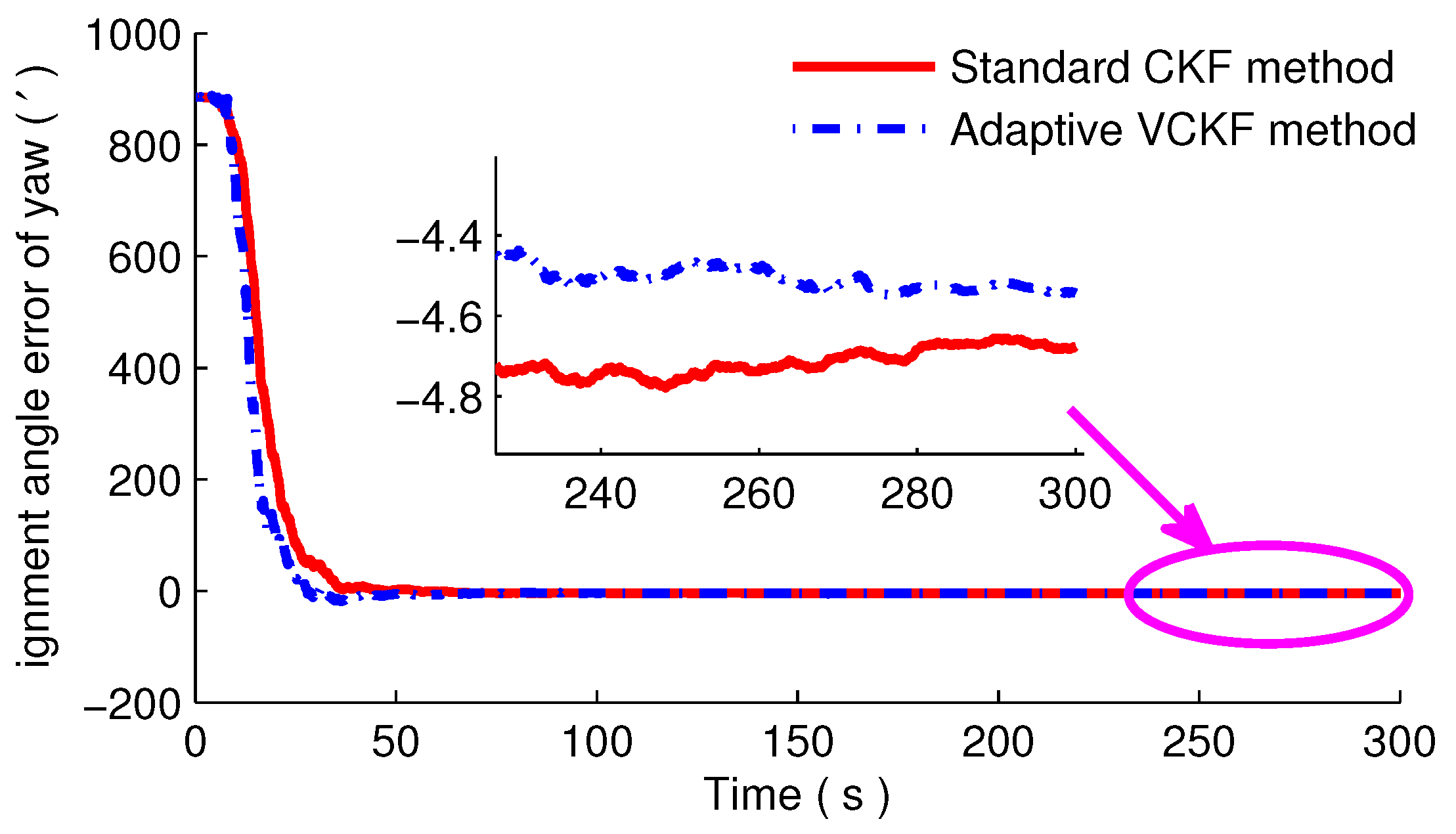
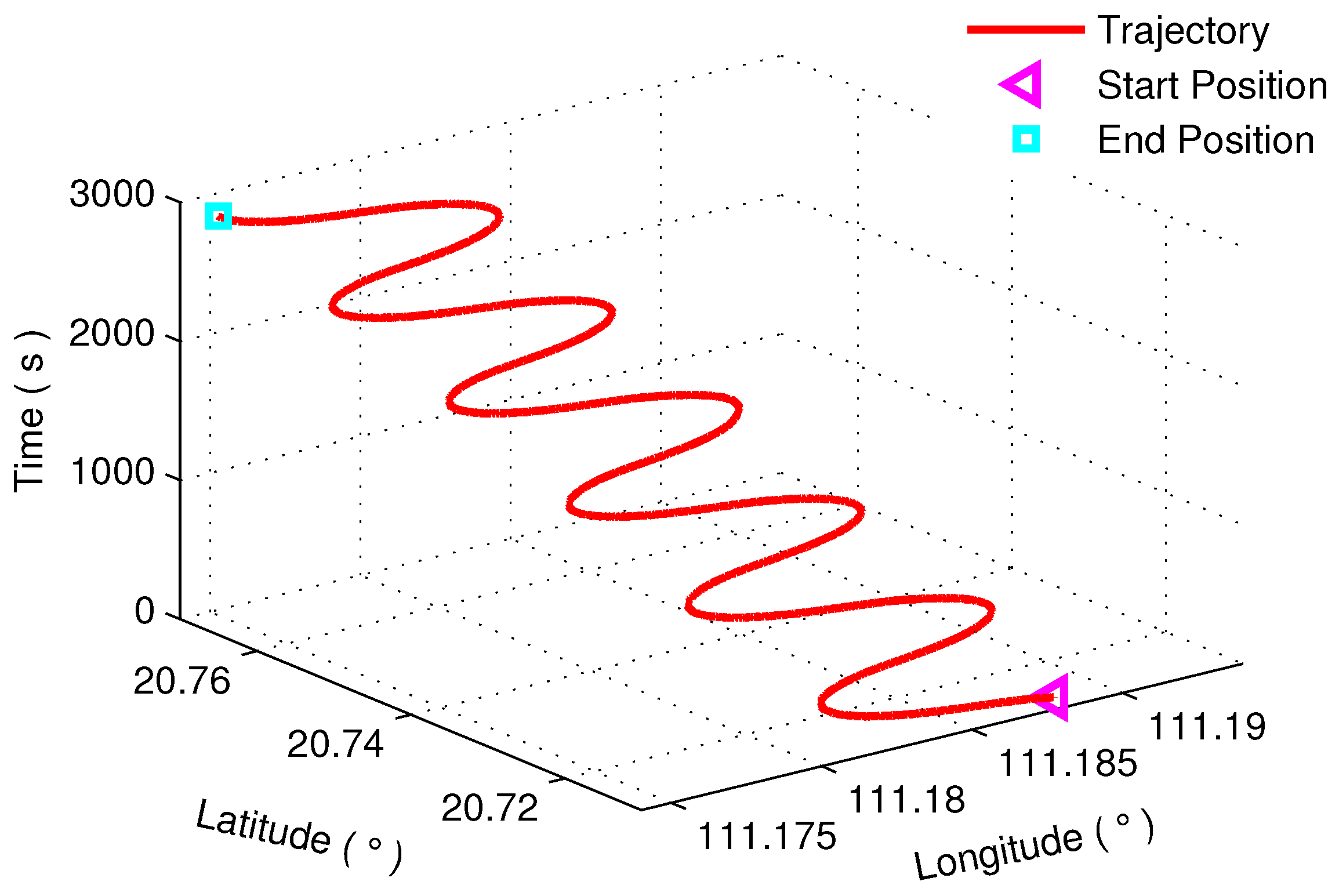
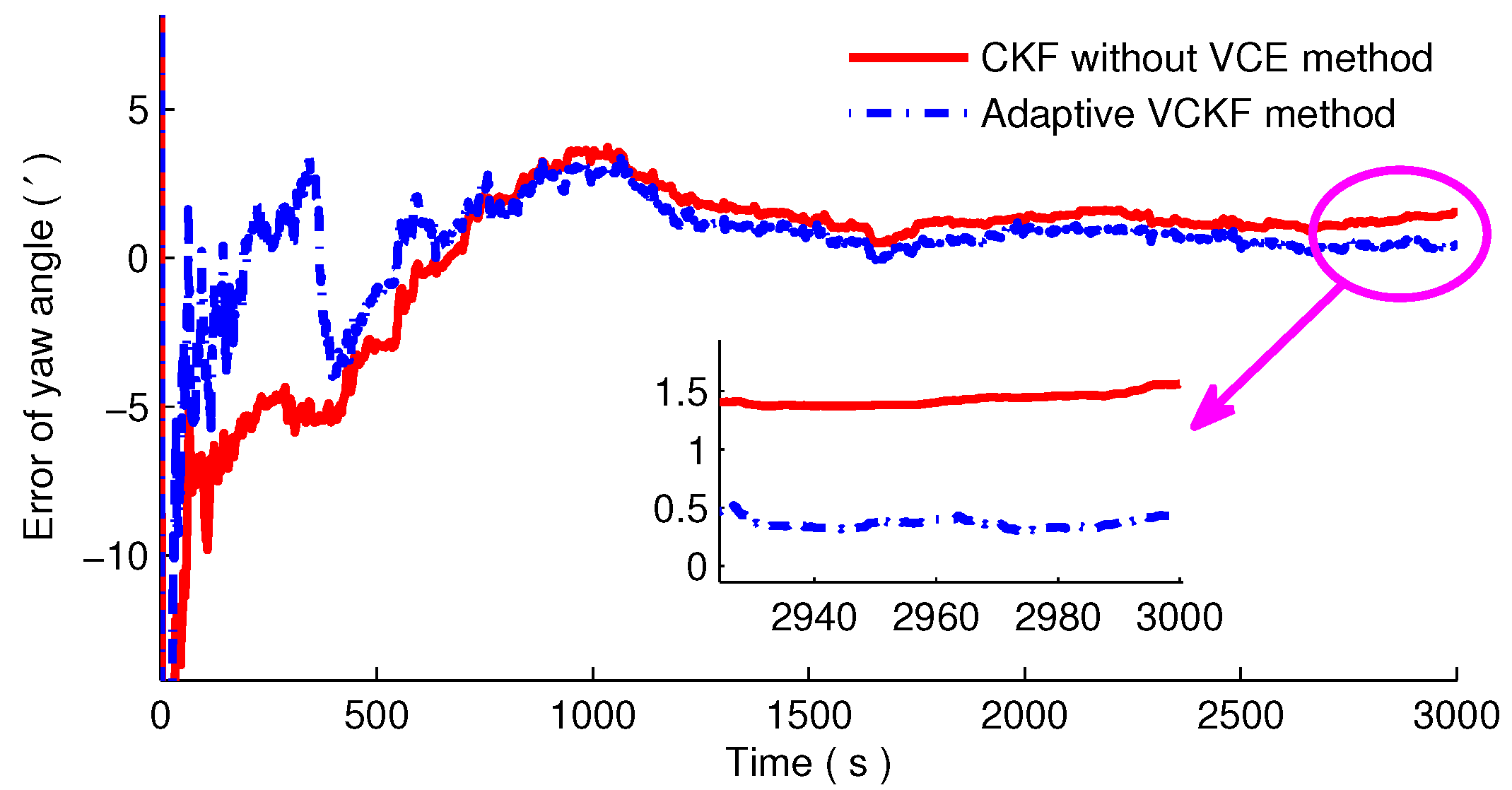
4. Simulations and Experiments
4.1. Simulation and Analysis
4.2. Experiment and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. IEEE J. Ocean. Eng. 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Lu, L.; Wu, W. A Novel Scheme for DVL-Aided SINS In-Motion Alignment Using UKF Techniques. Sensors 2013, 13, 1046–1063. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Li, W.; Yan, M.; Yang, S.X. The path planning of AUV based on DS information fusion map building and bio-inspired neural network in unknown dynamic environment. Int. J. Adv. Robot. Syst. 2014, 11, 34. [Google Scholar] [CrossRef]
- Li, D.; Ji, D.; Liu, J.; Lin, Y. A multi-model EKF integrated navigation algorithm for deep water AUV. Int. J. Adv. Robot. Syst. 2016, 13, 1–15. [Google Scholar] [CrossRef]
- Chang, L.; Li, J.; Chen, S. Initial Alignment by Attitude Estimation for Strapdown Inertial Navigation Systems. IEEE Trans. Instrum. Meas. 2015, 64, 784–794. [Google Scholar] [CrossRef]
- Tan, C.; Zhu, X.; Su, Y.; Wang, Y.; Wu, Z.; Gu, D. A New Analytic Alignment Method for a SINS. Sensors 2015, 15, 27930–27953. [Google Scholar] [CrossRef] [PubMed]
- Dorveaux, E.; Boudot, T.; Hillion, M.; Petit, N. Combining inertial measurements and distributed magnetometry for motion estimation. In Proceedings of the American Control Conference (ACC), San Francisco, CA, USA, 29 June–1 July 2011; pp. 4249–4256. [Google Scholar]
- Gao, W.; Deng, L.; Yu, F.; Zhang, Y.; Sun, Q. A novel initial alignment algorithm based on the interacting multiple model and the Huber methods. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 910–915. [Google Scholar]
- Han, S.; Wang, J. A Novel Initial Alignment Scheme for Low-Cost INS Aided by GPS for Land Vehicle Applications. J. Navig. 2010, 63, 663–680. [Google Scholar] [CrossRef]
- Xiong, J.; Guo, H.; Yang, Z. A two-position SINS initial alignment method based on gyro information. Adv. Space Res. 2014, 53, 1657–1663. [Google Scholar] [CrossRef]
- Hu, Z.; Su, Y. Initial alignment of the MEMS inertial measurement system assisted by magnetometers. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 276–280. [Google Scholar]
- Gao, W.; Zhang, Y.; Wang, J. A Strapdown Interial Navigation System/Beidou/Doppler Velocity Log Integrated Navigation Algorithm Based on a Cubature Kalman Filter. Sensors 2014, 14, 1511–1527. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Zhu, Z.H. Fractional-Order Tension Control Law for Deployment of Space Tether System. J. Guid. Control Dyn. 2014, 37, 157–167. [Google Scholar] [CrossRef]
- Atia, M.M.; Liu, S.; Nematallah, H.; Karamat, T.B.; Noureldin, A. Integrated Indoor Navigation System for Ground Vehicles With Automatic 3-D Alignment and Position Initialization. IEEE Trans. Veh. Technol. 2015, 64, 1279–1292. [Google Scholar] [CrossRef]
- Ali, J.; Mirza, M.R.U.B. Initial orientation of inertial navigation system realized through nonlinear modeling and filtering. Measurement 2011, 44, 793–801. [Google Scholar] [CrossRef]
- Han, H.; Xu, T.; Wang, J. Tightly Coupled Integration of GPS Ambiguity Fixed Precise Point Positioning and MEMS-INS through a Troposphere-Constrained Adaptive Kalman Filter. Sensors 2016, 16, 1057. [Google Scholar] [CrossRef] [PubMed]
- Athans, M.; Wishner, R.; Bertolini, A. Suboptimal state estimation for continuous-time nonlinear systems from discrete noisy measurements. IEEE Trans. Autom. Control 1968, 13, 504–514. [Google Scholar] [CrossRef]
- Haykin, S. Chapter 7: The Unscented Kalman Filter; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; pp. 221–280. [Google Scholar]
- Sun, G.; Zhu, Z.H. Fractional-Order Dynamics and Control of Rigid-Flexible Coupling Space Structures. J. Guid. Control Dyn. 2015, 38, 1324–1329. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman Filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature Kalman Filtering for Continuous-Discrete Systems: Theory and Simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Wang, J.G.; Gopaul, N.; Scherzinger, B. Simplified Algorithms of Variance Component Estimation for Static and Kinematic GPS Single Point Positioning. J. Glob. Position. Syst. 2009, 8, 43–52. [Google Scholar] [CrossRef]
- Zhang, L. Robust H-infinity CKF/KF hybrid filtering method for SINS alignment. IET Sci. Meas. Technol. 2016, 10, 916–925. [Google Scholar] [CrossRef]
- Narasimhappa, M.; Rangababu, P.; Sabat, S.L.; Nayak, J. A modified Sage-Husa adaptive Kalman filter for denoising Fiber Optic Gyroscope signal. In Proceedings of the 2012 Annual IEEE India Conference (INDICON), Kochi, India, 7–9 December 2012; pp. 1266–1271. [Google Scholar]
- Jin, M.; Zhao, J.; Jin, J.; Yu, G.; Li, W. The adaptive Kalman filter based on fuzzy logic for inertial motion capture system. Measurement 2014, 49, 196–204. [Google Scholar] [CrossRef]
- Chang, L.; Li, K.; Hu, B. Huber’s M-estimation-based process uncertainty robust filter for integrated INS/GPS. IEEE Sens. J. 2015, 15, 3367–3374. [Google Scholar] [CrossRef]
- Wang, R.; Xiong, Z.; Liu, J.Y.; Li, R.; Peng, H. SINS/GPS/CNS information fusion system based on improved Huber filter with classified adaptive factors for high-speed UAVs. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 441–446. [Google Scholar]
- Yu, F.; Sun, Q.; Lv, C.; Ben, Y.; Fu, Y. A SLAM Algorithm Based on Adaptive Cubature Kalman Filter. Math. Probl. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Available online: http://www.ixblue.com/products/phins/ (accessed on 18 July 2017).


| Parameters | Sets |
|---|---|
| Initial latitude | |
| Initial longitude | |
| Initial horizontal velocity | m/s |
| Gravity acceleration | m/s |
| Initial horizontal misalignment angles | |
| Initial vertical misalignment angles | Group 1: ; |
| Group 2: ; | |
| Group 3: ; | |
| Constant biases of the accelerometers | |
| Random noise of the accelerometers | |
| Constant drifts of the gyroscopes | /h |
| Random noise of the gyroscopes | /h |
| Sampling frequency | 100 Hz |
| Groups | Error of Yaw Angle () | |
|---|---|---|
| CKF without VCE Method | Adaptive VCKF Method | |
| Group 1 | −4.05 | −3.86 |
| Group 2 | −4.40 | −4.19 |
| Group 3 | −4.71 | −4.54 |
| Parameters | Values | |
|---|---|---|
| Gyroscope | Dynamic range | /s |
| Bias stability | /h | |
| random walk | /h | |
| Scale factor stability | 50 ppm | |
| Accelerometer | Dynamic range | g |
| Bias stability | mg | |
| random walk | mg | |
| Scale factor stability | 50 ppm | |
| DVL | Frequency | 600 kHz |
| Accuracy | mm/s | |
| Maximum Altitude | 110 m | |
| Minimum Altitude | 0.3 m | |
| Maximum Velocity | kn | |
| Maximum Ping Rate | 5/s |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Li, Y.; Sun, Q.; Zhang, Y. An Adaptive Initial Alignment Algorithm Based on Variance Component Estimation for a Strapdown Inertial Navigation System for AUV. Symmetry 2017, 9, 129. https://doi.org/10.3390/sym9080129
Dong Q, Li Y, Sun Q, Zhang Y. An Adaptive Initial Alignment Algorithm Based on Variance Component Estimation for a Strapdown Inertial Navigation System for AUV. Symmetry. 2017; 9(8):129. https://doi.org/10.3390/sym9080129
Chicago/Turabian StyleDong, Qianhui, Yibing Li, Qian Sun, and Ya Zhang. 2017. "An Adaptive Initial Alignment Algorithm Based on Variance Component Estimation for a Strapdown Inertial Navigation System for AUV" Symmetry 9, no. 8: 129. https://doi.org/10.3390/sym9080129






