Effect of Constitutive Equations on Springback Prediction Accuracy in the TRIP1180 Cold Stamping

Abstract

This study aimed to evaluate the effect of constitutive equations on springback prediction accuracy in cold stamping with various deformation modes. This study investigated the ability of two yield functions to describe the yield behavior: Hill’48 and Yld2000-2d. Isotropic and kinematic hardening models based on the Yoshida-Uemori model were adopted to describe the hardening behavior. The chord modulus model was used to calculate the degradation of the elastic modulus that occurred during plastic loading. Various material tests (such as uniaxial tension, tension-compression, loading-unloading, and hydraulic bulging tests) were conducted to determine the material parameters of the models. The parameters thus obtained were implemented in a springback prediction finite element (FE) simulation, and the results were compared to experimental data. The springback prediction accuracy was evaluated using U-bending and T-shape drawing. The constitutive equations wielded significant influence over the springback prediction accuracy. This demonstrates the importance of selecting appropriate constitutive equations that accurately describe the material behaviors in FE simulations.

1. Introduction

In recent years, lightweight vehicles have gained attention as fuel efficiency and gas emission regulations become increasingly stringent [1]. As weight reduction has become a key goal, many researchers have devoted significant efforts to selecting the materials for manufacturing automotive parts. Advanced high strength steel (AHSS) has been widely used in the automotive industry for its light weight, crashworthiness, and productivity. However, it is difficult to achieve dimensional accuracy with AHSS because its higher elastic recovery and yield strength cause excessive springback [2]. Fabricating a target product shape with AHSS is challenging for part manufacturers, requiring a considerable amount of time as well as additional costs to modify tools for this springback.

Finite element (FE) simulation may be applied to describe AHSS material behaviors and springback, as this provides a cost-effective and reliable method for predicting springback. The constitutive equations used in FE simulations strongly influence the accuracy of the prediction results. Thus, many researchers have suggested varying constitutive equations. Multiple equations have been used to describe the hardening behavior of AHSS, including the nonlinear kinematic hardening model proposed by Chaboche [3], the kinematic hardening model based on cyclic plasticity suggested by Yoshida, and the distortional hardening model recommended by Barlat. In addition, Hill’48 and Yld2000-2d have been widely used to model the anisotropic behavior of AHSS.

Many published studies have investigated the influence of constitutive equations on simulated prediction results. Lee et al. [4] performed a springback evaluation of automotive sheets based on an isotropic kinematic hardening model and anisotropic yield functions. It was found that the hardening behaviors, including Bauschinger and transient elements, were well represented by the modified Chaboche model. Furthermore, the work-hardening data for dual phase steel (DP steel) was found to better conform to a power law-type hardening law than to the Voce-type law. Zang et al. [5] developed an elasto-plastic constitutive model based on one-surface plasticity. Their results demonstrated that the resulting material model is able to accurately predict springback when materials show a constant offset in permanent softening. Furthermore, Larsson et al. [6] concluded that neither isotropic nor kinematic hardening models were sufficient to describe the plastic-hardening behavior seen in non-linear strain paths. Thus, Larsson employed a combined isotropic-kinematic hardening model to evaluate the effects of springback in steel sheets. Eggertsen et al. [7] predicted the springback using various hardening models and yield functions. The Yoshida-Uemori hardening model has been shown to yield results that fit experimental measurements better than other options. Kim et al. [8] performed die compensation based on the Yld2000-2d yield function and Yoshida-Uemori hardening model. It was concluded that the dimensional accuracy of AHSS products can be achieved efficiently through die compensation using the material models in the multi-stage stamping process. Previous studies have demonstrated that the descriptions of anisotropic behavior, the Bauschinger effect, transient behavior, and the permanent softening effect are important. Successful springback prediction via FE simulation is principally dependent on selecting accurate yield criterion, hardening models, and material coefficients [9]. However, the above studies dealt with simply configured products such as those used in U-bending tests [10] and did not focus on AHSS products with various deformation modes. Therefore, it is necessary to evaluate the effect of the constitutive equations on springback prediction accuracy in AHSS cold stamping with multiple deformation modes.

The objective of this study was to evaluate the effect of constitutive equations on springback prediction accuracy in TRIP1180 cold stamping. In this study, two types of yield function were considered to describe the yield behavior: Hill’48 and the Yld2000-2d. Isotropic and kinematic hardening models based on the Yoshida-Uemori model were also adopted to describe the hardening behavior. The chord modulus model was utilized in the FE simulation alongside the hardening model constants. Various material tests, such as uniaxial tension, tension–compression, loading–unloading, and hydraulic bulging tests were conducted to determine material parameters for the models. The obtained parameters were utilized in the FE simulation to predict springback, and the results were compared with experimental data. In addition, U-bending and T-shape drawing were employed to evaluate the accuracy of the springback predictions.

2. Constitutive Equations for the TRIP1180 Sheet Steel

A TRIP1180 steel sheet with a thickness of 1.0 mm was investigated in this study. The TRIP1180 was used as received. The constitutive equations Hill’48 and Yld2000-2d were used to describe its yield behavior. Moreover, isotropic and kinematic hardening models based on the Yoshida-Uemori model were adopted to express hardening behavior. The chord modulus model was used to describe the degradation of the elastic modulus that occurs during plastic loading. The material constants of TRIP1180 for the constitutive equations were obtained from uniaxial tension, tension-compression, loading-unloading, and hydraulic bulging tests.

2.1. Yield Function

Yield functions define the transition of a material from elastic to plastic behavior in complex stress states. In this study, the Hill’48 and Yld2000-2d yield functions were used to evaluate the anisotropic yield behavior of TRIP1180. In order to determine the material parameters of the yield functions, ASTM E8 standard uniaxial tension tests were performed on specimens using a MTS universal testing machine for different rolling directions (0°, 45°, 90°), and hydraulic bulge tests were conducted to obtain a stable biaxial stress-strain curve with an Erichsen bulge tester. The biaxial yield stress and biaxial anisotropic plasticity coefficients were derived from the developed curve. A mechanical measurement device was placed on the top of the specimen to allow in-plane elongation and curvature measurements using an extensometer. The membrane stress and thickness strain were calculated using these measurements as described in the literature [11]. The yield stress in balanced biaxial tension (${\sigma }_b$) was calculated based on the work-equivalence principle by comparing the bulge and uniaxial tension flow curves. The results of these tests are shown in Figure 1.

2.1.1. Hill’48 Yield Function

The anisotropic yield criterion proposed by Hill [12] is one of the most widely used yield functions. The Hill’48 yield function is also easy to express, and as such has been widely used to investigate the effect of anisotropy on springback, especially in steel sheets. This function is defined as follows:

$$2f(\sigma )=F{({\sigma }_{yy}-{\sigma }_{zz})}^2+G{({\sigma }_{zz}-{\sigma }_{xx})}^2+H{({\sigma }_{xx}-{\sigma }_{yy})}^2+2(L{{\sigma }^2}_{yz}+M{{\sigma }^2}_{zx}+N{{\sigma }^2}_{xy})=1$$

(1)

Under plane stress conditions (σ_zz = σ_yz = σ_zx = 0, L = M = 0), the Hill’48 model can be mathematically represented as follows:

$$2f(\sigma )=(G+H){{\sigma }^2}_{xx}+(F+H){{\sigma }^2}_{yy}-2H{\sigma }_{xx}{\sigma }_{yy}+2N{{\sigma }^2}_{xy}=1$$

(2)

where σ_xx, σ_yy, and σ_zz are the normal stresses in the rolling, transverse, and thickness directions, respectively; σ_xy, σ_yz, and σ_zx are the shear stresses in the xy, yz, and zx planes, respectively; and F, G, H, and N are the anisotropic coefficient parameters. The material parameters of the Hill’48 yield function are principally obtained from Lankford values at angles of 0°, 45°, and 90° to the rolling direction. The anisotropic parameters F, G, H and N can be formulated in terms of the r-values r₀, r₄₅, r₉₀ as follows:

$$F=\frac{r_0}{r_{90}(1+r_{90})},G=\frac{1}{(1+r_0)},H=\frac{r_0}{(1+r_0)},N=\frac{(r_0+r_{90})(1+2r_{45})}{2r_{90}(1+r_0)}$$

(3)

The mechanical properties and material constants thus determined are summarized in

Table 1. Material properties of TRIP1180 steel.

Test Direction	E0 (GPa)	YS (MPa)	UTS (MPa)	Elongation (%)	R-Value
Rolling direction (0°)	200.5	861.9	1180	17.2	0.795
Diagonal direction (45°)	200.7	866.6	1175	16.0	0.958
Transverse direction (90°)	206.3	866.2	1182	14.9	0.967

and

Table 2. Material constants of TRIP1180 for the Hill’48 yield function.

Material	F	G	H	N
TRIP1180	0.4580	0.5571	0.4429	1.480

.

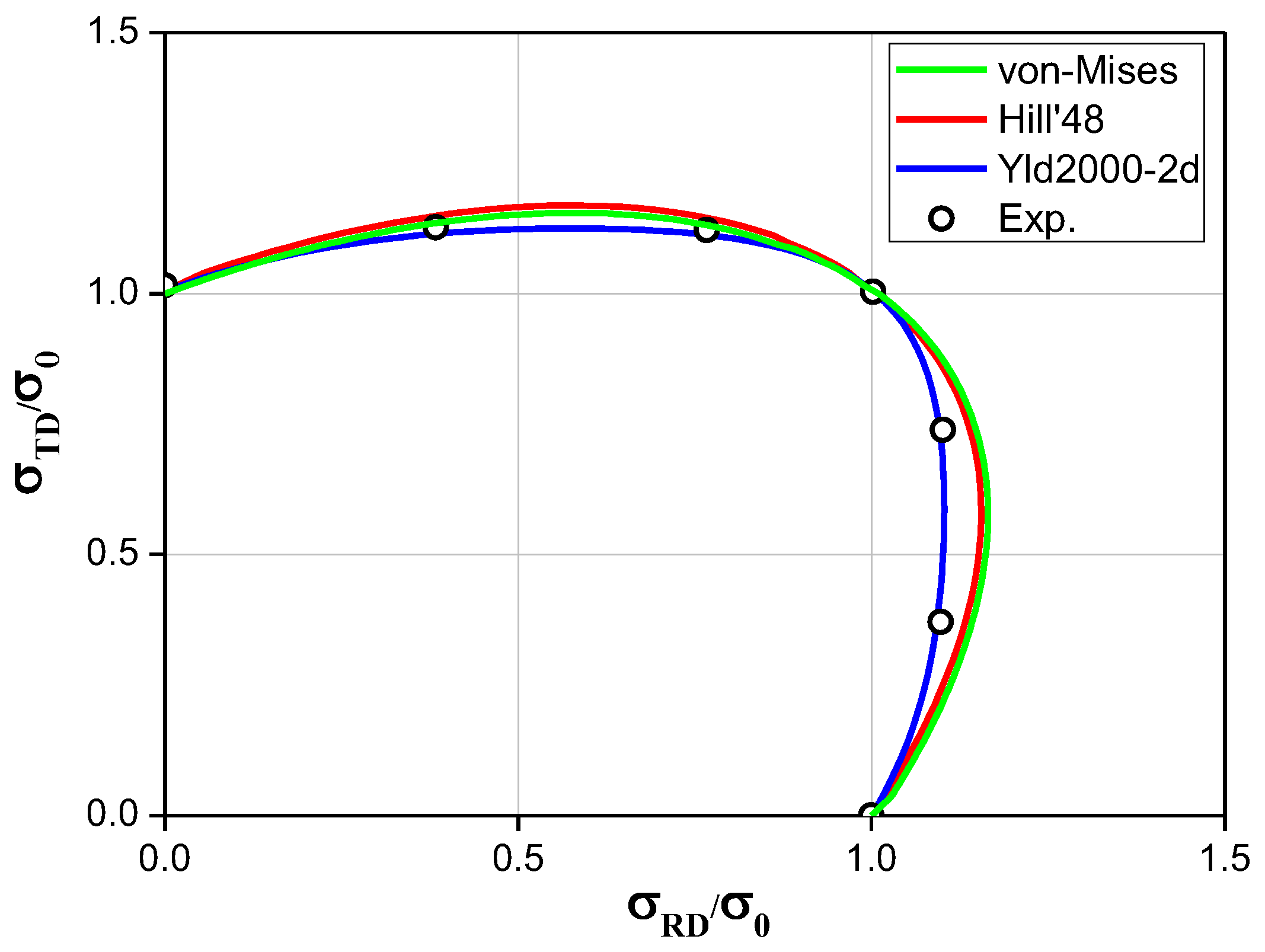
2.1.2. Yld2000-2d Yield Function

The Yld2000-2d function [13] proposed by Barlat et al. can describe yield behaviors for various deformation modes. This yield function has eight anisotropic coefficients related to the experimental yield stresses (σ₀, σ₄₅, σ₉₀, σ_b) and anisotropic parameters (r₀, r₄₅, r₉₀, r_b). This function can be expressed as shown in Equation (4):

$$f=\frac{{\varphi }^{\prime }+{\varphi }^{″}}{2},f={\left|X_1^{\prime }-X_2^{\prime }\right|}^a+{\left|2X_2^{″}+X_1^{″}\right|}^a+{\left|2X_1^{″}+X_2^{″}\right|}^a=2\overline{\sigma }$$

(4)

where $\overline{\sigma }$ is the effective stress and $a$ is a constant related to the crystalline structure of the material, which was set to 6 in this study (for FCC, $a=8$ and for BCC $a=6$, thus, for TRIP1180 $a=6$). In Equation (4), ${\varphi }^{\prime }={\left|X_1^{\prime }-X_2^{\prime }\right|}^a$ and ${\varphi }^{″}={\left|2X_2^{″}+X_1^{″}\right|}^a+{\left|2X_1^{″}+X_2^{″}\right|}^a$ where $X_1$ and $X_2$ are the principal values of the matrices, $X^{\prime }$ and $X^{″}$, whose components are obtained from the following linear transformations of the Cauchy stress ($\sigma$) and deviatoric Cauchy stress (${\sigma }^{\prime }$), respectively:

$$X^{\prime }=C^{\prime }{\sigma }^{\prime }=C^{\prime }T\sigma =L^{\prime }\sigma ,X^{″}=C^{″}{\sigma }^{\prime }=C^{″}T\sigma =L^{″}\sigma$$

(5)

where

$$\left[\begin{array}{l}{L}_{11}^{\prime }\\ L_{12}^{\prime }\\ L_{21}^{\prime }\\ L_{22}^{\prime }\\ L_{66}^{\prime }\end{array}\right]=\left[\begin{array}{ccc}2/3& 0& 0\\ -1/3& 0& 0\\ 0& -1/3& 0\\ 0& 2/3& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\alpha }_7\end{array}\right],\left[\begin{array}{l}{L}_{11}^{″}\\ L_{12}^{″}\\ L_{21}^{″}\\ L_{22}^{″}\\ L_{66}^{″}\end{array}\right]=\frac{1}{9}\left[\begin{array}{ccccc}-2& 2& 8& -2& 0\\ 1& -4& -4& 4& 0\\ 4& -4& -4& 1& 0\\ -2& 8& 2& -2& 0\\ 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\alpha }_3\\ {\alpha }_4\\ {\alpha }_5\\ {\alpha }_6\\ {\alpha }_8\end{array}\right]$$

(6)

The material constants (eight anisotropic coefficients) included in the ${\mathbf{L}}^{\prime }$ and ${\mathbf{L}}^{″}$ tensors can be determined according to the rolling direction using the yield stress and anisotropic coefficient (three uniaxial yield stresses, three r-values in the three material directions, and the balanced-biaxial r-values and yield stress: σ₀, σ₄₅, σ₉₀, σ_b, r₀, r₄₅, r₉₀ and r_b). This calculation procedure involves solving a system of nonlinear equations. This was performed in the current experiment by using the Newton-Raphson iteration method. The determined anisotropic coefficients are summarized in

Table 3. Material constants of TRIP1180 using the Yld2000-2d yield function.

α1	α2	α3	α4	α5	α6	α7	α8
0.9471	1.0199	0.9867	0.9925	1.0141	0.9815	0.9910	1.0007

.

Based on previous experimental results, the yield surface of the von-Mises, Hill’48, and Yld2000-2d models can be plotted alongside experimental results. The yield surface results are shown in Figure 2. It can be seen that the Yld2000-2d model matches well with the experimental results.

2.2. Hardening Model

In plasticity, the hardening rule is used to describe the behavior of a material during plastic deformation. In this study, the isotropic and Yoshida-Uemori kinematic hardening models were applied to evaluate the hardening behavior of TRIP1180. In order to accurately predict the springback, it is essential to analyze the stress-strain behaviors of sheet metals during tension-compression loading. For this reason, tension-compression tests were performed on a specimen modified from the standard SEP1240 [14] with a gauge length of 50 mm, as depicted in Figure 3a. A vertical load was applied to the uniform elongation portion of center of the specimen to prevent buckling, as shown in Figure 3b. This allowed tension-compression tests to be performed reliably.

2.2.1. Isotropic Hardening Model

When expansion of the yield surface is uniform in all directions in the stress space, the hardening behavior is referred to as isotropic. The Swift isotropic hardening model [15] used in this study can successfully describe isotropic behavior under these conditions. The Swift isotropic hardening model is defined as follows:

$$\overline{\sigma }=K{({\overline{\epsilon }}_0+{\overline{\epsilon }}_{\mathrm{p}})}^n$$

(7)

where $\overline{\sigma }$ is the effective stress and ${\overline{\epsilon }}_p$ is the effective strain (total true strain minus recoverable strain). Thus, ${\overline{\epsilon }}_p$ represents the residual true strains after elastic unloading. Constants K, n, and ε₀ are material constants related to the hardening behavior. The material parameters of the Swift hardening model were principally obtained via uniaxial tension tests, and the determined material constants are summarized in

Table 4. Coefficients of the Swift isotropic hardening model for TRIP1180.

Material	K (MPa)	n	${\mathsf{\epsilon }}_0$
TRIP1180	1672.8	0.1044	4.8605E-14

.

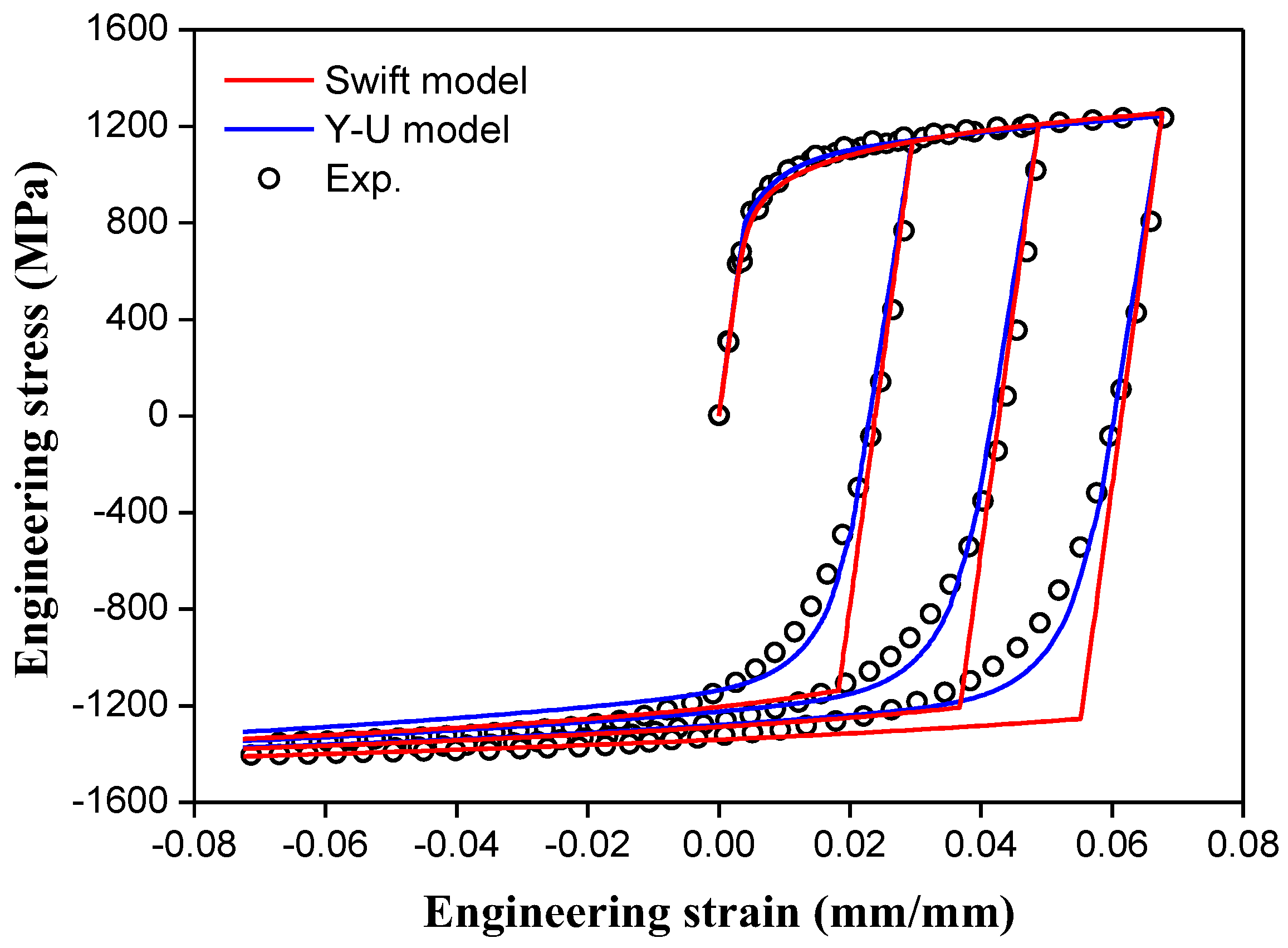
2.2.2. Yoshida-Uemori Hardening Model

As the material behavior is considerably complex during cyclic loading, a hardening rule should be able to accurately predict deformation behavior during cyclic loading. The Yoshida-Uemori model [16] is one of the most sophisticated models and can reproduce transient Bauschinger effects, permanent softening, and work hardening stagnation during large elasto-plastic deformation.

The Yoshida-Uemori model accounts for both the translation and expansion of the bounding surface, while the active yield surface evolves in a kinematic manner. A schematic of yield surfaces according to the Yoshida-Uemori model was presented in Chongthairungruang et al. [17]. The relative displacement of the two yield surfaces in a bounding surface can be defined as follows:

$${\alpha }_{*}=\alpha -\mathsf{\beta }$$

(8)

where α represents the current center of the yield surface, β represents the center of the bounding surface, and ${\alpha }_{*}$ represents the relative position of the two surfaces. An additional definition for ${\alpha }_{*}$ is given in Equation (9), which determines the relative movement of the yield and bounding surfaces:

$$\begin{array}{l}{\alpha }_{*}=C\left[\left(\frac{a}{Y}\right)(\sigma -\alpha )-\sqrt{\frac{a}{{\overline{\alpha }}_{*}}}{\alpha }_{*}\right]\dot{\overline{\epsilon }}\\ a=B+R-Y\end{array}$$

(9)

where B represents the initial size of the bounding surface, R represents the isotropic hardening component, Y represents the initial yield strength, and C is a material parameter of the kinematic yield surface hardening rule. The isotropic and kinematic hardening behaviors of the bounding surface can be defined as follows:

$$dR=m(R_{\mathrm{sat}}-R)\dot{\overline{\epsilon }}$$

(10)

$$d\beta =m\left(\frac{2}{3}b{D}^p-\beta \right)\dot{\overline{\epsilon }}$$

(11)

where R_sat is the saturated value of the isotropic hardening stress R for an infinitely large plastic strain and m is a material parameter controlling the rate of isotropic hardening. $D^p$ is an increment of the plastic deformation rate and b is a material constant. The Yoshida-Uemori model constants were derived via inverse finite element optimization. Inverse optimization was performed using Matlab’s fminsearch function, which identifies the constant value that minimizes the error value relative to the tension-compression experiment results using the Nelder-Mead method [18]. The Yoshida-Uemori model constants determined for the TRIP1180 sheets are presented in

Table 5. Material constants of TRIP1180 for the Yld2000-2d yield function.

Y	B	Rsat	b	m	C1	C2	εp,ref
800	284.9	294.2	88	9.62	366.8	366.8	0.005

.

A comparison of the experimental stress-strain curves and the calculated results based on the selected hardening models is shown in Figure 4. It can be observed that the Yoshida-Uemori hardening model matches well with the experimental results and captures the Bauschinger effect.

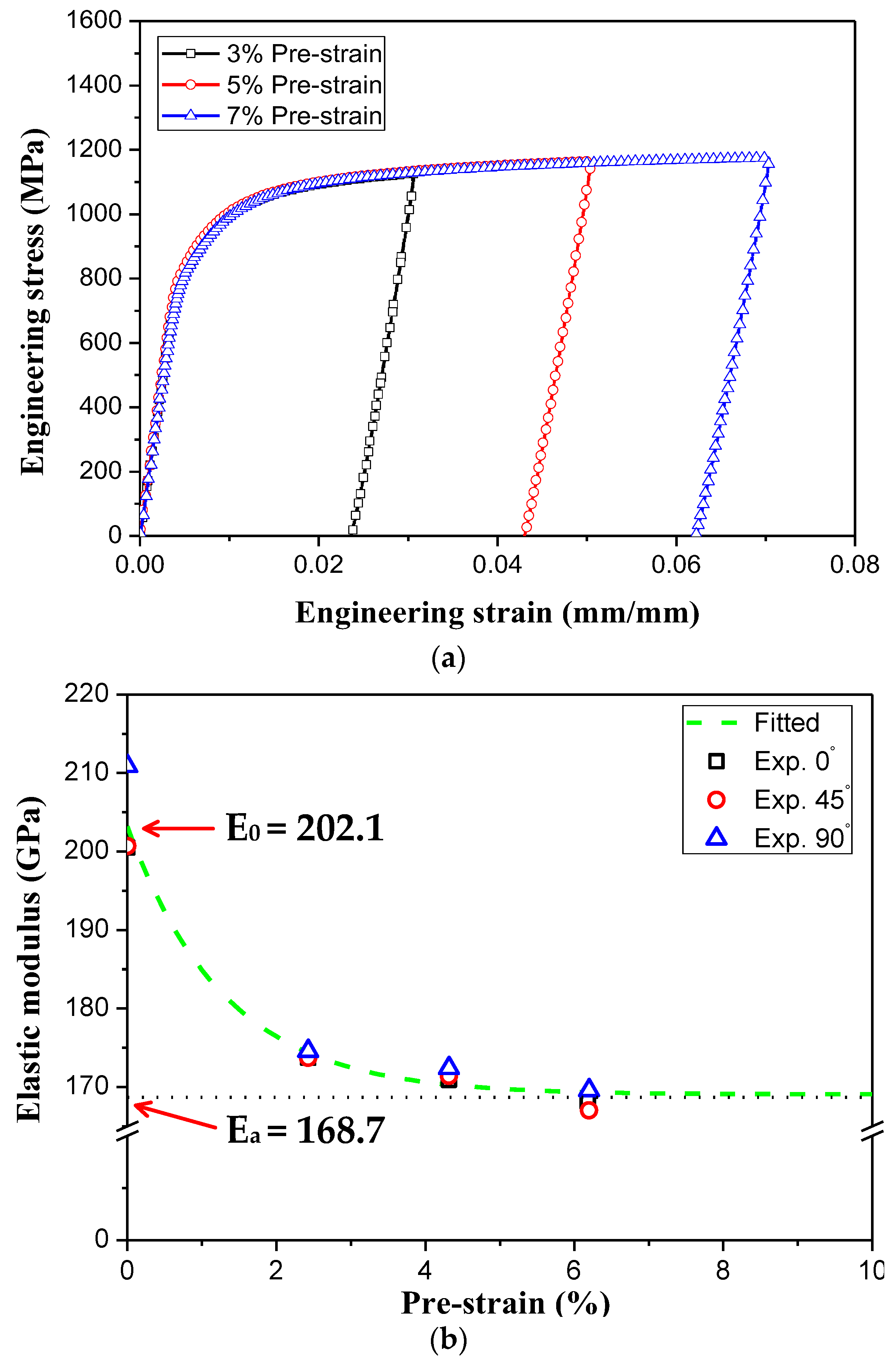
2.3. Chord Modulus Model

In order to determine the material constants of the chord modulus model, ASTM E8 standard loading–unloading tests were performed on specimens using a MTS universal testing machine for different rolling directions (0°, 45°, 90°). The elastic modulus changes during plastic deformation are reflected in the chord modulus model. The results of this test are shown in Figure 5. Generally, the elastic modulus of steel sheets decreases as the effective strain increases [19,20]. The initial elastic modulus under uniaxial tension, denoted as E₀, was determined using the linear regression fitting method. The elastic moduli for pre-strained sheet specimens were defined as the slope of a straight line drawn through the two stress–strain end points at a corresponding prescribed plastic strain. Changes in the chord modulus were applied to the FE simulation along with the hardening model constants. This phenomenon was formulated as shown in Equation (12):

$$E=E_0-(E_0-E_a)[1-\exp (-{\mathsf{\xi }\overline{\epsilon }}_{\mathrm{p}})]$$

(12)

where E represents the unloading elastic model under uniaxial tension, E_a represents the chord modulus obtained under an infinitely large plastic pre-strain, and ${\overline{\epsilon }}_{\mathrm{p}}$ and $\mathsf{\xi }$ are material parameters determining the rate at which E decreases. The optimized constants are given in

Table 6. Material constants of TRIP1180 softening behavior.

Material	E0 (GPa)	Ea (GPa)	ξ
TRIP1180	202.1	168.7	72.9

.

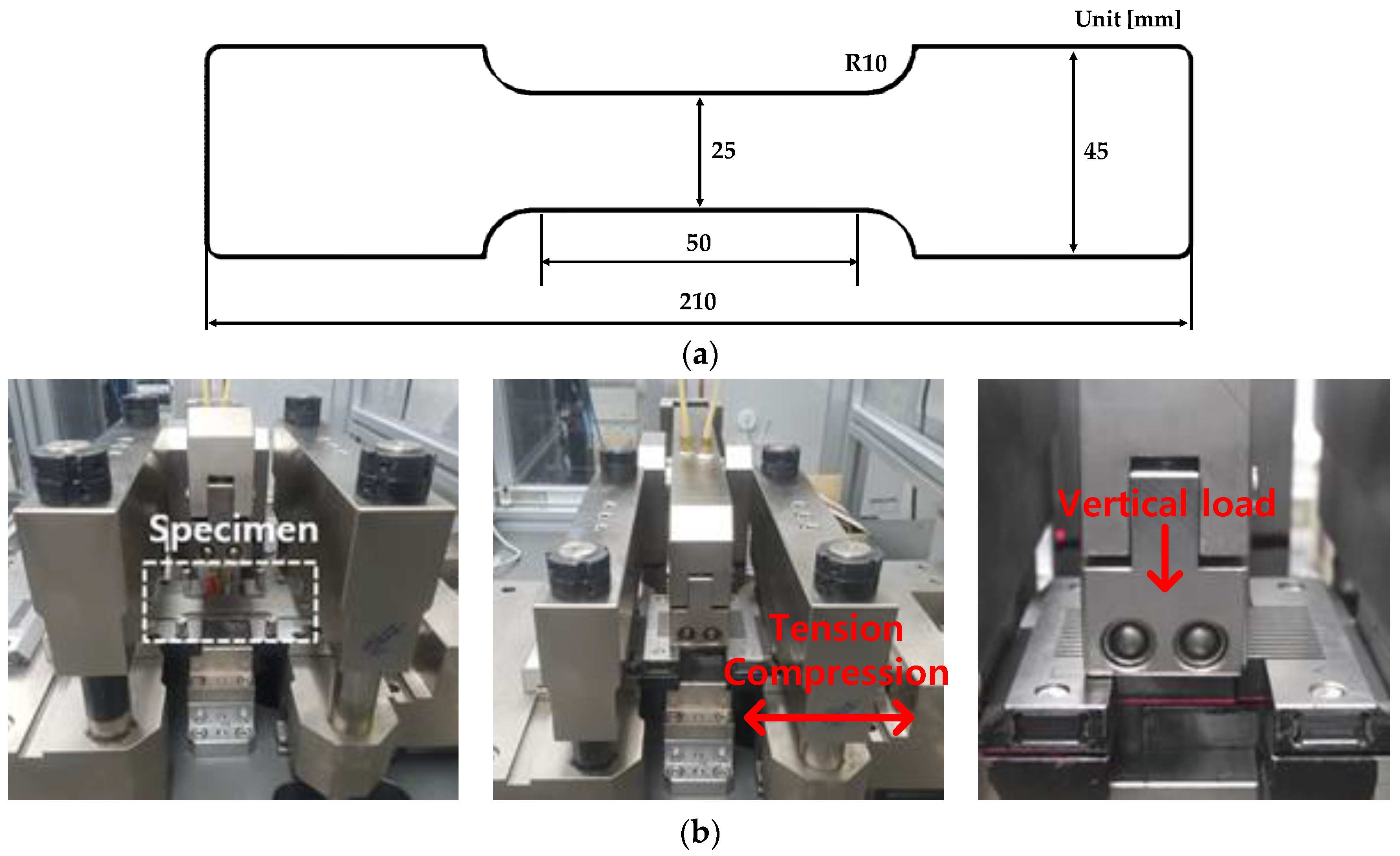
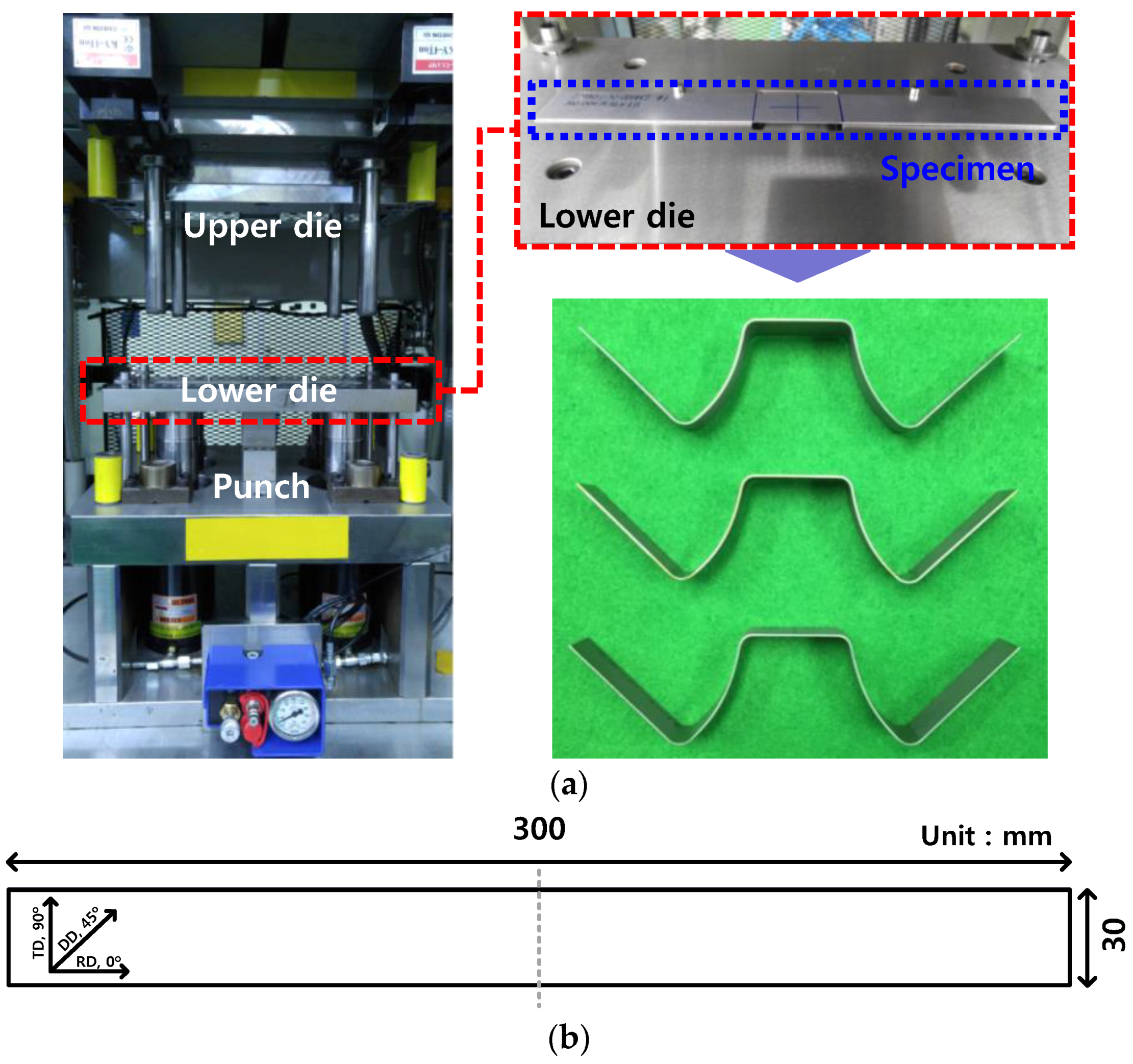
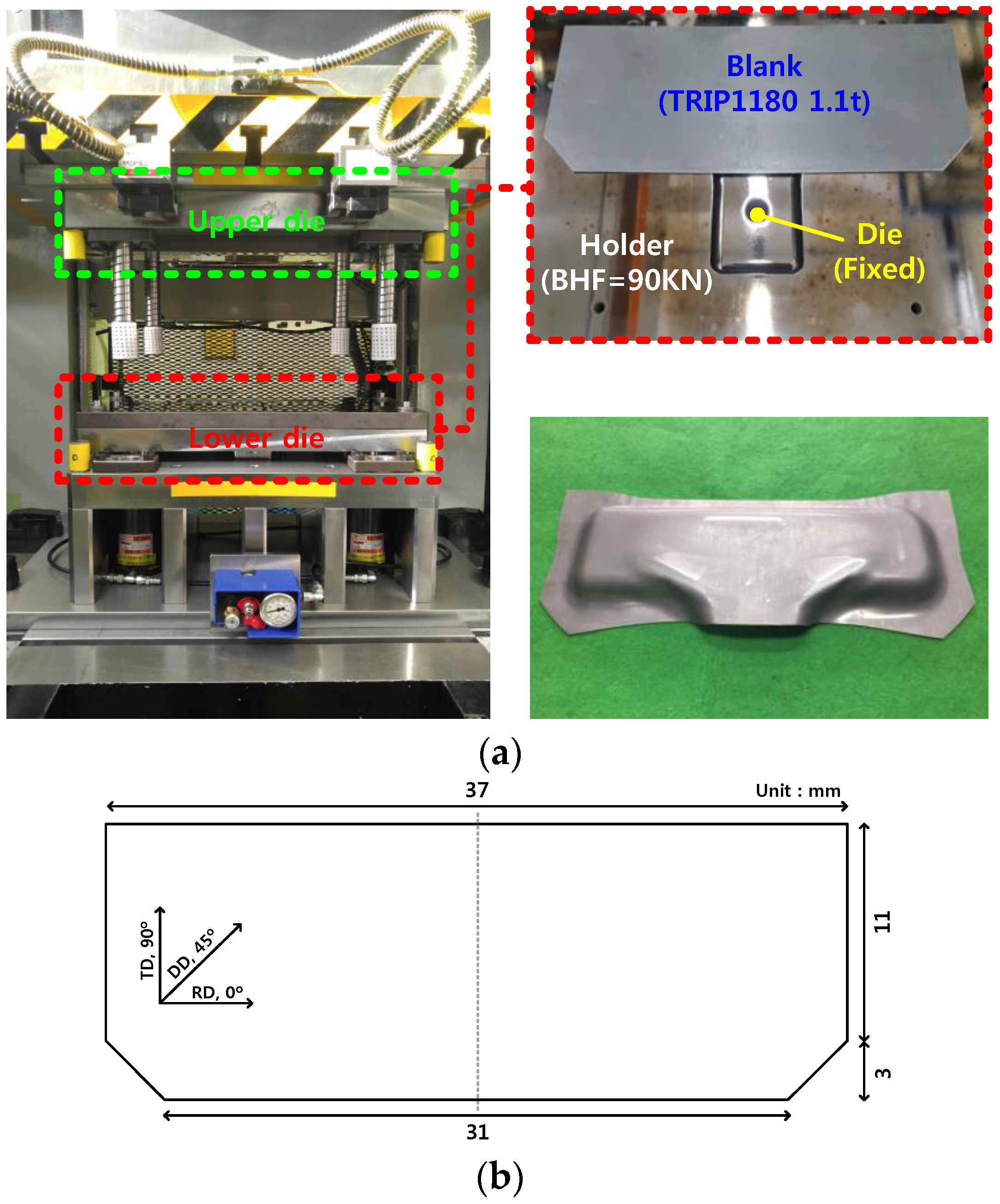
3. Test Conditions

In this study, FE simulations and experiments were performed for various forming processes including U-bending and T-shape drawing. A commercial program (PamStamp 2G) was used to perform the FE simulation. The experimental and analytical results were compared using various constitutive equations and the material constants determined in Section 2. Both U-bending and T-shape drawing were employed to evaluate the accuracy of springback predictions.

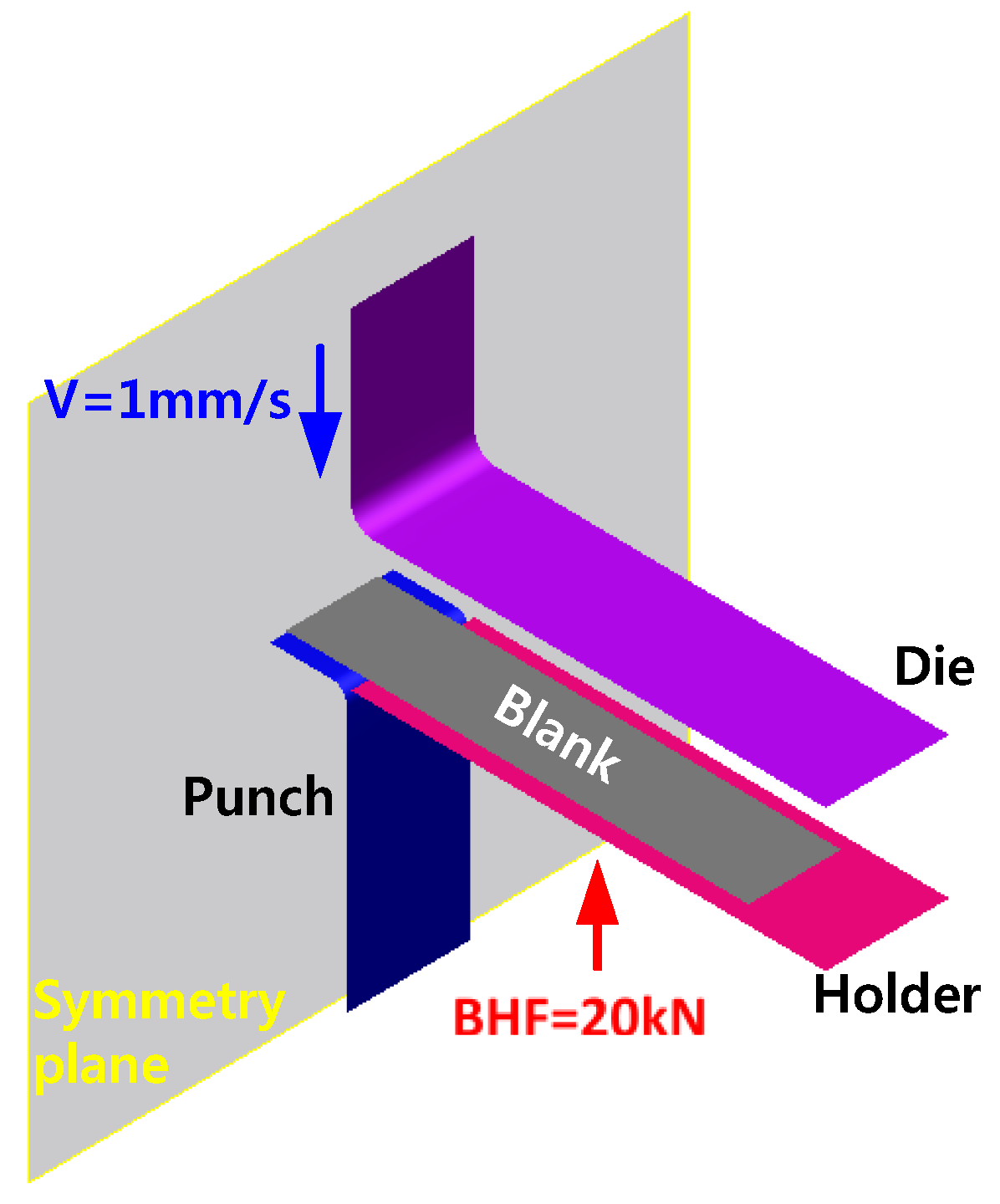
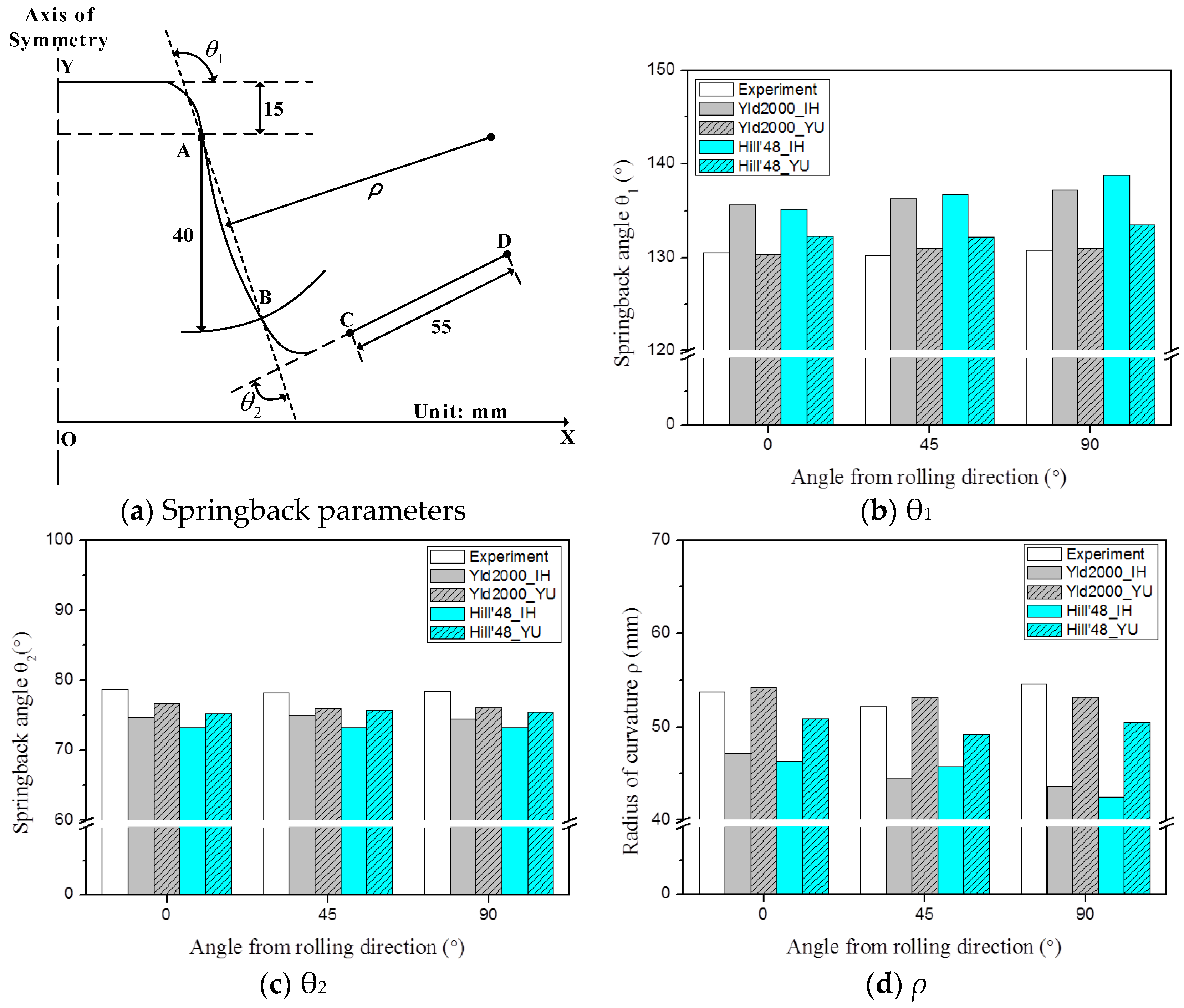
3.1. U-Bending Test

Previous works have confirmed the U-bending test to be a significant verification model for springback prediction [21,22,23]. The tools used in U-bending are shown in Figure 6, consisting of a punch, blank holder, and die. The dimension of the blank was 300.0 mm × 30.0 mm × 1.0 mm. The gap between the die and the punch was designed to be 1.1 mm. Testing was conducted using a 200-ton servo press machine. The total punch stroke was 60.0 mm, with a punch speed of 1 mm/s and a blank holding force of 20 kN. Additional tests were performed in various rolling directions (0°, 45°, 90°). Each set of experimental conditions was repeated five times to ensure the reliability of the experiment. After stamping, the final dimensions of the formed specimens were measured along the middle cross section using a laser coordinate measuring machine (a two-dimensional inspection machine), allowing for comparison between the experimental and FE simulation results.

To evaluate the springback behavior observed in the U-bending tests, FE simulations were conducted for forming and springback analysis. The analytical model was designed to mimic the experiment, though only a half model of the tools and blank was simulated as shown in Figure 7, considering the geometric symmetry of the test. The specimen used for FEA was a Belytschko-Lin-Tsay (BLT) shell element of uniform size (1.0 mm × 1.0 mm) with five integration points in the thickness direction. The die was assumed to be a rigid body. The FE simulation conditions were identical to the experimental conditions. The Coulomb friction coefficient between the die and specimen was set to 0.12, a value that assumed an unlubricated condition. In the FE simulation, mass-scaling and mesh-refinement techniques were applied to ensure the efficiency of the analysis. The shapes of the specimens calculated in the FE simulations were compared to those from the experimental results [24].

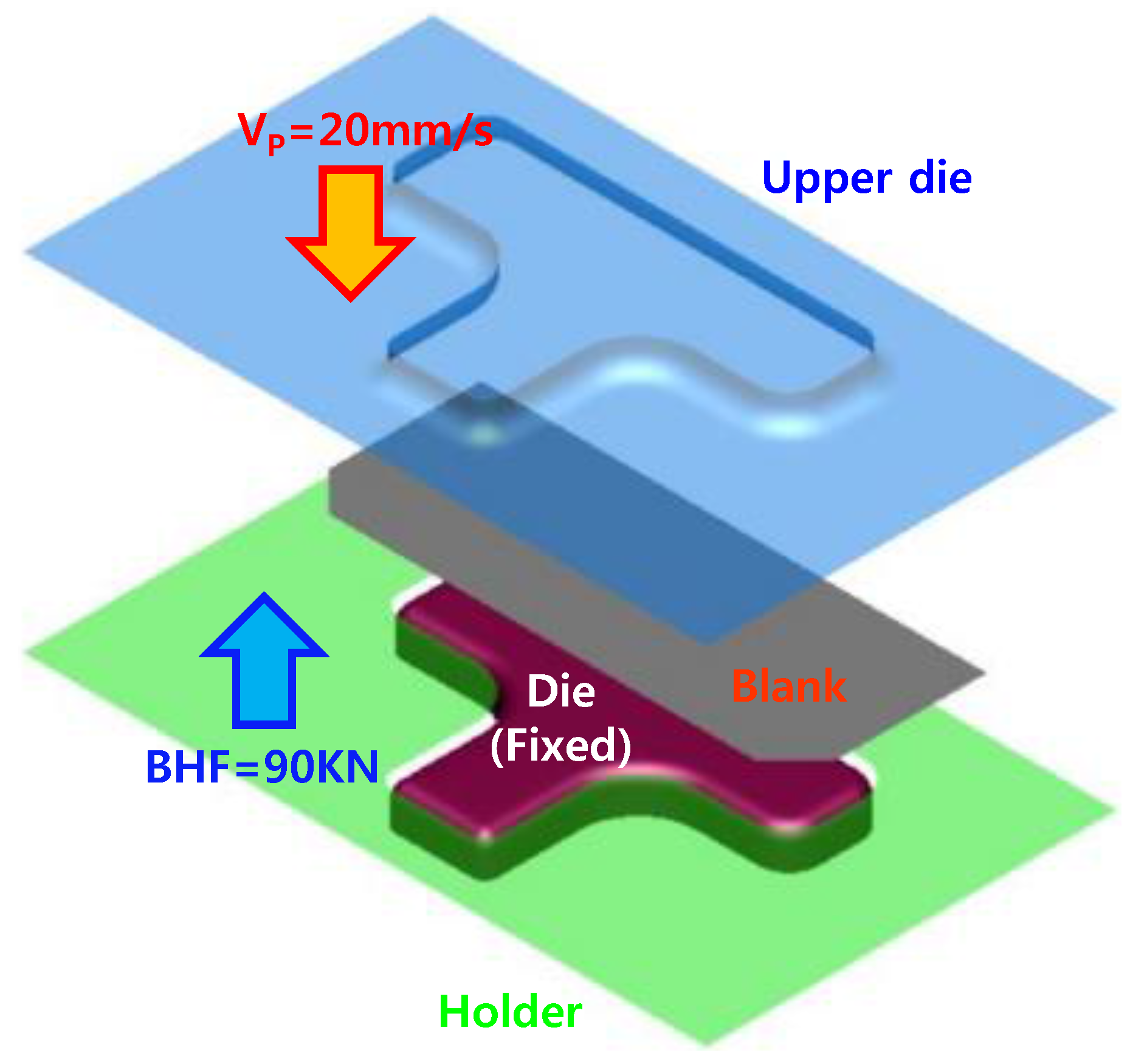
3.2. T-Shape Drawing Test

In this study, a T-shape drawing test was performed to evaluate the effect of the constitutive equations on the prediction accuracy of springback in complex deformation modes. The blank size used in T-shape drawing and the experimental set-up for the T-shape drawing test, consisting of a punch, blank holder, and die, are shown in Figure 8. The gap between the die and punch was designed to be 1.1 mm, and the test was conducted using a 200-ton servo press machine. The total punch stroke was 22.0 mm, with a punch speed of 20 mm/s and blank holding force of 90 kN. Experiments were repeated five times to ensure reliability. After stamping, the final dimensions of the formed specimens were measured using a 3D optical scanning system (three-dimensional inspection equipment), allowing for comparison between the experimental and FE simulation results.

To investigate the springback behavior during T-shape drawing tests, FE simulations were conducted for forming and springback analysis. The analytical model was designed to mimic the experiments, and Figure 9 shows the FE model that was used. A significant number of conditions for the T-shape drawing FE simulation were equivalent to those in the U-bending test simulation and the experimental conditions of the T-shape drawing test. The shapes of the specimens determined via FE simulations were compared with those obtained experimentally. In this study, a commercial reverse-design program (Geomagic Design X), was employed to quantitatively compare the configurations. For this comparison, the experimental results were input as the reference configuration to measure the dimensional errors between the experimental and analytical results.

4. Results and Discussion

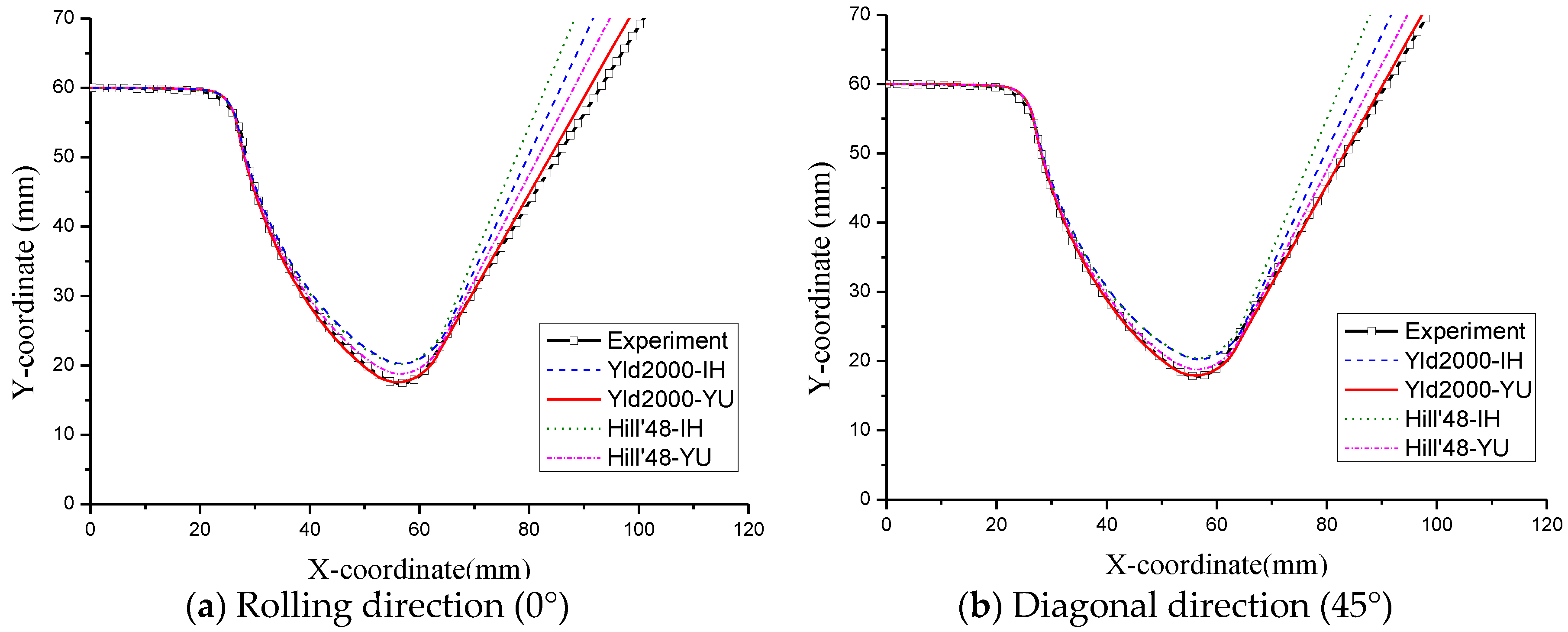
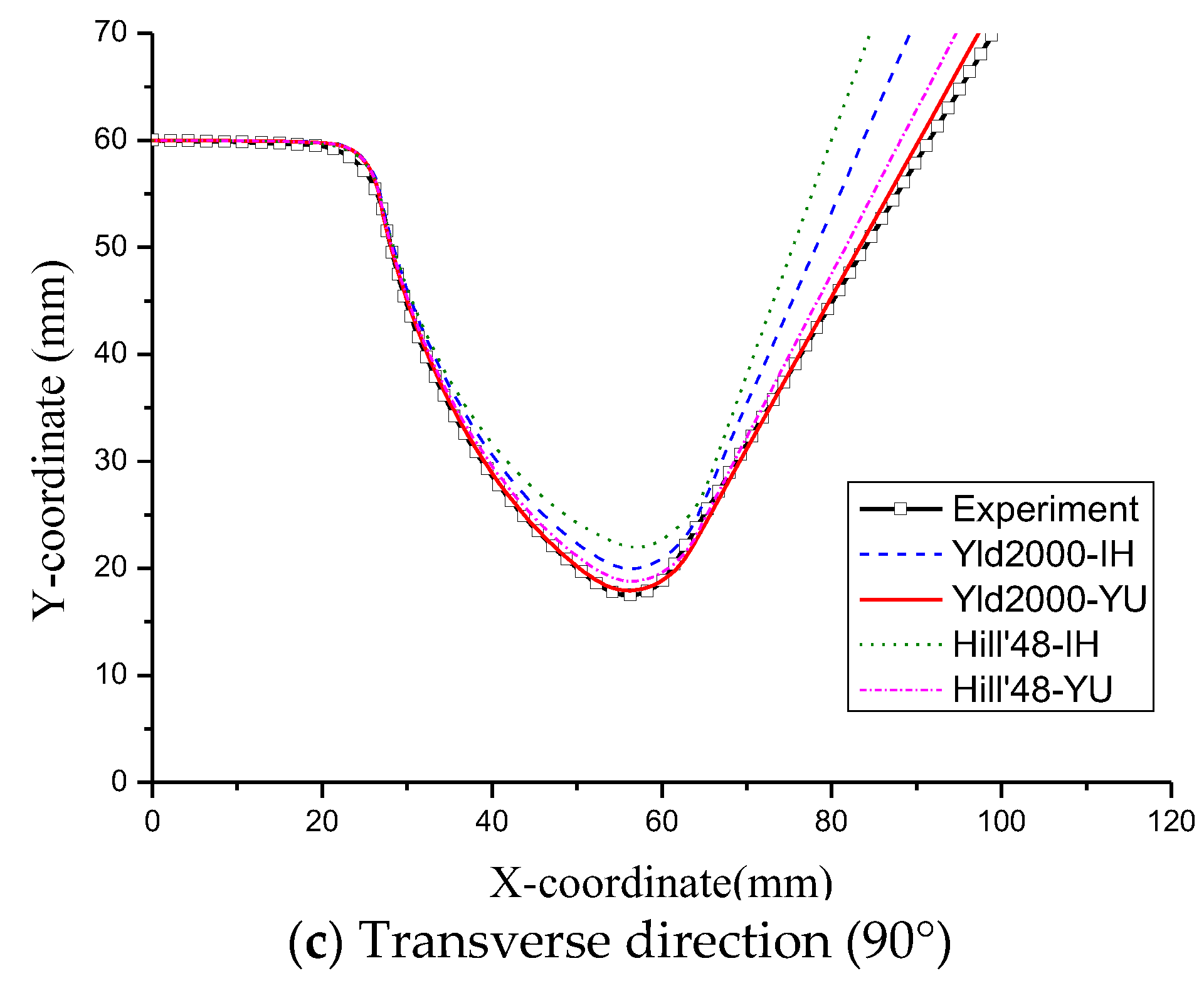
4.1. Springback Prediction for U-Bending Test

In order to determine the springback prediction accuracy dependent on the constitutive equations, the predicted U-bending test results were compared to the experimental results. The result is shown in Figure 10. The combination of the Hill’48 yield function and isotropic hardening model resulted in specimen shapes different from those observed experimentally. The combined Yld2000-2d yield function and Yoshida-Uemori model, however, predicted shapes that were similar to those of the manufactured parts.

Springback parameters were employed in this study to quantitatively compare the springback. In Figure 11a, the springback parameters of the defined Numisheet’93 benchmark problem are shown [25]. The 2D draw-bending test proposed as a benchmark problem in Numisheet’93 involves two-dimensional blank holders to show both the effects of the material as well as the process parameters. As previously mentioned, when the results of the combined Yld2000-2d yield function and Yoshida-Uemori model were used, the prediction accuracy for springback was excellent in various rolling directions, including 0°, 45°, and 90°, as shown in Figure 11.

Comparing the predicted and experimental results from the U-bending test, the hardening model was the predominant influence on springback prediction accuracy. When an isotropic hardening model was used, the predicted shape differed significantly from the experimental results. However, when the Yoshida-Uemori model was used, the predicted shape was similar to the experimental results. This demonstrates that the Yoshida–Uemori model resulted in better springback predictions relative to the isotropic hardening model, which is consistent with improved approximations of the reverse-loading curves. For the U-bending test, the deformation mode of the sheet was a uniaxial tension mode, and the sheet was deformed with nonlinear loading conditions. The anisotropic behavior in the uniaxial tension mode could be described well by both the Hill’48 and Yld2000-2d yield functions. However, the hardening behavior from the nonlinear loading conditions is only described by the Yoshida-Uemori model because this model effectively considers changes in the elastic modulus due to pre-strain, the Bauschinger effect, and transient behavior. Furthermore, since the inflow amount of the test specimen was large during the U-bending test, the tension-compression behavior is repeated at the wall of the test specimen as the experiment progresses, as shown in Figure 12. This increases the importance of considering nonlinear loading conditions.

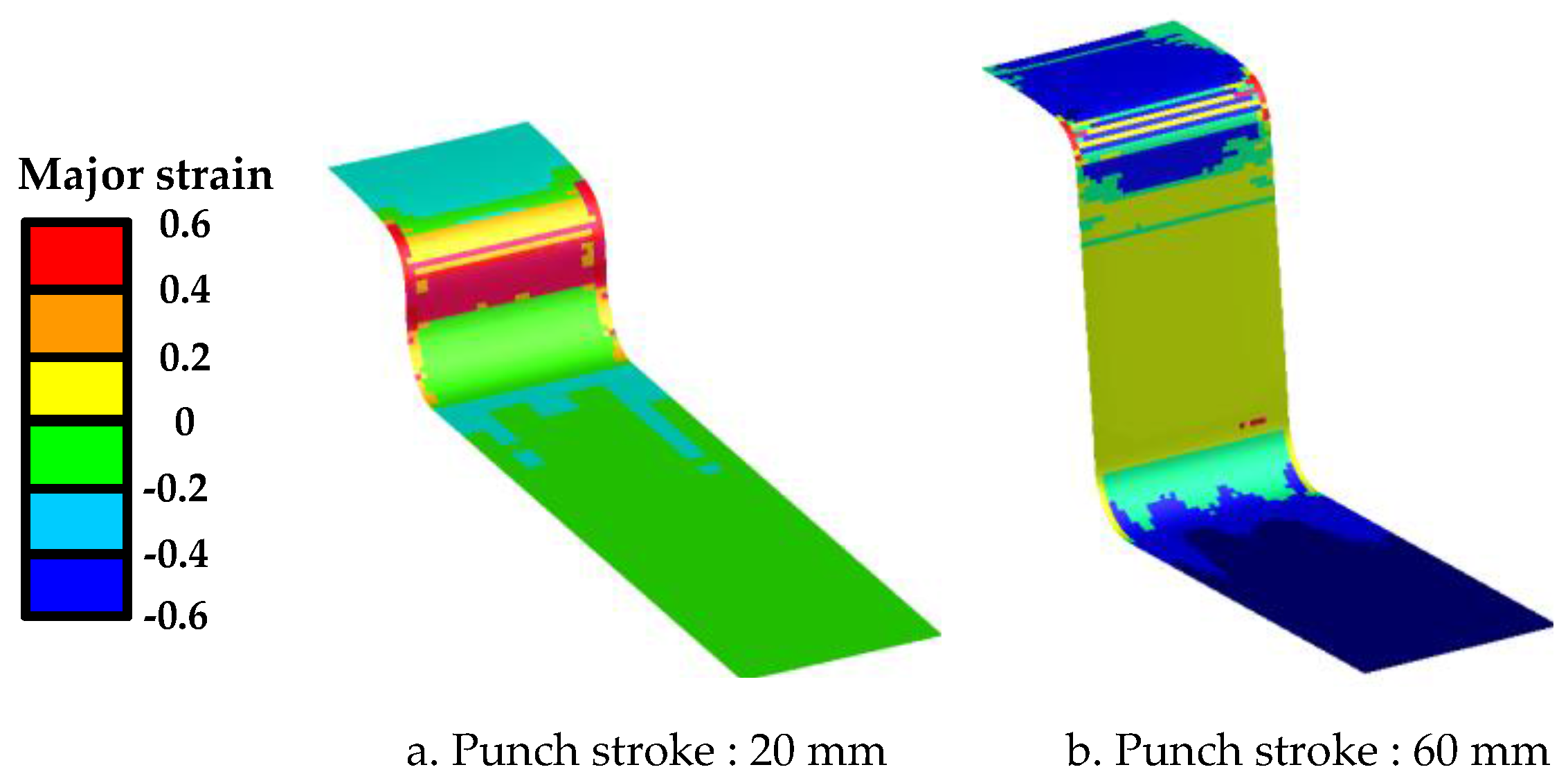
4.2. Springback Prediction for T-Shape Drawing Test

In order to investigate the effects of the constitutive equations on springback prediction accuracy, the predicted and experimental results of the T-shape drawing test were compared, as shown in Figure 13. The springback prediction accuracies in T-shape drawing displayed the same tendencies observed in the U-bending test. The results of the Yld2000-2d yield function and Yoshida-Uemori model combination demonstrated an agreement rate of 82.21%, whereas the combined result of the Hill’48 yield function and isotropic hardening model showed low prediction accuracy with an agreement rate of 73.54%. In this study, the agreement rate was defined as follows:

$$\mathrm{Agreement}\mathrm{rate}=\frac{A_{\pm 0.5}}{A_{\mathrm{total}}}\times 100(\%)$$

(13)

where A_±0.5 represents the area within an allowable tolerance of ±0.5 mm and A_total represents the total area of the manufactured part. The allowable tolerance was that acceptable variation from the specified dimensions. In this study, the differences between the analytical and experimental results defined using the Geomagic Design X program should be within ±0.5 mm.

When the predicted and experimental results for the T-shape drawing test were compared, it was observed that the yield function was the predominant influence on springback prediction accuracy. Although the uniaxial deformation mode is dominant in U-bending, T-shape drawing has various deformation modes. Additionally, since the inflow amount of the test specimen is small during the T-shape drawing, it is more important to consider the biaxial Lankford value and yield stress than to consider the non-linear condition. When the Hill’48 yield function was used, the predicted shapes differed greatly from those observed experimentally. However, when Yld2000-2d was used, the predicted shape was similar to the experimental results. In the T-shape drawing test, various deformation modes such as the biaxial tension, plane strain, and deep drawing modes were represented, as shown in Figure 14, and the sheet was deformed with an approximately linear loading condition. The hardening behavior in the linear loading condition could be described well by both the isotropic and Yoshida-Uemori hardening models. However, the yield behaviors for various deformation modes are only described by the Yld2000-2d yield function because it considers Lankford values and yield stresses according to the rolling direction and biaxial deformation mode.

5. Conclusions

In this study, FEA and experiments were conducted to evaluate the effect of constitutive equations on springback prediction accuracy for the cold stamping of a TRIP1180 sheet. Based on the experimental and analytical results, the following conclusions can be drawn:

• Uniaxial tension, bulge, tension-compression, and loading-unloading tests were conducted to investigate anisotropy, nonlinear hardening behavior, and changes in the elastic modulus of a TRIP1180 sheet. The material constants of various constitutive equations were determined based on the experimental results, and were implemented in FE simulations for modeling and analyzing springback.
• FE simulations and experiments were performed to evaluate springback behavior in U-bending and T-shape drawing tests. In both cases, the Yld2000-2d yield function and Yoshida-Uemori model showed excellent prediction accuracy, whereas the Hill’48 yield function and isotropic hardening model showed low prediction accuracy.
• In the U-bending test, the hardening model had a more dominant influence on the prediction accuracy of springback than the yield function due to the nonlinear loading conditions. The hardening behavior observed under nonlinear loading conditions was only described by the Yoshida-Uemori model, because it effectively considered changes in the elastic modulus due to the pre-strain, the Bauschinger effect, and transient behavior.
• In the T-shape drawing test, the yield function had a more dominant influence on the prediction accuracy of springback than the hardening model because various deformation modes were present. The yield behavior for various deformation modes was only described by the Yld2000-2d yield function because this function considered the Lankford values and yield stresses according to the rolling direction and biaxial deformation mode.
• To predict the springback present in AHSS cold stamping, it is necessary to use appropriate constitutive equations according to the forming process. Furthermore, these constitutive equations need to accurately describe the yield behavior, elastic modulus changes, and hardening behavior for a variety of deformation modes.