Indistinguishability Operators Applied to Task Allocation Problems in Multi-Agent Systems

Featured Application

Indistinguishability can provide a new family of response functions that could be applied to implement a new generation of swarm-like methods to carry out missions, like for example, allocate tasks to a set of robots in different environments. Actually, this paper provides a first implementation of this kind of systems.

Abstract

In this paper we show an application of indistinguishability operators to model response functions. Such functions are used in the mathematical modeling of the task allocation problem in multi-agent systems when the stimulus, perceived by the agent, to perform a task is assessed by means of the response threshold model. In particular, we propose this kind of operators to represent a response function when the stimulus only depends on the distance between the agent and a determined task, since we prove that two celebrated response functions used in the literature can be reproduced by appropriate indistinguishability operators when the stimulus only depends on the distance to each task that must be carried out. Despite the fact there is currently no systematic method to generate response functions, this paper provides, for the first time, a theoretical foundation to generate them and study their properties. To validate the theoretical results, the aforementioned indistinguishability operators have been used to simulate, with MATLAB, the allocation of a set of tasks in a multi-robot system with fuzzy Markov chains.

1. Introduction

The distribution of a determined number of tasks among a group of agents is a problem intensely studied in different fields, such as economics or robotics (we refer the reader, for instance, to [1,2,3] for a deeper treatment of the topic). It consists in allocating a collection of labors on a number of agents in the most efficient way, i.e., in such a way that the best agent is selected to perform each one of the labors to be carried out. This problem, commonly referred to as the task allocation problem, is still an open issue in real environments where the agents have a limited number of resources to obtain the optimal allocation. One of those challenging environments is the one formed by two or more autonomous robots that cooperatively perform a common mission, from now on referenced as multi-robot systems.

Among all the methods proposed to address the task allocation problem, this paper focuses on swarm methods, which are inspired by insect colonies where an intelligent behavior emerges from the interaction of very simple skills running on each agent (see [4,5]). Concretely, this work focuses on the so-called Response Threshold Method (RTM). In these methods each involved agent has an associated task response threshold and task stimulus. The task stimulus value indicates how attractive the task is for the agent and its threshold is a parameter of the system. Thus, an agent starts the execution of a task following a probability function, referenced as response function and denoted as P, that depends on both aforementioned values. As the probability of executing a task only depends on the current task, or state, the decision process can be modeled as a probabilistic Markov chain. Some examples of methods based on Response Threshold can be found in [6,7,8,9]. This classical probabilistic approach presents some well known disadvantages (see [10]), for instance problems associated with the selection of the probability function (response function) when more than two tasks are considered, asymptotic converge to a system’s stable state, and so on. Due to the inconveniences, in [10] new possibilistic theoretical formalism for a RTM was proposed. The RTM is implemented considering transition possibilities (response functions) instead of transition probabilities (response functions) and possibilistic Markov chains (also known as fuzzy Markov chains) instead of the classical probabilistic ones. The theoretical and empirical results demonstrated, among other advantages, that fuzzy Markov chains applied to task allocation problems require very few steps to converge to a stable state.

As will be proved for the first time in this paper, the most widely used response functions are a specific kind of mathematical functions called indistinguishability operators. This work demonstrates that indistinguishability operators, in general, are useful in modeling the response probability function in response threshold task allocation problems in those cases in which the stimulus of each agent of the group only depends on the distance to each task that must be carried out. Hence, the aim of this paper from a theoretical point of view is twofold. On the one hand, we will use a well-known technique to induce indistinguishability operators in order to provide a few examples that could be useful in modeling response functions. On the other hand, we will show that two popular response functions exposed in [11] can be reproduced from indistinguishability operators. Thus, this paper provides a new systematic method to generate response functions.

This paper extends the previous work in [10,12] in order to apply the indistinguishability operators as possibility transition functions to allocate tasks in a multi-robot system with fuzzy Markov chains. As tested in the aforementioned references, each robot uses a fuzzy Markov chain to decide the next task to execute. This paper also extends these previous works with new simulations performed with MATLAB in order to test the system’s behavior in environments with tasks placed in clusters or groups. The results show that, on the one hand, convergence time does not depend on the tested indistinguishability operator used as the possibility transition function. On the other hand, the simulations also show that the placement of the objects clearly impacts on the system performance. In all cases, the fuzzy Markov chains always outperform their probabilistic counterpart.

The paper is organized as follows. In Section 2, the main concepts on Response Threshold Methods are reviewed. In Section 3, we recall all pertinent aspects of indistinguishability operators necessary to our subsequent discussion. In Section 4, first we illustrate the well-known technique for generating indistinguishability operators from distances by means of two illustrative examples. After this, we show that a celebrated response function, which appears in [11], can be retrieved from an appropriate indistinguishability operator and the referenced technique. Furthermore, inspired by the so-called classical exponential response function given in [13], we introduce a new indistinguishability operator. The numerical values admit the same interpretation as the aforementioned paradigmatic exponential response function. We also show that the exponential response function can be exactly retrieved from the introduced indistinguishability operator by means of a known technique to induce distances from indistinguishability operators. Section 5.1 reviews the basics of possibilistic theory and fuzzy Markov chains. In Section 5, the possibilistic multi-robot task allocation problem will be posed. Moreover, the basics of possibilistic theory and fuzzy Markov chains will be reviewed. Then, in Section 6, we will show the experimental results. In Section 7, the proposed task will be generalized and we will propose a real example of how to apply the methodology. Finally, Section 8 presents the conclusions and future work.

2. Swarm Task Allocation: Response Threshold

In this section we will introduce the main concepts of classical (probabilistic) Response Threshold Methods (RTMs) and we will motivate that their response functions can be assimilated to indistinguishability operators. It must be recalled that classical RTMs are modeled using probabilistic Markov chains.

As was mentioned in Section 1, one way to model the probability transition function of the aforementioned Markov chain is by means of the so-called stimulus and response thresholds. Concretely, the stimulus expresses the need perceived by the agent to develop a task and the threshold determines the tendency of an agent to respond to stimulus intensity and, therefore, to make the task. In [11], a method was proposed, based on response functions, to model the aforesaid probability when the response threshold is fixed over time. In the aforesaid reference, the probability response function $P(s,\theta )$ can be defined by

$$P(s,\theta )=\frac{s^n}{s^n+{\theta }^n},$$

(1)

where s denotes, for each agent, the intensity of a stimulus to carry out a particular task and $\theta$ denotes the threshold for each agent and task. Notice that, according to [11], $n>1$ (with $n\mathbb{N}$) determines the steepness of the threshold. Of course, the numerical value $P(s,\theta )$ can be interpreted as follows. On one hand, values of the stimulus intensity much smaller than threshold (denoted by $s<<\theta$) implies response values (probabilities of engaging task performance) close to 0. On the other hand, stimulus intensity much greater than the threshold (denoted by $s>>\theta$) means probability of engaging task performance close to 1.

Other authors have used response functions of type (1) in order to model the probability of engaging tasks performance in multi-robot task allocation. We can find an instance in [14] where a mathematical model was proposed to assign particular events to individual robots in such a way that each robot is limited to one task at time. Concretely, they assume that each robot senses the need to handle the closest task. In this direction, the stimulus produced by a task e for a robot r was taken as the inverse of the distance between the task and the robot, i.e., $s=\sigma (r,e)=\frac{1}{d(r,e)}$. Then, the probability response function is formulated as follows.

$$P(s,\theta )=\frac{\sigma {(r,e)}^n}{\sigma {(r,e)}^n+{\theta }^n}.$$

(2)

As was pointed out in [14], the best performance was achieved with the inverse of the expected distance between tasks D, i.e., $\theta =\frac{1}{D}$. In this case, $s<<\theta$, or equivalently $d(r,a)>>D$, implies low response to engage the task, and $s>>\theta$, or equivalently $d(r,e)<<D$, implies high motivation to take on the task.

A straightforward computation yields that (2) can be transformed into the response function

$$P(s,D)=\frac{D^n}{D^n+d{(r,e)}^n},$$

(3)

Notice that the expression (3) maintains the essential properties of the response function (2). It must be stressed that these kind of response functions have been recently applied to possibilistic multi-robot task allocation problems (see [10] for more details).

Expression (3) has motivated this paper, since, as we will show in Section 4, $P(s,D)$ is an indistinguishability operator (see Section 3).

3. Preliminaries on Indistinguishability Operators

The concept of triangular norm, briefly t-norm, appeared in the literature as a tool to manage the triangle inequality in the construction of metric spaces that take, as values, a probability distribution instead of a positive real number. Since then, they have played an essential role in fuzzy logic and many authors have contributed to the development of this kind of binary operation. Our basic reference for t-norms and all related notions is [15].

Let us recall that a t-norm is a function $T:{[0,1]}^2\to [0,1]$ such that for all $x,y,z\in [0,1]$ the following four axioms are satisfied:

(T1) $T(x,y)=T(y,x)$;						(Commutativity)
(T2) $T(x,T(y,z\left)\right)=T\left(T\right(x,y),z)$;						(Associativity)
(T3) $T(x,y)\ge T(x,z)$; where $y\ge z$						(Monotonicity)
(T4) $T(x,1)=x$.						(Boundary Condition)

An interesting subclass of t-norms in our subsequent study are the so-called Archimedean, which are defined as follows.

A t-norm is called Archimedean if for each $x,y\in ]0,1[$ there exists $n\in \mathbb{N}$ such that $x^{\left(n\right)}<y$, where $x^{\left(n\right)}=T(x,\dots ,x)$n-times.

Archimedean t-norms are exactly those t-norms that satisfy $T(x,x)<x$ for each $x\in ]0,1[$ whenever T is, in addition, continuous. Two well-known examples of continuous Archimedean t-norms are the usual product $T_P$ and the Luckasievicz t-norm $T_L$, where $T_P(x,y)=x·y$ and $T_L(x,y)=max\{x+y-1,0\}$ for all $x,y\in [0,1]$. An example of continuous t-norm that is non-Archimedean is the minimum t-norm $T_M$, i.e., $T_M(x,y)=\min \{x,y\}$ for all $x,y\in [0,1]$. These t-norms are the most commonly used in Fuzzy Logic.

A concept related to a t-norm, which will play an important role in this paper, is the notion of the pseudo-inverse and an additive generator. The notion of the pseudo-inverse is given as follows:

Let $f:[0,1]\to [0,\infty ]$ be a strictly decreasing continuous function provided that $f\left(1\right)=0$. Then, the pseudo-inverse$f^{(-1)}:[0,\infty ]\to [0,1]$ of f is defined as follows.

$$f^{(-1)}\left(y\right)=f^{-1}\left(\min \{f\left(0\right),y\}\right)=max\{0,f^{-1}\left(y\right)\}.$$

(4)

Moreover, given a t-norm T, a strictly decreasing continuous function $f_T:[0,1]\to [0,\infty ]$ is said to be an additive generator of T provided that $f_T\left(1\right)=0$ and

$$T(x,y)=f_T^{(-1)}(f_T\left(x\right)+f_T\left(y\right)).$$

(5)

Note that in this case, the t-norm is continuous.

It is known that each t-norm with an additive generator is Archimedean. However, the converse of the former assertion is not true in general. The next result states that continuous t-norms always admits an additive generator.

Theorem 1.

A mapping $T:[0,1]\times [0,1]\to [0,1]$ is a continuous Archimedean t-norm if and only if there exists a continuous additive generator $f_T$ of T.

Let us note that if T is a t-norm and $f_T$ is an additive generator of T, then this additive generator multiplied by a positive constant is again an additive generator of T, i.e., if $f_T$ is an additive generator of T, then the function $f_{T,\theta }$ is again an additive generator of T, where $f_{T,\theta }\left(x\right)=\theta ·f_T\left(x\right)$ for all $x\in [0,1]$ and each $\theta \in ]0,\infty [$. Furthermore, if $f_T^{(-1)}$ is the pseudo-inverse of an additive generator $f_T$, then it is easy to verify that the pseudo-inverse of the additive generator $f_{T,\theta }$ is given by $f_{T,\theta }^{(-1)}\left(y\right)=f_T^{(-1)}(\frac{y}{\theta })$ for all $y\in [0,\infty ]$.

We have introduced some details about t-norms that will be necessary later on. Now, we are able to recall the concept of the T-indistinguishability operator. This concept was introduced in 1982 by E. Trillas as a way to measure the degree of equivalence, in fuzzy logic, between the elements of a set X (see [16,17]).

Let X be a nonempty set and let T be a t-norm, we will say that a fuzzy set $E:X\times X\to [0,1]$ is a T-indistinguishability operator if it satisfies, for each $x,y,z\in X$, the following:

(E1) $E(x,x)=1$;						(Reflexivity)
(E2) $E(x,y)=E(y,x)$;						(Symmetry)
(E3) $E(x,z)\ge T\left(E\right(x,y),E(y,z\left)\right)$.						(Transitivity)

A T-indistinguishability operator E is said to separate points provided that $E(x,y)=1\iff x=y$ for all $x,y\in X$. The notion of indistinguishability operators is essentially interpreted as a measure of similarity (in contrast to dissimilarity modeled by pseudo-metrics). Thus, $E(x,y)$ matches up with the degree of indistinguishability between the objects x and y. In fact, the greater $E(x,y)$, the more similar are x and y. In such a way that when $x=y$, the measure of similarity is exactly $E(x,x)=1$.

Since Trillas introduced the notion of the indistinguishability operator, many authors have contributed to the development of a theory in which this concept plays an essential role. We focus our attention on a method to construct T-indistinguishability operators from distances and vice-versa (for a detailed treatment of the topic we refer the reader to [18,19]).

The next proposition provides a technique that allows us to construct distances from indistinguishability operators.

Theorem 2.

Let X be a nonempty set and let $T^{\ast }$ be a t-norm with additive generator $f_{T^{\ast }}:[0,1]\to [0,\infty ]$. Let $d_E:X\times X\to [0,\infty ]$ be the function defined by

$$d_E(x,y)=f_{T^{\ast }}\left(E(x,y)\right)$$

for all $x,y\in X$. If T is a t-norm, then the following assertions are equivalent.

(1) 

$T^{\ast }\le T$ (i.e., $T^{\ast }(x,y)\le T(x,y)$ for all $x,y\in X$).

(2) 

For any T-indistinguishability operator E on X that separates points the function $d_E$ is a distance on X.

The following result develops a technique that allows the induction of indistinguishability operators from distances.

Theorem 3.

Let d be a distance on a nonemprty set X and let T be a continuous Archimedean t-norm with additive generator $f_T$. Then, the fuzzy set $E_T:X\times X\to [0,1]$, given by $E_T(x,y)=f_T^{(-1)}\left(d(x,y)\right)$ for all $x,y\in X$, is a T-indistinguishability operator that separates points on X.

Recall that a distance on a nonempty set X is a fucntion $d:X\times X\to [0,\infty ]$ satisfying the following axioms for all $x,y,z\in X$.

(d1) 

$d(x,y)=0\iff x=y$;

(d2) 

$d(x,y)=d(y,x)$;

(d3) 

$d(x,z)\le d(x,y)+d(y,z)$.

4. T-Indistinguishability Operators, Distances and Response Functions

In this section we will apply Theorems 2 and 3 for some particular t-norms in order to construct two indistinguishability operators that allow the reproduction of two celebrated response functions that appear in [11]. In this direction we first provide a few examples of T-indistinguishability operators that separate points with the aim of illustrating such a technique, due to the lack of this sort of examples in the literature.

4.1. Examples

We begin by applying the aforesaid construction to the Luckasievicz t-norm $T_L$, which is continuous and Archimedean (see Section 3).

A ${\mathit{T}}_{\mathit{L}}$-indistinguishability operator

Let d be a distance on a nonempty set X and consider the Luckasiewicz t-norm $T_L$. It is clear that the function $f_{T_L}:[0,1]\to [0,\infty ]$, given by $f_{T_L}\left(x\right)=1-x$ for all $x\in [0,1]$, is an additive generator of $T_L$. Applying (4), an easy computation shows that the pseudo-inverse $f_{T_L}^{(-1)}$ of the additive generator $f_{T_L}$ is given by

$$f_{T_L}^{(-1)}\left(y\right)=max\{0,1-y\}$$

for all $y\in [0,\infty ]$. Then, using the construction of Theorem 3, i.e., $E_{T_L}(x,y)=f_{T_L}^{(-1)}\left(d(x,y)\right)$ for all $x,y\in X$, we obtain a $T_L$-indistinguishability operator on X that separates points, which has the following expression:

$$E_{T_L}(x,y)=\left\{\begin{array}{cc}1-d(x,y),\hfill & \mathrm{if} 0\le d(x,y)<1;\hfill \\ 0,\hfill & \mathrm{elsewhere},\hfill \end{array}\right.$$

for all $x,y\in X$.

A ${\mathit{T}}_{\mathit{P}}$-indistinguishability operator

Let d be a distance on a nonempty set X and consider the product t-norm $T_P$. It is clear that the function $f_{T_P}:[0,1]\to [0,\infty ]$, given by $f_{T_P}\left(x\right)=-log\left(x\right)$ for all $x\in [0,1]$, is an additive generator of $T_P$. The pseudo-inverse $f_{T_P}^{(-1)}$ of $f_{T_P}$ is given by

$$f_{T_P}^{(-1)}\left(y\right)={\mathsf{e}}^{-y}$$

for all $y\in [0,\infty ]$. Then, using the construction of Theorem 3, i.e., $E_{T_P}(x,y)=f_{T_P}^{(-1)}\left(d(x,y)\right)$ for all $x,y\in [0,1]$, we obtain the following expression:

$$E_{T_P}(x,y)={\mathsf{e}}^{-d(x,y)}$$

for all $x,y\in X$. As in the above example, Theorem 3 ensures that $E_{T_P}$ is a $T_P$-indistinguishability operator on X that separates points.

After presenting these two easy yet illustrative preceding examples, which are constructed by means of the most commonly continuous Archimedean t-norms used in fuzzy logic, we will continue showing that the response function P, given by (3), is an indistinguishability operator that opens a wide range of potential applications from a mixed framework based on indistinguishability operators and distances to task allocation problems in multi-agent systems.

4.2. P as an Indistinguishability Operator

Consider the family of t-norms ${\left(T_{Dom}^{\lambda }\right)}_{\lambda \in [0,\infty ]}$ due to Dombi. Recall, according to [15], that such a family of t-norms is given by:

$$T_{Dom}^{\lambda }(x,y)=\left\{\begin{array}{cc}{T}_D(x,y),\hfill & \mathrm{if} \lambda =0;\hfill \\ T_M(x,y),\hfill & \mathrm{if} \lambda =\infty ;\hfill \\ \frac{1}{1+{\left({\left(\frac{1-x}{x}\right)}^{\lambda }+{\left(\frac{1-y}{y}\right)}^{\lambda }\right)}^{\frac{1}{\lambda }}},\hfill & \mathrm{elsewhere},\hfill \end{array}\right.$$

where $T_D$ is the drastic t-norm (see [15]).

According to [15], the t-norm $T_{Dom}^{\lambda }$ is continuous and Archimedean for each $\lambda \in ]0,\infty [$. Moreover an additive generator of $T_{Dom}^{\lambda }$ is given by

$$f_{T_{Dom}^{\lambda }}\left(x\right)={\left(\frac{1-x}{x}\right)}^{\lambda }$$

for all $x\in [0,1]$ and for each $\lambda \in ]0,\infty [$. It is not hard to verify that the pseudo-inverse of this additive generator $f_{T_{Dom}^{\lambda }}^{(-1)}$ is given by

$$f_{T_{Dom}^{\lambda }}^{(-1)}\left(y\right)=\frac{1}{1+y^{\frac{1}{\lambda }}}$$

for all $y\in [0,\infty ]$ and for each $\lambda \in ]0,\infty [$.

Taking into account the preceding facts, we are able to prove that P is in fact an indistinguishability operator constructed from a Dombi t-norm. To this end, assume that d is a distance on X and let $T_{Dom}^{\lambda }$ be a Dombi t-norm for an arbitrary $\lambda \in ]0,\infty [$. By Theorem 3, we obtain a $T_{Dom}^{\lambda }$-indistinguishability operator $E_{T_{Dom}^{\lambda }}$ that separates points by means of $E_{T_{Dom}^{\lambda }}(x,y)=f_{T_{Dom}^{\lambda }}^{(-1)}\left(d(x,y)\right)$ for all $x,y\in X$. It follows that

$$E_{T_{Dom}^{\lambda }}(x,y)=\frac{1}{1+d{(x,y)}^{\frac{1}{\lambda }}}$$

for all $x,y\in X$.

Next fix $n\in \mathbb{N}$ and take $\lambda =\frac{1}{n}$. Then, we have that $f_{T_{Dom}^{\frac{1}{n}},\theta }$ is also an additive generator of $T_{Dom}^{\frac{1}{n}}$, where

$$f_{T_{Dom}^{\frac{1}{n}},\theta }\left(x\right)=\theta ·f_{T_{Dom}^{\frac{1}{n}}}\left(x\right)=\theta ·{\left(\frac{1-x}{x}\right)}^{\frac{1}{n}}$$

for all $x\in X$ and for each $\theta \in ]0,\infty [$.

Now, we will apply Theorem 3 through $f_{T_{Dom}^{\frac{1}{n}},\theta }$. Since the pseudo-inverse $f_{T_{Dom}^{\frac{1}{n}},\theta }^{(-1)}$ of $f_{T_{Dom}^{\frac{1}{n}},\theta }$ is given by

$$f_{T_{Dom}^{\frac{1}{n}},\theta }^{(-1)}\left(y\right)=f_{T_{Dom}^{\frac{1}{n}}}^{(-1)}\left(\frac{y}{\theta }\right)=\frac{1}{1+{\left(\frac{y}{\theta }\right)}^n}=\frac{{\theta }^n}{{\theta }^n+y^n}.$$

Therefore, $E_{T_{Dom}^{\frac{1}{n}}}$ is a $T_{Dom}^{\frac{1}{n}}$-indsitinguishability operator with

$$E_{T_{Dom}^{\frac{1}{n}}}(x,y)=f_{T_{Dom}^{\frac{1}{n}},\theta }^{(-1)}\left(d(x,y)\right)=\frac{{\theta }^n}{{\theta }^n+d{(x,y)}^n}$$

(6)

for all $x,y\in X$. Since P given by (3) matches up with the preceding one, we conclude that the response function P is a $T_{Dom}^{\frac{1}{n}}$-indsitinguishability operator that separates points.

4.3. An Exponential Response Function and Indistinguishability Operators

In [13] (see also [11]), an exponential response function was introduced in order to model honey bee division of labor by means of response thresholds. In particular, the exponential response function of an agent taken under consideration was the following.

$$P_{exp}(s,\theta )=1-{\mathsf{e}}^{-\frac{s}{\theta }},$$

(7)

where s denotes the intensity of the stimulus for an agent to carry out a task and $\theta$ is the threshold. Note that, as in the case of response function (1), the probability of engaging task performance is small for $s<<\theta$, and is close to 1 for $s>>\theta$.

Our final goal of this section is twofold. On one hand, we provide an example of an indistinguishability operator that exhibits a behavior similar to response function (7) and, thus, it could be used in task allocation problems. On the other hand, we are able to retrieve exactly, from the generated indistinguishability operator and through the technique stated in Theorem 2, the response function (7) when it depends on the distance between an agent and a task.

Next consider the family of t-norms ${\left(T_{AA}^{\lambda }\right)}_{\lambda \in [0,\infty ]}$ introduced by Aczél and Alsina. Recall, according to [15], that such a family is given as follows:

$$T_{AA}^{\lambda }(x,y)=\left\{\begin{array}{cc}{T}_D(x,y),\hfill & \mathrm{if} \lambda =0;\hfill \\ T_M(x,y),\hfill & \mathrm{if} \lambda =\infty ;\hfill \\ {\mathsf{e}}^{-{\left({(-logx)}^{\lambda }+{(-logy)}^{\lambda }\right)}^{\frac{1}{\lambda }}},\hfill & \mathrm{elsewhere}.\hfill \end{array}\right.$$

Following [15], for each $\lambda \in ]0,\infty [$ we have that $T_{AA}^{\lambda }$ is continuous and Archimedean. Moreover, an additive generator of $T_{AA}^{\lambda }$ is given by

$$f_{T_{AA}^{\lambda }}\left(x\right)={(-log\left(x\right))}^{\lambda }$$

for all $x\in [0,1]$. A straightforward computation shows that the pseudo-inverse $f_{T_{AA}^{\lambda }}^{(-1)}$ of $f_{T_{AA}^{\lambda }}$ is given as follows.

$$f_{T_{AA}^{\lambda }}^{(-1)}\left(y\right)=e^{-\left(y^{\frac{1}{\lambda }}\right)},$$

for all $y\in [0,\infty ]$ and for each $\lambda \in ]0,\infty [$.

In the light of the exposed facts, we are able to introduce the announced indistinguishability operator. To this end, assume that d is a distance on a nonempty set X and let $T_{AA}^{\lambda }$ be an Aczél-Alsina t-norm for $\lambda \in ]0,\infty [$. Applying Theorem 3, we obtain the $T_{AA}^{\lambda }$-indistinguishability operator $E_{T_{AA}^{\lambda }}$ given by

$$E_{T_{AA}^{\lambda }}(x,y)=e^{-\left(d{(x,y)}^{\frac{1}{\lambda }}\right)}$$

for all $x,y\in X$. Notice that $E_{T_{AA}^{\lambda }}$ separates points.

Now, following similar arguments to those given in Subsection 4.2, we obtain, for each $n\in \mathbb{N}$ and $\theta \in ]0,\infty [$, the following indistinguishability operator from the preceding one.

$$E_{T_{AA}^{\frac{1}{n}}}(x,y)=e^{-\frac{d{(x,y)}^n}{{\theta }^n}}.$$

(8)

Of course, one can observe that the last operator presented involves the same elements of function (3). Indeed, this operator depends simultaneously on the distance $d(x,y)$, on a threshold parameter $\theta$, and it contains the non-linearity constant n. Besides, the nature of this indistinguishability operator is an exponential function as a response function (7). Nevertheless, a slight difference between them must be stressed with the aim of interpreting the operator given in (8) as a response function. It is clear that in (8), s must be considered as the inverse of the distance with the aim that the indistinguishability operator in (8) can be interpreted as a response function. Indeed, s must be understood as the inverse of distance in order to preserve the essence of the impact of the stimulus s in the expression of a response function. Thus, we have that the operator given by (8) acts as response function since it satisfies the following: $d(x,y)>>\theta$ implies probability response close to 0 and $d(x,y)<<\theta$ returns a probability response close to 1. It follows that the idea of “an agent is high motivated for performing closer tasks” is preserved. The fact that the operator in (8) can be interpreted as a response function inspires that several families of indistinguishability operators that can be proposed and tested with a large number of experiments in order to be compared with previous response functions used in the literature and, thus, to determine if indistinguishability operators are an appropriate mathematical tool for task allocation problems.

Finally, we show that, in addition, the indistinguishability operator given by (8) allows the retrieval of exactly the response function (7). Hence, indistinguishability operators can still be used for generating response function even in those cases in which the stimulus s cannot be understood as the inverse of the distance. Indeed, note that $T_L\le T_{AA}^1=T_P$ and, thus, Theorem 2 guarantees that the function given by $d_{E_{T_{AA}^1}}=f_{T_L}(E_{T_{AA}^1})=1-E_{T_{AA}^1}$ is a distance on X. However, such a function matches up with the exponential response function given by (7).

5. Possibilistic Task Allocation

In this section, we will see how to use possibilistic Markov chains for developing a RTM in order to allocate a set of robots to tasks using the aforementioned indistinguishability operators (see (1) and (8)). Firstly, we will introduce the theoretical foundations of the possibilistic Markov chains and then we will describe how to adapt the indistinguishability operators to the multi-robot task allocation problem. Although the implementation proposed in this section only considers robots, it can be easily extended to more generic multi-agent scenarios.

5.1. Possibilistic Markov Chains: Theory

As was proved in [10], possibilistic Markov chains provide a lot of advantages and outperform their probabilistic counterpart when they are applied to task allocation problems. This section summarizes the main theoretical concepts of possibilistic (fuzzy) Markov chains.

Following [20], we can define a possibility Markov (memoryless) process as follows: let $S=\left\{s_1,\dots ,s_m\right\}$ ($m\in \mathbb{N}$) denote a finite set of states. If the system is in the state $s_i$ at time $\tau$ ($\tau \in \mathbb{N}$), then the system will move to the state $s_j$ with possibility $p_{ij}$ at time $\tau +1$. Let $x\left(\tau \right)=(x_1\left(\tau \right),\dots ,x_m\left(\tau \right))$ be a fuzzy state set, where $x_i\left(\tau \right)$ is defined as the possibility that the state $s_i$ will occur at time $\tau$ for all $i=1,\dots ,m$. Notice that ${\bigvee }_{i=1}^m{x}_i\left(\tau \right)\le 1$ where ∨ stands for the maximum operator on $[0,1]$. In the light of the preceding facts, the evolution of the fuzzy Markov chain in time is given by

$$x_i\left(\tau \right)=\underset{j=1}{\overset{m}{\bigvee }}{p}_{ji}\wedge x_j(\tau -1),$$

where ∧ stands for the minimum operator on $[0,1]$. The preceding expression admits a matrix formulated as follows.

$$x\left(\tau \right)=x(\tau -1)\circ M=x\left(0\right)\circ M^{\tau },$$

(9)

where $M={\left\{p_{ij}\right\}}_{i,j=1}^m$ is the fuzzy transition matrix, ∘ is the matrix product in the max-min algebra $\left(\right[0,1],\vee ,\wedge )$, and $x\left(\tau \right)=\left(x_1\left(\tau \right),\dots ,x_m\left(\tau \right)\right)$ is the possibility distribution at time $\tau$.

Taking into account the preceding matrix notation and following [20], a possibility distribution $x\left(\tau \right)$ of the system states at time $\tau$ is said to be stationary, or stable, whenever $x\left(\tau \right)=x\left(\tau \right)\circ M$. During experiments, explained in Section 6, each state will be a task to execute and, therefore, m will stand for the number of tasks.

One of the main advantages of possibilistic Markov chains with respect to their probabilistic counterparts is given by the fact that under certain conditions, provided in [21] by J. Duan, the system converges to a stationary state in, at most, $m-1$ steps.

5.2. Possibilistic Multi-Robot Task Allocation

Formally, the problem to solve could be defined as follows. Let $l,m\in \mathbb{N}$, R be the set of robots with $R=\{r_1,\dots ,r_l\}$, and T be the set of tasks to carry out with $T=\{t_1,\dots ,t_m\}$. Both, tasks and robots are placed in an environment.

According to the classical RTMs (see Section 2), for each robot $r_k$ and for each task $t_j$, a stimulus $s_{r_k,t_j}\in \mathbb{R}$ that represents how suitable $t_j$ is for $r_k$ is defined. Besides, a threshold value $\theta$ is assigned to each robot $r_k$. Thus, a robot $r_k$, allocated at task $t_i$, will select a task $t_j$ to execute with a possibility $E_{T_{Dom}^{\frac{1}{n}}}(t_i,t_j)$ according to a fuzzy Markov decision chain. In the following, the stimulus of each robot $r_k$ to transit from task $t_i$ to task $t_j$ only depends on the distance between the tasks that will be denoted by $d(t_i,t_j)$. So, the stimulus of each robot $r_k$ to transit from $t_i$ to task $t_j$ is given as follows.

$$s_{t_i,t_j}=\left\{\begin{array}{cc}\frac{1}{d(t_i,t_j)}\hfill & \mathrm{if} d(t_i,t_j)\ne 0\hfill \\ \infty \hfill & \mathrm{if} d(r_k,t_j)=0\hfill \end{array}\right..$$

(10)

This stimulus $s_{r_k,t_j}$ allows us to obtain, by means of the indistinguishability operator (6), the following possibilistic transition function (response function),

$$p_{ij}=E_{T_{Dom}^{\frac{1}{n}}}(t_i,t_j)=\frac{{\theta }^n}{{\theta }^n+d{(t_i,t_j)}^n}.$$

(11)

If the same stimulus (distance) is applied to the indistinguishability operator (8), then the following possibilistic transition function (response function), is obtained:

$$p_{ij}=E_{T_{AA}^{\frac{1}{n}}}(t_i,t_j)=e^{-\frac{d{(t_i,t_j)}^n}{{\theta }^n}}.$$

(12)

From now on, we will reference the response function given by (12) as the Exponential Possibility Response Function (EPRF) and the response function given by (11) as the Original Possibility Response Function (OPRF). Furthermore, as the transition functions EPRF and OPRF are indistinguishability operators. We will use both terms—transition possibility and indistinguishability operator—equally.

As was proved in [12] (see also [10]), when either response functions (or indistinguishability operators), (11) or (12), are used as a possibility transition, the obtained fuzzy Markov chain holds the Duan’s convergence requirements. Therefore, we can ensure that the system converges to a stationary state in at most $m-1$ steps. It must be recalled that, in general, the convergence of the probabilistic Markov chains is only guaranteed asymptotically.

6. Experimental Results

In this section, we will show the experiments carried out to compare the number of steps required to converge to a stationary state using probabilistic and possibilistic Markov chains induced from the indistinguishability operators given in (6) and (8).

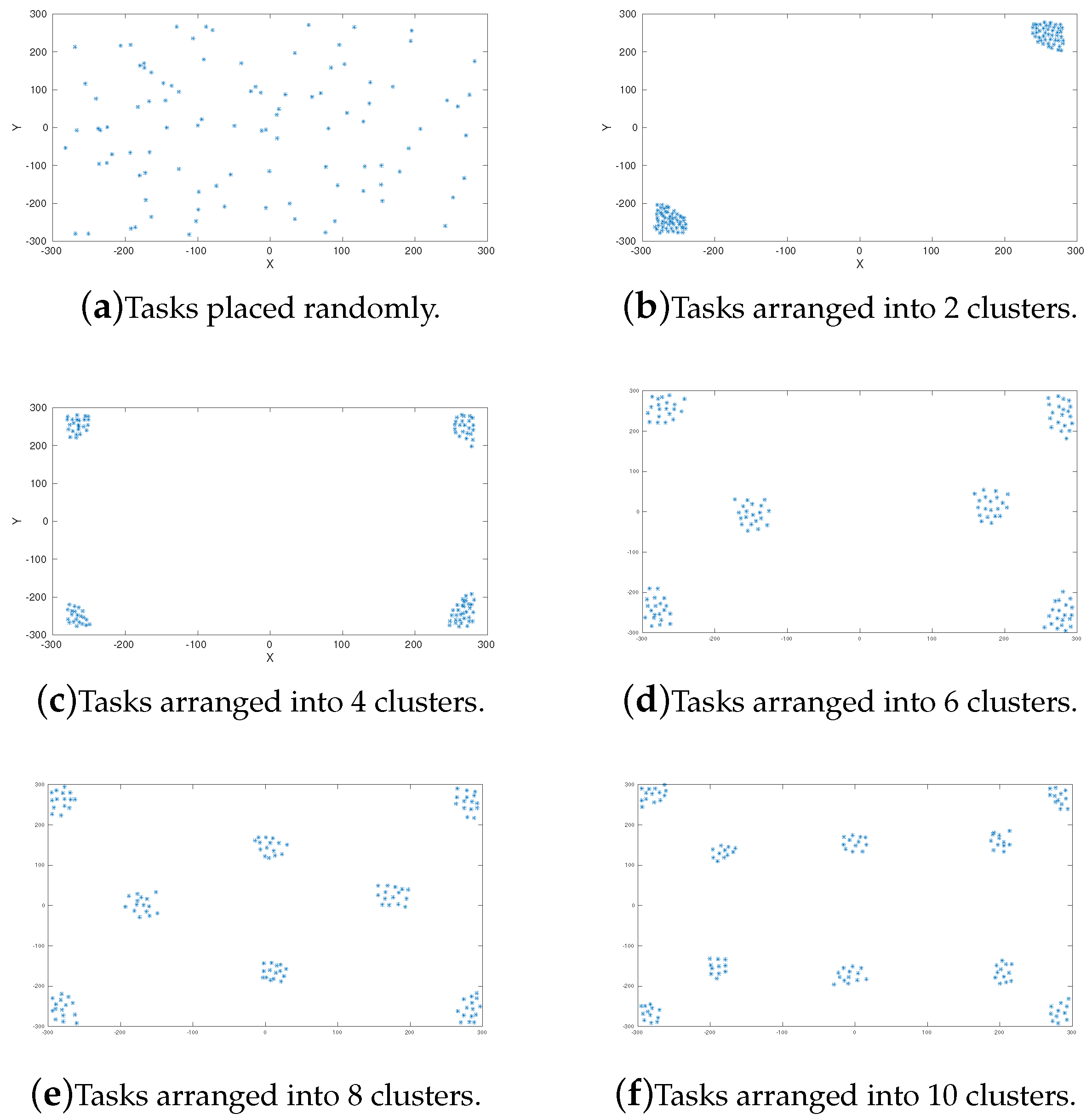
The robots must perform the task according to the stimulus defined in Section 5 under different configurations of the system: different positions of the objects, parameters of the possibility response functions ($\theta$ and the power n), and number of tasks. All the experiments have been carried out using MATLAB with different synthetic environments. Figure 1 shows the six types of environment used during the experiments, depending on the position of the tasks: randomly placed (Figure 1a), tasks grouped into two clusters (Figure 1b), tasks grouped into four clusters (Figure 1c), tasks grouped into six clusters (Figure 1d), tasks grouped into eight clusters (Figure 1e), and tasks grouped into 10 clusters (Figure 1f). This section extends the previous work given in [12] in order to consider clustered tasks.

As pointed out in Section 2, the threshold value $\theta$ must depend on the position of the tasks. During the performed experiments, $\theta$ will depend on the maximum distance between tasks as follows.

$$\theta =\frac{d_{max}}{nTH},$$

(13)

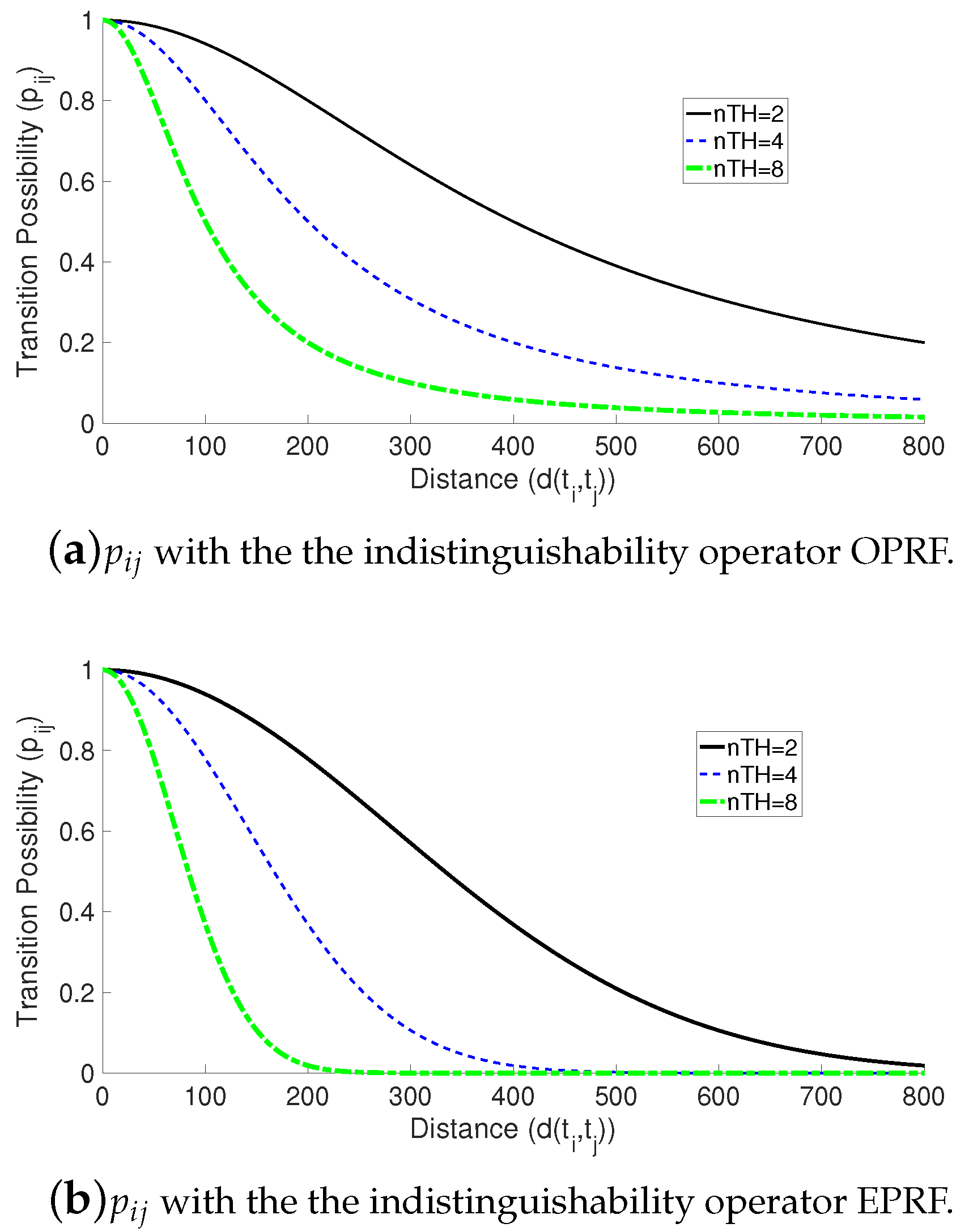
where $d_{max}$ is the maximum distance between two objects and $nTH$ is a parameter of the system. In our simulations, $d_{max}$ is constant and equal to 800.5 units. In order to see the impact of the parameter $nTH$ on the transition possibility ($p_{ij}$) from a task $t_i$ to the task $t_j$, Figure 2 shows the values of $p_{ij}$ using the indistinguishability operators OPRF (Figure 2a) and EPRF (Figure 2b) with $nTH=2,4,8$ and the power value $n=2$. It should be noted that if the distance is equal to 0 ($d(t_i,t_j)=0$) then $t_j=t_i$ and $p_{ij}=p_{ii}$ is the possibility of remaining in the current task.

Whichever possibility response function is used, (11) or (12), the possibilistic transition matrix for each robot, M, must be transformed into a probabilistic matrix for the possibilistic and probabilistic Markov chains results to be comparable. To make this conversion, we use the transformation proposed in [22], where each element of M is normalized (divided by the sum of all the elements in its row) meeting the conditions of a probability distribution.

6.1. Experiments with Randomly Placed Objects

This section focuses on experiments with tasks placed randomly, as can be seen in Figure 1a. All the experiments have been performed with 500 different environments, with different number of tasks ($m=50,100$) and different values of the power n in the expression of the indistinguishability operators (11) and (12). The threshold $\theta$ values under consideration are obtained from (13), setting $nTH=2,4,8$.

In [12], it was shown that OPRF and EPRF in these randomly generated environments needed the same number of steps to converge. This number of steps does not depend on $\theta$ nor the power value n. This is because the minimum between two transition possibilities is the same regardless of the indistinguishability operator (OPRF or EPRF) or parameters are used. Therefore, the result of the composition of two matrices with a max-min algebra does not depend on the operator. Informally, this fact can be seen in the following way. Recall that, as was introduced in Section 5.1, the composition of a possibilistic matrix with itself, $M^2=M\circ M$, is calculated as follows.

$$p_{ij}^2=\underset{k=1}{\overset{m}{\bigvee }}{p}_{ik}\wedge p_{kj},$$

(14)

where $M^2={\{p_{ij}^2\}}_{i,j=1}^m$. The minimum of two possibilities $(p_{ik}\wedge p_{kj}$) must be either $p_{ik}$ or $p_{kj}$ and it does not depend on the indistinguishability operator used ((11) or (12)). Therefore, the composition of the matrices given by Equation (14) is also independent of the indistinguishability operator, as well as the values of the power matrix $M^{\tau }$. From the matrix formulation of the system’s evolution (see Equation (9)) and the convergence condition given in Section 5.1, it can be seen that the number of steps until convergence does not depend on the indistinguishability operator nor its parameters. Future works will analyse, on one hand, if there are other indistinguishability operators that do not exhibit this property and, on the other hand, if this property is preserved when the matrix composition is based on the use of triangular conorm-triangular norm algebras different from the max-min one.

These simulations also show that only a 50% of the 500 environments could converge to a stationary state when probabilistic Markov chains are used. In contrast with fuzzy Markov chains, all the experiments converge and they required less than 25 steps. This shows that fuzzy Markov chains with indistinguishability operators always outperform their probability counterpart. Figure 3 shows the mentioned percentage of experiments that, using probabilistic Markov chains, do converge with 100 randomly placed tasks.

6.2. Clustered Environments

This section shows the results obtained using environments with the tasks arranged in the groups or clusters, shown in Figure 1b,c. As occurred in Section 6.1, the obtained results are very similar whichever indistinguishability operator is applied, OPRF or EPRF. Therefore, even if the tasks are arranged into clusters, both indistinguishability operators present an equivalent behavior and they are not affected by its parameters.

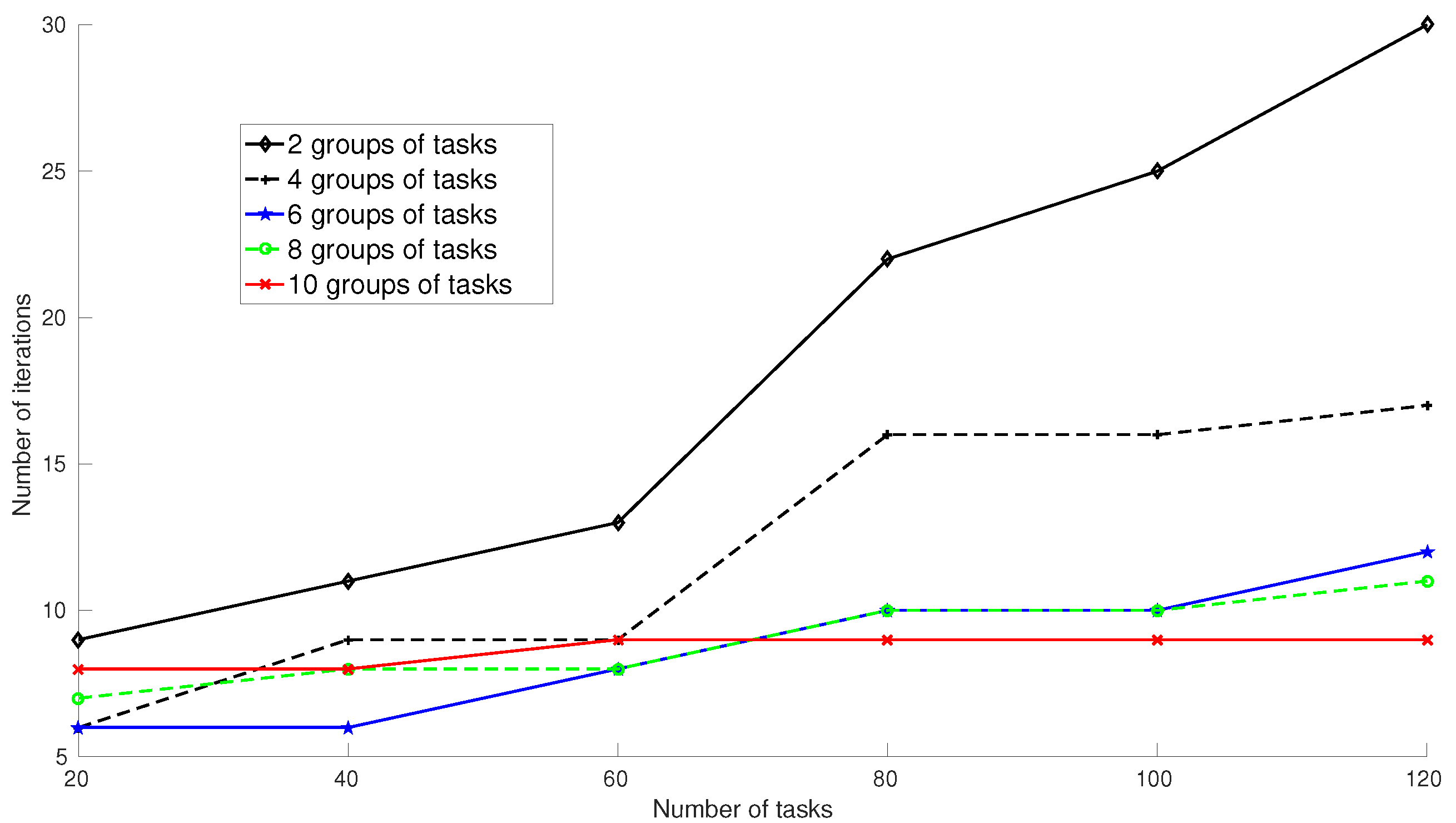
Figure 4 shows the number of iterations required to converge with fuzzy Markov chains with two, four, six, eight and 10 clusters of tasks and different number of tasks ($m=20,40,60,80,100,120$). As can be observed, the number of clusters has a great impact on the system. In general, if there is a greater number of clusters, the number of steps required to converge decreases. For example, the environment with 10 groups needs a significantly lower number of iterations to converge compared to the environment with two clusters, whatever number of tasks is under consideration. Moreover, from a certain number of clusters, between eight and 10, the number of iterations needed to converge is not reduced and remains constant whatever number of tasks are considered. From these results, we can see that, with fuzzy Markov chains, the number of steps to converge to a stable state depends only on the placement of tasks and not on the parameters of possibility transition function. Recall that the number of iterations required to converge is the same whichever indistinguishability operators are under consideration. Future works will analyze in detail the reason of this behavior. Moreover, more experiments will be conducted using clusters with different characteristics, such as placement in the environment, size, and so on.

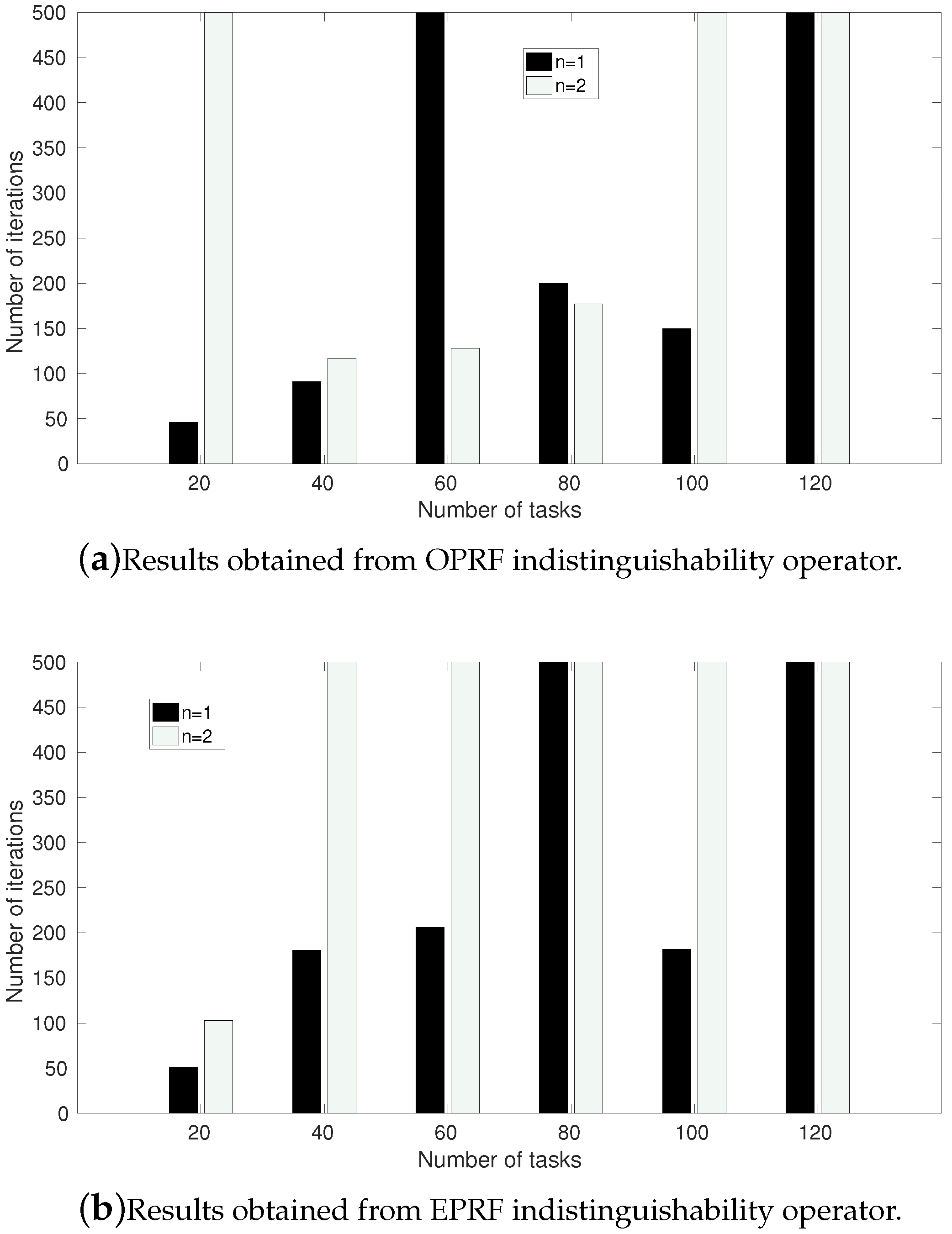
Figure 5 shows the number of steps required to converge with several number of tasks ($m=20,40,60,80,100,120$), a single environment with two clusters of tasks, $nTH=2$ and probabilistic Markov chains. When the number of iterations is equal to 500, the chain does not converge. Figure 5a shows this number of steps with the indistinguishability operator OPRF and Figure 5b with the indistinguishability operator EPRF, when the evolution of the process is modelled as a probabilistic Markov chain. These results show that the value n has a great impact on the results and that, in general, the exponential transition requires a greater number of steps to converge compared to its original counterpart. Furthermore, the indistinguishability operator has a great impact on the number of steps required to converge when probabilistic Markov chains are considered. It must be recalled that with possibilistic Markov chains both indistinguishability operators provide very similar results and it must be stressed that with possibilistic Markov chains, in general, the convergence is not guaranteed in a finite amount of steps.

7. Generalization of the Results

Firstly, this section provides a recapitulation of the main results of the paper, together with a generalization of them to other kinds of missions. Moreover, it provides some realistic application where the proposed task allocation approach can be applied.

As a recapitulation of the paper, it must be recalled that, as defined in Section 3, an indistinguishability operator provides the degree of equivalence, in fuzzy logic, between the elements of a set X. Thus, an indistinguishability operator E gives a numerical value between 0 and 1 ($E:X\times X\to [0,1]$) that must be interpreted as the measure of similarity between two elements. In our case, the set X can be considered as the set of tasks to be carried out. We have demonstrated that two of the most used response functions, Original Possibility Response Function (OPRF) and Exponential Possibility Response Function (EPRF) (see Equations (10) and (11)), are indistinguishability operators when both depend on the distance between the robot and the task to execute. Moreover, a max-min algebra has been used to compose the fuzzy transition matrices (see Equation (9)). The fuzzy Markov chains obtained from the indistinguishability operators converge to a stationary state in, at most, $m-1$ steps, where m is the number of tasks (see Section 5.1). In contrast, the probabilistic Makov chain used by the classical RTM methods, in general, converge asymptotically. The aforementioned points could be considered as a methodology where firstly, the system’s designer should choose one algebra and one indistinguishability operator and then model the behaviour of each robot as a fuzzy Markov chain.

In order to validate our approach, Section 5.2 and Section 6 provide an example of a foraging-like mission. This kind of mission, where the robots must gather or execute a set of tasks placed in an environment, is one of the most common mission used to evaluate multi-robot systems (see [3,14,23]). Despite its simplicity, many more complex and realistic missions are similar to it. For example, consider a scenario where the robots must search and rescue the victims of an earthquake. A human operator can mark on a map the regions of interest—where is it more plausible to find victims. Each task, or cluster of tasks, can be considered a region of interest where a robot, after reaching one of them, starts the rescue operation. Each robot would implement the aforementioned possibilistic Markov chain and decide autonomously the next task to carry out. In order to take this decision, the next task to execute will be randomly selected from the fuzzy state vector $x\left(\tau \right)$ (see Equation (9)).

8. Conclusions and Further Work

We have shown that the two most famous response functions given in literature are retrieved as particular cases from appropriate indistinguishability operators. This fact opens a wide range of potential applications from a mixed framework based on indistinguishability operators and distances to task allocation problems in multi-agent systems. We have applied the mentioned indistinguishability operators to allocate tasks to a group of robots according to a fuzzy Markov chain. We have shown that the results are very similar whichever indistinguishability operator is applied and, thus, both present equivalent behavior. The simulations extend the results previously obtained in [12] to analyze environments where the tasks are arranged in groups or clusters. The results show that the number of iterations required to converge with fuzzy Markov chains only depend on the placement of tasks in the environment and that they are not affected by the reminder of parameters of the system, whichever indistinguishability operator is applied. In contrast, when probabilistic Markov chains were used, this number of steps also depends on the indistinguishability operator. The theoretical and empirical obtained results in this paper open a wide range of potential applications from a mixed framework based on indistinguishability operators and distances to task allocation problems in multi-agent systems when fuzzy Markov chains are under consideration.

We plan to propose several families of indistinguishability operators to perform a large number of experiments in order to compare the new results with those provided by the task allocation methods that implement the two aforesaid response functions. An implementation of these methods on real robots is also under consideration.