Time Series Prediction Based on Adaptive Weight Online Sequential Extreme Learning Machine
Abstract
:1. Introduction
2. Preliminaries
2.1. Optimization Extreme Learning Machine
2.2. Online Sequential Extreme Learning Machine
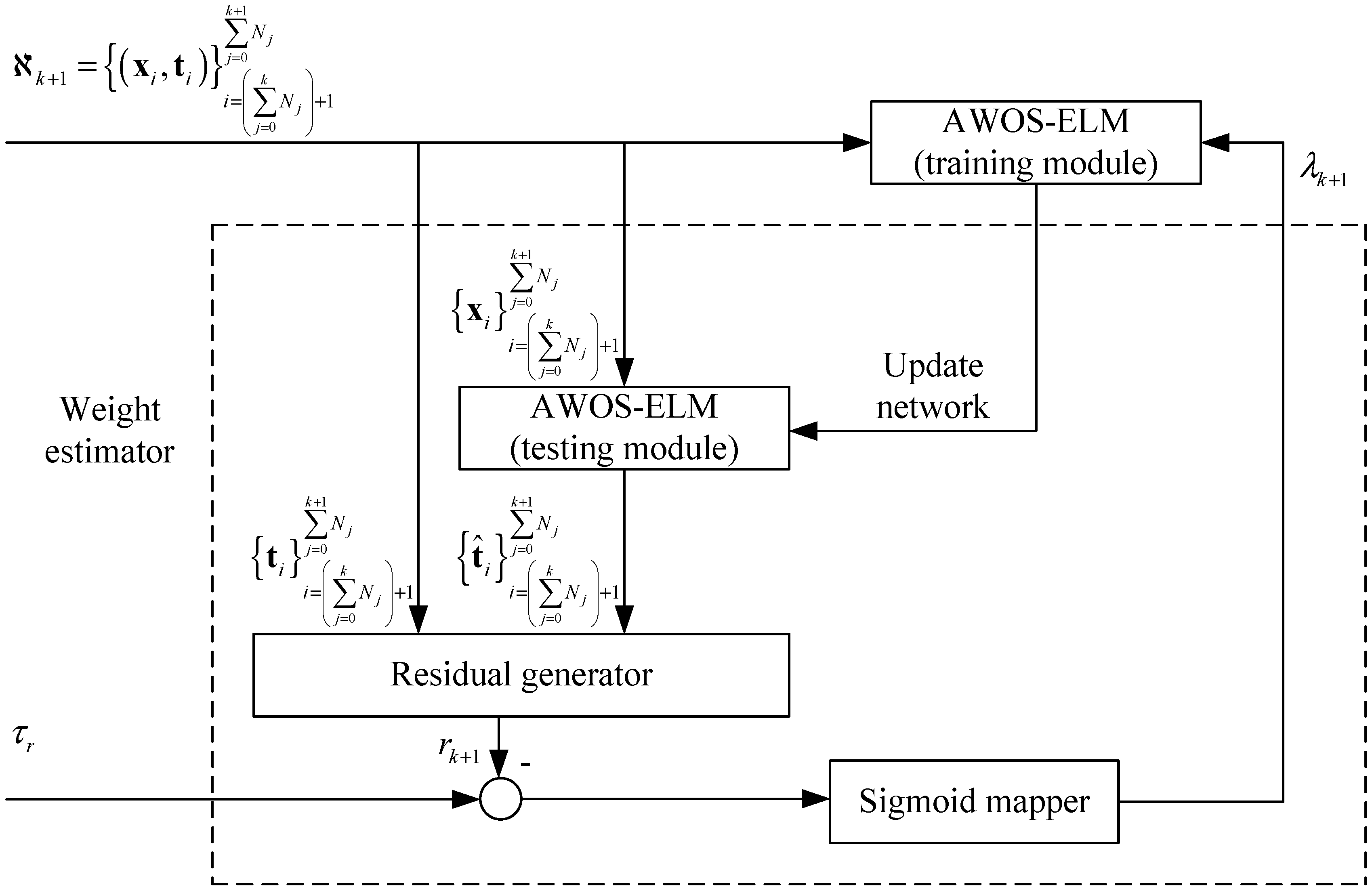
3. The Proposed Adaptive Weight Online Sequential Extreme Learning Machine
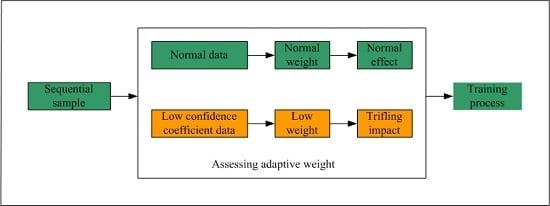
3.1. Integrated Structure
3.2. Formula Derivation
- (1)
- Configure the learning parameters randomly, and set ;
- (2)
- Calculate and according to Equations (9) and (10);
- (3)
- Set .
- (1)
- Assess the confidence coefficient of this new data chunk according to the test module in Figure 1, and determine the corresponding weight ;
- (2)
- Calculate the partial and as Equations (11) and (12);
- (3)
- Compute in an iterative way in accordance with Equations (21)–(23);
- (4)
- Set and go to Step 2 until all the training data chunks are used for the learning process.
4. Experiments
4.1. Benchmark Data Sets
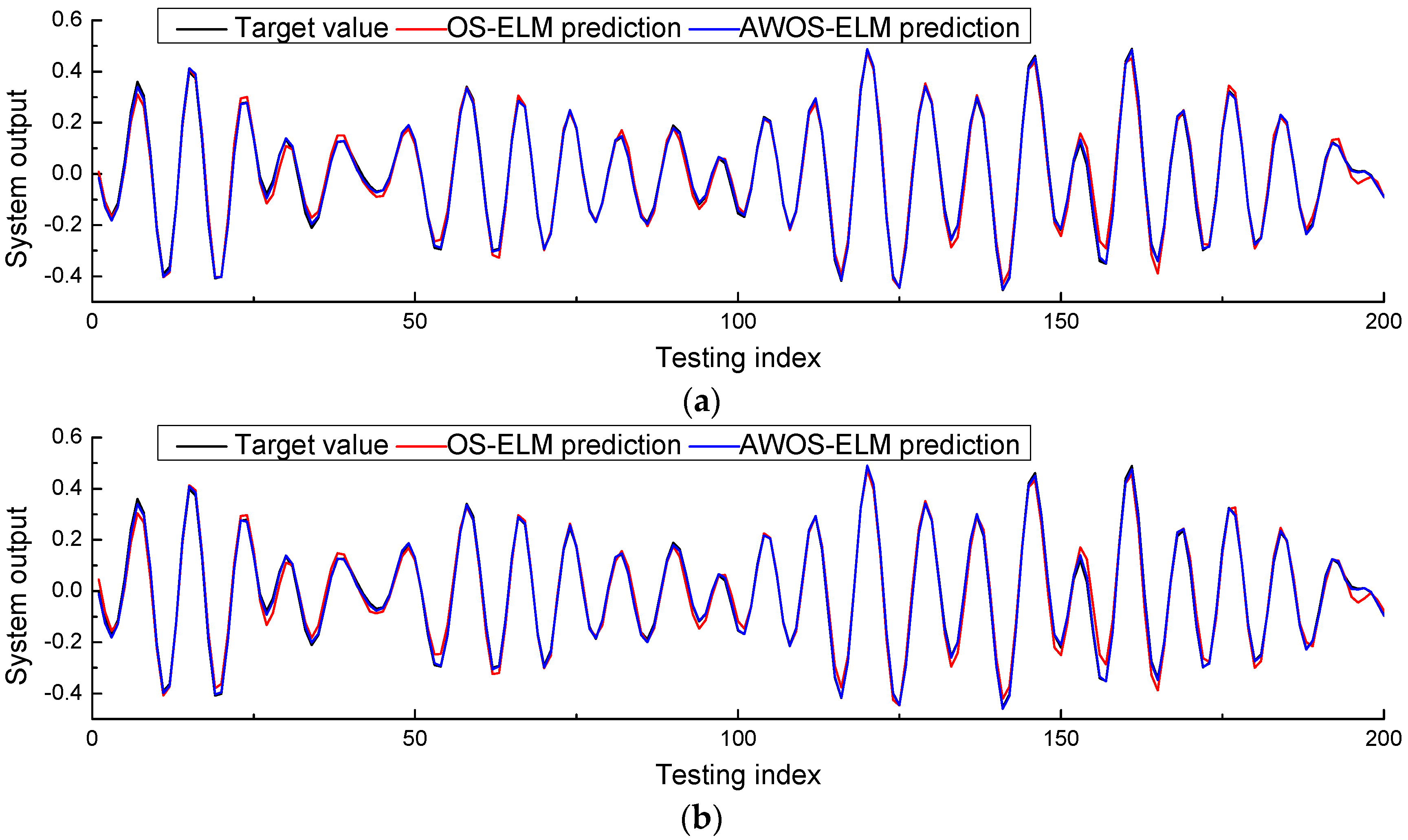
4.2. Robot Arm Example
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shukla, A.K.; Garde, Y.A.; Jain, I. Forecast of Weather Parameters Using Time Series Data. MAUSAM 2014, 65, 209–520. [Google Scholar]
- Kato, R.; Nagao, T. Stock Market Prediction Based On Interrelated Time Series Data. In Proceedings of the IEEE Symposium on Computers & Informatics, Penang, Malaysia, 18–20 March 2012.
- Soni, S.K.; Chand, N.; Singh, D.P. Reducing the Data Transmission in WSNs Using Time Series Prediction Model. In Proceedings of the IEEE International Conference on Signal Processing, Communications and Computing, Hong Kong, China, 13–15 August 2012.
- Hulsmann, M.; Borscheid, D.; Friedrich, C.M.; Reith, D. General Sales Forecast Models for Automobile Markets and Their Analysis. Trans. Mach. Learn. Data Min. 2011, 5, 65–86. [Google Scholar]
- Gooijer, J.G.D.; Hyndman, R.J. 25 Years of Time Series Forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, S.B. Time Series Analysis: Forecasting and Control. J. Oper. Res. Soc. 1976, 22, 199–201. [Google Scholar]
- Smith, C.; Jin, Y. Evolutionary Multi-objective Generation of Recurrent Neural Network Ensembles for Time Series Prediction. Neurocomputing 2014, 143, 302–311. [Google Scholar] [CrossRef] [Green Version]
- Donmanska, D.; Wojtylak, M. Application of Fuzzy Time Series Models for Forecasting Pollution Concentrations. Expert Syst. Appl. 2012, 39, 7673–7679. [Google Scholar] [CrossRef]
- Kumar, N.; Jha, G.K. A Time Series ANN Approach for Weather Forecasting. Int. J. Control Theory Comput. Model 2013, 3, 19–25. [Google Scholar] [CrossRef]
- Claveria, O.; Torra, S. Forecasting Tourism Demand to Catalonia: Neural Networks vs. Time Series Models. Econ. Model 2014, 36, 220–228. [Google Scholar] [CrossRef] [Green Version]
- Flores, J.J.; Graff, M.; Rodriguez, H. Evolutive Design of ARMA and ANN Models for Time Series Forecasting. Renew. Energ. 2012, 44, 225–230. [Google Scholar] [CrossRef]
- Adhikari, R. A Neural Network Based Linear Ensemble Framework for Time Series Forecasting. Neurocomputing 2015, 157, 231–242. [Google Scholar] [CrossRef]
- Kumar, D.A.; Murugan, S. Performance Analysis of Indian Stock Market Index Using Neural Network Time Series Model. In Proceedings of the International Conference on Pattern Recognition, Informatics and Mobile Engineering, Salem, India, 21–22 February 2013.
- Yoon, H.; Hyun, Y.; Ha, K.; Lee, K.; Kim, G. A Method to Improve the Stability and Accuracy of ANN- and SVM-Based Time Series Models For Long-Term Groundwater Level Predictions. Comput. Geosci. 2016, 90, 144–155. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L.; Siew, C.K. Universal Approximation Using Incremental Constructive Feedforward Networks with Random Hidden Nodes. IEEE T. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004.
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: Theory and Applications. Neurocomputing. 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Hosseinioun, N. Forecasting Outlier Occurrence in Stock Market Time Series Based on Wavelet Transform and Adaptive ELM Algorithm. J. Math. Financ. 2016, 6, 127–133. [Google Scholar] [CrossRef]
- Dash, R.; Dash, P.K.; Bisoi, R. A Self Adaptive Differential Harmony Search Based Optimized Extreme Learning Machine for Financial Time Series Prediction. Swarm Evol. Comput. 2014, 19, 25–42. [Google Scholar] [CrossRef]
- Liang, N.Y.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE T. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhou, H.M.; Ding, X.J.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Ding, X.; Zhou, H. Optimization Method Based Extreme Learning Machine for Classification. Neurocomputing. 2010, 74, 155–163. [Google Scholar] [CrossRef]
- Deng, C.Y. A Generalization of the Sherman-Morrison-Woodbury Formula. Appl. Math. Lett. 2011, 24, 1561–1564. [Google Scholar] [CrossRef]
- Guo, W.; Xu, T.; Tang, K. M-Estimator-Based Online Sequential Extreme Learning Machine For Predicting Chaotic Time Series with Outliers. Neural Comput. Appl. 2016, 2016, 1–18. [Google Scholar] [CrossRef]
- EI-Sayed, A.M.; Salman, S.M.; Elabd, N.A. On a Fractional-Order Delay Mackey-Glass Equation. Adv. Differ. Equ. 2016, 2016, 1–11. [Google Scholar]
- Berezowski, M.; Grabski, A. Chaotic and Non-chaotic Mixed Oscillations in a Logistic Systems with Delay. Chaos Solitons Fractals 2002, 14, 1–6. [Google Scholar] [CrossRef]
- Balasundaram, S.; Kapil, D.G. Lagrangian Support Vector Regression via Unconstrained Convex Minimization. Neural Net. 2014, 51, 67–79. [Google Scholar] [CrossRef] [PubMed]

| Data Sets | Hidden Node Type | Algorithms | RMSE | Hidden Nodes Number | Chunk Size | Training Time/s | ||
|---|---|---|---|---|---|---|---|---|
| Logistic | Sigmoid function | OS-ELM | 0.0164 | 0.0046 | 50 | - | 10 | 0.0924 |
| AWOS-ELM | 0.0041 | 0.0010 | 50 | 0.09 | 10 | 0.0914 | ||
| Radial basis function | OS-ELM | 0.0099 | 0.0023 | 50 | - | 10 | 0.1919 | |
| AWOS-ELM | 0.0039 | 0.0007 | 50 | 0.09 | 10 | 0.1913 | ||
| Mackey-Glass | Sigmoid function | OS-ELM | 0.0370 | 0.0021 | 25 | - | 5 | 0.1638 |
| AWOS-ELM | 0.0234 | 0.0026 | 25 | 0.1 | 5 | 0.1675 | ||
| Radial basis function | OS-ELM | 0.0362 | 0.0028 | 25 | - | 5 | 0.2764 | |
| AWOS-ELM | 0.0199 | 0.0024 | 25 | 0.1 | 5 | 0.2845 | ||
| Sunspot | Sigmoid function | OS-ELM | 0.0859 | 0.0006 | 40 | - | 10 | 0.0612 |
| AWOS-ELM | 0.0833 | 0.0006 | 40 | 0.15 | 10 | 0.0596 | ||
| Radial basis function | OS-ELM | 0.0844 | 0.0005 | 40 | - | 10 | 0.1251 | |
| AWOS-ELM | 0.0831 | 0.0004 | 40 | 0.15 | 10 | 0.1236 | ||
| Pseudo periodic synthetic series | Sigmoid function | OS-ELM | 0.0342 | 0.0007 | 20 | - | 15 | 0.1760 |
| AWOS-ELM | 0.0094 | 0.0004 | 20 | 0.1 | 15 | 0.1847 | ||
| Radial basis function | OS-ELM | 0.0365 | 0.0016 | 20 | - | 15 | 0.2577 | |
| AWOS-ELM | 0.0219 | 0.0025 | 20 | 0.1 | 15 | 0.2671 | ||
| Milk production | Sigmoid function | OS-ELM | 0.0561 | 0.0096 | 15 | - | 1 | 0.0062 |
| AWOS-ELM | 0.0394 | 0.0110 | 15 | 0.12 | 1 | 0.0056 | ||
| Radial basis function | OS-ELM | 0.0638 | 0.0101 | 15 | - | 1 | 0.0125 | |
| AWOS-ELM | 0.0506 | 0.0097 | 15 | 0.12 | 1 | 0.0103 | ||
| Electricity production | Sigmoid function | OS-ELM | 0.0301 | 0.0053 | 12 | - | 1 | 0.0168 |
| AWOS-ELM | 0.0265 | 0.0034 | 12 | 0.08 | 1 | 0.0165 | ||
| Radial basis function | OS-ELM | 0.0566 | 0.0233 | 12 | - | 1 | 0.0315 | |
| AWOS-ELM | 0.0406 | 0.0124 | 12 | 0.08 | 1 | 0.0303 |
| Data Sets | Sigmoid Hidden Node | Radial Basis Function Hidden Node | ||
|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | |
| Logistic | 0.7366 | 0.4403 | 0.7855 | 0.4080 |
| Mackey-Glass | 0.8750 | 0.3311 | 0.8748 | 0.3313 |
| Sunspot | 0.6440 | 0.4729 | 0.6447 | 0.4726 |
| Pseudo periodic synthetic series | 0.8726 | 0.3338 | 0.8592 | 0.3476 |
| Milk production | 0.8615 | 0.3435 | 0.9009 | 0.2959 |
| Electricity production | 0.8857 | 0.3152 | 0.9176 | 0.2741 |
| Hidden Node Type | Algorithms | RMSE | Hidden Nodes Number | Chunk Size | Training Time/s | ||
|---|---|---|---|---|---|---|---|
| Sigmoid function | OS-ELM | 0.0207 | 0.0004 | 45 | - | 5 | 0.1401 |
| AWOS-ELM | 0.0081 | 0.0004 | 45 | 0.04 | 5 | 0.1426 | |
| Radial basis function | OS-ELM | 0.0198 | 0.0006 | 45 | - | 5 | 0.3738 |
| AWOS-ELM | 0.0084 | 0.0007 | 45 | 0.04 | 5 | 0.4115 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Huang, J.; Lu, F. Time Series Prediction Based on Adaptive Weight Online Sequential Extreme Learning Machine. Appl. Sci. 2017, 7, 217. https://doi.org/10.3390/app7030217
Lu J, Huang J, Lu F. Time Series Prediction Based on Adaptive Weight Online Sequential Extreme Learning Machine. Applied Sciences. 2017; 7(3):217. https://doi.org/10.3390/app7030217
Chicago/Turabian StyleLu, Junjie, Jinquan Huang, and Feng Lu. 2017. "Time Series Prediction Based on Adaptive Weight Online Sequential Extreme Learning Machine" Applied Sciences 7, no. 3: 217. https://doi.org/10.3390/app7030217