Stochastic Model Predictive Control for Urban Traffic Networks
Abstract
:1. Introduction
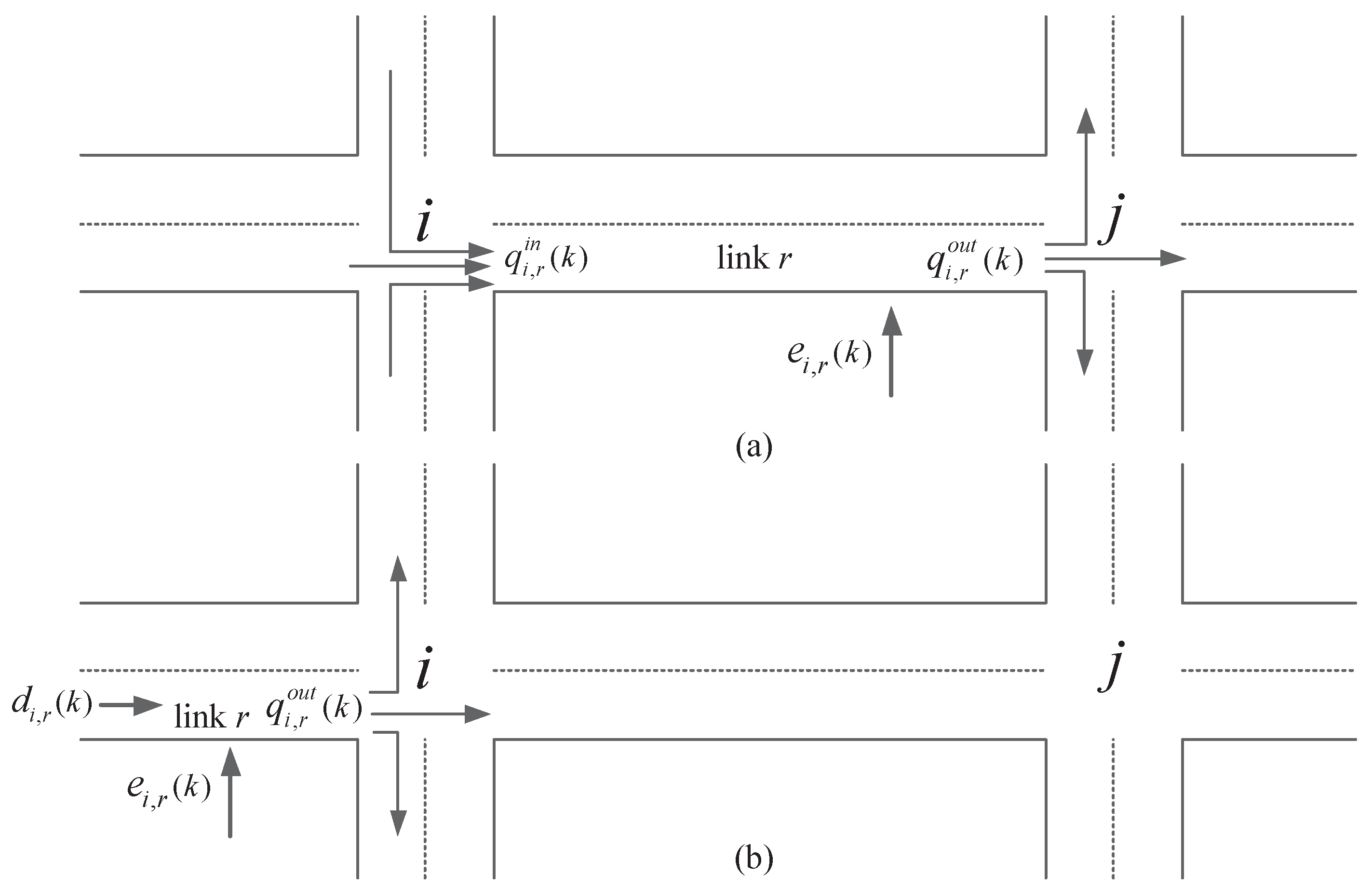
2. Modeling of Traffic Dynamics
2.1. Notations
2.2. Traffic Dynamics
3. Stochastic MPC-Based Model
3.1. Uncertainty
3.2. Constraints
3.3. MPC Framework
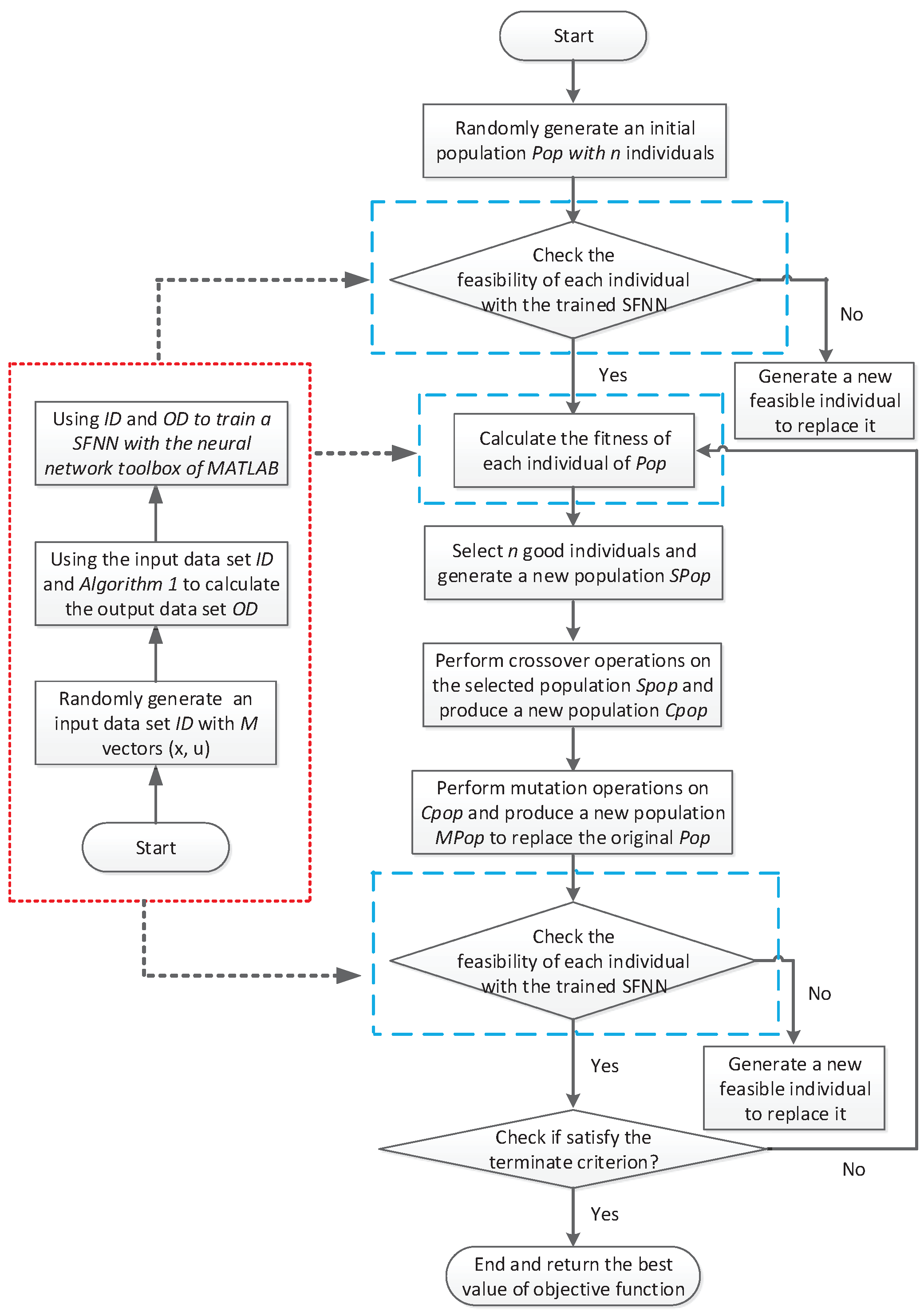
4. Optimization Method
4.1. Stochastic Simulation
| Algorithm 1 Stochastic Simulation for Uncertain Functions. |
|
4.2. Uncertain Function Approximation
4.3. Hybrid Intelligent Algorithm
| Algorithm 2 Hybrid Intelligent Algorithm |
|
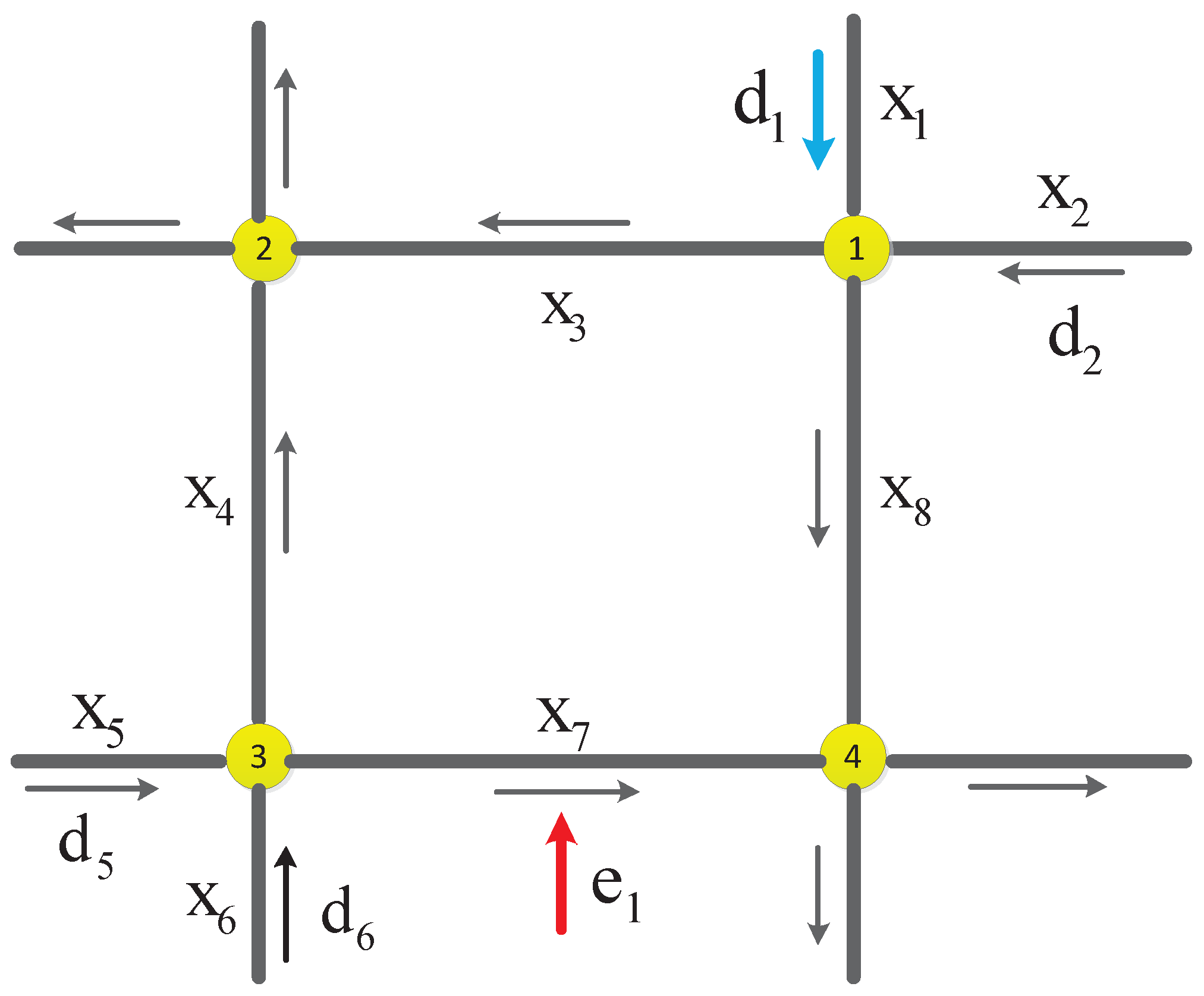
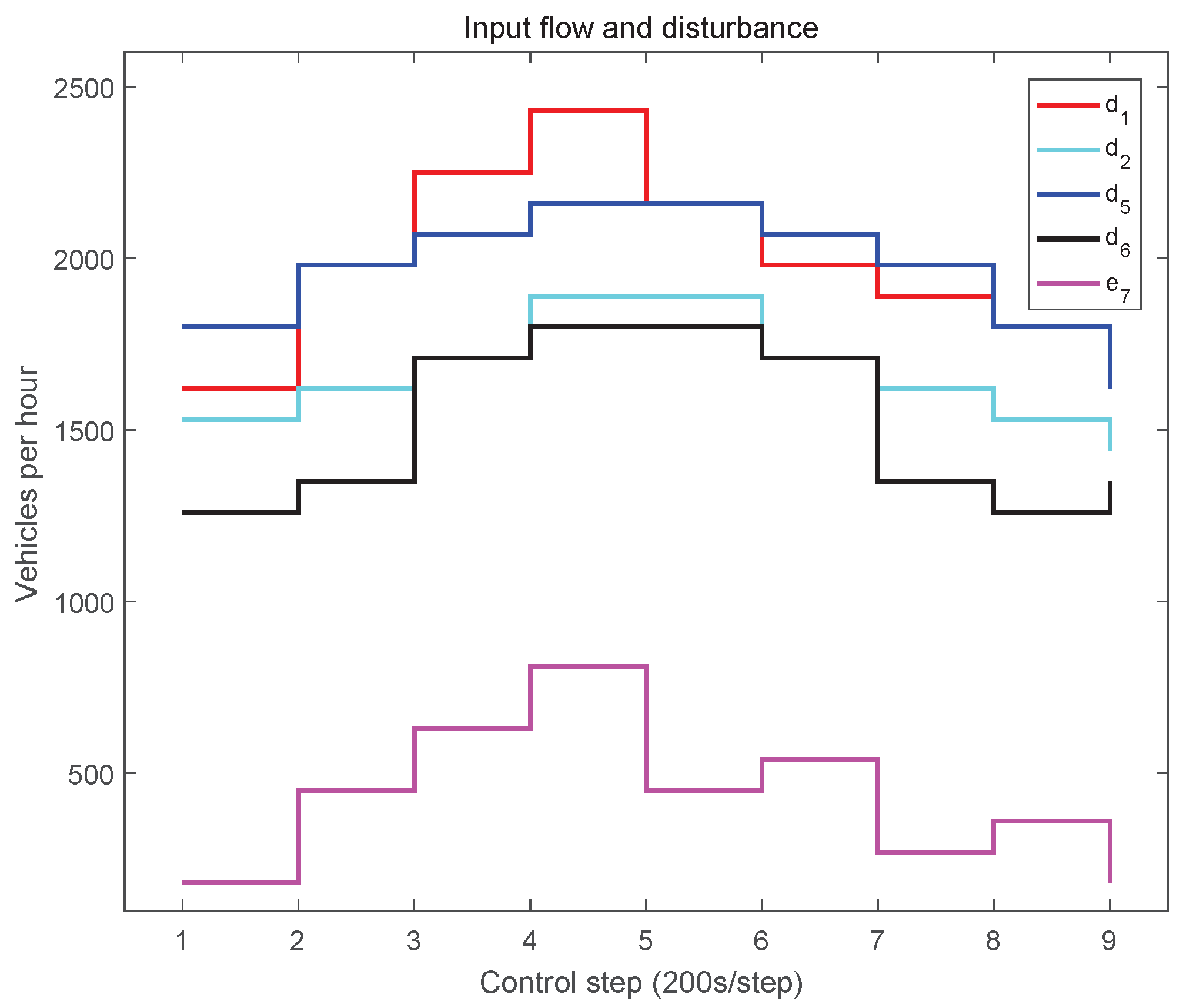
5. Simulation Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Porche, I.; Lafortune, S. Adaptive Look-ahead Optimization of Traffic Signals. J. Intell. Transp. Syst. 1999, 4, 209–254. [Google Scholar]
- Xie, X.F.; Smith, S.F.; Lu, L.; Barlow, G.J. Schedule-driven intersection control. Transp. Res. C Emerg. Technol. 2012, 24, 168–189. [Google Scholar] [CrossRef]
- Gartner, N.H.; Pooran, F.J.; Andrews, C.M. Optimized policies for adaptive control strategy in real-time traffic adaptive control systems: Implementation and field testing. Transp. Res. Rec. J. Transp. Res. Board 2002, 1811, 148–156. [Google Scholar] [CrossRef]
- Robertson, D.I.; Bretherton, R.D. Optimizing networks of traffic signals in real time: The SCOOT method. IEEE Trans. Veh. Technol. 1991, 40, 11–15. [Google Scholar] [CrossRef]
- Lowrie, P. The Sydney coordinated adaptive traffic system-principles, methodology, algorithms. In Proceedings of the International Conference on Road Traffic Signaling, London, UK, 30 March–1 April 1982; pp. 60–67. [Google Scholar]
- Gartner, N.H. OPAC: A demand-responsive strategy for traffic signal control. Transp. Res. Rec. J. Transp. Res. Board 1983, 906, 75–81. [Google Scholar]
- Henry, J.J.; Farges, J.L.; Tuffal, J. The PRODYN real time traffic algorithm. In Proceedings of the 4th Ifac/ifip/ifors Conference on Control in Transportation Systems, Baden-Baden, Germany, 20–22 April 1983; pp. 305–310. [Google Scholar]
- Sen, S.; Head, K.L. Controlled optimization of phases at an intersection. Transp. Sci. 1997, 31, 5–17. [Google Scholar] [CrossRef]
- Gazis, D.C.; Potts, R.B. The oversaturated intersection. In International Symposia on Traffic Theory, 2nd ed.; International Business Machines Corporation: London, UK, 1963; pp. 221–237. [Google Scholar]
- Diakaki, C.; Papageorgiou, M.; Aboudolas, K. A multivariable regulator approach to traffic-responsive network-wide signal control. Control Eng. Pract. 2002, 10, 183–195. [Google Scholar] [CrossRef]
- Aboudolas, K.; Papageorgiou, M.; Kosmatopoulos, E. Store-and-forward based methods for the signal control problem in large-scale congested urban road networks. Transp. Res. C Emerg. Technol. 2009, 17, 163–174. [Google Scholar] [CrossRef]
- Aboudolas, K.; Papageorgiou, M.; Kouvelas, A.; Kosmatopoulos, E. A rolling-horizon quadratic-programming approach to the signal control problem in large-scale congested urban road networks. Transp. Res. Part C Emerg. Technol. 2010, 18, 680–694. [Google Scholar] [CrossRef]
- Tettamanti, T.; Varga, I. Distributed traffic control system based on model predictive control. Civ. Eng. 2010, 54, 3–9. [Google Scholar] [CrossRef]
- De Oliveira, L.B.; Camponogara, E. Multi-agent model predictive control of signaling split in urban traffic networks. Transp. Res. C Emerg. Technol. 2010, 18, 120–139. [Google Scholar] [CrossRef]
- Camponogara, E.; Scherer, H.F. Distributed optimization for model predictive control of linear dynamic networks with control-input and output constraints. IEEE Trans. Autom. Sci. Eng. 2011, 8, 233–242. [Google Scholar] [CrossRef]
- Lin, S.; De Schutter, B.; Xi, Y.; Hellendoorn, H. Efficient network-wide model-based predictive control for urban traffic networks. Trans. Res. C Emerg. Technol. 2012, 24, 122–140. [Google Scholar] [CrossRef]
- Lin, S.; De Schutter, B.; Xi, Y.; Hellendoorn, H. Fast model predictive control for urban road networks via MILP. IEEE Trans. Intell. Transp. Syst. 2011, 12, 846–856. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, Y. Coordinate model predictive control with neighbourhood optimisation for a signal split in urban traffic networks. IET Intell. Transp. Syst. 2012, 6, 372–379. [Google Scholar] [CrossRef]
- Ye, B.L.; Wu, W.; Zhou, X.; Mao, W.; Li, J. A signal split optimization approach based on model predictive control for large-scale urban traffic networks. In Proceedings of the 2013 IEEE International Conference on Automation Science and Engineering (CASE), Madison, WI, USA, 17–20 Augest 2013; pp. 904–909. [Google Scholar]
- Ye, B.L.; Wu, W.; Mao, W. Distributed Model Predictive Control Method for Optimal Coordination of Signal Splits in Urban Traffic Networks. Asian J. Control 2015, 17, 775–790. [Google Scholar] [CrossRef]
- Ye, B.L.; Wu, W.; Li, L.; Mao, W. A hierarchical model predictive control approach for signal splits optimization in large-scale urban road networks. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2182–2192. [Google Scholar] [CrossRef]
- Yin, Y. Robust optimal traffic signal timing. Transp. Res. B Methodol. 2008, 42, 911–924. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, Y.; Lou, Y. Robust signal timing for arterials under day-to-day demand variations. Transp. Res. Rec. J. Transp. Res. Board 2010, 2010, 156–166. [Google Scholar] [CrossRef]
- Tamas, T.; Tamas, L.; Balazs, K.; Tamas, P.; Istvan, V. Robust control for urban road traffic networks. IEEE Trans. Intell. Transp. Syst. 2014, 15, 385–398. [Google Scholar]
- Liu, S.; Sadowska, A.; Frejo, J.R.D.; Núñez, A.; Camacho, E.F.; Hellendoorn, H.; De Schutter, B. Robust receding horizon parameterized control for multi-class freeway networks: A tractable scenario-based approach. Int. J. Robust Nonlinear Control 2016, 26, 1211–1245. [Google Scholar] [CrossRef]
- Zhou, X.; Ye, B.L.; Lu, Y.; Xiong, R. A Novel MPC with Chance Constraints for Signal Control in Urban Traffic Networks. In Proceedings of the 19th World Congress of International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014; pp. 11311–11317. [Google Scholar]
- Liu, B. Theory and Practice of Uncertain Programming, 2nd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Wang, T.; Gao, H.; Qiu, J. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 416–425. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Liu, J.; Thomas, D.B.; Cheung, P.Y. Neural Network Based Reinforcement Learning Acceleration on FPGA Platforms. ACM SIGARCH Comput. Archit. News 2017, 44, 68–73. [Google Scholar] [CrossRef]
- Ganjehkaviri, A.; Jaafar, M.M.; Hosseini, S.E.; Barzegaravval, H. Genetic algorithm for optimization of energy systems: Solution uniqueness, accuracy, Pareto convergence and dimension reduction. Energy 2017, 119, 167–177. [Google Scholar] [CrossRef]
- Guarnaccia, C. Acoustical noise analysis in road intersections: A case study. In Proceedings of the 11th WSEAS International Conference on Acoustics and Music: Theory and Applications, Iasi, Romania, 13–15 June 2010; pp. 13–15. [Google Scholar]
- Park, B.; Messer, C.; Urbanik, T. Traffic signal optimization program for oversaturated conditions: Genetic algorithm. Transp. Res. Rec. J. Transp. Res. Board 2002, 1683, 133–142. [Google Scholar] [CrossRef]
- Arel, I.; Liu, T.; Urbanik, A.; Kohls, G. Reinforcement learning-based multi-agent system for network traffic signal control. IET Intell. Transp. Syst. 2010, 4, 128–135. [Google Scholar] [CrossRef]
- Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer: Berlin, Germany, 2013. [Google Scholar]
- Portilla, C.; Valencia, F.; Espinosa, J.; Núñez, A.; De Schutter, B. Model-based predictive control for bicycling in urban intersections. Transp. Res. C Emerg. Technol. 2016, 70, 27–41. [Google Scholar] [CrossRef]
- Jamshidnejad, A.; Papamichail, I.; Papageorgiou, M.; De Schutter, B. A mesoscopic integrated urban traffic flow-emission model. Transp. Res. C Emerg. Technol. 2017, 75, 45–83. [Google Scholar] [CrossRef]
- Alaa, H.A.; Richard, C.P. Optimal design of aquifer cleanup systems under uncertainty using a neural network and a genetic algorithm. Water Resour. Res. 1999, 35, 2523–2532. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
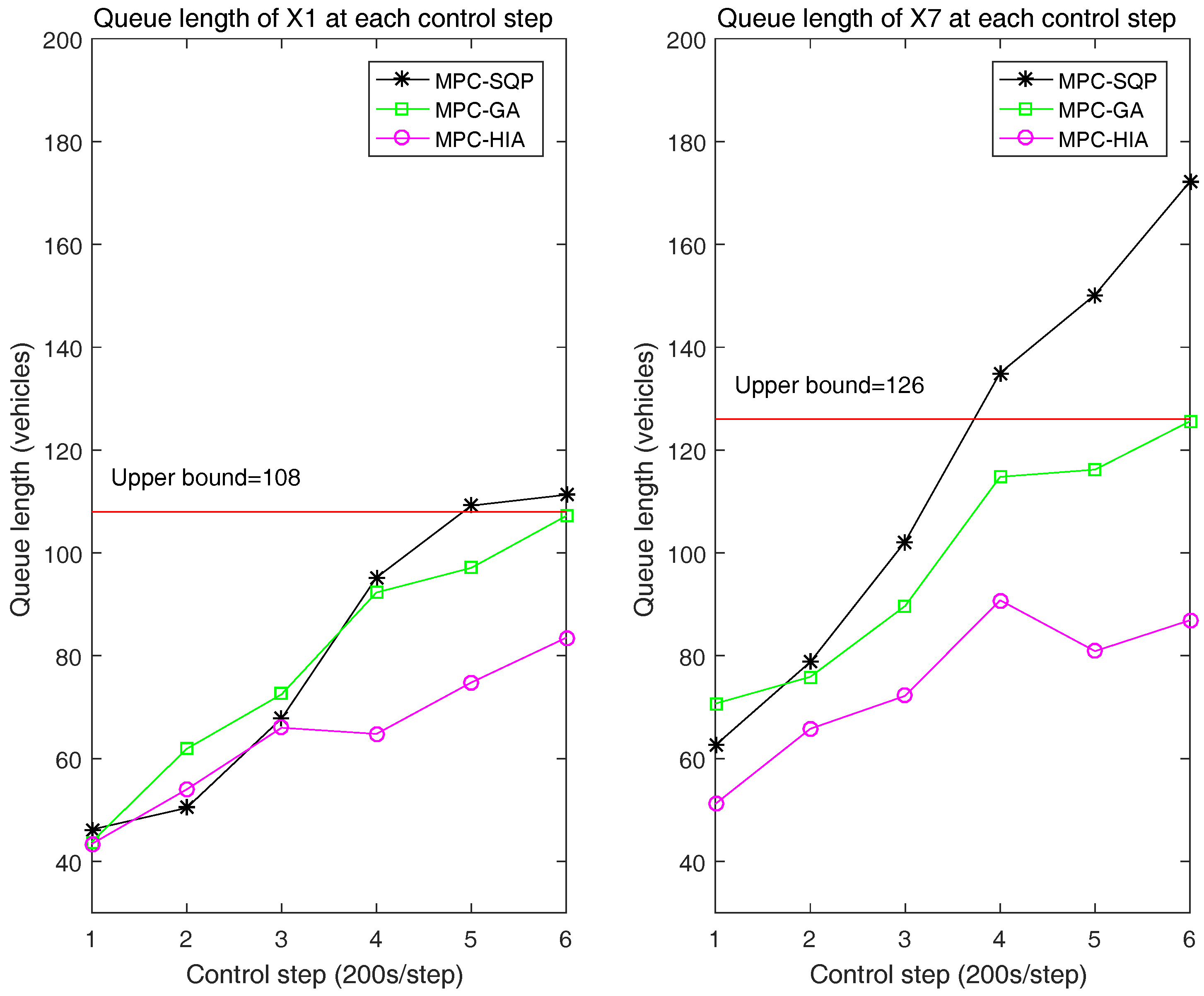
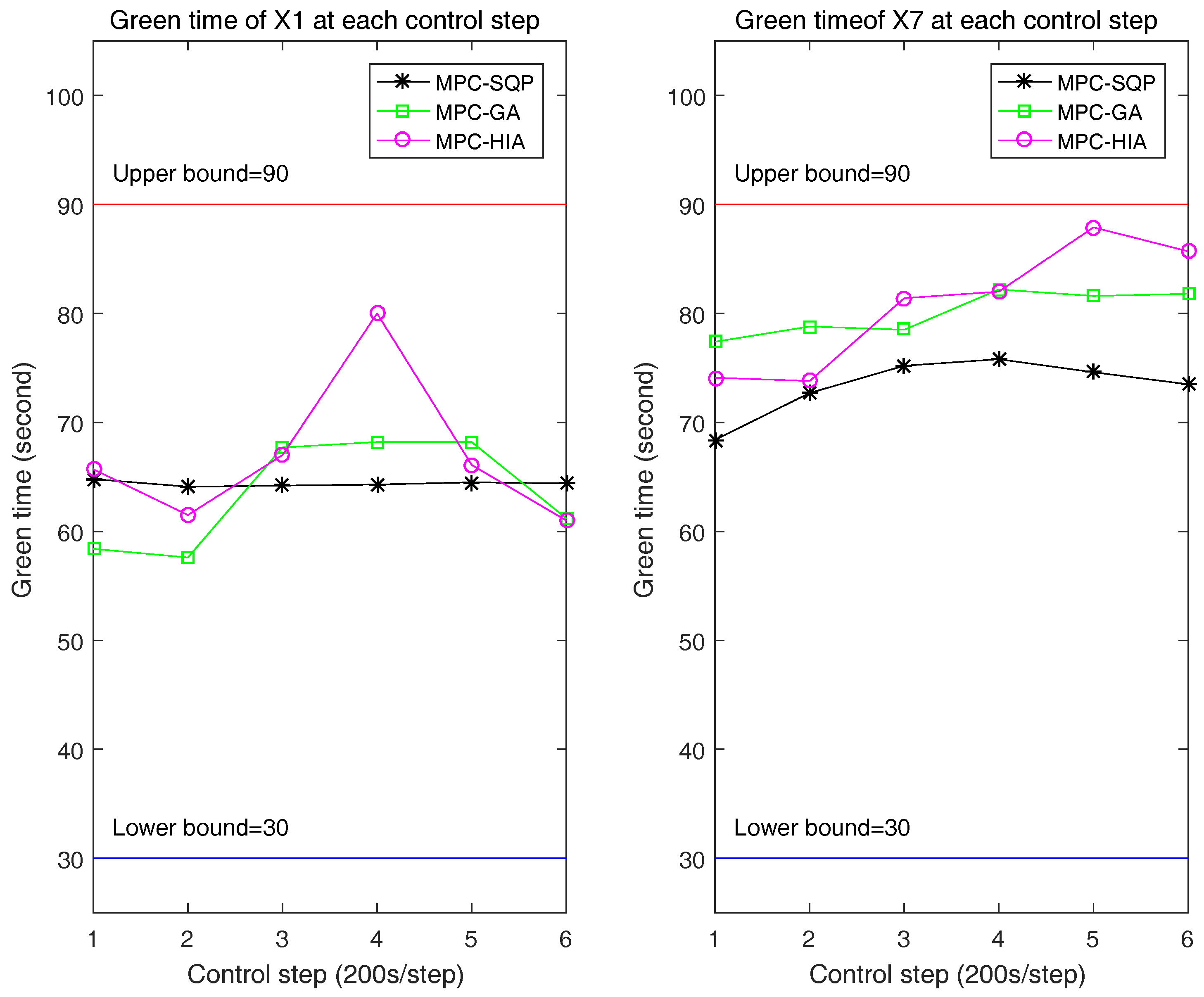
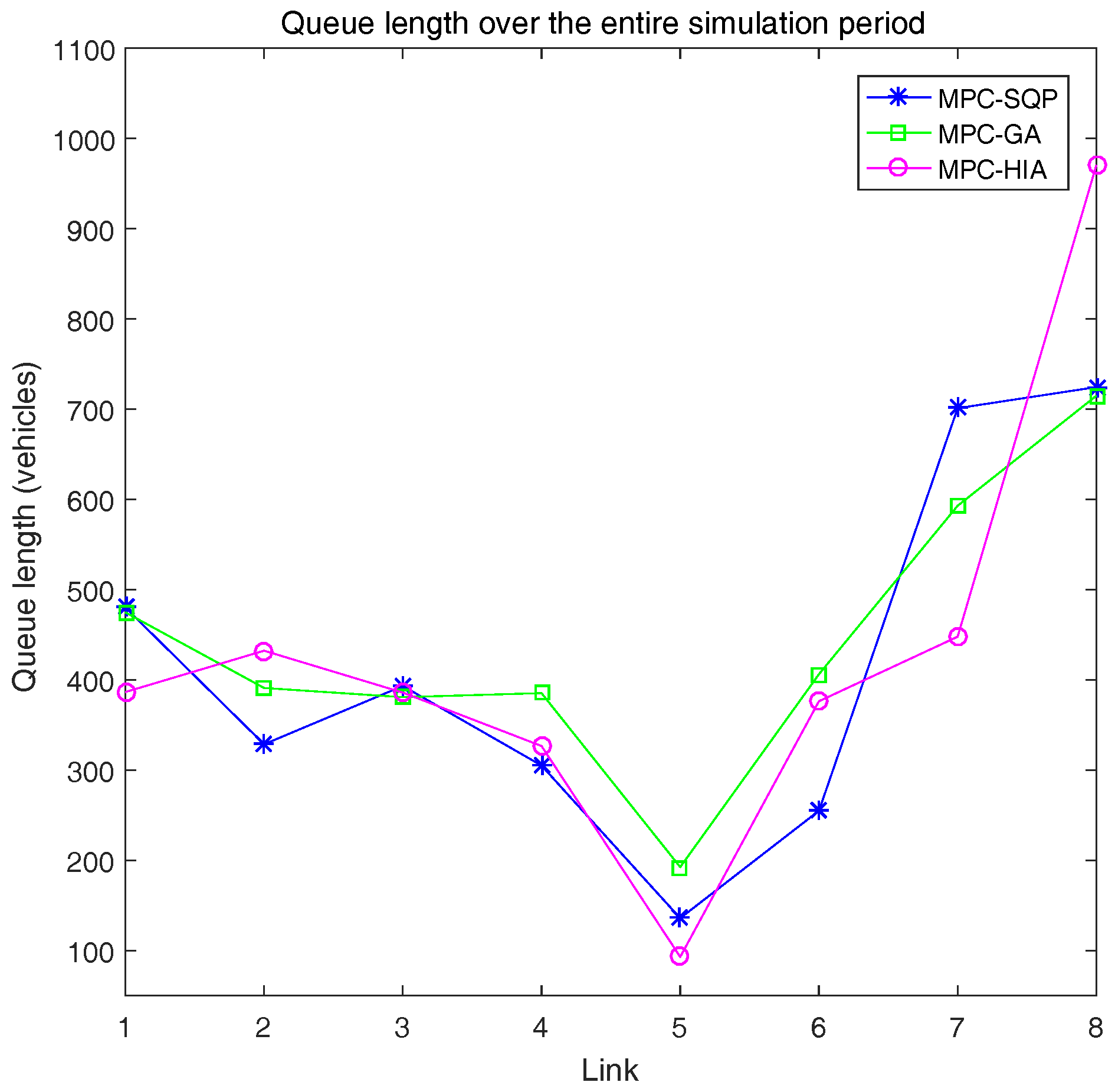
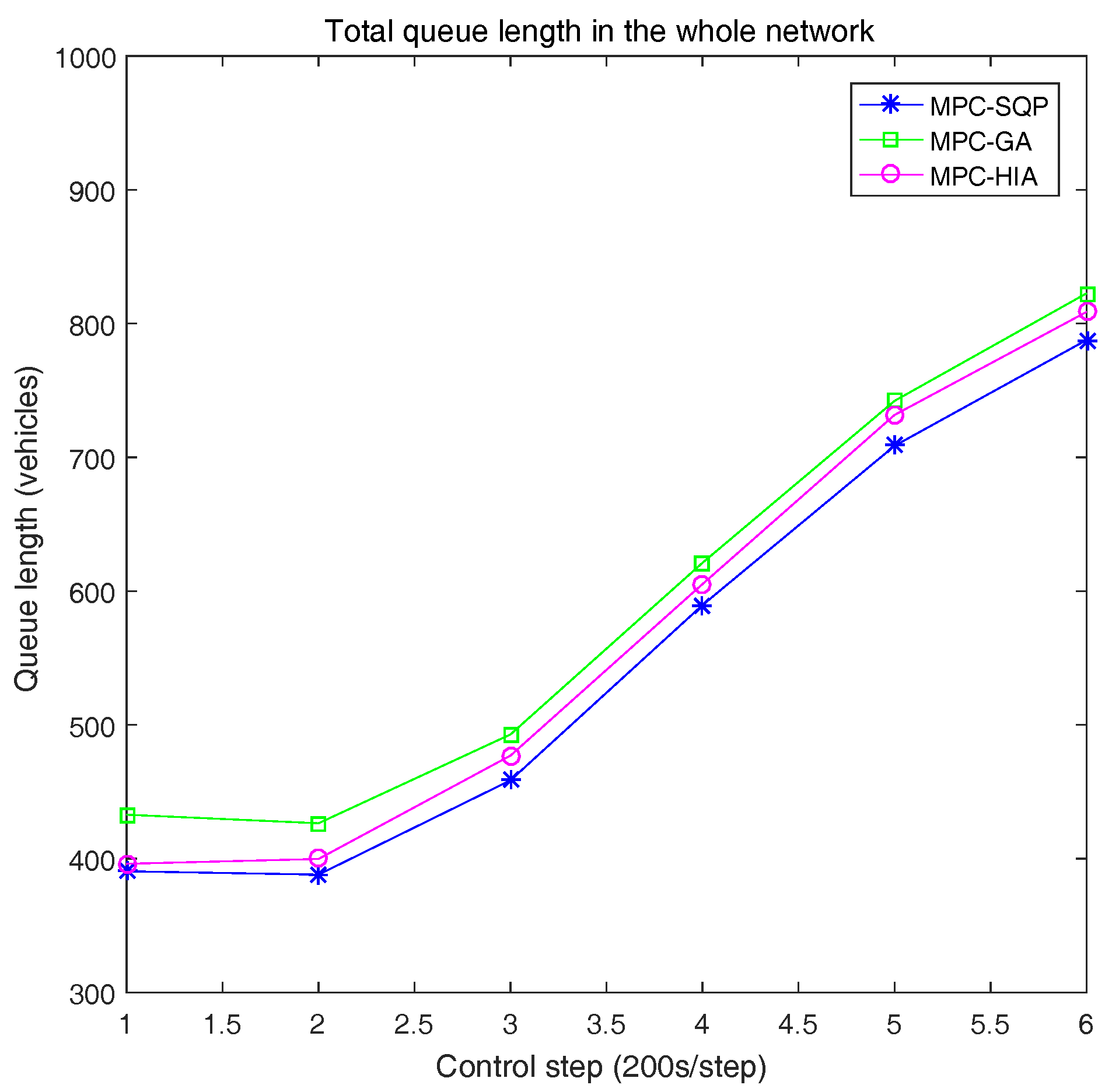
| Variable | Parameter | Simulation Value |
|---|---|---|
| C | common cycle time | 120 s |
| L | lost time | 8 s |
| S | saturation flow rate | 3600 veh/h |
| T | control interval | 200 s |
| l | average vehicle length | 5 m |
| P | prediction horizon length | 3 |
| u | constraint on green time |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
|---|---|---|---|---|---|---|---|---|
| x1 | - | - | 0.3 | - | - | - | - | 0.7 |
| x2 | - | - | 0.8 | - | - | - | - | 0.2 |
| x3 | - | - | - | - | - | - | - | - |
| x4 | - | - | - | - | - | - | - | - |
| x5 | - | - | - | 0.6 | - | - | 0.4 | - |
| x6 | - | - | - | 0.2 | - | - | 0.8 | - |
| x7 | - | - | - | - | - | - | - | - |
| x8 | - | - | - | - | - | - | - | - |
| Uncertain Variable | |||||||
| 16128 | 0 | 108 | |||||
| 0 | 6912 | 216 | 108 | ||||
| 10368 | 108 | 162 | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, B.-L.; Wu, W.; Gao, H.; Lu, Y.; Cao, Q.; Zhu, L. Stochastic Model Predictive Control for Urban Traffic Networks. Appl. Sci. 2017, 7, 588. https://doi.org/10.3390/app7060588
Ye B-L, Wu W, Gao H, Lu Y, Cao Q, Zhu L. Stochastic Model Predictive Control for Urban Traffic Networks. Applied Sciences. 2017; 7(6):588. https://doi.org/10.3390/app7060588
Chicago/Turabian StyleYe, Bao-Lin, Weimin Wu, Huimin Gao, Yixia Lu, Qianqian Cao, and Lijun Zhu. 2017. "Stochastic Model Predictive Control for Urban Traffic Networks" Applied Sciences 7, no. 6: 588. https://doi.org/10.3390/app7060588





