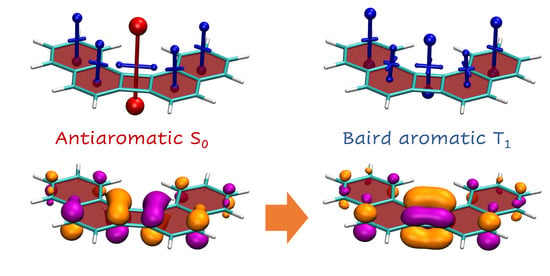
Exploitation of Baird Aromaticity and Clar’s Rule for Tuning the Triplet Energies of Polycyclic Aromatic Hydrocarbons
Abstract
1. Introduction
2. Theory
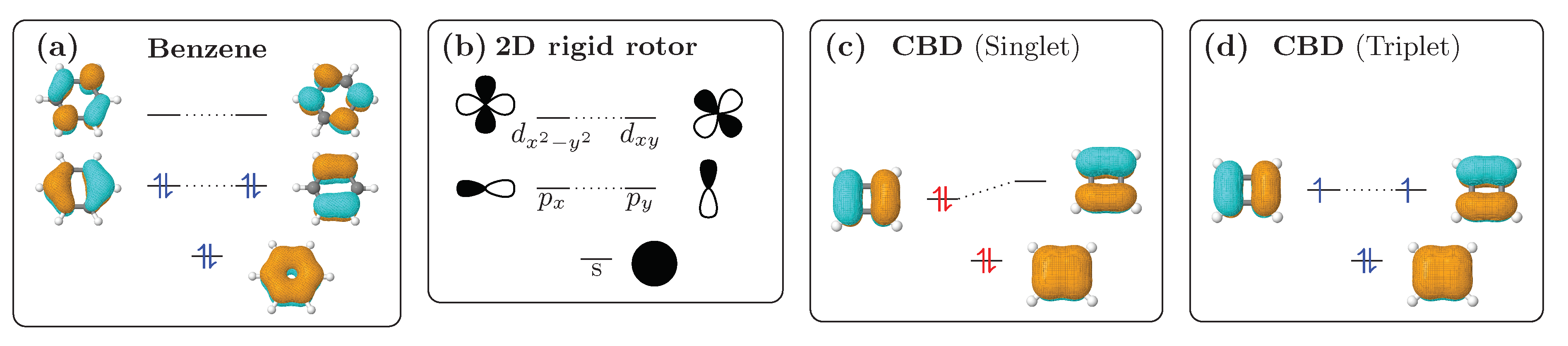
2.1. Aromaticity—The Rigid Rotor Viewpoint
2.2. Definition and Interpretation of the Chemical Shielding Tensors
2.3. Visualisation of Chemical Shielding Tensors (VIST)
2.4. Computational Details
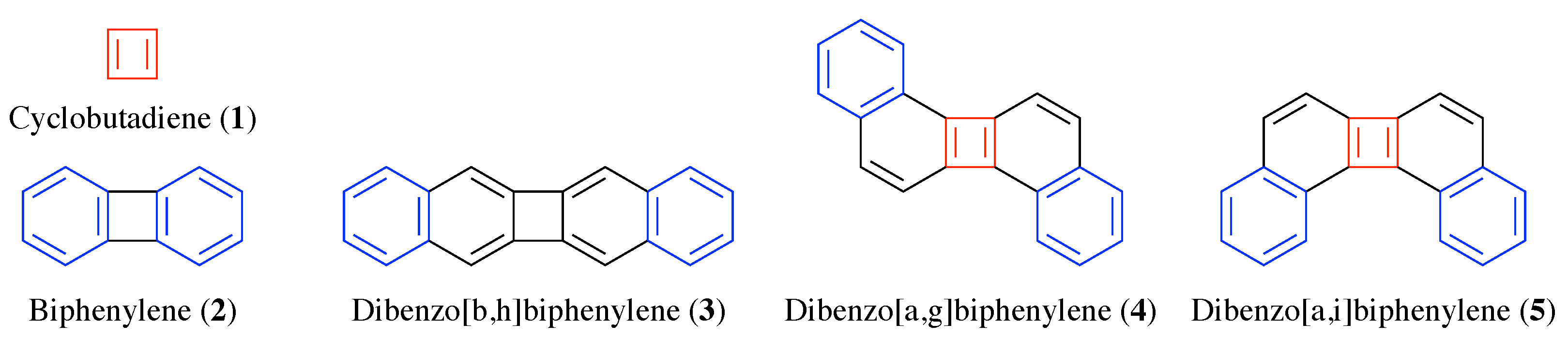
3. Results
3.1. Energetics
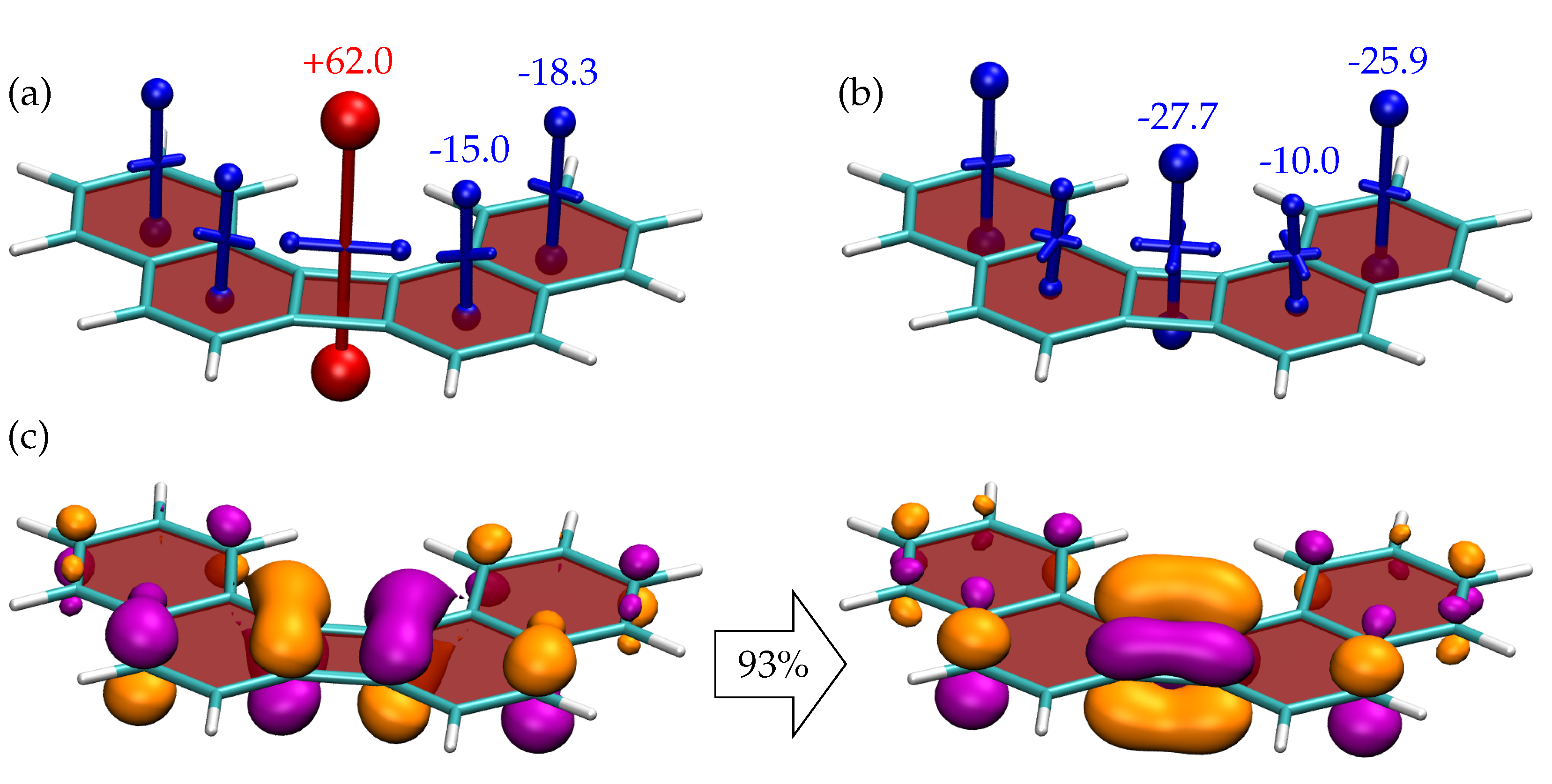
3.2. Shielding Tensors for the Building Blocks
3.3. Shielding Tensors for Biphenylene Derivatives
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anthony, J.E. The larger acenes: Versatile organic semiconductors. Angew. Chem. Int. Ed. 2008, 47, 452–483. [Google Scholar] [CrossRef]
- Chu, C.W.; Shao, Y.; Shrotriya, V.; Yang, Y. Efficient photovoltaic energy conversion in tetracene-C 60 based heterojunctions. Appl. Phys. Lett. 2005, 86, 1–3. [Google Scholar] [CrossRef]
- Smith, M.B.; Michl, J. Singlet fission. Chem. Rev. 2010, 110, 6891–6936. [Google Scholar] [CrossRef]
- Schultz, J.D.; Shin, J.Y.; Chen, M.; O’Connor, J.P.; Young, R.M.; Ratner, M.A.; Wasielewski, M.R. Influence of Vibronic Coupling on Ultrafast Singlet Fission in a Linear Terrylenediimide Dimer. J. Am. Chem. Soc. 2021. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Yang, G.; Duan, Y.; Geng, Y.; Wu, Y.; Su, Z. The relationship between intermolecular interactions and charge transport properties of trifluoromethylated polycyclic aromatic hydrocarbons. Org. Electron. 2014, 15, 1896–1905. [Google Scholar] [CrossRef]
- Hepp, A.; Heil, H.; Weise, W.; Ahles, M.; Schmechel, R.; von Seggern, H. Light-Emitting Field-Effect Transistor Based on a Tetracene Thin Film. Phys. Rev. Lett. 2003, 91, 157406. [Google Scholar] [CrossRef] [PubMed]
- Soe, W.H.; Manzano, C.; de Mendoza, P.; McGonigal, P.R.; Echavarren, A.M.; Joachim, C. Long starphene single molecule NOR Boolean logic gate. Surf. Sci. 2018, 678, 163–168. [Google Scholar] [CrossRef]
- Gantenbein, M.; Li, X.; Sangtarash, S.; Bai, J.; Olsen, G.; Alqorashi, A.; Hong, W.; Lambert, C.J.; Bryce, M.R. Exploring antiaromaticity in single-molecule junctions formed from biphenylene derivatives. Nanoscale 2019, 11, 20659–20666. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.H.; Wang, L.; Li, S.; Zhang, W.D.; He, G.; Wang, D.; Hou, S.M.; Wan, L.J. Single-Molecule Conductance through an Isoelectronic B–N Substituted Phenanthrene Junction. J. Am. Chem. Soc. 2020, 142, 8068–8073. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, H.; Sangtarash, S.; Lambert, C.J. Enhancing the thermoelectric figure of merit in engineered graphene nanoribbons. Beilstein J. Nanotechnol. 2015, 6, 1176–1182. [Google Scholar] [CrossRef] [PubMed]
- Delouche, T.; Vacher, A.; Caytan, E.; Roisnel, T.; Le Guennic, B.; Jacquemin, D.; Hissler, M.; Bouit, P.A. Multi-Stage Redox Systems Based on Dicationic P-Containing Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2020, 26, 8226–8229. [Google Scholar] [CrossRef] [PubMed]
- Holec, J.; Cogliati, B.; Lawrence, J.; Berdonces-Layunta, A.; Herrero, P.; Nagata, Y.; Banasiewicz, M.; Kozankiewicz, B.; Corso, M.; Oteyza, D.G.; et al. A Large Starphene Comprising Pentacene Branches. Angew. Chemie Int. Ed. 2021, 60, 7752–7758. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Abadía, M.; Strutynski, K.; Lerma-Berlanga, B.; Stoppiello, C.; Khlobystov, A.; Martí-Gastaldo, C.; Saeki, A.; Melle-Franco, M.; Mateo-Alonso, A. π-Interpenetrated 3D Covalent Organic Frameworks from Distorted Polycyclic Aromatic Hydrocarbons. Angew. Chem. Int. Ed. 2021, anie.202100434. [Google Scholar] [CrossRef] [PubMed]
- Schaberle, F.A.; Serpa, C.; Arnaut, L.G.; Ward, A.D.; Karlsson, J.K.G.; Atahan, A.; Harriman, A. The Photophysical Properties of Triisopropylsilyl-ethynylpentacene—A Molecule with an Unusually Large Singlet-Triplet Energy Gap—In Solution and Solid Phases. Chemistry 2020, 2, 545–564. [Google Scholar] [CrossRef]
- Aster, A.; Zinna, F.; Rumble, C.; Lacour, J.; Vauthey, E. Singlet Fission in a Flexible Bichromophore with Structural and Dynamic Control. J. Am. Chem. Soc. 2021, 143, 2361–2371. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Mukamel, S. Optical-Cavity Manipulation of Conical Intersections and Singlet Fission in Pentacene Dimers. J. Phys. Chem. Lett. 2021, 12, 2052–2056. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Zeng, Z.; Wu, J. Zethrenes, extended p-quinodimethanes, and periacenes with a singlet biradical ground state. Acc. Chem. Res. 2014, 47, 2582–2591. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Müller, T.; Plasser, F.; Lischka, H. Polyradical Character of Triangular Non-Kekulé Structures, Zethrenes, p-Quinodimethane-Linked Bisphenalenyl, and the Clar Goblet in Comparison: An Extended Multireference Study. J. Phys. Chem. A 2016, 120, 1625–1636. [Google Scholar] [CrossRef] [PubMed]
- Hinkel, F.; Freudenberg, J.; Bunz, U.H.F. A Stable pi-Conjugated Singlet Biradical. Angew. Chem. Int. Ed. 2016, 55, 9830–9832. [Google Scholar] [CrossRef] [PubMed]
- Chaolumen; Murata, M.; Wakamiya, A.; Murata, Y. Dithieno-Fused Polycyclic Aromatic Hydrocarbon with a Pyracylene Moiety: Strong Antiaromatic Contribution to the Electronic Structure. Org. Lett. 2017, 19, 826–829. [Google Scholar] [CrossRef]
- Stoycheva, J.; Tadjer, A.; Garavelli, M.; Spassova, M.; Nenov, A.; Romanova, J. Boron-Doped Polycyclic Aromatic Hydrocarbons: A Molecular Set Revealing the Interplay between Topology and Singlet Fission Propensity. J. Phys. Chem. Lett. 2020, 11, 1390–1396. [Google Scholar] [CrossRef]
- Pinheiro, M.; Machado, F.B.C.; Plasser, F.; Aquino, A.J.A.; Lischka, H. A systematic analysis of excitonic properties to seek optimal singlet fission: The BN-substitution patterns in tetracene. J. Mater. Chem. C 2020, 8, 7793–7804. [Google Scholar] [CrossRef]
- Intorp, S.N.; Hodecker, M.; Müller, M.; Tverskoy, O.; Rosenkranz, M.; Dmitrieva, E.; Popov, A.A.; Rominger, F.; Freudenberg, J.; Dreuw, A.; et al. Quinoidal Azaacenes: 99 % Diradical Character. Angew. Chem. Int. Ed. 2020, 59, 12396–12401. [Google Scholar] [CrossRef]
- Plasser, F.; Pašalic, H.; Gerzabek, M.H.; Libisch, F.; Reiter, R.; Burgdörfer, J.; Müller, T.; Shepard, R.; Lischka, H. The multiradical character of one- and two-dimensional graphene nanoribbons. Angew. Chem. Int. Ed. 2013, 52, 2581–2584. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Small, D.W.; Epifanovsky, E.; Head-Gordon, M. Coupled-Cluster Valence-Bond Singles and Doubles for Strongly Correlated Systems: Block-Tensor Based Implementation and Application to Oligoacenes. J. Chem. Theory Comput. 2017, 13, 602–615. [Google Scholar] [CrossRef] [PubMed]
- Ryerson, J.L.; Zaykov, A.; Aguilar Suarez, L.E.; Havenith, R.W.A.; Stepp, B.R.; Dron, P.I.; Kaleta, J.; Akdag, A.; Teat, S.J.; Magnera, T.F.; et al. Structure and photophysics of indigoids for singlet fission: Cibalackrot. J. Chem. Phys. 2019, 151, 184903. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem—I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Clar, E. The Aromatic Sextet; Wiley: London, UK, 1972. [Google Scholar]
- Baird, N.C. Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest 3ππ* State of Cyclic Hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. [Google Scholar] [CrossRef]
- Ottosson, H. Exciting excited-state aromaticity. Nat. Chem. 2012, 4, 969–971. [Google Scholar] [CrossRef] [PubMed]
- Fallon, K.J.; Budden, P.; Salvadori, E.; Ganose, A.M.; Savory, C.N.; Eyre, L.; Dowland, S.; Ai, Q.; Goodlett, S.; Risko, C.; et al. Exploiting Excited-State Aromaticity To Design Highly Stable Singlet Fission Materials. J. Am. Chem. Soc. 2019, 141, 13867–13876. [Google Scholar] [CrossRef] [PubMed]
- El Bakouri, O.; Smith, J.R.; Ottosson, H. Strategies for Design of Potential Singlet Fission Chromophores Utilizing a Combination of Ground-State and Excited-State Aromaticity Rules. J. Am. Chem. Soc. 2020, 142, 5602–5617. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lin, L.; Yang, J.; Wu, Y.; Wang, H.; Zhu, J.; Yao, J.; Fu, H. Singlet Fission in a Pyrrole-Fused Cross-Conjugated Skeleton with Adaptive Aromaticity. J. Am. Chem. Soc. 2020, 142, 10235–10239. [Google Scholar] [CrossRef] [PubMed]
- Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Matito, E.; Duran, M.; Solà, M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem. Phys. 2005, 122, 014109. [Google Scholar] [CrossRef]
- Zhu, J.; An, K.; Schleyer, P.v.R. Evaluation of Triplet Aromaticity by the Isomerization Stabilization Energy. Org. Lett. 2013, 15, 2442–2445. [Google Scholar] [CrossRef]
- Ligabue, A.; Pincelli, U.; Lazzeretti, P.; Zanasi, R. Current density maps, magnetizability, and nuclear magnetic shielding tensors for anthracene, phenanthrene, and triphenylene. J. Am. Chem. Soc. 1999, 121, 5513–5518. [Google Scholar] [CrossRef]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the induced current density (ACID), a general method to quantify and visualize electronic delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; von Ragué Schleyer, P. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Plasser, F.; Glöcklhofer, F. Visualisation of chemical shielding tensors (VIST) to elucidate aromaticity and antiaromaticity. Eur. J. Org. Chem. 2021. [Google Scholar] [CrossRef]
- Takano, H.; Ito, T.; Kanyiva, K.S.; Shibata, T. Recent Advances of Biphenylene: Synthesis, Reactions and Uses. Eur. J. Org. Chem. 2019, 2019, 2871–2883. [Google Scholar] [CrossRef]
- Ayub, R.; Bakouri, O.E.; Jorner, K.; Solà, M.; Ottosson, H. Can Baird’s and Clar’s Rules Combined Explain Triplet State Energies of Polycyclic Conjugated Hydrocarbons with Fused 4nπ- and (4n + 2)π-Rings? J. Org. Chem. 2017, 82, 6327–6340. [Google Scholar] [CrossRef] [PubMed]
- Milanez, B.D.; Chagas, J.C.V.; Pinheiro, M., Jr.; Aquino, A.J.A.; Lischka, H.; Machado, F.B.C. Effects on the aromaticity and on the biradicaloid nature of acenes by the inclusion of a cyclobutadiene linkage. Theor. Chem. Acc. 2020, 139, 1–10. [Google Scholar] [CrossRef]
- Platt, J.R. Classification of Spectra of Cata-Condensed Hydrocarbons. J. Chem. Phys. 1949, 17, 484–495. [Google Scholar] [CrossRef]
- Michl, J. Magnetic circular dichroism of cyclic .pi.-electron systems. 1. Algebraic solution of the perimeter model for the A and B terms of high-symmetry systems with a (4N + 2)-electron [n]annulene perimeter. J. Am. Chem. Soc. 1978, 100, 6801–6811. [Google Scholar] [CrossRef]
- Fleischhauer, J.; Höweler, U.; Michl, J. Magnetic circular dichroism of non-aromatic cyclic π-electron systems. 2. [1] The perimeter model for high-symmetry ’unaromatic’ and ’ambiaromatic’ molecules derived from 4N-electron [n]annulenes. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1999, 55, 585–606. [Google Scholar] [CrossRef]
- Monaco, G.; Zanasi, R. Assessment of Ring Current Models for Monocycles. J. Phys. Chem. A 2014, 118, 1673–1683. [Google Scholar] [CrossRef] [PubMed]
- Steiner, E.; Fowler, P.W. Four- and two-electron rules for diatropic and paratropic ring currents in monocyclic π systems. Chem. Commun. 2001, 1, 2220–2221. [Google Scholar] [CrossRef]
- Atkins, P.W. Physical Chemistry, 5th ed.; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Dias, F.B.; Penfold, T.J.; Monkman, A.P. Photophysics of thermally activated delayed fluorescence molecules. Methods Appl. Fluoresc. 2017, 5, 012001. [Google Scholar] [CrossRef]
- Chen, X.K.; Kim, D.; Brédas, J.L. Thermally Activated Delayed Fluorescence (TADF) Path toward Efficient Electroluminescence in Purely Organic Materials: Molecular Level Insight. Acc. Chem. Res. 2018, 51, 2215–2224. [Google Scholar] [CrossRef]
- Kimber, P.; Plasser, F. Toward an understanding of electronic excitation energies beyond the molecular orbital picture. Phys. Chem. Chem. Phys. 2020, 22, 6058–6080. [Google Scholar] [CrossRef]
- Ito, T.; Hayashi, Y.; Shimizu, S.; Shin, J.Y.; Kobayashi, N.; Shinokubo, H. Gram-Scale Synthesis of Nickel(II) Norcorrole: The Smallest Antiaromatic Porphyrinoid. Angew. Chemie Int. Ed. 2012, 51, 8542–8545. [Google Scholar] [CrossRef]
- Corminboeuf, C.; Heine, T.; Seifert, G.; Von Ragué Schleyer, P.; Weber, J. Induced magnetic fields in aromatic [n]-annulenes—Interpretation of NICS tensor components. Phys. Chem. Chem. Phys. 2004, 6, 273–276. [Google Scholar] [CrossRef]
- Stanger, A. NICS – Past and Present. Eur. J. Org. Chem. 2020, 2020, 3120–3127. [Google Scholar] [CrossRef]
- Cheeseman, J.R. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 1996, 104, 5497–5509. [Google Scholar] [CrossRef]
- Heine, T.; Corminboeuf, C.; Seifert, G. The magnetic shielding function of molecules and pi-electron delocalization. Chem. Rev. 2005, 105, 3889–3910. [Google Scholar] [CrossRef] [PubMed]
- Facelli, J.C. Chemical shift tensors: Theory and application to molecular structural problems. Prog. Nucl. Magn. Reson. Spectrosc. 2011, 58, 176–201. [Google Scholar] [CrossRef]
- Ramsey, N.F. Magnetic shielding of nuclei in molecules. Phys. Rev. 1950, 78, 699–703. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent advances in wave function-based methods of molecular-property calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef] [PubMed]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Zhao, L.; Grande-Aztatzi, R.; Foroutan-Nejad, C.; Ugalde, J.M.; Frenking, G. Aromaticity, the Hückel 4 n+2 Rule and Magnetic Current. ChemistrySelect 2017, 2, 863–870. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian-Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Martin, R.L. Natural transition orbitals. J. Chem. Phys. 2003, 118, 4775–4777. [Google Scholar] [CrossRef]
- Plasser, F.; Lischka, H. Analysis of Excitonic and Charge Transfer Interactions from Quantum Chemical Calculations. J. Chem. Theory Comput. 2012, 8, 2777–2789. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Grimme, S.; Parac, M. Substantial errors from time-dependent density functional theory for the calculation of excited states of large pi systems. ChemPhysChem 2003, 4, 292–295. [Google Scholar] [CrossRef]
- Mewes, S.A.; Plasser, F.; Dreuw, A. Universal Exciton Size in Organic Polymers is Determined by Non-Local Orbital Exchange in TDDFT. J. Phys. Chem. Lett. 2017, 8, 1205–1210. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Krylov, A.I.; Gill, P.M. Q-Chem: An engine for innovation. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 317–326. [Google Scholar] [CrossRef]
- Plasser, F.; Wormit, M.; Dreuw, A. New tools for the systematic analysis and visualization of electronic excitations. I. Formalism. J. Chem. Phys. 2014, 141, 024106. [Google Scholar] [CrossRef] [PubMed]
- Andersson, K.; Malmqvist, P.A.; Roos, B.O.; Sadlej, A.J.; Wolinski, K. Second-order perturbation theory with a CASSCF reference function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Galván, F.I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Zobel, J.P.; Nogueira, J.J.; González, L. The IPEA dilemma in CASPT2. Chem. Sci. 2017, 8, 1482–1499. [Google Scholar] [CrossRef]
- Ghigo, G.; Roos, B.O.; Malmqvist, P.A. A modified definition of the zeroth-order Hamiltonian in multiconfigurational perturbation theory (CASPT2). Chem. Phys. Lett. 2004, 396, 142–149. [Google Scholar] [CrossRef]
- Pierloot, K.; Dumez, B.; Widmark, P.O.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta 1995, 90, 87–114. [Google Scholar] [CrossRef]
- Plasser, F.; Mewes, S.A.; Dreuw, A.; González, L. Detailed Wave Function Analysis for Multireference Methods: Implementation in the Molcas Program Package and Applications to Tetracene. J. Chem. Theory Comput. 2017, 13, 5343–5353. [Google Scholar] [CrossRef] [PubMed]
- Malmqvist, P.A.k.; Roos, B.O. The CASSCF state interaction method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Plasser, F. TheoDORE: A toolbox for a detailed and automated analysis of electronic excited state computations. J. Chem. Phys. 2020, 152, 084108. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Supporting Research Data Available: Molecular Coordinates; Input/Output Files for Q-Chem, OpenMolcas, Gaussian, and TheoDORE. Available online: https://doi.org/10.17028/rd.lboro.14139824 (accessed on 9 April 2021).
- Karadakov, P.B. Ground- and excited-state aromaticity and antiaromaticity in benzene and cyclobutadiene. J. Phys. Chem. A 2008, 112, 7303–7309. [Google Scholar] [CrossRef] [PubMed]
- Pathak, S.; Bast, R.; Ruud, K. Multiconfigurational self-consistent field calculations of the magnetically induced current density using gauge-including atomic orbitals. J. Chem. Theory Comput. 2013, 9, 2189–2198. [Google Scholar] [CrossRef] [PubMed]
- Lischka, H.; Nachtigallová, D.; Aquino, A.J.A.; Szalay, P.; Plasser, F.; Machado, F.B.C.; Barbatti, M. Multireference Approaches for Excited States of Molecules. Chem. Rev. 2018, 118, 7293–7361. [Google Scholar] [CrossRef]
- Vijay, V.; Madhu, M.; Ramakrishnan, R.; Benny, A.; Hariharan, M. Through-space aromatic character in excimers. Chem. Commun. 2020, 56, 225–228. [Google Scholar] [CrossRef]
- Plasser, F. Entanglement Entropy of Electronic Excitations. J. Chem. Phys. 2016, 144, 194107. [Google Scholar] [CrossRef] [PubMed]
- Plasser, F. Visualisation of Electronic Excited-State Correlation in Real Space. ChemPhotoChem 2019, 3, 702–706. [Google Scholar] [CrossRef]
- Van Meer, R.; Gritsenko, O.V.; Baerends, E.J. Physical meaning of virtual kohn-sham orbitals and orbital energies: An ideal basis for the description of molecular excitations. J. Chem. Theory Comput. 2014, 10, 4432–4441. [Google Scholar] [CrossRef]
- Krylov, A.I. From orbitals to observables and back. J. Chem. Phys. 2020, 153, 080901. [Google Scholar] [CrossRef]
- Sekiguchi, A.; Matsuo, T.; Watanabe, H. Synthesis and Characterization of a Cyclobutadiene Dianion Dilithium Salt: Evidence for Aromaticity. J. Am. Chem. Soc. 2000, 122, 5652–5653. [Google Scholar] [CrossRef]
- Bäppler, S.A.; Plasser, F.; Wormit, M.; Dreuw, A. Exciton analysis of many-body wave functions: Bridging the gap between the quasiparticle and molecular orbital pictures. Phys. Rev. A 2014, 90, 052521. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Stanger, A. The NICS-XY-scan: Identification of local and global ring currents in multi-ring systems. Chem. Eur. J. 2014, 20, 5673–5688. [Google Scholar] [CrossRef] [PubMed]
- Van Damme, S.; Acke, G.; Havenith, R.W.; Bultinck, P. Can the current density map topology be extracted from the nucleus independent chemical shifts? Phys. Chem. Chem. Phys. 2016, 18, 11746–11755. [Google Scholar] [CrossRef] [PubMed]





| Diamagnetic Shielding () | Paramagnetic Deshielding () | |
|---|---|---|
| Aromatic | 0 | |
| Antiaromatic |
| Molecule | ||||
|---|---|---|---|---|
| 1 | Cyclobutadiene | 0.133 (0.183) | - | - |
| 2 | Biphenylene | 1.920 (1.765) | - | - |
| 3 | Dibenzo[b,h]biphenylene | 2.638 (2.243) | 0.000 (0.000) | 2.638 (2.243) |
| 4 | Dibenzo[a,g]biphenylene | 1.032 (0.894) | 0.508 (0.594) | 1.541 (1.488) |
| 5 | Dibenzo[a,i]biphenylene | 1.008 (0.814) | 0.514 (0.598) | 1.522 (1.412) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plasser, F. Exploitation of Baird Aromaticity and Clar’s Rule for Tuning the Triplet Energies of Polycyclic Aromatic Hydrocarbons. Chemistry 2021, 3, 532-549. https://doi.org/10.3390/chemistry3020038
Plasser F. Exploitation of Baird Aromaticity and Clar’s Rule for Tuning the Triplet Energies of Polycyclic Aromatic Hydrocarbons. Chemistry. 2021; 3(2):532-549. https://doi.org/10.3390/chemistry3020038
Chicago/Turabian StylePlasser, Felix. 2021. "Exploitation of Baird Aromaticity and Clar’s Rule for Tuning the Triplet Energies of Polycyclic Aromatic Hydrocarbons" Chemistry 3, no. 2: 532-549. https://doi.org/10.3390/chemistry3020038
APA StylePlasser, F. (2021). Exploitation of Baird Aromaticity and Clar’s Rule for Tuning the Triplet Energies of Polycyclic Aromatic Hydrocarbons. Chemistry, 3(2), 532-549. https://doi.org/10.3390/chemistry3020038