Passive Athermal Optical Design Method Considering Thermal-Induced Surface Deformation
Abstract
:1. Introduction
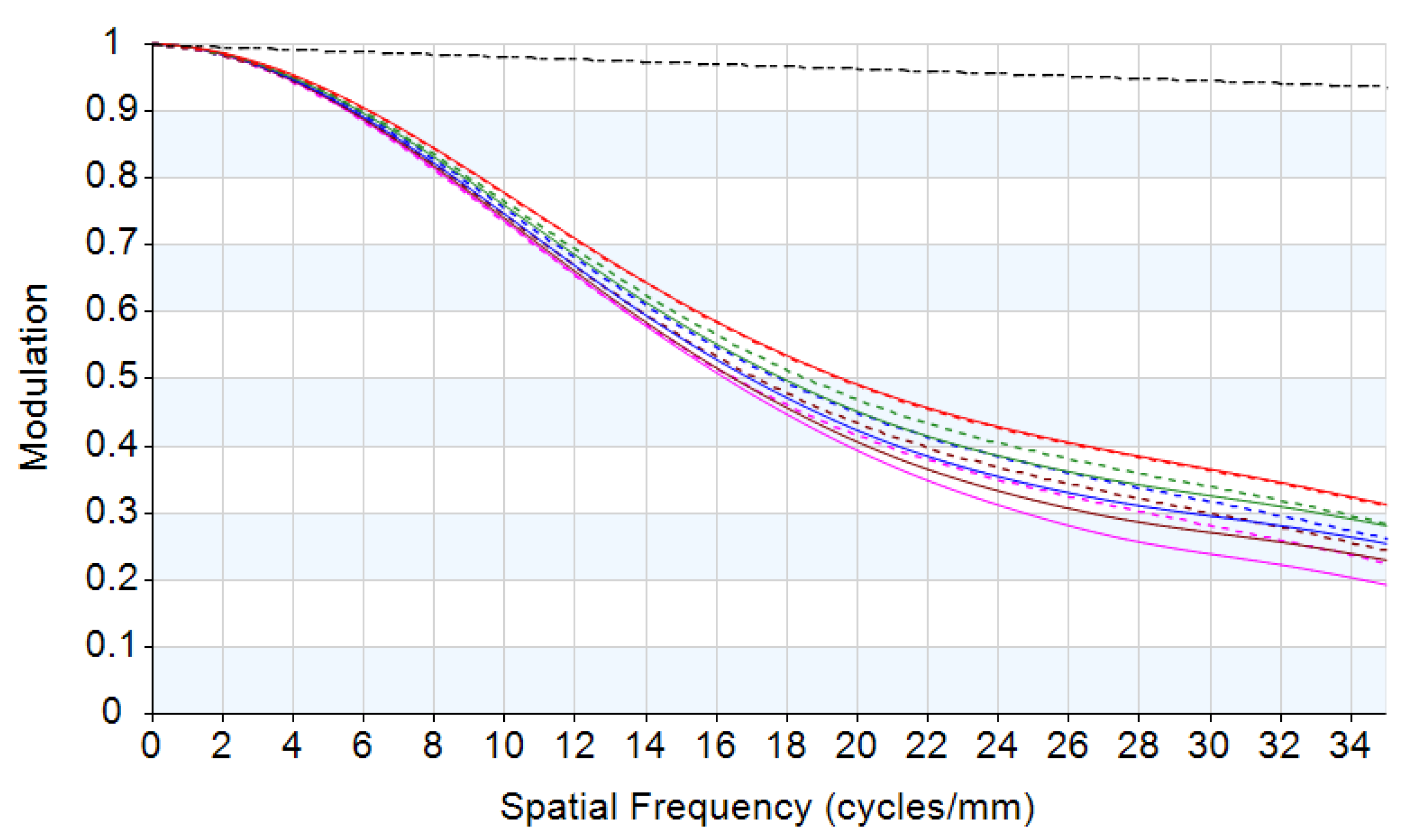
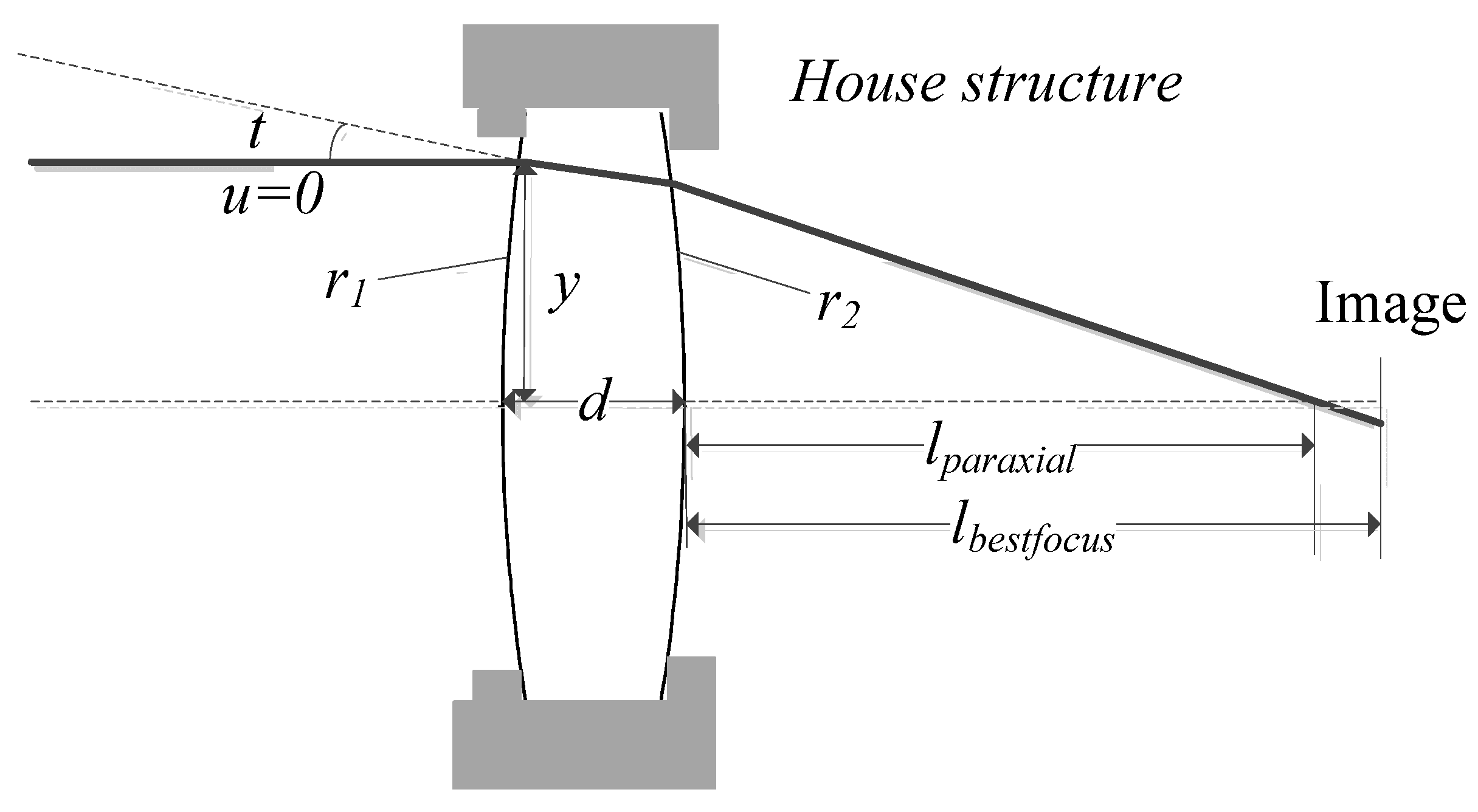
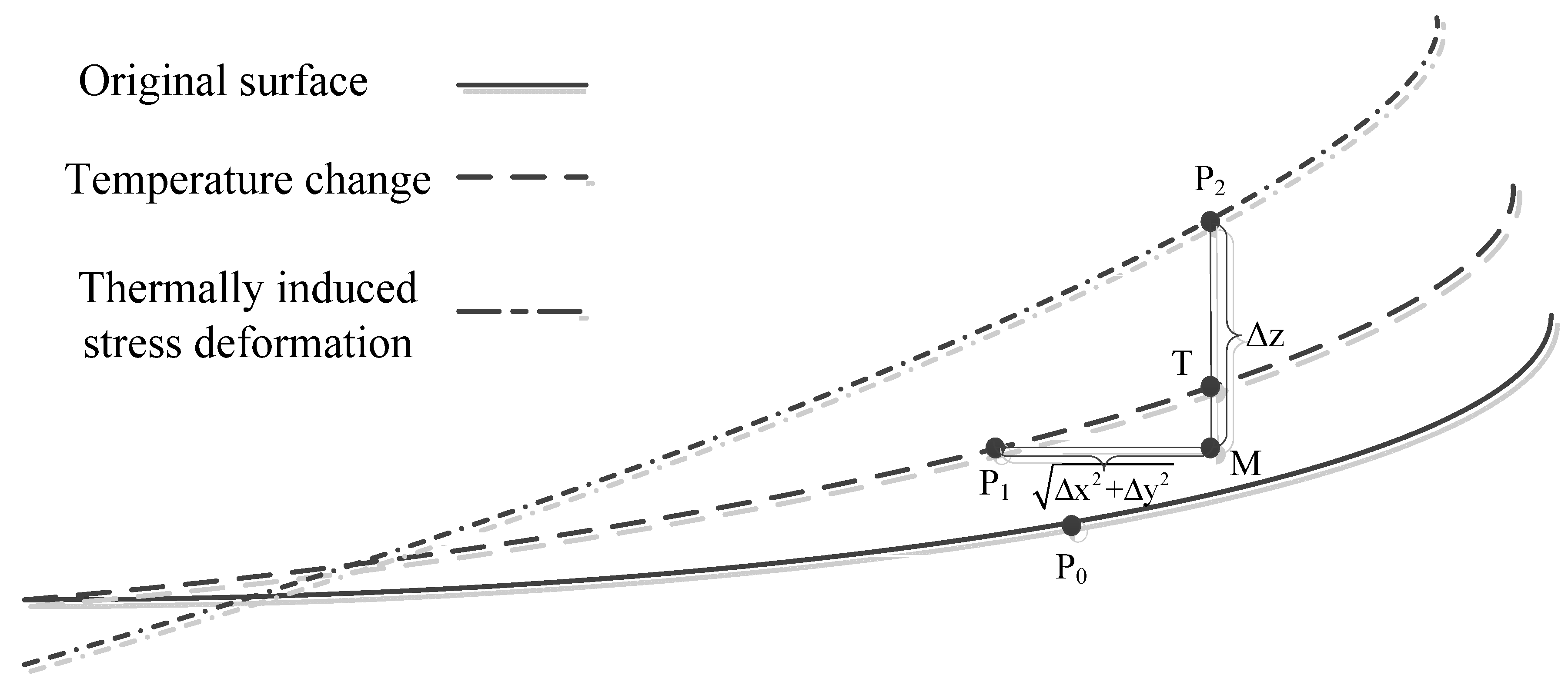
2. Degradation of Image Quality Caused by Thermal-Induced Surface Deformation
3. Materials and Methods
3.1. Optical Optimizability Based on Wavefront Aberration Theory
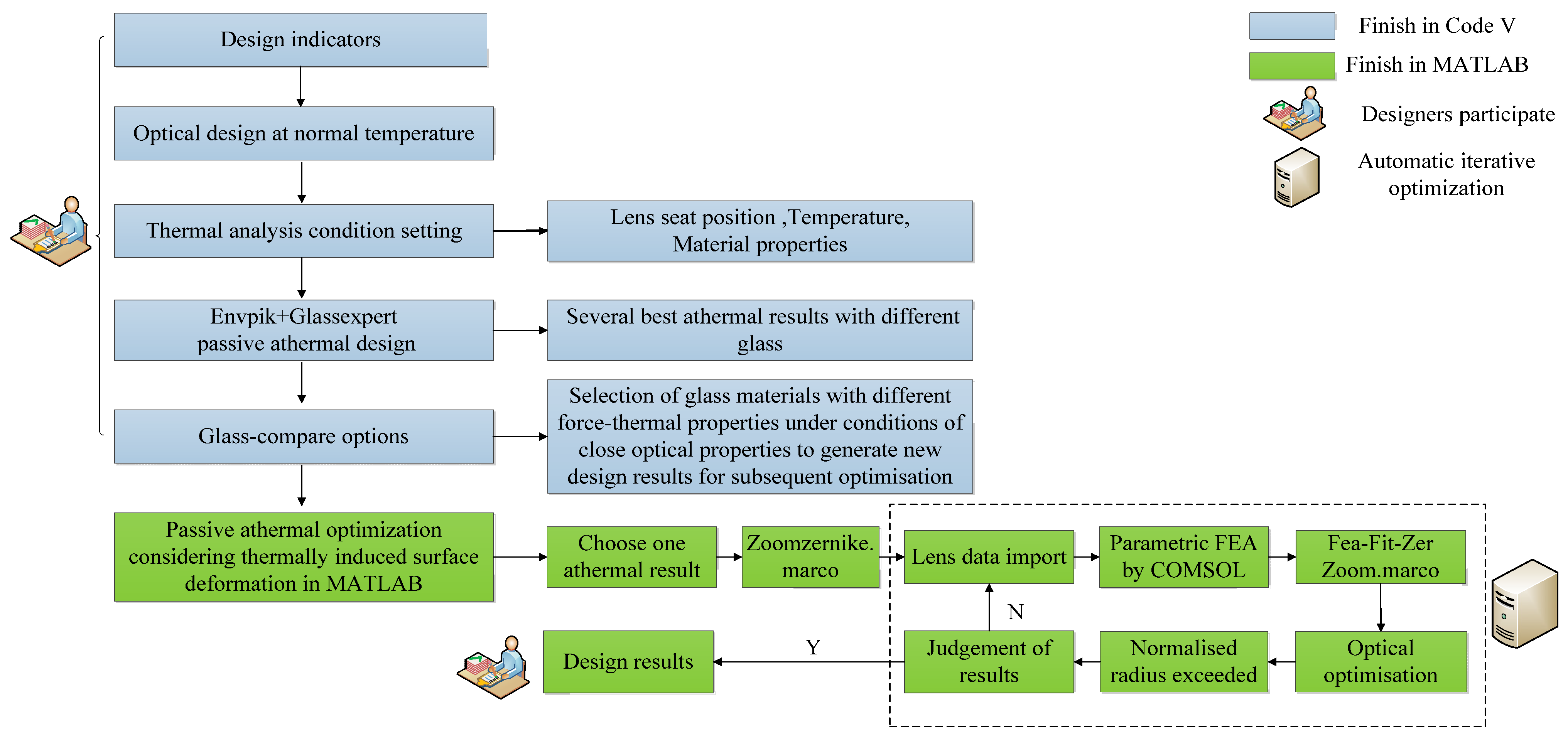
3.2. Process of Passive Athermal Optical Design Method while Considering Thermal-Induced Surface Deformation
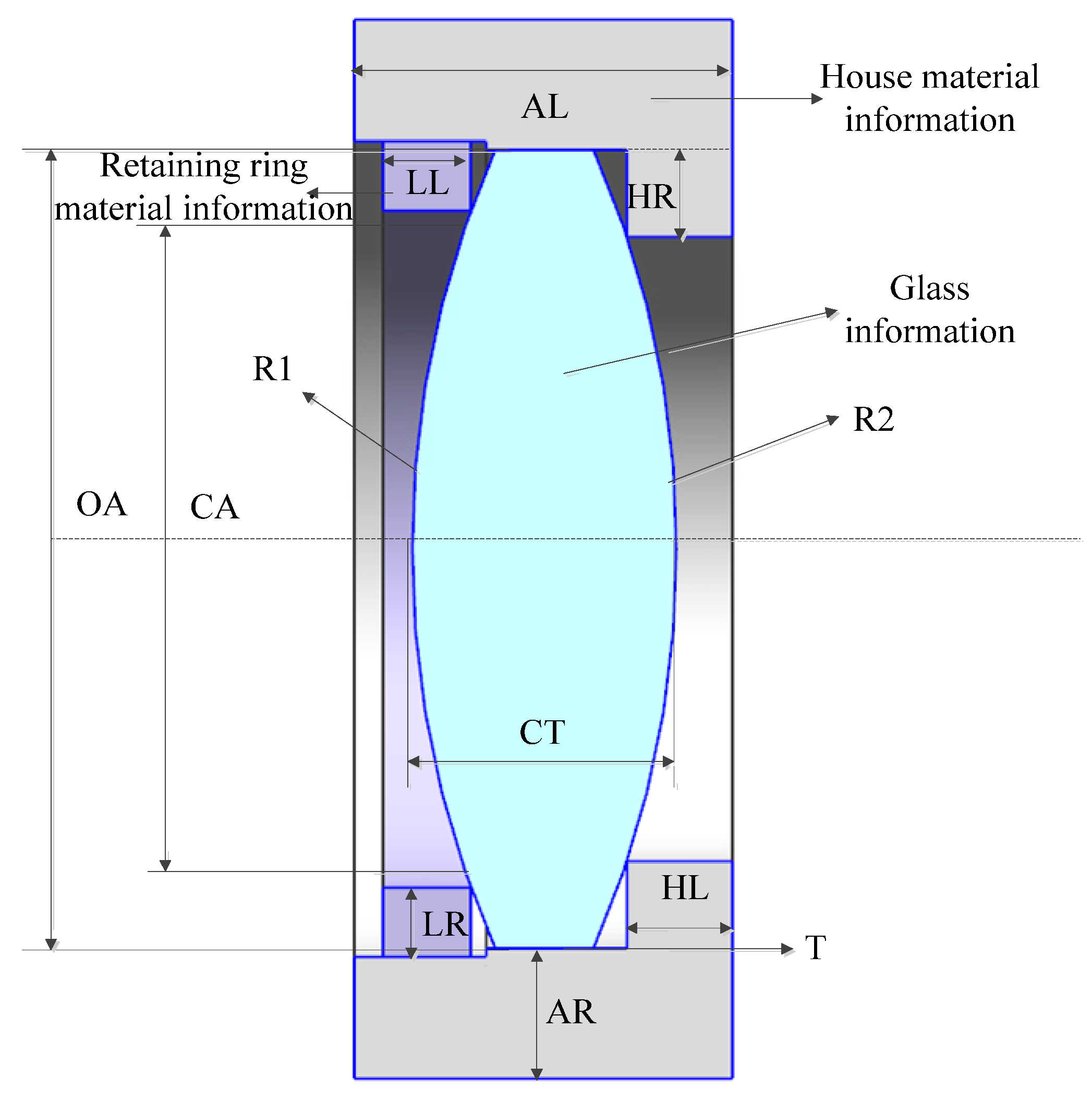
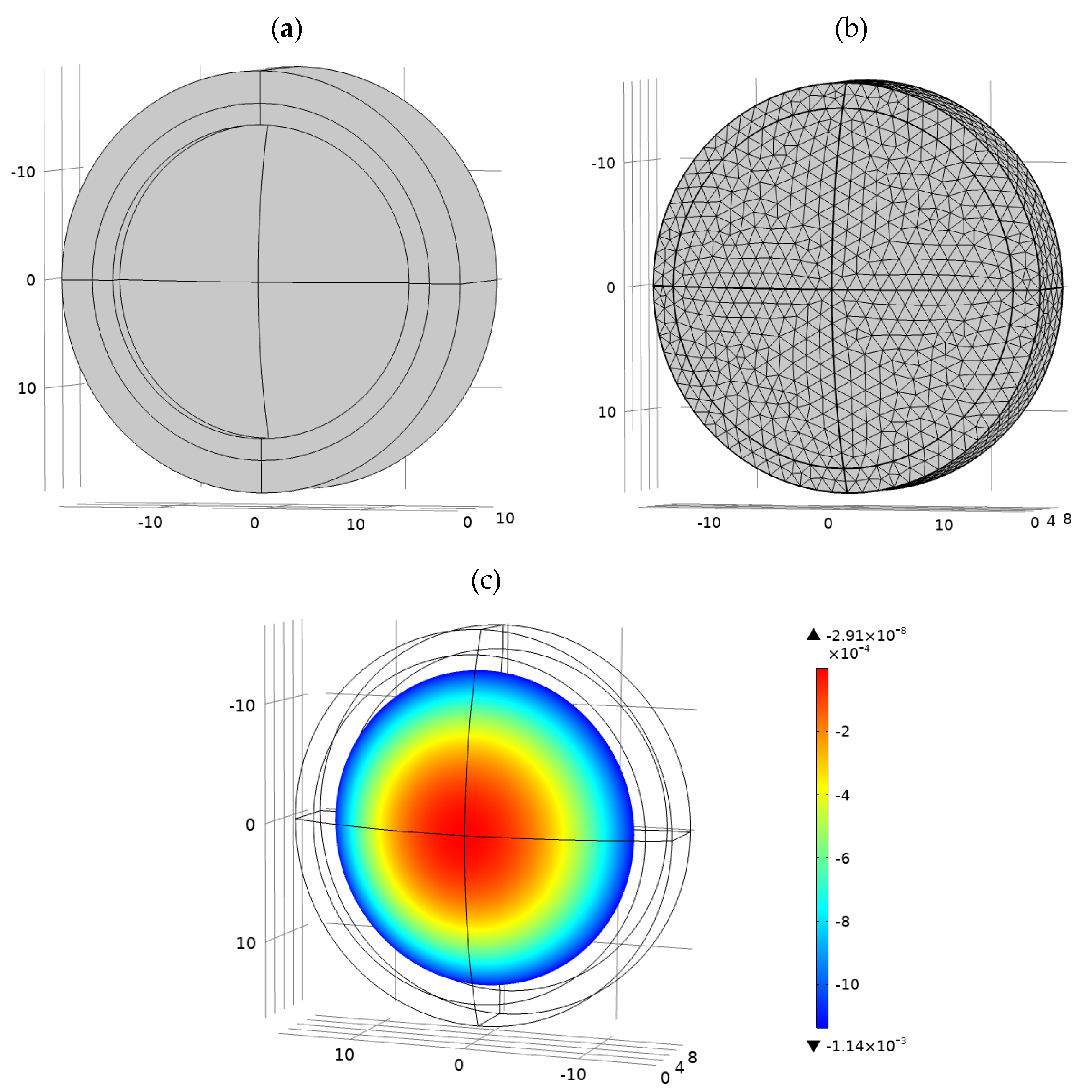
3.3. Parametric FEA
3.4. Transferring FEA Results to Zernike Surface Coefficients
4. Design Examples
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jamieson, T.H. Thermal effects in optical systems. Opt. Eng. 1981, 20, 156–160. [Google Scholar] [CrossRef]
- Nasyrov, A.R. Methods of athermalization of optical systems in thermal imaging devices. J. Opt. Technol. 2017, 84, 205–206. [Google Scholar] [CrossRef]
- An, X.Q.; Wang, Q.; Song, B. Athermal design of compact uncooled optical system with large relative aperture. Laser Infrared 2015, 45, 795–799. [Google Scholar] [CrossRef]
- Cheng, X.M.; Yang, Y.K.; Hao, Q. Analysis of the effects of thermal environment on optical systems for navigation guidance and control in supersonic aircraft based on empirical equations. Sensors 2016, 16, 1717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, W.S.; Huang, C.M.; Lin, J.S. Discussion of temperature, TV distortion, and lateral color of a 4 megapixel DLP projector lens. OSA Contin. 2019, 2, 3188–3203. [Google Scholar] [CrossRef]
- Xie, N.; Cui, Q.F.; Sun, L.; Wang, J.F. Optical athermalization in the visible waveband using the 1+Σ method. Appl. Opt. 2019, 58, 635–641. [Google Scholar] [CrossRef] [PubMed]
- Michels, G.J.; Genberg, V.L. Analysis of thermally loaded transmissive optical elements. In Proceedings of the Optical Modeling and Performance Predictions VI, San Diego, CA, USA, 27 September 2013. [Google Scholar] [CrossRef]
- Lim, T.Y.; Kim, Y.S.; Park, S.C. Graphical selection of optical materials using an expanded athermal glass map and considering the housing material for an athermal and achromatic design. J. Opt. Soc. Korea 2015, 19, 531–536. [Google Scholar] [CrossRef] [Green Version]
- Lim, T.Y.; Park, S.C. Achromatic and athermal lens design by redistributing the element powers on an athermal glass map. Opt. Express 2016, 24, 18049–18058. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.R. An optically athermalized lens covering a 200-degree temperature range. In Proceedings of the International Conference on Space Optics-ICSO 2018, Chania, Greece, 9–12 July 2019. [Google Scholar] [CrossRef] [Green Version]
- Sahin, F.E. Long-range, high-resolution camera optical design for assisted and autonomous driving. Photonics 2019, 6, 73. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; Wang, H.; Liu, Y.; Xue, Y.; Xiang, B.; Liu, J.; Xie, Y.; Liu, M.; Wu, L. Athermalization for the supporting structure of space camera primary and secondary mirrors. In Proceedings of the Third International Conference on Photonics and Optical Engineering, Xi’an, China, 24 January 2019. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, H.; Chen, Y.; Zhang, G.; Zhang, Z.; Peng, J.; Zhao, Z.; Yan, A. Optimization thermal design method for space cameras based on thermo-optical analysis and Taguchi method. Opt. Eng. 2020, 59, 075101. [Google Scholar] [CrossRef]
- Juergens, R.C.; Coronato, P.A. Improved method for transfer of FEA results to optical codes. In Proceedings of the Novel Optical Systems Design and Optimization VI, San Diego, CA, USA, 6 November 2003. [Google Scholar] [CrossRef]
- Coronato, P.A.; Juergens, R.C. Transferring FEA results to optics codes with Zernikes: A review of techniques. In Proceedings of the Optomechanics 2003, San Diego, CA, USA, 27 October 2003. [Google Scholar] [CrossRef]
- Doyle, K.B.; Genberg, V.L.; Michels, G.J.; Bisson, G.R. Optical modeling of finite element surface displacements using commercial software. In Proceedings of the Optical Modeling and Performance Predictions II, San Diego, CA, USA, 24 August 2005. [Google Scholar] [CrossRef]
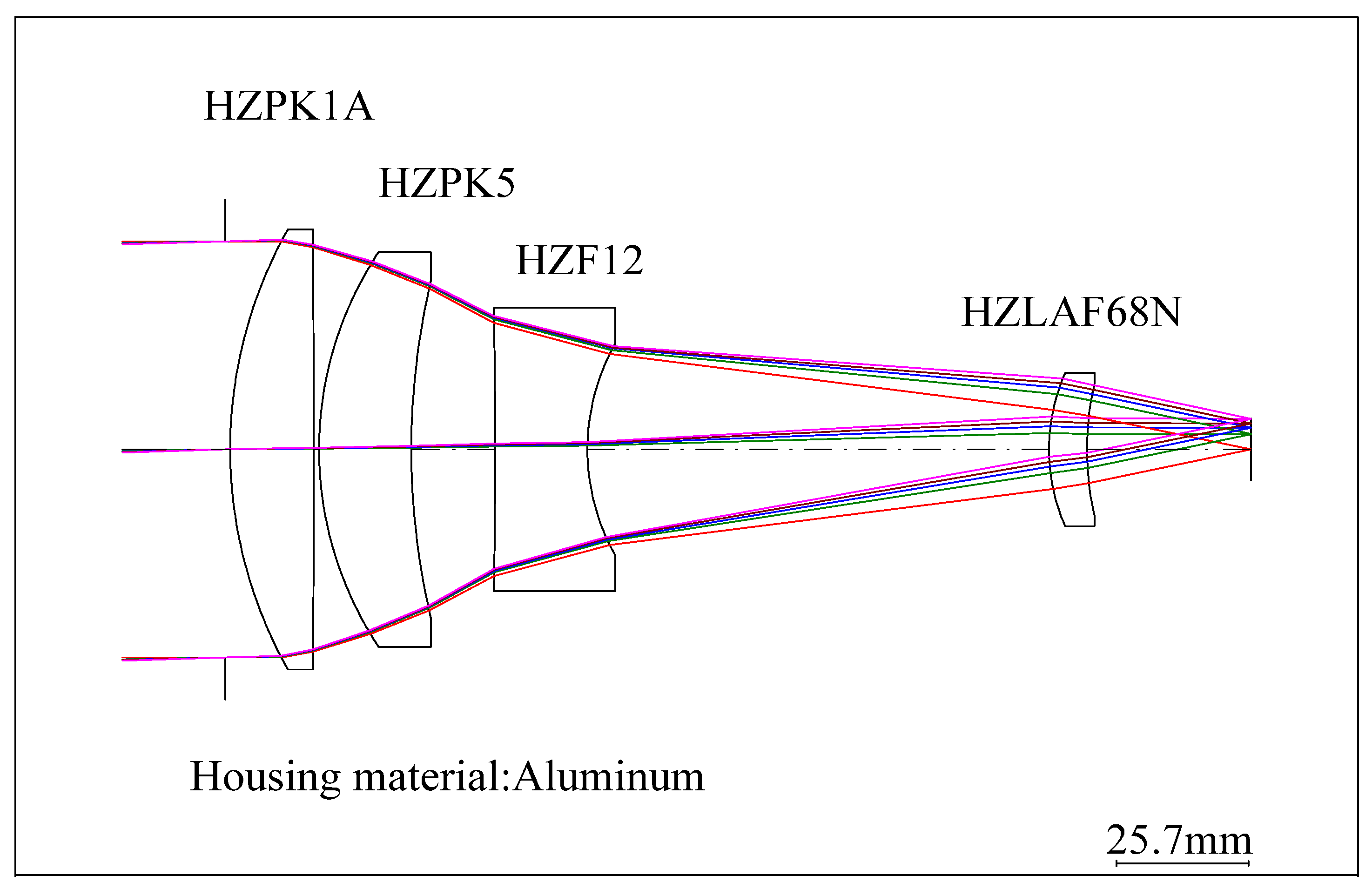

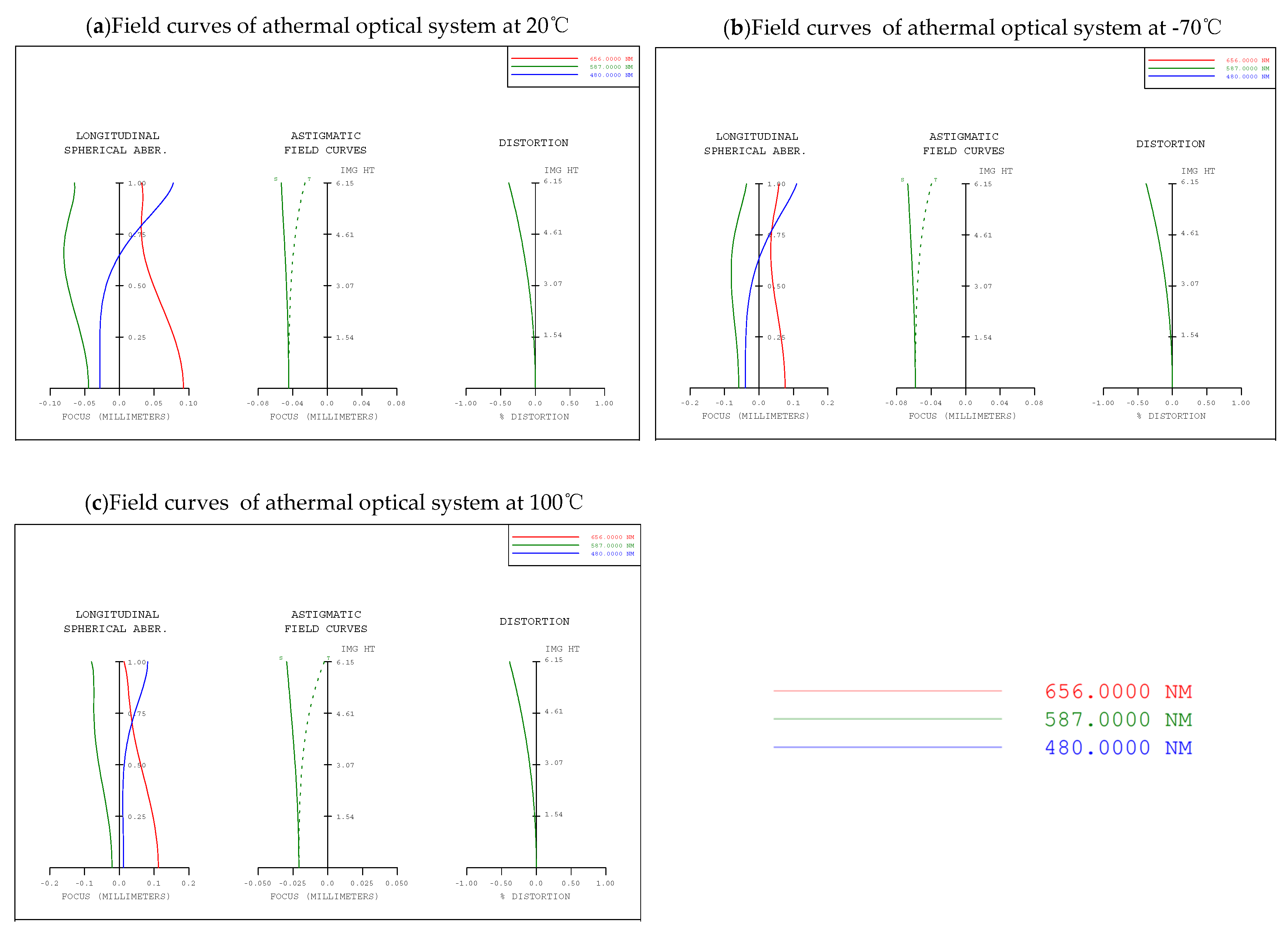
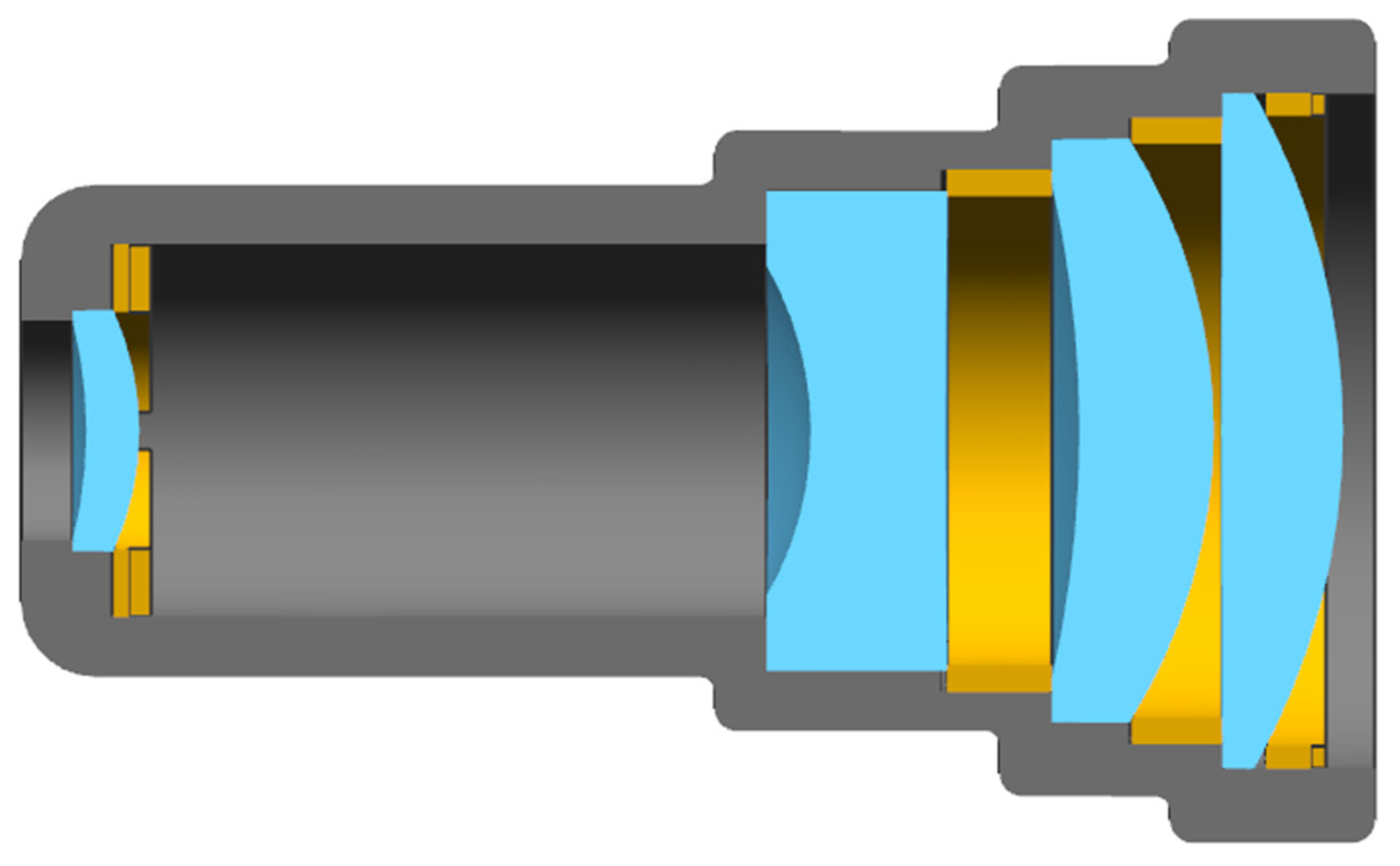
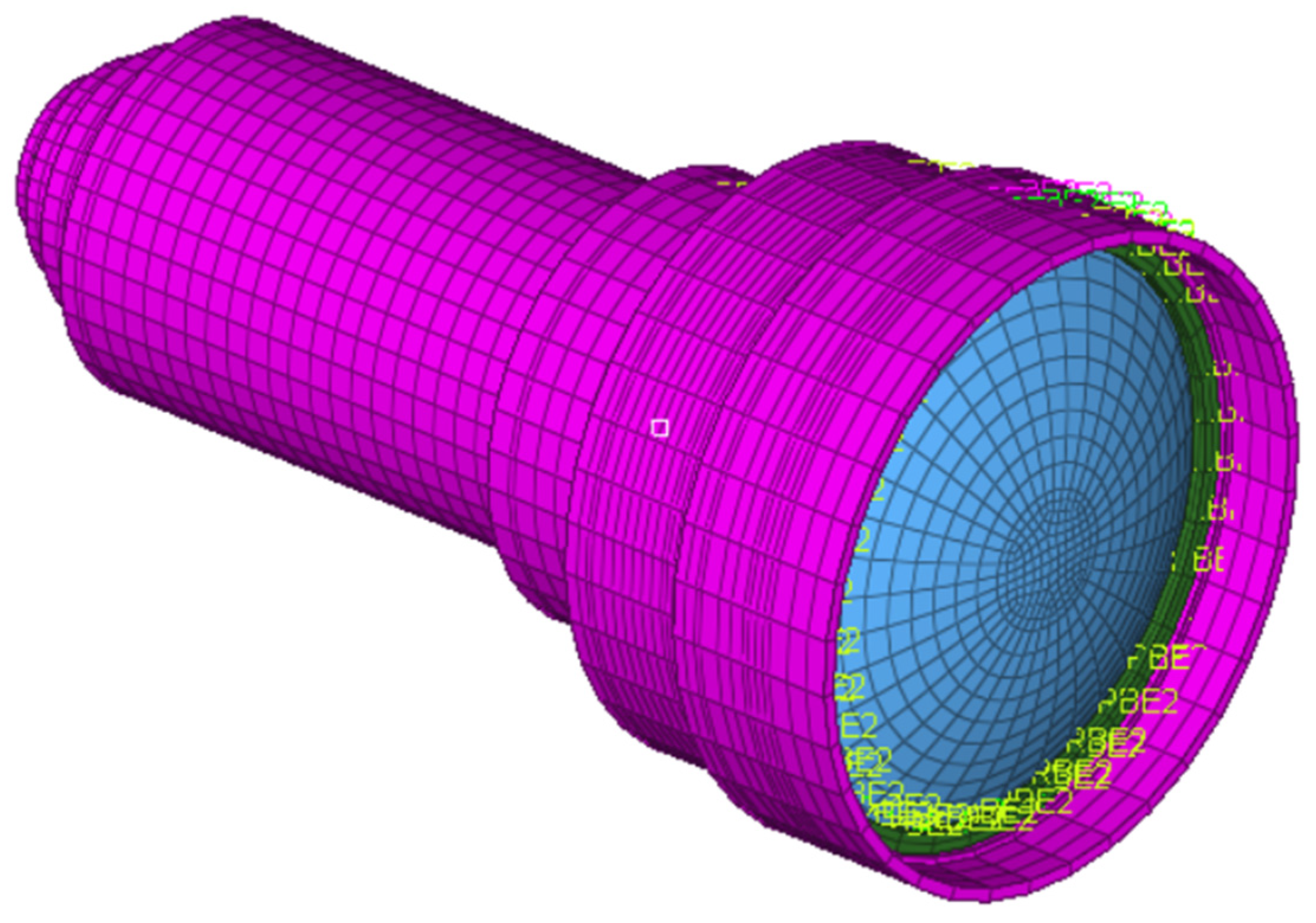


| Parameters | Value |
|---|---|
| Focal length | 200 mm |
| Wavelength | 480 nm–656 nm |
| Temperature range | −70 °C to 100 °C |
| Detector size | 9.6 mm × 7.68 mm |
| Housing material | Aluminum (αh = 230 × 10−6/°C) |
| Surface Number | Radius mm | Thickness mm | Material | Aperture mm |
|---|---|---|---|---|
| STO | - | 1.0 | - | 83.22 |
| 2 | 91.7341 | 16.3192 | HZPK1A | 84.05 |
| 3 | −6251.0594 | 1.0 | - | 81.98 |
| 4 | 72.9254 | 18.0 | HZPK5 | 75.26 |
| 5 | 150.6297 | 16.3414 | - | 66.28 |
| 6 | −1564.9886 | 18.0 | HZF12 | 53.48 |
| 7 | 44.2488 | 89.9915 | - | 41.30 |
| 8 | 38.9401 | 7.3875 | HZLAF68N | 28.34 |
| 9 | 60.3417 | 31.9604 | - | 25.68 |
| Image | - | - | - | 12.29 |
| Temperature Status | Normalized Field | RMS (waves@587nm) | P–V (waves@587nm) |
|---|---|---|---|
| 0 | 0.796 | 2.627 | |
| 20 °C | 0.5 | 0.877 | 3.180 |
| 1 | 0.980 | 3.311 | |
| 0 | 0.745 | 2.428 | |
| −70 °C | 0.5 | 0.833 | 3.010 |
| 1 | 0.943 | 3.126 | |
| 0 | 0.723 | 2.383 | |
| 100 °C | 0.5 | 0.807 | 2.924 |
| 1 | 0.914 | 3.158 |
| Temperature Status | Normalized Field | RMS (waves@587nm) | P–V (waves@587nm) |
|---|---|---|---|
| 0 | 1.629 | 5.226 | |
| −70 °C | 0.5 | 1.697 | 5.964 |
| 1 | 1.778 | 6.155 |
| Parameter Name | Parameter Meaning | Parametric Modeling Calculation Method |
|---|---|---|
| R1 | Radius 1 | R1 = Radius 1 |
| R2 | Radius 2 | R2 = Radius 2 |
| CT | Center thickness | CT = Center thickness |
| CA | Clear aperture | CA = Clear aperture |
| OA | Outer aperture | OA = Outer aperture |
| Fixed surface | Fixed surface | Front or back |
| LL | Retaining ring width | default: LL = OA/20 or customize |
| LR | Retaining ring thickness | default: LR = OA/20 or customize |
| HL | Lens room mounting width | default: LL = OA/15 or customize |
| HR | Lens room mounting thickness | default: LR = OA/18 or customize |
| AL | Lens room width | default: AL = lens edge thickness + HL + LL + 2 mm or customize |
| AR | Lens room thickness | default: AR = OA/7 or customize |
| T | Clearance between lens and lens holder | default: T = 0 or customize |
| House material information | Young’s modulus, Thermal expansion coefficient, Poin’s ratio | Assignment |
| Retaining ring material information | Young’s modulus, Thermal expansion coefficient, Poisson’s ratio | Assignment |
| Glass material information | Young’s modulus, Thermal expansion coefficient, Poisson’s ratio | Assignment |
| Result | Glass 1 | Glass 2 | Glass 3 | Glass 4 | Error Function |
|---|---|---|---|---|---|
| 1 | HZPK1A | HZPK5 | HZF12 | HZLAF68N | 48.5786 |
| 2 | HZPK1A | HZPK5 | HZF12 | HZLAF53B | 48.6393 |
| 3 | HZPK2A | HZPK5 | HZF12 | DZLAF52LA | 52.1341 |
| 4 | HFK61 | HZPK5 | HZF12 | DZLAF52LA | 82.9771 |
| 5 | HZPK5 | HZPK5 | HZF12 | DZLAF52LA | 92.6081 |
| 6 | HZK9B | HZPK5 | HZF52 | HZLAF75A | 98.1187 |
| Optimization Iteration Round | Error Function Before | Error Function After | Exceed the Normalized Radius |
|---|---|---|---|
| 1 | 111.07 | 83.60 | No |
| 2 | 85.19 | 68.85 | No |
| 3 | 64.45 | 62.44 | No |
| 4 | 61.33 | 59.73 | No |
| 5 | 59.88 | 56.83 | No |
| 6 | 56.83 | 56.72 | No |
| Temperature Status | Normalized Field | RMS (waves@587nm) | P–V (waves@587nm) |
|---|---|---|---|
| 0 | 0.991 | 3.272 | |
| 20 °C | 0.5 | 1.084 | 3.911 |
| 1 | 1.244 | 4.274 | |
| 0 | 1.107 | 4.412 | |
| −70 °C | 0.5 | 1.176 | 4.897 |
| 1 | 1.400 | 5.595 | |
| 0 | 0.881 | 2.901 | |
| 100 °C | 0.5 | 0.981 | 3.539 |
| 1 | 1.140 | 3.891 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Wang, C.; Yu, Y.; Liu, Z.; He, F. Passive Athermal Optical Design Method Considering Thermal-Induced Surface Deformation. Photonics 2021, 8, 396. https://doi.org/10.3390/photonics8090396
Liu T, Wang C, Yu Y, Liu Z, He F. Passive Athermal Optical Design Method Considering Thermal-Induced Surface Deformation. Photonics. 2021; 8(9):396. https://doi.org/10.3390/photonics8090396
Chicago/Turabian StyleLiu, Tao, Chong Wang, Yi Yu, Zhenyu Liu, and Fengyun He. 2021. "Passive Athermal Optical Design Method Considering Thermal-Induced Surface Deformation" Photonics 8, no. 9: 396. https://doi.org/10.3390/photonics8090396
APA StyleLiu, T., Wang, C., Yu, Y., Liu, Z., & He, F. (2021). Passive Athermal Optical Design Method Considering Thermal-Induced Surface Deformation. Photonics, 8(9), 396. https://doi.org/10.3390/photonics8090396




