On-Orbit Geometric Calibration from the Relative Motion of Stars for Geostationary Cameras
Abstract
:1. Introduction
2. Methodology
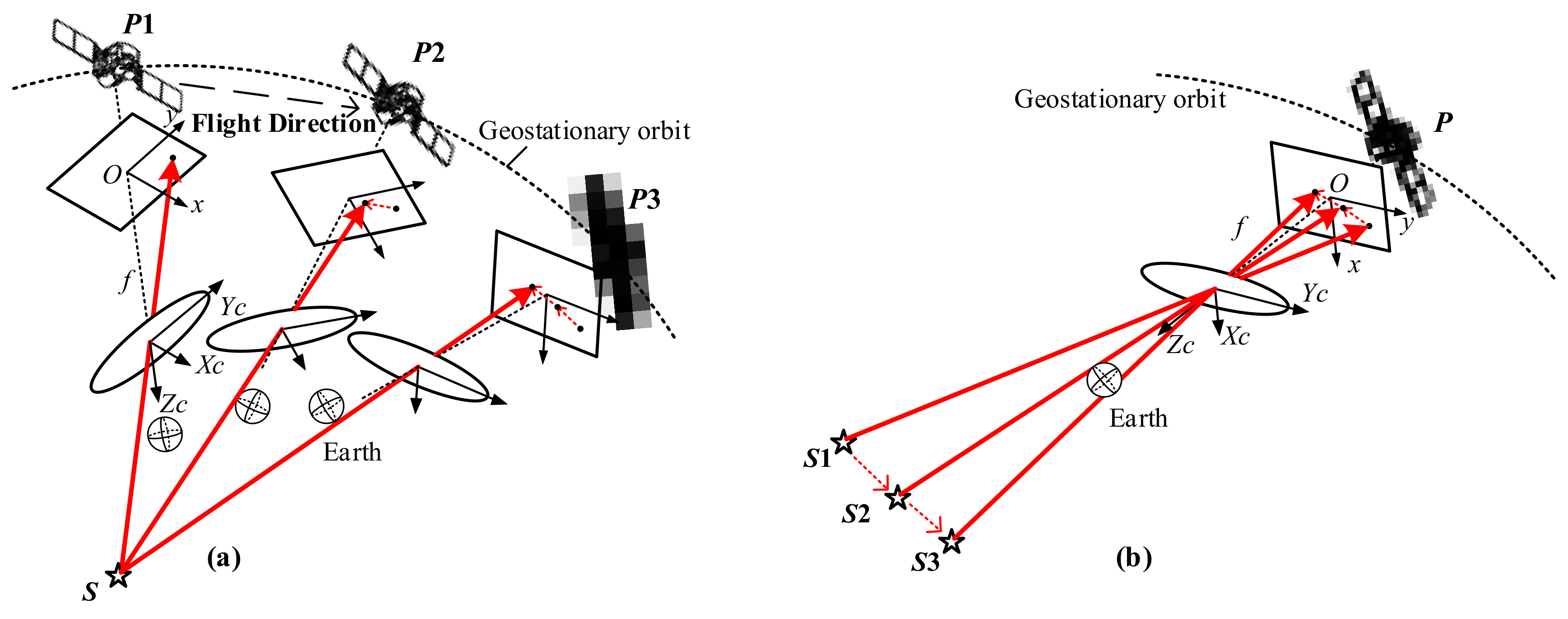
2.1. Preprocessing of Stellar Trajectory
2.2. Geometric Calibration Model
2.3. Model Solution Method
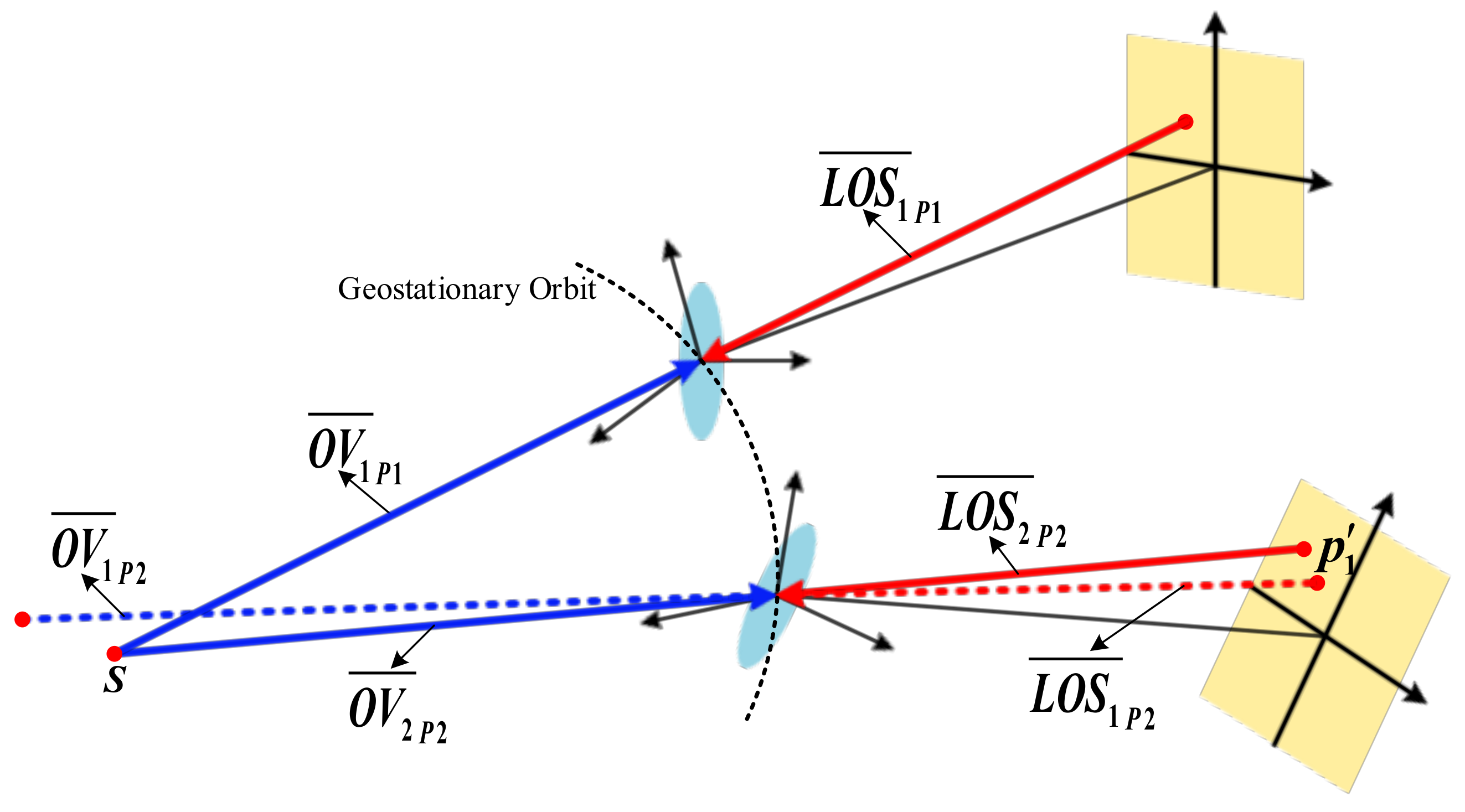
2.3.1. Relative Motion Transformation
2.3.2. Model Solving
2.3.3. Representation of Error
3. Experiment and Results
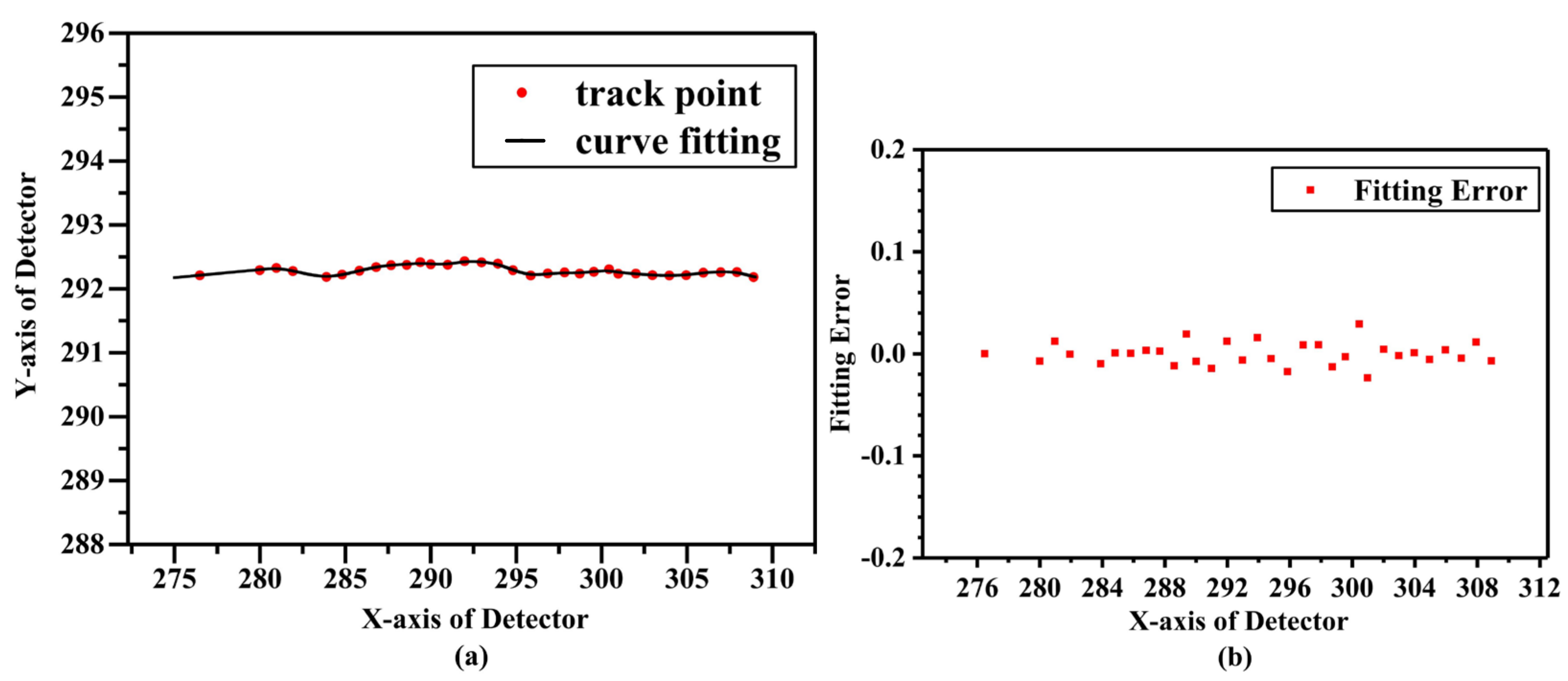
3.1. Trajectory Fitting Results
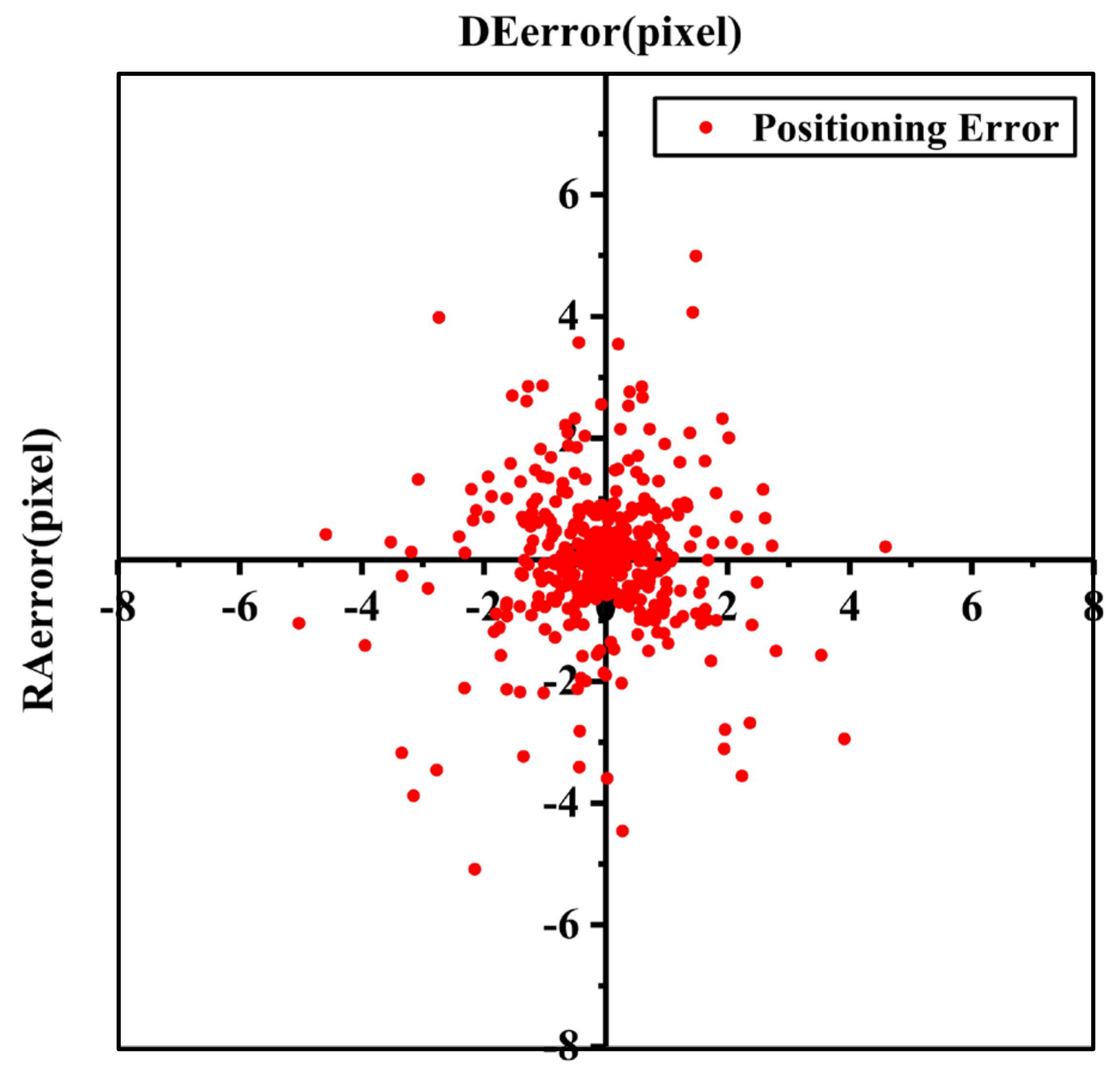
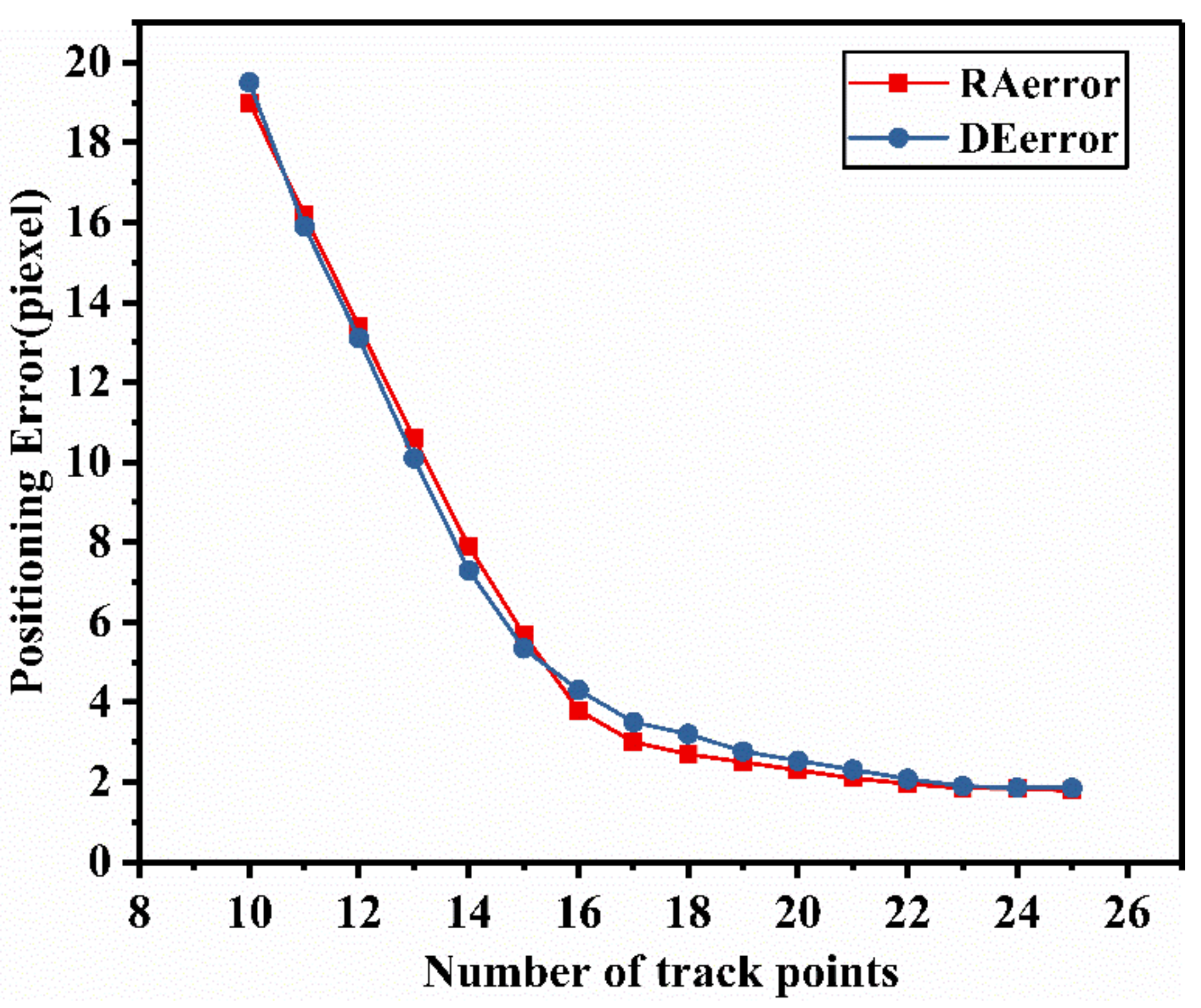
3.2. Results of Positioning Errors
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asaoka, S.; Nakada, S.; Umehara, A.; Ishizaka, J.; Nishijima, W. Estimation of spatial distribution of coastal ocean primary production in Hiroshima Bay, Japan, with a geostationary ocean color satellite. Estuar. Coast. Shelf Sci. 2020, 244, 106897. [Google Scholar] [CrossRef]
- Bhatt, R.; Doelling, D.R.; Haney, C.; Spangenberg, D.A.; Scarino, B.; Gopalan, A. Clouds and the Earth’s Radiant Energy System strategy for intercalibrating the new-generation geostationary visible imagers. J. Appl. Remote Sens. 2020, 14, 032410. [Google Scholar] [CrossRef]
- Miura, T.; Nagai, S. Landslide Detection with Himawari-8 Geostationary Satellite Data: A Case Study of a Torrential Rain Event in Kyushu, Japan. Remote Sens. 2020, 12, 1734. [Google Scholar] [CrossRef]
- Li, X.; Yang, L.; Su, X.; Hu, Z.; Chen, F. A Correction Method for Thermal Deformation Positioning Error of Geostationary Optical Payloads. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7986–7994. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, X.; Gong, J. In-Orbit Geometric Calibration and Validation of ZY-3 Three-Line Cameras Based on CCD-Detector Look Angles. Photogramm. Rec. 2015, 30, 211–226. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, Y.; Tian, Y.; He, L.; Wang, Y. A New On-Orbit Geometric Self-Calibration Approach for the High-Resolution Geostationary Optical Satellite GaoFen4. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1670–1683. [Google Scholar] [CrossRef]
- Liu, T.; Burner, A.W.; Jones, T.W.; Barrows, D.A. Photogrammetric techniques for aerospace applications. Prog. Aerosp. Sci. 2012, 54, 1–58. [Google Scholar] [CrossRef]
- Jacobsen, K. Issues and methods for in-flight and on-orbit calibration. In Post-Launch Calibration of Satellite Sensors: Proceedings of the International Workshop on Radiometric and Geometric Calibration, December 2003, Mississippi, USA; ISPRS Book Series 2; CRC Press: Boca Raton, FL, USA, 2004; pp. 83–92. [Google Scholar]
- Zhou, G.; Jiang, L.; Liu, N.; Li, C.; Li, M.; Sun, Y.; Yue, T. Advances and perspectives of on-orbit geometric calibration for high-resolution optical satellites. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2123–2126. [Google Scholar]
- Mulawa, D. On-orbit geometric calibration of the OrbView-3 high resolution imaging satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 1–6. [Google Scholar]
- De Lussy, F.; Greslou, D.; Dechoz, C.; Amberg, V.; Delvit, J.M.; Lebegue, L.; Blanchet, G.; Fourest, S. Pleiades HR in Flight Geometrical Calibration: Location and Mapping of the Focal Plane. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 519–523. [Google Scholar] [CrossRef] [Green Version]
- Greslou, D.; de Lussy, F.; Delvit, J.M.; Dechoz, C.; Amberg, V. Pleiades-Hr Innovative Techniques for Geometric Image Quality Commissioning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 543–547. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, M.; Zhu, Y. On-Orbit Calibration of Installation Parameter of Multiple Star Sensors System for Optical Remote Sensing Satellite with Ground Control Points. Remote Sens. 2020, 12, 1055. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hu, Z.; Jiang, L.; Yang, L.; Chen, F. GCPs Extraction With Geometric Texture Pattern for Thermal Infrared Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Zhang, Y.; Zhang, Z.; Xiao, X.; Yu, Y.; Wang, L. A Spliced Satellite Optical Camera Geometric Calibration Method Based on Inter-Chip Geometry Constraints. Remote Sens. 2021, 13, 2832. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z. Camera Geometric Calibration Using Dynamic Single-Pixel Illumination with Deep Learning Networks. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2550–2558. [Google Scholar] [CrossRef]
- Radhadevi, P.; Müller, R.; D’Angelo, P.; Reinartz, P. In-flight Geometric Calibration and Orientation of ALOS/PRISM Imagery with a Generic Sensor Model. Photogramm. Eng. Remote Sens. 2011, 77, 531–538. [Google Scholar] [CrossRef]
- Yang, B.; Pi, Y.; Li, X.; Yang, Y. Integrated geometric self-calibration of stereo cameras onboard the ZiYuan-3 satellite. ISPRS J. Photogramm. Remote Sens. 2020, 162, 173–183. [Google Scholar] [CrossRef]
- Tang, Y.; Wei, Z.; Wei, X.; Li, J.; Wang, G. On-Orbit Calibration of Installation Matrix between Remote Sensing Camera and Star Camera Based on Vector Angle Invariance. Sensors 2020, 20, 5667. [Google Scholar] [CrossRef] [PubMed]
- Grodecki, J.; Dial, G. IKONOS Geometric Accuracy Validation; International archives of photogrammetry remote sensing and spatial information sciences; Leibniz University Hannover Institute of Photogrammetry and GeoInformation: Hannover, Germany, 2012; p. 34. [Google Scholar]
- Helder, D.; Coan, M.; Patrick, K.; Gaska, P. IKONOS geometric characterization. Remote Sens. Environ. 2003, 88, 69–79. [Google Scholar] [CrossRef]
- Dial, G.; Bowen, H.; Gerlach, F.; Grodecki, J.; Oleszczuk, R. IKONOS satellite, imagery, and products. Remote Sens. Environ. 2003, 88, 23–36. [Google Scholar] [CrossRef]
- Valorge, C.; Meygret, A.; Lebègue, L. 40 years of experience with SPOT in-flight Calibration. In Post-Launch Calibration of Satellite Sensors; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Radhadevi, P.V.; Solanki, S.S. In-flight geometric calibration of different cameras of IRS-P6 using a physical sensor model. Photogramm. Rec. 2008, 23, 69–89. [Google Scholar] [CrossRef]
- Crespi, M.; Colosimo, G.; De Vendictis, L.; Fratarcangeli, F.; Pieralice, F. GeoEye-1: Analysis of Radiometric and Geometric Capability. In International Conference on Personal Satellite Services; Springer: Berlin/Heidelberg, Germany, 2010; pp. 354–369. [Google Scholar]
- Aguilar, M.A.; del Mar Saldana, M.; Aguilar, F.J. Assessing geometric accuracy of the orthorectification process from GeoEye-1 and WorldView-2 panchromatic images. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 427–435. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Aguilar, F.J.; Saldaña, M.D.M.; Fernández, I. Geopositioning Accuracy Assessment of GeoEye-1 Panchromatic and Multispectral Imagery. Photogramm. Eng. Remote Sens. 2012, 78, 247–257. [Google Scholar] [CrossRef]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.-P. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Wang, J.; Zhang, L.; Zhang, G.; Li, X.; Wu, J. Geometric Processing and Accuracy Verification of Zhuhai-1 Hyperspectral Satellites. Remote Sens. 2019, 11, 996. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Cheng, Y.; Chang, X.; Jin, S.; Zhu, Y. On-orbit geometric calibration and geometric quality assessment for the high-resolution geostationary optical satellite GaoFen4. ISPRS J. Photogramm. Remote Sens. 2017, 125, 63–77. [Google Scholar] [CrossRef]
- Dong, Y.; Fan, D.; Ma, Q.; Ji, S.; Ouyang, H. Automatic on-orbit geometric calibration framework for geostationary optical satellite imagery using open access data. Int. J. Remote Sens. 2019, 40, 6154–6184. [Google Scholar] [CrossRef]
- Zhukov, B.S.; Kondratieva, T.V.; Polyanskiy, I.V. Correction of automatic image georeferencing for the KMSS-2 multispectral satellite imaging system on board Meteor-M No. 2-2 satellite. Sovrem. Probl. Distantsionnogo Zondirovaniya Zemli Kosm. 2021, 18, 75–81. [Google Scholar] [CrossRef]
- Ye, S.; Zhang, C.; Wang, Y.; Liu, D.; Du, Z.; Zhu, D. Design and implementation of automatic orthorectification system based on GF-1 big data. Trans. Chin. Soc. Agric. Eng. 2017, 33 (Suppl. 1), 266–273. [Google Scholar]
- Seo, D.; Hong, G.; Jin, C. KOMPSAT-3A direct georeferencing mode and geometric Calibration/Validation. In Proceedings of the 36th Asian Conference on Remote Sensing: Fostering Resilient Growth in Asia, ACRS 2015, Quezon City, Philippines, 24–28 October 2015. [Google Scholar]
- Liu, L.; Xie, J.; Tang, X.; Ren, C.; Chen, J.; Liu, R. Coarse-to-Fine Image Matching-Based Footprint Camera Calibration of the GF-7 Satellite. Sensors 2021, 21, 2297. [Google Scholar] [CrossRef] [PubMed]
- Takenaka, H.; Sakashita, T.; Higuchi, A.; Nakajima, T. Geolocation Correction for Geostationary Satellite Observations by a Phase-Only Correlation Method Using a Visible Channel. Remote Sens. 2020, 12, 2472. [Google Scholar] [CrossRef]
- Chen, B.; Li, X.; Zhang, G.; Guo, Q.; Wu, Y.; Wang, B.; Chen, F. On-orbit installation matrix calibration and its application on AGRI of FY-4A. J. Appl. Remote Sens. 2020, 14, 024507. [Google Scholar] [CrossRef]
- Delvit, J.M.; Greslou, D.; Amberg, V.; Dechoz, C.; Delussy, F.; Lebegue, L.; Latry, C.; Artigues, S.; Bernard, L. Attitude assessment using Pleiades-HR capabilities. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 525–530. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Shin, D. On-Orbit Camera Misalignment Estimation Framework and Its Application to Earth Observation Satellite. Remote Sens. 2015, 7, 3320–3346. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Kim, E.; Chung, D.-W.; Seo, O.-C. Geometric Calibration Using Stellar Sources in Earth Observation Satellite. Trans. Jpn. Soc. Aeronaut. Space Sci. 2009, 52, 104–107. [Google Scholar] [CrossRef]
- Christian, J.A.; Benhacine, L.; Hikes, J.; D’Souza, C. Geometric Calibration of the Orion Optical Navigation Camera using Star Field Images. J. Astronaut. Sci. 2016, 63, 335–353. [Google Scholar] [CrossRef]
- Fourest, S.; Kubik, P.; Lebègue, L.; Déchoz, C.; Lacherade, S.; Blanchet, G. Star-Based Methods for Pleiades HR Commissioning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 513–518. [Google Scholar] [CrossRef] [Green Version]
- Guan, Z.; Jiang, Y.; Wang, J.; Zhang, G. Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite. Remote Sens. 2019, 11, 2081. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.J.; Ma, K. Study on the precision of feature point centroid extraction based on imaging angle. Laser J. 2018, 39, 90–99. [Google Scholar]
- Liu, Y.; Yang, L.; Chen, F.-S. Multispectral registration method based on stellar trajectory fitting. Opt. Quantum Electron. 2018, 50, 189. [Google Scholar] [CrossRef]



| Items | Detailed Parameters |
|---|---|
| Orbit altitude | 36,000 km |
| Focal length | 1250 mm (short-wave infrared) |
| Array sensor information | 1024 × 1024 HgCdTe |
| Pixel size | 25 μm (short-wave infrared) |
| Accuracy of attitude measurements |
| SSE | R-Square | RMSE | |
|---|---|---|---|
| Orbit altitude | 0.003856 | 0.9776 | 0.01728 |
| Initial Positioning Errors | Positioning Errors after Calibration | |||||
|---|---|---|---|---|---|---|
| RAerror/Pixel | DEerror/Pixel | RAerror/Pixel | Absolute Error/Pixel | DEerror/Pixel | Absolute Error/Pixel | |
| 2nd August | −10.384 | −20.247 | −0.616 | 0.616 | −0.080 | 0.08 |
| 3rd August | −5.081 | −20.430 | −0.086 | 0.086 | 0.099 | 0.099 |
| 4th August | −6.402 | −20.508 | −0.484 | 0.484 | 2.892 | 2.892 |
| 5th August | −5.181 | −20.624 | −0.464 | 0.464 | 1.233 | 1.233 |
| 6th August | −5.336 | −20.563 | −1.210 | 1.21 | −0.233 | 0.233 |
| 7th August | −5.877 | −20.557 | −0.017 | 0.017 | −0.127 | 0.127 |
| 8th August | −7.975 | −20.208 | −0.110 | 0.11 | −0.008 | 0.008 |
| 9th August | −4.686 | −20.414 | −0.063 | 0.063 | 0.027 | 0.027 |
| 10th August | −5.713 | −21.664 | 1.642 | 1.642 | −0.736 | 0.736 |
| 11th August | −8.704 | −20.375 | −0.568 | 0.568 | 0.468 | 0.468 |
| 12th August | −4.839 | −21.312 | −0.100 | 0.1 | −0.446 | 0.446 |
| 13th August | −5.371 | −21.283 | −0.271 | 0.271 | −0.437 | 0.437 |
| 14th August | −8.423 | −20.874 | −1.571 | 1.571 | 0.025 | 0.025 |
| 15th August | −8.366 | −21.446 | −2.038 | 2.038 | 0.984 | 0.984 |
| 16th August | −5.023 | −22.626 | 1.076 | 1.076 | 2.793 | 2.793 |
| 17th August | −7.060 | −21.679 | −0.280 | 0.28 | −1.177 | 1.177 |
| 18th August | −8.879 | −20.206 | 3.712 | 3.712 | 1.505 | 1.505 |
| 19th August | −7.201 | −22.269 | 0.511 | 0.511 | 1.013 | 1.013 |
| 20th August | −7.743 | −21.209 | −0.888 | 0.888 | 1.864 | 1.864 |
| 21st August | −7.658 | −22.182 | −1.128 | 1.128 | 0.921 | 0.921 |
| Mean | −6.795 | −21.004 | −0.148 | 0.84175 | 0.529 | 0.8534 |
| CL | mu | muci | sigma | sigmaci | |
|---|---|---|---|---|---|
| RAerror | 95% | −0.0611 | (−0.1661, 0.0440) | 1.1187 | (1.0492, 1.1982) |
| DEerror | 0.0234 | (−0.0870, 0.1338) | 1.1754 | (1.1024, 1.2589) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Li, X.; Li, L.; Yang, L.; Yang, L.; Hu, Z.; Chen, F. On-Orbit Geometric Calibration from the Relative Motion of Stars for Geostationary Cameras. Sensors 2021, 21, 6668. https://doi.org/10.3390/s21196668
Jiang L, Li X, Li L, Yang L, Yang L, Hu Z, Chen F. On-Orbit Geometric Calibration from the Relative Motion of Stars for Geostationary Cameras. Sensors. 2021; 21(19):6668. https://doi.org/10.3390/s21196668
Chicago/Turabian StyleJiang, Linyi, Xiaoyan Li, Liyuan Li, Lin Yang, Lan Yang, Zhuoyue Hu, and Fansheng Chen. 2021. "On-Orbit Geometric Calibration from the Relative Motion of Stars for Geostationary Cameras" Sensors 21, no. 19: 6668. https://doi.org/10.3390/s21196668
APA StyleJiang, L., Li, X., Li, L., Yang, L., Yang, L., Hu, Z., & Chen, F. (2021). On-Orbit Geometric Calibration from the Relative Motion of Stars for Geostationary Cameras. Sensors, 21(19), 6668. https://doi.org/10.3390/s21196668








