A Secure and Efficient Handover Authentication Protocol for Wireless Networks
Abstract
: Handover authentication protocol is a promising access control technology in the fields of WLANs and mobile wireless sensor networks. In this paper, we firstly review an efficient handover authentication protocol, named PairHand, and its existing security attacks and improvements. Then, we present an improved key recovery attack by using the linearly combining method and reanalyze its feasibility on the improved PairHand protocol. Finally, we present a new handover authentication protocol, which not only achieves the same desirable efficiency features of PairHand, but enjoys the provable security in the random oracle model.1. Introduction
In today's world, wireless communication networks are ubiquitous, and mobile handheld devices, such as PDAs, smart phones and laptop PCs, have a wide influence on various aspects of people's lives. To overcome the restriction of geographical coverage, seamless access services are highly desirable for WLANs and mobile wireless sensor networks (WSNs), but how to ensure the security and efficiency of this process is still challenging. Recently, as a promising seamless access control technology, handover authentication protocols have received much attention [1–12]. A handover authentication scenario is always assumed to involve three kinds of parties: mobile nodes (MNs), access points (APs) and the authentication server (AS). An MN is a registered user on AS, who accesses its subscribed services by connecting any AP. An AP acts as a guarantor for vouching for an MN as a legitimate subscriber. When an MN leaves the service area of the current AP (e.g., AP1) and tries to connect a new AP (e.g., AP2), the new AP will start its handover authentication process to identify the MN. If the authentication succeeds, a session key will be built between the MN and AP2 to escort the MN's later access. Otherwise, the requirement for accessing will be rejected by AP2. A promising application of this kind of protocol appears in three-tiered mobile WSNs [13], which consist of a base station, access points, mobile agents and sensor nodes. In the highest layer, the base station works as the AS to deploy access points and to register mobile agents by granting the corresponding authentication keys. The access points are the APs with the task of receiving and verifying the message from the medium layer. The medium layer is composed of the mobile agents, which can be mobile phones, vehicles, men and even animal, acting as the MNs and responsible for gathering data from the sensor nodes in the lowest layer and, then, forwarding to the upper layer.
Recently, He et al. [14] introduced an interesting handover authentication protocol, named PairHand. For improving the communication efficiency and reducing the burden on AS, PairHand only requires two handshakes between MN and AP for mutual authentication and key establishment, instead of relying on the participation of AS. Furthermore, considering the high cost and the inconvenience of revoking users due to using a group signature in the authentication process, PairHand makes its construction directly based on the pairing-based cryptography and uses a pool of shorter-lived pseudonyms to protect users' privacy. Unfortunately, shortly after, He et al. [15] found that there is a serious design weakness in PairHand protocol that enables an adversary to easily obtain the private key from the message transported in the first round of the protocol and presented an improvement by utilizing a composite order bilinear group, claiming that the improved version fixes the security problem without losing any of the desirable feature of PairHand. However, Yeo et al. [16] showed that if an attacker obtains multiple authenticated messages generated with the same pseudo-ID, it will be likely to recover the private key of the mobile node. Furthermore, Yeo et al. [16] and Tsai et al. [17] pointed out another dilemma of the improved version that suggested that the 160-bit composite is insecure, but using a 1,024-bit composite-order group will lead to a great drop in the efficiency. At the same time, Tsai et al. [17] presented a provably secure handover authentication protocol, which solves the above security problem, but increases the size of the public key.
In this paper, we provide a linear combination method to reduce the number of captured signatures corresponding to the same pseudo-ID required by the key recovery attack on the improved PairHand [15]. By repeatedly linearly combining arbitrary two-captured signatures from the same pseudo-ID in a random way, the attacker can compute out the private key of MN with a very high probability. To improve the security without losing the desirable features, we present a new handover authentication protocol that overcomes the security weakness of the original PairHand and achieves the same level of high efficiency. Finally, in the random oracle model, we prove that this protocol enjoys both semantic security and authentication security.
2. The Bilinear Maps and Complexity Implications
In this section, we briefly recall bilinear maps and some difficult problems that will be used in the followings.
Let





Bilinearity: e(aP, bQ) = (P, Q)ab for ∀P, Q ∈
and ∀a,
Non-degeneracy: e(P, P) ≠ 1 for P ≠ 0.
Computability: there exists an efficient algorithm to compute e(P, Q) for ∀P, Q ∈
.
Computational Diffie–Hellman (CDH) assumption: Given P, aP and bP for some a, , it is computationally intractable to compute the value abP.
Bilinear Diffie–Hellman (BDH) assumption: Given P, aP, bP and cP for some a, b, , it is computationally intractable to compute the value e(P, P)abc.
3. Security Model
Generally, there are two kinds of handovers: a hard handover and a soft handover. The difference between them is that in a hard handover, the former connection with AP1 is broken before the new connection is established between MN and AP2, while in a soft handover, MN can retain the connection with AP1 after building the new connection with AP2. For simplicity, it is assumed that there is no communication among APs and that handover authentication protocols perform in the hard handover model. In the following, we present the formal security model for handover authentication protocols, which follows the approach initiated by Bellare and Rogway [18,19] and modified by Bresson et al. [20].
3.1. Communication Model
Protocol participants: In the model, there are two kinds of participants: mobile node MN and access point AP, which have unique identities IDMN and IDAP, respectively. Each instance of a participant (U or V) is molded as an oracle, denoted by ( , respectively), meaning the n-th running instance of the participant MN (AP, respectively).
Protocol execution: In the model, it is assumed that an adversary

(1) Execute( , ): This query models passive attacks, where the attacker gets access to honest executions between instances and by eavesdropping. The output of this query is the complete transcript that was transported during the honest execution of the protocol.
(2) Send( , M): This query models an active attack against an MN or AP, in which the adversary sends a message to the instance . The output of this query is the message that the instance generates upon receipt of the message M.
(3) Reveal( ): This query models the misuse of session keys. Only if the session key of the instance is defined, the query is available and returns to the adversary the session key.
(4) Test( ): This query is to measure the semantic security of the session key of instance : If the session key is not defined, it returns ⊥. Otherwise, it returns either the session key held by the instance if b = 0 or a random number of the same size if b = 1, where b is the hidden bit previously selected at random before the protocol runs.
(5) Corrupt(IDU): This query models the exposure of the long-term secret key. When the adversary makes this query, the oracle returns the private key corresponding to IDU.
3.2. Security Definitions
Notation: An instance is said to be opened if the query Reveal( ) has been made by the adversary. We say an instance is unopened if it is not opened. An instance is said to be accepted if it goes into an accept state after receiving the last expected protocol message.
Partnering: We say two instances and are partners if the following conditions are met: (1) they are an MN and an AP, respectively; (2) both and are accepted; (3) both and share the same session ID sid; (4) the partner identification for is and vice versa; and (5) no instance other than and accepts with a partner identification equal to or .
Freshness: If an instance has been accepted, both the instance and its partner are unopened and they are both instances of honest clients, we say the instance is fresh.
Semantic security: The security notion is defined in the context of executing an ID-based handover authentication protocol P in the presence of an adversary





We say a handover authentication protocol P is semantically secure if the advantage is negligible.
Authentication security: To measure the security of a handover authentication protocol resisting the impersonation attacks, we consider the mutual authentication between MN and AP. We denote by
(or
, respectively) the probability that an adversary

4. Review of the Protocol
In this section, we review He et al.'s improved protocol [15], which is very similar to the original PairHand and consists of four phases: system initialization, handover authentication, batch authentication and denial-of-service (DoS) attack resistance. The only differences between the two versions appear at the selection of the group order in the system initialization phase and the computation of the hash value of the authentication message in the handover authentication phase, and our attack is exactly to address these two phases. Below, we only review the first two phases of the improved PairHand protocol. For more details, please refer to [14].
4.1. System Initialization
The AS randomly chooses a value s ∈
as the master key and a generator P of




For the registration of a qualified MN i with real identity IDi, AS generates a family of unlinkable pseudo-IDs PID = {pid1, pid2, ⋯}, computes the public key H1(pidj) and the corresponding private key s · H1(pidj) for each pseudo-ID pidj ∈ PID and, finally, securely sends to MN i all tuples (pidj, sH1(pidj)). The use of shorter-lived pseudonyms is to protect each MN's privacy, preventing them from being traced.
4.2. Handover Authentication
When an MN, say i, moves into the communication range of a new AP (AP2), a handover authentication process, which is shown in Figure 1, will be performed between MN i and AP2 in the following steps.
(1) MN i firstly picks an unused pseudo-ID pidi from his pseudo-ID family and the corresponding private key sH1(pidi). Then, MN i generates an authentication message as Mi = pidi‖IDAP2‖ts, where ts is a timestamp, which is used to resist against replay attacks and “‖” denotes the concatenation of messages and checks whether H2(Mi) and q are co-prime or not. If H2(Mi) and q are not co-prime, it does nothing; otherwise, it continues to append redundant bits rb into Mi until H2(Mi) and q are not co-prime. After that, MN i computes the signature σi = H2(Mi) · sH1(pidi) and unicasts the access request message {Mi, σi} to AP2. Finally, MN i computes the session key with AP2 as Ki−2 = e(sH1(pidi), H1(IDAP2)).
(2) Upon receiving the request message {Mi, σi}, AP2 firstly checks whether the timestamp ts is valid. If invalid, the request is rejected. Otherwise, AP2 verifies if e(σi, P) = e(H2(Mi) · H1 (IDpidi), Ppub). If true, AP2 computes the session key K2−i = e(H1(pidi), sH1(IDAP2)) and the authentication code Aut = H2(K2−i‖pidi‖IDAP2) and, then, sends the tuple {pidi, IDAP2, Aut} to MN i.
(3) Upon receipt of the message {pidi, IDAP2, Aut}, MN i computes the verification code Ver = H2(Ki−2‖pidi‖IDAP2) and compares it with Aut. If they are equal, MN i confirms that AP2 is legitimate, and the generated session key is valid. Otherwise, MN i cancels the connection.
(4) At last, AP2 securely transports {Mi, σi} to AS. By receiving this message, AS can identify the real identity of MN i according to the pseudo-ID in Mi.
After successfully executing the handover protocol, MN i and AP2 share a session key, since Ki−2 = e(sH1(pidi)),H1(IDAP2)) = e(H1(pidi),H1(IDAP2))s = e(H1(pidi),sH1(IDAP2)) = K2−i. Furthermore, the use of a pseudo-ID enables unilateral anonymous authentication for the MN i, and each session is uniquely identified by (pidi, IDAP2).
5. Attack on the Protocol
For the original PairHand protocol, what enables an attacker to recover the private key sH1(pidi) is that when H2(Mi) and q are co-prime, he can use the inverse u of H2(Mi) modulo q to get u· σi = u · H2(Mi) · sH1(pidi) = sH1(pidi)(modq), since u · H2(Mi) = 1(modq). The countermeasures of He et al. [15] are to restrict the group order q to be a composite and to append redundant bits into the request message Mi to ensure that the resulting H2(Mi) and q are not co-prime. By doing this, it seems that the private key sH1(pidi) will not be exposed by the signature σi, since there is no modular inverse for H2(Mi).
However, the following attack will show that He et al.'s improved protocol [15] does not eradicate the design weakness. Our attack is based on the assumption [6] that adversary





 directly computes
by using Mi and
and checks whether β and q are co-prime. If yes, it generates
and computes the private key sH1(pidi) = γ · α. Otherwise, it reselects random values x1, x2 and computes α and β again, until β and q are co-prime.
directly computes
by using Mi and
and checks whether β and q are co-prime. If yes, it generates
and computes the private key sH1(pidi) = γ · α. Otherwise, it reselects random values x1, x2 and computes α and β again, until β and q are co-prime.As q is a randomly generated system parameter, Mi and are random messages and x1 and x2 are randomly chosen from ℤp, we can approximately view q and as two independent random numbers. Let {p1, p2, p3, ⋯} denote the ascending sequence of all prime numbers, and let pk be the largest prime number less than q. The probability that β is divisible by a prime pi is , where i ≤ k, and the same fact holds for q. Therefore, the probability that the two numbers β and q are both divisible by this prime number is , whilst the probability that at least one of them is not is . Thus, the probability of the success of our attack for one time, Psuccess, which is equal to the probability that β and q are co-prime, is:
Obviously, a natural way to cope with the above attack is to ensure that each pseudo-ID is used only one time, regardless of whether the AP responds correctly, which will require different signatures to correspond to different pseudo-IDs. As a consequence, it is impossible for an adversary to compute out the private key by using linear combinations of two signatures. However, this countermeasure will largely reduce the availability of the handover authentication protocol and give rise to more serious security problems, as shown as follows. When an MN moves and leaves from the service range of its old AP, it will attempt to connect to and identify a new AP by instantly sending authentication messages. Once a pseudo-ID is used only one time, an attempt to connect will cost one pseudo-ID of the MN, which will cause a great waste on the pseudo-IDs and force the MN to store a much larger number of pseudo-IDs. However, mobile nodes are often lightweight devices and have limited storage spaces, this makes them unable to afford a large number of redundant pseudo-IDs. Additionally, the increase of the number of pseudo-IDs will lead to the growth of the length of pseudo-IDs, which deeply affects the efficiency of the computation and the communication of the whole wireless network. More seriously, if there is an adversary who always interrupts the request authentication message of an MN, the MN will eventually use up all its pseudo-IDs and be out of the service of the system, due to instantly repeating the request. Such an attack can be avoided by using additional precautions, such as delaying the response or introducing exponentially increasing delays after failed attempts and switching to other AP after an excessive amount of failures. However, all of these measures are very costly and can cause more additional risks, which is contrary to the design rational of PairHand.
6. Our Handover Authentication Protocol
According to the above analysis, the point to overcome the security weakness of the two PairHand protocols is to provide a secure authentication mechanism for the first message transmission. Below, we provide a simple scheme, which not only eliminates the security risks mentioned above, but greatly preserves the desirable efficiency features of the original protocol. Similar to PairHand, the proposed scheme is composed of four phases: system initialization, handover authentication, batch authentication and DoS attack resistance, where the first phase and the fourth phase are the same as those of the PairHand protocol. For the sake of completeness, all of the four phases are fully described in the following.
6.1. System Initialization
Let






The AS randomly chooses a value
as the master key, computes the corresponding public key Ppub = sP and selects two cryptographic hash functions H1 and H2, where H1 : {0, 1}∗ →



For the registration of a qualified MN i with real identity IDi, AS generates a family of unlinkable pseudo-IDs PID = {pid1, pid2, ⋯}, computes the public key H1(pidj) and the corresponding private key s · H1(pidj) for each pseudo-ID pidj ∈ PID and, finally, securely sends to MN i all tuples (pidj, sH1(pidj)).
6.2. Handover Authentication
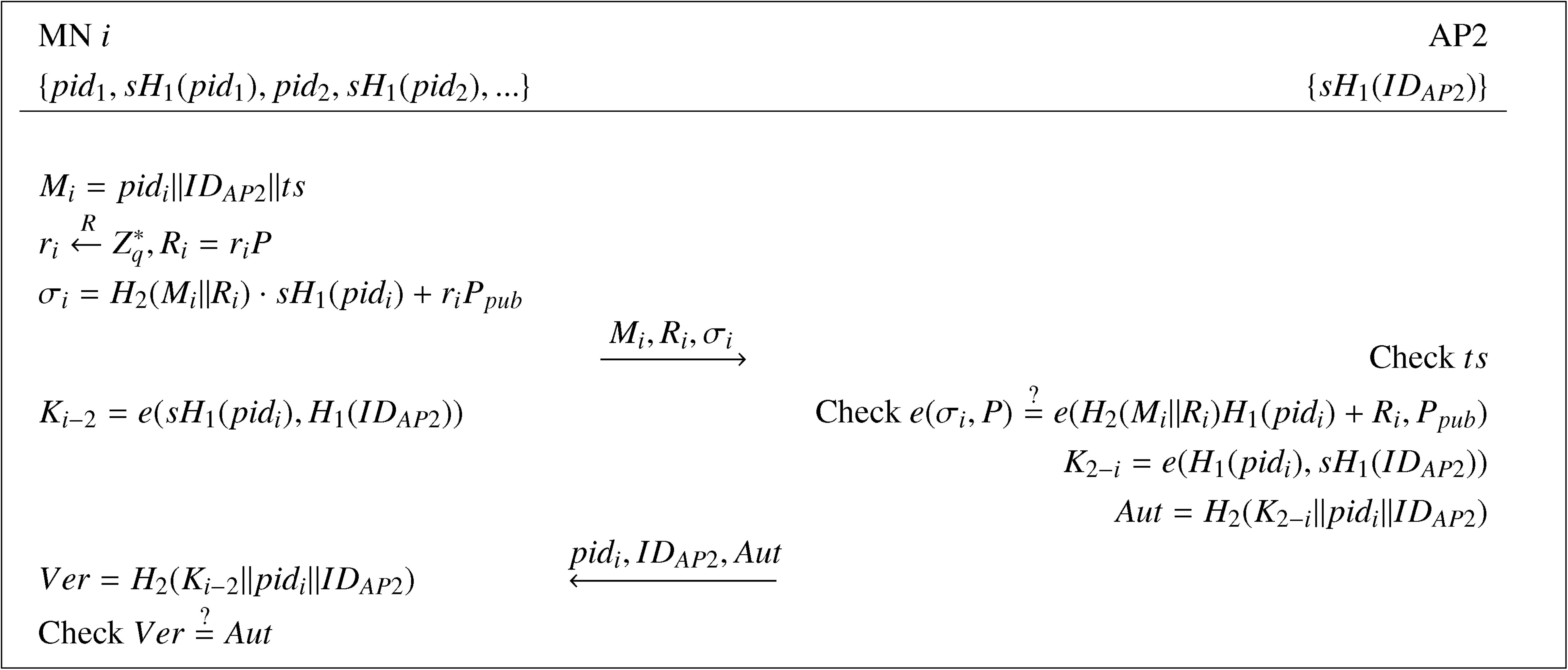
When an MN, say i, moves into the communication range of a new AP (AP2), a handover authentication process will be performed between MN i and AP2 in the following steps.
(1) MN i firstly picks an unused pseudo-ID pidi and the corresponding private key sH1(pidi) and computes Mi = (pidi‖IDAP2‖ts), where ts is the timestamp. Then, MN i chooses a random value , which is a nonce, computes Ri = riP and σi = H2(Mi‖Ri) · sH1(pidi) + riPpub and unicasts the access request message Mi and its signature pair (Ri, σi) to AP2. Finally, it computes the session key with AP2 as Ki−2 = e(sH1(pidi), H1(IDAP2)).
(2) Upon receiving the message {Mi, ri, σi}, AP2 checks the timestamp ts. If invalid, the request is rejected. Otherwise, AP2 verifies if e(σi, P)=e(H2(Mi‖Ri)H1(pidi) + Ri, Ppub). If true, AP2 computes the session key K2−i = e(H1(pidi), sH1(IDAP2)) and the authentication code Aut = H2(K2−i‖pidi‖IDAP2) and, then, sends the tuple {pidi, IDAP2, Aut} to MN i.
(3) Upon receipt of the message {pidi, IDAP2, Aut}, MN i computes the verification code Ver = H2(Ki−2‖pidi‖IDAP2) and compares it with Aut. If they are equal, MN i confirms that AP2 is legitimate and that the generated session key is valid. Otherwise, MN i cancels the connection.
(4) At last, AP2 securely transports {Mi, σi} to AS. By receiving this message, AS can identify the real identity of MN i according to the pseudo-ID in Mi.
The handover authentication phase of the proposed scheme is also shown in Figure 2.
6.3. Batch Authentication
A mass of signature verifications is likely to cause the potential bottleneck at APs. Batch authentication [14] is a desirable feature to solve the problem, which allows APs to verify multiple signatures simultaneously. Its advantage lies in that the total computation cost in the verification performed by APs can be apparently reduced.
Our protocol still enjoys the batch authentication feature. Suppose n request messages {M1, R1, σ1}, {M2, R2, σ2}, ⋯, {Mn, Rn, σn}, come simultaneously from n distinct MNs, MN 1, MN 2, ⋯, MN n, respectively The target AP can perform a batch verification on these n signatures as follows:
From the above equation, it is obvious that the computation cost of verifying n signatures is dramatically reduced to n point multiplication and two pairing operations by using the batch processing.
6.4. DoS Attack Resistance
In the handover authentication circumstance, DoS attack is an attempt to exhaust the resources of AP and AS and make them unavailable to its intended partners. A usual manner adopted by the adversary is to inject bogus access requests to the networks, forcing the APs to perform expensive cryptographic verifications and eventually exhaust their resources.
The proposed scheme still adopts the polynomial-based lightweight verification of PairHand [14] to resist the DoS attack. In the system initialization phase, AS randomly generates a bivariate t-degree polynomial over a prime field Fp, such that f(x, y) = f(y, x). When MN i registers to AS, for each pseudo-ID pidi, AS computes f(pidi, y), which is a polynomial share of f(x, y), and then securely transmits them to MN i. Furthermore, AS computes and deliveries f(IDAP, y) to each AP, where IDAP is the identity of the AP. As the evaluation of the polynomial is very fast [14], each AP can perform a lightweight verification on the access request from MN i by checking f(pidi, IDAP) ≟ f(IDAP, pidi), where the former is computed by MN i with f(pidi, y) at point IDAP and the later is done by the AP with f(IDAP, y) at point pidi. Once an AP is under attack, it starts the above measure, adding “Yes” and its identity into the beacon messages. As a result, DoS attack can be effectively mitigated, since each AP can promptly verify the authorized user with the communication key before conducting expensive cryptographic verifications.
6.5. Security Analysis
Theorem 1
Assume hash functions H1 and H2 are random oracles. Let 






Proof
Suppose that the attacker







Without loss of generality, we assume that for any pseudo-ID, the adversary


H1-query: When
invokes an H1 query for pidi,
checks whether pidi = pidU. If yes,
returns aP. Otherwise,
returns a randomly selected value h ∈
and appends < pidi, h > into the list LH1.
H2-query: When
invokes an H2 query for messages (m, R),
returns a random number and stores < m, R, t >.
Corrupt-query: If the queried pseudo-ID is legal and is not equal to pidU,
searches the corresponding item in the list LH1 according to the pseudo-ID and then returns the secret key. Otherwise,
returns ⊥.
Execute-query: This query is responded to by invoking the corresponding S end queries.
Send-query: When
invokes a send query, simulator
extracts pidi involved in the query and uses it to invoke query H1. Then,
randomly chooses ri, , computes σi = riPpub, Ri = riP − tH1(pidi) and stores the item < m, Ri, t > in the list LH2. Finally, it outputs (pidi, Ri, σi). If there is no collision of queries to the random oracle during the process,
can successfully simulate the protocol environment in front of
, due to the fact that the probabilities of the duple (α, β, γ, δ), such that , α, γ, δ ∈
and e(γ, P) = e(βα + δ, sP) appear, the following two distributions Γ and Γ′ are the same.
According to the Forking lemma [21], if



Additionally, the probability of that the two forged authentication messages correspond to pidU is . As a result, the upper bound of the expected time for breaking the CDH problem will be expanded -times the one in the Forking lemma.
Theorem 2
Assume hash functions H1 and H2 are random oracles. Let 



Proof
Let (P, aP, bP, sP) be the BDH instance provided to the simulator









H1-query: If
makes an H1 query for pidU,
returns aP. If the query is for the AP identification IDV,
returns bP. Otherwise,
returns a randomly selected value h ∈
and adds < pidi, h > or < IDV, h > into the list LH1.
H2-query: When
invokes an H2 query for messages M,
chooses a random number t ∈ ℤq, stores < M, t > the list LH2 and then returns it.
Corrupt-query: If the queried identity is legal and is not equal to pidU and IDV,
searches the corresponding item in the list LH1 according to the identity and then returns the secret key. Otherwise,
returns ⊥.
Execute-query: This query is responded to by invoking the corresponding S end queries.
Send-query: There are two types of S end queries: MN-to-AP and AP-to-MN, denoted by S end1 and Send2, respectively.
answers them by invoking the H1 and H2 queries.
If the query is Send1, simulator
randomly chooses ri, and computes σi = riPpub, Ri = riP − tH1(pidi) by invoking H1 queries with IDi. Then, it adds the item (m, Ri, t) in the list LH2 and outputs message tuple (pidi, Ri, σi).
If the query is S end2, simulator
checks whether e(σi, P)=e(H2(Mi‖Ri)H1(pidi) + Ri, Ppub). If false,
outputs “⊥”. Otherwise,
chooses a random value k ∈
and computes aut = H2(k‖pidi‖IDj) by making the H2 query. Finally, it returns the message tuple (aut‖pidi‖IDj).
The success of




Theorem 3
Assume hash functions H1 and H2 are random oracles. If the protocol enjoys the mutual authentication security, it is also semantically secure.
Proof
To prove the semantic security for the protocol, we apply the same simulation way used in proving Theorem 2. Let F1 (or F2, respectively) denote the event that the attacker successfully forges an MN-to-AP (or AP-to-MN, respectively) authentication message. Let S0 (or S1, respectively) denote the event that in the real (or simulated, respectively) attacking game, the attacker successfully guess the challenge bit involved in the Test oracle. If both the events F1 and F2 do not happen, the real and simulated games proceed identically, and we get the following equation:
6.6. Performance Comparison
Compared with the existing handover authentication protocols, the proposed protocol has the advantage in communication, computation and security. For those protocols prior to PairHand [1–4,6–10,12], its superiority comes through the low burden on AS, the two-run handshakes between MN and AP, the batch authentication and the privacy protection for MN. To evaluate its advantage over the post-PairHand protocols [14,15,17], we mainly consider its performance superiority on secret key size, computational cost and security features. In Table 1, we present the comparison results on these aspects among He et al.'s improved PairHand [15], Tsai et al.'s [17] protocol and our scheme. For computational cost, we focus on the time spent on the high cost operations, such as the time spent on the paring operations (Tp), the time spent on the multiplications on the elliptic curve (Tm) and the time spent on the search for non-co-primes (Ts), while the time spent on highly efficient operations, such as the hash function and the scalar addition on the elliptic curve, is neglected. The estimate of the time consumption at an MN is based on He et al.'s work in [14,15], where by using the MNT curve with the order of 160 bits and the degree k = 6 and the MIRACL and PBC libraries (c/c++), an MN runs on an 800 MHz processor. To evaluate the length of the messages transmitted in the protocol execution, we assume that the lengths of pidi, ts and IDAP2 are four, two and four bytes, respectively. We notice that the computational time of our protocol and Tsai et al.'s protocol are much lower than He et al.'s protocol, due to their prime-order work groups. This is because the composite order in He et al.'s protocol should be at least 1024-bit to be infeasible to factorize, while a 160-bit prime order is enough to achieve the same security level. An estimation [23] shows that the composite-order pairing is roughly 50-times slower than its prime-order counterpart. For security, both our scheme and Tsai et al.'s protocol enjoy provable security, but He et al.'s protocol does not. In terms of the secret key size, our protocol is superior to Tsai et al.'s protocol and is the same as the original PairHand protocol [14]. As a result, our scheme can be easily implanted to the running environment of the original PairHand protocol without any change to the public and private parameters.
7. Conclusions
In this paper, in reviewing the PairHand family protocols, we present a stronger key recovery attack on an improved PairHand protocol, which requires less signatures to be generated with the same private key compared with the existing attacks. Consequently, we present a new handover authentication protocol and prove its security in the random oracle model. Compared with the two latest handover authentication protocols, the proposed protocol has the advantages of efficiency and security.
Acknowledgments
The work is partially supported by the Fundamental Research Funds for the Central Universities under Grant No.2012JBM104.
Author Contributions
Weijia Wang is the principal researcher of this study and main author of this work. Lei Hu has contributed to the revision of this paper and provided insightful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, J.; Jung, S. A secure and efficient handover authentication based on light-weight Diffie-Hellman on mobile node in FMIPv6. IEICE Trans. Commun. 2008, E-91B, 605–608. [Google Scholar]
- Choi, J.; Jung, S. A handover authentication using credentials based on chameleon hashing. IEEE Commun. Lett. 2010, 14, 54–56. [Google Scholar]
- Choi, J.; Jung, S.; Kim, Y.; Yoo, M. A Fast and Efficient Handover Authentication Achieving Conditional Privacy in V2I Networks. In Smart Spaces and Next Generation Wired/Wireless Networking; Balandin, S., Moltchanov, D., Koucheryavy, Y., Eds.; Springer: Berlin, Germany, 2009; pp. 291–300. [Google Scholar]
- Chang, C.-C.; Lee, C.-Y.; Chiu, Y.-C. Enhanced authentication scheme with anonymity for roaming service in global mobility networks. Comput. Commun. 2009, 32, 611–618. [Google Scholar]
- Chang, C.-C.; Tsai, H.-C. An anonymous and self-verified mobile authentication with authenticated key agreement for large-scale wireless networks. IEEE Trans. Wirel. Commun. 2010, 9, 3346–3353. [Google Scholar]
- He, D.; Bu, J.; Chan, S.; Chen, C.; Yin, M. Privacy-preserving universal authentication protocol for wireless communications. IEEE Trans. Wirel. Commun. 2011, 10, 431–436. [Google Scholar]
- He, D.; Ma, M.; Zhang, Y.; Chen, C.; Bu, J. A strong user authentication scheme with smart cards for wireless communications. Comput. Commun. 2011, 34, 367–374. [Google Scholar]
- Hsiang, H.-C.; Shih, W.-K. Improvement of the secure dynamic ID based remote user authentication scheme for multi-server environment. Comput. Stand. Interfaces. 2009, 31, 1118–1123. [Google Scholar]
- Kim, Y.; Ren, W.; Jo, J.; Yang, M.; Jiang, Y.; Zheng, J. SFRIC: A secure fast roaming scheme in wireless LAN using ID-based cryptography. Proceedings of the IEEE International Conference on Communications (ICC '07), Glasgow, UK, 24–28 June 2007; pp. 1570–1575.
- Liao, Y.-P.; Wang, S.-S. A secure dynamic ID based remote user authentication scheme for multi-server environment. Comput. Stand. Interfaces. 2009, 31, 24–29. [Google Scholar]
- Yang, G. Comments on “An anonymous and self-verified mobile authentication with authenticated key agreement for large-scale wireless networks”. IEEE Trans. Wirel. Commun. 2011, 10, 2015–2016. [Google Scholar]
- Yang, G.; Huang, Q.; Wong, D.S.; Deng, X. Universal authentication protocols for anonymous wireless communications. IEEE Trans. Wirel. Commun. 2010, 9, 168–174. [Google Scholar]
- Munir, S.; Ren, B.; Jiao, W.; Wang, B.; Xie, D.; Ma, J. Mobile Wireless sensor Network: Architecture and Enabling Technologies for Ubiquitious Computing. Proceedings of the 21st International Conference on Advanced Information Networking and Applications Workshops (AINAW'07), Ontario, Canada, 21–23 May 2007; pp. 113–120.
- He, D.; Bu, J.; Chan, S.; Chen, C. Secure and efficient handover authentication based on bilinear pairing functions. IEEE Trans. Wirel. Commun. 2012, 11, 48–53. [Google Scholar]
- He, D.; Chen, C.; Chan, S.; Bu, J. Analysis and Improvement of a Secure and Efficient Handover Authentication for Wireless Networks. IEEE Commun. Lett. 2012, 16, 1270–1273. [Google Scholar]
- Yeo, S.; Yap, W.-S.; Liu, J.; Henricksen, M. Comments on “ Analysis and improvement of a secure and efficient handover authentication based on bilinear pairing functions”. IEEE Commun. Lett. 2013, 17, 1521–1523. [Google Scholar]
- Tsai, J.; Lo, N.; Wu, T. Secure handover authentication protocol based on bilinear Pairings. Wirel. Pers. Commun. 2013, 73, 1037–1047. [Google Scholar]
- Bellare, M.; Rogaway, P. Entity authentication and key distribution. In Advances in Cryptology—CRYPTO'93; Springer: Berlin/Heidelberg, Germany, 1993; pp. 232–249. [Google Scholar]
- Bellare, M.; Rogaway, P. Provably-Secure Session Key Distribution: The Three Party Case. Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing (STOC'95), Las Vegas, NV, USA, 29 May–1 June 1995; pp. 57–66.
- Bresson, E.; Chevassut, O.; Pointcheval, D. Provably Authenticated Group Diffie-Hellman Key Exchange-The Dynamic Case. In Advances in Cryptology—ASIACRYPT 2001; Boyd, C., Ed.; Springer: Berlin, Germany, 2001; pp. 290–309. [Google Scholar]
- Pointcheval, D.; Stern, J. Security arguments for digital signatures and blind signatures. J. Crytol. 2000, 13, 361–396. [Google Scholar]
- Shoup, V. Sequences of games: A tool for taming complexity in security proofs. 2004. Available online: http://www.shoup.net/papers/games.pdf (accessed on 26 June 2014). [Google Scholar]
- Gilbert, H. Converting pairing-based cryptosystems from composite-order groups to prime-order groups. In Advances in Cryptology—EUROCRYPT 2010; Gilbert, H. Springer: Berlin, Germany, 2010; pp. 44–61. [Google Scholar]

| He et al. [15] | Tsai et al. [17] | Ours | |
|---|---|---|---|
| The number of private keys | 1 | 1 | 1 |
| The number of Public keys | 1 | 2 | 1 |
| Provably secure | No | Yes | Yes |
| MN Anonymity | Yes | Yes | Yes |
| MN unlinkability | Yes | Yes | Yes |
| MN computational cost | 1Tp + 1Tm + 1Ts | 1Tp + 1Tm | 1Tp + 1Tm |
| The computation time consumption at an MN | ≈ 299.332 ms | ≈ 7.564 ms | ≈ 7.564 ms |
| AP computational cost | 1Tp | 1Tp | 1Tp |
| The length of the transmitted messages | 166 bytes | 78 bytes | 78 bytes |
| Work group | composite order | prime order | prime order |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, W.; Hu, L. A Secure and Efficient Handover Authentication Protocol for Wireless Networks. Sensors 2014, 14, 11379-11394. https://doi.org/10.3390/s140711379
Wang W, Hu L. A Secure and Efficient Handover Authentication Protocol for Wireless Networks. Sensors. 2014; 14(7):11379-11394. https://doi.org/10.3390/s140711379
Chicago/Turabian StyleWang, Weijia, and Lei Hu. 2014. "A Secure and Efficient Handover Authentication Protocol for Wireless Networks" Sensors 14, no. 7: 11379-11394. https://doi.org/10.3390/s140711379
APA StyleWang, W., & Hu, L. (2014). A Secure and Efficient Handover Authentication Protocol for Wireless Networks. Sensors, 14(7), 11379-11394. https://doi.org/10.3390/s140711379




