An Accurate and Generic Testing Approach to Vehicle Stability Parameters Based on GPS and INS
Abstract
:1. Introduction
2. Related Work
3. Objective Fuzzy Logic System and Subtractive Clustering Method
3.1. Objective Fuzzy Logic System


3.2. Fuzzy Logic Subtractive Cluster Approach

- : If x is A1 then
- : If x is A2 then
4. Models of Vehicle Testing
4.1. Dynamical Model of Vehicle
- (1)
- Automobile vertical and pitch motions are ignored;
- (2)
- The dynamic characteristics of the four tires are same;
- (3)
- The influence of air resistance is ignored;
- (4)
- The effect of sprung mass is ignored [37].

4.2. Model of Two-Stage Kalman Filter

4.3. Vehicle Stability Parameters Calculation
4.3.1. Vehicle Heading Angle Calculation
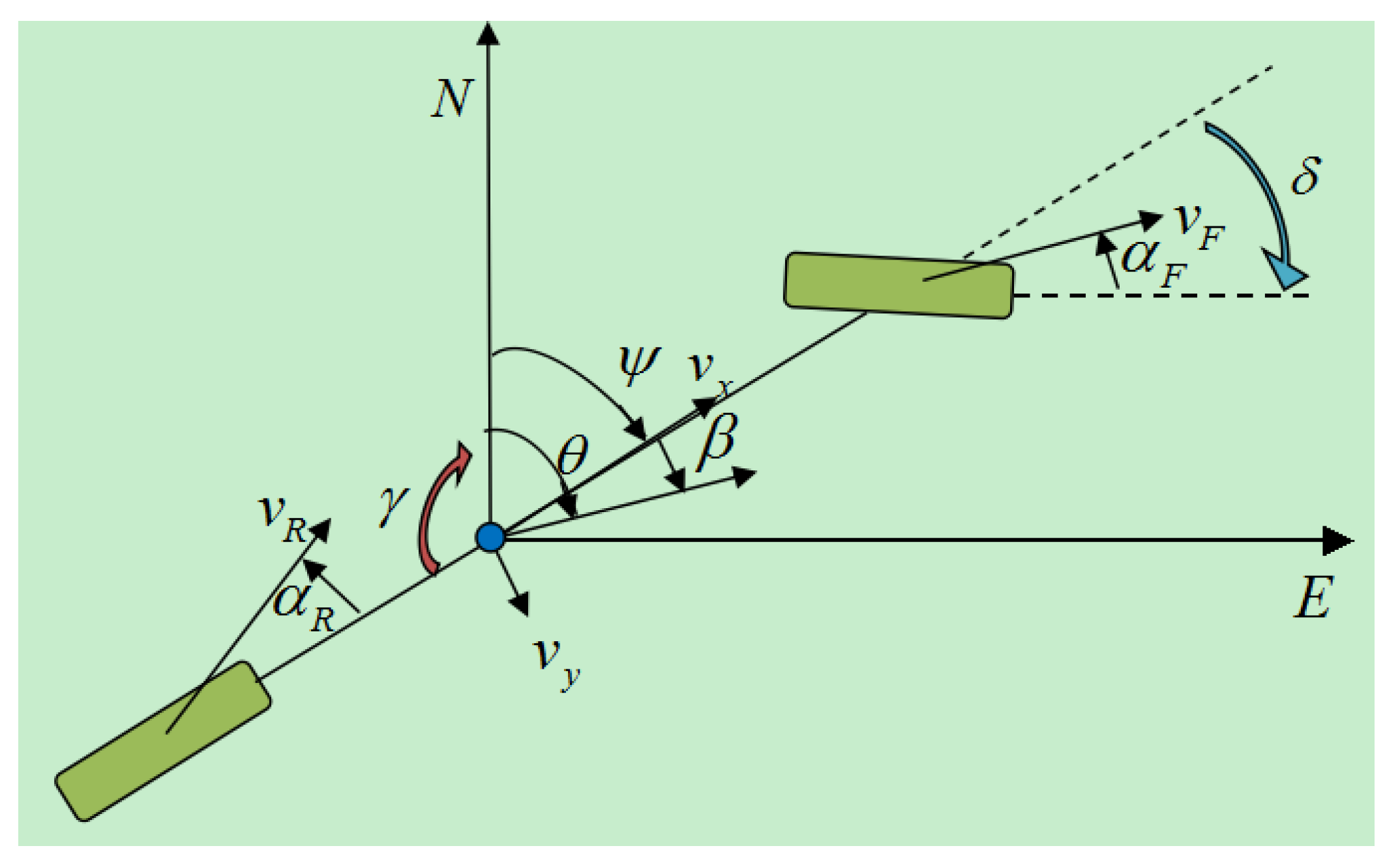
4.3.2. Vehicle Vertical and Horizontal Velocity Calculation
4.3.3. Vehicle Sideslip Angle Calculation
5. Simulation and Application
| Symbols | Meaning | Values | Symbols | Meaning | Values |
|---|---|---|---|---|---|
| Vehicle mass | 1704.7 kg | Front suspension stiffness | 47,298 N·m/Rad | ||
| Suspended mass | 152.6 kg | Rear suspension stiffness | 37,311 N·m/Rad | ||
| Front axle to centroid distance | 1.035 m | Front suspension damp | 2823 (N·m)/(rad/s) | ||
| Distance from centroid to rear axle | 1.655 m | Rear suspension roll damp | 2653 (N·m)/(rad/s) | ||
| Distance between front wheels | 1.535 m | Wheel inertia | 0.99 kg·m2 | ||
| Distance between rear wheels | 1.535 m | Wheel radius | 0.313 m | ||
| Centroid height | 0.542 m | Front wheel cornering stiffness | 55,095 N/rad | ||
| Roll inertia | 744.0 kg·m2 | Rear wheel cornering stiffness | 55,095 N/rad | ||
| Yaw inertia | 3048.1 kg·m2 | Front windward area | 1.8 m2 |
5.1. Simulation






5.2. Experimental Apparatus

| Band | 1.575 GHz |
|---|---|
| Type of Receiver | Carrier phase smoothing function, L1, C/A code. |
| Maximum data update rate | Heading and position are 20 Hz |
| Horizontal positioning accuracy | single machine: <2.5 m (95%, No SA); E-Dif: <1.0 m (95%, 30 min). DGPS: <0.5 m (95%); L-Dif: <0.2 m (95%) |
| Heading accuracy | <0.25° RMS, baseline is 0.5 m; <0.15° RMS, 1.0 m baseline; <0.10° RMS, 2.0 m baseline |
| Pitch/roll | <1° RMS |
| Angular rate | 90°/s (max) |
| Maximum speed | 515 m/s |
| Maximum elevation | 18.288 m |
| Speed and accuracy | 0.05 m/s |
5.3. Measurement Experiment






6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yi, K.S.; Chung, T.Y.; Kim, J.T.; Yi, S.J. An Investigation into Differential Braking Strategies for Vehicle Stability Vontrol. J. Automob. Eng. 2003, 217, 1081–1093. [Google Scholar] [CrossRef]
- Sugiyama, M.; Inoue, H.; Uchida, K.; Monzaki, S.; Inagaki, S.; Kido, S. Development of VSC (Vehicle Stability Control) System. TOYOTA Tech. Rev. 1997, 2, 61–68. [Google Scholar]
- Bauer, P.; Vanek, B.; Peni, T.; Zsedrovits, T.; Pencz, B.; Zarandy, A.; Bokor, J. Aircraft Trajectory Tracking with Large Sideslip Angles for Sense and Avoid Intruder State Estimation. In Proceedings of the 22nd Mediterranean Conference on Control and Automation (MED 2014), Palermo, Italy, 18 November 2014; pp. 1287–1292.
- Boada, B.L.; Boada, M.J.L.; Gauchía, A.; Olmeda, E.; Díaz, V. Sideslip angle estimator based on ANFIS for vehicle handling and stability. J. Mech. Sci. Tech. 2015, 29, 1473–1481. [Google Scholar] [CrossRef]
- Baffet, G.; Charara, A.; Lechner, D.; Thomas, D. Experimental Evaluation of Tire-Road Forces and Sideslip Angle Observers. In Proceedings of the 2007 9th European Control Conference (ECC 2007), Kos, Greece, 25 March 2015; pp. 625–631.
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Pennycott, A. Comparison of feedback control techniques for torque-vectoring control of fully electric vehicles. IEEE Trans. Veh. Tech. 2014, 63, 3612–3623. [Google Scholar] [CrossRef]
- Chadli, M.; Elhajjaji, A. Moment robust output controller to improve vehicle stability. In Proceedings of the 2009 10th European Control Conference (ECC 2009), Budapest, Hungary, 26 March 2015; pp. 4792–4797.
- Caroux, J.; Lamy, C.; Basset, M.; Gissinger, G.-L. Sideslip Angle Measurement, Experimental Characterization and Evaluation of Three Different Principles. In Proceedings of the 6th IFAC Symposium on Intelligent Autonomous Vehicles (IAV2007), Toulouse, France, 3–5 September 2007; pp. 505–510.
- Miao, Z.; Zhang, H.; Zhang, J.; Geng, R. Fuzz Interpolation in GPS/INS Data Fusion. In Proceedings of the 2010 IEEE International Conference on Information and Automation (ICIA 2010), Harbin, China, 20–23 June 2010; pp. 1587–1592.
- Baffet, G.; Charara, A.; Lechner, D. Experimental evaluation of a sliding mode observer for tire-road forces and an extended Kalman filter for vehicle sideslip angle. In Proceedings of the 46th IEEE Conference on Decision and Control 2007 (CDC), New Orleans, LA, USA, 12–14 December 2007; pp. 3877–3882.
- Khodabandeh, A.; Teunissen, P.J.G. Array-based satellite phase bias sensing: Theory and GPS/BeiDou/QZSS results. Meas. Sci. Tech. 2014, 25, 634–649. [Google Scholar] [CrossRef]
- Odolinski, R.; Odijk, D.; Teunissen, P.J.G. Combined GPS and BeiDou Instantaneous RTK Positioning. Navig. J. Inst. Navig. 2014, 61, 135–148. [Google Scholar] [CrossRef]
- Leung, K.T.; Whidborne, J.; Purdy, D.; Dunoyer, A. Ideal Vehicle Sideslip Estimation Using Consumer Grade GPS and INS; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Matsui, T.; Suganuma, N.; Fujiwara, N. Measurement of vehicle sideslip angle using stereovision. Trans. Jap. Soc. Mech. Eng. Part. C 2005, 71, 3202–3207. [Google Scholar] [CrossRef]
- Ding, Q.; Peng, Z.; Liu, T.; Tong, Q. Multi-sensor building fire alarm system with information fusion technology based on D-S evidence theory. Algorithms 2014, 7, 523–537. [Google Scholar] [CrossRef]
- Chen, H.; Gao, B.; Xu, F. Review on vehicle sideslip angle estimation. J. Mech. Eng. 2013, 49, 76–94. [Google Scholar] [CrossRef]
- Miao, Z.; Zhang, H. Data fusion modeling for an RT3102 and dewetron system application in hybrid vehicle stability testing. Algorithms 2015, 8, 632–644. [Google Scholar] [CrossRef]
- You, S.-H.; Hahn, J.-O.; Lee, H. New adaptive approaches to real-time estimation of vehicle sideslip angle. Control Eng. Pract. 2009, 17, 1367–1379. [Google Scholar] [CrossRef]
- Solmaz, S.; Corless, M.; Shorten, R. A methodology for the design of robust 0rollover prevention controllers for automotive vehicles with Active steering. Int. J. Control 2007, 11, 1763–1779. [Google Scholar] [CrossRef]
- Jun, L. Research and Simulation of Vehicle Stability Control Strategy. Master’s Thesis, Wuhan University of Science and Technology, Wuhan, China, 2006. [Google Scholar]
- Yang, F.; Li, Y.; Ku, H.; Rong, X.; Song, R. Attached to real-time estimation of coefficient of extended state observer based on the pavement. J. Agric. Mach. 2010, 8, 6–9. [Google Scholar]
- Huang, D.Y.; Chen, C.H.; Hu, W.C.; Yi, S.C.; Lin, Y.F. Feature-based vehicle flow analysis and measurement for a real-time traffic surveillance system. J. Inf. Hiding Multimedia Signal Process. 2012, 3, 282–296. [Google Scholar]
- Pan, J.S.; Ma, S.; Chen, S.H.; Yang, C.S. Vision-based vehicle forward collision warning system using optical flow algorithm. J. Inf. Hiding Multimedia Signal Process. 2015, 6, 1029–1042. [Google Scholar]
- Yu, C.-C.; Liu, T. Full control modes of a four-wheeled vehicle with zero body-sideslip angle and zero body motions. Int. J. Veh. Des. 2005, 38, 79–95. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J. In Robust Sideslip Angle Estimation for Lightweight Vehicles Using Smooth Variable Structure Filter. In Proceedings of the ASME 2013 Dynamic Systems and Control Conference (DSCC 2013), Palo Alto, CA, USA, 21–23 October 2013.
- Sicard, N.; Aryadinata, Y.S.; Lopez, F.D.R.; Laurent, A.; Flores, P.M.Q. Multi-core parallel gradual pattern mining based on multi-precision fuzzy orderings. Algorithms 2013, 6, 747–761. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H. Vehicle stability control system based on direct measurement of body sideslip angle. In Proceedings of the 2009 2nd Conference on Power Electronics and Intelligent Transportation System (PEITS 2009), Shenzhen, China, 19–20 December 2009; pp. 365–368.
- Kirstin, L. Validating GPS Based Measurements for Vehicle Control. In Proceedings of the ASME Dynamic Systems and Control Division, Orlando, OL, USA, 5 November 2005; pp. 583–592.
- Shuai, Z.; Zhang, H.; Wang, J.; Li, J.; Ouyang, M. Combined AFS and DYC control of four-wheel-independent-drive electric vehicles over CAN Network with time-varying delays. IEEE Trans. Veh. Tech. 2014, 63, 591–602. [Google Scholar] [CrossRef]
- Goggia, T.; Sorniotti, A.; de Novellis, L.; Ferrara, A.; Gruber, P.; Theunissen, J.; Steenbeke, D.; Knauder, B.; Zehetner, J. Integral sliding mode for the torque-vectoring control of fully electric vehicles: Theoretical design and experimental assessment. IEEE Trans. Veh. Tech. 2015, 64, 1701–1715. [Google Scholar] [CrossRef]
- Nguyen, B.M.; Wang, Y.; Fujimoto, H.; Hori, Y. Electric vehicle stability control based on disturbance accommodating Kalman filter using GPS. In Proceedings of the 2013 IEEE International Conference on Mechatronics (ICM 2013), Vicenza, Italy, 23 July 2013; pp. 382–387.
- Hahn, J.O.; Rajamani, R.; Alexander, L. GPS-based real-time identification of tire-road friction coefficient. IEEE Trans. Control. Syst. Tech. 2002, 10, 331–343. [Google Scholar] [CrossRef]
- Bevly, D.M.; Ryu, J.; Gerdes, J.C. Integrating INS sensors with GPS measurements for continuous estimation of vehicle sideslip, roll, and tire cornering stiffness. IEEE Trans. Intell. Transp. Syst. 2006, 7, 483–493. [Google Scholar] [CrossRef]
- Ryu, J.; Nardi, F.; Moshchuk, N. Vehicle sideslip angle estimation and experimental validation. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, (IMECE 2013), San Diego, CA, USA, 15–21 November 2013.
- Miao, Z.; Zhang, H.; Zhang, J.; Geng, R. A fuzz application in GPS/INS navigation. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Shanxi, China, 22–24 October 2010; pp. V8609–V8613.
- Xie, S.; Wei, L. Nonlinear estimation of vehicle sideslip angle based on RLS. Zhongguo Jixie Gongcheng 2014, 25, 278–283. [Google Scholar]
- Gao, B.; Chen, H.; Chen, W.; Xu, F. Fusion estimation of vehicle sideslip angle. Autom. Eng. 2013, 35, 716–722. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Z.; Zhang, H.; Zhang, J. An Accurate and Generic Testing Approach to Vehicle Stability Parameters Based on GPS and INS. Sensors 2015, 15, 30469-30486. https://doi.org/10.3390/s151229812
Miao Z, Zhang H, Zhang J. An Accurate and Generic Testing Approach to Vehicle Stability Parameters Based on GPS and INS. Sensors. 2015; 15(12):30469-30486. https://doi.org/10.3390/s151229812
Chicago/Turabian StyleMiao, Zhibin, Hongtian Zhang, and Jinzhu Zhang. 2015. "An Accurate and Generic Testing Approach to Vehicle Stability Parameters Based on GPS and INS" Sensors 15, no. 12: 30469-30486. https://doi.org/10.3390/s151229812
APA StyleMiao, Z., Zhang, H., & Zhang, J. (2015). An Accurate and Generic Testing Approach to Vehicle Stability Parameters Based on GPS and INS. Sensors, 15(12), 30469-30486. https://doi.org/10.3390/s151229812





