An Integrated Instrumentation System for Velocity, Concentration and Mass Flow Rate Measurement of Solid Particles Based on Electrostatic and Capacitance Sensors
Abstract
:1. Introduction
2. Measurement Principle
2.1. Particle Velocity Measurement Based on Electrostatic Sensors
2.2. Particle Concentration Measurement with Capacitance Sensor
3. Design of the Integrated Instrumentation System
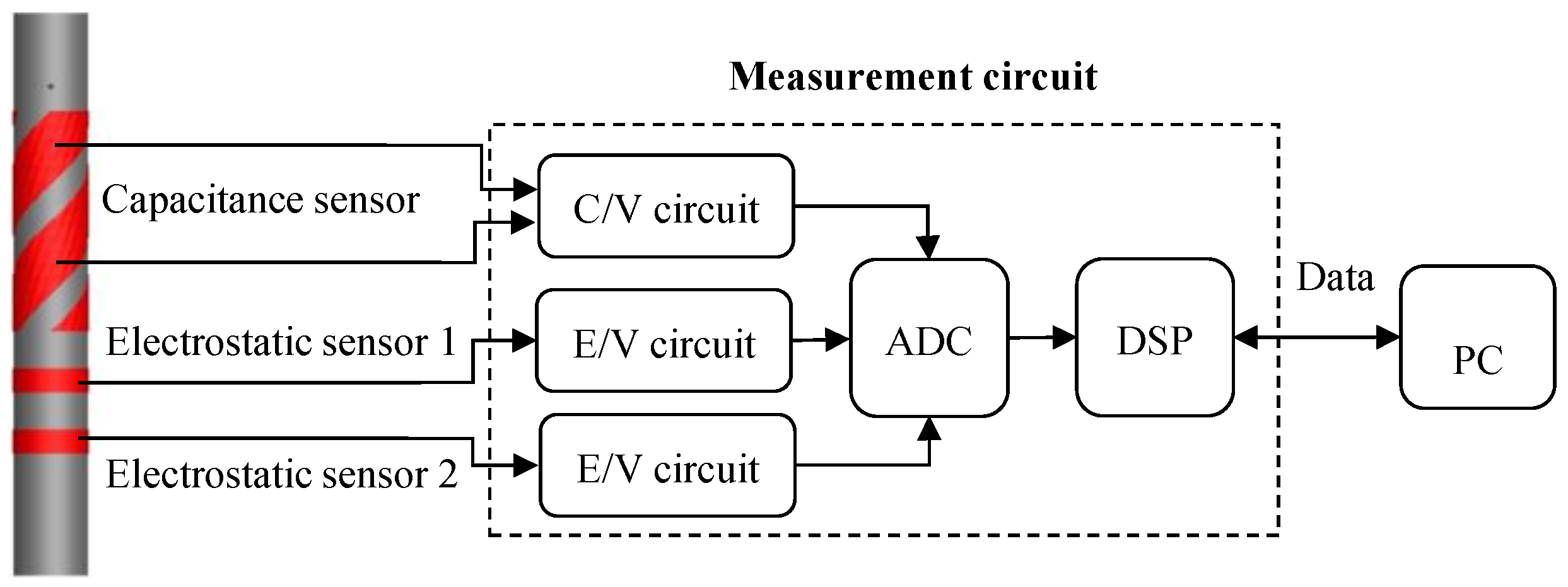




4. Experimental Results and Discussion
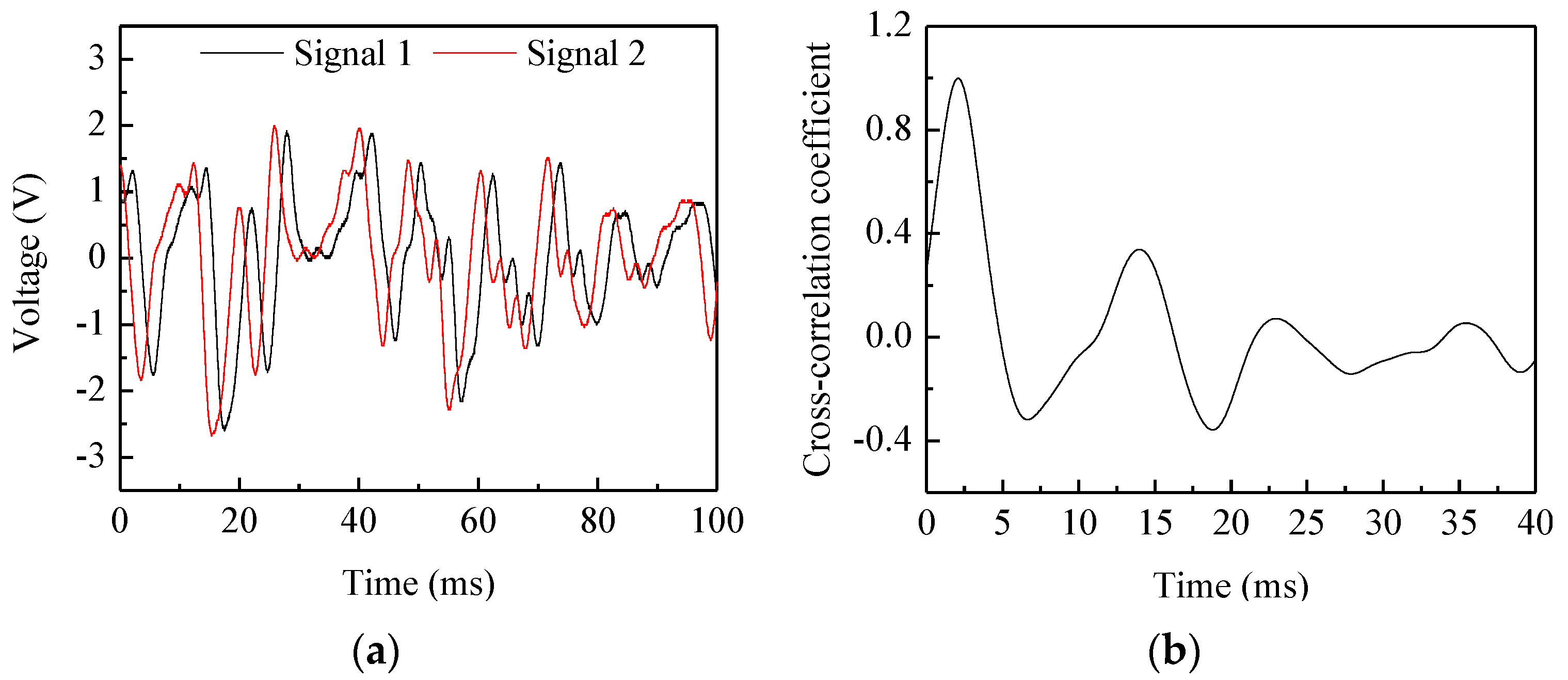
4.1. Tests on a Pulley Rig

| Type | b | h | Area | Volume Fraction |
|---|---|---|---|---|
| #1 | 8 mm | 5 mm | 43.9 mm2 | 2.23% |
| #2 | 13 mm | 8 mm | 80.7 mm2 | 4.11% |
| #3 | 17 mm | 11 mm | 143.0 mm2 | 7.28% |




4.2. Calibration of the Capacitance Sensor


4.3. Measurements on a Gravity-Fed Rig




5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zheng, Y.; Liu, Q. Review of techniques for the mass flow rate measurement of pneumatically conveyed solids. Measurement 2011, 44, 589–604. [Google Scholar] [CrossRef]
- Cai, X.; Li, J.; Ouyang, X.; Zhao, Z.; Su, M. In-line measurement of pneumatically conveyed particles by a light transmission fluctuation method. Flow Meas. Instrum. 2005, 16, 315–320. [Google Scholar] [CrossRef]
- Nieuwland, J.J.; Meijer, R.; Kuipers, J.A.M.; van Swaaij, W.P.M. Measurements of solids concentration and axial solids velocity in gas-solid two-phase flows. Powder Technol. 1996, 87, 127–139. [Google Scholar] [CrossRef]
- Song, D.; Peng, L.; Lu, G.; Yang, S.; Yan, Y. Velocity measurement of pneumatically conveyed particles through digital imaging. Sens. Actuators A Phys. 2009, 149, 180–188. [Google Scholar] [CrossRef]
- Carter, R.M.; Yan, Y. An instrumentation system using combined sensing strategies for online mass flow rate measurement and particle sizing. IEEE Trans. Instrum. Meas. 2005, 54, 1433–1437. [Google Scholar] [CrossRef]
- Albion, K.; Briens, L.; Briens, C.; Berruti, F. Flow regime determination in horizontal pneumatic transport of fine powders using non-intrusive acoustic probes. Powd. Technol. 2007, 172, 157–166. [Google Scholar] [CrossRef]
- Tallon, S.; Davis, C.E. Use of the attenuation of acoustic pulsed waves for concentration measurement in gas-solid pipe flow. AIChE Symp. Ser. 1997, 93, 136–140. [Google Scholar]
- Barratt, I.R.; Yan, Y.; Byrne, B. A parallel-beam radiometric instrumentation system for the mass flow measurement of pneumatically conveyed solids. Meas. Sci. Technol. 2001, 12, 1515–1528. [Google Scholar] [CrossRef]
- Tajdari, T.; Rahmat, M.F. Review of Electrostatic Sensor Applications. J. Teknol. 2014, 70, 7–12. [Google Scholar] [CrossRef]
- Yan, Y.; Byrne, B.; Woodhead, S.; Coulthard, J. Velocity measurement of pneumatically conveyed solids using electrodynamic sensors. Meas. Sci. Technol. 1995, 6, 515–537. [Google Scholar] [CrossRef]
- Gajewski, J.B. Electrostatic nonintrusive method for measuring the electric charge, mass flow rate, and velocity of particulates in the two-phase gas–solid pipe flows—its only or as many as 50 years of historical evolution. IEEE Trans. Ind. Appl. 2008, 44, 1418–1430. [Google Scholar] [CrossRef]
- Qian, X.; Huang, X.; Hu, Y.; Yan, Y. Pulverized coal flow metering on a full-scale power plant using electrostatic sensor arrays. Flow Meas. Instrum. 2014, 40, 185–191. [Google Scholar] [CrossRef]
- Li, J.; Fu, F.; Li, S.; Xu, C.; Wang, S. Velocity characterization of dense phase pneumatically conveyed solid particles in horizontal pipeline through an integrated electrostatic sensor. Int. J. Multiph. Flow 2015, 76, 198–211. [Google Scholar] [CrossRef]
- Yang, W.Q.; Beck, M.S. An intelligent cross correlator for pipeline flow velocity measurement. Flow Meas. Instrum. 1998, 8, 77–84. [Google Scholar] [CrossRef]
- Zhang, J.; Coulthard, J. Theoretical and experimental studies of the spatial sensitivity of an electrostatic pulverised fuel meter. J. Electrost. 2005, 63, 1133–1149. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Li, J.; Wang, S. A spatial filtering velocimeter for solid particle velocity measurement based on linear electrostatic sensor array. Flow Meas. Instrum. 2012, 26, 68–78. [Google Scholar] [CrossRef]
- Li, J.; Xu, C.; Wang, S. Spatial filtering characteristics of electrostatic sensor matrix for local velocity measurement of pneumatically conveyed particles. Measurement 2014, 53, 194–205. [Google Scholar] [CrossRef]
- Elkow, K.J.; Rezkallah, K.S. Void fraction measurements in gas-liquid flows under 1-g and μ-g conditions using capacitance sensors. Int. J. Multiph. Flow 1997, 23, 815–829. [Google Scholar] [CrossRef]
- Hu, H.; Xu, T.; Hui, S.; Zhou, Q. A novel capacitive system for the concentration measurement of pneumatically conveyed pulverized fuel at power stations. Flow Meas. Instrum. 2006, 17, 87–92. [Google Scholar] [CrossRef]
- Yang, W.Q.; Liu, S. Role of tomography in gas/solids flow measurement. Flow Meas. Instrum. 2000, 11, 237–244. [Google Scholar] [CrossRef]
- Arko, A.; Waterfall, R.C.; Beck, M.S.; Dyakowski, T.; Sutcliffe, P.; Byars, M. Development of Electrical Capacitance Tomography for Solids Mass Flow Measurement and Control of Pneumatic Conveying Systems. In Proceedings of the 1st World Congress on Industrial Process Tomography, Buxton, Greater Manchester, UK, 14–17 April 1999; pp. 140–146.
- Zhang, W.; Wang, C.; Wang, Y. Parameter selection in cross-correlation-based velocimetry using circular electrostatic sensors. IEEE Trans. Instrum. Meas. 2010, 59, 1268–1275. [Google Scholar] [CrossRef]
- Xu, L.A. Cross-Correlation Flow Measurement Technique; Tianjin University Publishing House: Tianjin, China, 1988. [Google Scholar]
- Jaworek, A.; Krupa, A.; Trela, M. Capacitance sensor for void fraction measurement in water/steam flows. Flow Meas. Instrum. 2004, 15, 317–324. [Google Scholar] [CrossRef]
- Li, H.; Yang, D.; Cheng, M. Sensitivity analysis of capacitance sensor with helical shaped surface plates. CIESC J. 2011, 62, 2292–2297. [Google Scholar]
- Abouelwafa, M.S.A.; Kendall, E.J.M. The use of capacitance sensors for phase percentage determination in multiphase pipelines. IEEE Trans. Instrum. Meas. 1980, 29, 24–27. [Google Scholar] [CrossRef]
- Tollefsen, J.; Hammer, E.A. Capacitance sensor design for reducing errors in phase concentration measurements. Flow Meas. Instrum. 1998, 9, 25–32. [Google Scholar] [CrossRef]
- Yang, W.Q.; York, T.A. New AC-based capacitance tomography system. IEE Proc. Sci. Meas. Technol. 1999, 146, 47–53. [Google Scholar] [CrossRef]
- Li, J.; Kong, M.; Xu, C.; Wang, S.; Wang, S. Influence of particle electrification on AC-based capacitance measurement and its elimination. Measurement 2015, 76, 93–103. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Kong, M.; Xu, C.; Wang, S.; Fan, Y. An Integrated Instrumentation System for Velocity, Concentration and Mass Flow Rate Measurement of Solid Particles Based on Electrostatic and Capacitance Sensors. Sensors 2015, 15, 31023-31035. https://doi.org/10.3390/s151229843
Li J, Kong M, Xu C, Wang S, Fan Y. An Integrated Instrumentation System for Velocity, Concentration and Mass Flow Rate Measurement of Solid Particles Based on Electrostatic and Capacitance Sensors. Sensors. 2015; 15(12):31023-31035. https://doi.org/10.3390/s151229843
Chicago/Turabian StyleLi, Jian, Ming Kong, Chuanlong Xu, Shimin Wang, and Ying Fan. 2015. "An Integrated Instrumentation System for Velocity, Concentration and Mass Flow Rate Measurement of Solid Particles Based on Electrostatic and Capacitance Sensors" Sensors 15, no. 12: 31023-31035. https://doi.org/10.3390/s151229843
APA StyleLi, J., Kong, M., Xu, C., Wang, S., & Fan, Y. (2015). An Integrated Instrumentation System for Velocity, Concentration and Mass Flow Rate Measurement of Solid Particles Based on Electrostatic and Capacitance Sensors. Sensors, 15(12), 31023-31035. https://doi.org/10.3390/s151229843





