Heat Transfer and Friction Characteristics of the Microfluidic Heat Sink with Variously-Shaped Ribs for Chip Cooling
Abstract
:1. Introduction
2. Problem Description

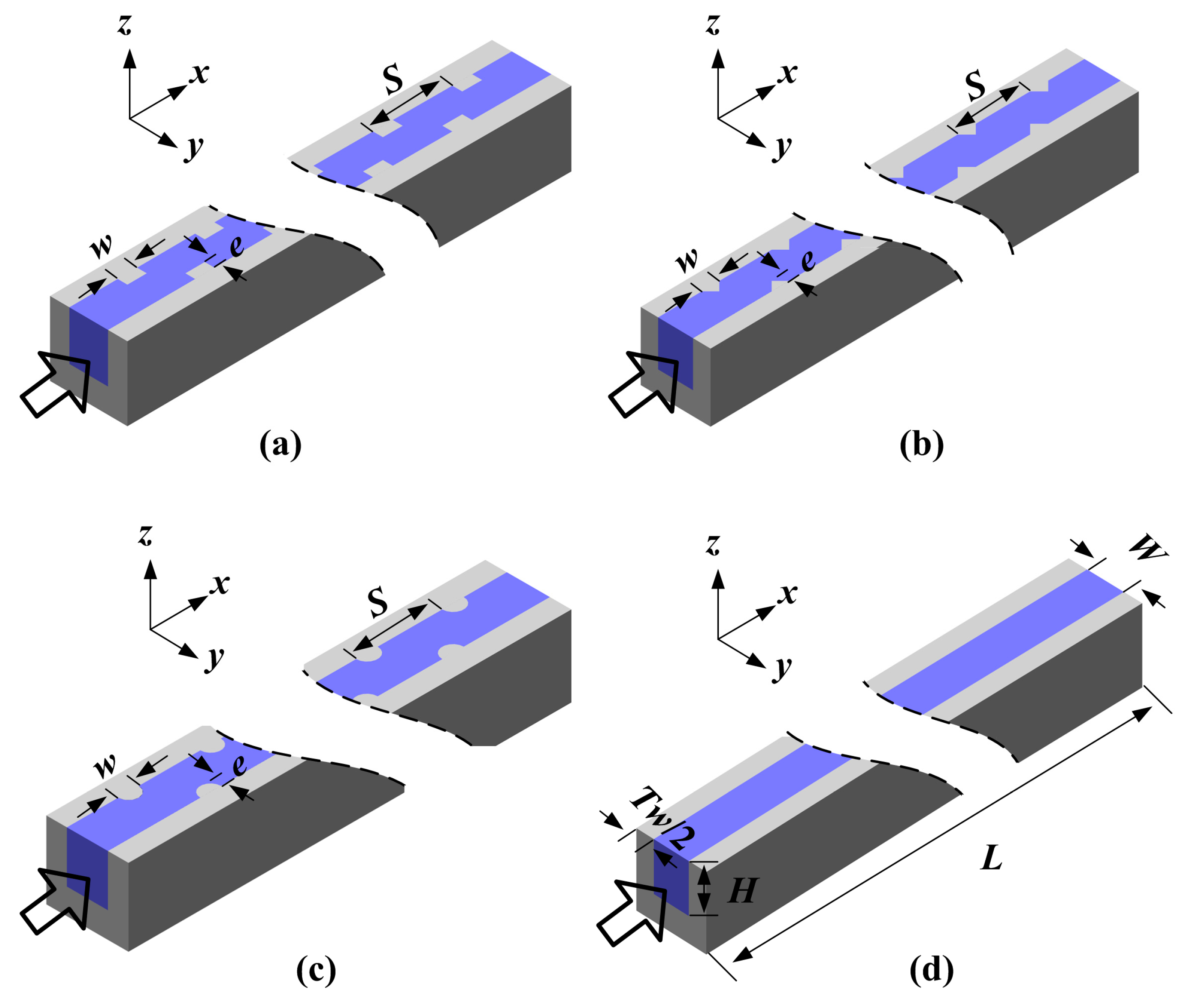
| Characteristic | Values (μm) |
|---|---|
| Channel width W | 425 |
| Channel height H | 500 |
| Channel length L | 10,000 |
| Thickness of the wall tw | 300 |
| Cover height hc | 450 |
| Substrate height hs | 1000 |
| Rib height e | 100 |
| Rib width w | 200 |
| Rib spacing S | 800 |
3. Experimental Work
3.1. Fabrication



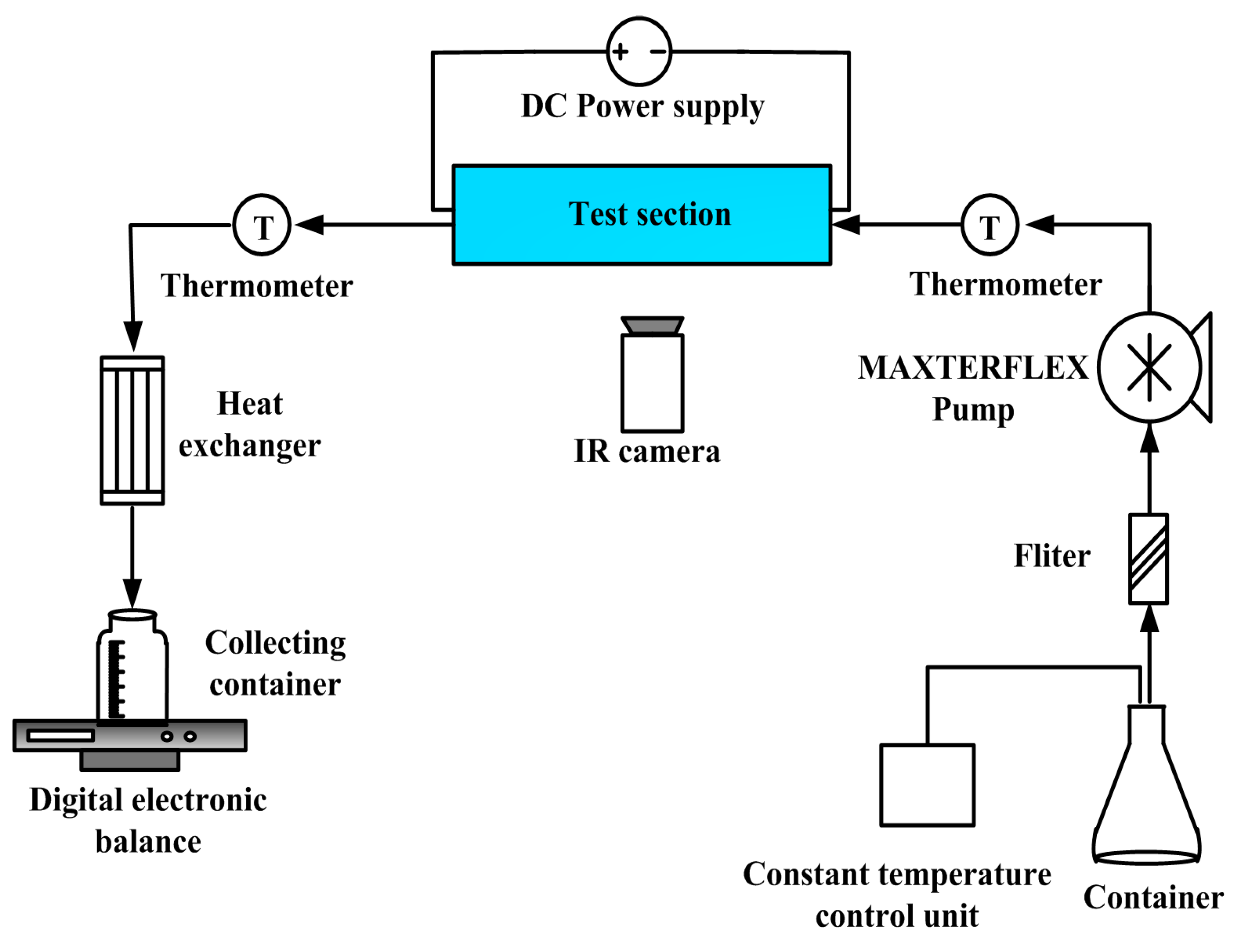
3.2. Experimental Setup
4. Numerical Work
4.1. Computational Domain
4.2. Governing Equations and Boundary Conditions
- (1)
- The fluid flow is steady and incompressible, and laminar flow prevails across the microchannels.
- (2)
- The solid and fluid properties are constant.
- (3)
- The effect of gravity, radiation heat transfer and viscous dissipation are negligible.
4.3. Grid Independence Test
5. Data Reduction
6. Results and Discussion
6.1. Flow Characteristic

6.2. Heat Transfer Characteristic


6.3. Friction Characteristic

6.4. Thermo-Hydraulic Performance

7. Conclusions
- (1)
- The presence of micro-ribs in the microchannels is an effective technique to improve the heat transfer characteristic.
- (2)
- Compared to the smooth microchannel, the rectangular, triangular and semicircular ribs all provide a higher Nusselt number for microchannels, and their maximum enhancement of the average Nusselt number has been found to be 1.65-times, 1.99-times and 1.85-times, respectively.
- (3)
- Due to the barrier effect of ribs, the apparent friction factor for rectangular ribbed microchannel, triangular ribbed microchannel and semicircular ribbed microchannel increases by 0.96~4.28-times, 0.63~6.67-times and 0.76~3.99-times, respectively.
- (4)
- For Re > 600, the thermo-hydraulic performance of ribbed microchannels is not better than that of the conventional smooth microchannel. Therefore, the ribbed microchannels are suitable for the operating condition of Re < 600.
Nomenclature
| A | area, m2 |
| Cp | specific heat, J·kg−1·K−1 |
| Dh | hydrodynamic diameter, m |
| e | rib height, m |
| f | frictional factor |
| H | the height of a microchannel, m |
| h | heat transfer coefficient, W·m−2·K−1 |
| L | the length of a microchannel, m |
| ṁ | mass flow rate, kg·s−1 |
| Nu | Nusselt number |
| P | pumping power, W |
| p | pressure, Pa |
| Q | total heat transfer, W |
| q | heat flux, W·m−2 |
| ΔT | temperature difference, K |
| T | temperature, K |
| t | thickness, m |
| S | pitch of the rib, m |
| u | velocity, m·s−1 |
| ū | mean flow velocity, m·s−1 |
| V | volumetric flow rate, m3·s−1 |
| W | the width of a microchannel, m |
| w | width, m |
Greek symbols
| μ | dynamic viscosity, Pa·s |
| ρ | density, kg·m−3 |
| λ | thermal conductivity, W·m−1·K−1 |
Subscripts
| c | cover |
| cr | cross |
| ch | channel |
| f | fluid |
| in | inlet |
| out | outlet |
| s | substrate |
| w | wall |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tuckerman, D.B.; Pease, R.F.W. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, EDL-2, 126–129. [Google Scholar]
- Yi, P.; Kayani, A.A.; Chrimes, A.F.; Ghorbani, K.; Nahavandi, S.; Kalantar-zadeh, K.; Khoshmanesh, K. Thermal analysis of nanofluids in microfluidics using an infrared camera. Lab Chip 2012, 12, 2520–2525. [Google Scholar] [CrossRef] [PubMed]
- Yi, P.; Khoshmanesh, K.; Chrimes, A.F.; Campbell, J.L.; Ghorbani, K.; Nahavandi, S.; Rosengarten, G.; Kalantar-zadeh, K. Dynamic Nanofin Heat Sinks. Adv. Energy Mater. 2014, 4. [Google Scholar] [CrossRef]
- Yi, P.; Khoshmanesh, K.; Campbell, J.L.; Coughlan, P.; Ghorbani, K.; Kalantar-zadeh, K. Investigation of different nanoparticles for magnetophoretically enabled nanofin heat sinks in microfluidics. Lab Chip 2014, 14, 1604–1613. [Google Scholar] [CrossRef] [PubMed]
- Wee, H.; Zhang, Q.; Ligrani, P.M.; Narasimhan, S. Numerical predictions of heat transfer and flow characteristics of heat sinks with ribbed and dimpled surfaces in laminar flow. Numer. Heat Transf. Part A Appl. 2008, 53, 1156–1175. [Google Scholar] [CrossRef]
- Desrues, T.; Marty, P.; Fourmigué, J. Numerical prediction of heat transfer and pressure drop in three-dimensional channels with alternated opposed ribs. Appl. Therm. Eng. 2012, 45, 52–63. [Google Scholar] [CrossRef]
- Cheng, Y. Numerical simulation of stacked microchannel heat sink with mixing-enhanced passive structure. Int. Commun. Heat Mass Transf. 2007, 34, 295–303. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.D.; Zhou, M.Z.; Li, J.; Qi, J.Z. Optimum thermal design of interrupted microchannel heat sink with rectangular ribs in the transverse microchambers. Appl. Therm. Eng. 2013, 51, 880–889. [Google Scholar] [CrossRef]
- Ann, J.; Choi, H.; Lee, J.S. Large eddy simulation of flow and heat transfer in a channel roughened by square or semicircle ribs. Trans. ASME J. Turbomach. 2005, 127, 263–269. [Google Scholar]
- Kamali, R.; Binesh, A.R. The importance of rib shape effects on the local heat transfer and flow friction characteristics of square ducts with ribbed internal surfaces. Int. Commun. Heat Mass Transf. 2008, 35, 1032–1040. [Google Scholar] [CrossRef]
- Zhang, C.B.; Chen, Y.P.; Shi, M.H. Effects of roughness elements on laminar flow and heat transfer in microchannels. Chem. Eng. Process. 2010, 49, 1188–1192. [Google Scholar] [CrossRef]
- Kandlikar, S.; Garimella, S.; Li, D.; Colin, S.; King, M.R. Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Amsterdam, the Netherlands, 2005. [Google Scholar]
- Incropera, F.; DeWitt, D. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Bucci, A.; Celata, G.P.; Cumo, M.; Serra, E.; Zummo, G. Water single-phase fluid flow and heat transfer in capillary tubes. In Proceedings of the ASME 2003 1st International Conference on Microchannels and Minichannels, New York, NY, USA, 24–25 April 2003; pp. 319–326.
- Park, J.S.; Han, J.C.; Huang, Y.; Ou, S.; Boyle, R.J. Heat transfer performance comparisons of five different rectangular channels with parallel angled ribs. Int. J. Heat Mass Transf. 1992, 35, 2891–2903. [Google Scholar] [CrossRef]
- Kleiner, M.B.; Kuhn, S.A.; Haberger, K. High performance forced air cooling scheme employing microchannel heat exchangers. IEEE Trans. Compon. Packag. Manuf. Technol. Part A 1995, 18, 795–804. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements; University Science Books: Sausalito, CA, USA, 1996. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.-L.; Yang, D.-W.; Wang, Y.; Niu, D.; Zhao, X.-L.; Ding, G.-F. Heat Transfer and Friction Characteristics of the Microfluidic Heat Sink with Variously-Shaped Ribs for Chip Cooling. Sensors 2015, 15, 9547-9562. https://doi.org/10.3390/s150409547
Wang G-L, Yang D-W, Wang Y, Niu D, Zhao X-L, Ding G-F. Heat Transfer and Friction Characteristics of the Microfluidic Heat Sink with Variously-Shaped Ribs for Chip Cooling. Sensors. 2015; 15(4):9547-9562. https://doi.org/10.3390/s150409547
Chicago/Turabian StyleWang, Gui-Lian, Da-Wei Yang, Yan Wang, Di Niu, Xiao-Lin Zhao, and Gui-Fu Ding. 2015. "Heat Transfer and Friction Characteristics of the Microfluidic Heat Sink with Variously-Shaped Ribs for Chip Cooling" Sensors 15, no. 4: 9547-9562. https://doi.org/10.3390/s150409547
APA StyleWang, G.-L., Yang, D.-W., Wang, Y., Niu, D., Zhao, X.-L., & Ding, G.-F. (2015). Heat Transfer and Friction Characteristics of the Microfluidic Heat Sink with Variously-Shaped Ribs for Chip Cooling. Sensors, 15(4), 9547-9562. https://doi.org/10.3390/s150409547






