Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor
Abstract
:1. Introduction
2. Model Analysis and Simulation
2.1. Kinematical Analogy of Skid-Steering with Differential Drive
- (1)
- the mass center of the robot is located at the geometric center of the body frame;
- (2)
- the two wheels of each side rotate at the same speed;
- (3)
- the robot is running on a firm ground surface, and four wheels are always in contact with the ground surface.
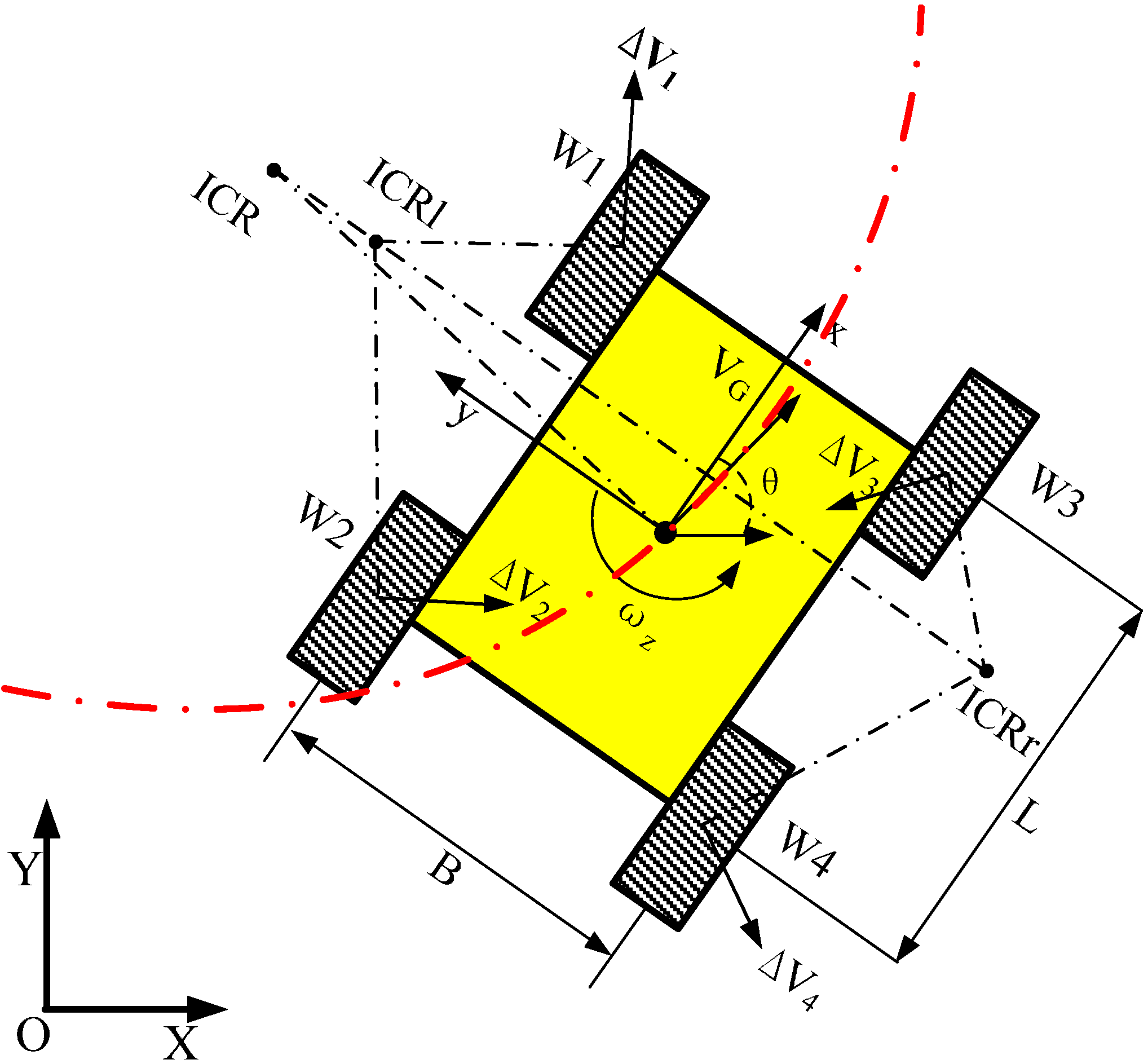

2.2. Dynamic Model for Kinematics Parameters Relationship
2.2.1. Skid-Steering Mobile Robot Dynamic Model


2.2.2. Dynamic Simulation
| Key Parameters | Symbol | Value |
|---|---|---|
| Mass of robot (kg) | m | 31 |
| Width of robot (m) | B | 0.40 |
| Length of robot (m) | L | 0.31 |
| Length of C (m) | C | 0.24 |
| Radius of tire (m) | R | 0.11 |
| Width of wheel (m) | b | 0.05 |
| Shear deformation modulus (m) | 0.00054 | |
| Coefficient of rolling resistance | 0.0371 | |
| Coefficient of friction, of | 0.4437 | |
| Coefficient of friction, of | 0.3093 |

3. Laser-Scanner-Based Experimental Kinematics Method
3.1. Proposed Algorithm
3.2. Laser-Scanner-Based Localization Method and Experiment Setup



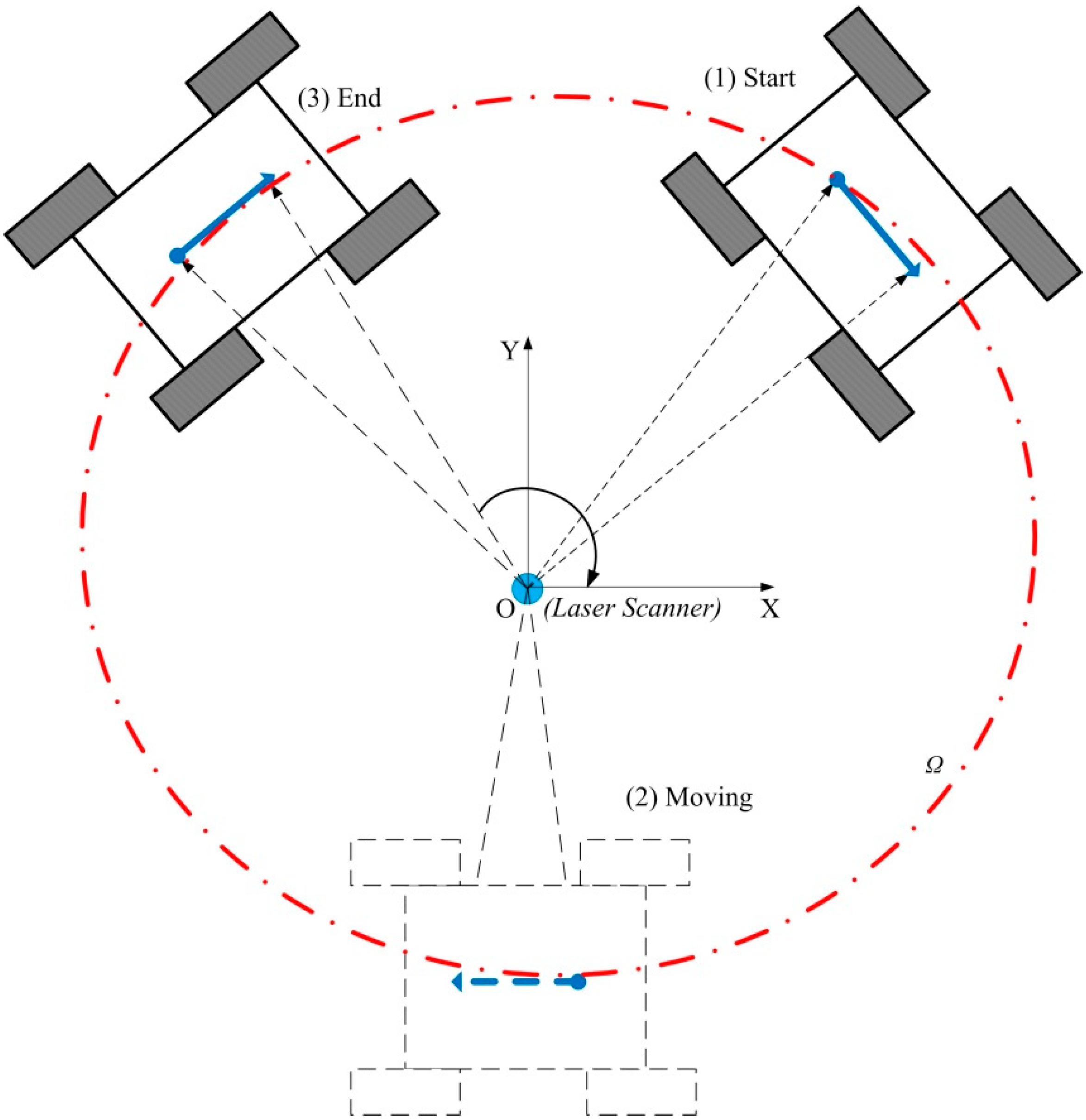
3.3. Errors Analysis
3.4. Results

| Test Parameters | (m) | (m) | Max. Error (m) |
|---|---|---|---|
| Width of the Plate () | 0.2890 | 0.003 | −0.01 |


| Parameters | Max. Relative Error | ||
|---|---|---|---|
| 0 | 1.4662 | 0.0033 | 0.34% |
| 1 | 1.4480 | 0.0065 | 0.59% |
| 2 | 1.4394 | 0.0055 | 0.62% |
| 3 | 1.4341 | 0.0068 | 0.71% |
| 4 | 1.4215 | 0.0080 | −0.92% |
| 5 | 1.4232 | 0.0050 | 0.52% |
| 6 | 1.4165 | 0.0077 | 0.77% |
| 7 | 1.4115 | 0.0043 | 0.30% |

3.5. Dead-Reckoning Validation


| NO. | (m) | (m) | (rad) |
|---|---|---|---|
| P3-AT model | 0.0169 | 0.0101 | 0.0438 |
| Proposed model | 0.0273 | 0.0119 | 0.0778 |

4. Conclusions/Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yi, J.; Wang, H.P.; Zhang, J.; Song, D. Kinematic modeling and analysis of skid-steered mobile robots with applications to low-cost inertial-measurement-unit-based motion estimation. IEEE Trans. Robot. 2009, 25, 1087–1097. [Google Scholar] [CrossRef]
- Mandow, A.; Martinez, J.L.; Morales, J.; Blanco, J.; García-Cerezo, A.J.; Gonzalez, J. Experimental kinematics for wheeled skid-steer mobile robots. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1222–1227.
- Yi, J.; Zhang, J.; Song, D.; Jayasuriya, S. IMU-based localization and slip estimation for skid-steered mobile robots. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 2845–2850.
- Caracciolo, L.; Luca, A.D.; Iannitti, S. Trajectory tracking control of a four-wheel differentially driven mobile robot. In Proceedings of IEEE/RSJ International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 2632–2638.
- Yi, J.; Song, D.; Zhang, J.; Goodwin, Z. Adaptive trajectory tracking control of skid-steered mobile robots. In Proceedings of IEEE/RSJ International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 2605–2610.
- Kozlowski, K.; Pazderski, D. Modeling and control of a 4-wheel skid-steering mobile robot. Int. J. Appl. Math. Comput. Sci. 2004, 14, 477–496. [Google Scholar]
- Martinez, J.L.; Mandow, A.; Morales, J.; Pedraza, S.; García-Cerezo, A.J. Approximating kinematics for tracked mobile robots. Int. J. Robot. Res. 2005, 24, 867–878. [Google Scholar] [CrossRef]
- Yu, W.; Chuy, O.; Collins, E.G.; Hollis, P. Dynamic Modeling of a Skid-Steered Wheeled Vehicle with Experimental Verification. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 4211–4219.
- Yu, W.; Chuy, O.; Collins, E.G.; Hollis, P. Analysis and experimental verification for dynamic modeling of a skid-steered wheeled vehicle. IEEE Trans. Robot. 2010, 26, 340–353. [Google Scholar] [CrossRef]
- Maalouf, E.; Saad, M.; Saliah, H. A higher level path tracking controller for a four-wheel differentially steered mobile robot. Robot. Auton. Syst. 2006, 54, 23–33. [Google Scholar] [CrossRef]
- Kozlowski, K.; Pazderski, D. Practical stabilization of a skid-steering mobile robot—A kinematic-based approach. In Proceedings of IEEE 3rd Conference on Mechatronics, Budapest, Hungary, 3 July 2006; pp. 519–524.
- Le, A.; Rye, D.; Durrant-Whyte, H. Estimation of track-soil interactions for autonomous tracked vehicles. In Proceedings of IEEE/RSJ International Conference on Robotics and Automation, Albuquerque, NM, USA, 10–14 April 1997; pp. 1388–1393.
- Moosavian, S.A.A.; Kalantari, A. Experimental slip estimation for exact kinematics modeling and control of a tracked Mobile Robot. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 95–100.
- Anousaki, G.; Kyriakopoulos, K. A dead-reckoning scheme for skid-steered vehicles in outdoor environments. In Proceedings of IEEE/RSJ International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; pp. 580–585.
- Anousaki, G.; Kyriakopoulos, K. Simultaneous localization and map building of skid-steered robots. IEEE Robot. Autom. Mag. 2007, 14, 79–89. [Google Scholar] [CrossRef]
- Wong, J.; Chiang, C. A general theory for skid steering of tracked vehicles on firm ground. Proceedings of the Institution of Mechanical Engineers. Available online: http://pid.sagepub.com/content/215/3/343.full.pdf (accessed on 23 April 2015).
- Wong, J. Theory of Ground Vehicles, 3rd ed.; Wong, J., Ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 389–418. [Google Scholar]
- Martinez, J.L.; Gonzalez, J.; Morales, J.; Mandow, A.; García-Cerezo, A.J. Mobile robot motion estimation by 2D scan matching with genetic and iterative closest point algorithms. J. Field Robot. 2006, 23, 21–34. [Google Scholar] [CrossRef]
- Duan, Z.; Cai, Z.; Min, H. Robust Dead Reckoning System for Mobile Robots Based on Particle Filter and Raw Range Scan. Sensors 2014, 14, 16532–16562. [Google Scholar] [CrossRef] [PubMed]
- Technical Description: Pioneer P3-AT Mobile Robot. Available online: http://www.mobilerobots.com (accessed on 11 February 2015).
- Technical Description: LMS400 Laser Measurement Sensor. Available online: http://www.sick.com (accessed on 11 February 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Wu, Y.; Liang, J.; Han, C.; Chen, J.; Zhao, Q. Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor. Sensors 2015, 15, 9681-9702. https://doi.org/10.3390/s150509681
Wang T, Wu Y, Liang J, Han C, Chen J, Zhao Q. Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor. Sensors. 2015; 15(5):9681-9702. https://doi.org/10.3390/s150509681
Chicago/Turabian StyleWang, Tianmiao, Yao Wu, Jianhong Liang, Chenhao Han, Jiao Chen, and Qiteng Zhao. 2015. "Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor" Sensors 15, no. 5: 9681-9702. https://doi.org/10.3390/s150509681
APA StyleWang, T., Wu, Y., Liang, J., Han, C., Chen, J., & Zhao, Q. (2015). Analysis and Experimental Kinematics of a Skid-Steering Wheeled Robot Based on a Laser Scanner Sensor. Sensors, 15(5), 9681-9702. https://doi.org/10.3390/s150509681





