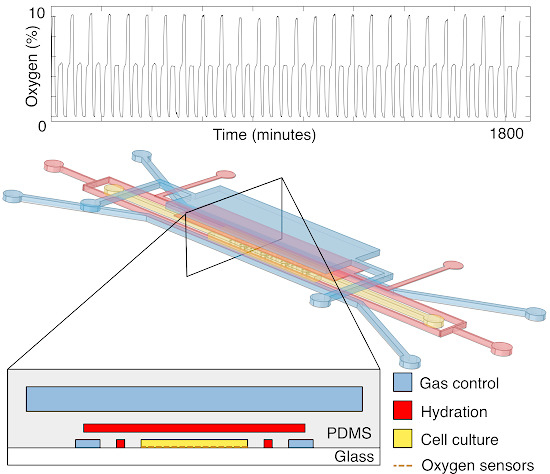
Designing a Microfluidic Device with Integrated Ratiometric Oxygen Sensors for the Long-Term Control and Monitoring of Chronic and Cyclic Hypoxia
Abstract
:1. Introduction
1.1. Importance of Precise Oxygen Control in Hypoxia Studies
1.2. Clinical Relevance of Oxygen Gradients and Cyclic Hypoxia
1.3. Harnessing Small Size Scales: Microfluidic Oxygen Control with Optical Oxygen Sensing
1.3.1. Microfluidic Oxygen Control Devices
1.3.2. Optical Oxygen Sensors
1.3.3. Microfluidic Devices for Cyclic (Transient) Oxygen Profiles
2. Experimental Section
2.1. Fabrication of Optical Oxygen Sensors and Microfluidic Oxygen Control Device
2.1.1. Design of Oxygen Control Device

2.1.2. Fabrication of Oxygen Control Device
2.1.3. Fabrication of Optical Oxygen Sensors and Integration with Microfluidic Oxygen Control Device
2.2. Measurement Setup for Oxygen Sensors
2.3. Calibration of Optical Oxygen Sensors
2.3.1. Sensor Calibration Setup
2.3.2. Image Processing
2.4. Finite-Element Modeling of Oxygen Control Device

2.5. Measurements of Oxygen Equilibration Times, Time-Varying Oxygen Levels and Oxygen Gradients
3. Results and Discussion
3.1. Calibration Results and Sensor Limits of Detection

3.2. Improvement of Ratiometric Oxygen Sensor Stability by Pre-Bleaching and Multiple Calibrations

3.3. Validation of Oxygen Control within the Device Using Finite-Element Modeling

| Q (µL/min) | ū (m/s) | Re | Pe | Ō2 (%) | O2 max (%) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 3.46 × 10−2 | 5.75 × 10−2 |
| 0.5 | 1.10 × 10−4 | 2.97 × 10−5 | 0.150 | 3.41 × 10−2 | 5.10 × 10−2 |
| 1 | 2.19 × 10−4 | 5.94 × 10−5 | 0.301 | 3.46 × 10−2 | 4.90 × 10−2 |
| 3 | 6.57 × 10−4 | 1.78 × 10−4 | 0.903 | 8.96 × 10−2 | 0.503 |
| 5 | 1.10 × 10−3 | 2.97 × 10−4 | 1.50 | 0.382 | 2.12 |
| 10 | 2.19 × 10−3 | 5.94 × 10−4 | 3.01 | 2.01 | 7.33 |
| 15 | 3.29 × 10−3 | 8.91 × 10−4 | 4.51 | 3.86 | 11.2 |
3.4. Oxygen Gradients within the Microfluidic Device

3.5. Oxygen Switching Times and Time-Varying Oxygen Profiles


4. Conclusions/Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Asthana, A.; Kisaalita, W.S. Microtissue size and hypoxia in HTS with 3D cultures. Drug Discov. Today 2012, 17, 810–817. [Google Scholar] [CrossRef] [PubMed]
- Amberger-Murphy, V. Hypoxia helps glioma to fight therapy. Curr. Cancer Drug Targets 2009, 9, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Favaro, E.; Lord, S.; Harris, A.L.; Buffa, F.M. Gene expression and hypoxia in breast cancer. Genome Med. 2011, 3. [Google Scholar] [CrossRef] [PubMed]
- Brizel, D.M.; Sibley, G.S.; Prosnitz, L.R.; Scher, R.L.; Dewhirst, M.W. Tumor hypoxia adversely affects the prognosis of carcinoma of the head and neck. Int. J. Radiat. Oncol. Biol. Phys. 1997, 38, 285–289. [Google Scholar] [CrossRef]
- Evans, S.M.; Judy, K.D.; Dunphy, I.; Jenkins, W.T.; Hwang, W.T.; Nelson, P.T.; Lustig, R.A.; Jenkins, K.; Magarelli, D.P.; Hahn, S.M.; et al. Hypoxia is important in the biology and aggression of human glial brain tumors. Clin. Cancer Res. 2004, 10, 8177–8184. [Google Scholar] [CrossRef] [PubMed]
- Vaupel, P. Hypoxia and aggressive tumor phenotype: Implications for therapy and prognosis. Oncologist 2008, 13, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Chaudary, N.; Hill, R.P. Hypoxia and metastasis in breast cancer. Breast Dis. 2007, 26, 55–64. [Google Scholar]
- Pettersen, E.O.; Ebbesen, P.; Gieling, R.G.; Williams, K.J.; Dubois, L.; Lambin, P.; Ward, C.; Meehan, J.; Kunkler, I.H.; Langdon, S.P.; et al. Targeting tumour hypoxia to prevent cancer metastasis. From biology, biosensing and technology to drug development: The metoxia consortium. J. Enzyme Inhib. Med. Chem. 2014, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Koumenis, C.; Wouters, B.G. “Translating” tumor hypoxia: Unfolded protein response (UPR)-Dependent and UPR-independent pathways. Mol. Cancer Res. 2006, 4, 423–436. [Google Scholar] [CrossRef] [PubMed]
- Nagelkerke, A.; Bussink, J.; Mujcic, H.; Wouters, B.; Lehmann, S.; Sweep, F.; Span, P. Hypoxia stimulates migration of breast cancer cells via the perk/atf4/lamp3-arm of the unfolded protein response. Breast Cancer Res. 2013, 15. [Google Scholar] [CrossRef] [PubMed]
- Gleadle, J.M.; Ratcliffe, P.J. Induction of hypoxia-inducible factor-1, erythropoietin, vascular endothelial growth factor, and glucose transporter-1 by hypoxia: Evidence against a regulatory role for src kinase. Blood 1997, 89, 503–509. [Google Scholar] [PubMed]
- Bellot, G.; Garcia-Medina, R.; Gounon, P.; Chiche, J.; Roux, D.; Pouysségur, J.; Mazure, N.M. Hypoxia-induced autophagy is mediated through hypoxia-inducible factor induction of BNIP3 and BNIP3L via their BH3 domains. Mol. Cell. Biol. 2009, 29, 2570–2581. [Google Scholar] [CrossRef] [PubMed]
- Simon, M.C.; Keith, B. The role of oxygen availability in embryonic development and stem cell function. Nat. Rev. Mol. Cell. Biol. 2008, 9, 285–296. [Google Scholar] [CrossRef] [PubMed]
- Millman, J.R.; Tan, J.H.; Colton, C.K. The effects of low oxygen on self-renewal and differentiation of embryonic stem cells. Curr. Opin. Organ. Transplant. 2009, 14, 694–700. [Google Scholar] [CrossRef] [PubMed]
- Helmlinger, G.; Yuan, F.; Dellian, M.; Jain, R.K. Interstitial ph and po(2) gradients in solid tumors in vivo: High-resolution measurements reveal a lack of correlation. Nat. Med. 1997, 3, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Erickson, K.; Braun, R.A.; Yu, D.H.; Lanzen, J.; Wilson, D.; Brizel, D.M.; Secomb, T.W.; Biaglow, J.E.; Dewhirst, M.W. Effect of longitudinal oxygen gradients on effectiveness of manipulation of tumor oxygenation. Cancer Res. 2003, 63, 4705–4712. [Google Scholar] [PubMed]
- Subarsky, P.; Hill, R. The hypoxic tumour microenvironment and metastatic progression. Clin. Exp. Metastasis 2003, 20, 237–250. [Google Scholar] [CrossRef] [PubMed]
- Graeber, T.G.; Osmanian, C.; Jacks, T.; Housman, D.E.; Koch, C.J.; Lowe, S.W.; Giaccia, A.J. Hypoxia-mediated selection of cells with diminished apoptotic potential in solid tumours. Nature 1996, 379, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Verduzco, D.; Lloyd, M.; Xu, L.; Ibrahim-Hashim, A.; Balagurunathan, Y.; Gatenby, R.A.; Gillies, R.J. Intermittent hypoxia selects for genotypes and phenotypes that increase survival, invasion, and therapy resistance. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Chaplin, D.J.; Olive, P.L.; Durand, R.E. Intermittent blood flow in a murine tumor: Radiobiological effects. Cancer Res. 1987, 47, 597–601. [Google Scholar] [PubMed]
- Cárdenas-Navia, L.; Mace, D.; Richardson, R.; Wilson, D.; Shan, S.; Dewhirst, M. The pervasive presence of fluctuating oxygenation in tumors. Cancer Res. 2008, 68, 5812–5819. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.A.; Chaplin, D.J. Detection of microregional fluctuations in erythrocyte flow using laser doppler microprobes. In Oxygen Transport to Tissue XVII; Ince, C., Kesecioglu, J., Telci, L., Akpir, K., Eds.; Springer US: Istanbul, Turkey, 1996; Volume 388, pp. 367–371. [Google Scholar]
- Cairns, R.A.; Kalliomaki, T.; Hill, R.P. Acute (cyclic) hypoxia enhances spontaneous metastasis of kht murine tumors. Cancer Res. 2001, 61, 8903–8908. [Google Scholar] [PubMed]
- Matsumoto, S.; Yasui, H.; Mitchell, J.B.; Krishna, M.C. Imaging cycling tumor hypoxia. Cancer Res. 2010, 70, 10019–10023. [Google Scholar] [CrossRef] [PubMed]
- Groisman, A.; Adler, M.; Polinkovsky, M.; Gutierrez, E. Generation of oxygen gradients with arbitrary shapes in a microfluidic device. Lab Chip 2010, 10, 388–391. [Google Scholar]
- Lam, R.H.W.; Kim, M.-C.; Thorsen, T. A microfluidic oxygenator for biological cell culture. In Proceedings of the International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 2489–2492.
- Lam, R.H.; Kim, M.C.; Thorsen, T. Culturing aerobic and anaerobic bacteria and mammalian cells with a microfluidic differential oxygenator. Anal. Chem. 2009, 81, 5918–5924. [Google Scholar] [CrossRef] [PubMed]
- Thomas, P.C.; Raghavan, S.R.; Forry, S.P. Regulating oxygen levels in a microfluidic device. Anal. Chem. 2011, 83, 8821–8824. [Google Scholar] [CrossRef] [PubMed]
- Forry, S.P.; Locascio, L.E. On-chip CO2 control for microfluidic cell culture. Lab Chip 2011, 11, 4041–4046. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.A.; King, A.D.; Shih, H.C.; Peng, C.C.; Wu, C.Y.; Liao, W.H.; Tung, Y.C. Generation of oxygen gradients in microfluidic devices for cell culture using spatially confined chemical reactions. Lab Chip 2011, 11, 3626–3633. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, W.; Wang, Y.; Wang, J.C.; Tu, Q.; Liu, R.; Wang, J. Construction of oxygen and chemical concentration gradients in a single microfluidic device for studying tumor cell-drug interactions in a dynamic hypoxia microenvironment. Lab Chip 2013, 13, 695–705. [Google Scholar] [CrossRef] [PubMed]
- Brennan, M.D.; Rexius-Hall, M.L.; Elgass, L.J.; Eddington, D.T. Oxygen control with microfluidics. Lab Chip 2014, 14, 4305–4318. [Google Scholar] [CrossRef] [PubMed]
- Wood, D.K.; Soriano, A.; Mahadevan, L.; Higgins, J.M.; Bhatia, S.N. A biophysical indicator of vaso-occlusive risk in sickle cell disease. Sci. Transl. Med. 2012, 4. [Google Scholar] [CrossRef] [PubMed]
- Grist, S.M.; Chrostowski, L.; Cheung, K.C. Optical oxygen sensors for applications in microfluidic cell culture. Sensors 2010, 10, 9286–9316. [Google Scholar] [CrossRef] [PubMed]
- Mills, A. Optical oxygen sensors. Platin. Metals Rev. 1997, 41, 115–127. [Google Scholar]
- Trettnak, W.; Kolle, C.; Reininger, F.; Dolezal, C.; OLeary, P. Miniaturized luminescence lifetime-based oxygen sensor instrumentation utilizing a phase modulation technique. Sens. Actuators B Chem. 1996, 36, 506–512. [Google Scholar] [CrossRef]
- Liebsch, G.; Klimant, I.; Frank, B.; Holst, G.; Wolfbeis, O.S. Luminescence lifetime imaging of oxygen, pH, and carbon dioxide distribution using optical sensors. Appl. Spectrosc. 2000, 54, 548–559. [Google Scholar] [CrossRef]
- Xu, H.; Aylott, J.W.; Kopelman, R.; Miller, T.J.; Philbert, M.A. A real-time ratiometric method for the determination of molecular oxygen inside living cells using sol-gel-based spherical optical nanosensors with applications to rat c6 glioma. Anal. Chem. 2001, 73, 4124–4133. [Google Scholar] [CrossRef] [PubMed]
- Cywinski, P.J.; Moro, A.J.; Stanca, S.E.; Biskup, C.; Mohr, G.J. Ratiometric porphyrin-based layers and nanoparticles for measuring oxygen in biosamples. Sens. Actuators B Chem. 2009, 135, 472–477. [Google Scholar] [CrossRef]
- Mayr, T.; Borisov, S.M.; Abel, T.; Enko, B.; Waich, K.; Mistlberger, G.; Klimant, I. Light harvesting as a simple and versatile way to enhance brightness of luminescent sensors. Anal. Chem. 2009, 81, 6541–6545. [Google Scholar] [CrossRef]
- Ungerbock, B.; Mistlberger, G.; Charwat, V.; Ertl, P.; Mayr, T. Oxygen imaging in microfluidic devices with optical sensors applying color cameras. Procedia Eng. 2010, 5, 456–459. [Google Scholar] [CrossRef]
- Ungerbock, B.; Charwat, V.; Ertl, P.; Mayr, T. Microfluidic oxygen imaging using integrated optical sensor layers and a color camera. Lab Chip 2013, 13, 1593–1601. [Google Scholar] [CrossRef] [PubMed]
- Ehgartner, J.; Wiltsche, H.; Borisov, S.M.; Mayr, T. Low cost referenced luminescent imaging of oxygen and pH with a 2-CCD colour near infrared camera. Analyst 2014, 139, 4924–4933. [Google Scholar] [CrossRef] [PubMed]
- Groisman, A.; Polinkovsky, M.; Gutierrez, E.; Levchenko, A. Fine temporal control of the medium gas content and acidity and on-chip generation of series of oxygen concentrations for cell cultures. Lab Chip 2009, 9, 1073–1084. [Google Scholar]
- Oppegard, S.C.; Nam, K.H.; Carr, J.R.; Skaalure, S.C.; Eddington, D.T. Modulating temporal and spatial oxygenation over adherent cellular cultures. PLoS ONE 2009, 4. [Google Scholar] [CrossRef] [PubMed]
- Oppegard, S.C.; Blake, A.J.; Williams, J.C.; Eddington, D.T. Precise control over the oxygen conditions within the boyden chamber using a microfabricated insert. Lab Chip 2010, 10, 2366–2373. [Google Scholar] [CrossRef] [PubMed]
- Lo, J.F.; Wang, Y.; Blake, A.; Yu, G.; Harvat, T.A.; Jeon, H.; Oberholzer, J.; Eddington, D.T. Islet preconditioning via multimodal microfluidic modulation of intermittent hypoxia. Anal. Chem. 2012, 84, 1987–1993. [Google Scholar] [CrossRef] [PubMed]
- Mauleon, G.; Fall, C.P.; Eddington, D.T. Precise spatial and temporal control of oxygen within in vitro brain slices via microfluidic gas channels. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Martewicz, S.; Michielin, F.; Serena, E.; Zambon, A.; Mongillo, M.; Elvassore, N. Reversible alteration of calcium dynamics in cardiomyocytes during acute hypoxia transient in a microfluidic platform. Integr. Biol. Quant. Biosci. Nano Macro 2012, 4, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Ni, C.; Grist, S.M.; Bayly, C.; Cheung, K.C. Alginate core-shell beads for simplified three-dimensional tumor spheroid culture and drug screening. Biomed. Microdevices 2015, 17. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Grist, S.M.; Nasseri, S.S.; Cheng, E.; Hwang, Y.C.E.; Ni, C.; Cheung, K.C. Core-shell hydrogel beads with extracellular matrix for tumor spheroid formation. Biomicrofluidics 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Grist, S.M.; Cheng, E.; Yu, L.F.; Cheung, K.C. Modulated two-photon imaging of whole spheroids for three-dimensional cell cultures. In Proceedings of the 18th International Conference on Miniaturized Systems for Chemistry and Life Sciences, San Antonio, TX, USA, 26–30 October 2014.
- Grist, S.M.; Oyunerdene, N.; Flueckiger, J.; Chrostowski, L.; Cheung, K.C. Fabrication and laser patterning of polystyrene optical oxygen sensor films for lab-on-a-chip applications. Analyst 2014, 139, 5718–5727. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.C.; Lam, R.W.; Thorsen, T.; Asada, H.H. Mathematical analysis of oxygen transfer through polydimethylsiloxane membrane between double layers of cell culture channel and gas chamber in microfluidic oxygenator. Microfluid. Nanofluid. 2013, 15, 285–296. [Google Scholar] [CrossRef]
- Armbruster, D.A.; Pry, T. Limit of blank, limit of detection and limit of quantitation. Clin. Biochem. Rev. 2008, 29, S49–S52. [Google Scholar] [PubMed]
- Koren, K.; Borisov, S.M.; Klimant, I. Stable optical oxygen sensing materials based on click-coupling of fluorinated platinum(ii) and palladium(ii) porphyrins-a convenient way to eliminate dye migration and leaching. Sens. Actuators B Chem. 2012, 169, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Chu, C.S.; Lo, Y.L. Ratiometric fiber-optic oxygen sensors based on sol-gel matrix doped with metalloporphyrin and 7-amino-4-trifluoromethyl coumarin. Sens. Actuators B Chem. 2008, 134, 711–717. [Google Scholar] [CrossRef]
- Lehner, P.; Staudinger, C.; Borisov, S.M.; Klimant, I. Ultra-sensitive optical oxygen sensors for characterization of nearly anoxic systems. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grist, S.M.; Schmok, J.C.; Liu, M.-C.; Chrostowski, L.; Cheung, K.C. Designing a Microfluidic Device with Integrated Ratiometric Oxygen Sensors for the Long-Term Control and Monitoring of Chronic and Cyclic Hypoxia. Sensors 2015, 15, 20030-20052. https://doi.org/10.3390/s150820030
Grist SM, Schmok JC, Liu M-C, Chrostowski L, Cheung KC. Designing a Microfluidic Device with Integrated Ratiometric Oxygen Sensors for the Long-Term Control and Monitoring of Chronic and Cyclic Hypoxia. Sensors. 2015; 15(8):20030-20052. https://doi.org/10.3390/s150820030
Chicago/Turabian StyleGrist, Samantha M., Jonathan C. Schmok, Meng-Chi (Andy) Liu, Lukas Chrostowski, and Karen C. Cheung. 2015. "Designing a Microfluidic Device with Integrated Ratiometric Oxygen Sensors for the Long-Term Control and Monitoring of Chronic and Cyclic Hypoxia" Sensors 15, no. 8: 20030-20052. https://doi.org/10.3390/s150820030
APA StyleGrist, S. M., Schmok, J. C., Liu, M.-C., Chrostowski, L., & Cheung, K. C. (2015). Designing a Microfluidic Device with Integrated Ratiometric Oxygen Sensors for the Long-Term Control and Monitoring of Chronic and Cyclic Hypoxia. Sensors, 15(8), 20030-20052. https://doi.org/10.3390/s150820030