Universal Capacitance Model for Real-Time Biomass in Cell Culture
Abstract
:1. Introduction
1.1. Problem Statement
1.2. State of the Art
1.3. Novelty of This Approach
1.4. Goal
1.5. Roadmap and Workflow

2. Experimental Section
2.1. Process Setup
2.1.1. Data Source
| Run | Scale 1 (80 L) | Scale 2 (2 L) | Chapter | |||
|---|---|---|---|---|---|---|
| Clone A | Clone B | Clone C | Clone B | Clone D | Finding the best model | |
| A1 | x | |||||
| A2 | x | |||||
| A3 | x | |||||
| A4 | x | |||||
| A5 | x | |||||
| A6 | x | |||||
| A7 | x | |||||
| B1 | x | Variable selection | ||||
| B2 | x | |||||
| B3 | x | |||||
| B4 | x | |||||
| B5 | x | Transfer learning | ||||
| B6 | x | |||||
| C1 | x | Validation | ||||
| D1 | x | |||||
| D2 | x | |||||
2.1.2. Media
2.1.3. Cell Lines
2.1.4. Analytics
2.1.5. Multivariate Data Analysis
2.2. Acceptance Criteria and Control Specifications
CVRMSE
3. Results and Discussion
3.1. From Signal to Model

3.2. Finding the Best Model

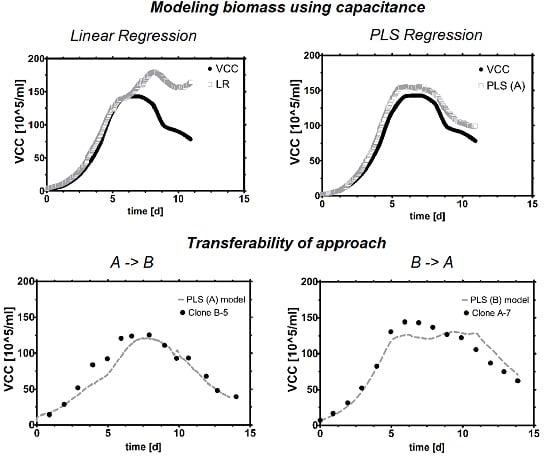
3.2.1. Linear Model
3.2.2. Multivariate Model
3.3. Multivariate Variable Selection
3.3.1. Scaling
3.3.2. Capacitance Maps
3.4. Transfer Learning

3.4.1. Direct Model Transfer

3.4.2. Attenuation Factor κ



3.4.3. Reasons for Transferability
3.5. Validation and Comparison with Literature

3.5.1. Scale to Scale Transferability
3.5.2. Clone to Clone Transferability
3.5.3. Internal Model Comparison

3.5.4. External Model Comparison
| Author | Year | CVRMSE | Comments | Ref |
|---|---|---|---|---|
| Noll | 1998 | n.a. | Linear model, R2 = 0.99, from a calibration curve with a serial dilution of a defined cell concentration | [8] |
| Cannizzaro | 2003 | 9%–22% Batch phase, 24%–36% perfusion fed-batch | PLS model, 1 and 2 principal components, only one run available for validation (2 runs available), perfusion process with high viability | [12] |
| Ansorge | 2007 | n.a. | Linear model, 20% change in cell size corresponds to the third power (80% variance) in permittivity signal; R2 = 0.99 provided for batch phase | [10] |
| Ansorge | 2010 | n.a. | No numeric performance parameters from the Cole-Cole model available. Linear model parameters: R2 = 0.74–0.89, capacitance vs. packed cell volume (PCV), two different clones in a fed-batch, only samples with viability >70% taken into account | [1] |
| Opel | 2010 | 7%–23% Mixed results, batch and fed-batch | PLS model, Result from cross validation with 5 principal components using 5 batches and 5 fed-batches as data source. Relative error is based on viable packed cell volume (vPCV) | [5] |
| Heinrich | 2011 | n.a. | No numeric performance parameters from the Cole-Cole model available. Linear model parameters: R2>0.98 for highly viable cells in perfusion | [45] |
| Parta | 2013 | 5%–45% without smoothing, 9%–15% with smoothing, all fed-batch | Three principal components, using always 1 out of 6 fed-batches for validation, with and without Savitzky-Golay smoothing to compensate extreme outliers | [39] |
| This contribution | 2014 | 7%–38% model A 9%–32% model B all fed-batch | Three principal components, one model (A or B) predicts VCC for 4 different clones and two different scales in a total of 16 orthogonal fed-batches | [-] |
4. Conclusions and Outlook
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| a1 − a17 | Capacitance 1–17 (pF/cm) |
| ANN | Artificial Neural Networks |
| B | Batch |
| FB | Fed-Batch |
| c1 − c17 | Coefficient 1–17 [-] |
| CHO | Chinese Hamster Ovary |
| CVRMSE | Coefficient of Variation of RMSE (Root Mean Square Error) |
| d | Offset (cells/mL) |
| fc | Capacitance at the critical frequency (pF/cm) |
| FQ | Frequencies |
| κ | Linear factor [-] |
| LR | Linear Regression |
| mab | Monoclonal antibody |
| MC | Mean Centering |
| MLR | Multiple Linear Regression |
| n | Number of measurements |
| PC | Principal Component |
| PCR | Principal Component Regression |
| PLS | Partial Least Squares |
| PLS-R | Partial Least Squares Regression |
| R2 | Regression Coefficient [-] |
| RMSE | Root Mean Square Error (cells/mL) |
| SD | Standardization |
| TCC | Total Cell Concentration (cells/mL) |
| VCC | Viable Cell Concentration (cells/mL) |
Estimated VCC from a prior model (cells/mL) | |
| y | Measured VCC (cells/mL) |
Average VCC (cells/mL) | |
Estimated VCC (cells/mL) |
References and Notes
- Ansorge, S.; Esteban, G.; Schmid, G. On-line monitoring of responses to nutrient feed additions by multi-frequency permittivity measurements in fed-batch cultivations of CHO cells. Cytotechnology 2010, 62, 121–132. [Google Scholar] [CrossRef] [PubMed]
- Yardley, J.E.; Todd, R.; Nicholson, D.J.; Barrett, J.; Kell, D.B.; Davey, C.L. Correction of the influence of baseline artefacts and electrode polarization on dielectric spectra. Bioelectrochemistry 2000, 51, 53–65. [Google Scholar] [CrossRef]
- Dabros, M.; Dennewald, D.; Currie, D.J.; Lee, M.H.; Todd, R.W.; Marison, I.W.; Stockar, U. Cole-Cole, linear and multivariate modeling of capacitance data for on-line monitoring of biomass. Bioprocess Biosyst. Eng. 2008, 32, 161–173. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.M.; Todd, R.W.; Bungard, S.J.; Lovitt, R.W.; Morris, J.G.; Kell, D.B. Dielectric permittivity of microbial suspensions at radio frequencies: A novel method for the real-time estimation of microbial biomass. Enzyme Microb. Technol. 1987, 9, 181–186. [Google Scholar] [CrossRef]
- Opel, C.F.; Li, J.; Amanullah, A. Quantitative modeling of viable cell density, cell size, intracellular conductivity, and membrane capacitance in batch and fed-batch CHO processes using dielectric spectroscopy. Biotechnol. Prog. 2010, 26, 1187–1199. [Google Scholar] [CrossRef] [PubMed]
- Favre, E.; Voumard, P.; von Stockar, U.; Péringer, P. A capacitance probe to characterize gas bubbles in stirred tank reactors. Chem. Eng. J. 1993, 52, 1–7. [Google Scholar] [CrossRef]
- Yardley, J.E.; Kell, D.B.; Barrett, J.; Davey, C.L. On-line, real-time measurements of cellular biomass using dielectric spectroscopy. Biotechnol. Genet. Eng. Rev. 2000, 17, 3–35. [Google Scholar] [CrossRef] [PubMed]
- Noll, T.; Biselli, M. Dielectric spectroscopy in the cultivation of suspended and immobilized hybridoma cells. J. Biotechnol. 1998, 63, 187–198. [Google Scholar] [CrossRef]
- Zeiser, A.; Bédard, C.; Voyer, R.; Jardin, B.; Tom, R.; Kamen, A.A. On-line monitoring of the progress of infection in .Sf-9 insect cell cultures using relative permittivity measurements. Biotechnol. Bioeng. 1999, 63, 122–126. [Google Scholar] [CrossRef]
- Ansorge, S.; Esteban, G.; Schmid, G. On-line monitoring of infected Sf-9 insect cell cultures by scanning permittivity measurements and comparison with off-line biovolume measurements. Cytotechnology 2007, 55, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Ansorge, S.; Lanthier, S.; Transfiguracion, J.; Henry, O.; Kamen, A. Monitoring lentiviral vector production kinetics using online permittivity measurements. Biochem. Eng. J. 2011, 54, 16–25. [Google Scholar] [CrossRef]
- Cannizzaro, C.; Gügerli, R.; Marison, I.; von Stockar, U. On-line biomass monitoring of CHO perfusion culture with scanning dielectric spectroscopy. Biotechnol. Bioeng. 2003, 84, 597–610. [Google Scholar] [CrossRef] [PubMed]
- Niklas, J.; Heinzle, E. Metabolic flux analysis in systems biology of mammalian cells. In Genomics and Systems Biology of Mammalian Cell Culture; Hu, W.S., Zeng, A.-P., Eds.; Springer: Berlin, Germany, 2012; pp. 109–132. [Google Scholar]
- Chen, Z.; Chen, Y.; Chen, J.; Shen, C. Effects of ammonium and lactate on hybridoma cell growth and metabolism. Chin. J. Biotechnol. 1992, 8, 255–261. [Google Scholar] [PubMed]
- Cruz, H.J.; Moreira, J.L.; Carrondo, M.J. Metabolic shifts by nutrient manipulation in continuous cultures of BHK cells. Biotechnol. Bioeng. 1999, 66, 104–113. [Google Scholar] [CrossRef]
- Templeton, N.; Dean, J.; Reddy, P.; Young, J.D. Peak antibody production is associated with increased oxidative metabolism in an industrially relevant fed-batch CHO cell culture. Biotechnol. Bioeng. 2013, 110, 2013–2024. [Google Scholar] [CrossRef] [PubMed]
- Zeng, A.-P.; Hu, W.-S.; Deckwer, W.-D. Variation of stoichiometric ratios and their correlation for monitoring and control of animal cell cultures. Biotechnol. Prog. 1998, 14, 434–441. [Google Scholar] [CrossRef] [PubMed]
- Ivorra, A. Bioimpedance monitoring for physicians: An overview. Cent. Nac. Microelectròn. Biomed. Appl. Gr. 2002, 1, 1–35. [Google Scholar]
- Garthwaite, P.H. An lnterpretation of partial least squares. J. Am. Stat. Assoc. 1994, 89, 122–127. [Google Scholar] [CrossRef]
- Wise, B.M. Properties of Partial Least Squares (PLS) Regression, and Differences between Algorithms; Technical Report; Eigenvector Research, Inc.: Manson, WA, USA, 2015. [Google Scholar]
- Lohninger, H.H. Datalab 3.5, A Programme for Statistical Analysis. 2000. Available online: http://datalab.epina.at/ (accessed on 28 August 2015).
- Rathore, A.S.; Mhatre, R. Quality by Design for Biopharmaceuticals: Principles and Case Studies; Wiley-Interscience: Hoboken, NJ, USA, 2011. [Google Scholar]
- Rosipal, R.; Krämer, N. Overview and recent advances in partial least squares. In Subspace, Latent Structure and Feature Selection; Saunders, C., Grobelnik, M., Gunn, S., Shawe-Taylor, J., Eds.; Springer: Berlin, Germany, 2006; pp. 34–51. [Google Scholar]
- Haenlein, M.; Kaplan, A.M. A beginner’s guide to partial least squares analysis. Underst. Stat. 2004, 3, 283–297. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Tobias, R.D. An introduction to partial least squares regression. In Proceedings of the 20th Annual SAS Users Group International Conference, Orlando, FL, USA, 2–5 April 1995.
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Pinto, R.C.V.; Marinho, P.A.N.; Oliveira, A.B.; Esteban, G.; Melo, P.A.; Medronho, R.A.; Castilho, L.R. Biomass monitoring and cho cell culture optimization using capacitance spectroscopy. In Cells and Culture; Noll, T., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 343–348. [Google Scholar]
- Wong, J. Implementation of Capacitance Probes for Continuous Viable Cell Density Measurements for 2K Manufacturing Fed-Batch Processes at Biogen Idec. Available online: http://www.infoscience.com/JPAC/ManScDB/JPACDBEntries/1394130144.pdf (accessed on 28 August 2015).
- Justice, C.; Brix, A.; Freimark, D.; Kraume, M.; Pfromm, P.; Eichenmueller, B.; Czermak, P. Process control in cell culture technology using dielectric spectroscopy. Biotechnol. Adv. 2011, 29, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Beving, H.; Eriksson, L.E.; Davey, C.L.; Kell, D.B. Dielectric properties of human blood and erythrocytes at radio frequencies (0.2–10 MHz); dependence on cell volume fraction and medium composition. Eur. Biophys. J. 1994, 23, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Gerckel, I.; Garcia, A.; Degouys, V.; Dubois, D.; Fabry, L.; Miller, A.O.A. Dielectric spectroscopy of mammalian cells. Cytotechnology 1993, 13, 185–193. [Google Scholar] [CrossRef]
- Kell, D.B.; Woodward, A.M.; Davies, E.A.; Todd, R.W.; Evans, M.F.; Rowland, J.J. Nonlinear dielectric spectroscopy of biological systems: Principles ans applications. In Nonlinear Dielectric Phenomena in Complex Liquids; Rzoska, S.J., Zhelezny, V.P., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 335–344. [Google Scholar]
- Markx, G.H.; Kell, D.B. Use of dielectric permittivity for the control of the biomass level during biotransformations of toxic substrates in continuous culture. Biotechnol. Prog. 1995, 11, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Ansorge, S.; Esteban, G.; Schmid, G. Multifrequency permittivity measurements enable on-line monitoring of changes in intracellular conductivity due to nutrient limitations during batch cultivations of CHO cells. Biotechnol. Prog. 2010, 26, 272–283. [Google Scholar] [CrossRef] [PubMed]
- David, J.; Nicholson, D.B.K. Deconvolution of the dielectric spectra of microbial cell suspensions using multivariate calibration and artificial neural networks. Bioelectrochem. Bioenerg. 1996, 39, 185–193. [Google Scholar]
- Lohninger, H. Teach/Me—Data Analysis, 1st ed.; Springer: Berlin, Germany, 1999. [Google Scholar]
- Beebe, K.R.; Pell, R.J.; Seasholtz, M.B. Chemometrics: A Practical Guide; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Párta, L.; Zalai, D.; Borbély, S.; Putics, A. Application of dielectric spectroscopy for monitoring high cell density in monoclonal antibody producing CHO cell cultivations. Bioprocess Biosyst. Eng. 2014, 37, 311–323. [Google Scholar] [CrossRef] [PubMed]
- El Wajgali, A.; Esteban, G.; Fournier, F.; Pinton, H.; Marc, A. Impact of microcarrier coverage on using permittivity for on-line monitoring high adherent Vero cell densities in perfusion bioreactors. Biochem. Eng. J. 2013, 70, 173–179. [Google Scholar] [CrossRef]
- Zeiser, A.; Elias, C.B.; Voyer, R.; Jardin, B.; Kamen, A.A. On-line monitoring of physiological parameters of insect cell cultures during the growth and infection process. Biotechnol. Prog. 2000, 16, 803–808. [Google Scholar] [CrossRef] [PubMed]
- Davey, C.L.; Markx, G.H.; Kell, D.B. Substitution and spreadsheet methods for analysing dielectric spectra of biological systems. Eur. Biophys. J. 1990, 18, 255–265. [Google Scholar] [CrossRef]
- Natschläger, T.; Zauner, B. Fused Stage-Wise Lasso—A Waveband Selection Algorithm for Spectroscopy. Available online: http://www.scch.at/de/publikationen/publication_id/802 (accessed on 19 August 2014).
- Torrey, L.; Shavlik, J. Transfer Learning. Available online: ftp://ftp.cs.wisc.edu/machine-learning/shavlik-group/torrey.handbook09.pdf (accessed on 28 August 2014).
- Heinrich, C.; Beckmann, T.; Büntemeyer, H.; Noll, T. Utilization of multifrequency permittivity measurements in addition to biomass monitoring. BMC Proc. 2011, 5. [Google Scholar] [CrossRef] [PubMed]
- MATLAB, Inc. Matlab 1-D Data Interpolation with Interp1. Available online: http://de.mathworks.com/help/matlab/ref/interp1.html (accessed on 28 August 2015).
- Motulsky, H. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting, 1st ed.; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Motulsky, H. Intuitive Biostatistics: A Nonmathematical Guide to Statistical Thinking, 3rd ed.; Oxford University Press: New York, NY, USA, 2013. [Google Scholar]
- Note: This contribution is provided together with sample data for frequencies and VCC, which were modified with regard to viable cell concentration by a linear factor between 0.5 and 2.0. The reader is invited to use the supplied excel sheet to estimate VCC with their own data or review historical bioreactor runs with one of our models.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konakovsky, V.; Yagtu, A.C.; Clemens, C.; Müller, M.M.; Berger, M.; Schlatter, S.; Herwig, C. Universal Capacitance Model for Real-Time Biomass in Cell Culture. Sensors 2015, 15, 22128-22150. https://doi.org/10.3390/s150922128
Konakovsky V, Yagtu AC, Clemens C, Müller MM, Berger M, Schlatter S, Herwig C. Universal Capacitance Model for Real-Time Biomass in Cell Culture. Sensors. 2015; 15(9):22128-22150. https://doi.org/10.3390/s150922128
Chicago/Turabian StyleKonakovsky, Viktor, Ali Civan Yagtu, Christoph Clemens, Markus Michael Müller, Martina Berger, Stefan Schlatter, and Christoph Herwig. 2015. "Universal Capacitance Model for Real-Time Biomass in Cell Culture" Sensors 15, no. 9: 22128-22150. https://doi.org/10.3390/s150922128
APA StyleKonakovsky, V., Yagtu, A. C., Clemens, C., Müller, M. M., Berger, M., Schlatter, S., & Herwig, C. (2015). Universal Capacitance Model for Real-Time Biomass in Cell Culture. Sensors, 15(9), 22128-22150. https://doi.org/10.3390/s150922128