Decoupling Control of Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension
Abstract
:1. Introduction
2. Design of Rebalance Loops
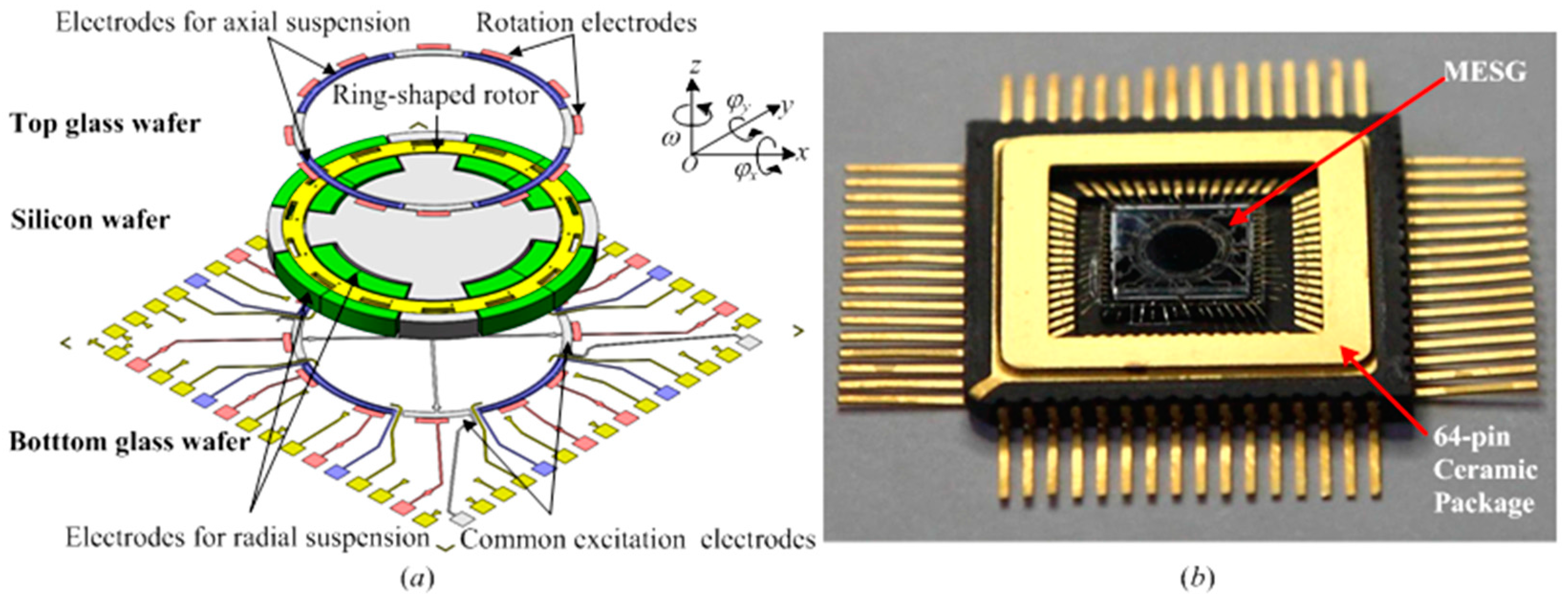
2.1. Description of the MEMS Spinning-Rotor Gyro
2.2. Stiffness Compensated Model
2.3. Inner-Loop and Outer-Loop Decoupling Compensation
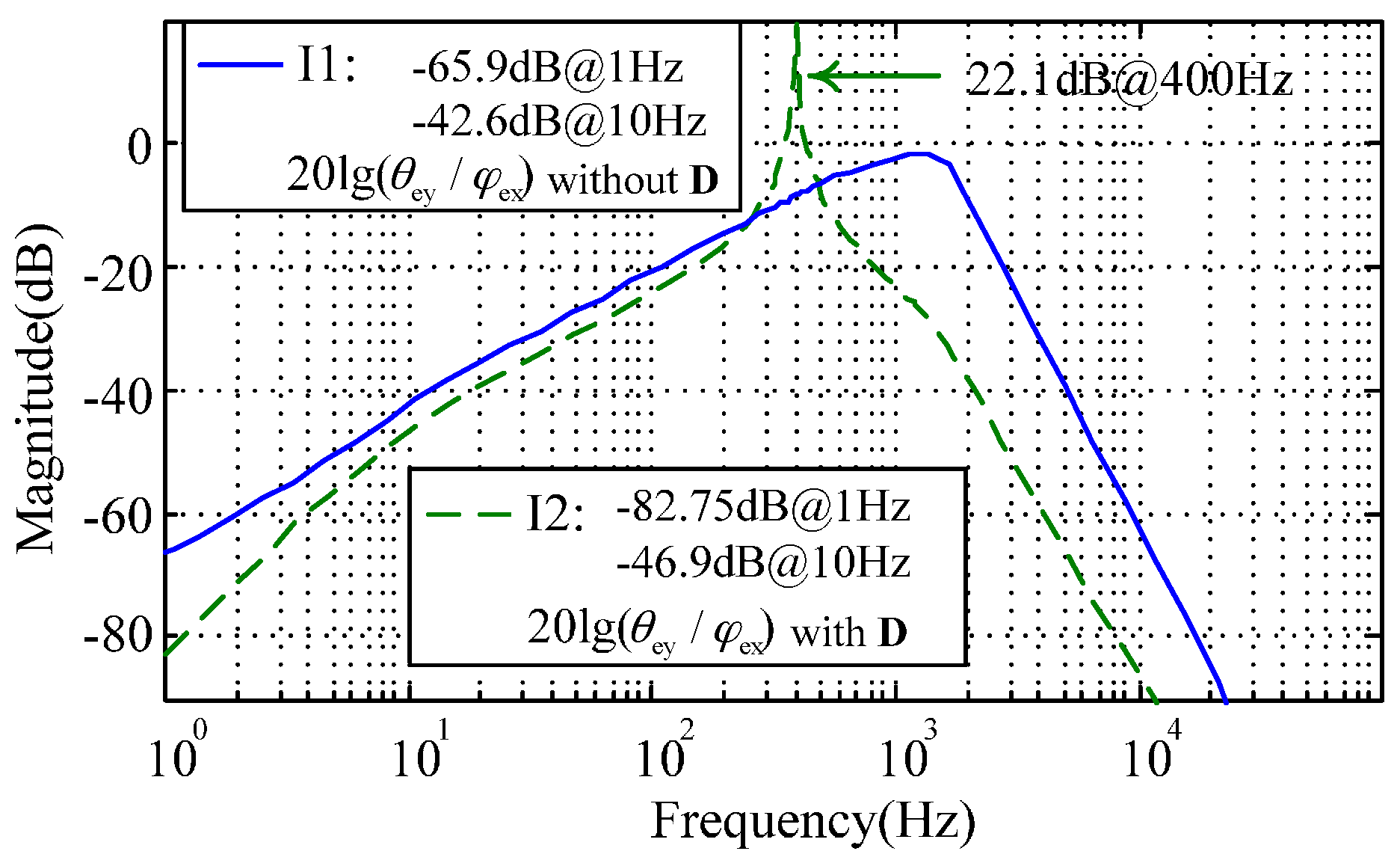
2.4. Verification Scheme for the Inner and Outer Loop Decoupling
3. Experiment Results and Discussion
3.1. Stiffness Compensation
3.2. Decoupling Compensation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xia, D.; Yu, C.; Kong, L. The development of micromachined gyroscope structure and circuitry technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhang, W.; Chen, W.; Li, K.; Dai, F.; Cui, F.; Wu, X.; Ma, G.; Xiao, Q. The development of micro-gyroscope technology. J. Micromech. Microeng. 2009, 19, 113001. [Google Scholar] [CrossRef]
- Robert, J.; Craig, G. Theory of operation of a two-axis-rate gyro. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 722–731. [Google Scholar]
- Bencze, W.J.; Eglington, M.E.; Brumley, R.W.; Buchman, S. Precision electrostatic suspension system for the Gravity Probe B relativity mission’s science gyroscopes. Adv. Space Res. 2007, 39, 224–229. [Google Scholar] [CrossRef]
- Han, F.; Gao, Z.; Li, D.; Wang, Y. Nonlinear compensation of active electrostatic bearings supporting a spherical rotor. Sens. Actuators A Phys. 2005, 119, 177–186. [Google Scholar] [CrossRef]
- Lu, Z.; Poletkin, K.; Hartogh, B.; Wallrabe, U.; Badilita, V. 3D micro-machined inductive contactless suspension: Testing and modeling. Sens. Actuators A Phys. 2014, 220, 134–143. [Google Scholar] [CrossRef]
- Han, F.; Wang, L.; Wu, Q.; Liu, Y. Performance of an active electric bearing for rotary micromotors. J. Micromech. Microeng. 2011, 21, 085027. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, W.; Zhao, X.; Wu, X.; Liu, W.; Huang, X.; Shao, S. The study of an electromagnetic levitating micromotor for application in a rotating gyroscope. Sens. Actuators A Phys. 2006, 132, 651–657. [Google Scholar] [CrossRef]
- Chan, M.; Yoxall, B.; Park, H.; Kang, Z.; Izyumin, I.; Chou, J.; Horsley, D.A. Design and characterization of MEMS micromotor supported on low friction liquid bearing. Sens. Actuators A Phys. 2012, 177, 1–9. [Google Scholar] [CrossRef]
- Wong, C.; Zhang, X.; Jacobson, S.A.; Epstein, A.H. A self-acting gas thrust bearing for high-speed microrotors. J. Microelectromech. Syst. 2004, 13, 158–164. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, N.; Liu, X.; Yin, L.; Li, H. Optimized geometry model for liquid-suspended miniature gyroscope. Micro Nano Lett. 2014, 9, 548–551. [Google Scholar] [CrossRef]
- Esashi, M. Micro /nano electro mechanical systems for practical applications. J. Phys. Conf. Ser. 2009, 187, 012001. [Google Scholar] [CrossRef]
- Fukuda, G.; Hayashi, S. The basic research for the new compass system using latest MEMS. Int. J. Mar. Navig. Saf. Sea Transp. 2010, 4, 317–322. [Google Scholar]
- Murakoshi, T.; Endo, Y.; Fukatsu, K.; Nakamura, S.; Esashi, M. Electrostatically levitated ring-shaped rotational-gyro accelerometer. Jpn. J. Appl. Phys. 2003, 42, 2468–2472. [Google Scholar] [CrossRef]
- Dillard, B.; Trent, V.; Greene, M.; Taylor, E. Radiation effects on multiple DOF MEMS inertial sensors. Nanophoton. Macrophoton. Space Environ. V 2011, 8164. [Google Scholar] [CrossRef]
- Nakamura, S. MEMS inertial sensor toward high accuracy and multi-axis sensing. In Proceedings of the 4th IEEE Conference on Sensors, Irvine, CA, USA, 31 October–3 November 2005; pp. 939–942.
- Damrongsak, B.; Kraft, M.; Rajgopal, S.; Mehregany, M. Design and fabrication of a micromachined electrostatically suspended gyroscope. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2008, 222, 53–63. [Google Scholar] [CrossRef]
- Cui, F.; Liu, W.; Chen, W.; Zhang, W.; Wu, X.S. Hybrid microfabrication and 5-DOF levitation of micromachined electrostatically suspended gyroscope. Electron. Lett. 2011, 47, 976–978. [Google Scholar] [CrossRef]
- Sun, B.; Han, F.; Li, L.; Wu, Q. Rotation control and characterization of high-speed variable-capacitance micromotor supported on electrostatic bearing. IEEE Trans. Ind. Electron. 2016, 63, 4336–4345. [Google Scholar] [CrossRef]
- Han, F.; Wu, Q.; Wang, L. Experimental study of a variable-capacitance micromotor with electrostatic suspension. J. Micromech. Microeng. 2010, 20, 115034. [Google Scholar] [CrossRef]
- Han, F.; Liu, Y.; Wang, L.; Ma, G. Micromachined electrostatically suspended gyroscope with a spinning ring-shaped rotor. J. Micromech. Microeng. 2012, 22, 105032. [Google Scholar] [CrossRef]
- Xia, D.; Yu, C.; Kong, L. A micro dynamically tuned gyroscope with adjustable static capacitance. Sensors 2013, 13, 2176–2195. [Google Scholar] [CrossRef] [PubMed]
- Ellis, C.D.; Wilamowski, B.M. Fabrication and control of an electrostatically levitated rotating gyro. Micro (MEMS) Nanotechnol. Sp. Def. Secur. II 2008, 6959. [Google Scholar] [CrossRef]
- Han, F.; Wu, Q.; Zhang, R.; Dong, J. Capacitive sensor interface for an electrostatically levitated micromotor. IEEE Trans. Instrum. Meas. 2009, 58, 3519–3526. [Google Scholar]
- Giindila, M.V.; Kraft, M. Electronic interface design for an electrically floating micro-disc. J. Micromech. Microeng. 2003, 13, S11–S16. [Google Scholar] [CrossRef]
- Watanabe, T.; Terasawa, T. An all-digital TAD-OFDM detection for sensor using TAD-digital synchronous detection. In Proceedings of the 17th IEEE ICECS, Athens, Greece, 12–15 December 2010; pp. 788–791.
- Kraft, M.; Damrongsak, B. Micromachined gyroscopes based on a rotating mechanically unconstrained proof mass. In Proceedings of the 2010 IEEE Sensors, Waikoloa, HI, USA, 1–4 November 2010; pp. 23–28.
- Ma, G.; Chen, W.; Xiao, Q.; Zhang, W.; Cui, F.; Li, K. Single-neuron spinning control system for a non-silicon micro machined rotational gyro. In Proceedings of the 4th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Shenzhen, China, 5–8 January 2009; pp. 282–285.
- Han, F.; Wu, Q.; Zhang, R. Modeling and analysis of a micromotor with an electrostatically levitated rotor. Chin. J. Mech. Eng. 2009, 22, 1–8. [Google Scholar] [CrossRef]
- Ma, G.; Chen, W.; Zhang, W.; Cui, F.; Li, K. Compact H∞ robust rebalance loop controller design for a micromachined electrostatically suspended gyroscope. ISA Trans. 2010, 49, 222–228. [Google Scholar] [CrossRef] [PubMed]
- Poletkin, K.; Wallrabe, U. Static behavior of closed-loop micromachined levitated two-axis rate gyroscope. IEEE Sens. J. 2015, 15, 7001–7008. [Google Scholar] [CrossRef]
- Torti, R.P.; Gondhalekar, V.; Tran, H.; Selfors, B.; Bart, S.; Maxwell, B. Electrostatically suspended and sensed micromechanical rate gyroscope. Sens. Imaging Vis. Control Guid. Aerosp. Veh. 1994, 2220. [Google Scholar] [CrossRef]










| Description (unit) | Value |
|---|---|
| Rotor axial moment of inertia Jz (kg·m2) | 1.43 × 10−12 |
| Rotor radial moment of inertia Je (kg·m2) | 7.17 × 10−13 |
| Spin rate of rotor (rpm) | 1.20 × 104 |
| Angular momentum of rotor H (kg·m2·s−1) | 1.80 × 10−9 |
| Torque-voltage coefficient Kv (Nm·V−1) | 1.94 × 10−9 |
| Voltage amplifier gain Ka | 2.54 |
| Angular position stiffness Kn (Nm·rad−1) | 3.36 × 10−6 |
| Sensitivity of position sensor Ks (V·rad−1) | 5.90 × 102 |
| Stiffness compensation coefficient Kc (V·rad−1) | 1.16 |
| Squeeze-film damping coefficient C (Nm·s·rad−1) | 4.21 × 10−11 |
| Orthogonal-damping elastic coefficient (Nm/rad) | 5.29 × 10−8 |
| Scale factor of the MESG (mV/°/s) | 16.05 |
| Measuring range of the MESG (°/s) | ±196.1 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Wang, S.; Li, H.; He, X. Decoupling Control of Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension. Sensors 2016, 16, 1747. https://doi.org/10.3390/s16101747
Sun B, Wang S, Li H, He X. Decoupling Control of Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension. Sensors. 2016; 16(10):1747. https://doi.org/10.3390/s16101747
Chicago/Turabian StyleSun, Boqian, Shunyue Wang, Haixia Li, and Xiaoxia He. 2016. "Decoupling Control of Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension" Sensors 16, no. 10: 1747. https://doi.org/10.3390/s16101747
APA StyleSun, B., Wang, S., Li, H., & He, X. (2016). Decoupling Control of Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension. Sensors, 16(10), 1747. https://doi.org/10.3390/s16101747





